Tehničko veleučilište u Zagrebu, Graditeljski odjel, 10000 Zagreb, Av. V. Holjevca 15, Hrvatska
mandi.orlic@tvz.hr
Sažetak
U članku se iznose dosadašnja iskustva o primjeni računalnog programa Maxima u nastavi predmeta Vjerojatnost i statistika, koji se izvodi na Politehničkom diplomskom specijalističkom stručnom studiju graditeljstva Tehničkog veleučilišta u Zagrebu. Opisuju se načini postizanja ishoda učenja navedenog predmeta primjenom programa Maxima, te se predlažu mogućnosti dodatne modernizacije spomenutog predmeta korištenjem ovog ili sličnih besplatnih računalnih programa. S ciljem boljeg prikaza teme u članak su uvršteni i zadaci, pri čemu je dana diskusija rješenja, koja su dobivena na dva načina: primjenom programa Maxima i klasičnim (“ručnim”) računanjem.
Ključni pojmovi: vjerojatnost, statistika, Maxima, besplatni računalni program
1Uvod
U prvom semestru Politehničkog diplomskog specijalističkog stručnog studija graditeljstva Tehničkog veleučilišta u Zagrebu izvodi se predmet Vjerojatnost i statistika. Cilj tog predmeta je upoznati studente s osnovnim pojmovima vjerojatnosti i metodama za statističku obradu podataka. Fond sati tog predmeta je 15+13+2, od čega je 15 sati predviđeno za predavanja, 13 sati za auditorne vježbe, a 2 sata za laboratorijske vježbe koje se održavaju u računalnom laboratoriju. Teme predviđene nastavnim planom i programom odnose se na: klasičnu definiciju vjerojatnosti, operacije među događajima, uvjetnu i totalnu vjerojatnost, diskretne i kontinuirane slučajne varijable, statističku populaciju i slučajni uzorak, grafičko prikazivanje statističkih podataka, procjenitelje, intervalnu procjenu očekivanja i varijance te testiranje hipoteza. Do ove akademske godine u sklopu laboratorijskih vježbi zadaci su se rješavali pomoću MS Excela. Međutim, kako se od akademske godine 2015./2016. u sklopu predmeta Računarstvo u graditeljstvu, koji se izvodi u prvom semestru preddiplomskog stručnog studija graditeljstva, obrađuje program Maxima, ove akademske godine umjesto MS Excela koristili smo program Maxima. Osim na predmetu Vjerojatnost i statistika Maximu koristimo i u sklopu ostalih matematičkih predmeta koji se izvode na studijima graditeljstva Tehničkog veleučilišta u Zagrebu, o čemu smo pisali u [1].
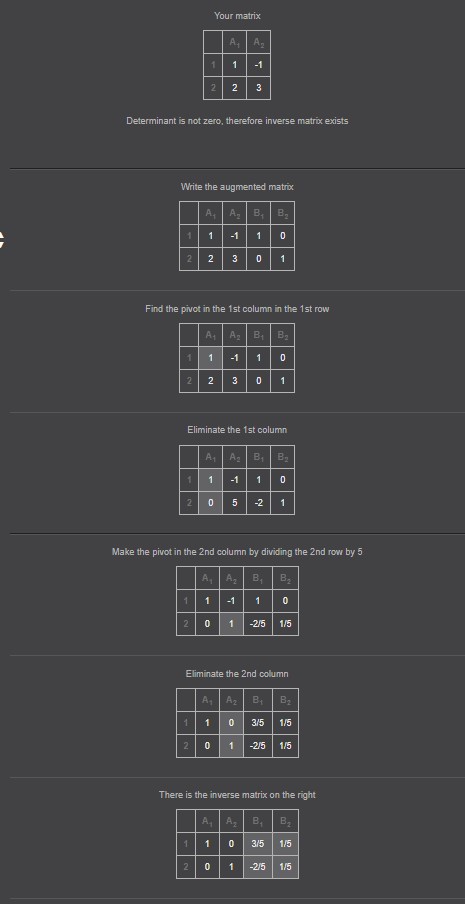
Računalni program Maxima, besplatni je program koji se može preuzeti na web adresi http://maxima.sourceforge.net/. Općenito, program je pogodan za različite algebarske operacije sa simboličkim i numeričkim izrazima, kao što su deriviranje, integriranje, razvoj u Taylorov red, Laplaceova transformacija, sustavi linearnih jednadžbi, vektori, matrice, statistika itd.
U ovom članku prikazano je kako se pomoću programa Maxima mogu riješiti neki od zadataka koji se obrađuju u sklopu nastave predmeta Vjerojatnost i statistika.
2Statističke funkcije programa Maxima
U ovom dijelu rada dan je pregled i opis onih funkcija programa Maxima, koje koristimo u sklopu nastave predmeta Vjerojatnost i statistika. To su funkcije iz paketa descriptive, distrib i stats.
Paket descriptive sadrži funkcije deskriptivne statistike i funkcije za grafički prikaz podataka. Sljedeće funkcije samo su neke od dostupnih funkcija ovog paketa. Njihov argument x može biti lista ili matrica.
|
\bullet |
Funkcija mean(x) računa uzoračku aritmetičku sredinu. |
|
\bullet |
Funkcija var(x) računa uzoračku varijancu. |
|
\bullet |
Funkcija var1(x) računa korigiranu uzoračku varijancu. |
|
\bullet |
Funkcija std(x) računa uzoračku standardnu devijaciju. |
|
\bullet |
Funkcija std1(x) računa korigiranu standardnu devijaciju. |
|
\bullet |
Funkcija histogram(x, opcije) koristi se za izradu histograma. |
Paket distrib sadrži funkcije za izračun vjerojatnosti diskretnih i kontinuiranih univarijatnih modela. Dalje su opisane one funkcije koje se odnose na slučajne varijable s normalnom odnosno binomnom razdiobom.
|
\bullet |
Za slučajnu varijablu s normalnom razdiobom N\left(m, s\right) funkcija:
|
- |
pdf_normal(x,m,s) za podatak x računa vrijednost funkcije gustoće vjerojatnosti, |
|
- |
cdf_normal(x,m,s) za podatak x računa vrijednost funkcije razdiobe vjerojatnosti, |
|
- |
mean_normal(m,s) računa vrijednost očekivanja, |
|
- |
var_normal(m,s) računa vrijednost varijance, |
|
- |
std_normal(m,s) računa vrijednost standardne devijacije. |
|
|
\bullet |
Za slučajnu varijablu s binomnom razdiobom B\left(n, p\right) funkcija:
|
- |
pdf_binomial(x,n,p) za podatak x računa vrijednost funkcije vjerojatnosti, |
|
- |
cdf_binomial(x,n,p) za podatak x računa vrijednost funkcije razdiobe, |
|
- |
mean_binomial(n,p) računa vrijednost očekivanja, |
|
- |
var_binomial(n,p) računa vrijednost varijance, |
|
- |
std_binomial(n,p) računa vrijednost standardne devijacije. |
|
Paket stats sadrži funkcije za izvođenje zaključaka o populaciji na temelju svojstava uzorka.
|
\bullet |
Funkcija test_mean(x,opcije) koristi se za testiranje hipoteza i određivanje intervala povjerenja za očekivanje s poznatom ili nepoznatom varijancom. Argument x može biti lista ili stupac matrice, a odnosi se na jednodimenzionalni slučajni uzorak normalno distribuirane slučajne varijable, dok se pod opcijama mogu unijeti sljedeći podaci:
|
- |
'mean poprima vrijednost očekivanja koju se želi provjeriti. |
|
- |
'alternative odnosi se na alternativnu hipotezu H_{1} i mogu se pridodati vrijednosti 'twosided, 'greater i 'less. |
|
- |
'dev poprima vrijednost 'unknown ili pozitivan realan broj, ovisno je li varijanca (standardna devijacija) uzorka poznata ili nepoznata. |
|
- |
'conflevel je razina pouzdanosti za interval povjerenja. Poprima vrijednosti iz intervala \left[0,1\right]. Ako se vrijednost razine pouzdanosti ne unese podrazumijeva se da iznosi 0.95. |
Izlaz funkcije test_mean je objekt koji prikazuje sljedeće rezultate:
|
- |
'mean_estimate prikazuje vrijednost uzoračke aritmetičke sredine, |
|
- |
'conf_level prikazuje razinu pouzdanosti definiranu od korisnika, |
|
- |
'conf_interval daje interval povjerenja za očekivanje normalne razdiobe, |
|
- |
'method prikazuje osnovne podatke o korištenoj razdiobi, |
|
- |
'hypotheses prikazuje vrijednosti hipoteza H_{0} i H_{1}, |
|
- |
'statistic daje vrijednost test-statistike, |
|
- |
'distribution prikazuje podatke o razdiobi statističkog uzorka, |
|
- |
'p_value daje p-vrijednost testa. |
|
|
\bullet |
Funkcija test_variance(x, opcije) koristi se za testiranje hipoteza te određivanje intervala povjerenja za varijancu. Argument i opcije definiraju se isto kao i kod funkcije test_mean. |
Prije zadavanja bilo koje funkcije iz navedenih paketa potrebno je učitati odgovarajući paket i to jednom od naredbi: load("descriptive")$, load("distrib")$ ili load("stats")$. Unutar jednog radnog lista paket je dovoljno učitati jednom bez obzira koliko se funkcija iz njega poziva. Više o ovim i ostalim funkcijama dostupnim u navedenim paketima može se pronaći u [2].
3Primjeri zadataka
U ovom poglavlju dani su primjeri zadataka i njihova rješenja koji se rješavaju u sklopu auditornih ("ručnim" putem) i laboratorijskih vježbi (upotrebom računalnog programa) na predmetu Vjerojatnost i statistika. Budući da se zbog ograničena vremena na laboratorijskim vježbama ne stigne u sklopu zadataka ponavljati teorijska podloga, rješavamo iste zadatke kao i na auditornim vježbama. Na taj način ne "trošimo" vrijeme na razumijevanje teksta zadatka i postavljanje problema, već su studenti usmjereni na razumijevanje naredbi programa Maxima i interpretaciju dobivenih rezultata. Najčešći problem s kojim se susrećemo na laboratorijskim vježbama vezan je uz poznavanje sintakse programa odnosno uz ispravan unos početnih podataka i interpretaciju dobivenih rezultata.
Zadatak 1. Godišnja količina oborina u nekom mjestu, izražena u l/m^{2}, je normalno distribuirana slučajna varijabla X \sim N\left(250, 40\right). Kolika je vjerojatnost da godišnja količina oborina bude između 235 i 260?
Rješenje:
Za slučajnu varijablu X \sim N\left(\mu, \sigma^{2}\right), slučajna varijabla sa standardnom normalnom razdiobom je X^{*} =\frac{X-\mu}{\sigma}, a vjerojatnost da normalno distribuirana slučajna varijabla X poprimi vrijednosti unutar segmenta \left[a, b\right] je
(1)
\begin{aligned} &P\left(a\leq X \leq b\right)=P\left(\frac{a-\mu}{\sigma} \leq X^{*} \leq \frac{b-\mu}{\sigma}\right)=F^{*}\left(\frac{b-\mu}{\sigma}\right) - F^{*}\left(\frac{a-\mu}{\sigma}\right)\,, \\ &\text{pri čemu je} \quad F^{*}(x)=\int_{-\infty}^{x} {\frac{1}{\sqrt{2\pi}} e^{-\frac{t^{2}}{2} } t}\,. \end{aligned}
Podintegralna funkcija f^{*}(x) je funkciju gustoće vjerojatnosti standardne normalne razdiobe ([3]). Vrijednosti funkcija F^{*} i f^{*}(x) čitaju se iz odgovarajućih tablica (vidjeti tablice u [4]).
Stoga, primjenom formule 1 vjerojatnost da godišnja količina oborina bude između 235 i 260 je:
\begin{aligned} P\left(235 \leq X \leq 260 \right)&=P\left(\frac{235-250}{\sqrt{40}} \leq X^{*} \leq \frac{260-250}{\sqrt{40}} \right)=P\left(-2.37 \leq X^{*} \leq 1.58 \right)\\ &=F^{*}(1.58)-F^{*}(-2.37)=0.942947-0.008894=0.9341\,. \end{aligned}
U programu Maxima vrijednosti funkcije F^{*}(x) mogu se izračunati, i to nešto preciznije, na sljedeći način. Najprije izračunamo vrijednosti \frac{a-\mu}{\sigma} i \frac{b-\mu}{\sigma} unošenjem naredbi:
\begin{aligned} & (235-250)/\texttt{sqrt(40)},\texttt{numer;}\\ & (260-250)/\texttt{sqrt(40)},\texttt{numer;} \end{aligned}
Nakon što stisnemo zajedno tipke SHIFT+ENTER Maxima će ispisati:
\begin{aligned} & -2.371708245126\\ & 1.58113883008\,.\\ \end{aligned}
Za izračun vrijednosti funkcije F^{*} koristimo funkciju cdf_normal(x,m,s), gdje x odgovara vrijednosti \frac{X-\mu}{\sigma}, \texttt{m}=0 i s=1. U novi red unesemo naredbu za učitanje paketa distrib, a potom zadamo odgovarajuću naredbu.
\begin{aligned} & \texttt{load(distrib)}\$ \\ &\texttt{cdf_normal}(1.58113883008,0,1)-\texttt{cdf_normal}(-2.371708245126,0,1); \end{aligned}
Kao izlaz zadane naredbe Maxima će ispisati:
0.9342238180929876\,.
Zadatak 2. Broj pogodaka u cilj u 10 gađanja je binomno distribuirana slučajna varijabla X \sim B\left(10, \frac{57}{100}\right). Kolika je vjerojatnost da se pogodi cilj barem 2 puta?
Rješenje:
Za binomno distribuiranu slučajnu varijablu X \sim B\left(n, p\right) funkcija vjerojatnosti dana je izrazom
(2)
P\left(X=k\right)=b\left(k;n,p\right)={n \choose k}p^{k}\left(1-p\right)^{n-k}\,,
gdje je n proizvoljan prirodan broj, k\leq n prirodan broj i p(0\lt p\lt 1) realan broj ([3]).
Vjerojatnost da se pogodi cilj barem 2 puta, uključuje događaje da se cilj pogodi dva ili tri ili četiri,..., ili deset puta. U ovom slučaju jednostavnije je izračunati vjerojatnost suprotnog događaja, koji uključuje događaje da se cilj nije pogodio te da se pogodio jednom. Stoga, primjenom formule 2 tražena vjerojatnost iznosi:
\begin{aligned} &P\left(X\geq 2\right)=1-P\left(X=0\right)-P\left(X=1\right)=\\ &=1-{10 \choose 0}\left(\frac{57}{100}\right)^{0}\left(1-\frac{57}{100}\right)^{10}-{10 \choose 1}\left(\frac{57}{100}\right)^{1}\left(1-\frac{57}{100}\right)^{9}=0.9969\,. \end{aligned}
U programu Maxima ovo možemo izračunati unošenjem sljedećih naredbi:
\begin{aligned} & \texttt{load(distrib)}\$ \\ &1-\texttt{pdf_binomial}(0,10,57/100)-\texttt{pdf_binomial}(1,10,57/100),\texttt{numer}; \end{aligned}
Izlaz ove naredbe je:
0.9969191072888272\,.
Zadatak 3. Stroj proizvodi limene ploče debljine 9.5 mm. Slučajno odabrane ploče na tom stroju imaju debljinu redom
8.65, \,9.90,\, 9.71,\, 9.60,\, 9.61,\, 10.21, \,11.29, \,9.70,\, 11.24, \,9.10,\, 11.35,\, 9.43\,.
Pretpostavimo li da je debljina ploče slučajna varijabla normalne razdiobe može li se uz razinu značajnosti od
\alpha=0.05 tvrditi da stroj proizvodi ploče debljine manje od propisane?
Rješenje:
Test-statistika
T=\frac{\bar{X}-\mu}{S}\sqrt{n} \sim t(n-1)
ima Studentovu t-razdiobu s n-1 stupnjeva slobode. Za određivanje vrijednosti test-statistike potrebno je odrediti aritmetičku sredinu i korigiranu standardnu devijaciju:
\begin{aligned} \bar{x}&=\frac{1}{n}\sum_{i=1}^{m}{x_{i} \cdot f_{i}}=9.9825\\ s^{2}&=\frac{1}{n-1}\sum_{i=1}^{m}\left(x_{i}-\bar{x}\right)^{2}\cdot f_{i}=0.7744 \quad \Rightarrow \quad s=0.87999. \end{aligned}
Tada test-statistika iznosi:
t=\frac{\bar{x}-\mu_{0}}{s}\sqrt{n}=\frac{9.9825-9.5}{0.87999}\sqrt{12}=1.8994\,.
Digresija: Vrijednosti aritmetičke sredine i standardne devijacije u programu Maxima mogu se izračunati na sljedeći način:
\begin{aligned} & \texttt{load(descriptive)}\$ \\ & \texttt{x:}\left[ 8.65, 9.90, 9.71, 9.60, 9.61, 10.21, 11.29, 9.70, 11.24, 9.10, 11.35, 9.43\right];\\ & \texttt{mean (x);}\\ & \texttt{std1 (x);} \end{aligned}
Izlazi ovih naredbi su:
\begin{aligned} &9.9825\\ &0.8799909606973759\,.\\ \end{aligned}
Postavljamo hipoteze
\begin{cases} H_{0}:&\mu=9.5\\ H_{1}:&\mu\lt 9.5 \end{cases}
Za ovako postavljene hipoteze kritično područje ili područje odbacivanja hipoteze H_{0} je \left[-\infty,t_{\alpha}\right\rangle. Vrijednost t_{\alpha} odredimo iz tablice Studentove t-razdiobe za n-1=11 stupnjeva slobode (vidjeti tablicu u [4] na stranici 231.):
t_{\alpha}=t_{0.05}=-t_{1-0.05}=-t_{0.95}=-1.85955\,,
odnosno kritično područje je \left\langle -\infty, -1.85955 \right\rangle\,. Kako vrijednost test-statistike t ne upada u kritično područje prihvaćamo hipotezu H_{0}, te odbacujemo hipotezu H_{1}, na razini značajnosti od 5\%. Prema tome, možemo reći da stroj ne proizvodi ploče debljine manje od propisanih 9.5 mm.
Zadatak ćemo u programu Maxima riješiti tako da ćemo prvo učitati paket stats, definirat ćemo skup podataka te potom zadati naredbu za lijevi jednostrani test. To činimo na sljedeći način:
\begin{aligned} &\texttt{load("stats")}\$ \\ &\texttt{x:}\left[ 8.65, 9.90, 9.71, 9.60, 9.61, 10.21, 11.29, 9.70, 11.24, 9.10, 11.35, 9.43\right];\\ &\texttt{test_{m}ean(x,'mean=9.5,'alternative='less,'conflevel=0.95);} \end{aligned}
Napomena: 'conflevel=0.95 je razina pouzdanosti i njegova vrijednost jednaka je 1-\alpha.
Maxima će rezultat zadane naredbe ispisati u obliku:
\begin{aligned} & \texttt{MEAN TEST}\\ &\texttt{mean_estimate=9.9825}\\ &\texttt{conf_level=0.95}\\ &\texttt{conf_interval=[-inf,10.43871131438427]}\\ &\texttt{method="Exact t-test. Unknown variance."}\\ &\texttt{hypotheses="H0: mean = 9.5 , H1: mean \lt 9.5"}\\ &\texttt{statistic}=1.899370679875383\\ &\texttt{distribution}=\texttt{[student_t,11]}\\ &\texttt{p_value}=0.9579800520853199 \end{aligned}
Na temelju dobivenih rezultata odgovor o odbacivanju ili prihvaćanju hipoteze H_{0} dajemo na temelju p-vrijednosti testa. Kako na auditornim vježbama, kao što je prethodno prikazano, odgovor o prihvaćanju hipoteze H_{0} dajemo na temelju vrijednosti test-statistike i kritičnog područja te se pojam p-vrijednosti ne spominje, ovdje je potrebno studentima dodatno pojasniti što ona predstavlja.
U slučaju lijevog jednostranog t-testa p-vrijednost jednaka je p=\mathbb{P}\left(T\leq \left.t \right|H_{0}\right), desnog jednostranog testa jednaka je p=\mathbb{P}\left(T \geq \left.t \right|H_{0}\right), dok je kod dvostranog testa p-vrijednost manja od brojeva 2\cdot \mathbb{P}\left(T\leq \left.t \right|H_{0}\right) i 2\cdot \mathbb{P}\left(T \geq \left.t \right|H_{0}\right). Na temelju p-vrijednosti možemo dati sljedeće zaključke:
|
\bullet |
ako je p \leq \alpha, onda se t nalazi u kritičnom području, pa odbacujemo H_{0} na razini značajnosti \alpha, |
|
\bullet |
ako je p \gt \alpha, onda se t ne nalazi u kritičnom području, pa prihvaćamo H_{0} na razini značajnosti \alpha. |
U našem slučaju je p=0.96\gt 0.05, pa stoga hipotezu H_{0} prihvaćamo na razini značajnosti od 0.05.
Zadatak 4. Za podatke dane u Zadatku 3. uz pouzdanost od 95\% odrediti interval povjerenja za očekivanje \mu=9.5.
Rješenje:
Interval povjerenja za očekivanje s nepoznatom varijancom i pouzdanošću \gamma je
(3)
\left\langle \bar{X}-t_{\frac{1+\gamma}{2}}\cdot \frac{S}{\sqrt{n}}, \bar{X}+t_{\frac{1+\gamma}{2}}\cdot \frac{S}{\sqrt{n}}\right\rangle\,,
gdje je t_{\frac{1+\gamma}{2}} kvantil Studentove t-razdiobe s n-1 stupnjeva slobode.
Vrijednost kvantila t_{\frac{1+\gamma}{2}} odredimo iz tablice Studentove t-razdiobe za n-1=11 stupnjeva slobode (vidjeti tablicu u [4] na stranici 231.):
t_{\frac{1+\gamma}{2}}= t_{\frac{1+0.95}{2}}= t_{0.975}= 2.201\,.
Tada je interval povjerenja na temelju formule 3 jednak:
\left\langle 9.9825-2.201 \cdot \frac{0.87999}{\sqrt{12}}, \,\, 9.9825+2.201 \cdot \frac{0.87999}{\sqrt{12}} \right\rangle =\left\langle 9.4234,\, 10.5416\right\rangle \,.
U programu Maxima interval povjerenja određuje se pomoću naredbe za određivanje dvostranog t-testa. U novi red unesemo naredbu:
\texttt{test_ {m}ean(x,'mean=9.5,'alternative='twosided,'conflevel=0.95);}
Maxima će rezultat zadane naredbe ispisati u obliku:
\begin{aligned} & \texttt{MEAN TEST}\\ &\texttt{mean_estimate=9.9825}\\ &\texttt{conf_level=0.95}\\ &\texttt{conf_interval=[9.423380425654932,10.54161957434507]}\\ &\texttt{method="Exact t-test. Unknown variance."}\\ &\texttt{hypotheses="H0: mean = 9.5 , H1: mean} \neq 9.5"\\ &\texttt{statistic}=1.899370679875383\\ &\texttt{distribution}=\texttt{[student_t,11]}\\ &\texttt{p_value}=0.08403989582936022 \end{aligned}
Sada je u četvrtom redu ispisan interval povjerenja za očekivanje s nepoznatom varijancom s pouzdanošću od 95\%.
4Zaključak
Od akademske godine 2015./2016. na stručnom studiju graditeljstva Tehničkog veleučilišta u Zagrebu računalni program Maxima obrađuje se u sklopu predmeta Računarstvo u graditeljstvu. U posljednje tri godine pokazalo se da ga studenti s lakoćom savladavaju te da ga uspješno primjenjuju u rješavanju zadataka u sklopu ostalih matematičkih predmeta (bilo na nastavi ili samostalno u sklopu seminarskih radova). Iz tog razloga, ali i zato što imamo mali broj sati predviđen za rad na računalu iz predmeta Vjerojatnost i statistika, odlučili smo se koristiti program Maxima, a ne neki, možda, prikladniji program za statističku obradu podataka (R, SPS i sl.).
U ovom trenutku postoje prijedlozi da se broj laboratorijskih vježbi poveća. Na taj način imali bi mogućnost raditi s oba programa, Excelom (kojeg smo do ove godine koristili) i Maximom. Iako se pokazalo da program Maxima u potpunosti zadovoljava sve nastavne potrebe matematičkih predmeta, koji se izvode na studijima graditeljstva, Excel je program koji će studenti u svom budećem poslu koristiti na svakodnevnoj razini i stoga je dobro u što većoj mjeri i u što različitije svrhe koristiti ga u sklopu nastave.
Bibliografija
|
[1] |
L. Marohnić, M. Orlić Bachler: Applications of free computational software in math courses at Zagreb University of Applied Sciences, Matematics Education as a Science and a Profession, Mathematics and Children 2017, Osijek, Hrvatska, 2017. |
|
[2] |
Maxima Manual, Version 5.41.0
Dostupno na: http://superk.physics.sunysb.edu/ mcgrew/phy310/documentation/maxima-reference.pdf |
|
[3] |
M. Orlić, T. Perkov: Repetitorij matematike za studente graditeljstva, Tehničko veleučilište u Zagrebu, Zagreb, 2014. |
|
[4] |
S. Suljagić: Vjerojatnost i statistika, interna skripta, Tehničko veleučilište u Zagrebu, Zagreb, 2003. |