Fakultet prirodoslovno matematičkih znanosti, Sveučilište u Mostaru, Mostar, Bosna i Hercegovina
ivansoco91@hotmail.com
Fakultet građevinarstva, arhitekture i geodezije, Sveučilište u Splitu, Split, Hrvatska
maja.andric@gradst.hr
Sažetak
Ovaj članak prezentira Beesackov dokaz Opialove nejednakosti te nekoliko jednostavnijih dokaza koji su netom uslijedili. Pritom se posebno promatra Beesackova metoda dokaza koja je doprinijela razvoju općenitijih nejednakosti Opailova tipa.
1Uvod
Godine 1960. poljski matematičar Zdzislaw Opial je objavio rad [7] dokazavši nejednakost koja sadržava funkciju i njenu derivaciju.
Teorem 1. (Opialova nejednakost) Neka je
f \in C^{1}[0,h] takva da je
f(0)=f(h)=0 i
f(t)\gt 0 za
t\in \left( 0,h\right). Tada vrijedi sljedeća nejednakost
(1)
\int_{0}^{h} \left|f(t)f'(t)\right| dt \leq \frac{h}{4}\int_{0}^{h}\left(f'\left(t\right)\right)^{2} dt,
gdje je konstanta
\frac{h}{4} najbolja moguća.
Ovo je prepoznato kao temeljni rezultat u analizi kvalitativnih uvjeta rješenja diferencijalnih jednadžbi. U proteklih pet desetljeća nastali su brojni radovi posvećni različitim poopćenjima i proširenjima Opialove nejednakosti. Više o ovome može se naći u monografiji Agarwala i Panga [1] koja daje pregled nejednakosti Opialova tipa i njihovih primjena u diferencijalnim i diferencijskim jednadžbama.
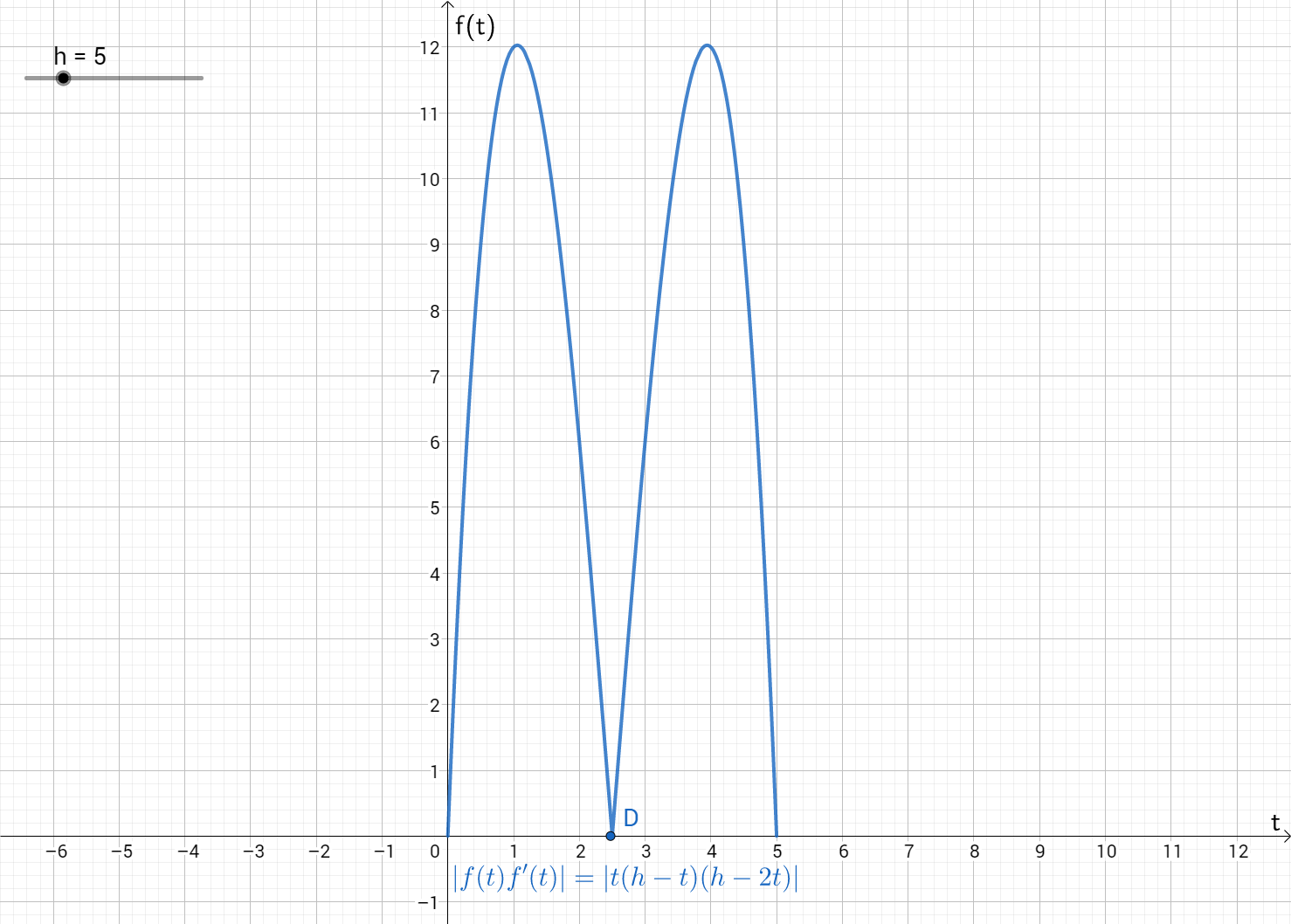
Promotrimo funkciju f(t)=t(h-t) koja zadovoljava uvjete Opialove nejednakosti. Graf funkcije je parabola (prikaz je za konkretni izbor parametra h) s nultočkama A(0,0) i B(h,0) te maksimumom u tjemenu C(\frac{h}{2},\frac{h^{2}}{4}):
Za nju vrijedi f'(t)=h-2t i |f(t)f'(t)|=|t(h-t)(h-2t)| uz graf
Koristeći nultočku D(\frac{h}{2},0) slijedi
\begin{eqnarray*} \int_{0}^{h} \left|f(t)f'(t)\right| dt &=& 2\int_{0}^{\frac{h}{2}} f(t)f'(t) dt\\ &=&\int_{0}^{\frac{h}{2}} d f^{2}(t) \ = \ f^{2}(\frac{h}{2}) - f^{2}(0)\ =\ \frac{h^{4}}{16}. \end{eqnarray*}
S desne strane Opialove nejednakosti imamo funkciju \left(f'(t)\right)^{2} = (h-2t)^{2}
\int_{0}^{h} \left(f'(t)\right)^{2} dt =\int_{0}^{h} (h-2t)^{2} dt= \frac{(h-2t)^{3}}{-6}\bigg|_{0}^{h}=\frac{h^{3}}{3}.
Zaključujemo
\frac{\int_{0}^{h} \left|f(t)f'(t)\right| dt}{\int_{0}^{h}\left(f'\left(t\right)\right)^{2} dt}=\frac{3h}{16}
što je manje od najbolje moguće konstante \frac{h}{4} (najbolja u smislu da je ona najmanji broj za koji nejednakost vrijedi).
Analogno, za funkciju f(t)=c\sin t, c\gt 0, t\in[0,\Pi], vrijedi
\int_{0}^{\Pi} \left|f(t)f'(t)\right| dt = c^{2}\int_{0}^{\Pi} \left|\sin t \cos t\right| dt= 2c^{2}\int_{0}^{\frac{\Pi}{2}} \sin t \cos t\, dt = c^{2},
i
\int_{0}^{\Pi} \left(f'(t)\right)^{2} dt = c^{2} \int_{0}^{\Pi} \cos^{2} t\, dt= c^{2}\frac{\Pi}{2}
odakle slijedi
\frac{\int_{0}^{\Pi} \left|f(t)f'(t)\right| dt}{\int_{0}^{\Pi}\left(f'\left(t\right)\right)^{2} dt}=\frac{2}{\Pi}\lt \frac{\Pi}{4}.
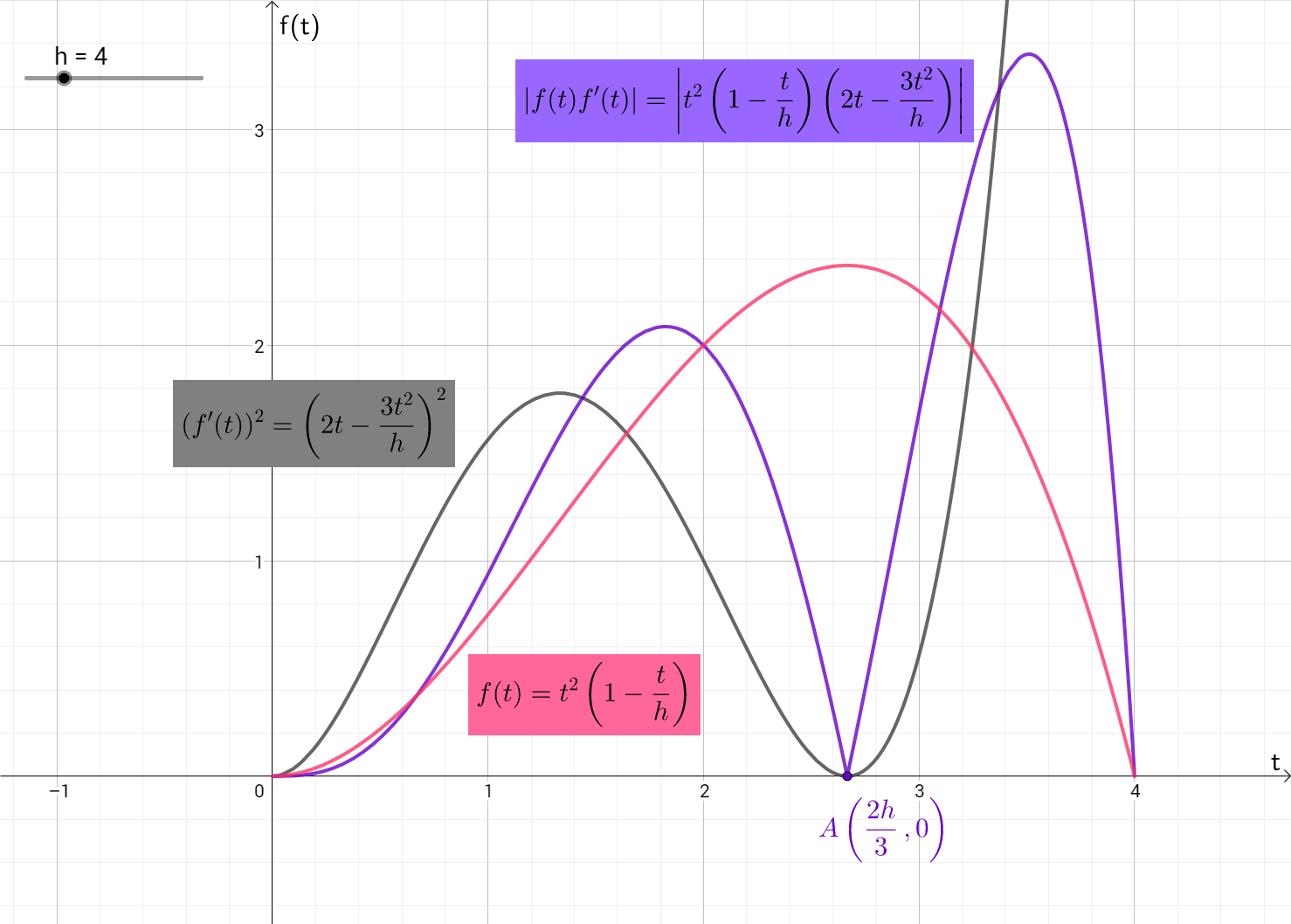
Promotrimo još funkciju f(t)=t^{2}\left(1-\frac{t}{h}\right) na [0,h]:
Vrijedi f'(t)=2t - \frac{3t^{2}}{h} i
\int_{0}^{h} \left|f(t)f'(t)\right|dt=\int_{0}^{\frac{2h}{3}} f(t)f'(t) dt- \int_{\frac{2h}{3}}^{h} f(t)f'(t) dt
\qquad\qquad=\frac{1}{2} f^{2}(t)\big|_{0}^{\frac{2h}{3}}-\frac{1}{2}f^{2}(t)\big|_{\frac{2h}{3}}^{h}=\frac{2^{4}h^{4}}{3^{6}},
\begin{eqnarray*} \int_{0}^{h} \left(f'(t)\right)^{2} dt &=&\int_{0}^{h} (2t-\frac{3t^{2}}{h})^{2} dt\\ &=&\int_{0}^{h} \left(4t^{2}-\frac{12t^{3}}{h} + \frac{9t^{4}}{h^{2}}\right) dt\\ &=&\left(\frac{4t^{3}}{3}-\frac{3t^{4}}{h} + \frac{9t^{5}}{5h^{2}}\right)\bigg|_{0}^{h}=\frac{2h^{3}}{15}, \end{eqnarray*}
\frac{\int_{0}^{h} \left|f(t)f'(t)\right| dt}{\int_{0}^{h}\left(f'\left(t\right)\right)^{2} dt}=\frac{2^{3} 5h}{3^{5}}\lt \frac{h}{4}.
Nakon Opialovog dokaza, uslijedio je Olechov rad ([6]) u kojem je pokazao da pretpostavke Opialovog teorema ne trebaju biti toliko stroge. U svom teoremu je dokazao da Opialova nejednakost vrijedi i za apsolutno neprekidne funkcije na [0,h] te da je uvjet f(t)\gt 0 suvišan. Uz sve to, Olechov dokaz je čak jednostavniji od Opialovog dokaza (pogledati članak [9]).
Teorem 2. (Olechova nejednakost) Neka je
f \in AC[0,h] i neka je
f(0)=f(h)=0. Tada za funkciju
f vrijedi nejednakost
(1). Nadalje, jednakost je zadovoljena ako i samo ako je
f=f_{0}, gdje je
f_{0} funkcija definirana s
(2)
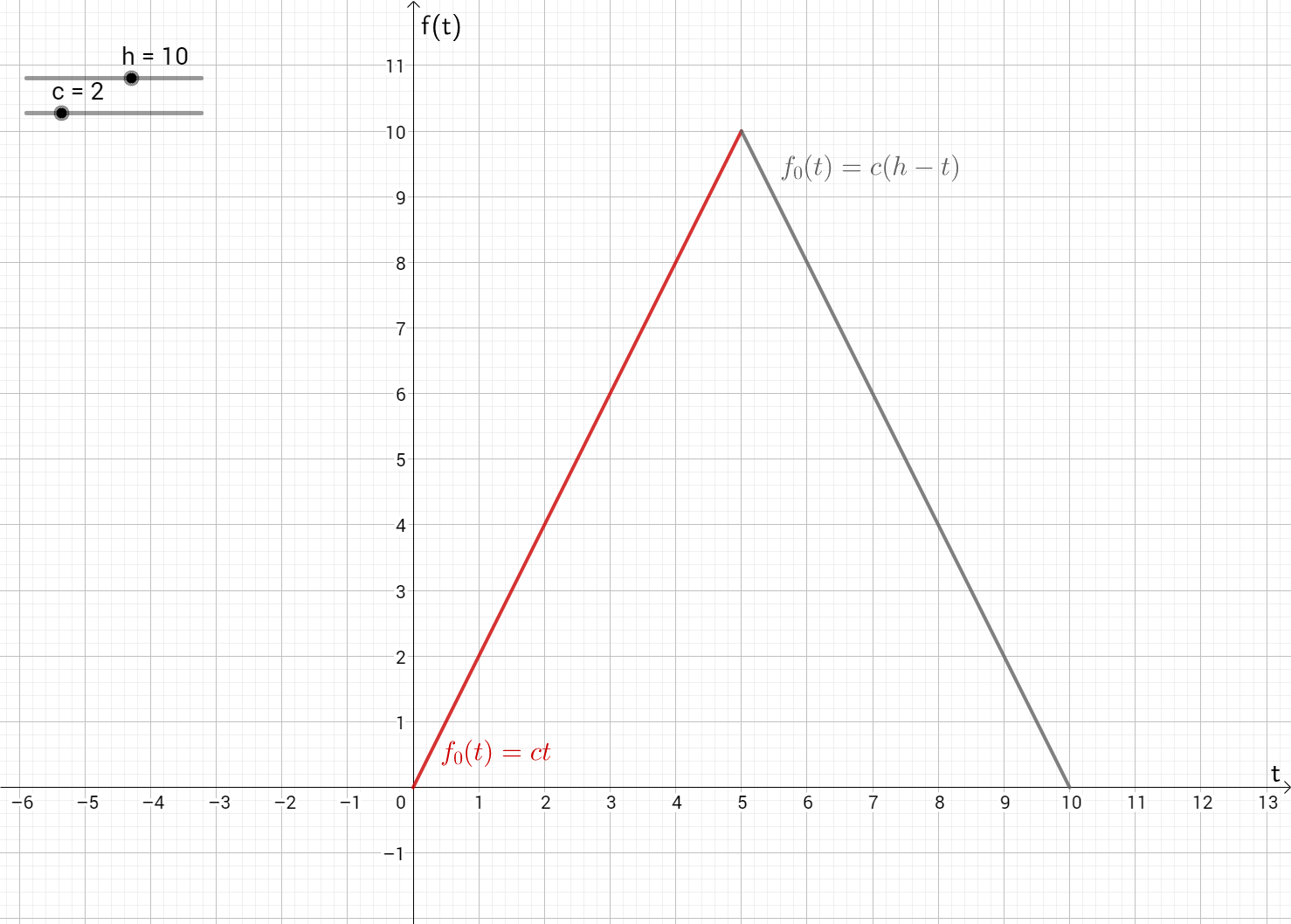
f_{0}(t)=\begin{cases} ct, & 0\leq t \leq \frac{h}{2} \\ c(h-t), & \frac{h}{2} \leq t \leq h \end{cases}
gdje je
c\gt 0 proizvoljna konstanta.
Na slici je prikazan graf funkcije f_{0} (za konkretne izbore c i h):
Za lijevi i desni limes funkcije u točki t=\frac{h}{2} vrijedi
\lim_{{t} \to {\frac{h}{2}^{-}}}\frac{f_{0}(t)-f_{0}(\frac{h}{2})}{t-\frac{h}{2}}=\frac{ct-c\frac{h}{2}}{t-\frac{h}{2}}=\frac{c(t-\frac{h}{2})}{t-\frac{h}{2}}=c
\lim_{{t} \to {\frac{h}{2}^{+}}}\frac{f_{0}(t)-f_{0}(\frac{h}{2})}{t-\frac{h}{2}}=\frac{c(h-t)-c\frac{h}{2}}{t-\frac{h}{2}}=\frac{-c(t-\frac{h}{2})}{t-\frac{h}{2}}=-c.
Iako ova funkcija nije derivabilna u t=\frac{h}{2}, možemo je aproksimirati funkcijama klase C^{1}[0,h] za koje vrijedi Opialova nejednakost (1) i tada je konstanta \frac{h}{4} najbolja moguća.
Cilj ovog rada je dati Beesackov dokaz Opialove nejednakosti te nekoliko jednostavnijih dokaza koji su netom uslijedili. Od posebne je važnosti sama Beesackova metoda dokaza jer je doprinijela razvoju općenitijih nejednakosti Opailova tipa.
1.1Osnovni pojmovi i rezultati
Neka je [a,b] interval u \mathbb{R}, gdje je -\infty \leq a \lt b \leq \infty. Prostor funkcija na [a,b] koje imaju neprekidne derivacije do uključivo reda n, n\in \mathbb{N}, označavamo s C^{n}[a,b], tj.
C^{n}[a,b]=\lbrace f:[a,b]\rightarrow \mathbb{R} : f^{(k)} \in C[a,b], k=0,1,\ldots,n\rbrace .
Posebno, C^{0}[a,b]=C[a,b], tj. prostor neprekidnih funkcija na [a,b].
U teoriji mjere izmjerive funkcije imaju jednako važnu ulogu kao što je imaju neprekidne funkcije u topologiji. Opširnije o samoj teoriji može se pogledati u knjizi [3] iz koje dajemo kratki pregled nužan za ovaj članak: ako promatramo skup \mathbb{R}, onda za područje definicije mjere \mu uzimamo pogodnu familiju podskupova od \mathbb{R} kako bi svakom podskupu A pridružili neki broj \mu(A) kao njegovu mjeru. Pritom prazan skup treba biti izmjeriv (mjere nula) kao i otvoreni skupovi koji su u matematici fundamentalni. Uzimajući još u obzir familiju izmjerivih skupova koja treba biti zatvorena na formiranje prebrojivih unija i zatvorena na komplementiranje, generalizacijom dolazimo do definicije \sigma-algebre.
Familiju
\mathcal{A} podskupova skupa
X nazivamo
\sigma-algebra skupova na skupu
X, ako ona ima sljedeća svojstva:
|
\bullet |
[(\sigma 1)] X \in \mathcal{A}, |
|
\bullet |
[(\sigma 2)] A \in \mathcal{A} \Longrightarrow A^{c} \in \mathcal{A}, |
|
\bullet |
[(\sigma 3)] unija prebrojivo mnogo elemenata iz \mathcal{A} je element iz \mathcal{A}. |
Za uređeni par (X,\mathcal{A}) kažemo da je izmjeriv prostor, a elemente iz \mathcal{A} nazivamo izmjerivim skupovima.
Neka su (X,\mathcal{A}) i (Y,\mathcal{B}) izmjerivi prostori, A \subseteq X skup i f : A \rightarrow Y funkcija. Funkcija f je izmjeriva u paru \sigma-algebri \mathcal{A} i \mathcal{B}, ili kraće \mathcal{A}-\mathcal{B} izmjeriva, ako je f^{-1}(B) \in \mathcal{A} za svaki B \in \mathcal{B}. Pritom f^{-1}(B) označava original skupa B, tj.
f^{-1}(B) = \lbrace x \in A : f(x) \in B \rbrace \subseteq {A}.
S L_{p}[a,b],1 \leq p \lt \infty, označavamo Lebesgueov prostor izmjerivih funkcija f za koje vrijedi \int_{a}^{b} |f(t)|^{p} dt \lt \infty, uz normu
\Vert f\Vert _{p}=\big(\int_{a}^{b}|f(t)|^{p} dt \big)^{\frac{1}{p}}.
Za funkciju f:[a,b]\rightarrow \mathbb{R} kažemo da je apsolutno neprekidna na [a,b] ako za svaki pozitivan broj \varepsilon postoji pozitivan broj \delta takav da za svaku familiju disjunktnih otvorenih podintervala (a_{k},b_{k}) \subset [a,b] za koju vrijedi
\sum _{k}(b_{k}-a_{k})\lt \delta,
slijedi da je
\sum _{k}|f(b_{k})-f(a_{k})|\lt \varepsilon .
Prostor apsolutno neprekidnih funkcija na konačnom intervalu [a,b], tj. -\infty \lt a \lt b \lt \infty, označavamo s AC[a,b]. Taj se prostor podudara s prostorom primitivnih funkcija prostora L_{1}[a,b], tj. vrijedi
f \in AC[a,b]\quad \Leftrightarrow \quad f(x)=f(a)+\int_{a}^{x}\varphi(t)dt, \quad \varphi \in L_{1}[a,b]
te stoga za apsolutno neprekidnu funkciju f vrijedi f'(x)=\varphi(x) gotovo svuda na [a,b]. S AC^{n} [a,b], n\in \mathbb{N}, označavamo prostor
AC^{n} [a,b]= \lbrace f \in C^{n-1}[a,b]: f^{(n-1)} \in AC[a,b] \rbrace .
Očito je AC^{1}[a,b]=AC[a,b].
Za kraj, navedimo nejednakost koju ćemo često koristiti u svrhu dokaza.
Teorem 3. (Cauchy-Schwartzova nejednakost) Neka su
f i
g realne integrabilne funkcije na intervalu
[a,b]. Tada vrijedi
\int_{a}^{b} f(t)g(t) dt \ \leq \ \left( \int_{a}^{b} (f(t))^{2} dt\right)^{\frac{1}{2}}\left(\int_{a}^{b} (g(t))^{2} dt\right)^{\frac{1}{2}}.
2Beesackova nejednakost
Dvije godine nakon objavljivanja Opialove nejednakosti, točnije 1962., Beesack je dao još jednostavniji dokaz za apsolutno neprekidnu funkciju f na [0,h] koja zadovoljava uvjet f(0)=f(h)=0 (nastavljajući se na Olechov doprinos da je i uvjet pozitivnosti funkcije suvišan). Njegova verzija teorema koja koristi iščezavanje funkcije samo u jednoj granici intervala, danas je poznata pod nazivom Beesackova nejednakost:
Teorem 4. (Beesackova nejednakost) Neka je
f \in AC[0,a] i
f(0)=0. Tada vrijedi
(3)
\int_{0}^{a}|f(t)f'(t)| dt\ \leq\ \frac{a}{2} \int_{0}^{a}(f'(t))^{2} dt.
Štoviše, jednakost u
(3) vrijedi ako i samo ako je
f(t)=ct.
Osim Beesackovog dokaza, dat ćemo i nekoliko još jednostavnijih dokaza same nejednakosti (3).
2.1Beesackov dokaz Opialove nejednakosti
Beesack je bazirao svoj dokaz na elementarnim opažanjima, parcijalnoj integraciji, Cauchy-Schwartzovoj nejednakosti, te je u [2] pokazao kako se njegova metoda dokaza može koristiti za dobivanje općenitijih nejednakosti Opialova tipa.
Dokaz. Neka je
f \in AC[0,h],
f(0)=f(h)=0 i
0\lt \epsilon\lt \tau\lt h. Tada vrijedi
\begin{eqnarray*} 0 &\leq &\int_{\epsilon}^{\tau}\left[|f'(t)|-\frac{1}{t}|f(t)|\right]^{2} dt \\ &=&\int_{\epsilon}^{\tau}(f'(t))^{2}dt + \int_{\epsilon}^{\tau}\frac{(f(t))^{2}}{t^{2}}dt - 2\int_{\epsilon}^{\tau}\frac{1}{t}|f(t)f'(t)|dt, \end{eqnarray*}
odnosno
(4)
2\int_{\epsilon}^{\tau}\frac{1}{t}|f(t)f'(t)|dt \leq \int_{\epsilon}^{\tau}(f'(t))^{2} dt + \int_{\epsilon}^{\tau}\frac{(f(t))^{2}}{t^{2}}dt,
gdje su lijeva i desna strana jednake ako i samo ako je
f(t)=ct.
Parcijalnom integracijom dobijemo
(5)
\begin{eqnarray} {2 \int_{\epsilon}^{\tau} \frac{1}{t}|f(t)f'(t)|dt}\\ &=&2\left[\left(\frac{1}{t}\int_{0}^{t}|f(s)f'(s)|ds\right)\Bigg|_{\epsilon}^{\tau} - \left(-\int_{\epsilon}^{\tau}\frac{1}{t^{2}}\left[\int_{0}^{t}|f(s)f'(s)|ds\right]dt\right)\right]\nonumber \\ \nonumber &=&\frac{2}{\tau}\int_{0}^{\tau}|f(s)f'(s)|ds-\frac{2}{\epsilon}\int_{0}^{\epsilon}|f(s)f'(s)|ds\\ &&+\ 2\int_{\epsilon}^{\tau}\frac{1}{t^{2}}\left[\int_{0}^{t}|f(s)f'(s)|ds\right]dt. \end{eqnarray}
Iz
(4) i
(5) dobijemo
(6)
\begin{eqnarray} {\frac{2}{\tau}\int_{0}^{\tau}|f(t)f'(t)|dt}\\ \nonumber &\leq & \int_{\epsilon}^{\tau}(f'(t))^{2}dt + \int_{\epsilon}^{\tau} \frac{1}{t^{2}}\left[(f(t))^{2}-2\int_{0}^{t}|f(s)f'(s)|ds\right]dt\\ && + \ \frac{2}{\epsilon}\int_{0}^{\epsilon}|f(t)f'(t)|dt. \end{eqnarray}
Budući je
0 \ \leq\ (f(t))^{2}=2\int_{0}^{t}f(s)f'(s)ds \ \leq \ 2\int_{0}^{t}|f(s)f'(s)|ds,
slijedi da je
(f(t))^{2}- 2\int_{0}^{t}|f(s)f'(s)|ds \leq 0. Stoga iz
(6) dobijemo
(7)
\frac{2}{\tau}\int_{0}^{\tau}|f(t)f'(t)|dt \ \leq \ \int_{\epsilon}^{\tau}(f'(t))^{2} dt + \frac{2}{\epsilon} \int_{0}^{\epsilon}|f(t)f'(t)|dt,
gdje jednakost vrijedi ako i samo ako je
f(t)=ct. Podsjetimo se da funkcija ima polinomijalni rast ako postoje
M,x_{0},c takvi da vrijedi
|f(x)| \leq M|x^{c}|,\quad \text{za svaki} \ \ x\gt x_{0}
i to označavamo s
f(x)=o(x^{c}), c\gt 1.
Kako je
f' \in L_{2}[0,\tau], slijedi da je
f(t)=o(t^{\frac{1}{2}}) kad
t \rightarrow 0^{+}, tj.,
|f(t)| \leq kt^{\frac{1}{2}}, gdje je
k\gt 0 konstanta. Sada po Cauchy-Schwartzovoj nejednakosti imamo
(8)
\begin{eqnarray} \int_{0}^{\epsilon}|f(t)f'(t)|dt &\leq& k\int_{0}^{\epsilon} t^{\frac{1}{2}}|f'(t)|dt\\ & \leq& k\left(\int_{0}^{\epsilon}(t^{\frac{1}{2}})^{2} dt\right)\left(\int_{0}^{\epsilon}(f'(t))^{2} dt \right)\nonumber\\ & =&\frac{k\epsilon}{\sqrt{2}}\left(\int_{0}^{\epsilon}(f'(t))^{2} dt \right)^{\frac{1}{2}}. \end{eqnarray}
Iz
(7) i
(8) slijedi
(9)
\frac{2}{\tau}\int_{0}^{\tau}|f(t)f'(t)|dt \ \leq\ \int_{\epsilon}^{\tau}(f'(t))^{2}dt + \sqrt{2}k \left(\int_{0}^{\epsilon}(f'(t))^{2} dt\right)^{\frac{1}{2}}.
Kad
\epsilon \rightarrow 0^{+}, u
(9) dobijemo
(10)
\int_{0}^{\tau}|f(t)f'(t)|dt \ \leq\ \frac{\tau}{2}\int_{0}^{\tau}(f'(t))^{2}dt,
gdje opet jednakost vrijedi samo ako je
f(t)=ct.
Neka sada u
(10) vrijedi
f(t)=f(h-t). Tada je
\int_{0}^{\tau}|f(h-t)f'(h-t)|dt \ \leq\ \frac{\tau}{2}\int_{0}^{\tau}(f'(h-t))^{2} dt,
što je uz supstituciju
s=h-t jednako
(11)
\int_{h-\tau}^{h}|f(s)f'(s)|ds \ \leq \ \frac{\tau}{2}\int_{h-\tau}^{h}(f'(s))ds.
Ako u
(10) i
(11) uvrstimo
\tau=\frac{h}{2}, onda dobijemo
\int_{0}^{\frac{h}{2}}|f(s)f'(s)|ds \leq \frac{h}{4}\int_{0}^{\frac{h}{2}}(f'(s))^{2} ds ,
te
\int_{\frac{h}{2}}^{h}|f(s)f'(s)|ds \leq \frac{h}{4} \int_{\frac{h}{2}}^{h}(f'(s))^{2} ds .
Zbrajanjem ovih dviju nejednakosti direktno dobijemo Opialovu nejednakost
(1).
\ \blacksquare
Napomena. Opialova nejednakost
(1) vrijedi čak i ako funkcija
f ima prekid u
t=\frac{h}{2} uz uvjet da je
f apsolutno neprekidna na oba podintervala
[0,\frac{h}{2}] i
[\frac{h}{2},h] te ako vrijedi da je
f(0)=f(h)=0.
Iz gornjeg dokaza je očito da je za dokazati Opialovu nejednakost (1) dovoljno dokazati Teorem 4.
Modifikacijom svog dokaza Beesack je pokazao kako dobiti poopćenja Opialove nejednakosti (za detalje pogledati [2]), kao što je npr. nejednakost
\int_{a}^{b}q(t)|f(t)f'(t)| dt\ \leq\ \frac{1}{2} \int_{a}^{b}\frac{dt}{p(t)}\int_{a}^{b}p(t)q(t)(f'(t))^{2} dt,
gdje je na [a,b] funkcija p pozitivna i neprekidna, q pozitivna, neprekidna i nerastuća, a f apsolutno neprekidna uz f(a)=0.
2.2Levinsonov dokaz Beesackove nejednakosti
Levinsonov dokaz Beesackove nejednakosti je proširenje na kompleksne funkcije ([4]). No tada se desna strana u (3) treba zamijeniti s \frac{a}{2}\int_{0}^{a}|f'(t)|^{2} dt nakon čega dokaz slijedi dvostrukom primjenom Cauchy-Schwartzove nejednakosti.
Dokaz. Po Cauchy-Schwartzovoj nejednakosti imamo
(12)
\int_{0}^{a} \left|f(t)f'(t)\right| dt \ \leq\ \int_{0}^{a}\left| t^{\frac{-1}{2}} \int_{0}^{t}f'(s)ds\right| \left|t^{\frac{1}{2}}f'(t)\right|dt \leq (AB)^{\frac{1}{2}},
gdje su
A i
B
(13)
A=\int_{0}^{a}t^{-1} \left| \int_{0}^{t} f'(s) ds \right|^{2} dt, \qquad B=\int_{0}^{a}t\left|f'(t)\right|^{2} dt.
Nadalje, koristeći ponovno Cauchy-Schwartzovu nejednakosti dobijemo
\left| \int_{0}^{t} f'(s) ds \right|2 \leq \left(\int_{0}^{t}ds\right)\left(\int_{0}^{t}\left|f'(s)\right|^{2} ds\right) = t \int_{0}^{t}\left|f'(s)\right|^{2} ds,
gdje jednakost vrijedi samo ako je
f'(t)=c gotovo svuda. Slijedi
(14)
A \leq \int_{0}^{a}\left(\int_{0}^{t}\left|f'(s)\right|^{2} ds\right) dt = \int_{0}^{a}(a-t)|f'(t)|^{2} dt .
Kako je
(AB)^{\frac{1}{2}} \leq \frac{(A+B)}{2}, iz
(12)-
(14) slijedi Beesackova nejednakost
(3). Konačno, jednakost u
(3) vrijedi ako i samo ako je
f'(t)=c gotovo svuda, što uz početni uvjet
f(0)=0 implicira da je
f(t)=ct.
\ \blacksquare
2.3Mallowsov dokaz Beesackove nejednakosti
Još jednostavniji dokaz Beesackove nejednakosti dao je Mallows ([5]), vjerujući da je postigao kako navodi "the ultimate in simplicity".
Dokaz. Neka je
y(t)=\int_{0}^{t}f'(s) ds,
t \in [0,a], tako da je
|f(t)|\leq y(t). Tada je
(15)
2\int_{0}^{a}|f(t)f'(t)|dt \ \leq\ 2\int_{0}^{a}y(t)y'(t)dt=y^{2}(a).
Koristeći Cauchy-Schwartzovu nejednakost slijedi
(16)
\begin{eqnarray} y^{2}(a)&=&\left(\int_{0}^{a}|f'(t)|dt\right)^{2} \\ \nonumber &\leq& \left(\int_{0}^{a}dt\right)\left(\int_{0}^{a}(f'(t))^{2} dt\right)\\ &=& a\int_{0}^{a}(f'(t))^{2} dt. \end{eqnarray}
Sada koristeći
(15) i
(16) dobijemo
2\int_{0}^{a}|f(t)f'(t)|dt \leq y^{2}(a) \leq a\int_{0}^{a}(f'(t))^{2} dt,
iz čega slijedi Beesackova nejednakost
(3). Analogno prethodnom razmatranju, jednakost u
(16), pa dakle i u
(3), vrijedi ako i samo ako je
f(t)=ct.
\ \blacksquare
2.4Pedersonov dokaz Beesackove nejednakosti
Posljednji dokaz Beesackove nejednakosti koji dajemo je Pedersonov ([8]). Razmotrio je integral simetrične funkcije nad trokutom i nad kvadratom, te kao i svi prethodnici iskoristio Cauchy-Schwartzovu nejednakost u dokazu.
Dokaz. Prvo napravimo početnu procjenu
(17)
\int_{0}^{a}|f(t)f'(t)|dt\ \leq\ \int_{0}^{a}\int_{0}^{t}|f'(s)f'(t)| dsdt.
Budući je integral simetrične integralne funkcije nad trokutom
0\leq s \leq t,
0\leq t \leq a jednak polovini integrala nad kvadratom
0\leq s \leq a,
0\leq t \leq a, onda vrijedi
(18)
\begin{eqnarray} \int_{0}^{a}\int_{0}^{s}|f'(s)f'(t)| dsdt &=&\frac{1}{2}\int_{0}^{a}\int_{0}^{a}|f'(s)f'(t)|dsdt\\ &=&\frac{1}{2}\left(\int_{0}^{a} |f'(t)|dt\right)^{2} . \end{eqnarray}
Sada po Cauchy-Schwartzovoj nejednakosti slijedi
\begin{eqnarray*} \frac{1}{2}\left(\int_{0}^{a}|f'(t)|dt\right)^{2} &\leq& \frac{1}{2}\left(\int_{0}^{a}dt\right)\left(\int_{0}^{a}(f'(t))^{2} dt\right)\\ &=&\frac{a}{2}\int_{0}^{a}(f'(t))^{2} dt\end{eqnarray*}
što u kombinaciji s
(17) i
(18) daje Beesackovu nejednakost
(3).
\ \blacksquare
Bibliografija
|
[1] |
R. P. Agarwal, P. Y. H. Pang, Opial Inequalities with Applications in Differential and Difference Equations, Kluwer Academic Publishers, Dordrecht, Boston, London (1995). |
|
[2] |
P. R. Beesack, On an integral inequality of Z. Opial, Trans. Amer. Math. Soc.104 (1962), 470–475. |
|
[3] |
D. Jukić, Mjera i integral, Sveučilište J. J. Strossmayera, Odjel za matematiku, Osijek (2012). |
|
[4] |
N. Levinson, On an inequality of Opial and Beesack, Proc. Amer. Math. Soc. 15 (1964), 565–566. |
|
[5] |
C. L. Mallows, An even simpler proof of Opial's inequality, Proc. Amer. Math. Soc. 16 (1965), 173. |
|
[6] |
C. Olech, A simple proof of a certain result of Z. Opial, Ann. Polon. Math. 8 (1960), 61–63. |
|
[7] |
Z. Opial, Sur une inegalite, Ann. Polon. Math. 8 (1960), 29–32. |
|
[8] |
R. N. Pederson, On an inequality of Opial, Beesack and Levinson, Proc. Amer. Math. Soc. 16 (1965), 174. |
|
[9] |
I. Sočo, M. Andrić, Opialova nejednakost, Osječki Mat. List 16 (2) (2016), 169–180. |