U srednjem vijeku matematika se dijelila na aritmetiku, glazbu, geometriju i astronomiju, takozvani Quadrivium. Kasnija podjela matematike je naravno isključivala glazbu, ali veza matematike i glazbe ostala je dublja nego što bismo očekivali. Ta veza seže još od Pitagore iz Samosa koji ju je prvi put primijetio, do današnjih modernih primjena teorije grupa na teoriju glazbe koje zahvaljujemo prvenstveno njemačkom teoretičaru glazbe Hugu Riemannu, koji se bavio odnosima među glazbenim tonovima i intervalima, s naglaskom na zamjenu tada postojećih načina zapisivanja akorda i glazbenih događaja oznakama koje bi bile primjerenije analizi atonalne glazbe koja se počela pojavljivati u 19. stoljeću, te američkom teoretičaru glazbe Davidu Lewinu koji je počeo primjenjivati Riemannove oznake da opiše pokrete među glazbenim događajima i bio začetnik teorije transformacija u glazbi (koju često nazivamo i Neo-Riemannova teorija).
Glazba i matematika su neraskidivo povezane. Žice žičanih instrumenata vibriraju određenim frekvencijama. Zvučni valovi opisuju se matematičkim jednadžbama. Tehnlogija nužna za izradu digitalne snimke glazbe počiva na matematici. Na posljetku, matematika je jezik koji znanstvenici koriste da opišu svijet oko nas, kojeg je glazba dio. Pitanje koje se tada nameće samo po sebi je - ako možemo modelirati zvuk matematičkim jednadžbama, možemo li naći jednadžbu koja opisuje glazbene kompozicije? Odgovor na to pitanje je naravno niječan, takva jednadžba ne postoji. Ali, sve muzičke kompozicije posjeduju određene matematičke strukture, i te matematičke strukture nisu opisane jednadžbama, već matematičkom teorijom grupa. Glazbena teorija nam daje konceptualne kategorije da organiziramo i razumijemo glazbu. Teorija grupa opisuje načine na koje su skupovi tonova povezani i kako ih se može transformirati iz jednog u drugog. Na taj način, pomaže ne samo slušaču da čuje glazbu na novi način, već i kompozitoru pri analizi i stvaranju novog djela, te glazbenom izvođaču u prepoznavanju istih i srodnih dijelova u glazbi, što mu olakšava pamćenje i kasnije izvođenje glazbenog djela.
Što je teorija grupa i kako može pomoći u teoriji glazbe? Koncept binarne operacije jedan je od najstarijih u matematici, seže još od starih Egipćana i Babilonaca koji su već imali metode za računanje suma i produkata pozitivnih brojeva. Kako je vrijeme prolazilo, matematičari su shvatili da je od tablica zbrajanja i množenja mnogo važniji skup brojeva na kojem se operacija izvodi (u ovom slučaju prirodni brojevi), i sama binarna operacija koja se izvodi (u ovom slučaju to je zbrajanje ili množenje). Binarna operacija i skup na kojem se operacija izvodi, zajedno s određenim svojstvima koja moraju vrijediti i koja skupu daju strukturu, čine matematički pojam grupe. Teorija grupa je vrlo utjecajna grana matematike koja se primjenjuje na gotovo sve druge matematičke discipline i brojne druge znanosti. Generalne teorije struktura su vrlo moćni alati, jer kad god netko pokaže da objekti koje proučava čine određenu strukturu (u ovom slučaju strukturu grupe), odmah može primijeniti mnoštvo rezultata iz teorije grupa na svoje objekte. Nema potrebe za ponovnim dokazivanjem rezultata za svaki objekt posebno.
U ovom poglavlju uvodimo neke osnovne pojmove iz teorije grupa i teorije glazbe koje ćemo koristiti u daljnjim razmatranjima.
Da bi mogli iskoristiti matematičku teoriju, najprije moramo konstruirati preslikavanje između naših 12 tonova i elemenata \mathbb{Z}_{12}. To činimo na sljedeći način:
Sada je lako zapisati na primjer C-dur ljestvicu: {C, D, E, F, G, A, B}={0, 2, 4, 5, 7, 9, 11}. Nas će osobito zanimati skupovi nota koje se odsviraju istovremeno, takozvani akordi. Među njima posebno se ističu grupe od tri note koje nazivamo trijade. Postoji \binom{12}{3}=220 podskupova od 3 note iz skupa od 12 nota, no osobito su važni (zbog razloga što se od njih sastoji veliki dio glazbe, to su kombinacije koje ljudskom uhu zvuče posebno ugodno) oni koji čine takozvane durske i molske akorde. Tri note koje su dio durskih i molskih akorda nazivaju se redom: prva (eng. root), treća i peta. Na primjer, C-dur akord {C, E, G} je u našem zapisu { 0,4, 7}. Durske i molske akorde definiramo na sljedeći način:
Napomenimo da su akordi skupovi tonova i kao takvi nisu uređeni (to jest nije nam bitan poredak tonova). Za naše kasnije glazbene analize u nekim situacijama ćemo koristiti uređene, a nekada neuređene skupove. Ukoliko će nam poredak biti bitan, koristit ćemo oznake \langle i \rangle za početak i kraj akorda.
Osnovne operacije na akordima (a i na većim dijelovima melodijske linije) su transpozicija i inverzija. Kada slušamo melodiju koja se sastoji od nekoliko frekvencija zapravo čujemo intervale među pojedinim notama. Odnos među tim intervalima je ono što čini melodiju privlačnom. Transpozicija matematički definira ono što glazbenici i kompozitori vrlo često čine: izvođenje melodije na višim ili nižim frekvencijama na način koji čuva intervale. Inverzija također varira melodiju na način da je intervalski zvuk melodije očuvan, iako intervali nisu sasvim očuvani.
\begin{eqnarray*}T_{n}(\lbrace a,b,c\rbrace )=\lbrace a+n, b+n, c+n\rbrace ,\end{eqnarray*}
\begin{eqnarray*}T_{n}(\lbrace a,b,c\rbrace )=\lbrace -a+n, -b+n, -c+n\rbrace .\end{eqnarray*}
\begin{eqnarray*} T_{0}(\lbrace 0,4,7\rbrace )=\lbrace 0,4,7\rbrace\\\ T_{1}(\lbrace 0,4,7\rbrace )=\lbrace 1,5,8\rbrace\\\\\ \vdots\\\\ T_{12}(\lbrace 0,4,7\rbrace )=\lbrace 0,4,7\rbrace =T_{0}(\lbrace 0,4,7\rbrace )\\\ T_{13}(\lbrace 0,4,7\rbrace )=\lbrace 1,5,8\rbrace =T_{1}(\lbrace 0,4,7\rbrace ) \end{eqnarray*}
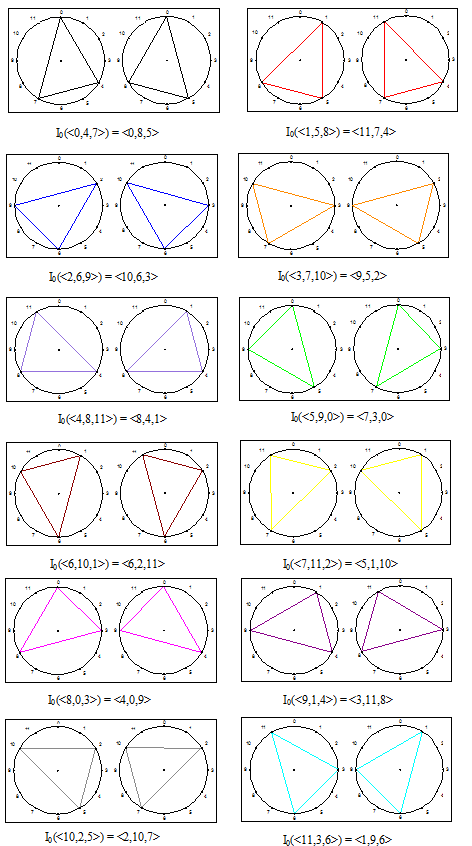
Transpozicije se geometrijski mogu prikazati kao rotacije trokuta po 12 točaka ravnomjerno raspoređenih po kružnici. Vrhovi trokuta predstavljaju sve tonove akorda. Takva reprezentacija za C-dur akord prikazana je na Slici 2. Analogno, ima i samo 12 različitih inverzija istog akorda (I_{12}=I_{0}). Geometrijski, inverzije I_{0} se mogu prikazati kao refleksije trokuta u odnosu na vertikalnu os koja prolazi kroz točke 0 i 6 na kružnici. Slika 3 prikazuje svih 12 inverzija C-dur akorda, iako to na prvi pogled nije jasno. Naime, u namjeri da ilustriramo refleksije, slika prikazuje inverziju svih transpozicija sa Slike 2, to jest I_{0}(T_{n}\lbrace 0,4,7\rbrace ) što je po Lemi 3.5 jednako I_{n}(\lbrace 0,4,7\rbrace ), pa to zapravo jesu sve inverzije C-dur akorda.
Definicija 11.[2] Skup svih transpozicija i inverzija označavamo s
\;{T}{I}\; i definiramo kao:
\begin{eqnarray*}\;{T}{I}\;=\lbrace T_{n}, I_{n}|n\in\mathbb{Z}_{12}\rbrace.\end{eqnarray*}
Skup\;{T}{I}\;ima sljedeća korisna svojstva:
Lema 1.[2] U skupu
\;{T}{I}\; vrijede relacije:
\begin{eqnarray*} T_{m}\circ T_{n}=T_{m+n}\\\ T_{m}\circ I_{n}=I_{m+n}\\\ I_{m}\circ T_{n}=I_{m-n}\\\ I_{m}\circ I_{n}=T_{m-n}\end{eqnarray*}
Dokaz. Za prvu relaciju imamo:
\begin{eqnarray*}(T_{m}\circ T_{n})(x)=T_{m}(T_{n}(x))=T_{m}(x+n)= (x+n)+m=x+(n+m)=T_{m+n}(x). \end{eqnarray*}
Analogno za preostale relacije.
\ \blacksquare
Slika 2: Transpozicije C-dur akorda \lbrace 0,4,7\rbrace
Slika 3: Inverzije C-dur akorda \lbrace 0,4,7\rbrace
Teorem 12. [2] Skup
\;{T}{I}\; s operacijom kompozicije funkcija je grupa
.
Dokaz. Skup
\;{T}{I}\; je zatvoren na kompoziciju po Lemi 3.5. Kompozicija funkcija je asocijativna operacija. Nadalje, vrijedi:
\begin{eqnarray*} T_{0}\circ T_{n}=T_{0+n}=T_{n}\\\ T_{n}\circ T_{0}=T_{n+0}=T_{n}\\\ T_{0}\circ I_{n}=I_{0+n}=I_{n}\\\ I_{n}\circ T_{0}=I{n-0}=I_{n}\end{eqnarray*}
pa je
T_{0} neutralni element. Vrijedi i:
\begin{eqnarray*}T_{n}\circ T_{12-n}=T_{n+12-n}=T_{12}=T_{0},\\\ T_{12-n}\circ T_{n}=T_{12-n+n}=T_{12}=T_{0}, \end{eqnarray*}
pa je inverzni element za transpozicije
T_{n}^{-1}=T_{12-n}. Za inverzije imamo:
\begin{eqnarray*} I_{n}\circ I_{n}=T_{n-n}=T_{0} \end{eqnarray*}
pa je
I_{n}^{-1}=I_{n}. Dakle,
\;{T}{I}\; je grupa.
\ \blacksquare
Primijenimo elemente grupe \;{T}{I}\; na analiziranje Fuge 6 u d-molu iz prve knjige Dobro ugođeni klavir Johanna Sebastiana Bacha. Fuga obično počinje uvođenjem glavne teme koju nazivamo subjekt. Subjekt se kasnije stalno ponovno vraća u raznim varijacijama. Svaka fuga ima višestruke transpozicije i inverzije. Subjekt Fuge 6, nazovimo ga P, počinje u prvom taktu: \begin{eqnarray*} \langle D, E, F, G, E, F, D, C\sharp , D, B\sharp , G,A\rangle= \langle 2, 4, 5, 7, 4, 5, 2, 1,2, 10, 7,9\rangle . \end{eqnarray*} U trećem taktu imamo:
\begin{eqnarray*} \langle A, B, C, D, B, C,A, G\sharp,A, F, D, E\rangle= \langle 9,11,0,2,11,0,9,8,9,5,2,4\rangle,\end{eqnarray*}
a to je T_{7}(P). U osmom taktu pojavljuje se ovakav oblik subjekta:
\begin{eqnarray*} \langle E, F, G, A, F, B\flat , G, F\sharp , G, E\flat , C\sharp , D\rangle= \langle 4, 5, 7, 9, 5, 10,7,6,7,3,1,2\rangle . \end{eqnarray*}
Ovdje je prvih pet tonova skoro T_{2} prvih pet tonova u P, dok su idućih pet tonova i dvanaesti ton T_{5} korespondirajućih tonova u P. Nadalje imamo u 13., 17., 18. i 21. taktu redom:
\begin{eqnarray*} \langle A, B, C\sharp , D, B, C\sharp , A, G\sharp , A, F, D, E\rangle= \langle 9, 11, {\textbf{1}}, 2, 11, {\textbf{1}}, 9, 8, 9, 5, 2,4\rangle ,\\\\\langle A, B, C, D, B, C\sharp , A, G\sharp , A, F, D, E\rangle= \langle 9, 11, 0, 2, 11, {\textbf{1}}, 9, 8, 9, 5, 2,4\rangle ,\\\\\langle A, B, C\sharp , D, B, C , A, G\sharp , A, F, D, E\rangle= \langle 9, 11, {\textbf{1}}, 2, 11, 0, 9, 8, 9, 5, 2,4\rangle ,\\\\\langle A, B, C\sharp , D, B, C\sharp , A, G\sharp , A, F, D, E\rangle= \langle 9, 11, {\textbf{1}}, 2, 11, {\textbf{1}}, 9, 8, 9, 5, 2,4\rangle , \end{eqnarray*}
koji su svi T_{7}(P), ako izuzmemo istaknute jedinice. Transpozicija T_{7} je vrlo važna u glazbi. Ovdje je nalazimo pet puta već u prvoj polovici djela. Fuga 6 bogata je i inverzijama, na primjer u 14. i 22. taktu nalazimo:
\begin{eqnarray*} \langle E, D, C\sharp, B, D, C\sharp , E, F, E, A, C, B\flat \rangle= \langle 4,2,1,11,2,1,4,5,4,{\textbf{9}}, {\textbf{0}}, {\textbf{1}0}\rangle ,\\\\\langle E, D, C\sharp, B, D, C\sharp , E, F, E, G, B\flat , A\rangle= \langle 4,2,1,11,2,1,4,5,4,{\textbf{7}}, {\textbf{1}0}, {\textbf{9}}\rangle , \end{eqnarray*}
što je gotovo I_{6}(P) (samo su zadnja tri tona izmijenjena). I ostatak kompozicije sadrži transpozicije i inverzije, a čitava kompozicija sadrži i druge matematičke forme kojima ćemo se baviti kasnije.
Posve drugačija glazba od prethodno razmatrane fuge je opera Tristan i Izolda Richarda Wagnera. Promotrimo transkripciju za klavir uvoda u tu operu (koji je inače ozloglašen po svojoj otpornosti na analizu tradicionalnim metodama glazbene teorije) i analizirajmo ga na transpozicije i inverzije. Označimo s P_{i} skup tonova koje čujemo za vrijeme i-tog ciklusa transkripcije. Na primjer, P_{2}=\lbrace F, B, D\sharp , A\rbrace. Tada, nakon pažljive analize, zamjećujemo sljedeći uzorak:
\begin{array}{cccc} P_{1}& P_{2}& P_{3}& P_{4} \\\ P_{5}& P_{6}& P_{7}& P_{8}\\\ P_{9}& \:& P_{12}& P_{13}\\\\\hline \lbrace 0,2,5,8\rbrace& \lbrace 0,2,6,8\rbrace& \lbrace 0,2,6,8\rbrace& \lbrace 0,2,5,8\rbrace\end{array}
Ova tablica znači da se svi skupovi P_{1} u prvom stupcu mogu transponirati ili invertirati u \lbrace 0,2,5,8\rbrace, analogno vrijedi i za preostala tri stupca. Ta sličnost koja se vidi matematički, glazbeno se čuje u kompoziciji i čini je zanimljivijom slušaču.
4PLR grupa
Osim transpozicija i inverzija na skupu akorda \mathbb{M} definiramo još tri transformacije: suprotnu (P), zamjenu vodećeg tona (L), i paralelnu (R). Za dva akorda kažemo da su suprotni (eng. parallel) ako imaju isto ime, ali su suprotnog tipa (u smislu da li se radi o duru ili molu). Na primjer, P C-dur preslikava u c-mol. Dva akorda su paralelni (eng. relative), ako su suprotnog tipa i prvi ton (eng. root) mola je tri polustupnja ispod prvog tona dura. Na primjer, paralelni mol C-duru je a-mol. Konačno, zamjena vodećeg tona (eng. leading tone exchange) dobila je ime po činjenici da se ton koji je pola stupnja ispod bilo kojeg tona naziva vodeći ton polaznog tona. Dur akordu funkcija L zamjenjuje osnovni ton njegovim vodećim tonom i time dur prelazi u mol (na primjer, preslikava C-dur u e-mol). Za mol akord vrijedi inverzna operacija (prelazak na ton pola stupnja iznad). Slijede matematičke definicije transformacija P, L i R i nekoliko primjera.
Definicija 13. [2] Neka su
x=\langle a,b,c\rangle,
Y=\langle A,B,C\rangle \in \mathbb{M}, gdje je
x molski a
Y durski akord. Tada definiramo funkcije
P,
L i
R:\mathbb{M}\to\mathbb{M} sa:
\begin{eqnarray*} P(x)=P(\langle a,b,c\rangle)=\langle a,b+1,c\rangle,\\\ P(Y)=P(\langle A,B,C\rangle)=\langle A,B-1,C\rangle,\\\ L(x)=P(\langle a,b,c\rangle)=\langle c+1,a,b\rangle,\\\ L(Y)=P(\langle A,B,C\rangle)=\langle B,C, A-1\rangle,\\\ R(x)=P(\langle a,b,c\rangle)=\langle b,c,a-2\rangle,\\\ R(Y)=P\langle A,B,C\rangle)=\langle C+2,A,B\rangle.\end{eqnarray*}
Na primjer,
\begin{eqnarray*} P(c)=P(\langle 0,3,7\rangle)=\langle 0,4,7\rangle=C, \:\:P(F)=P(\langle 5,9,0\rangle)=\langle 5,8,0\rangle=f,\\\ L(e)=L(\langle 4,7,11\rangle )=\langle 0,4,7\rangle = C, \:\: L(G)=L(\langle7,11,2\rangle)=\langle 11,2,6\rangle=b,\\\ R(b)=R(\langle11,2,6\rangle )=\langle 2,6,9\rangle=D,\:\: R(A)=R(\langle 9,1,4\rangle )=\langle 6,1,9\rangle=f\sharp. \end{eqnarray*}
Primijetimo da svaka od ovih transformacija zadržava dva tona polaznog akorda istima. Također, funkcije P, L i R imaju svojstvo da je P^{2}=L^{2}=R^{2}=identiteta. Pokažimo to za funkciju P: P^{2}(\langle a,b,c\rangle)=P\circ P(\langle a,b,c\rangle)= P(\langle a,b+1,c\rangle)=\langle a,(b+1)-1,c\rangle =\langle a,b,c\rangle. Slično vrijedi i P^{2}(\langle A,B,C\rangle)=\langle A,B,C\rangle. Još jedno korisno svojstvo dano je u propoziciji:
Propozicija 14. [2] Za
n,k\in \mathbb{Z} takve da je
n\equiv k mod12 vrijedi
\begin{eqnarray*}(L\circ R)^{n}=(L\circ R)^{k}\:\:{\text{i}}\:\: R\circ (L\circ R)^{n}=R\circ (L\circ R)^{k}. \end{eqnarray*}
Dokaz. Imamo
\begin{eqnarray*}(L\circ R)^{3}(\lbrace A,B,C\rbrace )=(L\circ R)^{2}(L\circ R(\lbrace A,B,C\rbrace ))=(L\circ R)^{2}(\lbrace B+1,C+2, A\rbrace )\\\ =(L\circ R)(\lbrace C+3,A+2,B+1\rbrace )=\lbrace A+3,B+3,C+3\rbrace .\:\:\:\end{eqnarray*}
To iskoristimo da dobijemo
\begin{eqnarray*}(L\circ R)^{12}((\lbrace A,B,C\rbrace )=(L\circ R)^{9}((L\circ R)^{3}(\lbrace A,B,C\rbrace )=\cdots=\\\\lbrace A+12,B+12,C+12\rbrace =\lbrace A,B,C\rbrace . \end{eqnarray*}
Analogni rezultat dobije se i za molski akord. Znači da vrijedi
(1)
\begin{eqnarray}(L\circ R)^{12}=(L\circ R)^{0}=\text{identiteta}. \end{eqnarray}
Jer je
n\equiv k mod12
\Rightarrow n=12q+k pa je
\begin{eqnarray*}(L\circ R)^{n}=(L\circ R)^{12q+k}=(L\circ R)^{12q}(L\circ R)^{k}=(L\circ R)^{k}. \end{eqnarray*}
Druga jednakost slijedi odmah iz prve.
\ \blacksquare
Definirajmo sada skup \;{P}{L}{R}\;:
Definicija 15. [2] Skup svih
P,
L i
R funkcija označavamo sa
\;{P}{L}{R}\; i definiramo kao
\begin{eqnarray*}\;{P}{L}{R}\;=\lbrace (L\circ R)^{n},R\circ (L\circ R)^{n}|n\in \mathbb{Z}_{12}\rbrace . \end{eqnarray*}
Na prvi pogled se čini čudno što u definiciji skupa \;{P}{L}{R}\;ne spominjemo eksplicitno funkcije P i L. Međutim, možemo generirati sve elemente skupa \mathbb{M} (pa tako i sve funkcije \;{P}{L}{R}\; skupa) bez korištenja funkcija P i L. Specijalno, lako se pokaže da je
\begin{eqnarray*} P=R\circ (L\circ R)^{3}\:\:{\text{i}}\:\: L=R\circ(L\circ R)^{11}. \end{eqnarray*}
Zbog Propozicije 14. vidimo da skup \;{P}{L}{R}\;, kao i skup \;{T}{I}\;, ima samo 24 različita elementa. Vrijedi sljedeći teorem:
Teorem 16. [2] Skup
\;{P}{L}{R}\; uz operaciju kompozicije funkcija je grupa.
Dokaz. Lako se pokaže da je kompozicija dobro definirana operacija i da se svaka kompozicija funkcija
P,
L i
R nalazi u skupu
\;{P}{L}{R}\;. Kompozicija funkcija je asocijativna operacija po definiciji. Iz Propozicije 14. vidimo da je neutralni element (identiteta) također u skupu
\;{P}{L}{R}\;. Ostaje još provjeriti invertibilnost. U skupu
\;{P}{L}{R}\; imamo dvije vrste elemenata, oblika
(L\circ R)^{n} i
R\circ (L\circ R)^{n}. Vidimo da vrijedi
(R\circ (L\circ R)^{n})^{2}=identiteta, pa je
(R\circ (L\circ R)^{n})^{-1}=R\circ (L\circ R)^{n}. Pomoću (
1) pokaže se i da je
(L\circ R)^{n}\circ(L\circ R)^{k}=(L\circ R)^{k}\circ (L\circ R)^{n}=identiteta, uz
k\in\mathbb{Z} takav da je
k\equiv -n mod12, pa je
((L\circ R)^{n})^{-1}=(L\circ R)^{k}, i
\;{P}{L}{R}\; je grupa.
\ \blacksquare
Grupe \;{P}{L}{R}\; i \;{T}{I}\; vežu mnoga zanimljiva matematička svojstva, na primjer one su izomorfne i dualne [7], ali to ostaje tema za drugi članak.
Primijenimo elemente \;{P}{L}{R}\; grupe na primjere iz glazbe. Elvisova progresija I-VI-IV-V-I je klasičan motiv iz rock glazbe 50-ih godina i može se naći u mnogim pjesmama. Ona je zapravo dijagram na Slici 4.
U prvi krug upišemo C-dur akord i primijenimo funkcije kako je nacrtano. Dobijemo progresiju: C-dur, a-mol, F-dur, G-dur, C-dur. Ta progresija nalazi se i na primjer u hitu iz 80-ih Stand by me. Drugi dobar primjer je pjesma Beatlesa Oh Darling, koja ima glavnu progresiju E-dur, A-dur, E-dur, f\sharp-mol, D-dur, b-mol, E-dur, b-mol, E-dur i A-dur. Fokusirajmo se samo na 4 unutarnja akorda, f\sharp-mol, D-dur, b-mol i E-dur. Oni formiraju dijagram koji vidimo na Slici 5.
Slika 5: Beatles akordi
Kao što vidimo, matematikom se uspješno mogu analizirati i djela popularne, a ne samo klasične glazbe.
5Beethovenova 9. simfonija, put na torusu i druge primjene
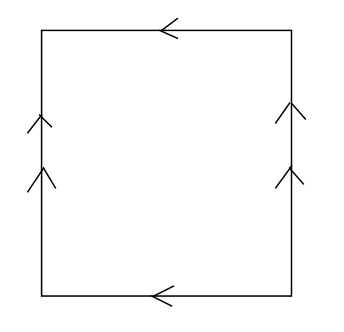
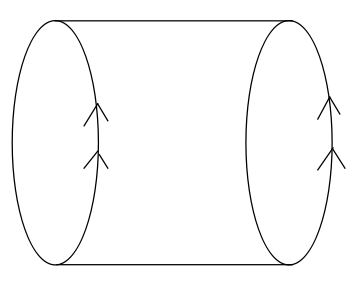
Topologija je grana matematike koja se bavi kvalitativnim svojstvima geometrijskih objekata. Na primjer, neka od klasičnih topoloških pitanja bila bi: da li je geometrijski objekt povezan, da li ima granice, da li ima rupe? U toplogiji smatramo kružnicu i rub kvadrata (prazan kvadrat) istim objektima jer se jedan može preoblikovati u drugi - oba su povezana, oba imaju prazninu u sredini, dok je na primjer segment pravca kvalitativno različit od njih jer ima granice (dva kraja) te nema prazninu u sredini. Topologija je kao geometrija gumenih tjela - zamislimo da su naši objekti od meke rastezljive gume i smatramo ih istima ukoliko se jedan može rastegnuti, stisnuti ili na bilo koji drugi način preoblikovati u drugi. Jedan od osobito zanimljivih objekata u toplogiji je torus. Da dobijemo torus, počinjemo od punog kvadrata kao na Slici 6.a. Strelice predstavljaju mjesta po kojima ćemo lijepiti da dobijemo torus. Najprije zalijepimo horizontalne linije s jednostrukim strelicama skupa i dobijemo cilindar prikazan na Slici 6.b. Nakon toga zalijepimo dvije kružnice na kojima se nalaze dvostruke strelice i dobijemo torus (Slika 6.c.). Kao što vidimo, torus izgleda kao napuhana automobilska guma.
Slika 6: a) kvadrat\quad\qquad\qquad b) cilindar \qquad\qquad\qquad c) torus\qquad\qquad
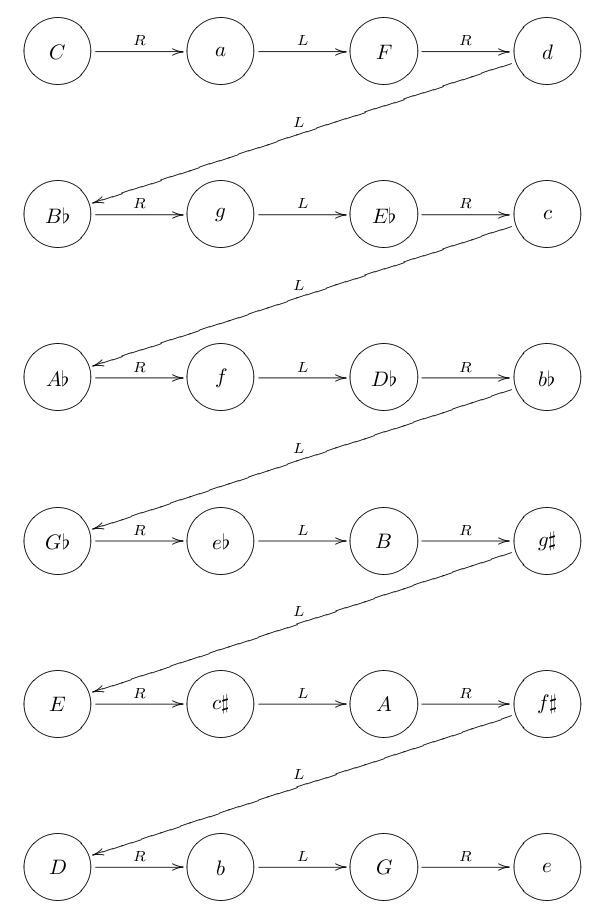
Torus, \;{P}{L}{R}\; grupa i 9. simfonija Ludwiga van Beethovena povezani su na zanimljiv i neočekivan način. U taktovima 143-176 simfonije nailazimo na niz od 19 akorda, koji je prvi primijetio Cohn u [6]:
\begin{eqnarray*} C,a,F,d,B\flat, g,E\flat,c,A\flat,f,D\flat,b\flat,G\flat,e\flat,B,g\sharp,E,c\sharp,A.\end{eqnarray*}
Čitav taj niz možemo dobiti naizmjeničnim primjenjivanjem funkcija R i L, kao što vidimo na Slici 7.
Slika 7: Beethovenova progresija
Zadnjih 5 akorda sa slike Beethoven nije dodao u svoju simfoniju, ali nadopunom njih dobili smo svih 24 različitih akorda, i niti jedan se nije ponovio. Graf na slici, osim što pokazuje taj iznenađujući uzorak, odlikuje se i time što svaki akord za svoje susjede ima akorde koji su mu najsličniji i razlikuju se od njega samo u jednom tonu (glazbeno također ti akordi zajedno zvuče osobito ugodno).
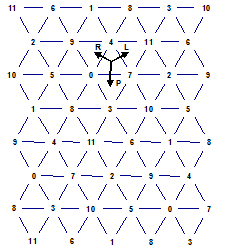
Geometrijska reprezentacija P, L i R funkcija poznata je pod nazivom Tonnetz (njem. mreža tonova). Vrhovi predstavljaju tonove, a trokuti akorde koji se sastoje od tonova u vrhovima. Kao što smo ranije spomenuli, funkcije P, L i R preslikavaju akorde u akorde koji se razlikuju u samo jednom tonu, odnosno svaki trokut Tonnetza preslikava se u njemu susjedne na način prikazan na Slici 8.
Slika 8: Tonnetz
Uočimo da se vrhovi na slici počinju nakon nekog vremena ponavljati. Ako sada spojimo vrhove u prvom i u zadnjem retku slike, a zatim (s malim pomakom ukoso-gore) vrhove u prvom i zadnjem stupcu (spajamo iste vrhove s istima, na način kao što smo ranije spajali stranice kvadrata u torus), vidimo da smo dobili torus. Naš graf devete simfonije možemo lako pronaći na Slici 8., pronađemo trokute koji odgovaraju akordima iz Slike 7. i spojimo ih kao na Slici 7. Zbog toga možemo reći da Beethovenova 9. simfonija iscrtava put na torusu.
Da li postoji još primjena promatranja simetrije u glazbi korištenjem matematike, osim pomoći kompozitorima u skladanju, muzičarima u učenju i slušačima glazbe, koji bez znanja matematike nikad ne bi čuli torus u Beethovenovoj simfoniji? Algoritmi bazirani na teoretskim razmatranjima iz teorije grupa uspješno su implementirani za računala i računalo može samo skladati, generiranjem takozvanih Vuza kanona [8]. Mi smo se ovdje koncentrirali na evropsku i američku glazbu, ali matematika se uspješno primjenjuje na svu glazbu. Vrlo zanimljiva je primjena na indijsku glazbu koja je utemeljena na ragama (glazbene ljestvice s karakterističnim uzorcima specifičnim za indijsku glazbu) prikazanima kao nizovima cijelih brojeva [9]. Brojni dodatni primjeri veze matematike i glazbe mogu se pronaći i u izvrsnoj knjizi [10]. Konačno, ovaj članak je prikaz samo nekih važnih struktura iz teorije grupa koje nalazimo u glazbenim kompozicijama. Bogatstvo simetrija, uzoraka i transformacija među njima u glazbi je veliko, a teorija grupa vrlo pogodan alat za njihovo izučavanje.
Bibliografija
|
[1] |
Horvatić, K. Linearna algebra, I. dio , Matematički odjel PMF-a, Sveučilište u Zagrebu, Zagreb, 1995. |
|
[2] |
Aceff-Sánchez, A.; Augustin-Aquino, O.A.; Lluis-Puebla. E.; Montiel, M.; du Plessis, J. An introduction to Group Theory. Applications to Mathematical Music Theory., Bookboon Ventus publishing Aps, 2012. |
|
[3] |
Fiore, T.M. Music and Mathematics, Lecture notes, Department of Mathematics and Statistics, University of Michigan, 2011. |
|
[4] |
Milnor, J.W. Topology from the Differentiable Viewpoint, The University Press of Virginia, Charlottesville, 1965. |
|
[5] |
Mendelson, B. Introduction to topology, Dover Publications, 1990. |
|
[6] |
Cohn, R. Neo-Riemannian operations, parsimonious trichords and their Tonnetz representations. Journal of Music Theory, 41 1997., 1–66. |
|
[7] |
Crans, A.; Fiore, T.; Satyendra, R. Musical Actions of Dihedral Groups, The American Mathematical Monthly, vol. 116, no. 6, June 2009, p. 479–495. |
|
[8] |
Andreatta, M. On group-theoretical methods applied to music: some compositional and implementational aspects, Osnabrück, Germany, Electronic Publishing Osnabrück, 2004. |
|
[9] |
Balasubramanian, K. Combinatorial Enumeration of Ragas (Scales of Integer Sequences) of Indian Music, Journal of Integer Sequences, Vol.5, 2002., p. 1–21 |
|
[10] |
Benson, J.D. Music: A Mathematical Offering, Cambridge University Press, 2006.
|