O zlatnom rombu
U ovom članku definirat ćemo zlatni romb, objasnit ćemo neka njegova svojstva i pokazati neke konstrukcije vezane uz zlatni romb, a koje se mogu izvesti ravnalom i šestarom.
Zlatni rez i zlatni pravokutnik su omiljena tema u matematici, odnosno geometriji, a i u umjetnosti. O njima je napisano zaista mnoštvo radova. Poznat je i pojam zlatnog romba, ali se on u literaturi nešto rjeđe spominje. Stoga ćemo u ovom radu definirati zlatni romb, te navesti njegova najvažnija svojstva i načine konstrukcija.
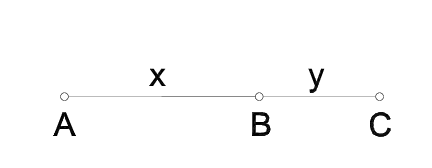
Dužina (\overline{AC}) je podijeljena u zlatnom rezu ako je omjer većeg dijela dužine (\overline{AB}) prema manjem dijelu dužine (\overline{BC}) jednak omjeru cijele dužine (\overline{AC}) prema većem dijelu dužine (\overline{AB}) (vidjeti Sliku 1).
Broj \varphi nazivamo zlatni broj. Jednakost (1) može se zapisati i u ekvivalentnom obliku:
Za pregledne podatke o zlatnom rezu i dvjema osnovnim konstrukcijama vezanima uz zlatni rez zainteresiranoga čitatelja upućujemo na članak
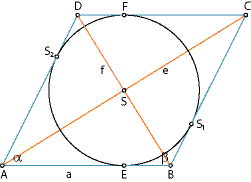
Zlatni romb je romb kojemu je omjer duljine veće dijagonale (e) i manje dijagonale (f) jednak zlatnom broju \varphi (vidjeti Sliku 2). Preciznije, vrijede sljedeće jednakosti:
Napomena: Ne istaknemo li drugačije, u iskazima i dokazima svih svojstava zlatnoga romba koristimo oznake sa Slike 2.
Pokažimo najprije da su svi zlatni rombovi slični. U tu ćemo svrhu najprije izračunati mjere unutrašnjih kutova proizvoljnoga zlatnoga romba.
Propozicija 1. (prema
Dokaz: Prisjetimo se da je romb četverokut kojemu su dijagonale međusobno okomite, a ujedno su i simetrale unutrašnjih kutova romba (tj. kutova \alpha i \beta). Promotrimo bilo koji od četiriju pravokutnih trokutova na koje je romb podijeljen svojim dijagonalama. Duljine kateta toga trokuta su \frac{e}{2} i \frac{f}{2} , duljina hipotenuze a, a mjere šiljastih kutova \frac{\alpha}{2} i \frac{\beta}{2}. Primjenom (
Odatle slijedi:
što je i trebalo dokazati. (Pretvorbe mjera kutova u stupnjeve prepuštamo čitatelju.) \square
Korolar 1. Svi zlatni rombovi su slični.
Dokaz: Prema Propoziciji 1, mjere svih unutrašnjih kutova romba su konstante. Zbog toga tvrdnja korolara izravno slijedi iz definicije sličnosti dvaju mnogokuta (vidjeti npr.
Zbog netom dokazanoga svojstva, zlatni romb je potpuno određen zadavanjem jedne od dviju dijagonala ili osnovice romba. Razmotrimo zasebno svaki pojedini slučaj. Radi jasnoće i preglednosti, relacije formuliramo u obliku propozicija.
Najprije iskažimo jednakost koju ćemo često koristiti u nastavku teksta.
Lema 1. Za zlatni broj \varphi vrijedi jednakost:
Dokaz: Izravnim uvrštavanjem \varphi=\frac{1+\sqrt{5}}{2} u navedenu jednakost ili uočavanjem da je \varphi rješenje kvadratne jednadžbe x^{2}-x-1=0. Detalje prepuštamo čitatelju. \square
Propozicija 2. Neka je zadan zlatni romb čija je duljina osnovice a. Tada su:
Dokaz: Prema Pitagorinu poučku vrijedi:
Iz (
Iz (
Time je propozicija dokazana. \square
Propozicija 3. Neka je zadan zlatni romb kojemu je duljina veće dijagonale e. Tada su:
Dokaz: Prva jednakost odmah slijedi iz (
Propozicija 4. Neka je zadan zlatni romb kojemu je duljina manje dijagonale f. Tada su:
Dokaz: Prva jednakost odmah slijedi iz (
Izvedimo sada izraze za površinu zlatnoga romba.
Propozicija 5. Površina zlatnoga romba (P) dana je sljedećim izrazima:
Dokaz: Romb je četverokut s okomitim dijagonalama, pa se njegova površina može izračunati prema formuli:
Sada prva jednakost odmah slijedi uvrštavanjem (
a odatle izravno slijedi treća jednakost. \square
Svakom rombu se može upisati kružnica. Njezin je promjer jednak visini romba. Ekvivalentno, polumjer rombu upisane kružnice jednak je polovici visine romba. Izraze za izračunavanje toga polumjera u slučaju zlatnoga romba navodimo u sljedećoj propoziciji.
Propozicija 6. Polumjer zlatnom rombu upisane kružnice (r) dan je sljedećim izrazima:
Dokaz: Neka je v duljina visine romba. Znamo da je v=2 r, pa uvrštavanjem toga izraza u formulu za površinu romba P=a v dobijemo:
Ako u (
Ako u (
Naposljetku, ako u (
Napomena: Zlatnom rombu nije moguće opisati kružnicu. Podsjetimo, rombu se može opisati kružnica ako i samo ako je romb kvadrat.
Propozicija 7. Dirališta zlatnom rombu upisane kružnice dijele stranice romba u omjeru \varphi : \frac{1}{\varphi}.
Dokaz: Budući da dijagonale bilo kojega romba dijele romb na četiri sukladna trokuta, tvrdnju propozicije dovoljno je dokazati samo za jednu stranicu romba. Stoga bez smanjenja općenitosti odaberimo stranicu \overline{AB} i diralište E. Iz (
Dijeljenjem tih jednakosti odmah dobivamo |\overline{AE}|:|\overline{BE}|=\varphi : \frac{1}{\varphi}, što je i trebalo pokazati. \square
U prethodnoj smo točki pokazali da je za jednoznačno određivanje zlatnoga romba dovoljno zadati jednu od dijagonala ili osnovicu romba. Zbog toga razlikujemo tri osnovne konstrukcije zlatnoga romba:
1.Konstrukcija ako je zadana duljina osnovice (a).
2.Konstrukcija ako je zadana duljina veće dijagonale (e).
3.Konstrukcija ako je zadana duljina manje dijagonale (f).
Svaka od ovih konstrukcija zasniva se na konstrukciji pravokutnoga trokuta kojemu je omjer duljina kateta jednak zlatnom broju. Stoga ćemo najprije opisati tu konstrukciju.
Dokažimo najprije sljedeću propoziciju.
Propozicija 8. Neka je \Delta ABC pravokutan trokut kojemu su duljine kateta a i b. Pretpostavimo da je a:b=\varphi. Tada je \Delta ABC jednoznačno određen zadavanjem duljine bilo koje svoje stranice.
Dokaz: Bez smanjenja općenitosti možemo pretpostaviti da su kutovi u trokutu \Delta ABC označeni standardno (tj. nasuprot katete a se nalazi kut \alpha itd.).
Pretpostavimo najprije da je zadana duljina bilo koje katete. Tada iz omjera a:b=\varphi najprije izračunamo duljinu preostale katete. Duljinu hipotenuze c potom izračunamo npr. koristeći Pitagorin poučak. Time je dokazana tvrdnja propozicije za ovaj slučaj.
Preostaje razmotriti slučaj kad je zadana duljina hipotenuze c. Iz pretpostavke
a:b=\varphi slijedi:
pa primjenom trigonometrijskih relacija u pravokutnom trokutu (vidjeti
Odatle slijedi da su jednoznačno određene i duljine obiju kateta, što smo i htjeli pokazati. \square
Radi jednostavnosti, u nastavku pretpostavljamo da je \Delta ABC pravokutan trokut kojemu su duljine kateta a i b takve da je a:b=\varphi. Analogno kao u dokazu Propozicije 8., pretpostavljamo da su sve ostale oznake veličina u \Delta ABC standardne.
Pokažimo da se \Delta ABC može konstruirati ako je zadana duljina bilo koje njegove stranice. Sve konstrukcije izvodimo ravnalom i šestarom. Radi jasnoće i preglednosti izlaganja, svaku od triju mogućih konstrukcija formuliramo u obliku zadatka.
Zadatak 1. Konstruirajte \Delta ABC ako je zadana duljina katete a.
Rješenje: Iz pretpostavke zadatka i ranije pretpostavke o standardnim oznakama veličina u \Delta ABC zaključujemo da je zadana dužina \overline{BC} takva da je |\overline{BC}|=a. Trokut će biti potpuno konstruiran kad odredimo preostali vrh A. Točka C mora biti vrh pravoga kuta trokuta \Delta ABC, pa su koraci konstrukcije sljedeći:
Korak 1. Iz točke C uzdignemo okomicu p na polupravac CB. Radi određenosti, u daljnjem smatramo da je p polupravac kojemu je C početna točka.
Korak 2. Nacrtamo kružni luk sa središtem u točki C i polumjerom r_{1}=\overline{BC}. Taj kružni luk siječe polupravac p u točki D.
Korak 3. Odredimo polovište P dužine \overline{BC}.
Korak 4. Nacrtamo kružni luk sa središtem u točki P i polumjerom r_{2}=\overline{PD}. Taj luk siječe pravac CB u točki E.
Korak 5. Nacrtamo kružni luk sa središtem u točki C i polumjerom r_{3}=\overline{CE}. Taj luk siječe polupravac p u traženoj točki A.
Dokaz konstrukcije: Vidjeti rješenje Zadatka 1 u
Zadatak 2. Konstruirajte \Delta ABC ako je zadana duljina katete b.
Rješenje: Iz pretpostavke zadatka i ranije pretpostavke o standardnim oznakama veličina u \Delta ABC zaključujemo da je zadana dužina \overline{AC} takva da je |\overline{AC}|=b. Trokut će biti potpuno konstruiran kad odredimo preostali vrh B. Točka C mora biti vrh pravoga kuta trokuta, pa su koraci konstrukcije sljedeći:
Korak 1. Iz točke C uzdignemo okomicu p na polupravac CA. Ponovno radi jednostavnosti i jednoznačnosti rješenja, u daljnjem smatramo da je p polupravac kojemu je C početna točka.
Korak 2. Odredimo polovište P dužine \overline{AC}.
Korak 3. Nacrtamo kružni luk sa središtem u točki C i polumjerom r_{1}=\overline{CP}. Taj luk siječe polupravac p u točki D.
Korak 4. Nacrtamo kružni luk sa središtem u točki D i polumjerom r_{2}=\overline{AD}. Taj luk siječe polupravac p u traženoj točki B.
Dokaz konstrukcije: Zapravo treba dokazati da je |\overline{BC}|=a. Iz Koraka 3 i 4 slijedi B,D\in p. Iz Koraka 1 zaključujemo da je p okomit na polupravac CA, pa su trokutovi ABC i ACD pravokutni trokutovi s pravim kutom u vrhu C. Iz Koraka 2 i Koraka 3 slijedi |\overline{CD}|=|\overline{CP}|=\frac{b}{2}, dok iz Koraka 4 slijedi |\overline{BD}|=|\overline{AD}|. Primjenom Pitagorina poučka na trokut ACD dobivamo:
S druge strane, pretpostavka a:b=\varphi je ekvivalentna s a=\varphi b, pa iz dobivenih jednakosti zaključujemo da je |\overline{BC}|=a, što smo i željeli dokazati. \square
Zadatak 3. Konstruirajte \Delta ABC ako je zadana duljina hipotenuze c.
Rješenje: \Delta ABC je najbrže i najlakše konstruirati tako da se najprije konstruira zlatni romb čija osnovica ima duljinu c. Ovu konstrukciju izložit ćemo u sljedećoj točki.
Dokaz konstrukcije: Pretpostavimo da smo konstruirali zlatni romb ABCD kojemu je c duljina osnovice. Neka je S sjecište njegovih dijagonala. Tada je traženi trokut npr. \Delta ABS (ili, općenito, bilo koji trokut određen dvama susjednima vrhovima romba i točkom S). Ispravnost ovoga zaključka slijedi iz definicije zlatnoga romba i činjenice da su dijagonale bilo kojega romba međusobno okomite. Detalje prepuštamo čitatelju. \square
Već smo ranije istaknuli (vidjeti primjedbu neposredno iza Korolara 1) da je zlatni romb jednoznačno određen zadavanjem bilo koje njegove dijagonale ili njegove osnovice. Stoga ćemo razmotriti konstrukciju romba u svakom od tih slučajeva. Radi jasnoće i preglednosti, konstrukcije ćemo ponovno formulirati u obliku zadataka.
U svim konstrukcijama pretpostavljamo da je ABCD zlatni romb kojemu su \overline{AC} veća dijagonala, \overline{BD} manja dijagonala i S sjecište tih dijagonala.
Zadatak 4. Konstruirajte zlatni romb kojemu je zadana duljina veće dijagonale e.
Rješenje: U skladu s pretpostavkama, zadana nam je \overline{AC} takva da je |\overline{AC}|=e. Koraci konstrukcije su sljedeći:
Korak 1. Odredimo polovište P dužine \overline{AC}.
Korak 2. Konstrukcijom opisanom u rješenju Zadatka 1 konstruiramo pravokutan trokut APB čija je veća kateta \overline{AP}.
Korak 3. Nacrtamo kružni luk sa središtem u točki P i polumjerom r=\overline{PB}. Taj luk će presjeći pravac PB u točkama B i D.
Korak 4. Četverokut ABCD je traženi zlatni romb.
Dokaz konstrukcije: Prema Koracima 1 i 3, P je zajedničko polovište dužina \overline{AC} i \overline{BD}. To znači da je četverokut ABCD paralelogram. Prema Koraku 2, trokut APB je pravokutan trokut, pa su dijagonale \overline{AC} i \overline{BD} četverokuta ABCD okomite. Odatle slijedi da je četverokut ABCD romb. Prema konstrukciji iz Koraka 2 vrijedi omjer |\overline{AP}|:|\overline{BP}|=\varphi. Budući da su |\overline{AP}|=\frac{e}{2} i |\overline{BP}|=\frac{f}{2}, zaključujemo da je \varphi =|\overline{AP}|:|\overline{BP}|=\frac{e}{2}:\frac{f}{2}=e:f, pa je ABCD zlatni romb. \square
Zadatak 5. Konstruirajte zlatni romb kojemu je zadana duljina manje dijagonale f.
Rješenje: U skladu s pretpostavkama, zadana nam je \overline{BD} takva da je |\overline{BD}|=f . Koraci konstrukcije su sljedeći:
Korak 1. Odredimo polovište P dužine \overline{BD}.
Korak 2. Konstrukcijom opisanom u rješenju Zadatka 2 konstruiramo pravokutan trokut APB čija je manja kateta \overline{BP}.
Korak 3. Nacrtamo kružni luk sa središtem u točki P i polumjerom r=\overline{AP}. Taj luk će presjeći pravac AP u točkama A i C.
Korak 4. Četverokut ABCD je traženi zlatni romb.
Dokaz konstrukcije: Jednak je dokazu konstrukcije iz Zadatka 4, pa ga izostavljamo. \square
Preostalo je razmotriti slučaj konstrukcije zlatnoga romba u slučaju kad je zadana duljina osnovice romba. U tu ćemo svrhu najprije riješiti sljedeći zadatak.
Zadatak 6. (prilagođeno prema
Rješenje: Promotrimo pravokutnik A_{1}B_{1}C_{1}D_{1} čije su duljine stranica 4 i 2. Radi određenosti, zapišimo:
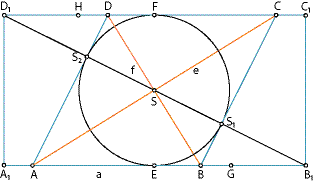
U taj pravokutnik upišimo kružnicu k polumjera 1 čije je središte u sjecištu dijagonala pravokutnika. Dijagonala \overline{B_{1}D_{1}} siječe kružnicu k u točkama S_{1} i S_{2}. U tim točkama povucimo tangente t_{1} i t_{2} na kružnicu k. Neka su:
Tada je četverokut ABCD traženi zlatni romb (vidjeti Sliku 3).
Dokaz konstrukcije I. Naznačit ćemo samo glavne korake dokaza, a detalje prepuštamo čitatelju. Smjestimo pravokutnik A_{1}B_{1}C_{1}D_{1} u pravokutni koordinatni sustav u ravnini tako da središte pravokutnika, tj. sjecište S njegovih dijagonala bude u ishodištu koordinatnoga sustava. Neka su vrhovi pravokutnika A_{1}=(-2,-1),B_{1}=(2,-1),C_{1}=(2,1),D_{1}=(-2,1). Jednadžba kružnice k sa središtem u S=(0,0) i polumjerom r=1 je x^{2}+y^{2}=1. Jednadžba pravca na kojemu leži dijagonala \overline{B_{1}D_{1}} je y=-\frac{1}{2} x. Taj pravac siječe kružnicu k u točkama S_{1}=\bigg( \frac{2}{5} \sqrt{5},-\frac{1}{5} \sqrt{5}\bigg) i S_{2}=\bigg( -\frac{2}{5} \sqrt{5},\frac{1}{5} \sqrt{5}\bigg). Jednadžba tangente povučene na kružnicu k u točki S_{1} je t_{1}... y=2 x-\sqrt{5}, a jednadžba tangente povučene na kružnicu k u točki S_{2} je t_{2}... y=2 x+\sqrt{5}. Presiječemo li pravce t_{1} i t_{2} s pravcima y=-1 (pravac na kojemu leži stranica \overline{A_{1}B_{1}}) i y=1 (pravac na kojemu leži stranica \overline{C_{1}D_{1}}), uz oznake definirane u opisu konstrukcije dobit ćemo:
Sada se lako provjeri da je ABCD romb čija osnovica ima duljinu \sqrt{5}. Preostaje provjeriti da je ABCD zlatni romb. Sjecište dijagonala romba je također točka S, odnosno ishodište. Lako izračunamo:
pa je:
što smo i željeli pokazati. \square
Dokaz konstrukcije II. Ovaj dokaz je elegantniji od prvoga jer ne koristi koordinatizaciju. Zbog toga ćemo u potpunosti obrazložiti svaki njegov korak. Koristimo oznake sa Slike 3 i iz konstrukcije. Pritom napominjemo da je točka E polovište stranice \overline{A_{1}B_{1}}, a točka F polovište stranice \overline{C_{1}D_{1}}.
Pokažimo najprije da je četverokut ABCD paralelogram. Prema konstrukciji, pravac na kojemu leži dijagonala \overline{BD} prolazi središtem kružnice k, pa je dužina \overline{S_{1}S_{2}} promjer kružnice k. Pravci t_{1} i t_{2} su tangente na kružnicu k, pa su okomiti na dužinu \overline{S_{1}S_{2}}, a time i na dijagonalu \overline{BD}. To znači da su pravci t_{1} i t_{2} usporedni (okomiti su na istu dužinu \overline{S_{1}S_{2}}). Odatle slijedi da je stranica \overline{BC} četverokuta ABCD usporedna sa stranicom \overline{AD}. Usporednost stranica \overline{AB} i \overline{CD} slijedi izravno iz usporednosti stranica \overline{A_{1}B_{1}} i \overline{C_{1}D_{1}} koja vrijedi jer je A_{1}B_{1}C_{1}D_{1} pravokutnik. Time smo pokazali da je četverokut ABCD paralelogram.
Pokažimo da je paralelogram ABCD romb. U tu je svrhu dovoljno dokazati da je |\overline{AB}|=|\overline{AD}|. Površina paralelograma ABCD dana je izrazima P_{ABCD}=|\overline{AB}| v_{1}=|\overline{AD}| v_{2}, gdje su v_{1} i v_{2} duljine visina povučenih na stranicu \overline{AB}, odnosno \overline{AD}. Primijetimo da je dužina \overline{EF} visina na stranicu \overline{AB} (jer sa stranicama \overline{AB} i \overline{CD} zatvara pravi kut), te da je iz analognoga razloga dužina \overline{S_{1}S_{2}} visina na stranicu \overline{AD}. No, |\overline{EF}|=|\overline{S_{1}S_{2}}|=2 jer su te dužine promjeri kružnice k. Dakle, vrijedi jednakost v_{1}=v_{2}, pa sada iz |\overline{AB}| v_{1}=|\overline{AD}| v_{2} izravno slijedi |\overline{AB}|=|\overline{AD}|.
Izračunajmo duljinu stranice romba ABCD. Uočimo da je \Delta EBS\cong \Delta SS_{2}D. Oba trokuta su pravokutna (prvi ima pravi kut kod vrha E, a drugi kod vrha S_{2}) i imaju dva para međusobno sukladnih stranica (|\overline{BS}|=|\overline{SD}|=\frac{f}{2} i |\overline{SE}|=|\overline{SS_{2}}|=2), pa primjenom Pitagorina poučka zaključujemo da je i preostali par stranica međusobno sukladan. Preciznije, vrijedi jednakost:
Nadalje, uočimo da je \Delta EB_{1}S\sim \Delta S_{1}BB_{1}. Oba trokuta su pravokutna i imaju zajednički (šiljasti) kut kod vrha B_{1}, pa su i preostala dva kuta tih trokutova sukladna. Stoga navedena sličnost slijedi iz poučka K-K o sličnosti trokutova (vidjeti npr.
U taj razmjer uvrstimo:
Naposljetku, uočimo da je \Delta EB_{1}S\sim \Delta S_{2}AB_{1} iz istih razloga kao i \Delta EB_{1}S\sim \Delta S_{1}BB_{1}. Tako dobivamo razmjer:
Budući da su
Tako iz (
Preostaje pokazati da je ABCD zlatni romb. Uočimo da je \Delta ASD\sim \Delta ASS_{2}. Oba trokuta su pravokutna i imaju zajednički kut kod vrha A, pa sličnost ponovno slijedi iz poučka K-K o sličnosti trokutova. Tako dobivamo razmjer:
pa zbog |\overline{SS_{2}}|=1, (
što smo i htjeli pokazati. Time je dokaz završen. \square
Zadatak 7. Konstruirajte zlatni romb kojemu je zadana duljina osnovice a.
Rješenje: Koristimo rješenje Zadatka 6. Koraci konstrukcije su sljedeći:
Korak 1. Postupkom opisanim u rješenju Zadatka 6 konstruiramo zlatni romb ABCD čija osnovica ima duljinu \sqrt{5}.
Korak 2. U šestar uzmemo dužinu duljine a. Zabodemo šestar u vrh A i presiječemo polupravce AB i AD. Tako dobivamo točke P\in AB i T\in AD.
Korak 3. Zabodemo šestar u vrh P i nacrtamo kružnicu polumjera a sa središtem u P. Potom zabodemo šestar u vrh T i nacrtamo kružnicu polumjera a sa središtem u T. Nacrtane kružnice se sijeku u točkama A (koju znamo otprije) i R. Četverokut APRT je traženi zlatni romb.
Dokaz konstrukcije: Prema Korolaru 1, svi zlatni rombovi su slični. Stoga je dovoljno dokazati da su rombovi ABCD i APRT slični, odnosno da su im odgovarajući kutovi sukladni. Oba romba imaju zajednički (šiljasti) kut \alpha kod vrha A, pa i njihovi tupi kutovi moraju biti sukladni (mjera tih kutova jednaka je \pi -\alpha radijana). \square
Konstrukcija zlatnoga romba opisana u rješenju Zadatka 6 ima neke zanimljive posljedice. Naime, u toj smo konstrukciji, osim zlatnoga romba, konstruirali i dužinu \overline{AS_{2}} čija je duljina jednaka \varphi, te dužinu \overline{DS_{2}} čija je duljina jednaka \frac{\sqrt{5}-1}{2}, odnosno zbog (
Propozicija 9. (prema
Dokaz: Radi kratkoće zapisa, označimo x:=|\overline{AE}|,y:=|\overline{BE}|,z:=|\overline{BG}|,w:=|\overline{CH}|. Uočimo da vrijede relacije:
Zbog njih, te zbog (
Pokažimo da je z=\frac{1}{\varphi^{2}}. Prema pretpostavci je |\overline{EG}|=1, pa koristeći Lemu 1 imamo:
Preostaje pokazati da je w=\varphi^{2}. Uočimo da je \Delta FDS\cong \Delta SEB. To znači da je |\overline{FD}|=|\overline{EB}|=y=\frac{1}{\varphi}. Prema pretpostavci je |\overline{FH}|=1, pa slijedi:
Tako ponovno koristeći Lemu 1 dobivamo:
što je i trebalo pokazati. Detalje prepuštamo čitatelju. \square
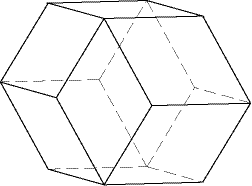
Spomenimo zaključno i posebnu zanimljivost vezanu uz zlatni romb. On se pojavljuje usko vezan uz dodekaedar Bilinskoga (vidjeti Sliku 4). Taj dodekaedar je 1960. otkrio hrvatski matematičar Stanko Bilinski (1909. - 1998.) i nazvao ga rompski dodekaedar druge vrste. Riječ je o konveksnom poliedru kojemu su svih 12 strana sukladni zlatni rombovi. Tim je otkrićem profesor Bilinski pokazao da postoji i rompski dodekaedar kojemu je omjer dijagonala bilo koje strane različit od \sqrt{2}. Dotad se, naime, smatralo da su strane svakoga rompskoga dodekaedra rombovi kojima je omjer dijagonala \sqrt{2}:1. Zbog toga je novootkriveni rompski dodekaedar nazvan prema profesoru Bilinskom, čime je svjetska matematička zajednica dala (još jedno) zasluženo priznanje istaknutim hrvatskim matematičarima. Zainteresiranoga čitatelja upućujemo na članak
Konstrukcije koje su opisane u ovom članku jednostavno je izvesti u GeoGebri. Primjeri koje su izradili autori članka dostupni su na Internetu zajedno s uputama namijenjenima korisnicima, i to:
1) Primjer za pravokutni trokut kojemu je omjer duljina kateta jednak zlatnom broju, odnosno konstrukciju opisanu u Zadatku 2:
https://www.geogebra.org/m/WnUqk86T
2) Primjer za zlatni romb kojemu je zadana duljina veće dijagonale, odnosno konstrukciju opisanu u Zadatku 4:
https://www.geogebra.org/m/X6eSRuMQ
3) Primjer za zlatni romb kojemu je zadana duljina manje dijagonale, odnosno konstrukciju opisanu u Zadatku 5:
https://www.geogebra.org/m/tqAUNwM6
4) Primjer za zlatni romb kojemu je zadana duljina stranice, odnosno konstrukciju opisanu u Zadatku 7:
https://www.geogebra.org/m/rsksFeGv
U istom primjeru pokazana je i konstrukcija zlatnoga romba kojemu je duljina stranice \sqrt{5} jediničnih dužina, odnosno konstrukcija opisana u Zadatku 6.
U ovom smo članku izložili još jednu od mnogobrojnih primjena zlatnoga reza u geometriji. Definirali smo pojam zlatnoga romba, naveli njegova osnovna svojstva i detaljno opisali moguće načine njegova konstruiranja. Pritom treba posebno istaknuti da su sve opisane konstrukcije izvodljive samo ravnalom i šestarom, a za dokazivanje njihove valjanosti posve je dovoljno poznavanje elementarne (srednjoškolske) geometrije.
I ovim radom nastojali smo dati svoj doprinos nastojanjima da se potpuno neopravdano zanemarene geometrijske teme uvrste u nastavne programe matematičkih predmeta na tehničkim stručnim studijima koji se izvode na našim veleučilištima i samostalnim visokim školama. Uvjereni smo da bi takve teme vrlo pozitivno utjecale na zanimljivost tih predmeta, a samim time i na popularizaciju matematike, odnosno nastavak "razbijanja" tradicionalnih stereotipa o matematici kao "bauku".
| [1] | M. Katić Žlepalo, B. Kovačić: O zlatnom trokutu, Math.e, Hrvatsko matematičko društvo, Zagreb, 2017. |
| [2] | B. Pavković, D. Veljan: Elementarna matematika 1, školska knjiga, Zagreb, 2004. |
| [3] | B. Pavković, D. Veljan: Elementarna matematika 2, školska knjiga, Zagreb, 1994. |
| [4] | E. W. Weisstein: Golden Rhombus, (javno dostupno na: http://mathworld.wolfram.com/GoldenRhombus.html 15.8.2017.) |
| [5] | A. Bogomolny: Golden Ratio via Golden Rhombus (javno dostupno na: http://www.cut-the-knot.org/do_you_know/GoldenRatioMolokach.shtml, 15.8.2017.) |
| [6] |
B. Gruenbaum: The Bilinski dodecahedron and assorted parallelohedra, zonohedra, monohedra, isozonohedra, and otherhedra, The Mathematical Intelligencer, 32 (4), 2010. |