Bojan Kovačić i Tihana Strmečki, Tehničko
veleučilište, Zagreb
Problemi
razdiobe ulaganja općenito podrazumijevaju određivanje razdiobe određenoga
novčanog iznosa na određeni broj gospodarskih grana tako da ukupna očekivana neto-dobit
nastala tim ulaganjima bude maksimalna. U ovu kategoriju pripada i problem
minimizacije troškova proizvodnje: ako u jednakim vremenskim intervalima treba
proizvesti određenu količinu nekoga proizvoda i ako su poznati troškovi
proizvodnje u svakom pojedinom intervalu, valja napraviti raspored proizvodnje
tako da ukupni troškovi budu minimalni. Navedene probleme, njihovo matematičko
modeliranje i rješavanje metodama dinamičkoga programiranja opisujemo na nizu
primjera, pri čemu uz neke dajemo postupak rjeąavanja s pomoću računalnoga
programa WinQSB.[1]
Radi
boljega razumijevanja navedenih metoda, navodimo objašnjenja njihovih osnovnih pojmova.
Dinamičko programiranje
je metoda rješavanja složenih problema koji imaju određenu pravilnost u
strukturi. Riječ programiranje dolazi iz vremena prije nastanka
računalnog programiranja, a sinonim je riječi optimizacija. Koristi se u
slučajevima u kojima problem ima optimalnu podstrukturu −
mogućnost rastava na manje potprobleme iste vrste i neznatno razlikovanje
potproblema od problema s nivoa iznad (problemi koji se svode na znatno manji
potproblem rješavaju se drugim metodama). Rješavanju se može pristupati
tehnikama „od vrha prema dnu“ ili „od dna prema vrhu“, pri čemu se dobiveni
rezultati spremaju u tablicu za buduće korištenje, čime se izbjegava ponovno
računanje. Traženo rješenje dobije se rekurzivno iz optimalnih rješenja
potproblema, preko Bellmanove jednadžbe (Richard Bellman, 1953.). Ovakva metoda
memoizacije puno je brža od metode u
kojoj se svaki put nanovo rješava svaki manji korak, koji se ne javlja nužno
prvi put.
Kod problema koji imaju
računalnu primjenu, bitan je broj koraka implementacije danog zadatka. Manji
broj koraka omogućuje brže i učinkovitije rješavanje, zbog čega je ocjenjivanje
broja operacija važan kriterij za odabir načina rješavanja.
U primjerima ovoga
članka korišteni su matematički modeli s cjelobrojnim koeficijentima i
cjelobrojnim varijablama[2].
Zbog primijenjene metode dinamičkog programiranja nije moguće računanje s
realnim brojevima. Međutim, u praksi se kao mjerne jedinice varijabli u modelu
vrlo često pojavljuju desetine, stotine, tisuće i milijuni (novčanih jedinica
ili proizvoda), što može znatno usporiti postupak rješavanja. U takvim
slučajevima pogodno je redefinirati mjerne jedinice varijabli tako da se kao
nova mjerna jedinica uzme neki višekratnički oblik polazne mjerne jedinice
(npr. valutna jedinica 1000 kn umjesto valutne jedinice 1 kn). Osnovne
prednosti takvoga redefiniranja su smanjenje ukupnoga broja potrebnih računskih
operacija i povećavanje brzine izračuna optimalnoga rješenja, a osnovni nedostatak je smanjenje mogućnosti dobivanja
preciznijih informacija o optimalnom rješenju. Naime, zbog cjelobrojnosti svih
varijabli u matematičkom modelu, i optimalno rješenje je cjelobrojno, pa ćemo
tako npr. u problemu čije je „stvarno“ optimalno rješenje x*
= 1234.56 [kn] odabirom valutne jedinice 1000 kn umjesto valutne jedinice 1 kn
dobiti optimalno rješenje y* = 1 [000 kn], tj. y*
= 1000 [kn] koje se bitno razlikuje od rješenja x*. Zbog toga prigodom
eventualnoga redefiniranja mjernih jedinica treba odabrati što manje
višekratničke oblike polaznih mjernih jedinica kako se ne bi izgubilo na
preciznosti izračuna optimalnoga rješenja.
Spomenuti program WinQSB
već
pri odabiru numeričkih vrijednosti strogo većih od 500 pokazuje vlastita
ograničenja i zahtijeva bitno dulje trajanje izračuna, pa je u primjeni toga
programa redefiniranje mjernih jedinica pogodno u slučajevima u kojima je
relativna većina svih numeričkih vrijednosti strogo veća od 500.[3] U Primjerima
4. i 6. posebno ćemo analizirati utjecaj takvoga redefiniranja na preciznost
izračuna optimalnoga rješenja.
Radi
kraćeg i jednostavnijeg zapisa, označavamo:
[n]0
:= {0, 1, 2… n} = prvih n + 1 elemenata skupa N0
:= {0, 1, 2…};
[n]
:= {1, 2… n} = skup prvih n prirodnih brojeva.
Primjer 1. Uprava neke tvrtke želi uložiti
najviše 8 n.j.[4]
u tri odjela te tvrtke tako da iznos svakoga pojedinog uloga bude cjelobrojan
te da se u svaki odjel uloži najviše 5 n.j. (dakle, moguće je da se u neki
odjel ne uloži ništa, kao i da se ne uloži sav predviđeni kapital.) Kriterij za
razdiobu ulaganja su ostvarene neto-dobiti u pojedinim odjelima koje linearno
ovise o iznosima uloženoga kapitala. Uloži li se po 1 n.j. u svaki odjel, prvi
odjel ostvarit će neto-dobit od 4 n.j., drugi odjel neto-dobit od 5 n.j., a
treći odjel neto-dobit od 2 n.j. Formirajmo odgovarajući matematički model, pa
odredimo optimalan iznos ulaganja u svaki odjel tako da ukupna neto-dobit bude
maksimalna.
Matematički model: Za svaki \(i\in [3]\) označimo s xi
iznos ulaganja u i–ti odjel. Ukupna neto-dobit D(x1,
x2, x3) nastala tim ulaganjima iznosi
D(x1, x2,
x3) = 4 ×
x1 + 5 × x2
+ 2 × x3.
Stoga
je matematički model promatranoga problema:
maksimizirati D(x1, x2,
x3) = 4 ×
x1 + 5 × x2
+ 2 × x3
pod
uvjetima
x1 + x2
+ x3 ≤ 8
x1, x2,
x3 ∈ [5]0.
Analitičko rješenje: Traženi iznos
možemo izračunati koristeći se tzv. pohlepnim principom: uzmemo
najveći mogući kapital i uložimo najviše što možemo u profitabilniji od dvaju
promatranih odjela, ostatak potom u manje profitabilan odjel itd. U ovom
slučaju to znači da svih 8 n.j. ulažemo tako da maksimalno dopuštenih 5 n.j.
uložimo u drugi (profitabilniji) odjel, a ostatak od 8 – 5 = 3 n.j. uložimo u
prvi odjel, pa će ukupna optimalna neto-dobit iznositi 5 × 5 + 4 × 3 = 37 n.j.
Rješavamo
li problem dinamičkim programiranjem, osnovna je ideja podijeliti problem u tri
faze tako da se za svaki \(i\in [3]\), u i–toj fazi rješavanja promatra
ulaganje kapitala u odjele 1… i pri čemu se u izračunima u dotičnoj fazi
koriste optimalne vrijednosti dobivene u prethodnim fazama. Radi kraćega
zapisa, označimo C := [8]0.
Dakle, u
prvoj fazi određujemo optimalnu neto-dobit kad se kapital ulaže samo u prvi
odjel. Uz ulaganje 1 n.j. u prvi odjel ostvaruje se neto-dobit od 4 n.j., pa će
za ulog od x1 n.j. ostvarena neto-dobit iznositi 4 × x1
n.j. Primijetimo da, zbog uvjeta zadatka, ne znamo točan iznos ukupno uloženoga
kapitala, nego znamo jedino da je taj iznos neki prirodan broj najviše jednak 8
(ekvivalentno, ukupni uloženi kapital je neki element skupa C,
ali ne znamo koji je to točno element). Stoga za svaki \(c \in C\)
računamo vrijednosti realne funkcije \(f:C\to \mathbb{R}\)
definirane s:
\(f_1\)(c) = 4 × c.
Te
su vrijednosti, zapravo, optimalne neto-dobiti u slučaju kad ukupni
kapital od c n.j. ulažemo samo u prvi odjel. Odmah napomenimo da za
vrijednosti \(c \in C\) takve
da je c ≥ 5 stavljamo \(f_1\)(c)
= \(f_1\)(5) jer ukupno ulaganje u prvi odjel ne može biti strogo
veće od 5 n.j. Tako dobivamo sljedeću tablicu:
|
c
|
\(f_1\)(c)
|
\({x_1}^*\)
|
|
0
|
0
|
0
|
|
1
|
4
|
1
|
|
2
|
8
|
2
|
|
3
|
12
|
3
|
|
4
|
16
|
4
|
|
5
|
20
|
5
|
|
6
|
20
|
5
|
|
7
|
20
|
5
|
|
8
|
20
|
5
|
Tablica 1. Optimalne vrijednosti funkcije \(f_1\)
Vrijednost
\({x_1}^*\) označava optimalno ulaganje u
prvi odjel za koje se postiže pripadna optimalna vrijednost \(f_1\)(c).
U prvoj je fazi ovaj zapis praktički nepotreban, ali će nam poslužiti u
sljedećim dvjema fazama.
U
drugoj fazi razmatramo slučaj ulaganja kapitala samo u prvi i drugi
odjel. Pretpostavimo da ukupno ulažemo c n.j., pri čemu je \(c\in C\). Za
svaki \(i \in [2]\) označimo s xi
iznos koji ulažemo u i–ti odjel. Tada mora vrijediti jednakost
x1 + x2
= c,
iz
koje je
x1 = c – x2.
Neto-dobit
koju će ostvariti drugi odjel iznosi 5 × x2 n.j., a optimalna neto-dobit
koju će ostvariti prvi odjel, prema definiciji funkcije \(f_1\),
iznosi \(f_1\)(x1), tj. \(f_1\)(c
– x2) n.j. Stoga za svaki \(c \in C\)
računamo vrijednosti realne funkcije \(f_2:C\to \mathbb{R}\)
definirane s:
\[f_2(c)=
\max_{\begin{subarray}{l} 0
\leqslant {x_2} \leqslant \min \left\{ {c,5} \right\} \\ {x_2} \in \mathbb{Z}
\end{subarray}} \left[ {5 \cdot {x_2} + {f_1}(c - {x_2})} \right].\]
Te
su vrijednosti, zapravo, optimalne neto-dobiti ako ukupni kapital od c
n.j. uložimo samo u prvi i drugi odjel. Uvjeti pri kojima određujemo maksimum
posljedice su zahtjeva da iznos x2 mora biti cjelobrojan i ne
smije premašiti niti ukupni kapital od c n.j., niti 5. n.j. Radi
ilustracije postupka, prikazujemo izračun vrijednosti f2(4) i
f2(8):
\[ f_2(4)=\max_{\begin{subarray}{l} 0 \leqslant
{x_2} \leqslant \min \left\{ {4,5} \right\} \\ {x_2} \in \mathbb{Z}
\end{subarray}} \left[ {5 \cdot {x_2} + {f_1}(4 - {x_2})} \right] =
\max_{0 \leqslant {x_2} \leqslant 4} \left[ {5 \cdot {x_2} + {f_1}(4
- {x_2})} \right] = \] \( \max \{5 \cdot 0 + f_1(4 – 0), 5 \cdot 1 + f_1(4– 1), 5 \cdot 2 + f_1(4– 2), 5 \cdot 3 + f_1(4– 3), 5 \cdot 4 + f_1(4– 4)\} = \) \( \max \{0 + f_1(4), 5 + f_1(3), 10 + f_1(2),
15 + f_1(1), 20 + f_1(0)\} = \) \( \max \{0 +
16, 5 + 12, 10 + 8, 15 + 4, 20 + 0\} = 20; \)
\[ f_2(8)= \max_{\begin{subarray}{l} 0
\leqslant {x_2} \leqslant \min \left\{ {8,5} \right\} \\ {x_2} \in \mathbb{Z}
\end{subarray}} \left[ {5 \cdot {x_2} + {f_1}(8 - {x_2})} \right] =
\max_{0 \leqslant {x_2} \leqslant 5} \left[ {5 \cdot {x_2} + {f_1}(8
- {x_2})} \right] = \] \( \max \{5 \cdot 0 + f_1(8 – 0), 5 \cdot 1 + f_1(8
– 1), 5 \cdot 2 + f_1(8
– 2), 5 \cdot 3 + f_1(8
– 3), 5 \cdot 4 + f_1(8
– 4), 5 \cdot 5 + f_1(8
– 5)\} = \) \( \max \{0 + f_1(8), 5 + f_1(7),
10 + f_1(6),15 + f_1(5), 20 + f_1(4),
25 + f_1(3)\} = \) \( \max \{0 + 20, 5 + 20, 10 + 20, 15 + 20, 20 + 16,
25 + 12\} = 37.\)
Sve
vrijednosti funkcija \(f_1\) i \(f_2\) navedene su u
sljedećoj tablici:
|
c
|
\(f_1(c)\)
|
\(x_1^*\)
|
\(f_2(c)\)
|
\(x_2^*\)
|
|
0
|
0
|
0
|
0
|
0
|
|
1
|
4
|
1
|
5
|
1
|
|
2
|
8
|
2
|
10
|
2
|
|
3
|
12
|
3
|
15
|
3
|
|
4
|
16
|
4
|
20
|
4
|
|
5
|
20
|
5
|
25
|
5
|
|
6
|
20
|
5
|
29
|
5
|
|
7
|
20
|
5
|
33
|
5
|
|
8
|
20
|
5
|
37
|
5
|
Tablica 2. Optimalne vrijednosti funkcija \(f_1\)
i \(f_2\)
Vrijednost
\(x_2^*\) označava optimalno ulaganje u
drugi odjel za koje se postiže pripadna optimalna vrijednost f2(c).
Npr. za c = 4 optimalna se vrijednost f2(c) = f2(4)
= 20 postiže ulaganjem \(x_2^*\) = 4 n.j.
u drugi odjel.
U
trećoj fazi razmatramo ulaganje kapitala u sva tri odjela. Analogno kao
u drugoj fazi, pretpostavimo da ulažemo ukupno c n.j. pri čemu je \(c\in C\). Za
svaki \(i\in [3]\) označimo s xi
iznos uložen u i–ti odjel. Tada mora vrijediti jednakost
x1 + x2
+ x3 = c,
iz
koje je
x1 + x2
= c – x3.
Uložimo
li u treći odjel x3 n.j., neto-dobit koju će ostvariti taj
odjel iznosi 2 × x3
n.j., a optimalna neto-dobit koju će ostvariti prvi i drugi odjel
zajedno, prema definiciji funkcije f2, iznosi f2(x1
+ x2) n.j., odnosno f2(c – x3)
n.j. Stoga za svaki \(c\in C\) računamo vrijednosti realne funkcije \(f_3:C\to \mathbb{R}\)
definirane s
\[ f_3(c)= \max_{\begin{subarray}{l} 0
\leqslant {x_3} \leqslant \min \left\{ {c,5} \right\} \\ {x_3} \in \mathbb{Z}
\end{subarray}} \left[ {2 \cdot {x_3} + {f_2}(c - {x_3})} \right].\]
Te
su vrijednosti, zapravo, optimalne neto-dobiti ako ukupni kapital od c
n.j. uložimo u sva tri odjela. Uvjeti pri kojima određujemo maksimum posljedica
su zahtjeva da iznos x3 mora biti cjelobrojan i ne smije
premašiti niti ukupni kapital od c n.j., niti 5. n.j. Radi ilustracije
postupka, prikazujemo izračun vrijednosti f2(4) i f2(8):
f3(4) = \[ \max_{\begin{subarray}{l} 0
\leqslant {x_3} \leqslant \min \left\{ {4,5} \right\} \\ {x_3} \in \mathbb{Z}
\end{subarray}} \left[ {2 \cdot {x_3} + {f_2}(4 - {x_3})} \right] =
\max_{0 \leqslant {x_3} \leqslant 4} \left[ {2 \cdot {x_3} + {f_2}(4
- {x_3})} \right]\] = max {2 × 0 + f2(4 – 0), 2 × 1 + + f2(4
– 1), 2 × 2 + f2(4
– 2), 2 × 3 + f2(4
– 3), 2 × 4 + f2(4
– 4)} = max {0 + f2(4), 2 + f2(3), 4 + + f2(2),
6 + f2(1), 8 + f2(0)} = max {0 + 20, 2
+ 15, 4 + 10, 6 + 5, 8 + 0} = 20;
f3(8) = \[ \max_{\begin{subarray}{l} 0
\leqslant {x_3} \leqslant \min \left\{ {8,5} \right\} \\ {x_3} \in \mathbb{Z}
\end{subarray}} \left[ {2 \cdot {x_3} + {f_2}(8 - {x_3})} \right] =
\max_{0 \leqslant {x_3} \leqslant 5} \left[ {2 \cdot {x_3} + {f_2}(8
- {x_3})} \right]\] = max {2 × 0 + f2(8 – 0), 2 × 1 + + f2(8
– 1), 2 × 2 + f2(8
– 2), 2 × 3 + f2(8
– 3), 2 × 4 + f2(8
– 4), 2 × 5 + f2(8
– 5)} = max {0 + + f2(8), 2 + f2(7), 4
+ f2(6), 6 + f2(5), 8 + f2(4),
10 + f2(3)} = max {0 + 37, 2 + 33, 4 + 29, 6 + + 25, 8 +
20, 10 + 15} = 37.
Svih
9 vrijednosti svake od triju promatranih funkcija pregledno su dane u sljedećoj
tablici.
|
c
|
\(f_1(c)\)
|
\(
x_1^*\)
|
f2(c)
|
\(
x_2^*\)
|
f3(c)
|
\(
x_3^*\)
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
4
|
1
|
5
|
1
|
5
|
0
|
|
2
|
8
|
2
|
10
|
2
|
10
|
0
|
|
3
|
12
|
3
|
15
|
3
|
15
|
0
|
|
4
|
16
|
4
|
20
|
4
|
20
|
0
|
|
5
|
20
|
5
|
25
|
5
|
25
|
0
|
|
6
|
20
|
5
|
29
|
5
|
29
|
0
|
|
7
|
20
|
5
|
33
|
5
|
33
|
0
|
|
8
|
20
|
5
|
37
|
5
|
37
|
0
|
Tablica 3. Optimalne vrijednosti funkcija \(f_1\),
\(f_2\) i \(f_3\)
Optimalna
vrijednost funkcije f3 jednaka je 37 i postiže se za c
= 8, što znači da se optimalna ukupna neto-dobit ostvaruje ulaganjem cjelokupnoga
raspoloživog kapitala od 8 n.j. Odredimo pripadne optimalne iznose ulaganja u
svaki odjel.
Vrijednost
f3(8) = 37 postiže se kao zbroj 0 + 37, odnosno kao zbroj 0 +
f2(8), tj. kao zbroj 2 × ×
0 + f2(8 – 0). Odatle ''očitavamo'' da je optimalna
vrijednost varijable x3 jednaka \(x_3^*\) = 0, pa zaključujemo da u treći
odjel ne ulažemo ništa.
Vrijednost
f2(8) = 37 postiže se kao zbroj 25 + 12, odnosno kao zbroj 25
+ f_1(3), tj. kao zbroj 5 × 5 + f_1(8 – 5). Odatle
''očitavamo'' da je optimalna vrijednost varijable x2 jednaka
\(x_2^*\) = 5, pa u drugi odjel ulažemo
ukupno 5 n.j.
Vrijednost
\(f_1(3) = 12\) postiže se kao umnožak 4 × 3, pa je
optimalna vrijednost varijable x1 jednaka \(x_1^*\) = 3, stoga u prvi odjel ulažemo
ukupno 3 n.j.
Dobiveni
optimalan plan ulaganja možemo pregledno prikazati sljedećom tablicom:
|
odjel
|
optimalan
iznos ulaganja
[n.j.]
|
|
1
|
3
|
|
2
|
5
|
|
3
|
0
|
Tablica 4. Optimalan plan ulaganja – rješenje
Primjera 1
Pripadna
optimalna neto-dobit iznosi 37 n.j.
Rješenje s pomoću programa WinQSB: Program WinQSB
ne sadržava potprogram namijenjen rješavanju problema optimalne razdiobe
ulaganja, ali sadržava potprogram Dynamic Programming (u daljnjem tekstu
DP) namijenjen, među ostalim, rješavanju problema naprtnjače (ruksaka).
Unutar njega ne postoje druge aplikacije pogodne za rješavanje promatranog problema.
Ako je problem linearan, može se primijeniti potprogram Linear and Integer
Programming, ali uz znatne restrikcije ulaznih podataka.
Prije
nego što opišemo rješenje s pomoću programa WinQSB, ukratko ćemo navesti
osnovna obilježja problema naprtnjače.
Problem
naprtnjače
(engl. the knapsack problem) česta je tema na području primijenjene
matematike, financijske alokacije sredstava, kombinatorike i kriptografije.
Naziv problema proizlazi iz narodne predaje: kako lopov s naprtnjačom određenog
obujma može ukrasti predmete što veće vrijednosti[5], a da
pritom obujam ukradenih predmeta ne premaši obujam naprtnjače? Prvi pisani
tragovi o problemu datiraju iz 1897. godine, a u posljednjih nekoliko
desetljeća jednako se intenzivno proučavaju i teorija i praktična primjena.
Razlog tomu je modeliranje mnogih industrijskih, financijskih i kriptografskih
problema preko problema naprtnjače, poput kapitalnog budžetiranja, ukrcavanja
tereta, smanjivanja zaliha, izrade portfolija, kriptosustava itd.
Postoje tri osnovne
podjele problema naprtnjače. Prva razlikuje slučajeve u kojima postoji jedna
naprtnjača (single knapsack problem) od onih u kojima postoji više njih
(multiple knapsack problem). Sljedeća podjela odnosi se na „djeljivost“
predmeta. U cjelobrojnom problemu naprtnjače predmeti su „nedjeljivi“,
tj. ne možemo uzeti manji dio niti jednog predmeta, već samo predmet u cjelini.
U djeljivom problemu naprtnjače predmeti se mogu razdijeliti na manje
dijelove. U trećoj podjeli ograničen problem naprtnjače ograničava količinu
svakog predmeta s nekom cjelobrojnom vrijednosti, dok neograničen problem
naprtnjače ne postavlja nikakvu gornju granicu na broj komada pojedine
vrste predmeta.
S obzirom na vrstu
problema naprtnjače, može se primijeniti nekoliko različitih algoritama za
rješavanje: pohlepni algoritam (engl. greedy algorithm), granice
i grananje (engl. branch-and-bound), linearno programiranje,
dinamičko programiranje i drugi. U programu WinQSB za rješavanje
problema primjenjuje se dinamičko programiranje.
Tipičan
problem naprtnjače je sljedeći:
Problem 1. Putnik ima
naprtnjaču čija je najveća dopuštena nosivost M kg. Na odabir mu je
ponuđeno ukupno n vrsta namirnica: N1… Nn,
pri čemu su sve namirnice međusobno ravnopravne. Za svaki i \in [n] neka su vi
i mi redom vrijednost[6]
i masa namirnice Ni. Kako putnik treba napuniti naprtnjaču
namirnicama tako da ukupna masa svih namirnica stavljenih u naprtnjaču ne bude
veća od M kg i da ukupna vrijednost tih namirnica bude što veća?[7]
Za
svaki \(i \in [n] \)
definiramo varijable \(x_i\) s:
\[{x_i} = \left\{ \begin{gathered}
0,{\text{ ako namirnicu }}{N_i}{\text{ ne stavljamo u naprtnjaču;}} \\
1,{\text{ ako namirnicu }}{N_i}{\text{ stavljamo u naprtnjaču.}} \\
\end{gathered} \right.\]
Promatrani
problem možemo opisati sljedećim matematičkim modelom:
maksimizirati \(f({x_1},...,{x_n})
= \sum\limits_{i = 1}^n {{w_i} \cdot {x_i}} \)
pod
uvjetima
\[\begin{gathered} \sum\limits_{i = 1}^n {{a_i}
\cdot {x_i} \leqslant M,} \\ {x_i} \in \left\{ {0,1} \right\}{\text{,
za svaki }}i \in \left[ n \right] \end{gathered} \]
Ova
najčešća i najpoznatija formulacija ograničenog cjelobrojnog problema
naprtnjače poznata je kao 0 - 1 problem naprtnjače. Izraz „0-1“ potječe
od interpretacije varijabli xi: svaki predmet ili se uzima u
cijelosti ili se uopće ne uzima.
S
obzirom na to da imamo n vrsta namirnica, postoji ukupno \(2^n\) različitih mogućnosti
odabira. Jedan od načina određivanja optimalne mogućnosti je ispitivanje svih
kombinacija. Za to bi nam trebalo \(O({2^n})\) operacija, što najčešće nije najbolje
moguće vrijeme. Uz korištenje dinamičkog programiranja, rješavanje promatranoga
problema može se svesti na pseudopolinomijalno (u ovisnosti o \(C_0\)).
Problem
iz Primjera 1 možemo ''prevesti'' na sljedeći zatvoreni problem
naprtnjače:
Na
raspolaganju nam je po 5 komada svake od triju vrsta namirnica: N1,
N2 i N3 te naprtnjača kapaciteta 8
kg. Podaci o jediničnoj cijeni i jediničnoj masi svake namirnice navedeni su
u donjoj tablici.
|
namirnica
|
jedinična
cijena
[n.j.]
|
jedinična masa
[kg]
|
|
N1
|
4
|
1
|
|
N2
|
5
|
1
|
|
N3
|
2
|
1
|
Tablica 5. Ulazni podaci za zatvoreni problem
naprtnjače
Treba
odabrati namirnice što veće ukupne vrijednosti tako da njihova ukupna masa ne
bude veća od kapaciteta naprtnjače. Formirajmo odgovarajući matematički model, pa odredimo
optimalan izbor namirnica i pripadnu optimalnu ukupnu vrijednost.
Ovako
definiran problem ima isti matematički model kao i polazni problem, ali
s drugačijim interpretacijama varijabli, funkcije cilja i uvjeta. Takvi
se problemi uobičajeno nazivaju izomorfnima: njihovi matematički modeli
su jednaki do na interpretacije ulaznih i
izlaznih varijabli[8]
te se rješavaju istim metodama/algoritmima.
Pokretanjem
potprograma DP odaberimo tip Knapsack Problem (vidjeti Sliku 1).
Slika 1. Dijaloški okvir potprograma DP
Nazovimo
problem koji ćemo rješavati Primjer 1, tj. upišimo:
Problem
Title:
Primjer 1
Number
of Items:
3
Potom
kliknimo na OK. U sljedećem koraku unosimo ulazne podatke (vidjeti Sliku
2).
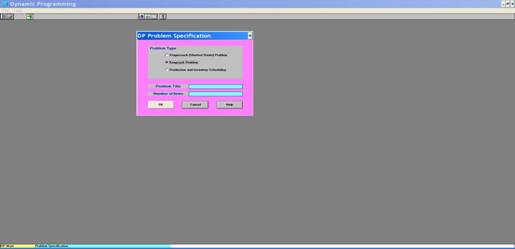
Slika 2. Unos ulaznih podataka
U
drugi stupac (Item Identification) upišimo redom O1, O2 i O3 jer će nam
takve oznake na kraju ''otkriti'' svotu uloženu u svaki pojedini odjel.
U
treći stupac (Units Available) upisujemo najveći mogući iznos koji može
biti uložen u svaki pojedini odjel. Ti iznosi su jednaki 5, pa upisujemo: 5, 5,
5.
U
četvrti stupac (Unit Capacity Required) treba upisati koeficijente uz
nepoznanice x1, x2 i x3 u
uvjetu x1 + x2 + x3 £ 8. Oni su
jednaki 1, pa u četvrti stupac upišimo: 1, 1, 1. Istaknimo odmah da su prigodom
modeliranja problema jednostavne razdiobe ulaganja koeficijenti u ovom stupcu uvijek
jednaki 1, dok kod problema složene razdiobe ulaganja (obrađenoga u točki 1.4.)
ti koeficijenti općenito mogu biti i nenegativni realni brojevi različiti od 1.
U
peti stupac (Return Function (X: Item ID)) upišimo redom
komponente funkcije cilja koje se odnose na odjel iz pripadnoga retka. Tako u
prvi redak toga stupca upišimo 4*X, u drugi 5*X, a u treći 2*X.
U
posljednji redak pored natpisa Capacity= upišimo ukupan iznos
kapitala, tj. 8.
Ovime
je unos ulaznih podataka završen. Kliknimo lijevom tipkom miša na izbornik Solve
and Analyze i odaberimo opciju Solve the Problem. Dobivamo izlaznu
tablicu sa svim potrebnim rezultatima (vidjeti Sliku 3).
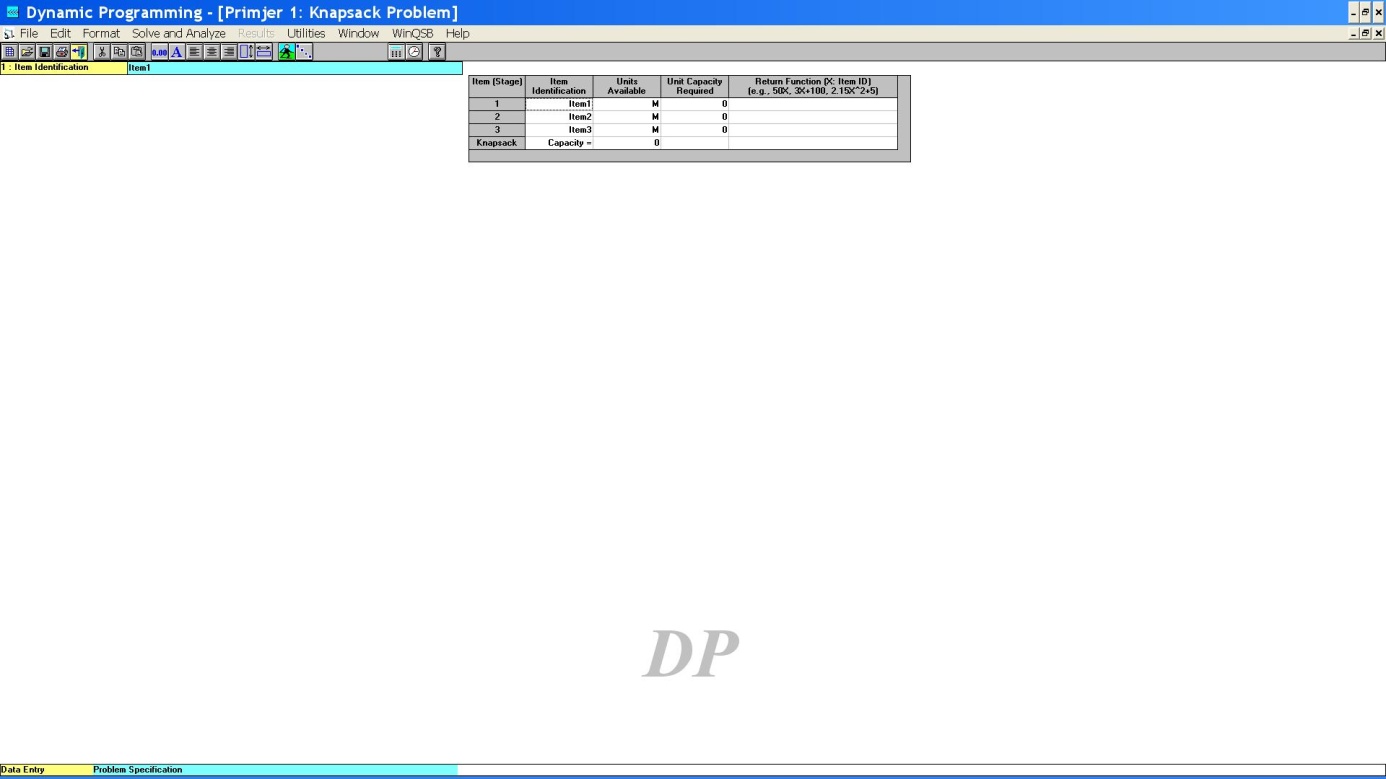
Slika 3. Izlazna tablica u Primjeru 1
Iz
trećega stupca (Decision Quantity (X)) očitavamo optimalan iznos
ulaganja u svaki pojedini odjel: u prvi odjel (O1) treba
uložiti 3 n.j., u drugi odjel (O2) 5 n.j., dok se u treći
odjel (O3) ne ulaže ništa. Optimalnu neto-dobit očitavamo iz
posljednjega retka (Total Return Value) i ona iznosi 37. n.j.
Na
navedenom primjeru može se vidjeti i razlog naziva jednostavna razdioba
ulaganja. Cjelokupni kapital dijeli se na međusobno ravnopravne
dijelove, tj. na početku nemamo razloga preferirati bilo koji odjel tvrtke.
Zbog toga se u uvjetu koji označava da zbroj svih uloženih iznosa mora biti
najviše jednak predviđenom kapitalu uz nepoznanice koje označavaju uložene
iznose kao koeficijenti pojavljuju jedinice. U gospodarskoj su praksi, međutim,
mogući i slučajevi kad se na početku, prema nekom kriteriju, rangiraju
ulaganja, pa se u takvim slučajevima govori o složenoj razdiobi ulaganja
u kojoj se pojavljuju tzv. težinski koeficijenti. O time se više može
naći npr. u [6].
Primjer 2. Problem optimalnog ulaganja
kapitala u razvoj određene regije ili određene gospodarske grane može se
definirati na sljedeći način: Za ostvarivanje bržega razvoja određene
gospodarske grane predviđen je kapital u iznosu od C0 n.j.
Taj kapital može se uložiti u ukupno n različitih tvrtki iz navedene
gospodarske grane. Ovisno o uloženom kapitalu, svaka pojedina tvrtka ostvarit
će dodatnu neto-dobit (razliku ukupne neto-dobiti i uloženoga kapitala). Treba
naći razdiobu raspoloživoga kapitala na navedene tvrtke tako da ukupna dodatna neto-dobit
(tj. zbroj dodatnih neto-dobiti svih n tvrtki) bude maksimalna.
Konkretno,
za ostvarivanje bržega razvoja određene gospodarske grane predviđen je kapital
u iznosu od C0 = 4.000.000,00 kn. Taj se kapital ulaže u
ukupno tri tvrtke − T1,
T2 i T3 − pri čemu se u svaku tvrtku ili
ne ulaže ništa ili se ulaže iznos koji je višekratnik broja 1.000.000 (nije
nužno uložiti sav predviđeni kapital). Očekivana dodatna neto-dobit koju će
ostvariti svaka tvrtka navedena je u sljedećoj tablici.
|
iznos ulaganja
(milijuna kn)
|
očekivana
dodatna neto-dobit tvrtke (milijuna kn)
|
|
T1
|
T2
|
T3
|
|
0
|
0
|
0
|
0
|
|
1
|
0.3
|
0.29
|
0.31
|
|
2
|
0.47
|
0.45
|
0.46
|
|
3
|
0.7
|
0.67
|
0.74
|
|
4
|
0.83
|
0.82
|
0.8
|
Tablica 6. Ulazni podaci za Primjer 2
a)
Odredimo
opći matematički model promatranoga problema uz pretpostavku da svi iznosi
ulaganja nužno moraju biti cjelobrojni (moguće je da se u neku tvrtku ne uloži
ništa).
b) Za konkretni
slučaj nađimo optimalnu razdiobu predviđenoga kapitala.
Opći matematički model: Za svaki
\(i\in [n] \)
označimo s xi iznos ulaganja u tvrtku Ti, a
fi(xi) pripadnu očekivanu dodatnu neto-dobit
[9]. Tada je ukupna očekivana dodatna neto-dobit od ulaganja u svih n tvrtki jednaka
f(x1, x2…
xn) = f1(x1) + f2(x2)
+… + fn(xn) = \(\sum\limits_{i = 1}^n {{f_i}({x_i})} \)
pa
zahtijevamo da vrijednost te funkcije bude maksimalna. Pogledajmo pripadne
uvjete uz koje tražimo maksimalnu vrijednost. Zbroj svih ulaganja ne smije biti
strogo veći od ukupnoga iznosa raspoloživoga kapitala C0, pa
mora vrijediti nejednakost
tj.
\( \sum\limits_{i = 1}^n
{{x_i}}\le C_0\).
Iznos
svakog ulaganja nužno mora biti cjelobrojan, a prema prirodi problema on mora
biti i nenegativan i najviše jednak C0. Zbog toga mora
vrijediti:
xi \in [C0]0,
za svaki \(i \in [n]\).
Prema
tome, traženi matematički model je:
maksimizirati f(x1, x2…
xn) = \(\sum\limits_{i = 1}^n
{{f_i}({x_i})} \)
pod
uvjetima
\(\sum\limits_{i = 1}^n {{x_i}} \le C_0\)
\(x_i \in \) [C0]0,
za svaki \(i \in [n]\).
b) U konkretnom su
slučaju n = 3 i C0 = 4.[10]
Odgovarajući matematički model je:
maksimizirati f(x1, x2,
x3) = f1(x1) + f2(x2)
+ f3(x3)
pod
uvjetima
\(x_i \in [4]_0 \),
za svaki \(i \in [3]\).
Stavimo
C := [4]0. Intuitivno možemo naslutiti da će se optimalna
vrijednost postići bude li uloženi iznos jednak C0. Problem
ćemo riješiti u ukupno tri faze.
U
prvoj fazi definirajmo realnu funkciju \(d_1:C\to \mathbb{R}\)
d1(c) = \(f_1\)(c).
d1(c) je
zapravo optimalna očekivana dodatna neto-dobit ako se ukupan iznos od c
milijuna kuna uloži isključivo u tvrtku T1. Ti iznosi već su
zadani u Tablici 6, pa ih pregledno prepišimo u sljedeću tablicu:
|
c
|
d1(c)
|
\(x_1^*\)
|
|
0
|
0
|
0
|
|
1
|
0.3
|
1
|
|
2
|
0.47
|
2
|
|
3
|
0.7
|
3
|
|
4
|
0.83
|
4
|
Tablica 7. Rezultati prve faze rješenja Primjera 2
Vrijednost
\(x_1^*\) označava optimalno ulaganje u
tvrtku T1 uz koju se postiže optimalna očekivana dodatna neto-dobit
d1(c). U ovom slučaju za svaki \(c\in C\)
vrijedi jednakost \(x_1^* = c\), ali, kako
smo vidjeli u Primjeru 1, u prvoj fazi ta jednakost općenito ne mora vrijediti.
U
drugoj fazi definirajmo realnu funkciju \(d_2:C\to \mathbb{R}\) s:
d2(c) =\( \max\limits_{\begin{subarray}{l} 0
\leqslant {x_2} \leqslant c \\ {x_2} \in C \end{subarray}} \left[
{{f_2}({x_2}) + {d_1}(c - {x_2})} \right]\).
d2(c) je
zapravo optimalna očekivana dodatna neto-dobit ako se ukupan iznos od c
milijuna kuna uloži samo u tvrtke T1 i T2.
Uloži li se iznos od x2 milijuna kuna u tvrtku T2,
očekivana dodatna neto-dobit tvrtke T2 iznosit će f2(x2).
Preostali iznos od c – x2 milijuna kuna ulaže se u
tvrtku T1, a prema definiciji funkcije d1, optimalna
očekivana dodatna neto-dobit nastala tim ulaganjem jednaka je d1(c
– x2). Zbroj tih dviju očekivanih dodatnih neto-dobiti treba
maksimizirati, pa odatle slijedi izraz iz definicije funkcije d2.
Detaljno
prikazujemo izračun vrijednosti d2(4):
\[ d_2(4)= \max_{\begin{subarray}{l} 0
\leqslant {x_2} \leqslant 4 \\ x_2 \in C \end{subarray}} \left[
{{f_2}({x_2}) + {d_1}(4 - {x_2})} \right]= \max_{x_2 \in C}
\left[ {{f_2}({x_2}) + {d_1}(4 - {x_2})} \right]=\] max{f2(0)
+ d1(4 – 0), f2(1) + + d1(4
– 1), f2(2) + d1(4 – 2), f2(3)
+ d1(4 – 3), f2(4) + d1(4
– 4)} = max{0 + 0.83, 0.29 + 0.7, 0.45 + 0.47, 0.67 + 0.3, 0.82 + 0} = 0.99.
Radi
potpunosti razmatranja, u sljedećoj tablici navodimo i vrijednosti funkcije d2
za preostale vrijednosti varijable c:
|
c
|
d1(c)
|
\(x_1^*\)
|
d2(c)
|
\(x_2^*\)
|
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0.3
|
1
|
0.3
|
0
|
|
2
|
0.47
|
2
|
0.59
|
1
|
|
3
|
0.7
|
3
|
0.76
|
1
|
|
4
|
0.83
|
4
|
0.99
|
1
|
Tablica 8. Rezultati prvih dviju faza rješenja
Primjera 2
Vrijednost
\(x_2^*\) označava optimalno ulaganje u
tvrtku T2 uz koju se postiže optimalna očekivana dodatna neto-dobit
d2(c). To optimalno ulaganje ''očitava'' se iz
postupka izračuna vrijednosti funkcije d2. Npr. d2(4)
= 0.99 dobiva se kao zbroj 0.29 + 0.7, tj. kao zbroj f2(1) +
d1(4 – 1). Odatle slijedi
\(x_2^* =
1\)
(i, naravno, \(x_1^* = 4 - x_2^* = 4 - 1 = 3\)) .
U
trećoj fazi definirajmo realnu funkciju \(d_3\to \mathbb{R}\) s
d3(c) =\( \max\limits_{\begin{subarray}{l} 0
\leqslant {x_3} \leqslant c \\ {x_3} \in C \end{subarray}} \left[
{{f_3}({x_3}) + {d_2}(c - {x_3})} \right]\).
d3(c) je
zapravo optimalna očekivana dodatna neto-dobit ako se ukupan iznos od c
milijuna kuna uloži u sve tri tvrtke. Uloži li se iznos od x3
milijuna kuna u tvrtku T3, očekivana dodatna neto-dobit
tvrtke T3 iznosit će f3(c).
Preostali iznos od c – x3 milijuna kuna ulaže se u
tvrtke T1 i T2, a prema definiciji funkcije
d2, optimalna očekivana dodatna neto-dobit nastala tim
ulaganjem jednaka je d2(c – x3).
Zbroj tih dviju očekivanih dodatnih neto-dobiti treba maksimizirati, pa odatle
slijedi izraz iz definicije funkcije d3.
Detaljno
prikazujemo izračun vrijednosti d3(4):
\[ d_3(4) = \max_{\begin{subarray}{l} 0
\leqslant {x_3} \leqslant 4 \\ {x_3} \in C \end{subarray}} \left[
{{f_3}({x_3}) + {d_2}(4 - {x_3})} \right] = \max_{\begin{subarray}{l} 0
\leqslant {x_3} \leqslant 4 \\ {x_3} \in C \end{subarray}} \left[
{{f_3}({x_3}) + {d_2}(4 - {x_3})} \right]= \] max{f3(0)
+ d2(4 – 0), f3(1) + d2(4
– 1), f3(2) + d2(4 – 2), f3(3)
+ d2(4 – 3), f3(4) + d2(4
– 4)} = max{0 + 0.99, 0.31 + 0.76, 0.46 + 0.59, 0.74 + 0.3, 0.8 + 0} = 1.07.
Radi
potpunosti razmatranja, u sljedećoj tablici navodimo i vrijednosti funkcije d3
za preostale vrijednosti varijable c:
|
c
|
d1(c)
|
\(x_1^*\)
|
d2(c)
|
\(x_2^*\)
|
d3(c)
|
\(x_3^*\)
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0.3
|
1
|
0.3
|
0
|
0.31
|
1
|
|
2
|
0.47
|
2
|
0.59
|
1
|
0.61
|
1
|
|
3
|
0.7
|
3
|
0.76
|
1
|
0.90
|
1
|
|
4
|
0.83
|
4
|
0.99
|
1
|
1.07
|
1
|
Tablica 9. Rezultati svih triju faza rješenja
Primjera 2
Iz
Tablice 9 vidimo da se najveća vrijednost funkcije d3, kako
smo i očekivali, postiže za c = 4. Dakle, treba uložiti sav predviđeni
kapital od 4.000.000,00 kn. Pripadni optimalni plan ulaganja ''očitava'' se iz
postupaka izračuna vrijednosti funkcija d1, d2
i d3 na sljedeći način:
Optimalna
vrijednost d3(4) = 1.07 dobiva se kao zbroj 0.31 + 0.76, tj.
kao zbroj f3(1) + d2(4 – 1). Odatle slijedi \(x_3^* = 1\). Optimalna vrijednost d2(4
– 1) = d2(3) = 0.76 dobiva se kao zbroj 0.29 + 0.47, tj. kao
zbroj f2(1) + d1(3 – 1). Odatle slijedi \(x_2^* = 1\) i \(x_1^*
= 3 - 1 = 2\). Tražena optimalna razdioba kapitala navedena je u Tablici
10.
|
Tvrtka
|
optimalan
iznos ulaganja
(milijuna kn)
|
|
T1
|
2
|
|
T2
|
1
|
|
T3
|
1
|
Tablica 10. Rješenje Primjera 2
Pripadna
optimalna očekivana dodatna neto-dobit iznosi 1.070.000,00 kn.
Kako
je istaknuto u uvodu, na problem optimizacije jednostavne razdiobe ulaganja
mogu se svesti različiti problemi minimizacije ukupnih troškova proizvodnje
nekoga proizvoda. Pokažimo to na primjerima.
Primjer 3. Tijekom tri mjeseca treba
proizvesti točno 12 komada nekoga proizvoda, pri čemu je najveći mogući
kapacitet proizvodnje 6 komada proizvoda mjesečno (moguće je da se u nekom
mjesecu ne proizvede niti jedan proizvod). Troškovi proizvodnje upravno su razmjerni kvadratima broja proizvedenih
proizvoda, te za svaki \( i \in [3]\) vrijedi: ako se u i–tom mjesecu
proizvede xi komada proizvoda, troškovi proizvodnje iznose wi
× \(x_i^2\) n.j., gdje su wi
strogo pozitivni realni parametri. Treba odrediti plan proizvodnje takav da
ukupni troškovi proizvodnje budu minimalni.
a) Odredimo opći
matematički model promatranoga problema.
b) Riješimo
problem za konkretne vrijednosti: w1 = 10, w2
= 24 i w3 = 32.
Matematički model: U postavci problema
već je naznačeno da s xi označavamo količinu (broj komada)
proizvoda proizvedenu u i–tom mjesecu. Ukupan zbroj svih količina mora
biti jednak 12, pa vrijedi jednakost:
x1 + x2
+ x3 = 12.
Troškovi
proizvodnje u prvom mjesecu su \(w_1\cdot x_1^2\), troškovi
proizvodnje u drugom mjesecu \(w_2\cdot x_2^2\), a troškovi
proizvodnje u trećem mjesecu \(w_3\cdot x_3^2\). Stoga ukupni
troškovi proizvodnje u navedena tri mjeseca iznose
f(x1, x2,
x3) = \( w_1\cdot x_1^2 + w_2\cdot x_2^2+ w_3\cdot x_3^2\).
Nadalje,
iz tipa promatranoga problema slijedi da vrijednosti varijabli xi
nužno moraju biti elementi skupa N0. Također, te vrijednosti
ne smiju biti strogo veće od 6 jer je najveći mogući kapacitet proizvodnje
jednak 6. Prema tome, matematički model promatranoga problema
glasi:
minimizirati f(x1, x2,
x3) = \( w_1\cdot x_1^2 + w_2\cdot x_2^2+ w_3\cdot x_3^2\)
pod
uvjetima
x1 + x2
+ x3 = 12,
\( x_1,x_2,x_3 \in [6]_0\).
Analitičko rješenje: Za w1
= 10, w2 = 24 i w3 = 32 dobivamo sljedeći
problem:
minimizirati f(x1, x2,
x3) = \( 10\cdot x_1^2 + 24\cdot x_2^2+ 32\cdot x_3^2\)
pod uvjetima
x1 + x2
+ x3 = 12,
\(x_1,x_2,x_3 \in [6]_0\).
I
ovdje bismo mogli razmišljati ''pohlepno'', tj. da u prvom mjesecu treba
proizvesti točno 6 komada proizvoda (jer su najmanji troškovi proizvodnje
upravo u tom mjesecu), a u drugom preostalih 6 (jer su troškovi proizvodnje u
drugom mjesecu manji nego u trećem). Stoga bi traženi plan mogao biti \(x_1^*\) = \(x_2^*\)
= 6, \(x_3^*\)= 0, a minimalni troškovi f(6,
6, 0) = 10 × 62 +
24 × 62 +
32 × 02 =
1224 n.j. Pokazat ćemo, međutim, da ovakav ''pohlepni'' pristup u ovom slučaju
ne daje optimalno rješenje.
Analogno
prethodnim primjerima, stavimo C := [12]0. Primijetimo da u
ovom primjeru unaprijed znamo točan ukupan broj komada proizvoda koje treba
proizvesti (to je 12), ali, radi ilustriranja tehnike dinamičkoga
programiranja, u svakoj ćemo fazi rješavanja problema izračunavati 13
odgovarajućih vrijednosti.
U
prvoj fazi za svaki \(c\in C\) računamo vrijednosti realne funkcije \(f_1:C\to \mathbb{R}\)
definirane s:
\(f_1(c)=10\cdot c^2 \).
Vrijednosti
funkcije \(f_1\) su optimalni troškovi proizvodnje ako se u
prvom mjesecu proizvede točno c komada proizvoda. Pritom za svaki \(c\in C\) takav
da je \(s\ge 7\) dogovorno
stavljamo da su troškovi proizvodnje beskonačni jer je najveći proizvodni
kapacitet, prema uvjetima zadatka, jednak 6. Tako dobivamo sljedeću tablicu:
|
c
|
\(f_1(c)\)
|
\(x_1^*\)
|
|
0
|
0
|
0
|
|
1
|
10
|
1
|
|
2
|
40
|
2
|
|
3
|
90
|
3
|
|
4
|
160
|
4
|
|
5
|
250
|
5
|
|
6
|
360
|
6
|
|
7
|
\(\infty\)
|
6
|
|
8
|
\(\infty\)
|
6
|
|
9
|
\(\infty\)
|
6
|
|
10
|
\(\infty\)
|
6
|
|
11
|
\(\infty\)
|
6
|
|
12
|
\(\infty\)
|
6
|
Tablica 11. Rezultati prve faze rješenja Primjera 3
Vrijednost
\(x_1^*\) označava optimalnu proizvodnju u
prvom mjesecu za koju se postiže pripadna optimalna vrijednost \(f_1(c)\).
Pritom smo u retcima u kojima je \(f_1(c) = \infty\) dogovorno pisali \(x_1^*\) = 6 zbog već istaknute činjenice da je
najveći mjesečni proizvodni kapacitet jednak 6.
U
drugoj fazi računamo vrijednosti realne funkcije \(f_2:C\to\mathbb{R}\)
definirane s:
U
ovoj fazi pretpostavljamo da se ukupno c komada proizvoda mora
proizvesti u prva dva mjeseca. Ako se u drugom mjesecu proizvede x2
proizvoda, u prvom se mora proizvesti ukupno c – x2
proizvoda. Troškovi proizvodnje u drugom mjesecu iznose 24 × \(x_2^2\) n.j., dok optimalni troškovi
proizvodnje u prvom mjesecu, prema definiciji funkcije \(f_1\),
iznose \(f_1(c-x_2)\) n.j. Zbroj tih
troškova jednak je ukupnim troškovima proizvodnje u prva dva mjeseca, pa taj
zbroj treba minimizirati imajući na umu uvjete da vrijednost varijable x2
mora biti cjelobrojna, ne veća od ukupne količine proizvoda koju treba
proizvesti i ne veća od najvećega mjesečnog kapaciteta proizvodnje. Odatle
slijedi izraz iz definicije funkcije f2.
Radi
ilustracije, izračunat ćemo f2(6) i f2(12),
pri čemu koristimo da vrijednosti \(f_1(7), f_1(8),\ldots,
f_1(12)\) ne postoje jer se niti u jednom mjesecu (pa posebno
niti u prvom mjesecu) ne može proizvesti strogo više od 6 komada proizvoda:
\[ f_2(6)= \min_{\begin{subarray}{l} 0
\leqslant x_2 \leqslant \min \left\{ 6,6 \right\} \\ x_2 \in \mathbb{Z}
\end{subarray}} \left[ {24 \cdot x_2^2 + {f_1}(6 - {x_2})} \right] =
\min_{0 \leqslant {x_2} \leqslant 6} \left[ {24 \cdot x_2^2 + {f_1}(6
- {x_2})} \right] = \] min {24 × 02 + f_1(6 – 0), 24 × 12 +
f_1(6 – 1), 24 × 22 + f_1(6 – 2), 24 × 32 +
f_1(6 – 3), 24 × 42 + f_1(6 – 4), 24 × 52 +
f_1(6 – 5), 24 × 62 + f_1(6 – 6)} = min
{0 + 360, 24 + 250, 96 + 160, 216 + 90, 384 + 40, 600 + 10, 864 + + 0} = 256;
\[ f_2(12) = \min_{\begin{subarray}{l} 0
\leqslant {x_2} \leqslant \min \left\{ {12,6} \right\} \\ {x_2} \in
\mathbb{Z} \end{subarray}} \left[ {24 \cdot x_2^2 + {f_1}(12 - {x_2})} \right]
= \min_{0 \leqslant {x_2} \leqslant 6} \left[ {24 \cdot x_2^2
+ {f_1}(12 - {x_2})} \right] = \] min {24 × 02 + f_1(12
– 0), 24 × 12 +
f_1(12 – 1), 24 × 22 + f_1(12 – 2), 24 × 32 +
f_1(12 – 3), 24 × 42 + f_1(12 – 4), 24 × 52 +
+ f_1(12 – 5), 24 × 62 + f_1(12 – 6)} =
min{24 × 62 +
f_1(6)} = 1224.
Izračunom
ostalih vrijednosti dobivamo sljedeću tablicu:
|
c
|
\(f_1(c)\)
|
\(x_1^*\)
|
f2(c)
|
\(x_2^*\)
|
|
0
|
0
|
0
|
0
|
0
|
|
1
|
10
|
1
|
10
|
0
|
|
2
|
40
|
2
|
34
|
1
|
|
3
|
90
|
3
|
64
|
1
|
|
4
|
160
|
4
|
114
|
1
|
|
5
|
250
|
5
|
184
|
1
|
|
6
|
360
|
6
|
256
|
2
|
|
7
|
\(\infty\)
|
6
|
346
|
2
|
|
8
|
\(\infty\)
|
6
|
456
|
2
|
|
9
|
\(\infty\)
|
6
|
576
|
3
|
|
10
|
\(\infty\)
|
6
|
744
|
4
|
|
11
|
\(\infty\)
|
6
|
960
|
5
|
|
12
|
\(\infty\)
|
6
|
1224
|
6
|
Tablica 12. Rezultati prve i druge faze rješenja
Primjera 3
Vrijednost
\(x_2^*\) označava optimalnu
proizvodnju u drugom mjesecu za koju se postiže pripadna optimalna vrijednost f2(c),
a može se ''očitati'' iz odgovarajućega izračuna vrijednosti f2(c).
Npr., f2(6) = 256 dobiva se kao zbroj 96 + 160, tj. kao 24 ·
22 + f1(6 – 2). Odatle slijedi \(x_2^*\) = 2 i \(x_1^*\) = 6 – 2 = 4.
U
trećoj fazi računamo vrijednosti realne funkcije \(f_3:C\to \mathbb{R}\)
definirane s :
f3(c) =\( \min\limits_{\begin{subarray}{l} 0
\leqslant {x_3} \leqslant \min \left\{ {c,6} \right\} \\ {x_3} \in \mathbb{Z}
\end{subarray}} \left[ {32 \cdot x_3^2 + {f_2}(c - {x_3})} \right]\).
U
ovoj fazi, pretpostavljamo, treba proizvesti ukupno c komada proizvoda u
sva tri mjeseca. Ako se u trećem mjesecu proizvede x3
proizvoda, u prva dva mjeseca treba proizvesti ukupno c – x3
proizvoda. Ukupni troškovi proizvodnje u trećem mjesecu iznose 32 × \(x_3^2\) n.j., dok optimalni troškovi
proizvodnje u prva dva mjeseca, u skladu s definicijom funkcije f2,
iznose f2(c – x3) n.j. Stoga ukupni
troškovi proizvodnje u sva tri mjeseca iznose 32 × \(x_3^2\)
+ f2(c – x3) n.j, pa taj zbroj treba
minimizirati imajući na umu početne uvjete na vrijednost varijable x3
(cijeli broj ne veći od ukupne količine proizvoda koju treba proizvesti i
najvećega mjesečnog kapaciteta proizvodnje). Radi ilustracije postupka
izračuna, detaljno prikazujemo izračun vrijednosti f3(6) i f3(12):
\[ f_3(6)= \min_{\begin{subarray}{l} 0
\leqslant {x_3} \leqslant \min \left\{ {6,6} \right\} \\ {x_3} \in \mathbb{Z}
\end{subarray}} \left[ {32 \cdot x_3^2 + {f_2}(6 - {x_3})} \right] =
\min_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant 6 \\ {x_3}
\in \mathbb{Z} \end{subarray}} \left[ {32 \cdot x_3^2 + {f_2}(6 - {x_3})}
\right] = \] min {32 ×
02 + f2(6 – 0), 32 × 12 + f2(6
– 1), 32 × 22 +
f2(6 – 2), 32 × 32 + f2(6 – 3), 32 × 42 +
f2(6 – 4), 32 × 52 + f2(6 – 5), 32 × 62 +
f2(6 – 6)} = min {256, 216, 242, 352, 546, 810, 1152} = 216;
\[ f_3(12)= \min_{\begin{subarray}{l} 0
\leqslant {x_3} \leqslant \min \left\{ {12,6} \right\} \\ {x_3} \in
\mathbb{Z} \end{subarray}} \left[ {32 \cdot x_3^2 + {f_2}(12 - {x_3})} \right]
= \min_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant 6
\\ {x_3} \in \mathbb{Z} \end{subarray}} \left[ {32 \cdot x_3^2 + {f_2}(12 -
{x_3})} \right] = \] min {32 × 02 + f2(12 – – 0), 32 × 12 +
f2(12 – 1), 32 × 22 + f2(12 – 2), 32 × 32 +
f2(12 – 3), 32 × 42 + f2(12 – 4), 32 × 52 +
+ f2(12 – 5), 32 × 62 + f2(12 – 6)} = min
{1224, 992, 872, 864, 968, 1146, 1408} = 864.
Izračunom
svih vrijednosti funkcije f3 dobivamo sljedeću tablicu:
|
c
|
\( f_1(c)\)
|
\(x_1^*\)
|
f2(c)
|
\(x_2^*\)
|
f3(c)
|
\(x_3^*\)
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
10
|
1
|
10
|
0
|
10
|
0
|
|
2
|
40
|
2
|
34
|
1
|
34
|
0
|
|
3
|
90
|
3
|
64
|
1
|
64
|
0
|
|
4
|
160
|
4
|
114
|
1
|
96
|
1
|
|
5
|
250
|
5
|
184
|
1
|
146
|
1
|
|
6
|
360
|
6
|
256
|
2
|
216
|
1
|
|
7
|
\(\infty\)
|
6
|
346
|
2
|
288
|
1
|
|
8
|
\(\infty\)
|
6
|
456
|
2
|
378
|
1
|
|
9
|
\(\infty\)
|
6
|
576
|
3
|
474
|
2
|
|
10
|
\(\infty\)
|
6
|
744
|
4
|
584
|
2
|
|
11
|
\(\infty\)
|
6
|
960
|
5
|
704
|
2
|
|
12
|
\(\infty\)
|
6
|
1224
|
6
|
864
|
3
|
Tablica 13. Rezultati svih triju faza rješenja
Primjera 3
Vrijednost
\(x_3^*\) označava optimalnu proizvodnju u
trećem mjesecu za koju se postiže pripadna optimalna vrijednost f3(c),
a ''očitava'' se iz odgovarajućeg izračuna vrijednosti funkcije f3.
Konkretno, za c = 12 minimalni ukupni troškovi proizvodnje iznose 864
n.j. Ti se troškovi dobiju kao zbroj 32 · 32 + f2(12
– 3), odnosno postižu se proizvodnjom točno \(x_3^*\)
= 3 komada proizvoda
u trećem mjesecu, te točno 12 – 3 = 9 proizvoda u prva dva mjeseca. Za c
= 9 odgovarajuća optimalna količina proizvodnje u drugom mjesecu je \(x_2^*\) = 3, pa u drugom mjesecu treba
proizvesti točno 3 proizvoda. Stoga u prvom mjesecu treba proizvesti točno \(x_1^*\) = 12 – (3 + 3) = 6 proizvoda.
Dakle,
traženi optimalni plan proizvodnje je:
|
Mjesec
|
optimalan broj
proizvoda
|
|
1.
|
6
|
|
2.
|
3
|
|
3.
|
3
|
Tablica 14. Rješenje Primjera 3
a
pripadni optimalni troškovi proizvodnje iznose f3(12) = 864
n.j.
Rješenje s pomoću programa WinQSB: U ovome ćemo
primjeru postupiti analogno Primjeru 1, ali uz jednu nužnu modifikaciju. Naime,
problem naprtnjače je maksimizacijski problem, tj. traži se
maksimizacija vrijednosti svih namirnica koje stavljamo u naprtnjaču. Stoga
potprogram DP pri rješavanju problema naprtnjače traži maksimum
funkcije cilja. No problem koji ovdje promatramo je minimizacijski
problem jer zahtijevamo minimizaciju ukupnih troškova. Na temelju standardne
veze između problema minimizacije i problema maksimizacije:
min f(x) = –max(–f(x)),
gdje
je f(x) funkcija cilja, polazni matematički model možemo zapisati
u obliku:
maksimizirati f(x1, x2,
x3) = –10 ×
\(x_1^2\) – 24 × \(x_2^2\) – 32 × \(x_3^2\)
pod
uvjetima
x1 + x2
+ x3 = 12,
\( x_1,x_2,x_3\in [6]_0 \).
Ovaj
problem možemo riješiti potpuno analogno kao i zatvoreni problem naprtnjače,
pri čemu modificiranu funkciju cilja npr. možemo shvatiti kao ukupne troškove
prijevoza svih vrsta namirnica (svaki negativni predznak uobičajeno ekonomski
interpretiramo kao trošak).
Pokrenimo
potprogram DP, odaberimo proceduru Knapsack Problem, nazovimo
problem koji ćemo rješavati Primjer 3 i, kao Number of Items
ponovno upišimo 3. Potom kliknimo na OK.
U
sljedećem koraku unesimo ulazne podatke.
U
drugi stupac (Item Identification) upišimo M1, M2 i M3. Te oznake sugerirat
će nam na koji se mjesec (prvi, drugi ili treći) odnosi odgovarajući rezultat.
U
treći stupac (Units Available) upišimo najveće moguće kapacitete
mjesečne proizvodnje. Sva tri kapaciteta su jednaka 6, pa u stupac unosimo tri
''šestice''.
U
četvrti stupac (Unit Capacity Required), kako smo već istaknuli u
rješenju Primjera 1, upisujemo tri ''jedinice''.
U
peti stupac (Return Function (X: Item ID)) upisujemo
pojedine komponente modificirane funkcije cilja, tj. funkcije cilja koja
se odnosi na odgovarajući problem maksimizacije. Upisujemo redom: –10*X^2,
-24*X^2 i -32*X^2.
U
posljednji redak tablice (Capacity =) upišimo ukupnu količinu proizvoda
koju treba proizvesti, tj. 12.
Time
je unos ulaznih podataka završen. Kliknimo na izbornik Solve and Analyze,
a potom na opciju Solve the Problem. Dobivamo tablicu u kojoj je
navedeno optimalno rješenje promatranoga problema.
To
optimalno rješenje očitavamo u trećem stupcu tablice (Decision Quantity).
Iz tog stupca proizlazi da u prvom mjesecu treba proizvesti 6 proizvoda, a u
drugom i trećem po 3 proizvoda. Ukupne minimalne troškove proizvodnje
''očitamo'' iz posljednjega retka (Total Return Value): ondje je naveden
broj –864. Negativan predznak, kako smo istaknuli, označava da je riječ o
troškovima, pa zaključujemo da su optimalni ukupni troškovi proizvodnje 864
n.j.
Primjer 4. Koristeći se programom WinQSB
analizirajmo što bi se dogodilo s optimalnim rješenjima Primjera 3 kada bi
najveći mjesečni kapacitet proizvodnje bio 6000 komada, a tromjesečna potražnja
12000 komada.[11].
Uzmemo
li kao mjernu jedinicu 1000 komada proizvoda, dobit ćemo sljedeći optimalan
plan:
|
mjesec
|
1.
|
2.
|
3.
|
|
optimalna
proizvodnja
[000 kom.]
|
6
|
3
|
3
|
Tablica 15. Prvi optimalan plan proizvodnje u
Primjeru 4
pri
čemu optimalni ukupni troškovi proizvodnje iznose 864 milijuna n.j. Taj se
optimalni plan dobije izravno iz gore navedenoga rješenja Primjera 3 uz nužno
redefiniranje odgovarajućih mjernih jedinica.
Uzmemo
li kao mjernu jedinicu 100 komada proizvoda, tj. da su mjesečni kapacitet
proizvodnje 60 [stotina komada proizvoda] i planirana tromjesečna potražnja 120
[stotina komada proizvoda], dobit ćemo sljedeći optimalan plan:
|
mjesec
|
1.
|
2.
|
3.
|
|
optimalna
proizvodnja
[stotina kom.]
|
60
|
34
|
26
|
Tablica 16. Drugi optimalan plan proizvodnje u
Primjeru 4
pri
čemu optimalni ukupni troškovi proizvodnje iznose 853 760 000 n.j. Dobiveni
optimalni plan očito se bitno razlikuje od plana navedenog u tablici 15.
Nadalje,
uzmemo li kao mjernu jedinicu 10 komada proizvoda, tj. da su mjesečni kapacitet
proizvodnje 600 [desetina komada proizvoda] i planirana tromjesečna potražnja
1200 [desetina komada proizvoda], dobit ćemo sljedeći optimalan plan:
|
mjesec
|
1.
|
2.
|
3.
|
|
optimalna
proizvodnja
[desetina kom.]
|
600
|
343
|
257
|
Tablica 17. Treći optimalan plan proizvodnje u
Primjeru 4
pri
čemu pripadni optimalni troškovi proizvodnje iznose 853 714 400 n.j. Isti
rezultat dobiva se ako se za mjernu jedinicu uzme 5 komada proizvoda. Izborom 1
komada proizvoda za mjernu jedinicu dobiva se poruka programa Subscript out
of range, tj. nemogućnost rješavanja problema. Stoga možemo zaključiti da
je optimalno rješenje \[(x_1^*,x_2^*,x_3^*) =
(6000,3430,2570)\] i da je u ovom slučaju za mjernu jedinicu proizvodnje
pogodno odabrati 10 komada proizvoda, a ne 1000 komada proizvoda, kako se
isprva čini.
Primjer 5. Tijekom jednoga mjeseca (4
tjedna) treba proizvesti točno 11 komada nekoga proizvoda. Troškovi proizvodnje
xi komada proizvoda u i–tom tjednu zadani su izrazom wi
×\(x_i^2\), gdje su wi
strogo pozitivni realni parametri. Tijekom jednoga tjedna moguće je proizvesti
najviše 5 komada proizvoda (moguće je da u jednom tjednu ne bude proizveden
niti jedan proizvod). Treba izraditi plan proizvodnje tako da ukupni troškovi
budu minimalni.
a)
Odredimo
matematički model promatranoga problema.
b) Riješimo model
za w1 = 12, w2 = 24, w3 =
40 i w4 = 30.
Matematički model: Ukupne
troškove proizvodnje računamo prema formuli
f (x1, x2,
x3, x4) =\(\sum\limits_{i
= 1}^4 {{w_i} \cdot x_i^2} \).
Ukupan
broj proizvedenih komada mora biti jednak 11, što znači da mora vrijediti
jednakost
\( \sum\limits_{i = 1}^4 {{x_i}} = 11\).
Budući
da se tijekom jednoga tjedna može proizvesti najviše 5 komada proizvoda i da
ukupan broj proizvedenih komada nužno mora biti prirodan broj ili nula, za
svaki \(i \in [4]\) vrijedi
uvjet \(x_i \in [5]_0\). Stoga odgovarajući matematički model glasi:
minimizirati f (x1, x2,
x3, x4) = \(\sum\limits_{i
= 1}^4 {{w_i} \cdot x_i^2} \)
pod
uvjetima
\(\sum\limits_{i =
1}^4 {{x_i}} = 11\);
\(x_i\in [5]_0\),
za svaki \(i \in [4]\).
b) U konkretnom je
slučaju matematički model sljedeći:
minimizirati f (x1, x2,
x3, x4) = \(12
\cdot x_1^2 + 24 \cdot x_2^2 + 40 \cdot x_3^2 + 30 \cdot x_4^2\)
pod
uvjetima
\(\sum\limits_{i =
1}^4 {{x_i}} = 11\);
\(x_i\in [5]_0\),
za svaki \(i \in [4]\).
Analitičko rješenje: Stavimo C
:= [11]0, pa za svaki \(c\in C\) računamo vrijednosti četiriju realnih
funkcija \(f_1,f_2,f_3,f_4:C\to \mathbb{R}\):[12]
f1(c) = 12 × c2;
f2(c) =\( \min\limits_{\begin{subarray}{l} 0
\leqslant {x_2} \leqslant \min \left\{ {c,5} \right\} \\ {x_2} \in \mathbb{Z}
\end{subarray}} \left[ {24 \cdot x_2^2 + {f_1}(c - {x_2})} \right]\);
f3(c) =\( \min\limits_{\begin{subarray}{l} 0
\leqslant {x_3} \leqslant \min \left\{ {c,5} \right\} \\ {x_3} \in \mathbb{Z}
\end{subarray}} \left[ {40 \cdot x_3^2 + {f_2}(c - {x_3})} \right]\);
f4(c) =\( \min\limits_{\begin{subarray}{l} 0
\leqslant {x_4} \leqslant \min \left\{ {c,5} \right\} \\ {x_4} \in \mathbb{Z}
\end{subarray}} \left[ {30 \cdot x_4^2 + {f_3}(c - {x_4})} \right]\).
Pri
izračunu vrijednosti ovih funkcija treba imati na umu da zbog polaznih uvjeta ne
postoje sljedeće vrijednosti:
-
\(f_1(6),f_1(7),\ldots,f_1(11) \) jer se u prvom (ali i bilo
kojem!) tjednu može proizvesti najviše 5 proizvoda;
-
f2(11) jer se u
prva (ali i bilo koja!) dva tjedna može proizvesti najviše 2 × 5 = 10
proizvoda.
Izračunom
svih vrijednosti definiranih realnih funkcija dobiva se sljedeća tablica:
|
c
|
\(f_1(c)\)
|
\(x_1^*\)
|
f2(c)
|
\(x_2^*\)
|
f3(c)
|
\(x_3^*\)
|
f4(c)
|
\(x_1^*\)
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
12
|
1
|
12
|
0
|
12
|
0
|
12
|
0
|
|
2
|
48
|
2
|
36
|
1
|
36
|
0
|
36
|
0
|
|
3
|
108
|
3
|
72
|
1
|
72
|
0
|
66
|
1
|
|
4
|
192
|
4
|
132
|
1
|
112
|
1
|
102
|
1
|
|
5
|
300
|
5
|
204
|
2
|
172
|
1
|
142
|
1
|
|
6
|
\(\infty\)
|
5
|
288
|
2
|
244
|
1
|
202
|
1
|
|
7
|
\(\infty\)
|
5
|
396
|
2
|
328
|
1
|
274
|
1
|
|
8
|
\(\infty\)
|
5
|
516
|
3
|
436
|
1
|
358
|
1
|
|
9
|
\(\infty\)
|
5
|
684
|
4
|
556
|
1, 2
|
448
|
2
|
|
10
|
\(\infty\)
|
5
|
900
|
5
|
676
|
2
|
556
|
2
|
|
11
|
\(\infty\)
|
5
|
\(\infty\)
|
5
|
844
|
2
|
676
|
2
|
Tablica 18. Rezultati svih četiriju faza rješenja
Primjera 5
(Zapis
1, 2 označava da se optimalna vrijednost odgovarajuće funkcije postiže za \(x_3^*\) = 1 i za \(x_3^*\) = 2).
Preostaje
''očitati'' rješenje postavljenoga problema. Optimalna vrijednost ukupnih
troškova proizvodnje 11 komada proizvoda jednaka je f4(11) =
676 n.j. Ta se vrijednost postiže za \(x_4^*\)
= 2, što znači da u četvrtom tjednu treba proizvesti točno dva proizvoda. Stoga
u prva tri tjedna treba proizvesti ukupno 11 – 2 = 9 proizvoda. Optimalni
troškovi proizvodnje točno 9 proizvoda u prva tri tjedna iznose f3(9)
= 556 n.j. i postižu se za \(x_3^*\) = 1 ili
\(x_3^*\) = 2. Zbog toga razlikujemo dvije
mogućnosti:
1)
U trećem tjednu proizvede se točno jedan proizvod (tj. \(x_3^*\) = 1). Tada u
prva dva tjedna treba proizvesti točno 9 – 1 = 8 proizvoda. Optimalni troškovi
proizvodnje 8 proizvoda u prva dva tjedna iznose f2(8) = 516
n.j. i postižu se za \(x_3^*\) = 3. Zbog toga u drugom tjednu
treba proizvesti točno 3 proizvoda, pa u prvom tjednu preostaje proizvesti
ukupno \(x_1^*\) = 8 – 3 = 5 proizvoda.
2)
U trećem tjednu proizvedu se točno dva proizvoda (tj. \(x_3^*\)= 2). Tada u prva dva tjedna treba
proizvesti točno 9 – 2 = 7 proizvoda. Optimalni troškovi proizvodnje 7
proizvoda u prva dva tjedna iznose f2(7) = 396 n.j. i postižu
se za \(x_2^*\) = 2. Stoga u drugom tjednu treba proizvesti
točno 2 proizvoda, pa u prvom tjednu preostaje proizvesti točno \(x_1^*\) = 7 – 2 = 5 proizvoda.
Tako
smo dobili ukupno dva optimalna plana proizvodnje:
Plan 1:
|
tjedan
|
1.
|
2.
|
3.
|
4.
|
|
optimalna
proizvodnja
[kom.]
|
5
|
3
|
1
|
2
|
Tablica 19. Prvi optimalan plan proizvodnje u
Primjeru 5
Plan 2:
|
tjedan
|
1.
|
2.
|
3.
|
4.
|
|
optimalna
proizvodnja
[kom.]
|
5
|
2
|
2
|
2
|
Tablica 20. Drugi optimalan plan proizvodnje u
Primjeru 5
Rješenje s pomoću programa WinQSB: Na ovom ćemo
primjeru uočiti jedan od glavnih nedostataka potprograma DP: nemogućnost
ispisa barem dvaju optimalnih rješenja (ako ona postoje, naravno). Naime,
potprogram će – kao izlazni rezultat – ispisati točno jedan optimalni plan i ne
postoji nikakva mogućnost da bilo kojom od implementiranih procedura dobijemo
ispis drugoga optimalnog plana.
Sâm
postupak rješavanja problema s pomoću programa WinQSB potpuno je
analogan onome iz prethodnoga primjera. Najprije problem minimizacije
''pretvorimo'' u problem maksimizacije:
maksimizirati f (x1, x2,
x3, x4) = \(
- 12 \cdot x_1^2 - 24 \cdot x_2^2 - 40 \cdot x_3^2 - 30 \cdot x_4^2\)
pod
uvjetima
x1 + x2
+ x3 + x4 = 11;
\( x_1,x_2,x_3,x_4 \in [5]_0 \).
Potom
pokrenemo potprogram DP, odaberemo proceduru Knapsack Problem,
nazovimo problem koji ćemo rješavati Primjer 5, a u pravokutnik
pored natpisa Number of Items upišimo 4. Potom kliknimo na OK.
Unesimo
ulazne podatke za razmatrani primjer na sljedeći način:
-
u
drugi stupac (Item Identification) upišimo: T1, T2, T3 i T4. Tako ćemo u
izlaznom rezultatu moći ''očitati'' opseg proizvodnje u svakom pojedinom
tjednu;
-
u
treći stupac (Units Available) upišimo maksimalne tjedne kapacitete
proizvodnje: oni su jednaki 5, pa upišimo ukupno četiri ''petice'';
-
u
četvrti stupac (Unit Capacity Required) upišimo onoliko ''jedinica''
koliko imamo tjedana: dakle, upišimo četiri ''jedinice'';
-
u
peti stupac (Return Function (X: Item ID)) upišimo
komponente modificirane funkcije cilja koje se odnose na svaki pojedini tjedan:
dakle, upišimo redom –12*X^2, –24*X^2, –40*X^2 i –30*X^2;
-
u
posljednji redak (Capacity=) upišimo ukupan broj komada proizvoda koje
treba proizvesti, tj. 11.
Ovime
je unos ulaznih podataka završen. Lijevom tipkom miša kliknimo na izbornik Solve
and Analyze i odaberimo opciju Solve the Problem. Kao rješenje
razmatranoga problema dobivamo samo Plan 2 iz analitičkoga rješenja,
tj. u prvom tjednu treba proizvesti 5 komada proizvoda, a u svakom od preostala
tri tjedna po dva komada proizvoda. Vrijednost Total Return Value = –676
znači da pripadni optimalni ukupni troškovi iznose 676 n.j.
Primjer 6. Analogno u Primjeru 4, koristeći
se računalnim programom WinQSB, analizirajmo što bi se dogodilo s optimalnim
rješenjima kada bi najveći tjedni kapacitet proizvodnje bio 5000 komada, a
mjesečna potražnja 11000 komada proizvoda.[13]
Uzmemo
li kao mjernu jedinicu 1000 komada, dobit ćemo sljedeći optimalan plan:
Plan 1*:
|
tjedan
|
1.
|
2.
|
3.
|
4.
|
|
optimalna
proizvodnja
[000 kom.]
|
5
|
2
|
2
|
2
|
Tablica 21. Prvi optimalan plan proizvodnje u
Primjeru 6
uz
pripadne optimalne troškove od 676 milijuna kuna. Primijetimo da je i plan
Plan 2*:
|
tjedan
|
1.
|
2.
|
3.
|
4.
|
|
optimalna
proizvodnja
[000 kom.]
|
5
|
3
|
1
|
2
|
Tablica 22. Drugi optimalan plan proizvodnje u
Primjeru 6
također
optimalan. Oba navedena plana mogu se dobiti izravno iz analitičkoga rješenja
Primjera 5 uz odgovarajuće redefiniranje mjernih jedinica, a drugi navedeni
plan (ponovno) nije moguće dobiti s pomoću programa WinQSB.
Uzmemo
li kao mjernu jedinicu 100 komada proizvoda, dobit ćemo sljedeći optimalan
plan:
Plan 1**:
|
tjedan
|
1.
|
2.
|
3.
|
4.
|
|
optimalna
proizvodnja [stotina
kom.]
|
50
|
25
|
15
|
20
|
Tablica 23. Treći optimalan plan proizvodnje u
Primjeru 6
Dakle,
u prvom tjednu treba proizvesti 5000 komada proizvoda, u drugom 2500 komada
proizvoda, u trećem 1500 komada proizvoda, a u četvrtom 2000 komada proizvoda
uz pripadne optimalne troškove od 660 milijuna n.j. Isti rezultat dobije se ako
se kao mjerne jedinice odaberu 10 komada proizvoda, odnosno 5 komada proizvoda.
Stoga je u ovom slučaju za mjernu jedinicu proizvodnje pogodno odabrati 100
komada proizvoda.
Zanimljivo
je primijetiti da je Plan 1**, grubo govoreći, aritmetička
sredina Planova 1* i 2*. Preciznije, optimalna proizvodnja
u i–tom tjednu prema Planu 1** je aritmetička sredina
optimalnih planova proizvodnje u istom tjednu dobivenih prema Planu 1*
i Planu 2*.
Zaključno
istaknimo da postoje još neki ekonomski problemi koji se mogu svesti na problem
jednostavne razdiobe ulaganja, ali ih zbog opsežnosti članka ovdje nismo
razmatrali. Čitatelje zainteresirane za daljnje primjene upućujemo na
literaturu [1] ili [5].
LITERATURA:
1. M.J. Beckmann: Dynamic
Programming of Economic Decisions, Springer–Verlag, New York, 1968
2. R. Bellman: Dynamic
Programming, Dover Publications, 2003
3. D. Kalpić, V.
Mornar: Operacijska istraživanja, ZEUS, Zagreb, 1996.
4. L. Neralić: Uvod
u matematičko programiranje 1, Element, Zagreb, 2003.
5. J. Petrić: Operaciona
istraživanja, Nauka, Beograd, 1997.
6. J. Petrić
et.al.: Operaciona istraživanja – zbirka rešenih zadataka, Nauka,
Beograd, 1996.
7.
H. Kellerer, U. Pferschy, D. Pisinger: Knapsack
Problems, Springer, 2004
8.
S. Martello, P. Toth: Knapsack Problems,
Wiley, 1990
[2] Iz navedenih razloga
u takvim slučajevima govorimo o cjelobrojnom programiranju.
[3] Navedeno svojstvo
programa WinQSB je, zapravo, njegova osnovna manjkavost jer smo,
prigodom rješavanja problema u kojima je relativna većina svih numeričkih
vrijednosti strogo veća od 500, zapravo prisiljeni na redefiniranje pripadnih
mjernih jedinica.
[4] Skraćenica za: novčanih
jedinica. U danom primjeru, taj iznos može biti višekratnik nekog elementa
iz skupa {1, 100, 1.000, 1.000.000 ... }.
[5] Vrijednost
predmeta obično se definira kao umnožak njegove mase (ili obujma) i jedinične
cijene (tj. cijene po jedinici mase ili obujma).
[6] Vrijednost namirnice
obično se definira kao umnožak njezine mase (ili obujma) i jedinične cijene
(tj. cijene po jedinici mase ili obujma).
[7] Pritom
pretpostavljamo da su sve vrijednosti M, vi i mi
nenegativne (to su tzv. prirodni uvjeti).
[8] Izomorfni
modeli se, dakle, mogu razlikovati u interpretacijama, ali ne i u tipovima
varijabli. Npr. ako su u modelu A varijable nužno cjelobrojne, a u
modelu B nužno realne, onda takvi modeli nisu izomorfni. Analogna
tvrdnja vrijedi i za (ne)jednadžbe koje opisuju uvjete.
[9] Označimo li sa S
skup svih mogućih iznosa ulaganja, onda je za svaki \( i \in [n]\) \(f_i:S\to \mathbb{R}\) realna
funkcija čije su vrijednosti u konkretnom slučaju zadane tablično, a ne
analitički (formulom). Zbog toga ovaj primjer ne rješavamo koristeći se
računalnim programom WinQSB.
[10] C = 4 posljedica je
zahtjeva da svi iznosi ulaganja moraju biti višekratnici broja 1.000.000. Bez
toga zahtjeva, tj. samo uz zahtjev cjelobrojnosti ulaganja, morali bismo uzeti C
= 4.000.000. Radi jednostavnosti i računanja s ''manjim brojevima'', valutna
jedinica kapitala u ovome je slučaju 1.000.000,00 kn.
[11] Svi ostali numerički
podaci ostaju neizmijenjeni.
[12] Preciznije,
problem se rješava u ukupno četiri faze, pri čemu se, za svaki \( i\in [4] \), u i–toj fazi
računaju vrijednosti funkcije fi.
[13] Svi ostali numerički
podaci ponovno ostaju neizmijenjeni.