|
Ivan Zirdum i Nela Bosner |
Moderna tehnologija i stalan porast broja stanovnika na Zemlji razlog su velike produkcije podataka. Svaki dan se proizvede ogromna količina novih podataka koje je potrebno spremati, obraditi, a često i slati. Zbog toga je bilo potrebno osmisliti načine za efikasno spremanje podataka kako bi oni zauzimali što je manje moguće prostora, a da glavna informacija bude očuvana. Lijep primjer toga je kompresija digitalne slike. Uzmimo za primjer sliku dimenzije 3000 \times 2000 piksela. Kako bismo takvu sliku spremili u memoriju potrebno nam je 3000 \cdot 2000 \cdot 24 = 144000000 bitova memorije (za pamćenje jednog piksela koristimo 24 bita) što iznosi 18 megabajta.
U ovom članku bavit ćemo se matričnom (tenzorskom) dekompozicijom koja nam omogućava da iz nekog skupa podataka, prikazanog pomoću matrice (tenzora), izdvojimo "najvažniji" dio, a ostatak izostavimo. Koristeći tu tehniku možemo komprimirati slike, razviti algoritme koji: klasificiraju rukom pisane znamenke, prepoznaju ljudska lica i još mnogo toga. Zamislite sada da ste zaposleni u pošti i da je vaša zadaća sortirati pristigla pisma prema poštanskom broju kako bi ona stigla na pravu adresu. Možda biste radije bili prometni policajac na autocesti koji je zadužen za praćenje brzine automobila koje ulaze u tunel. Vaš posao je snimiti tablice automobila koji ne poštuju ograničenje brzine, a zatim u bazi podataka registracija vozila pronaći tu tablicu te na priloženu adresu vlasnika poslati kaznu za prebrzu vožnju. Biste li svaki dan isti posao radili ručno ili biste radije pokušali taj postupak automatizirati? Srećom, ljudi su se već susreli s ovim problemom i smislili mnogo načina kako taj posao ubrzati i uštediti dragocjeno vrijeme. Svi navedeni problemi mogu se riješiti upotrebom jednog moćnog alata numeričke matematike koji ćemo vam pokušati približiti u ostatku ovog članka.
1Matrična dekompozicija singularnih vrijednosti (SVD)
Jedna od najkorisnijih dekompozicija i s teorijske strane (za dokazivanje) i s praktične strane, je dekompozicija singularnih vrijednosti (engl. singular value decomposition) ili, skraćeno, SVD. Sljedeći teorem pokazuje da za svaku matricu postoji takva dekompozicija.
Teorem 1. (SVD) Neka su
m i
nn \geq m prirodni brojevi te
A proizvoljna
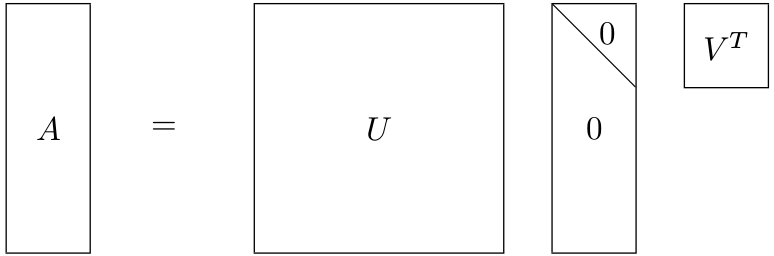
n \times m realna matrica. Tada postoji dekompozicija
gdje su
U \in \mathbb{R}^{n \times n} i
V \in \mathbb{R}^{m \times m} ortogonalne matrice, a
\Sigma \in \mathbb{R}^{n \times m} dijagonalna matrica,
\Sigma = diag( \sigma_{1}, \sigma_{2}, \cdots,\sigma_{m}),
\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{m} \geq 0 .
Ilustrirajmo SVD:
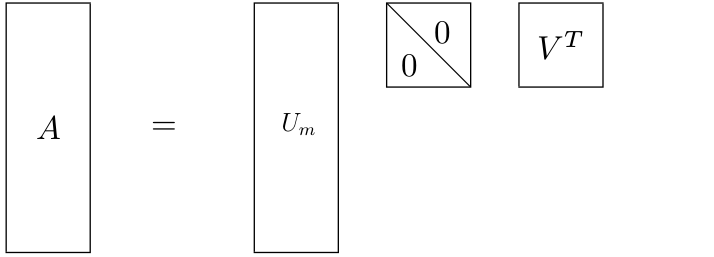
Ako U zapišemo kao U=(U_{m}\,U_{m}^{\perp}), gdje je U_{m} \in \mathbb{R}^{n \times m}, a \Sigma zapišemo kao \begin{pmatrix} \Sigma_{m} \\ 0 \end{pmatrix} gdje je \Sigma_{m} \in \mathbb{R}^{m\times m}, tada dobijemo tanki SVD.
A=U_{m} \Sigma_{m} V^{T},
Ilustirajmo sada tanki SVD:
Jako važnu primjenu SVD-a daje sljedeći teorem.
Teorem 2. Neka je
A = U_{m}\Sigma_{m} V^{T} dekompozicija singularnih vrijednosti (SVD) realne matrice
A tipa
n \times m,
n \geq m. Zapišimo matrice
U_{m} i
V iz SVD-a od
A u stupčanom obliku
U_{m} = (u_{1}, \cdots, u_{m}), \hspace{5mm} V = (v_{1}, \cdots, v_{m}).
Onda matricu
A možemo pisati kao zbroj matrica ranga 1
A= U_{m} \Sigma_{m} V^{T} = \sum_{i=1}^{m} \sigma_{i} u_{i} v_{i}^{T}.
Matricu
A_{k}, istog tipa kao i
A, ranga
rang(A_{k}) \leq k \lt m, koja je po 2-normi najbliža matrici
A, možemo zapisati kao
A_{k} = U_{m} \Sigma_{k} V^{T} = \sum_{i=1}^{k} \sigma_{i} u_{i} v_{i}^{T}
pri čemu je
\Sigma_{k} = diag(\sigma_{1}, \cdots , \sigma_{k}, 0, \cdots, 0).
Pritom je
||A-A_{k}||_{2} = \sigma_{k+1}
najmanja udaljenost između
A i svih matrica ranga najviše
k.
1.1Primjena dekompozicije matrice singularnih vrijednosti
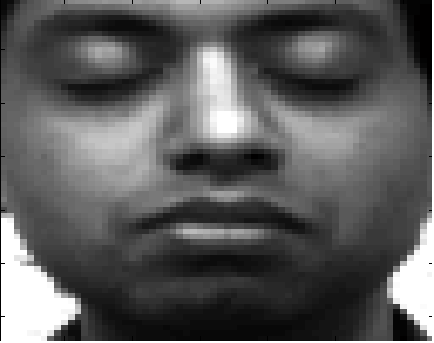
Jedna od primjena prethodnog teorema je kompresija slika. Neka je dana n \times m matrica A s elementima a_{i,j} \in [0,1]. Zamislimo da A predstavlja n \times m grayscale (crno-bijelu) sliku, gdje broj na (i,j) mjestu u matrici predstavlja intenzitet svjetlosti piksela na mjestu (i,j) na slici. Ako uzmemo da vrijednost nula predstavlja crno, a jedan bijelo, zanimljivo je pitanje što će se dogoditi kad napravimo A = U \Sigma V^{T}, a onda u matrici \Sigma posljednjih nekoliko ne-nul elemenata stavimo na nulu te promotrimo dobivenu sliku A_{k}, gdje je A_{k} = U \Sigma _{k} V^{T} = \sum_{i=1}^{k} \sigma_{i} u_{i} v_{i}^{T}, a \Sigma_{k} = diag(\sigma_{1}, \cdots, \sigma_{k}, 0, \cdots, 0).
Preciznije, neka je A = U \Sigma V^{T}, SVD matrice A. Prema teoremu 2 , vrijedi da je A_{k} = \sum_{i=1}^{k} \sigma_{i} u_{i} v_{i}^{T} najbolja aproksimacija matrice A matricom ranga k, u smislu ||A-A_{k}|| = \sigma_{k+1}. Da bismo spremili podatke u_{1}, \cdots , u_{k} te \sigma_{1}v_{1}, \cdots, \sigma_{k}v_{k} iz kojih možemo dobiti matricu A_{k} potrebno je pamtiti samo (m+n)\cdot k brojeva budući da su u_{i} i v_{i} vektori iz \mathbb{R}^{m} odnosno iz \mathbb{R}^{n}. S druge strane, za spremanje matrice A potrebno je pamtiti svih m \cdot n brojeva. Stoga, koristimo A_{k} kao kompresiju slike A.
2Tenzori
Do sada smo razmatrali linearnu algebru, gdje su glavni objekti vektori i matrice. Njih možemo smatrati kao jednodimenzionalna i dvodimenzionalna polja podataka. Tenzor je višedimenzionalni ekvivalent vektora i matrice i možemo ga predstaviti višedimenzionalnim poljem brojeva. Red tenzora jednak je broju indeksa potrebnih za indeksiranje njegovih elemenata. Primjerice, skalar možemo smatrati tenzorom reda 0, vektor tenzorom reda 1, a matricu tenzorom reda 2. Tenzori reda većeg ili jednakog 3 nazivaju se tenzorima višeg reda. Preciznije, tenzor reda N je element tenzorskog produkta N vektorskih prostora.
Red tenzora \mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}} je N. Elemente od \mathcal{A} označavamo s \mathcal{A}_{i_{1} i_{2} \dots i_{n}}, gdje su 1 \leq i_{n} \leq I_{n}, n = 1,2, \dots N.
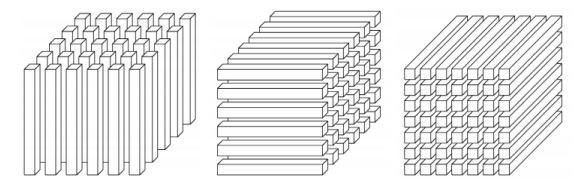
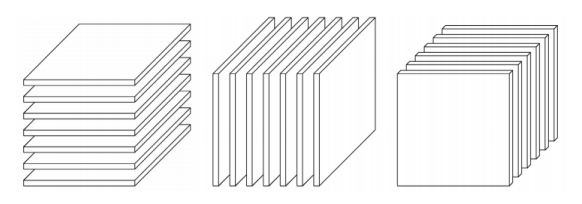
Svaki indeks u tenzoru nazivamo mod, a dimenzija pripadnog moda je broj različitih vrijednosti koje taj indeks može poprimiti. Unutar tenzora možemo indeksirati podtenzore ograničavanjem pojedinih indeksa. Primjerice, za tenzor \mathcal{A} = (a_{i_{1} i_{2} i_{3}}) \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}} reda 3 možemo fiksiranjem indeksa u modu 1,2 ili 3 definirati podtenzore kao \mathcal{A}_{i_{1} = n} = \mathcal{A}_{n::},\mathcal{A}_{i_{2} = n} = \mathcal{A}_{:n:} ili \mathcal{A}_{i_{3} = n} = \mathcal{A}_{::n}.
Primjetimo da su u tom slučaju dva indeksa slobodna pa su podtenzori zapravo novi tenzori reda 2, odnosno matrice. Posebno za slučaj tenzora reda 3 te podtenzore nazivamo horizontalnim, lateralnim i frontalnim odsječcima. Također možemo definirati i vektore po modu n na način da fiksiramo sve indekse osim jednoga, npr. vektor u modu 1 se dobije kao \mathcal{A}_{:i_{2} i_{3}}. Analogno za tenzor reda N možemo definirati podtenzore reda manjeg ili jednakog N. Na sljedećoj slici su prikazani primjeri podtenzora za tenzor reda 3.
|
MATLAB kod |
function Av=vekt_tenz_mod(A,tmod,j,k)
% Av=vekt_tenz_mod(A,mod,i1,i2) vraca vektor tenzora A reda
% 3 u modu tmod, sa preostalim indeksima fiksiranim na j i
% k.
tdim=size(A);
ind=1:3;
ip=ind(ind�=tmod);
Ap=permute(A,[tmod,ip]);
Av=reshape(Ap(:,j,k),tdim(tmod),1);
end
|
|
MATLAB kod |
function Ao=odsj_tenz_mod(A,tmod,i)
% Ao=odsj_tenz_mod(A,tmod,j,k) vraca odsjecak tenzora A
% reda 3 u modu tmod, za i_tmod=i.
tdim=size(A);
ind=1:3;
ip=ind(ind�=tmod);
Ap=permute(A,[ip,tmod]);
Ao=reshape(Ap(:,:,i),tdim(ip));
end
|
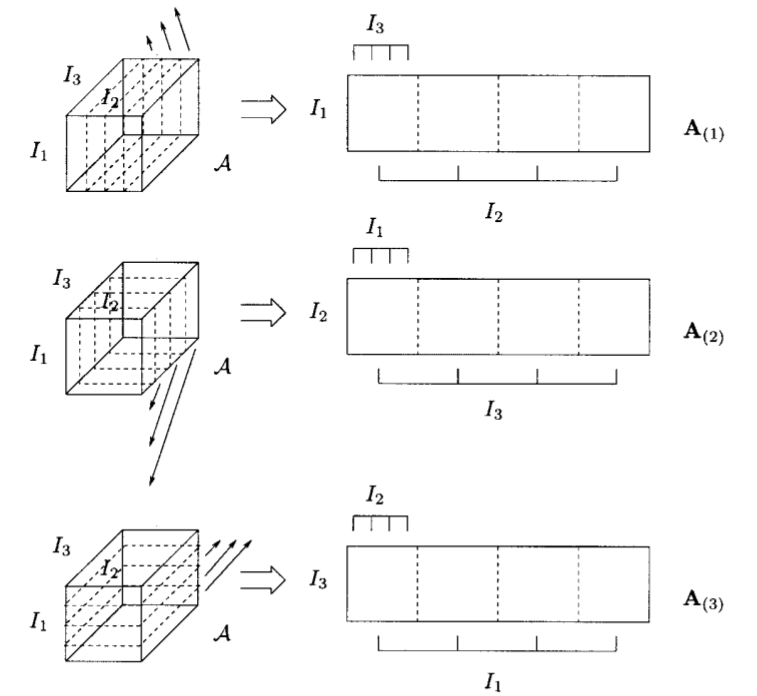
često je korisno prikazati tenzor u obliku matrice. Stoga definiramo matricu tenzora po modu n kao matricu A_{(n)} koja se dobije tako da vektore iz moda n složimo kao stupce u matricu A_{(n)}. Poredak kojim se vektori iz moda n preslikavaju u stupce nije bitan, dok god se isti poredak koristi u svim izračunima.
Matricizacija tenzora (eng. unfold) u modu n od \mathcal{A} označava se s
A_{(n)} \in {\mathbb{R}}^{I_{n} \times (I_{1} \times \dots \times I_{n-1} \times I_{n+1} \times \dots \times I_{N})}.
Tenzorski produkt u modu n tenzora \mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}} s matricom U \in \mathbb{R}^{J_{n} \times I_{n}}, označen s \mathcal{A} \times_{n}U, je
(I_{1} \times \dots \times I_{n-1} \times J_{n} \times I_{n+1} \times \dots \times I_{N})
tenzor čiji elementi su zadani s
(\mathcal{A} \times_{n} U)_{i_{1}i_{2} \dots i_{n-1}j_{n}i_{n+1} \dots i_{N} } \stackrel{def}{=}\sum_{i_{n}}^{}a_{i_{1}i_{2} \dots i_{n-1}i_{n}i_{n+1} \dots i_{N}}u_{j_{n}i_{n}}.
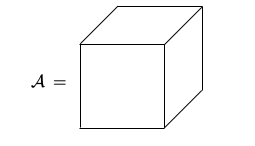
Zbog jednostavnosti ograničavamo se na tenzore reda 3, \mathcal{A} = (a_{ijk}) \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}}. Takav tenzor možemo vizualizirati na sljedeći način:
Uvedimo sada osnovne pojmove za tenzor reda 3, \mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}}. Dimenzije tenzora \mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3} } su: I_{1}, I_{2} i I_{3}.
2.1Osnovni koncepti tenzora
Prvo definiramo skalarni produkt dvaju tenzora istog reda i jednakih dimenzija:
Definicija 3. Skalarni produkt dvaju tenzora istih dimenzija
\mathcal{A},\mathcal{B} \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}} je suma umnožaka njihovih elemenata, tj.
(2)
\langle \mathcal{A},\mathcal{B} \rangle=\sum_{i,j,k} a_{ijk} b_{ijk}.
Pripadna norma je
Definicija 4. Norma tenzora
\mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}} je kvadratni korijen sume svih kvadrata njegovih elemenata, tj.
\Vert \mathcal{A}\Vert = \langle{\mathcal{A},\mathcal{A}}\rangle^{1/2}=\Bigg(\sum_{i,j,k} a_{ijk}^{2}\Bigg)^{1/2}.
Ako gledamo gornje definicije na matricama (dvodimenzionalnim tenzorima) vidimo da je to Frobeniusova norma.
Sljedeće što definiramo je množenje u modu 1 matrice s tenzorom.
Definicija 5. Množenje u modu
1 tenzora
\mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}} matricom
\mathcal{U}\in\mathbb{R}^{l_{0}\times I_{1}} u oznaci
\mathcal{A}\times_{1} U, je
l_{0}\times I_{2} \times I_{3} tenzor dan s
(\mathcal{A}\times_{1} U)(j,i_{2},i_{3})=\sum_{k=1}^{I_{1}} u_{j,k}a_{k,i_{2},i_{3}}.
Uspredbe radi, uočimo da za množenje matrica vrijedi
A \times_{1} U = UA, \hspace{5mm} (UA)(i,j)=\sum_{k=1}^{l}u_{i,k}a_{k,j}.
Znamo da je množenje matrica ekvivalentno množenju svakog stupca iz \mathcal{A} matricom U. Isto vrijedi i za množenje tenzora matricom u modu 1. Svi stupčani vektori iz tenzora \mathcal{A} se množe matricom U.
Slično množenje u modu 2 tenzora s matricom V
(\mathcal{A}\times_{2} V)(i_{1},j,i_{3})=\sum_{k=1}^{I_{2}}v_{j,k}a_{i_{1},k,i_{3}}
znači da su svi retci tenzora pomnoženi s matricom V. Opet uočavamo da je množenje u modu 2 matrice s V ekvivalentno matričnom množenju s V^{T} zdesna,
A\times_{2} V = AV^{T};
Množenje u modu 3 se dobije analogno.
Ponekad je zgodno matricizirati tenzor u matricu.
Matricizacija tenzora \mathcal{A} je definirana kroz tri moda (koristeći MATLAB-ovu notaciju):
\begin{align*} \text{unfold}_{1}(\mathcal{A}):=&A_{(1)}:=(\mathcal{A}(:,1,:)\hspace{5mm} \mathcal{A}(:,2,:) \hspace{5mm}\dots \hspace{5mm}\mathcal{A}(:,I_{2},:)) \hspace{1cm} \in \mathbb{R} ^{I_{1}\times I_{2} I_{3} }, \\ \text{unfold}_{2}(\mathcal{A}):=&A_{(2)}:=(\mathcal{A}(:,:,1)^{T}\hspace{5mm} \mathcal{A}(:,:,2)^{T} \hspace{5mm}\dots \hspace{5mm}\mathcal{A}(:,:,I_{3})^{T}) \hspace{4mm} \in \mathbb{R} ^{I_{2}\times I_{1} I_{3} }, \\ \text{unfold}_{3}(\mathcal{A}):=&A_{(3)}:=(\mathcal{A}(1,:,:)^{T}\hspace{5mm} \mathcal{A}(2,:,:)^{T} \hspace{5mm}\dots \hspace{5mm}\mathcal{A}(I_{1},:,:)^{T}) \hspace{5mm} \in \mathbb{R} ^{I_{3}\times I_{1} I_{2} }. \end{align*}
Vrijedi i sljedeće:
|
(1) |
{Stupčani vektori od \mathcal{A} su stupčani vektori od A_{(1)}}. |
|
(2) |
{Retci od \mathcal{A} su stupčani vektori od A_{(2)}}. |
|
(3) |
{Prostorni vektori od \mathcal{A} su stupčani vektori od A_{(3)}}. |
\text{Unfold}_{1} od \mathcal{A} je ekvivalentan dijeljenju tenzora na odsječke \mathcal{A}(:,i,:) (koji su matrice) i slaže ih u dugu matricu A_{(1)}.
|
MATLAB kod |
function Au=tenz_unfold(A,tmod)
% Au=tenz_unfold(A,tmod) vraca matricizaciju tenzora A reda
% 3 po modu tmod.
tdim=size(A);
Au=[];
io=mod(tmod,3)+1;
for i=1:tdim(io)
if (tmod==1)
Au=[Au,odsj_tenz_mod(A,2,i)];
else
Au=[Au,odsj_tenz_mod(A,io,i)'];
end
end
end
|
Kao što nam je korisno prikazati tenzor u obliku matrice tako nam je ponekad korisno tenzorificirati matricu odnosno matricu pretvoriti u tenzor. Tenzorifikacija je inverz matricizacije odnosno operator fold je inverz operatora unfold pa vrijedi
\text{fold}_{i}(\text{unfold}_{i}(\mathcal{A}))=\mathcal{A}.
|
MATLAB kod |
function A=tenz_fold(Au,tmod,tdim)
% A=tenz_fold(Au,tmod,tdim) tenzorificira matricu Au koja
% je matricizirana pomocu Au=tenz_unfold(A,tmod), natrag u
% polazni tenzor dimenzija tdim(1) x tdim(2) x tdim(3).
A=[];
[dim1,dim2]=size(Au);
if (dim1�=tdim(tmod) && dim2�=prod(tdim(tdim�=tmod)))
fprintf(1,'Krive dimenzije!\n');
return;
end
io=mod(tmod,3)+1; ib=mod(tmod-2,3)+1; bdim=tdim; bdim(io)=1;
for i=1:tdim(io)
switch(tmod)
case 1
A(:,i,:)=reshape(Au(:,(i-1)*tdim(ib)+1:
i*tdim(ib)),bdim);
case 2
A(:,:,i)=reshape(Au(:,(i-1)*tdim(ib)+1:
i*tdim(ib))',bdim);
case 3
A(i,:,:)=reshape(Au(:,(i-1)*tdim(ib)+1:
i*tdim(ib))',bdim);
end
end
end
|
Korištenjem unfold-fold operacija, možemo formulirati matrično množenje ekvivalentno u modu i tenzorskom množenju:
(3)
\mathcal{A}\times_{i}U=\text{fold}_{i}(U\ \text{unfold}_{i}(\mathcal{A}))=\text{fold}_{i}(UA_{(i)}).
|
MATLAB kod |
function B = tenz_mult(A, U, tmod)
% B = tenz_mult(A, U, mod) vraca tenzorski produkt u modu
% tmod tenzora A reda 3 sa matricom U.
B=[];
Au=tenz_unfold(A,tmod);
udim=size(U);
audim=size(Au);
if (udim(2)�=audim(1))
fprintf(1,'Krive dimenzije!\n');
return;
end
tdim = size(A);
switch(tmod)
case 1
B=tenz_fold(U*Au,tmod,[udim(1),tdim(2:3)]);
case 2
B=tenz_fold(U*Au,tmod,[tdim(1),udim(1),tdim(3)]);
case 3
B=tenz_fold(U*Au,tmod,[tdim(1:2),udim(1)]);
end
end
|
2.2Tenzorski SVD (HOSVD)
Matrični SVD može se generalizirati na više načina kako bi dobili tenzorski. Mi promatramo jedan koji se često naziva "Higher order SVD" (HOSVD).
Vidjeli smo da matrice možemo promatrati kao tenzore reda 2. Koristeći tenzorsku notaciju, jednadžbu (1) iz Teorema 1 (SVD) sada možemo zapisati kao
A = U\Sigma V^{T} = \Sigma \times_{1} U \times_{2} V = S \times_{1} U^{(1)} \times_{2} U^{(2)}
isto vrijedi i za tenzore višeg reda. O tome nam više govori sljedeći teorem.
Teorem 6. (HOSVD) Tenzor
\mathcal{A} \in \mathbb{R} ^{l \times m \times n} može se zapisati kao
(4)
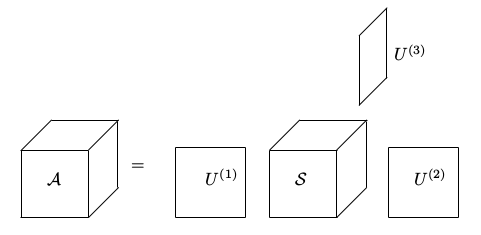
\mathcal{A} = \mathcal{S} \times_{1} U^{(1)} \times_{2} U^{(2)} \times_{3} U^{(3)},
gdje su
U^{(1)} \in \mathbb{R}^{l \times l},U^{(2)} \in \mathbb{R}^{m \times m} i
U^{(3)} \in \mathbb{R}^{n \times n} ortogonalne matrice.
\mathcal{S} je tenzor istih dimenzija kao
\mathcal{A}. Svaka dva odsječka tenzora
\mathcal{S} su ortogonalna u smislu skalarnog produkta:
\langle \mathcal{S}(i,:,:),\mathcal{S}(j,:,:) \rangle = \langle\mathcal{S}(:,i,:),\mathcal{S}(:,j,:)\rangle = \langle\mathcal{S}(:,:,i),\mathcal{S}(:,:,j)\rangle = 0
za
i \neq j. Singularne vrijednosti u modu 1 su definirane s
\sigma_{j}^{(1)} = ||\mathcal{S}(j,:,:)||_{F} , \hspace{1cm} j=1,\dots,l
i one su sortirane silazno
(5)
\sigma_{1}^{(1)} \geq \sigma_{2}^{(1)} \geq \dots \geq \sigma_{l}^{(1)} .
Singularne vrijednosti u ostalim modovima i njihovo sortiranje je analogno.
Ortogonalni tenzor \mathcal{S} nazivamo jezgreni tenzor tenzora \mathcal{A}. HOSVD je vizualiziran na Slici 8.
Koristeći tenzorsku dekompoziciju, svaki tenzor reda N možemo prikazati kao produkt
(6)
\mathcal{A}=\mathcal{S} \times_{1} U^{(1)} \times_{2} U^{(2)} \times_{3} \dots \times_{N} U^{(N)}
gdje nam je \mathcal{S} jezgreni tenzor, a U_{n},\ n=1,2, \dots ,N ortogonalne matrice.
Iz dokaza prethodnog teorema može se zapravo vidjeti kako se računa HOSVD određenog tenzora \mathcal{A}:
|
(1) |
Matrica U^{(i)} u modu i može se direktno naći kao lijeva singularna matrica od matricizacije tenzora \mathcal{A} u modu i: A_{(i)} = U^{(i)}\Sigma^{(i)} V^{(i)^{T}}. |
|
(2) |
Nakon toga, jezgreni tenzor \mathcal{S} može se izračunati prebacivanjem matrica singularnih vekotora na lijevu stranu u jednadžbi (6):
\mathcal{S} = \mathcal{A}\times_{1} U^{(1)^{T}} \times_{2} U^{(2)^{T}} \times_{3} \dots \times_{N} U^{(N)^{T}}.
|
Zbog toga se računanje HOSVD-a tenzora reda N svodi na računanje N različitih matričnih SVD-a matrica formata (I_{n} \times I_{1} I_{2} \cdots I_{n-1} I_{n+1} \cdots I_{N}).
Ponekad se događa da je dimenzija od jednog moda veća od produkta dimenzija drugih modova. Pretpostavimo, npr. da je \mathcal{A} \in \mathbb{R}^{l \times m \times n} gdje je l \gt mn. Može se pokazati da tada za tenzor \mathcal{S} vrijedi
(7)
\mathcal{S}(i,:,:) = 0, \hspace{1cm} i \gt mn,
i možemo odbiti dio s nulama tenzora \mathcal{S} te (4) napisati kao tanki HOSVD
(8)
\mathcal{A} = \widehat{\mathcal{S}} \times_{1} \widehat{U}^{(1)} \times_{2} U^{(2)} \times_{3} U^{(3)},
gdje je \widehat{\mathcal{S}} \in \mathbb{R}^{mn \times m \times n } i \widehat{U}^{(1)} \in \mathbb{R}^{l \times mn}.
|
MATLAB kod |
function [S,U1,U2,U3]=tenz_hosvd(A)
% [S,U1,U2,U3]=tenz_hosvd(A) racuna HOSVD tenzora A reda 3.
[U1,S1,V1]=svd(tenz_unfold(A,1));
[U2,S2,V2]=svd(tenz_unfold(A,2));
[U3,S3,V3]=svd(tenz_unfold(A,3));
S=tenz_mult(tenz_mult(tenz_mult(A,U1',1),U2',2),U3',3);
sdim=size(S);
%Slucaj tankog HOSVD-a
psd12=sdim(1)*sdim(2);
psd13=sdim(1)*sdim(3);
psd23=sdim(2)*sdim(3);
if (sdim(1)>psd23)
S=S(1:psd23,1:sdim(2),1:sdim(3));
U1=U1(1:sdim(1),1:psd23);
return;
end
if (sdim(2)>psd13)
S=S(1:sdim(1),1:psd13,1:sdim(3));
U2=U2(1:sdim(2),1:psd13);
return;
end
if (sdim(3)>psd12)
S=S(1:sdim(1),1:sdim(2),1:psd12);
U3=U3(1:sdim(3),1:psd12);
return;
end
|
2.3Aproksimacija tenzora HOSVD-om
I HOSVD se može koristiti za kompresiju tenzora. Budući da je masa jezgrenog tenzora \mathcal{S} koncentirana za male vrijednosti od sva tri indeksa, moguće je "stisnuti" podatke u sva tri moda HOSVD-om. Pretpostavimo sada da smo podatke stisnuli u manji tenzor gdje ćemo imati k_{i} stupaca u modu i. Neka je U_{k_{i}}^{(i)} = U^{(i)}(:,1:k_{i}) i \hat{\mathcal{S}} = \mathcal{S}(1:k_{1},1:k_{2},1:k_{3}). Zatim razmotrimo aproksimaciju
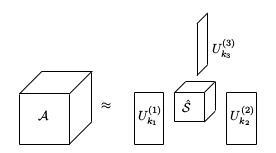
\mathcal{A}\approx \widehat{\mathcal{A}}=\widehat{\mathcal{S}}\times_{1} U_{k_{1}}^{(1)} \times_{2} U_{k_{2}}^{(2)} \times_{3} U_{k_{3}}^{(3)}.
Ilustrirajmo to na sljedećoj slici:
Na ovaj način smo uz minimalne gubitke uštedjeli memoriju. Tenzor \mathcal{A}\in \mathbb{R}^{l\times m \times n} ima ukupno l \cdot m \cdot n elemenata, dok za njegovu aproksimaciju \widehat{\mathcal{A}} moramo pamtiti ukupno k_{1} \cdot k_{2} \cdot k_{3} + l\cdot k_{1} + m\cdot k_{2} + n \cdot k_{3} elemenata.
Ako je tenzor \mathcal{A}\in \mathbb{R}^{1000\times 1000 \times 1000} onda on ima 1000 \cdot 1000 \cdot 1000 = 10^{9} elemenata, dok njegova aproksimacija \widehat{\mathcal{A}} za k_{1}=k_{2}=k_{3}=100 ima 10^{6} elemenata u \widehat{\mathcal{S}}, 1000 \cdot 100 = 10^{5} elemenata u U_{k_{1}}^{(1)},U_{k_{2}}^{(2)} i U_{k_{3}}^{(3)}, ukupno 1.3\cdot 10^{6} elemenata. što znaći da umjesto da koristimo 1 000 000 000 elemenata mi korisitmo samo 1 300 000 elemenata, a to je ušteda od 997 000 000 elemenata, odnosno umjesto da zauzmemo 3GB memorije zauzimamo samo 3.9MB.
3Prepoznavanje lica korištenjem HOSVD-a
Ljudska bića su vrlo vješta pri prepoznavanju lica čak i kada izraz lica, osvjetljenje, kut gledanja itd. variraju. Razviti automatske postupke za prepoznavanje lica koji su robusni s obzirom na različite uvjete, izazovan je istraživački problem koji je istražen pomoću nekoliko različitih pristupa. Analiza glavnih komponenti (eng. principal component analysis, PCA), temeljena na SVD-u, popularna je tehnika koja često ide pod imenom "eigenfaces". Međutim, ova metoda je najbolja kada su sve fotografije nastale pod sličnim uvjetima, i ne radi dobro kad se mijenjaju neki faktori okoline.
Nedavno su istraživane metode za multilinearnu analizu skupa fotografija. Konkretno, problem prepoznavanja lica razmatran je korištenjem tenzorskog modela, TensorFaces pristupa. I to tako da modovi tenzora predstavljaju drukčiji način gledanja, npr. osvjetljenje ili izraz lica, postalo je moguće poboljšati preciznost algoritma prepoznavanja u usporedbi s PCA metodom.
U ovom ćemo odsječku opisati metodu tenzorskog prepoznavanja lica, koja se odnosi na TensorFaces. Budući da se radi o fotografijama, koje se često pohranjuju kao matrice m \times n, s m i n reda 100-500, izračuni za svako lice koje treba identificirati su prilično teški. Razmotrit ćemo kako se tenzorski SVD (HOSVD) također može koristiti za smanjenje dimenzije u svrhu smanjenja broja operacija.
3.1Tenzorski prikaz fotografija
Pretpostavimo da imamo kolekciju fotografija od n_{p} osoba, gdje je svaka fotografija m_{i_{1}} \times m_{i_{2}} matrica s m_{i_{1}} m_{i_{2}} = n_{i} elemenata. Pretpostavljamo da su stupci fotografija složeni tako da svaka fotografija predstavlja vektor u \mathbb{R}^{n_{i}}. Nadalje pretpostavljamo da je svaka osoba fotografirana u n_{e} različitih izraza lica. često je n_{i} \geq 5000, i obično je n_{i} znatno veći od n_{e} i n_{p}. Takva kolekcija fotografija je spremljena u tenzor:
(9)
\mathcal{A} \in \mathbb{R}^{n_{i} \times n_{e} \times n_{p}}
Pozivamo se na različite modove kao što su mod fotografije (eng. the image mode), mod izraza lica (eng. the expression mod) i mod osobe (eng. the person mode), zbog toga korisitmo indekse i,e,p u (9).
Ako, primjerice, također imamo fotografije svake osobe s različitim osvjetljenjem, kutem gledanja, itd., onda bi mogli predstavljati kolekciju fotografija tenzorom višeg reda. Radi jednostavnosti ovdje promatramo samo tenzore reda 3. Generalizacija tenzorima višeg reda je jasna.
Primjer 7. Prethodno smo obradili fotografije od
10 osoba iz baze podataka Yale Face koje smo postavili na
112 \times 78 piksela i pohranili u vektor duljine 8736. Pet fotografija je prikazano na sljedećoj slici.
Svaka osoba je fotografirana u ukupno 11 različitih izraza lica.
Redosljed modova je naravno proizvoljan; u svrhu ilustriranja pretpostavljat ćemo redosljed iz (9). Međutim kako bi naglasili proizvoljnost, koristit ćemo oznaku \times _{e} za množenje tenzora matricom u modu izraza lica (the expression mode), i slično za druge modove. Sada pretpostavljamo da je n_{i} \gg n_{e} n_{p} i pišemo tanki HOSVD (Pogledati Teorem 6 i (8)),
\mathcal{A}= \mathcal{S} \times_{i} F \times_{e} G \times_{p} H,
gdje je \mathcal{S} \in \mathbb{R}^{n_{e}n_{p} \times n_{e} \times n_{p}} jezgra tenzora \mathcal{A}, F\in \mathbb{R}^{n_{i} \times n_{e}n_{p}} ima ortogonalne stupce, i G \in \mathbb{R}^{n_{e} \times n_{e}} i H \in \mathbb{R}^{n_{p} \times n_{p}} su ortogonalne matrice.
3.2Prepoznavanje lica
Sada ćemo razmatrati problem klasifikacije kako slijedi:
Za danu fotografiju nepoznate osobe, koju predstavlja vektor u \mathbb{R}^{n_{i}} odredit ćemo koju od n_{p} osoba predstavlja ili odlučiti da nepoznata osoba nije u bazi podataka.
Za klasifikaciju pišemo HOSVD (4) u sljedećem obliku:
(10)
\mathcal{A} = \mathcal{C}\times_{p} H, \hspace{1cm} \mathcal{C} = \mathcal{S}\times_{i} F \times_{e} G.
Za određeni izraz lica e imamo
(11)
\mathcal{A}(:,e,:)=\mathcal{C}(:,e,:)\times_{p} H.
Očito tenzore \mathcal{A}(:,e,:) i \mathcal{C}(:,e,:) možemo promatrati kao matrice, koje označavamo s A_{e} i C_{e}. Stoga, za sve izraze imamo linearne relacije
(12)
A_{e} = C_{e} H^{T}, \hspace{1cm} e=1,2,\cdots , n_{e}
Imajmo na umu da se ista (ortogonalna) matrica H pojavljuje u svih n_{e} relacija. S H^{T} = (h_{1} \cdots h_{n_{p}}), stupac p iz (12) može biti zapisan kao
(13)
a_{p}^{(e)} = C_{e} h_{p}
Možemo interpretirati (12) i (13) na sljedeći način:
Stupac p od matrice A_{e} sadrži sliku osobe p u izrazu e. Stupci matrice C_{e} su bazni vektori za izraz e, i red p matrice H, tj, h_{p}, sadrži koordinate fotografija osobe p u toj bazi. Nadalje isti h_{p} sadrži koordinate fotografija osobe p u svim izraznim bazama.
Zatim pretpostavimo da je z \in \mathbb{R}^{n_{i}} slika nepoznate osobe u nepoznatom izrazu (iz n_{e}) i da ju želimo klasificirati. Taj z ćemo zvati testna slika. Očito, ako je slika osobe p u izrazu e, onda su koordinate vektora z u toj bazi jednake koordinatama vektora h_{p}. Dakle, možemo klasificirati z računanjem njegovih koordinata u svim bazama ekspresije i provjeravajući, za svaki izraz, podudaraju li se koordinate od z (ili se gotovo podudaraju) s elementima bilo kojeg reda matrice H.
Koordinate od z u izraznoj bazi e mogu se naći rješavanjem problema najmanjeg kvadrata
(14)
\min_{\alpha_{e}} \Vert C_{e} \alpha_{e} - z\Vert _{2}
Klasifikacijski algoritam
for e = 1,2, \cdots, n_{e}
Riješi \text{min}_{\alpha_{e}} \Vert C_{e} \alpha_{e} - z\Vert _{2}
for p=1,2,\cdots, n_{p}
if \Vert \alpha_{e} - h_{p}\Vert _{2} \lt tol, onda klasificiraj kao osobu p i stani.
end
end
Količina posla u ovom algoritmu je velika: za svaku test sliku z moramo riješiti n_{e} problema najmanjih kvadrata (14) s C_{e} \in \mathbb{R}^{n_{i} \times n_{p}}.
4Primjeri dobiveni MATLAB rutinama
Program smo testirali na 10 osoba fotografiranih u 10 različitih ekspresija(izraza) lica. Fotografije su spremljene u matricu tako da svaki stupac predstavlja jednu fotografiju i to na način da prvih 10 stupaca predstavlja prvu osobu u svih 10 ekspresija, drugih 10 stupaca predstavlja drugu osobu itd. Svaka fotografija je dimenzije 64 \times 64 što znači da je matrica dimenzije 4096\times 100. Pogledajmo sada fotografije tih osoba u prvom izrazu lica:
Svaka od tih osoba je fotografirana u 10 različitih izraza lica, pa pogledajmo na prvoj osobi koji su to sve izrazi: \nopagebreak[4]
4.1Klasifikacija
Za potrebe prepoznavanja lica uzeli smo prvih 5 osoba u prve 3 ekspresije lica (15 fotografija) i stavili ih u bazu, te na njima "trenirali" program. Nakon toga smo izbacili te fotografije i na preostalim fotografijama testirali program. Preostalo je po 7 fotografija za svaku osobu koja je u bazi, a po 10 od osoba koje nisu u bazi (ukupno 35 fotografija osoba koje su u bazi i 50 fotografija osoba koje nisu u bazi). Naš cilj je da danu testnu fotografiju program klasificira kao jednu od tih 5 osoba ili da vrati: "Tražena osoba nije u bazi!". Odnosno, ukoliko je testna fotografija jedna od tih 7 fotografija da program prepozna tu osobu kao odgovarajuću osobu iz baze, a ako je jedna od 10 fotografija osoba koje nisu u bazi da vrati: "Tražena osoba nije u bazi!". Tolerancija u ovom radu iznosi 0.475, a do nje dolazimo eksperimentima.
Uzmimo sada za testnu fotografiju proizvoljnu fotografiju iz skupa od 35 fotografija osoba koje su u bazi i na njoj testirajmo program. Pogledajmo rezultate na sljedećim slikama: (Lijeva fotografija predstavlja osobu koju želimo klasificirati, a desna klasificiranu osobu.)
Vidimo da je program dobro prepoznao lica. Za sljedeće fotografije je program vratio: "Tražena osoba nije u bazi!".
što također vidimo da je dobro jer niti jedna od tih osoba nije u prvih 5 osoba na kojima smo trenirali naš program.
Napomenimo na kraju da program nije savršen i da se može dogoditi da krivo klasificira osobu. Primjer krive klasifikacije: Uzeli smo novu 11. osobu i pokušali je klasificirati.
Klasifikacija očito nije dobra jer to nisu iste osobe!
Da bismo to spriječili možemo smanjiti toleranciju, ali u tom slučaju se može dogoditi da osoba koja je u bazi ne bude prepoznata, odnosno da program vrati: "Tražena osoba nije u bazi!".
Pogledajmo i takav primjer: (Tolerancija u ovom primjeru iznosi 0.35).
Za gornju fotografiju je program vratio: "Tražena osoba nije u bazi!", a trebao ju je klasificirati kao:
Unatoč tome smatramo da je "manja" pogreška ako program ne prepozna osobu koju bi trebao, nego da osoba koja nije u bazi bude prepoznata kao neka osoba koja je u bazi. Iz tih razloga ipak uzimamo manju toleranciju do koje dolazimo eksperimentima.
Bibliografija
|
[1] |
L. Elden, Matrix methods in data mining and pattern recognition, Philadelphia, SIAM., 2007. |
|
[2] |
L. De Lathauwer, B. De Moor, and J. Vandewalle. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl., 21:1253-1278, 2000. |
|
[3] |
J. Demmel. Applied Numerical Linear Algebra. SIAM . MIT , 1996. |
|
[4] |
T. G. Kolda, Multilinear Operators for Higher Order Decompositions, Tech. Report SAND2006-2081, 2006. |
|
[5] |
Mladen Rogina, Sanja Singer, Saša Singer. Numerička analiza. PMF - Matematički odsjek, Zagreb, 2003. |
|
[6] |
Z. Drmač. Bilješke s predavanja iz kolegija Uvod u složeno pretraživanje podataka, PMF - Matematički odsjek, Zagreb, 2016. |
|
[7] |
A. Novak, D. Pavlović. Dekompozicija matrice na singularne vrijednosti i primjene. math.e, Zagreb, 2013.
|


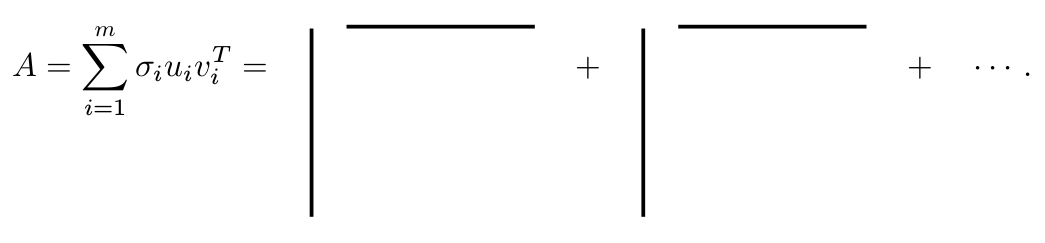





 s
s