Ključne riječi: Petersenov graf, stupanj, struk, dijametar, bridno kromatski broj, hipohamiltonov graf

Adresa: Odjel za matematiku, Sveučilište Josipa Jurja Strossmayera u Osijeku, Trg Ljudevita Gaja 6, 31000, Osijek,

Velik interes za proučavanje 3-regularnih grafova nastao je zahvaljujući problemu četiri boje kojeg je postavio matematičar F. Guthrie 1852. godine. Problem se svodi na bojanje država ucrtanih na zemljopisnoj karti tako da države koje imaju zajedničku granicu nisu obojane istom bojom. Guthrie je pretpostavio da je za takvo bojanje dovoljno uzeti četiri različite boje. Danas je njegova tvrdnja poznata kao Teorem o četiri boje, a jedan njegov ekvivalent je tvrdnja da je svaki planaran 3-regularan graf bez mostova 3-bridno obojiv. Zahvaljujući Teoremu o četiri boje, kojemu su matematičari bili posvećeni više od 150 godina, otkriven je Petersenov graf. Za nešto više saznanja o problemu četiri boje upućujemo čitatelje na npr. [2].

Petersenov graf je jednostavan 3-regularan graf s 10 vrhova i 15 bridova. Nazvan je po Juliusu Petersenu koji je 1898. godine ustanovio [15] da je upravo taj graf najmanji 3-regularan graf bez mostova koji nije 3-bridno obojiv. Ipak, prvu konstrukciju Petersenova grafa načinio je A.B. Kempe 1886. kada se bavio Desargueosovim konfiguracijama [11]. Uočio je da vrhovi Petersenova grafa reprezentiraju 10 pravaca Desargueosovih konfiguracija, a bridovi reprezentiraju parove pravaca koji se ne sijeku niti u jednoj od 10 točaka konfiguracije. Na slici 1, u prvom redu lijevo, je prikaz Petersenova grafa kakav se danas najčešće pojavljuje u literaturi. Odmah do njega je prikaz grafa kako ga je načinio Kempe.

Slika 1: Različiti prikazi Petersenova grafa u ravnini.

Julius Petersen nije poznat jedino zbog otkrića (Petersenova) grafa, već i po tome što je dao značajan doprinos teoriji grafova dokazavši tvrdnju koja danas nosi njegovo ime: Petersenov teorem. On glasi:

1-faktor je savršeno sparivanje u grafu, tj. podskup M skupa bridova sa svojstvom da niti jedan par bridova iz M nije incidentan s istim vrhom, a svaki vrh grafa je incidentan jednom bridu iz M. Petersenov graf je protuprimjer Taitovom 'teoremu' [18] vezanom za problem četiri boje koji glasi:

Drugim riječima, Tait je pogriješio kada je zaključio da se skup bridova 3-regularnog grafa može rastaviti na međusobno disjunktne podskupove pri čemu je svaki takav podskup savršeno sparivanje.

Od vremena kada je otkriveno njegovo prvo ekstremalno svojstvo pa do danas, Petersenov graf se pojavljuje kao protuprimjer raznim tvrdnjama za koje se dulje vrijeme smatralo da su istinite. Nije čudno da se danas Petersenov graf nalazi na stranicama raznih svjetskih matematičkih časopisa kao što su Journal of Graph Theory i Discrete Mathematics.

Rad je organiziran na slijedeći način: prvih 5 odjeljaka posvećeno je ekstremalnim svojstvima Petersenova grafa. Svako svojstvo je detaljno dokazano i popraćeno ne tako kratkim povijesnim okvirom. U zadnjem odjeljku navodimo i dokazujemo još nekoliko zanimljivih, a svakako netrivijalnih, svojstava Petersenova grafa. U radu koristimo mnoštvo pojmova iz teorije grafova za čije bi definicije bilo potrebno dodati još nekoliko stranica. Kako je rad ionako dosta opsežan, pokušali smo neke složenije pojmove definirati "usputno", i to tamo gdje se koriste. Definicije svih ostalih pojmova čitatelji mogu potražiti u [21]. Napomenimo još samo da se u radu, zbog jednostavnosti, koriste definicije i tvrdnje vezane isključivo za jednostavne grafove (iako mnoge vrijede i za multigrafove, odnosno, pseudografove). Evo nekoliko jednostavnih svojstava Petersenova grafa koja ćemo navesti bez dokaza:

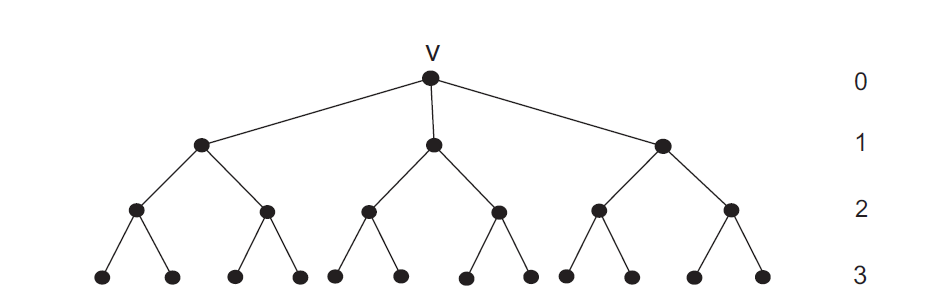
Udaljenost dva vrha u nekom grafu definiramo kao broj bridova u najkraćem putu koji ih povezuje. Dijametar grafa definiramo kao najveću udaljenost dva njegova vrha. Pretpostavimo da postoji povezan graf s n vrhova čiji je maksimalan stupanj \Delta, a dijametar je d. Zanima nas maksimalan broj vrhova koji može imati takav graf. Slučaj \Delta=d=1 je trivijalan: jedini graf dijametra 1 i maksimalnog stupnja 1 je potpun graf K_{2} pa je n=2. Petpostavimo stoga da je \Delta\geq 2 i d\geq 2. Konstruirajmo BFS (Breadth First Search) stablo sa korjenom v. Iz vrha v putem duljine 1 možemo posjetiti najviše \Delta vrhova. Iz vrha v putem duljine 2 možemo posjetiti najviše \Delta(\Delta-1) vrhova itd. Konačno, iz vrha v putem duljine d možemo posjetiti najviše \Delta(\Delta -1)^{d-1} vrhova. Vidi Sliku 2.

Slika 2: BFS stablo za \Delta=3 i d=3

Slijedi da je

Desna strana nejednadžbe (1) zove se Mooreova granica, u oznaci M_{\Delta,d}, prema američkom profesoru Edward Forrest Mooreu koji je pedesetih godina prošlog stoljeća postavio problem klasifikacije i karakterizacije grafova koji uz zadani maksimalan stupanj i dijametar imaju broj vrhova jednak M_{\Delta,d}. Takvi grafovi zovu se Mooreovi grafovi, a prvi su ih proučavali (i nadjenuli im ime) A.J.Hoffman i R.R.Singleton 1960. godine [9].

Mooreovi grafovi su nužno regularni grafovi stupnja \Delta, a njihova posebnost je u tome što su rijetki. Štoviše, ne postoje Mooreovi grafovi za slučaj \Delta\geq 3 i d\geq 3. Za d=1 i \Delta\geq 2 imamo potpune grafove K_{\Delta+1}, za \Delta=2 i d\geq 2 imamo cikluse C_{2d+1}, dok je za d=2 i \Delta\geq 3 dokazano [9] da postoje samo 2 Mooreova grafa: Petersenov graf (\Delta=3) i Hoffman-Singleton graf (\Delta=7) [22], dok je egzistencija Mooreovog grafa za \Delta=57 još uvijek otvoren problem u teoriji grafova (ukoliko bi postojao takav graf, broj vrhova bi mu bio 3250, a imao bi 92625 bridova).

Dakle, Petersenov graf pripada klasi izuzetno rijetkih grafova: Mooreovih grafova. Preciznije, on je jedini Mooreov graf stupnja 3 i dijametra 2. Sada je jasno da je Petersenov graf ujedno i najveći 3-regularan graf dijametra 2, jer prema formuli (1) svaki takav graf ne može imati više od 10 vrhova, a upravo toliko vrhova ima Petersenov graf. Jedinstvenost se lako dokaže konstrukcijom: nakon što konstruiramo BFS stablo sa 10 vrhova kao na Slici 3, potrebno je dodati još 6 bridova među listove e,f,g,h, i i j pazeći pritom da rezultirajući graf bude 3-regularan i da mu je dijametar 2. Jedini mogući način dodavanja tih 6 bridova prikazan je na Slici 3, a rezultirajući graf je Petersenov graf.

Slika 3:

Proučavanje Mooreovih grafova, pa tako i Petersenova grafa kao jednog specijalnog slučaja, utjecalo je na razvijanje posebnih grana teorije grafova kao što su Mooreove geometrije, Mooreove grupe, teorija antipodalnih grafova, teorija dizajna...

U nastavku ćemo se baviti problemom određivanja minimalnog mogućeg broja vrhova grafa ako je poznat minimalan stupanj i struk te uspostaviti vezu tog problema sa problemom određivanja najvećeg mogućeg broja vrhova grafa ako je poznat maksimalan stupanj i dijametar.

Ciklus u nekom grafu je put u kojemu se prvi i posljednji vrh podudaraju. Struk grafa definiramo kao duljinu najkraćeg ciklusa u grafu. Pretpostavimo da postoji povezan graf koji nije stablo takav da mu je minimalan stupanj jednak \delta\geq 2 i struk g\geq 3.
Za slučaj g=2k+1 krećemo najprije sa konstukcijom BFS stabla. Na razini 0 nalazi se korjen v. Na razini 1 najmanje je \delta vrhova, na razini 2 najmanje \delta(\delta-1) vrhova itd.... na razini k najmanje je \delta(\delta-1)^{k-1} vrhova. Za 1\leq i\leq k-1 ne postoje bridovi među vrhovima razine i jer bi u tom slučaju dobili cikluse duljine manje od g. Iz istog razloga ne postoje bridovi među vrhovima sa različitih razina. Jedino je moguće dodavati bridove među vrhove koji se nalaze na (k-1)-oj razini.

Slijedi

Za slučaj parnog struka, tj. g=2k, BFS stablo konstruiramo slično kao u prethodnom slučaju, ali smatramo da korjen čine dva vrha spojena bridom. Slijedi

Regularan graf s najmajim mogućim brojem vrhova koji je stupnja \Delta i struka g zove se (\Delta,g)-rešetka. W.T.Tutte [20] je među prvima proučavao takvu vrstu grafova, a kasnije su P.Erdös i H.Sachs [6] dokazali da (\Delta,g)-rešetke postoje za sve \Delta\geq 2 i g\geq 3. No, zanimljivo je da su i ovakvi grafovi vrlo rijetki. Do sada je pronađeno 38 grafova i to za \Delta\leq 14 i g\leq 12.

Slika 4: a) Potpun bipartitan graf K_{5,5} kao (5,4)-rešetka, b) potpun graf K_{10} kao (9,3)-rešetka, c) Haewoodov graf ili (3,6)-rešetka i d) McGeeov graf ili (3,7)-rešetka

Ako usporedimo desne strane nejednadžbi (1) i (2), ustanoviti ćemo da je svaka (\Delta,g)-rešetka ujedno i Mooreov graf ukoliko vrijedi g=2d+1. U takvoj rešetki broj vrhova jednak je M_{\Delta,d}. Drugim riječima, Mooreova granica M_{\Delta,d} ne daje samo maksimalan broj vrhova grafa sa maksimalnim stupnjem \Delta i dijametrom d, već daje i minimalan broj vrhova u regularnom grafu stupnja \Delta i struka 2d+1. S tim u vezi, dokazano je [16] da je svaki graf dijametra d i struka 2d+1 nužno regularan. Na ovaj način dolazimo do zaključka da Petersenov graf pripada još jednoj zanimljivoj klasi grafova: (\Delta,g)-rešetkama. Štoviše, Petersenov graf je jedina (3,5)-rešetka, tj. jedini najmanji 3-regularan graf struka 5. Minimalnost odmah slijedi iz formule (2), dok se jedinstvenost opet lako dokaže konstrukcijom. Potrebno je izgraditi BFS stablo s 10 vrhova kao na Slici 3, a zatim spojiti listove tog stabla pazeći na uvjete o stupnju i struku. Dokaz prepuštamo čitatelju.

Problem pravilnog bojanja bridova 3-regularnih grafova privukao je značajnu pažnju kada je P.G.Tait [18] ustanovio da je teorem o četiri boje ekvivalentan tvrdnji da je svaki planaran 3-regularan graf bez mostova 3-bridno obojiv. Ovdje pod pravilnim bojanjem podrazumijevamo bojanje bridova u kojem niti jedan par bridova incidentan sa istim vrhom nije obojan istom bojom. S tim u vezi definiran je bridno kromatski broj grafa kao minimalan broj boja potreban za pravilno bojanje njegovih bridova. Obzirom da je kasnije dokazano da je teorem o četiri boje istinit, znamo da ne postoji planaran 3-regularan graf bez mostova čije bridove ne možemo obojati sa tri boje. No, izuzetno je teško pronaći primjere neplanarnih grafove te vrste. Sve do 1975., kada je Isaacs konstruirao dvije beskonačne familije takvih grafova, samo je pet grafova sa navedenim svojstvima bilo poznato. Među njima je i Petersenov graf. Stoga je M.Gardner [7] odlučio nadjenuti im ime snarks, prema poznatoj baladi Lewisa Carolla: "The Hunting of the Snark", gdje je snark ime fiktivne teško uhvatljive životinje koju ni sam autor nije znao opisati kada su to od njega tražili čitatelji. Dakle, u teoriji grafova snark je netrivijalan 3-regularan graf koji nije 3-bridno obojiv. No, Vizingov teorem [21] kaže da u svakom jednostavnom grafu s maksimalnim stupnjem \Delta, bridno kromatski broj iznosi ili \Delta ili \Delta+1 pa snark možemo definirati i kao netrivijalan 3-regularan graf s bridno kromatskim brojem 4. Treba još objasniti što znači riječ "netrivijalan" u definiciji snark grafa.

Prvenstveno, to znači da graf nema mostova, tj. ne postoji brid čijim se uklanjanjem graf raspada na dvije komponente povezanosti. Također, "netrivijalan" ovdje znači da je struk grafa najmanje 5, jer ako bismo uzeli u obzir snarkove koji sadrže cikluse sa 2 ili 3 vrha, onda se uklanjanjem ili dodavanjem takvih ciklusa ništa ne mijenja, tj. graf i dalje neće biti 3-bridno obojiv. Snark nema ni cikluse duljine 4 jer se takvi grafovi mogu reducirati na manje snarkove. I na kraju, snark mora biti ciklički 4-bridno povezan, tj. potrebno je ukloniti najmanje 4 brida da bi se graf raspao na dvije komponene povezanosti tako da svaka komponenta sadrži ciklus. Za više detalja pogledati [14].

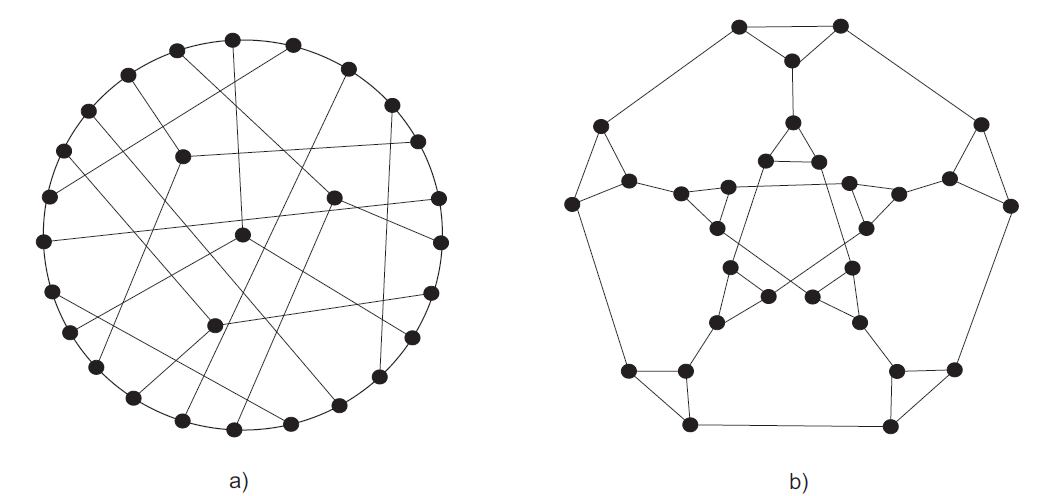
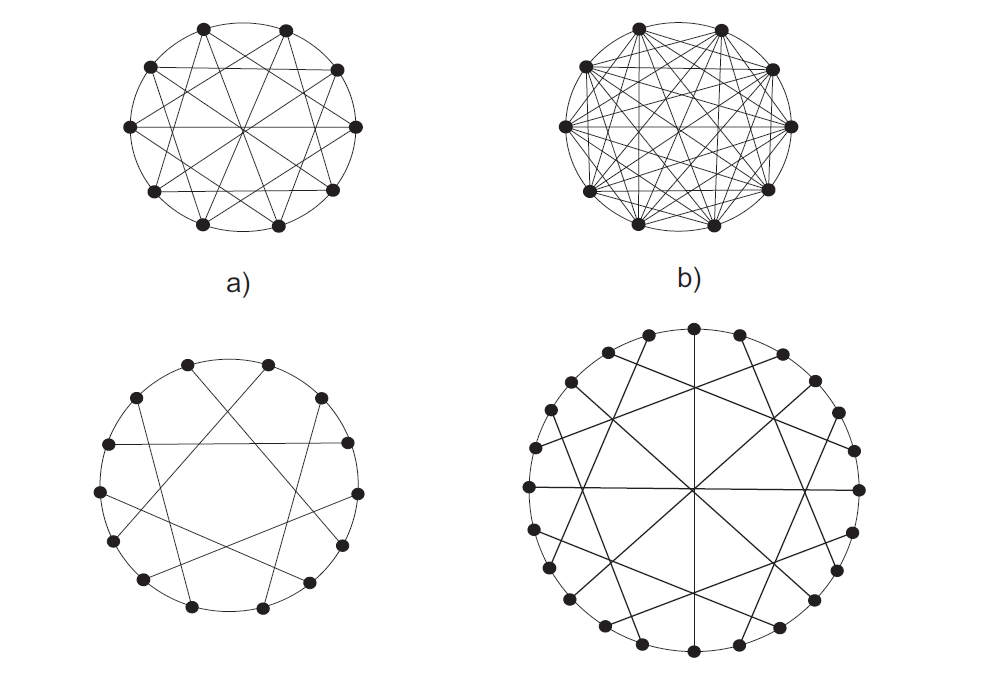
Prvi snark otkriven je 1898. i to je upravo Petersenov graf. Kasnije, 1946. hrvatski matematičar Danilo Blanuša pronalazi nova dva snarka, oba s 18 vrhova, a danas poznata pod nazivom Blanušini snarkovi. Vidi Sliku 4.5. pod a) i b). Četvrtog je snarka otkrio dvije godine kasnije Bill Tutte. Poznat je kao Descartesov snark i ima 210 vrhova. Godine 1973. otkriven je Szekeresov snark, a ima 50 vrhova. Zatim, 1975. godine Rufus Isaacs uspijeva konstruirati dvije beskonačne familije snarkova. Jedna se zove Cvjetni snarkovi, a druga dobiva naziv BDS snarkovi i uključuje sve ranije otkrivene snarkove osim Petersenova grafa. Primjer cvjetnog snarka nalazi se na Slici 5 c). Isaacs je uspio pronaći još jedan snark koji ne pripada niti jednoj od navedenih familija: Dvostruka zvijezda snark (30 vrhova). Vidi Sliku 5 d).

Slika 5: a) Prvi i b) drugi Blanušin snark, c) cvjetni snark s 20 vrhova i d) dvostruka zvijezda snark.

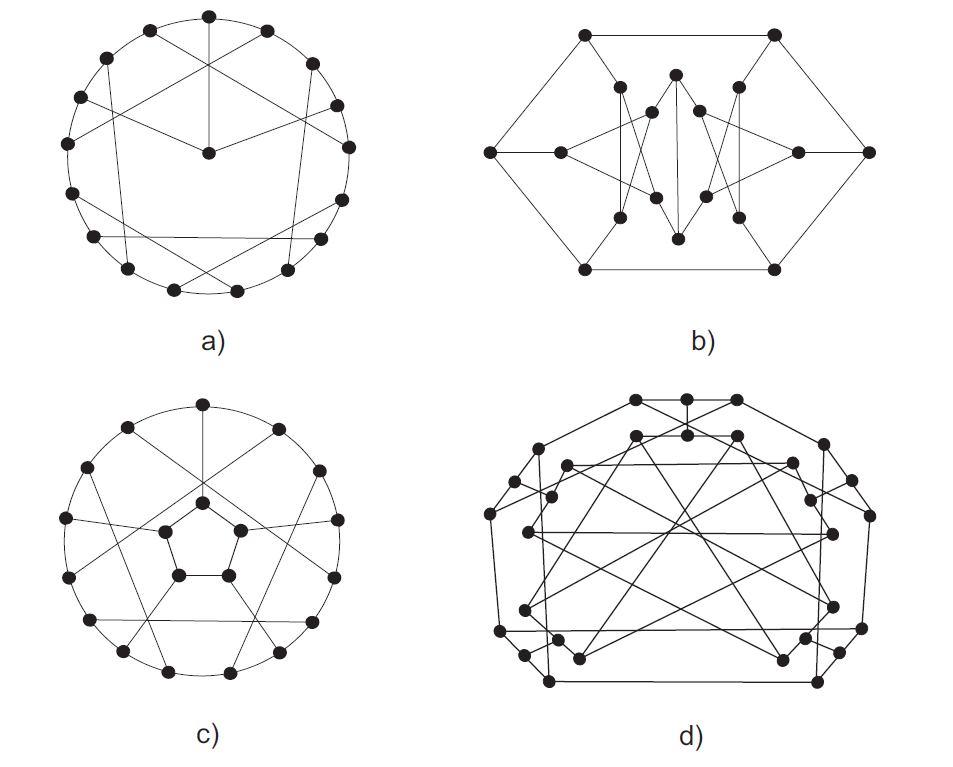
Napomena: Drugi Blanušin snark nalazi se u logotipu Hrvatskoga matematičkog društva (HMD), doduše, sa malo drugačijim ravninskim smještenjem.
Također, HMD je predložio hrvatskoj pošti da obilježi Svjetsku matematičku godinu 2000. (World Mathematical Year 2000) izdavanjem prigodne marke. Hrvatska pošta je taj prijedlog prihvatila, izdala marku i promovirala ju 15. lipnja 2000. godine na dan početka Drugog hrvatskog matematičkog kongresa.


Sada ćemo dokazati da je Petersenov graf najmanji snark i ujedno jedinstveni snark s 10 vrhova.

Neka je G snark i neka je X proizvoljan ciklički bridni rez u G. Tada se G-X sastoji od dvije komponente povezanosti pri čemu svaka sadrži ciklus s najmanje 5 vrhova jer je struk snarka najmanje 5. Slijedi |V(G)|\geq 10. No, obzirom da je Petersenov graf snark i ima 10 vrhova, zaključujemo da je on ujedno i najmanji snark. Ostaje još dokazati da bilo koji snark s 10 vrhova mora biti izomorfan sa Petersenovim grafom. Neka je G snark s 10 vrhova i neka je Y ciklički bridni rez u G. Tada svaka komponenta u G-Y ima 5 vrhova, zbog pretpostavke o struku grafa G. Ako bi |Y|=4, tada bi u svakoj komponenti povezanosti postojalo 4 vrha stupnja 2 i jedan vrh stupnja 3, što je nemoguće jer je u svakom grafu broj vrhova neparnog stupnja paran broj. Slučaj |Y|\gt 5 nije moguć jer bi tada ostalo najviše 9 bridova za dvije komponente u G-Y, a znamo da zbog pretpostavke o struku svaka komponenta mora imati najmanje 5 bridova. Slijedi |Y|=5. Neka je Y=\lbrace u_{i}v_{i}\,:\, 1\leq i\leq 5\rbrace. Dakle, G-Y se sastoji od dva 5-ciklusa. Pretpostavimo da jedan od tih ciklusa ima skup vrhova T=\lbrace u_{i}\,:\,1\leq i\leq 5\rbrace. Neka je v_{i} treći susjed od u_{i} koji ne pripada skupu T, i=1,\ldots,5. Kada bi vrijedilo v_{1}v_{2}\in E(G) ili v_{1}v_{5}\in E(G), tada bi G sadržavao ciklus s 4 vrha što ne može biti. Zbog 3-regularnosti grafa G, mora vrijediti v_{1}v_{3}\in E(G) i v_{1}v_{4}\in E(G). Slično zaključujemo da v_{2}v_{4}\in E(G), v_{2}v_{5}\in E(G) i v_{3}v_{5}\in E(G). Odavde slijedi da je G izomorfan Petersenovom grafu pa smo dokazali jedinstvenost.

Neka je G povezan graf. Hamiltonov put u G je put koji sadrži sve vrhove grafa G. Hamiltonov ciklus u G je ciklus koji sadrži sve vrhove od G. Graf je Hamiltonov ako sadrži Hamiltonov ciklus. Iako se problem egzistencije Hamiltonova puta i Hamiltonova ciklusa pojavio puno ranije, 1969. godine Lovasz [12] postavlja slutnju koja povezuje Hamiltonove puteve i Hamiltonove cikluse sa simetrijama u grafovima. Slutnja glasi:

Graf G je tranzitivan po vrhovima ako za svaki par vrhova u i v iz G postoji automorfizam na G koji preslikava u u v.
Do danas nije otkriven niti jedan graf koji je tranzitivan po vrhovima, a nema Hamiltonov put. No, iako se ta slutnja pokazala istinitom za razne klase grafova, dokaz još nije pronađen. Štoviše, gotovo svi grafovi koji su potvrđivali ovu slutnju ujedno su i Hamiltonovi. Da sada su poznata samo 4 izuzetka, tj. 4 povezana, po vrhovima tranzitivna grafa (s najmanje 3 vrha) koji nemaju Hamiltonov ciklus: Petersenov graf, Coxeterov graf i još dva grafa dobivena od njih zamjenom svakog vrha sa 3-ciklusom. Vidi Sliku 6. Postoji još jedan takav graf, ali se on zbog svoje trivijalnosti često izostavlja. Radi se o potpunom grafu s dva vrha K_{2}.

Stoga je alternativna, i pomalo nespretna, verzija Lovaszove slutnje:

Ovakva je slutnja dokazana za sve takve grafove sa p\gt 2 vrhova gdje je p prost broj [3], za sve takve grafove s 2p vrhova osim za Petersenov graf [1] te za slučajeve p^{2}, p^{3}, 2p^{2} i 3p [13].

Zanimljivo je da su svi navedeni protuprimjeri 3-regularni grafovi pa pokušaji dokazivanja ili opovrgavanja Lovaszove slutnje ne mogu zaobići detaljnu analizu 3-regularnih po vrhovima tranzitivnih grafova.

Slika 6: a) Coxeterov graf i b) graf nastao od Petersenova zamjenom vrhova sa trokutima.

Dokažimo najprije da Petersenov graf ne sadrži Hamiltonov ciklus. Pretpostavimo suprotno, tj. neka je C Hamiltonov ciklus u Petersenovom grafu. Tada se P sastoji od 10-ciklusa C i još 5 dodatnih bridova. Ako bi svaki takav brid spajao dijametralno suprotne vrhove u C, tada bi P sadržavao 4-ciklus što ne može biti obzirom da je struk od P jednak 5. Stoga postoji najmanje jedan brid koji spaja vrhove na udaljenosti 4 u C (ne može spajati vrhove na manjoj udaljenosti jer bismo u tom slučaju dobili cikluse sa 3 ili 4 vrha). Neka je e jedan takav brid. Označimo mu krajeve sa u i v, tj. e=uv. Odaberimo vrh w dijametralno suprotan jednom od vrhova u i v. Tada svaki brid s jednim krajem u w tvori ciklus s najviše 4 vrha pa je nemoguće dodati 5 novih bridova u C, a da dobiveni graf ima struk veći od 4. Time je dokaz završen.

Sada još treba pokazati da je Petersenov graf najmanji 3-regularan graf bez mostova koji nema Hamiltonov ciklus te da nema drugih grafova s 10 vrhova koji imaju ista svojstva.
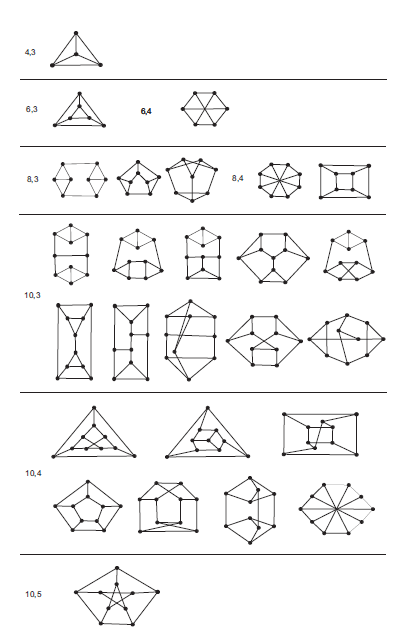
Svaki 3-regularan graf mora imati paran broj vrhova pa u obzir dolaze grafovi sa n=4,6,8,10 vrhova. \bullet Za n=4 imamo jedinstven 3-regularan graf, a to je potpun graf K_{4} koji je Hamiltonov. \bullet Za n=6 imamo samo dva neizomorfna 3-regularna grafa, jedan struka 3, a drugi struka 4. Graf struka 3 je trostrana prizma \Pi_{3}, a graf struka 4 je potpun bipartitan graf K_{3,3}. Za oba se grafa lako provjeri da su Hamiltonovi. \bullet Za n=8 imamo 5 takvih grafova, tri su struka 3, a ostala dva su struka 4. Vidi Sliku 7. Svi su ti grafovi Hamiltonovi.
\bullet Postoji 183-regularnih grafova s 10 vrhova koji nemaju mostova. Njih 12 ima struk 3, petero ih ima struk 4, a jedini graf struka 5 je Petersenov graf. Sa slike je vidljivo da svi ti grafovi, osim Petersenova grafa, sadrže Hamiltonov ciklus. U ovom dijelu rada dokazali smo da je Petersenov graf jedini najmanji 3-regularan graf bez mostova koji nema Hamiltonov ciklus, ali i više od toga: pokazali smo da je Petersenov graf jedan od rijetkih protuprimjera tvrdnji da je svaki povezan, po vrhovima tranzitivan graf ujedno i Hamiltonov.

Slika 7: 3-regularni grafovi bez mostova s 4,6,8, i 10 vrhova

Za graf G kažemo da je hipohamiltonov ako ne sadrži Hamiltonov ciklus, ali uklanjanjem proizvoljnog vrha iz G dobivamo Hamiltonov graf. Proučavanje takvih grafova počinje 1963. godine [17], a J.C.Herz, J.J.Duby i F.Vigue 1967.[8] dokazuju da je Petersenov graf najmanji hipohamiltonov graf. Hipohamiltonovi grafovi nisu rijetki. Do sada su otkriveni svi takvi grafovi sa najviše 17 vrhova, ali je dokazano da oni postoje i za svaki n\geq 18. Mnogi snarkovi su hipohamiltonovi grafovi. Navedimo nekoliko osnovnih svojstava hipohamiltonova grafa G. (i)G je 3-povezan, tj. potrebno je ukloniti najmanje 3 vrha da bi graf postao nepovezan. Ovo svojstvo se lako dokazuje. Ako iz G uklonimo samo jedan vrh, dobiti ćemo Hamiltonov graf, a to je povezan graf. Ako uklonimo dva vrha iz G, dobiti ćemo Hamiltonov put. Stoga je potrebno ukloniti najmanje 3 vrha da bi se graf raspao na najmanje dvije komponente povezanosti. (ii)\delta(G)\geq 3. Ukoliko bi postojao vrh stupnja 1 u G, tada bismo uklanjanjem njegovog susjeda dobili graf sa izoliranim vrhom. Ako bi G sadržavao vrh v stupnja 2, uklanjanjem jednog njegovog susjeda ne bismo dobili Hamiltonov graf jer bi u tom grafu v bio vrh stupnja 1. (iii)\displaystyle{\Delta(G)\leq \frac{n-1}{2}}. Neka je v vrh maksimalnog stupnja u G. Tada v ne može biti susjed sa 2 međusobno susjedna vrha u Hamiltonovom ciklusu C iz G-v jer bi u suprotnom G bio Hamiltonov graf. To je moguće jedino ako vrijedi gornja nejednakost. (iv) Ako G sadrži vrh v stupnja 3, tada v nije vrh ni jednog 3-ciklusa. Inače bi G bio Hamiltonov. Iako se čini da posljednja dva svojstva impliciraju nepostojanje 3-ciklusa u hipohamiltonovim grafovima, otkriveni su primjeri hipohamiltonovih grafova koji ih sadrže.

Dokaz da je Petersenov graf hipohamiltonov je jednostavan. Zbog svojstva tranzitivnosti po vrhovima, dovoljno je provjeriti da uklanjanjem jednog odabranog vrha dobivamo Hamiltonov graf. Minimalnost ćemo dokazati tako da pokažemo da niti jedan graf s manje vrhova nije hipohamiltonov. U tome će nam pomoći gore navedena svojstva hipohamiltonovih grafova, ali i Diracov teorem koji glasi:

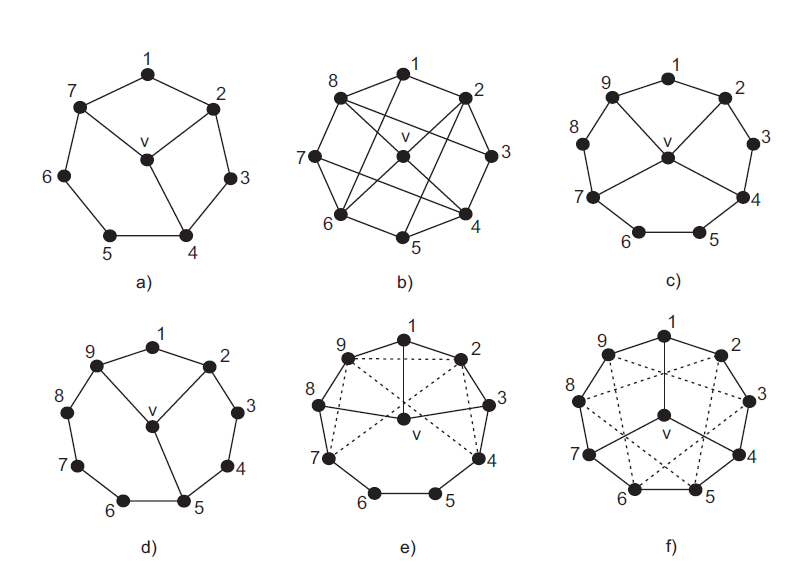
Zbog svojstva (ii) i Diracova teorema ne uzimamo u obzir grafove s manje od 7 vrhova. \bullet Pretpostavimo da postoji hipohamiltonov graf G sa 7 vrhova. Tada zbog Diracova teorema svi vrhovi moraju imati stupanj jednak 3. No, to je nemoguće jer je ukupan broj vrhova u grafu neparan broj. \bullet Slično zaključujemo da, ukoliko postoji, hipohamiltonov graf G s 8 vrhova mora biti 3-regularan. Fiksirajmo proizvoljan vrh v\in V(G). Neka je C Hamiltonov ciklus u G-v. Obzirom da je v susjed sa tri različita vrha u C, prema svojstvu (iv) niti jedan par takvih vrhova nije povezan bridom. Jedini mogući raspored susjeda od v prikazan je na Slici 8 a). Uz oznake kao na slici, v je susjed sa vrhovima 2, 4 i 7. Ostaju još vrhovi 1, 3, 5 i 6 koji moraju biti međusobno spojeni s još dva brida (jer |E(G)|=12). No, svaki mogući raspored bridova među njima daje Hamiltonov ciklus na G. Slijedi da ne postoji hipohamiltonov graf s 8 vrhova.

\bullet Neka |V(G)|=9. Slijedi 3\leq d(u)\leq 4\forall u\in V(G) i postoji barem jedan vrh, recimo v, stupnja 4. Samo je jedan mogući raspored vrhova-susjeda od v u Hamiltonovom ciklusu iz G-v. Vidi Sliku 8 b). Svaki od vrhova 1, 3, 5, 6 i 8 mora biti incidentan s još najmanje jednim novim bridom. Kada bi postojao brid između takvih vrhova, G bi bio Hamiltonov graf. Stoga svaki takav vrh mora biti susjed nekom susjedu od v. Jedini mogući raspored bridova među tim vrhovima prikazan je također na Slici 8 b). Dobiveni graf ima maksimalan mogući broj bridova, ali nije hipohamiltonov jer graf koji dobivamo uklanjanjem bilo kojeg vrha iz skupa \lbrace 2,4,6,8\rbrace ne sadrži Hamiltonov ciklus.

\bullet Neka |V(G)|=10. Vrijedi 3\leq d(u)\leq 4\forall u\in V(G). Neka postoji vrh v u G takav da d(v)=4. Jedini mogući raspored njegovih susjeda u Hamiltonovom ciklusu iz G-v prikazan je kao na Slici 8 c). Ne postoji brid među vrhovima iz skupa A=\lbrace 1,3,5,6,8\rbrace jer bi tada G bio Hamiltonov. Stoga svaki vrh iz skupa A mora biti povezan bridom s nekim vrhom iz skupa B=\lbrace 2,4,7,9\rbrace. Prema Dirichletovom principu, postoji vrh iz B koji će imati dva susjeda u A, a to ne može biti jer vrhovi iz B ne mogu biti stupnja većeg od 4. Zaključujemo da ne postoji vrh stupnja 4 u G.

Neka su svi vrhovi u G stupnja 3. Odaberemo proizvoljan vrh v u G. Svi mogući rasporedi vrhova-susjeda od v na Hamiltonovom ciklusu u G-v prikazani su na Slici 8 d), e) i f).
Promotrimo najprije Sliku 8 d). Vrh 1 može biti susjed jedino sa 7, jer svaki drugi brid incidentan s 1 daje Hamiltonov ciklus u G. No, tada je vrh 3 susjed sa 8 jer brid 3-6 daje Hamiltonov ciklus. Sada je nužno 4 susjed sa 6, no, tako dobiveni graf je Hamiltonov.

Na Slici 8 e) zabranjeni bridovi su označeni isprekidanom crtom. Ako imamo bridove 2-5 i 6-9, tada nužno imamo brid 4-7, ali tako dobiveni graf nije hipohamiltonov jer npr. uklanjanjem vrha 4 ne dobivamo Hamiltonov graf. Ako imamo bridove 2-6 i 5-9, onda opet nužno vrijedi 4-7, no, tada je G Hamiltonov graf. Slučaj na Slici 8 f) daje Petersenov graf. Evo kako: ukoliko bi postojao brid 2-9, onda nužno imamo bridove 3-5 i 6-8, ali takav G je Hamiltonov. Dakle, jedini dozvoljeni bridovi su 2-6, 5-9 i 3-8, što je upravo Petersenov graf. Dokaz da je Petersenov graf jedini najmanji hipohamiltonov graf je završen.

Slika 8: \,

U nastavku ćemo ćemo se pozabaviti još nekim, ne tako očitim, svojstvima Petersenova grafa.

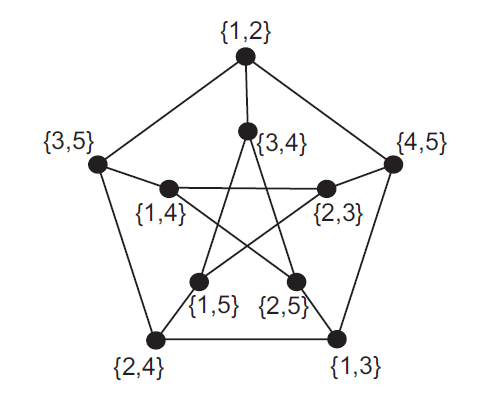
Neka su n i k prirodni brojevi. Kneserov graf K(n,k) je graf čiji vrhovi odgovaraju k-članim podskupovima skupa od n elemenata, a dva su vrha povezana bridom ako i samo ako odgovarajuća dva podskupa nemaju zajedničkih elemenata. Takve je grafove prvi proučavao Martin Kneser 1955. godine.

Najjednostavniji primjer Kneserovog grafa je potpun graf s n vrhova K(n,1)=K_{n}.

Slika 9: Petersenov graf kao Kneserov K(5,2) graf

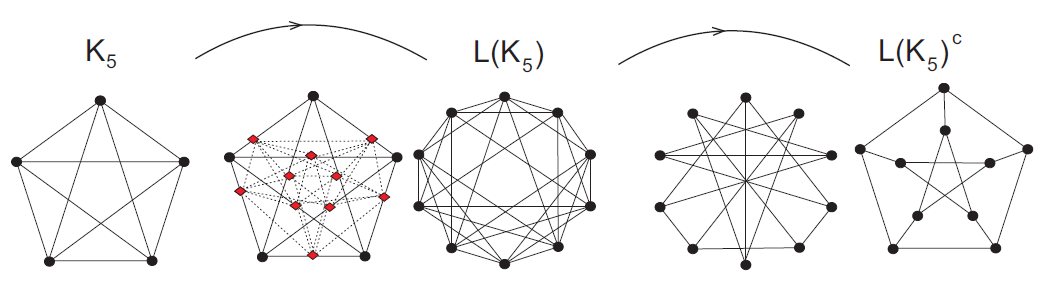
\bullet Petersenov graf je komplement linijskog grafa potpunog grafa K_{5}.

Linijski graf grafa G je graf L(G) sa skupom vrhova E(G), a dva vrha su spojena bridom ako i samo ako su odgovarajući bridovi od G incidentni sa istim vrhom. Komplement G^{c} grafa G je graf sa istim skupom vrhova V(G) kao i graf G, a dva vrha su susjedna u G^{c} ako i samo ako nisu susjedna u G. Na Slici 7.10. je prikazan postupak dobivanja Petersenova grafa primjenom dvije uzastopne unarne operacije nad K_{5}:

Slika 10: \, Petersenov graf kao (L(K_{5}))^{c}

Napomena: Svaki graf nastao komplementiranjem linijskog grafa potpunog grafa s n vrhova je Knesereov graf K(n,2).

Automorfizam grafa G je permutacija skupa vrhova V(G) koja čuva susjednost. Simetrična grupa S_{5} je grupa čiji su elementi sve n-permutacije n-članog skupa uz operaciju kompozicije tih permutacija. Već smo ustanovili da je Petersenov graf Kneserov graf K(5,2). Neka je dan skup A=\lbrace a,b,c,d,e\rbrace. Ako su \lbrace a,b\rbrace i \lbrace c,d\rbrace dva susjedna vrha Petersenova grafa, tada vrijedi \lbrace a,b\rbrace \cap\lbrace c,d\rbrace =\emptyset. No, tada je i \lbrace \sigma(a),\sigma(b))\rbrace \cap\lbrace \sigma(c),\sigma(d)\rbrace =\emptyset, gdje je \sigma bilo koja permutacija skupa A. Stoga svaka permutacija vrhova grafa preslikava susjedne vrhove u susjedne, a nesusjedne u nesusjedne, tj. svake dvije različite permutacije od S_{5} induciraju dva različita automorfizma na K(5,2). Stoga 120=|S_{5}|\leq |Aut(P)|. Dokaz da je |Aut(P)|\leq |S_{5}| je zahtjevniji pa ga izostavljamo.

Jako regularan graf s parametrima (n,k,\lambda,\mu) je k-regularan graf s n vrhova koji ispunjava slijedeća dva svojstva:

Obzirom da je struk Petersenova grafa jednak 5, jasno je da niti jedan par susjednih vrhova nema zajedničkih susjeda, tj. \lambda=0. Uzimajući u obzir i dijametar koji je jednak 2, slijedi \mu=1.

Neka je A matrica susjedstva Petersenova grafa P. Obzirom da je P3-regularan graf, vrijedi Au=3u, gdje je u vektor jedinica. Odmah je jasno da je 3 svojstvena vrijednost matrice A sa svojstvenim vektorom u. Obzirom da niti jedan par susjednih vrhova u P nema zajednički vrh, a svaki par nesusjednih vrhova ima zajednički vrh, za matricu A vrijedi jednadžba:

pri čemu je I jedinična matrica, a J matrica čiji su svi elementi jedinice.
Neka je \lambda svojstvena vrijednost od A različita od 3 te neka je v pripadni svojstveni vektor, tj. Av=\lambda v.
Slijedi v^{\tau}u=0 jer su svojstveni vektori simetrične realne matrice međusobno ortogonalni. Također vrijedi Jv=0.
Množenjem jednadžbe (3) sa v dobivamo

Obzirom da vrijedi v\neq 0, slijedi \lambda^{2}+\lambda-2=0. Rješenja ove kvadratne jednadžbe su \displaystyle{\lambda_{1}=-2} i \displaystyle{\lambda_{2}=1}. Kako jednadžba vrijedi za svaki svojstveni vektor različit od u, slijedi da su -2, 1 i 3 jedine svojstvene vrijednosti od A. Odredimo im kratnost. Poznato je [5] da je najveća svojstvena vrijednost matrice susjedstva jednostavnog grafa algebarske kratnosti 1. Uzimajući u obzir i to da je \displaystyle{\sum_{i=1}^{10}\lambda_{i}=\sum_{i=1}^{n} a_{ii}=0} (\displaystyle{a_{ii}} dijagonalni elementi od A), dobivamo sustav jednadžbi: -2a+1b+3=0, a+b+1=10 iz kojeg slijedi a=4, b=5. Spektar se, dakle, sastoji od svojstvenih vrijednosti: 3, \displaystyle{-2^{(4)}} i \displaystyle{1^{(5)}}.

Planarne grafove možemo smjestiti u ravninu ili na sferu tako da im se bridovi sijeku samo u vrhovima. Minora grafa G je graf dobiven nizom uklanjanja i kontraktiranja bridova i uklanjanja vrhova. Kontrakcija brida u grafu je uklanjanje brida uz identifikaciju vrhova-krajeva tog brida. Vrijedi Wagnerov teorem iz 1937. godine: "GrafG je planaran ako i samo ako mu ni K_{5} ni K_{3,3} nisu minore."} Da Petersenov graf ima minoru K_{5}, može se lako ustanoviti promatrajući njegov prikaz u prvom redu lijevo na Slici 1. Ukoliko kontraktiramo bridove incidentne vrhovima vanjskog ciklusa, a koji ne pripadaju tom ciklusu, dobiti ćemo K_{5}. Minoru K_{3,3} možemo formirati tako da npr. promatramo drugi po redu prikaz Petersenova grafa na Slici 1. Ako uklonimo središnji vrh i kontraktiramo brid incidentan svakom susjedu izbrisanog vrha, dobiti ćemo K_{3,3}.

Petersenov graf ima mnoštvo iznimnih svojstava zbog kojih zauzima vrlo važno mjesto u području teorije grafova. Vrlo često se pojavljuje kao protuprimjer raznim tvrdnjama o grafovima.
Citirati ćemo jednu popularnu izreku u teoriji grafova: