Uparena optimizacijska metoda
Luka Borozan, Slobodan Jelić, Domagoj Matijević, Domagoj Ševerdija
Sveučilište J.J. Strossmayera u Osijeku, Odjel za matematiku
lborozan@mathos.hr
Sveučilište J.J. Strossmayera u Osijeku, Odjel za matematiku
lborozan@mathos.hr
Sažetak
U ovom članku analiziramo metode gradijentnog i zrcalnog spusta u području konveksne optimizacije s danim naglaskom na njihove brzine konvergencije. Nadalje, uparujući dvije spomenute metode dobivamo takozvanu uparenu metodu čija analiza konvergencije pokazuje ubrzanje u odnosu na gradijentnu i zrcalnu metodu, te bilo koju drugu nama poznatu metodu prvoga reda.
Uvod
Probleme konveksne optimizacije često nalazimo kako u različitim područjima matematike i računarstva, tako i u primjeni. Do sada su razvijene mnoge metode konveksne optimizacije, primjerice metoda gradijentnog spusta, metoda najbržeg spusta, metoda zrcalnog spusta, metoda polovljenja, itd. Više o tim metodama može se naći u
Prvo ćemo ukratko objasniti metode gradijentnog i zrcalnog spusta, a potom ćemo konstruirati i opravdati uparenu metodu.
Metoda gradijentnog spusta
Metoda gradijentnog spusta ili gradijentna metoda jedna je od najstarijih i najjednostavnijih iterativnih metoda rješavanja problema konveksne optimizacije. Ona minimizira konveksnu, diferencijabilnu funkciju f po varijabli x \in S, gdje je S konveksan i zatvoren skup. Dodatno zahtijevamo da je \nabla f Lipschitz neprekidna na S s konstantom L. Prvo ćemo dati definiciju koraka (iteracije) metode gradijentnog spusta.
Definicija 1. Neka je x \in S. Iteracija gradijentne metode s duljinom koraka 1 / L je
\tilde{x} = \text{Grad}(x) = \text{argmin}_{y \in S} \left\lbrace f(x) + \frac{L}{2} \left\Vert y - x \right\Vert ^{2} + \langle \nabla f(x), y - x \rangle \right\rbrace .
Označimo \text{Prog}(x) = - \min_{y \in S} \left\lbrace \frac{L}{2} \left\Vert y - x \right\Vert ^{2} + \langle \nabla f(x), y - x \rangle \right\rbrace \geq 0. Primijetimo kako se gornja definicija koraka gradijentne metode bitno razlikuje od gradijentne metode kod koje je S = \mathbb{R}^{n} i \left\Vert \cdot \right\Vert = \left\Vert \cdot \right\Vert_{2}, tj. kod gradijentne metode bez ograničenja u euklidskoj normi (\text{Grad}(x) = x - \frac{1}{L}f'(x)). Više o gradijentnoj metodi u neeuklidskim normama može se pronaći u
Definicija 2. Neka je x \in \mathbb{R}^{n}, te \left\Vert\cdot\right\Vert norma na \mathbb{R}^{n}. Dualnu normu norme \left\Vert\cdot\right\Vert definiramo kao
\left\Vert x \right\Vert _{*} = \displaystyle \max \limits_{\left\Vert v \right\Vert = 1} v^{T}x.
Sljedeći teorem daje nam ocjenu smanjenja vrijednosti funkcije cilja metode gradijentnog spusta, te je dokazan po uzoru na
Dokaz. Neka je \tilde{x} = \text{Grad}(x). Imamo:
\begin{array}{lcl} \text{Prog}(x) & = & \displaystyle - \min_{y \in S} \left\lbrace \frac{L}{2} \left\Vert y - x \right\Vert ^{2} + \langle \nabla f(x), y - x \rangle \right\rbrace \\ & = & \displaystyle - \left( \frac{L}{2} \left\Vert \tilde{x} - x \right\Vert ^{2} + \langle \nabla f(x), \tilde{x} - x \rangle \right) \\ & = & \displaystyle f(x) - \left(\frac{L}{2} \left\Vert \tilde{x} - x \right\Vert ^{2} + \langle \nabla f(x), \tilde{x} - x \rangle + f(x) \right) \leq f(x) - f(\tilde{x}). \\ \end{array}
Posljednja nejednakost posljedica je sljedećeg izraza. Neka su x, y \in S.
\begin{array}{lcl} f(y) - f(x) & = & \displaystyle \int_{0}^{1} \langle \nabla f(x + t(y - x)), y - x \rangle \text{d}t \\ & = & \displaystyle \langle \nabla f(x), y - x \rangle + \int_{0}^{1} \langle \nabla f(x + t(y - x)) - \nabla f(x), y - x \rangle \text{d}t \\ & \leq & \displaystyle \langle \nabla f(x), y - x \rangle + \int_{0}^{1} \left\Vert \nabla f(x + t(y - x)) - \nabla f(x) \right\Vert_{*} \left\Vert y - x \right\Vert \text{d}t \\ & \leq & \displaystyle \langle \nabla f(x), y - x \rangle + \int_{0}^{1} tL \left\Vert y - x \right\Vert^{2} \text{d}t \\ & = & \displaystyle \langle \nabla f(x), y - x \rangle + \frac{L}{2}\left\Vert y - x \right\Vert^{2}. \\ \end{array}
Time je tvrdnja dokazana.
\ \blacksquare
Sada ćemo dati i ocjenu pogreške gradijentne metode.
Teorem 4.([2] ) Neka je x_{k} aproksimacija točke minimuma x^{*} dobivena k-tom iteracijom metode gradijentnog spusta s početnom aproksimacijom x_{0}. Tada vrijedi f(x_{k}) - f(x^{*}) \leq \mathcal{O} \left( \frac{L \left\Vert x_{0} - x^{*} \right\Vert^{2}_{2}}{k} \right). Nadalje, \varepsilon-aproksimaciju točke x^{*} postižemo u \Omega (\frac{L \left\Vert x_{0} - x^{*} \right\Vert^{2}_{2}}{\varepsilon}) iteracija.
Metoda zrcalnog spusta
Kao i kod metode gradijentnog spusta, tako i kod metode zrcalnog spusta pretpostavljamo da je f konveksna funkcija u varijabli x \in S, gdje je S konveksan i zatvoren skup, te da je Lipschitz neprekidna na S s konstantom K. Kako bismo mogli uvesti ovu metodu, potrebno nam je definirati nekoliko pojmova.
Definicija 5. Neka je f konveksna funkcija na \mathbb{R}^{n}. Kažemo da je \partial f(x) subgradijent od f u x ako je f(y) \geq f(x) + \langle \partial f(x), y - x\rangle, \quad \forall y \in \mathbb{R}^{n}.
Primjer 6. Za funkciju f(x) = |x| subgradijent \partial f možemo definirati na sljedeći način. Neka je x \in \mathbb{R}. Ako je x \lt 0, očito je \partial f(x) = -1, a ako je x \gt 0, očito je \partial f(x) = 1. Preostaje odrediti \partial f(0). Mora vrijediti |x| \geq \partial f(0) \cdot x. To je zadovoljeno za \partial f(0) \in \lbrace -1, 1\rbrace.
Sljedeća propozicija govori o subgradijentnom uvjetu ekvivalentnom Lipschitzovoj neprekidnosti kojeg ćemo dalje koristiti kako bismo definirali korak metode zrcalnog spusta.
Propozicija Neka je f konveksna funkcija na konveksnom skupu S. Tada je f Lipschitz neprekidna s konstantom K na S ako i samo ako za svaku točku x \in S vrijedi \left\Vert \partial f(x) \right\Vert_{*} \leq K, gdje je \partial f bilo koji subgradijent od f.
(\Rightarrow) Pretpostavimo da je f Lipschitz neprekidna s konstantom K na S, te {x, y \in S}. Neka je y - x = \text{argmax}_{\left\Vert z \right\Vert = 1} \langle \partial f(x), z \rangle. Tada vrijedi \left\Vert y - x \right\Vert = 1, te \langle \partial f(x), z \rangle = \left\Vert \partial f(x) \right\Vert_{*} po definiciji dualne norme. Koristeći pretpostavku o Lipschitz neprekidnosti od f, definiciju subgradijenta, te Cauchy-Schwarz-Bunyakovsky nejednakost imamo:
Iz \left\Vert y - x \right\Vert = 1 slijedi prva implikacija.
(\Leftarrow) Neka sada \forall x \in S vrijedi \left\Vert \partial f(x) \right\Vert_{*} \leq K. Neka je y \in S. Množeći definiciju subgradijenta s -1, te primjenom Cauchy-Schwarz-Bunyakovsky nejednakosti imamo:
Analogno, zamjenom uloga x i y dobivamo f(y) - f(x) \leq K \left\Vert x - y \right\Vert. Uparivanjem prethodne dvije nejednakosti dobivamo:
Time smo dokazali i drugu implikaciju, pa tako i tvrdnju propozicije.
K \left\Vert y - x \right\Vert \geq f(y) - f(x) \geq \langle \partial f(x), y - x \rangle = \left\Vert \partial f(x) \right\Vert_{*}.
Iz \left\Vert y - x \right\Vert = 1 slijedi prva implikacija.
(\Leftarrow) Neka sada \forall x \in S vrijedi \left\Vert \partial f(x) \right\Vert_{*} \leq K. Neka je y \in S. Množeći definiciju subgradijenta s -1, te primjenom Cauchy-Schwarz-Bunyakovsky nejednakosti imamo:
f(x) - f(y) \leq \langle \partial f(x), x - y \rangle \leq \left\Vert \partial f(x) \right\Vert_{*} \left\Vert x - y\right\Vert \leq K \left\Vert x - y \right\Vert.
Analogno, zamjenom uloga x i y dobivamo f(y) - f(x) \leq K \left\Vert x - y \right\Vert. Uparivanjem prethodne dvije nejednakosti dobivamo:
\max \lbrace f(y) - f(x), f(x) - f(y) \rbrace = \left\vert f(x) - f(y) \right\vert \leq K \left\Vert x - y \right\Vert.
Time smo dokazali i drugu implikaciju, pa tako i tvrdnju propozicije.
\ \blacksquare
U svrhu definiranja iteracije metode zrcalnog spusta trebaju nam i sljedeće definicije.
Definicija 7. Kažemo da je d : \mathbb{R}^{n} \times \mathbb{R}^{n} \rightarrow [0, \infty\rangle kvazimetrička funkcija ukoliko {\forall x, y \in \mathbb{R}^{n}} vrijedi d(x, y) = 0 \ \Leftrightarrow \ x = y.
Definicija 8. Neka je \phi 1-jako konveksna, diferencijabilna funkcija na \text{Int}S. Funkciju d : \text{Int}S \times S \rightarrow [0, \infty\rangle definiranu s d(x, y) = \phi(y) - \phi(x) - \langle \nabla\phi(x), y - x\rangle nazivamo Bregmanova divergencija.
Napomena Vrijedi d(x, y) \geq \displaystyle \frac{1}{2}\left\Vert x - y \right\Vert^{2}. Dokaz ove tvrdnje ćemo izostaviti.
Sada možemo definirati korak metode zrcalnog spusta.
Definicija 9. Iteracija metode zrcalnog spusta s duljinom \alpha \gt 0 dana je sljedećim izrazom:
gdje je \partial f neki subgradijent funkcije f.
\displaystyle \text{Mirr}(\alpha, x, \partial f) = \text{argmin}_{y \in S} \lbrace d(x, y) + \langle \alpha\partial f(x), y - x \rangle\rbrace,
gdje je \partial f neki subgradijent funkcije f.
Sljedeći rezultat govori o brzini konvergencije metode zrcalnog spusta. Dokaz mu je preuzet iz
Teorem 10. Ako je \tilde{x} = \text{Mirr}(\alpha, x, \partial f), gdje su \alpha \gt 0 duljina koraka, te \partial f neki subgradijent od f, tada \forall u \in S vrijedi:
\alpha(f(x) - f(u)) \leq \alpha \langle \partial f(x), x - u \rangle \leq \displaystyle \frac{\alpha^{2}}{2} \Vert \partial f(x) \Vert^{2}_{*} + d(x, u) - d(\tilde{x}, u).
Dokaz. Prva nejednakost slijedi iz definicije subgradijenta. Počnimo od izraza:
8 . Sada imamo:
\begin{array}{lcl} \langle \alpha \partial f(x), x - u \rangle & = & \langle \alpha \partial f(x), x - \tilde{x} \rangle + \langle \alpha \partial f(x), \tilde{x} - u \rangle. \\ \end{array}
Iz činjenice da je \tilde{x} dobiven minimizacijom po y \in S izraza d(x, y) + \langle \alpha \partial f(x), y \rangle, dobivamo da je \langle \partial_{2} d(x, \tilde{x}) + \alpha \partial f(x), u - \tilde{x}\rangle = 0, pa imamo:
\begin{array}{lcl} \langle \alpha \partial f(x), x - u \rangle & \leq & \langle \alpha \partial f(x), x - \tilde{x} \rangle + \langle -\partial_{2} d(x, \tilde{x}), \tilde{x} - u \rangle. \\ \\ \end{array}
Ocijenimo sada drugi sumand na lijevoj strani prethodne nejednakosti.
\begin{array}{lcl} \langle -\partial_{2} d(x, \tilde{x}), \tilde{x} - u \rangle & = & \langle \nabla \phi (x) - \nabla \phi (\tilde{x}), \tilde{x} - u \rangle \\ & = & (\phi (u) - \phi(x) - \langle \nabla \phi (x), u - x \rangle) - (\phi (u) - \phi(\tilde{x}) - \langle \nabla \phi (\tilde{x}), u - \tilde{x} \rangle) \\ & & - (\phi (\tilde{x}) - \phi(x) - \langle \nabla \phi (x), \tilde{x} - x \rangle) \\ & = & d(x, u) - d(\tilde{x}, u) - d(x, \tilde{x}) \leq d(x, u) - d(\tilde{x}, u) - \displaystyle \frac{1}{2} \Vert x - \tilde{x}\Vert^{2}. \\ \end{array}
Posljednja nejednakost slijedi iz svojstva Bregmanove divergencije danog u
\begin{array}{lcl} \langle \alpha \partial f(x), x - u \rangle & \leq & (\langle \alpha \partial f(x), x - \tilde{x} \rangle - \displaystyle \frac{1}{2} \Vert x - \tilde{x}\Vert^{2}) + (d(x, u) - d(\tilde{x}, u)). \\ & \leq & \displaystyle \frac{\alpha^{2}}{2} \Vert \partial f(\tilde{x}) \Vert^{2}_{*} + (d(x, u) - d(\tilde{x}, u)). \\ \end{array}
Posljednja nejednakost slijedi iz ab - \frac{1}{2}b^{2} \leq \frac{1}{2}a^{2}, \ a, b \in \mathbb{R}. Time je teorem dokazan.
\ \blacksquare
Za kraj, navedimo rezultat koji ocjenjuje pogrešku metode zrcalnog spusta.
Teorem 11. Neka je \bar{x} = \frac{1}{k}\sum_{i = 0}^{k - 1}x_{i} aritmetička sredina prvih k iteracija metode zrcalnog spusta, \Theta bilo koja gornja međa na d(x_{0}, x^{*}), gdje je x^{*} točka minimuma, te neka je \alpha = \frac{\sqrt{2 \Theta}}{K\sqrt{k}}. Vrijedi: f(\bar{x}) - f(x^{*}) \leq \frac{\sqrt{2\Theta}K}{\sqrt{k}}. Nadalje, \varepsilon-aproksimaciju točke x^{*} postižemo u \Omega(\frac{2\Theta K^{2}}{\varepsilon^{2}}) iteracija.
Dokaz prethodnog teorema može se pronaći u
Osvrt na metode gradijentnog i zrcalnog spusta
U praksi se pokazalo kako gradijentna metoda brzo konvergira dok je trenutna iteracija ”daleko” od optimalnog rješenja, dok metoda zrcalnog spusta konvergira brzo kada je ”blizu” optimuma. Zbog toga ćemo u nastavku razviti metodu koja će izmjenjivati korake gradijentne i metode zrcalnog spusta ovisno o tome koliko koja metoda pridonosi konvergenciji prema optimumu.
Napomena. U slučaju kada je \phi (x) = \frac{1}{2}\Vert x \Vert^{2}_{2} i \Vert \cdot \Vert = \Vert \cdot \Vert_{2} gradijentne i zrcalne iteracije su ekvivalentne.
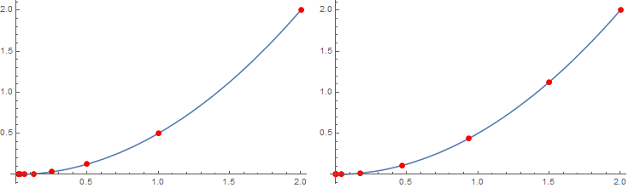
Primjer 12. Metodama gradijentnog i zrcalnog spusta minimizirat ćemo funkciju f(x) = \frac{x^{2}}{2} s početnom aproksimacijom x_{0} = 2 na segmentu [0, 2]. Istaknute točke na sljedeća dva grafa prikazuju iteracije dviju metoda s desna na lijevo.
Na slici 1 se jasno vidi kako je metoda gradijentnog spusta brža od metode zrcalnog spusta u prvih nekoliko iteracija. Također, uočavamo kako metoda zrcalnog spusta brže konvergira nakon prvih nekoliko iteracija. Ovim smo primjerom intuitivno opravdali konstrukciju metode koja uparuje gradijentnu i zrcalnu metodu.
Pojednostavljena uparena metoda
Pokušat ćemo konstruirati metodu koja uparuje metode gradijentnog i zrcalnog spusta s ciljem ubrzanja konvergencije. Ova metoda je prvi puta spomenuta u
Ideja pojednostavljenog algoritma je sljedeća:
| \bullet | postavimo tri početne iteracije x_{0} = y_{0} = z_{0}, |
| \bullet | u svakoj iteraciji k računamo vrijednosti x_{k + 1}, y_{k + 1}, z_{k + 1}, |
| \bullet | x_{k + 1} = \tau z_{k} + (1 - \tau)y_{k}, |
| \bullet | y_{k + 1} = \text{Grad}(x_{k + 1}), |
| \bullet | z_{k + 1} = \text{Mirr}(\alpha, x_{k + 1}, \partial f). |
Još nam preostaje razmotriti brojeve \alpha i \tau. Broj \alpha je zasada konstantna duljina koraka metode zrcalnog spusta, dok je \tau također privremeno konstantna težina pomoću koje kontroliramo utjecaj metoda gradijentnog i zrcalnog spusta na aproksimaciju rješenja. Sljedeći teorem nam daje osnovni rezultat koji će nam pomoći pri dokazivanju teorema o brzini konvergencije pojednostavljene uparene metode.
Teorem 13. Za svaki u iz \mathbb{R}^{n} imamo:
\begin{array}{lcl} \alpha \langle \nabla f(x_{k + 1}), z_{k} - u \rangle & \leq & \displaystyle \frac{\alpha^{2}}{2} \Vert \nabla f(x_{k + 1}) \Vert^{2}_{*} + d(z_{k}, u) - d(z_{k + 1}, u) \\ & \leq & \alpha^{2} L(f(x_{k + 1}) - f(y_{k + 1})) + d(z_{k}, u) - d(z_{k + 1}, u). \\ \end{array}
Dokaz. Dokaz prve nejednakosti identičan je dokazu Teorema 10 uz promijenjene oznake. Iz Teorema 3 imamo (uz promjenu oznaka) f(x_{k + 1}) - f(y_{k + 1}) \geq \text{Prog}(x_{k + 1}), gdje je
\begin{array}{lcl} \text{Prog}(x_{k + 1}) & = & \displaystyle - \min_{y \in \mathbb{R^{n}}} \left\lbrace \frac{L}{2} \Vert y - x_{k + 1} \Vert ^{2} + \langle \nabla f(x_{k + 1}), y - x_{k + 1} \rangle \right\rbrace \\ & = & \displaystyle -L \min_{y \in \mathbb{R^{n}}} \left\lbrace \frac{1}{2} \Vert x_{k + 1} - y \Vert ^{2} - \frac{1}{L} \langle \nabla f(x_{k + 1}), x_{k + 1} - y \rangle \right\rbrace \\ & \geq & \displaystyle -L \min_{y \in \mathbb{R^{n}}} \left\lbrace \frac{1}{2} \Vert x_{k + 1} - y \Vert ^{2} - \frac{1}{L} \Vert \nabla f(x_{k + 1}) \Vert_{*} \Vert x_{k + 1} - y \Vert \right\rbrace \\ & \geq & \displaystyle -L \min_{y \in \mathbb{R^{n}}} \left\lbrace -\frac{1}{2L^{2}} \Vert \nabla f(x_{k + 1}) \Vert^{2}_{*} \right\rbrace = \displaystyle \frac{1}{2L} \Vert \nabla f(x_{k + 1}) \Vert^{2}_{*}.\\ \end{array}
Koristeći nejednakost f(x_{k + 1}) - f(y_{k + 1}) \geq \frac{1}{2L} \Vert \nabla f(x_{k + 1}) \Vert^{2}_{*} slijedi i druga nejednakost.
\ \blacksquare
Iz prethodnog teorema vidimo kako je pogreška iteracije metode zrcalnog spusta \frac{\alpha^{2}}{2} \Vert \nabla f(x_{k + 1}) \Vert^{2}_{*} proporcionalna smanjenju vrijednosti funkcije cilja dobivenom gradijentnom iteracijom f(x_{k + 1}) - f(y_{k + 1}). Na taj način opravdavamo praktični rezultat (o brzini konvergencije gradijentne i zrcalne metode) iz prethodnog potpoglavlja.
Sada ćemo navesti rezultat koji daje brzinu konvergencije pojednostavljene uparene metode.
Teorem 14. Ukoliko odaberemo \tau \in (0, 1) takav da je \frac{1 - \tau}{\tau} = \alpha L, tada \forall u \in \mathbb{R}^{n} imamo:
\alpha \langle \nabla f(x_{k + 1}), x_{k + 1} - u \rangle \leq \alpha^{2} L (f(y_{k}) - f(y_{k + 1})) + (d(z_{k}, u) - d(z_{k + 1}, u)).
Dokaz. Primijetimo da za x_{k + 1} vrijedi \tau (x_{k + 1} - z_{k}) = (1 - \tau)(y_{k} - x_{k + 1}). Koristeći tu činjenicu i osnovna svojstva konveksnih funkcija imamo:
13 , uz \frac{1 - \tau}{\tau} = \alpha L dokazujemo tvrdnju.
\begin{array}{lcl} \alpha \langle \nabla f(x_{k + 1}), x_{k + 1} - u \rangle - \alpha \langle \nabla f(x_{k + 1}), z_{k} - u \rangle & = & \alpha \langle \nabla f(x_{k + 1}), x_{k + 1} - z_{k} \rangle \\ & = & \displaystyle \frac{1 - \tau}{\tau} \alpha \langle \nabla f(x_{k + 1}), x_{k + 1} - z_{k} \rangle \\ & \leq & \displaystyle \frac{1 - \tau}{\tau} \alpha (f(y_{k}) - f(x_{k + 1})). \\ \end{array}
Zbrajanjem gornjeg izraza i Teorema
\ \blacksquare
Preostaje nam još ocijeniti pogrešku.
Teorem 15. Neka je \Theta gornja ocjena vrijednosti d(x_{0}, x^{*}), gdje je x_{0} početna aproksimacija, a x^{*} točka minimuma. Ako je \bar{x} = \frac{1}{k}\sum_{i = 0}^{k - 1}x_{i} aritmetička sredina prvih k iteracija pojednostavljene uparene metode, te r \geq 0 takav da f(x_{0}) - f(x^{*}) \leq r, tada imamo: f(\bar{x}) - f(x^{*}) \leq \frac{2\sqrt{L \Theta r}}{k}. Nadalje, \varepsilon-aproksimaciju točke x^{*} postižemo u \mathcal{O}(\sqrt{\frac{L\Theta}{\varepsilon}}) iteracija.
Dokaz. Neka je \bar{x} = \frac{1}{k} \sum_{i = 0}^{k - 1} x_{i} suma prvih k iteracija pojednostavljene uparene metode. U iskazu Teorema 14 uzmimo da je u = x^{*}. Korištenjem Jensenove nejednakosti imamo:
k = \mathcal{O} \left( \sqrt{\frac{L\Theta}{\varepsilon}} + \sqrt{\frac{L\Theta}{2\varepsilon}} + \sqrt{\frac{L\Theta}{4\varepsilon}} + \dots \right) = \mathcal{O}\left( \sqrt{\frac{L\Theta}{\varepsilon}}\right) koraka. Time je tvrdnja dokazana.
\begin{array}{lcl} \alpha k (f(\bar{x}) - f(x^{*})) & = & \displaystyle \alpha k \left(f \left(\sum_{i = 0}^{k - 1} \frac{x_{i}}{k} \right) - f(x^{*})\right) \leq \displaystyle \alpha k \left( \sum_{i = 0}^{k - 1} \frac{1}{k} f(x_{i}) - f(x^{*}) \right) \\ & = & \displaystyle \alpha \sum_{i = 0}^{k - 1} (f(x_{i}) - f(x^{*})) \leq \displaystyle \alpha \sum_{i = 0}^{k - 1} \langle \nabla f(x_{i}), x_{i} - x^{*} \rangle \\ & \leq & \alpha^{2} L(f(y_{0}) - f(y_{k})) + d(x_{0}, x^{*}) - d(z_{k}, x^{*}) \leq \alpha^{2} Ld + \Theta, \\ \end{array}
gdje je d neka gornja međa za f(y_{0}) - f(y_{k}). Iz izbora \alpha = \sqrt{\frac{\Theta}{Ld}} slijedi f(\bar{x}) - f(x^{*}) \leq \frac{2\sqrt{\Theta Ld}}{k}. Drugim riječima, u k \geq 4\sqrt{\frac{L\Theta}{d}} koraka možemo doći do aproksimacije \bar{x} takve da je f(\bar{x}) - f(x^{*}) \leq \frac{d}{2}. Ako ovaj postupak ponovno pokrenemo nekoliko puta, prepolavljajući udaljenost do optimuma, dobivamo \varepsilon-aproksimaciju rješenja uk = \mathcal{O} \left( \sqrt{\frac{L\Theta}{\varepsilon}} + \sqrt{\frac{L\Theta}{2\varepsilon}} + \sqrt{\frac{L\Theta}{4\varepsilon}} + \dots \right) = \mathcal{O}\left( \sqrt{\frac{L\Theta}{\varepsilon}}\right) koraka. Time je tvrdnja dokazana.
\ \blacksquare
Iz posljednjeg dokaza možemo primijetiti kako se duljina koraka \alpha povećava svakim ponovnim pokretanjem algoritma, dok \tau pada. To znači da što smo bliže optimumu gradijentnoj metodi dajemo veću težinu, što možda nije intuitivno. Osim toga, kako bismo dodijelili vrijednosti \alpha i \tau, moramo dobro ocijeniti vrijednost \Theta, te dobro odabrati početnu aproksimaciju i vrijednost d. Još jedna negativna strana ovog algoritma je to što ga moramo pokretati više puta kako bismo postigli željenu preciznost. Sljedeća metoda koju ćemo konstruirati pokušat će savladati sve navedene prepreke.
Uparena metoda
Prilikom konstrukcije ove metode zadržat ćemo pretpostavke pojednostavljene uparene metode. Dodatno ćemo zahtijevati da je S \neq \mathbb{R}^{n} konveksan i zatvoren, tj. sada ćemo ograničenja uzeti u obzir.
Iteracija uparene metode slična je iteraciji pojednostavljene iterativne metode. Ona glasi:
| \bullet | postavimo 3 početne iteracije x_{0} = y_{0} = z_{0}, |
| \bullet | u svakoj iteraciji k računamo vrijednosti x_{k + 1}, y_{k + 1}, i z_{k + 1}, |
| \bullet | također, računamo \alpha_{k} i \tau_{k}, |
| \bullet | x_{k + 1} = \tau_{k} z_{k} + (1 - \tau_{k})y_{k}, |
| \bullet | y_{k + 1} = \text{Grad}(x_{k + 1}), |
| \bullet | z_{k + 1} = \text{Mirr}(\alpha_{k}, x_{k + 1}, \nabla f). |
Prvo ćemo izraziti \tau_{k} pomoću \alpha_{k}. Nadalje, \alpha_{k} ćemo birati tako da \tau_{k} bude iz intervala (0, 1], što će nam osigurati da iteracije ostanu unutar konveksnog skupa S. Sjetimo se, u pojednostavljenoj uparenoj metodi duljina koraka \tau_{k} bila je jednaka \frac{1}{\alpha_{k + 1} L + 1}. U uparenoj metodi, duljinu koraka \tau_{k} biramo na sličan način, o čemu govori sljedeća tvrdnja.
Teorem 16. Ukoliko je \tau_{k} = \frac{1}{\alpha_{k + 1} L}, tada za svaki u iz S vrijedi:
\begin{array}{lcl} \alpha_{k + 1} \langle \nabla f(x_{k + 1}), z_{k} - u \rangle & \leq & \alpha_{k + 1}^{2} L \text{Prog}(x_{k + 1}) + d(z_{k}, u) - d(z_{k + 1}, u) \\\ & \leq& \alpha_{k + 1}^{2} L (f(x_{k + 1}) - f(y_{k + 1})) + d(z_{k}, u) - d(z_{k + 1}, u). \end{array}
Dokaz. Ekvivalentno dokazu Teorema 10 , uz promjenu oznaka, imamo:
Koristeći prethodnu jednakost i definiciju od \text{Prog}(x_{k + 1}) imamo:
\begin{array}{lcl} \alpha_{k + 1} \langle \nabla f(x_{k + 1}), z_{k} - u \rangle & = & \langle \alpha_{k + 1} \nabla f(x_{k + 1}), z_{k} - z_{k + 1} \rangle + \langle \alpha_{k + 1} \nabla f(x_{k + 1}), z_{k + 1} - u \rangle \\ & \leq & \langle \alpha_{k + 1} \nabla f(x_{k + 1}), z_{k} - z_{k + 1} \rangle + \langle -\partial_{2} d(z_{k}, z_{k + 1}), z_{k + 1} - u \rangle \\ & = & \langle \alpha_{k + 1} \nabla f(x_{k + 1}), z_{k} - z_{k + 1} \rangle + d(z_{k}, u) - d(z_{k + 1}, u) - d(z_{k}, z_{k + 1}) \\ & \leq & (\langle \alpha_{k + 1} \nabla f(x_{k + 1}), z_{k} - z_{k + 1} \rangle - \displaystyle \frac{1}{2} \Vert z_{k} - z_{k + 1}\Vert^{2}) \ + \\ & & + \ (d(z_{k}, u) - d(z_{k + 1}, u)). \\ \end{array}
Neka je sad v = \tau_{k} z_{k + 1} + (1 - \tau_{k})y_{k} \in S. Tada vrijedi:
x_{k + 1} - v = (\tau_{k} z_{k} + (1 - \tau_{k} y_{k})) - v = \tau_{k} (z_{k} - z_{k + 1}).
Koristeći prethodnu jednakost i definiciju od \text{Prog}(x_{k + 1}) imamo:
\begin{array}{cl} & \langle \alpha_{k + 1} \nabla f(x_{k + 1}), z_{k} - z_{k + 1} \rangle - \displaystyle \frac{1}{2} \Vert z_{k} - z_{k + 1}\Vert^{2} \\ = & \displaystyle \frac{\alpha_{k + 1}}{\tau_{k}} \langle \nabla f(x_{k + 1}), x_{k + 1} - v \rangle - \displaystyle \frac{1}{2\tau_{k}^{2}} \Vert x_{k + 1} - v\Vert^{2} \\ = & \displaystyle \alpha_{k+ 1}^{2} L (\langle \nabla f(x_{k + 1}), x_{k + 1} - v \rangle - \frac{L}{2} \Vert x_{k + 1} - v\Vert^{2}) \\ \leq& \alpha_{k+ 1}^{2} L \cdot \text{Prog}(x_{k + 1}), \\ \end{array}
iz čega slijedi prva nejednakost tvrdnje teorema. Druga nejednakost slijedi iz analize metode gradijentnog spusta za koju vrijedi f(x_{k + 1}) - f(y_{k + 1}) \geq \text{Prog}(x_{k + 1}).
\ \blacksquare
Sljedeća nam tvrdnja donosi ocjenu pogreške iteracije uparene metode. Također, moći ćemo odrediti duljine koraka \alpha_{k}.
Teorem 17. Neka je u \in S. Vrijedi:
\alpha^{2}_{k + 1} Lf(y_{k + 1}) - (\alpha^{2}_{k + 1} L - \alpha_{k + 1}) f(y_{k}) + d(z_{k + 1}, u) - d(z_{k}, u) \leq \alpha_{k + 1} f(u).
Dokaz. Koristeći prethodni teorem, konveksnost od f, definicije od x_{k},y_{k} i z_{k}, te izbor \tau_{k} imamo:
\begin{array}{cl} & \alpha_{k + 1} (f (x_{k + 1}) - f(u)) \\ \leq & \alpha_{k + 1} \langle \nabla f(x_{k + 1}), x_{k + 1} - u \rangle \\ = & \alpha_{k + 1} \langle \nabla f(x_{k + 1}), x_{k + 1} - z_{k} \rangle + \alpha_{k + 1} \langle \nabla f(x_{k + 1}), z_{k} - u \rangle \\ = & \displaystyle \frac{(1 - \tau_{k})\alpha_{k + 1}}{\tau_{k}} \langle \nabla f(x_{k + 1}), y_{k} - x_{k + 1}\rangle + \alpha_{k + 1} \langle \nabla f(x_{k + 1}), z_{k} - u \rangle \\ \leq & \displaystyle \frac{(1 - \tau_{k})\alpha_{k + 1}}{\tau_{k}} (f(y_{k}) - f(x_{k + 1})) + \alpha_{k + 1} \langle \nabla f(x_{k + 1}), z_{k} - u \rangle \\ \leq & \displaystyle \frac{(1 - \tau_{k})\alpha_{k + 1}}{\tau_{k}} (f(y_{k}) - f(x_{k + 1})) + \alpha_{k + 1}^{2} L(f(x_{k + 1}) - f(y_{k + 1})) + d(z_{k}, u) -d(z_{k + 1}, u)\\ = & (\alpha^{2}_{k + 1}L - \alpha_{k + 1}) f(y_{k}) - \alpha^{2}_{k + 1}L f(y_{k + 1}) + \alpha_{k + 1}f(x_{k + 1}) + d(z_{k}, u) -d(z_{k + 1}, u). \\ \end{array}
Time je tvrdnja dokazana.
\ \blacksquare
Kako bismo mogli dokazati sljedeći teorem koji nam osigurava konvergenciju uparene metode, trebamo odabrati \alpha_{k} tako da je \alpha_{k}^{2}L \approx \alpha_{k + 1}^{2}L - \alpha_{k + 1}. Izaberimo \alpha_{k} = \frac{k + 1}{2L}. Tada je \alpha_{k}^{2}L = \alpha_{k + 1}^{2}L - \alpha_{k + 1} + \frac{1}{4L}.
Teorem 18. Neka je \Theta gornja ocjena vrijednosti d(x_{0}, x^{*}), gdje je x_{0} početna aproksimacija, a x^{*} optimum. U k-toj iteraciji uparene metode imamo: f(y_{k}) - f(x^{*}) \leq \frac{4 \Theta L}{(k + 1)^{2}}.
Dokaz. Teleskopiranjem prethodnog teorema za i = 0, \dots, k. Dobivamo:
\begin{array}{c} \alpha_{k}^{2} L f(y_{k}) + \displaystyle \sum_{i = 1}^{k - 1} \frac{1}{4L}f(y_{k}) + d(z_{k}, u) - d(z_{0}, u) \leq \sum_{i =0}^{k} \alpha_{k} f(u). \end{array}
Ukoliko uzmemo da je u = x^{*}, f(y_{i}) \geq f(x^{*}), d(z_{k}, u) \geq 0, te d(z_{0}, u) \leq \Theta imamo:
\begin{array}{rcl} \displaystyle \frac{(k + 1)^{2}}{4L^{2}} Lf(y_{k}) & \leq & \left( \frac{k(k + 3)}{4L} - \frac{k - 1}{4L} \right) f(x^{*}) + \Theta, \\ f(y_{k}) - f(x^{*}) &\leq& \displaystyle \frac{4 \Theta L}{(k + 1)^{2}}. \\ \end{array}
Time je tvrdnja dokazana.
\ \blacksquare
U nastavku slijedi algoritam uparene metode.
Algorithm 19.
Ulaz: funkcija f, x_{0} početna aproksimacija, k broj koraka
Izlaz: y_{k} za koji f(y_{k}) - f(x^{*}) \leq \frac{4 \Theta L}{(k + 1)^{2}}.
UparenaMetoda(f, x_{0}, k)
1. y_{0} = x_{0}, z_{0} = x_{0}
2. za i = 0, \dots, k radi
3. \tau_{i} = \frac{2}{i +2}
4. \alpha_{i + 1} = \frac{i + 1}{2L}
5. x_{i + 1} = \tau_{i} z_{i} + (1 - \tau)y_{i}
6. y_{i + 1} = \text{Grad}(x_{i + 1})
7. z_{i+ 1} = \text{Mirr}(\alpha_{i + 1}, x_{i + 1}, \nabla f)
8. vrati y_{k}
Ulaz: funkcija f, x_{0} početna aproksimacija, k broj koraka
Izlaz: y_{k} za koji f(y_{k}) - f(x^{*}) \leq \frac{4 \Theta L}{(k + 1)^{2}}.
UparenaMetoda(f, x_{0}, k)
1. y_{0} = x_{0}, z_{0} = x_{0}
2. za i = 0, \dots, k radi
3. \tau_{i} = \frac{2}{i +2}
4. \alpha_{i + 1} = \frac{i + 1}{2L}
5. x_{i + 1} = \tau_{i} z_{i} + (1 - \tau)y_{i}
6. y_{i + 1} = \text{Grad}(x_{i + 1})
7. z_{i+ 1} = \text{Mirr}(\alpha_{i + 1}, x_{i + 1}, \nabla f)
8. vrati y_{k}
U sljedećem primjeru ćemo vidjeti način na koji djeluje uparena metoda.
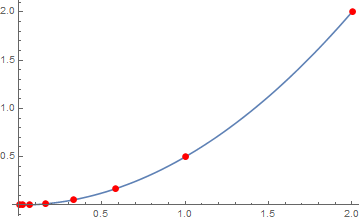
Primjer 20. Neka je funkcija f jednaka onoj u Primjeru 12 . Uz jednaku početnu aproksimaciju i ograničenja na varijable uparenom metodom dobivamo sljedeće aproksimacije.
Na Slici 3 vidimo kako uparena metoda zadržava dobra svojstva gradijentne metode na prvim iteracijama, te zrcalne metode na kasnijim iteracijama.
Tablica1 pokazuje aproksimacije minimuma dobivene gradijentnom, zrcalnom i uparenom metodom iz početne aproksimacije x = 5. Algoritam je stao kada je postignuta točnost 5 \cdot 10^{-4}.
Tablica
Zaključak
Ukratko smo, s teorijskog aspekta, analizirali algoritme gradijentnog i zrcalnog spusta. Utvrdili smo kako je, zbog svojstava ove dvije metode, njihovo uparivanje prirodno, te kako ono rezultira teorijski bržom metodom, takozvanom uparenom metodom. Prvo smo, na intuitivan način, konstruirali pojednostavljenu verziju uparene metode s konstantnom duljinom koraka i bez skupa ograničenja, a potom smo uveli varijabilne duljine koraka i konveksne skupove ograničenja.
Tablica 1: Iteracije gradijentne (G), zrcalne (Z) i uparene metode (U)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| G | 2.5 | 1.25 | 0.625 | 0.3125 | 0.1563 | 0.07813 | 0.03906 | 0.01953 | 0.009766 | 0.004883 | 0.00244 | 0.00122 | 0.00061 | 0.00031 |
| Z | 4.5146 | 3.638 | 2.5784 | 1.5771 | 0.8115 | 0.3388 | 0.1085 | 0.02424 | 0.003059 | 0.00009 | ||||
| U | 2.5 | 1.6667 | 0.8333 | 0.3333 | 0.1111 | 0.03175 | 0.007937 | 0.001764 | 0.00035 |
Bibliografija