Ivić, Kruno
Tehničko veleučilište Zagreb (student)
Graditeljski odjel |
Katić Žlepalo, Mirela
Tehničko veleučilište Zagreb
Graditeljski odjel
mkatic@tvz.hr |
Uremović, Boris
Tehničko veleučilište Zagreb
Graditeljski odjel |
1Uvod
Na Graditeljskom odjelu Tehničkog veleučilišta u Zagrebu u sklopu kolegija "Nacrtna geometrija u graditeljstvu 2", studenti samostalno rješavaju nekoliko zadataka, tzv. programa. Jedan od tih programa je i crtanje nekog zadanog objekta u kosoj aksonometriji. U ovom članku analizirat ćemo sličnosti i razlike između izrade programa iz kose aksonometrije ručno, u računalnom programu AutoCAD i u računalnom programu SketchUp.
2O kosoj aksonometriji
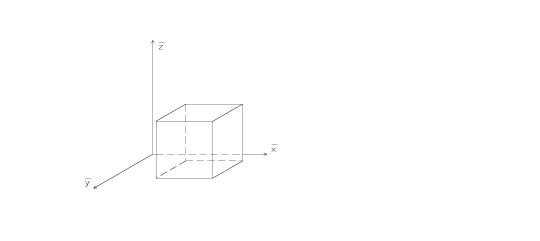
Kosa aksonometrija je metoda kosog paralelnog projiciranja na jednu ravninu slike pri čemu se objekt projicira na ravninu slike zajedno s prostornim koordinatnim sustavom u koji je smješten. Svatko je nekad nešto nacrtao ili barem skicirao metodom kose aksonometrije. Primjer za to je kocka na Slici 1 koja je nacrtana posebnom metodom kose aksonometrije koja se zove kosa projekcija. (Napomena: U kosoj projekciji najčešće su osi \overline{x} i \overline{z} pod pravim kutem.)
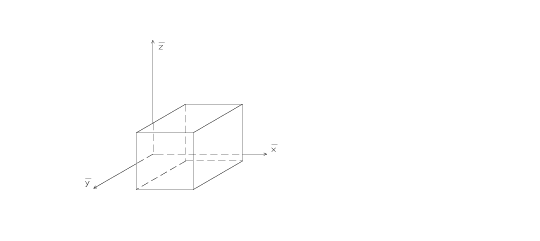
Kako bi se sačuvala prirodnost kosoaksonometrijske slike, odnosno omogućila zornost i što realniji prikaz prostornog objekta, što i je osnovna svrha ove metode, preporučeno je držati se nekih pravila. Primjerice, na Slici 1 brid kocke koji je paralelan s osi \overline{y} nacrtan je kraći nego bridovi paralelni s osima \overline{x} i \overline{z}. Ukoliko se svi bridovi nacrtaju jednakih duljina, kocka izgleda izduženo, kao kvadar (Slika 2).
Stoga je jedno od pravila kod kose aksonometrije korištenje prikrata - dakle bridove koji su paralelni s osima prikraćujemo i to uobičajeno na taj način da najviše prikratimo one bridove koji su paralelni s osi \overline{y}. Os \overline{z} se obično crta u vertikalnom položaju, a preporučeno je da kut među osima \overline{x} i \overline{z} bude između 100^{\circ} i 105^{\circ}, a kut među osima \overline{y} i \overline{z} između 110^{\circ} i 120^{\circ} ([2]).
U ovom članku nećemo se baviti prikratama nego ćemo zadatak pokazati u tzv. izometriji. Izometrija je kosa aksonometrija u kojoj su prikrate u smjeru sve tri osi jednake.
3Kosa aksonometrija - ručno i u AutoCAD-u
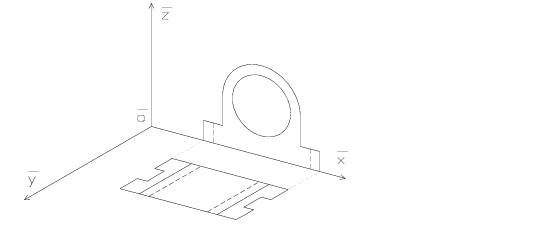
Kod ručnog crtanja i kod crtanja u AutoCAD-u počinje se jednako. Kut među osima \overline{x} i \overline{z} izabran je 105^{\circ}, a među osima \overline{y} i \overline{z}120^{\circ}. Zadatak smo odlučili crtati u izometriji, bez prikrata pa nanosimo one duljine koje su zadane u zadatku ([1], stranica 102, zadatak 28) da bismo ucrtali kosoaksonometrijski tlocrt i nacrt objekta (Slika 3). Pri tome treba paziti koji bridovi objekta su paralelni s osima koordinatnog sustava. Kružnica iz nacrta se u kosoj aksonometriji projicira u elipsu pri čemu je za konstrukciju elipse potrebno provesti tzv. Rytzovu konstrukciju.
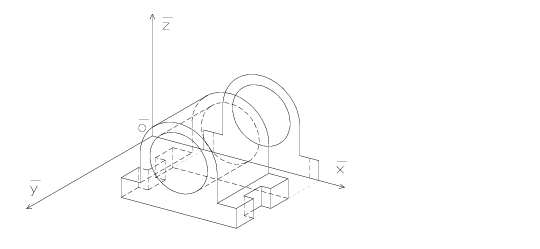
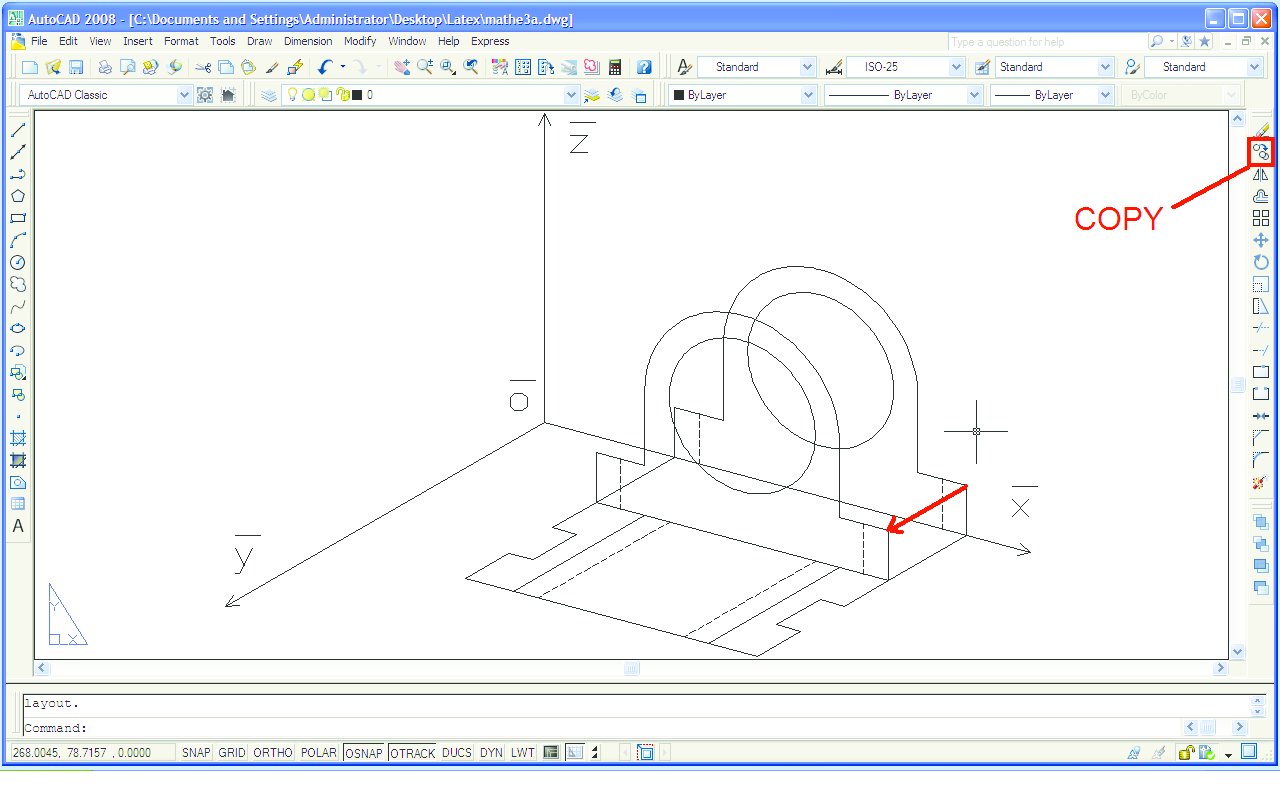
Nakon što konstruiramo kosoaksonometrijski tlocrt i nacrt, koristimo iz tlocrta zrake koje su paralelne s osi \overline{z}, a iz nacrta zrake koje su paralelne s osi \overline{y}, tražimo odgovarajuća sjecišta i spajamo cijelu kosoaksonometrijsku sliku objekta (Slika 4). Ovaj korak je u AutoCAD-u puno jednostavniji. Naime, jednom konstruiranu elipsu iz kosoaksonometrijskog nacrta dovoljno je samo translatirati na pripadno mjesto na slici objekta (naredbom Copy - Slika 5), dok je kod ručnog crtanja potrebno ponoviti konstrukciju elipse (ne nužno i Rytzovu konstrukciju). Osim toga, naredbom Copy moguće je istovremeno kopirati nekoliko linija, što je kod ručnog crtanja nemoguće. Uočimo da je očuvana paralelnost, dakle oni bridovi koji su međusobno paralelni u prostoru, paralelni su i na slici.
4Trodimenzionalni model u SketchUp-u i AutoCAD-u
SketchUp je besplatan program koji je zgodan za razvijanje prostornog zora jer je jednom nacrtani objekt moguće rotirati i gledati ga s raznih strana (naredbe Orbit, Pan, Zoom). Jedan od glavnih alata u SketchUp-u je Push/Pull pomoću kojeg je vrlo jednostavno dvodimenzionalnu sliku "izvući" u trodimenzionalni objekt ili na nekom trodimenzionalnom objektu "utisnuti" neki njegov dio i slično.
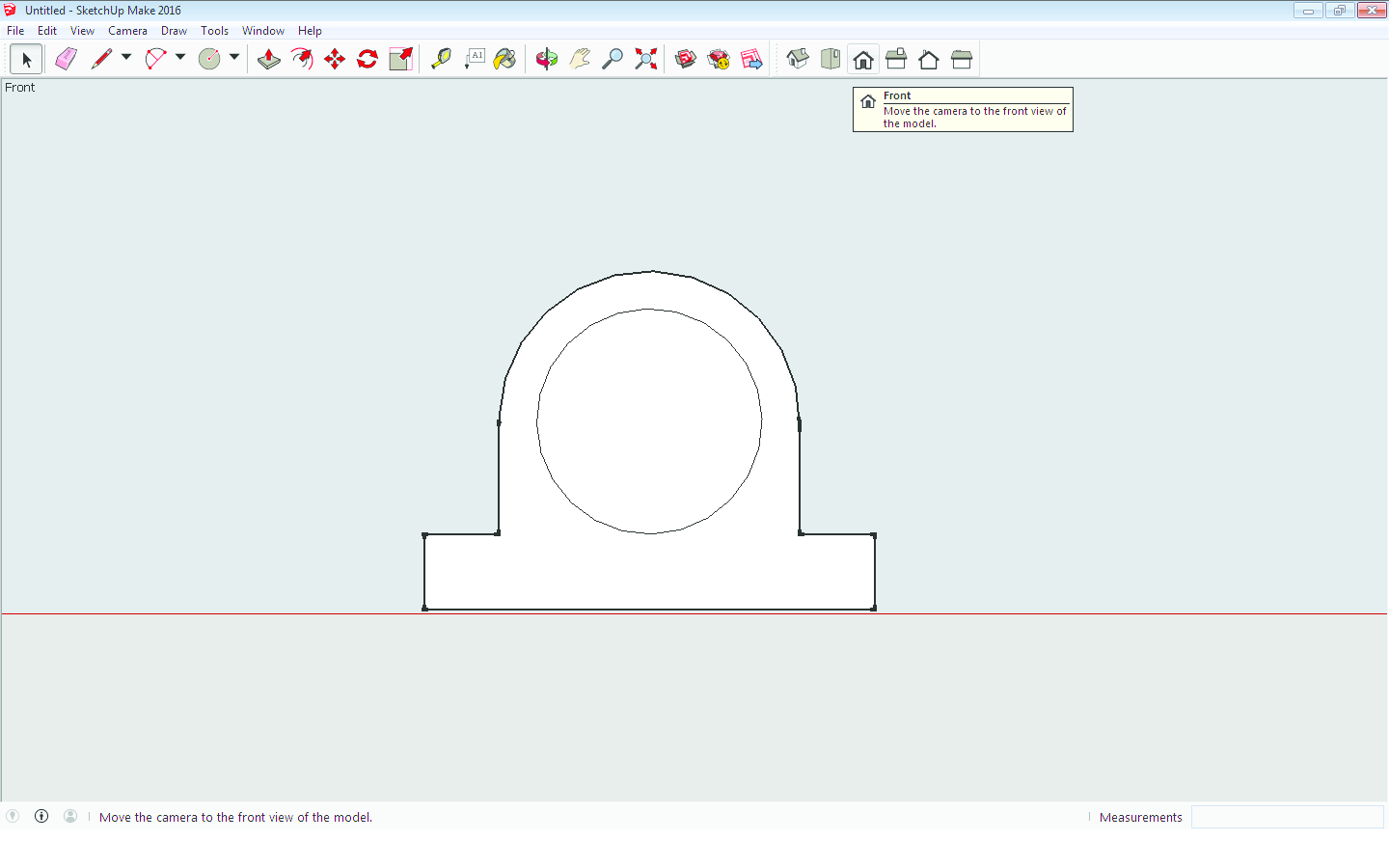
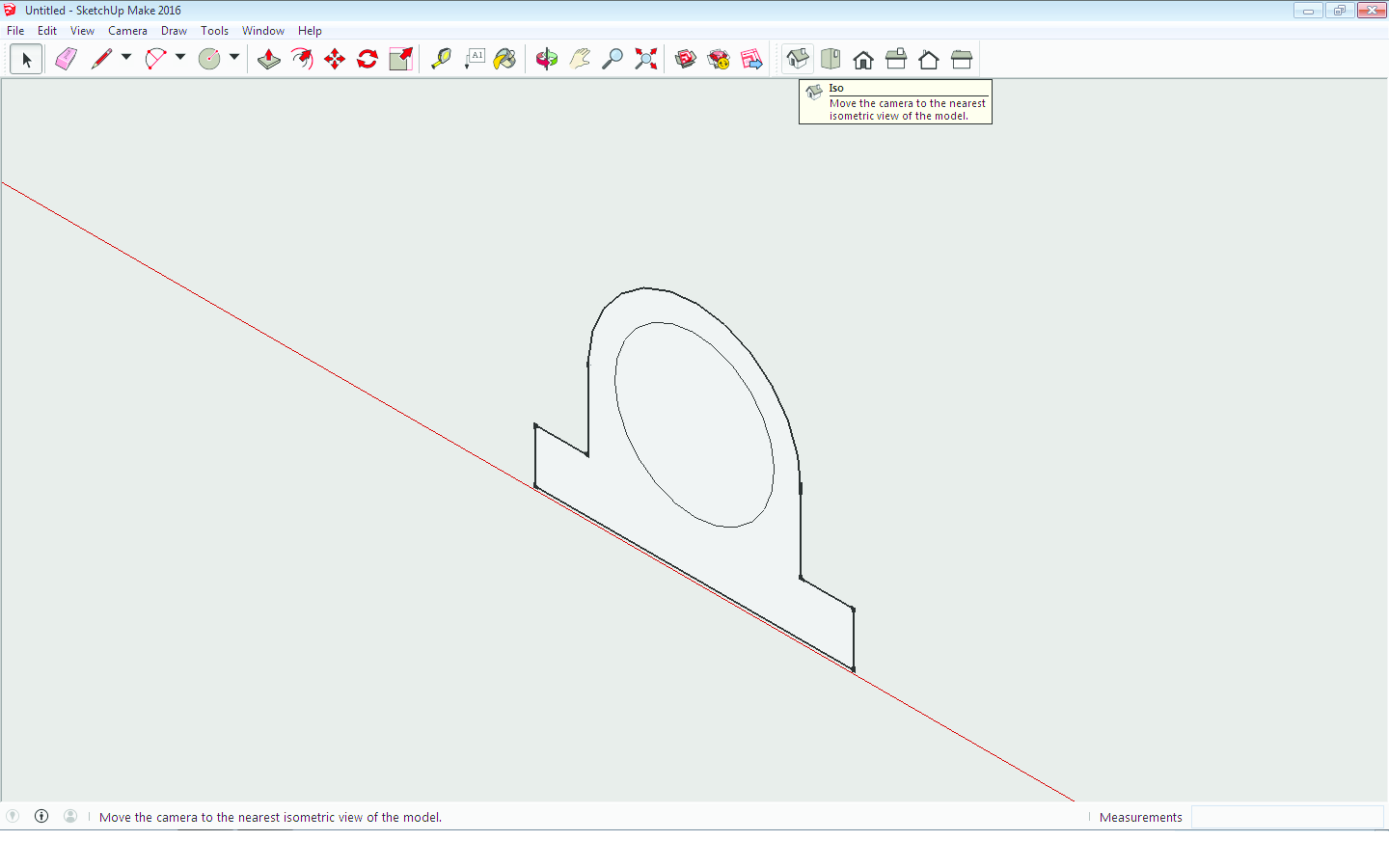
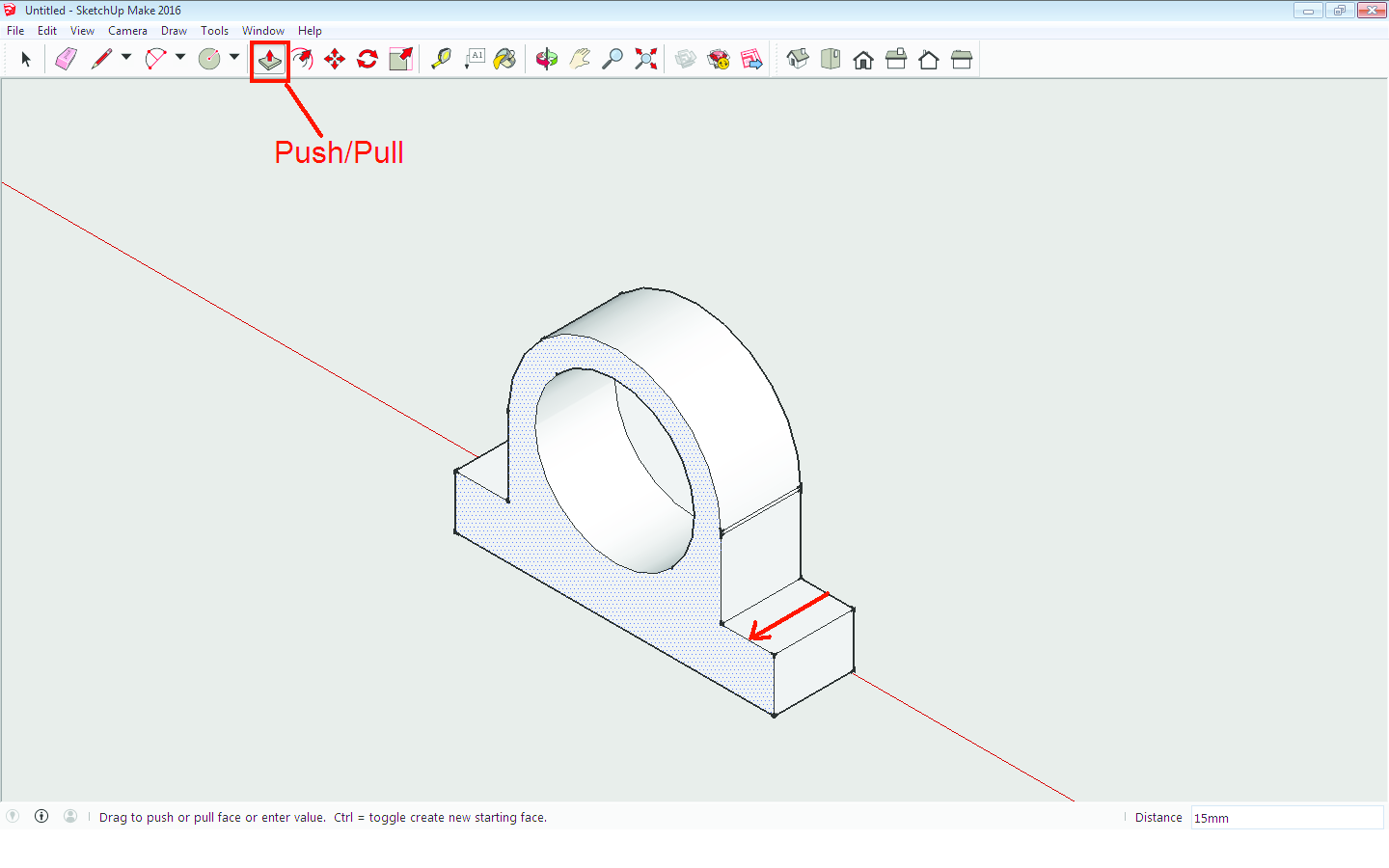
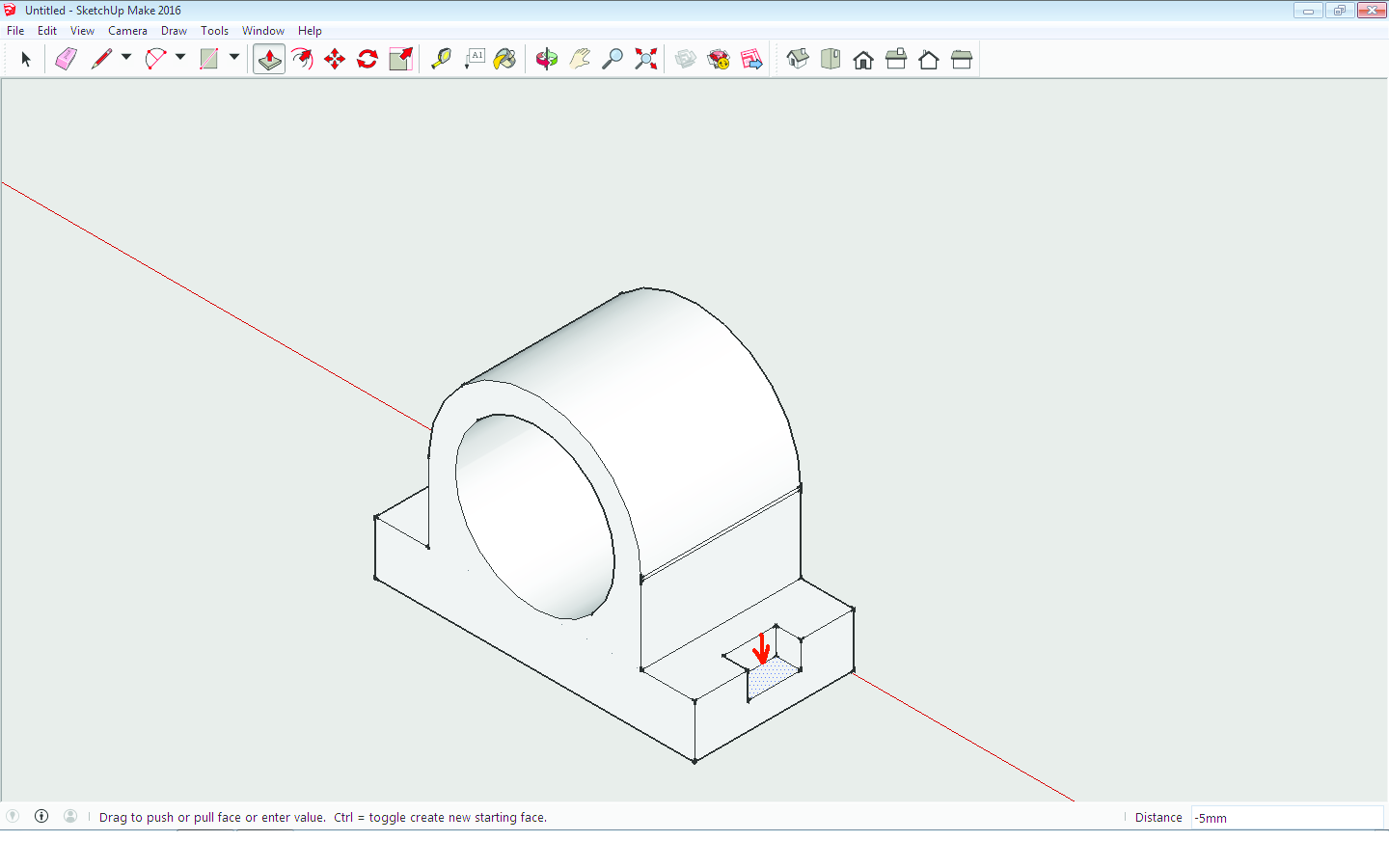
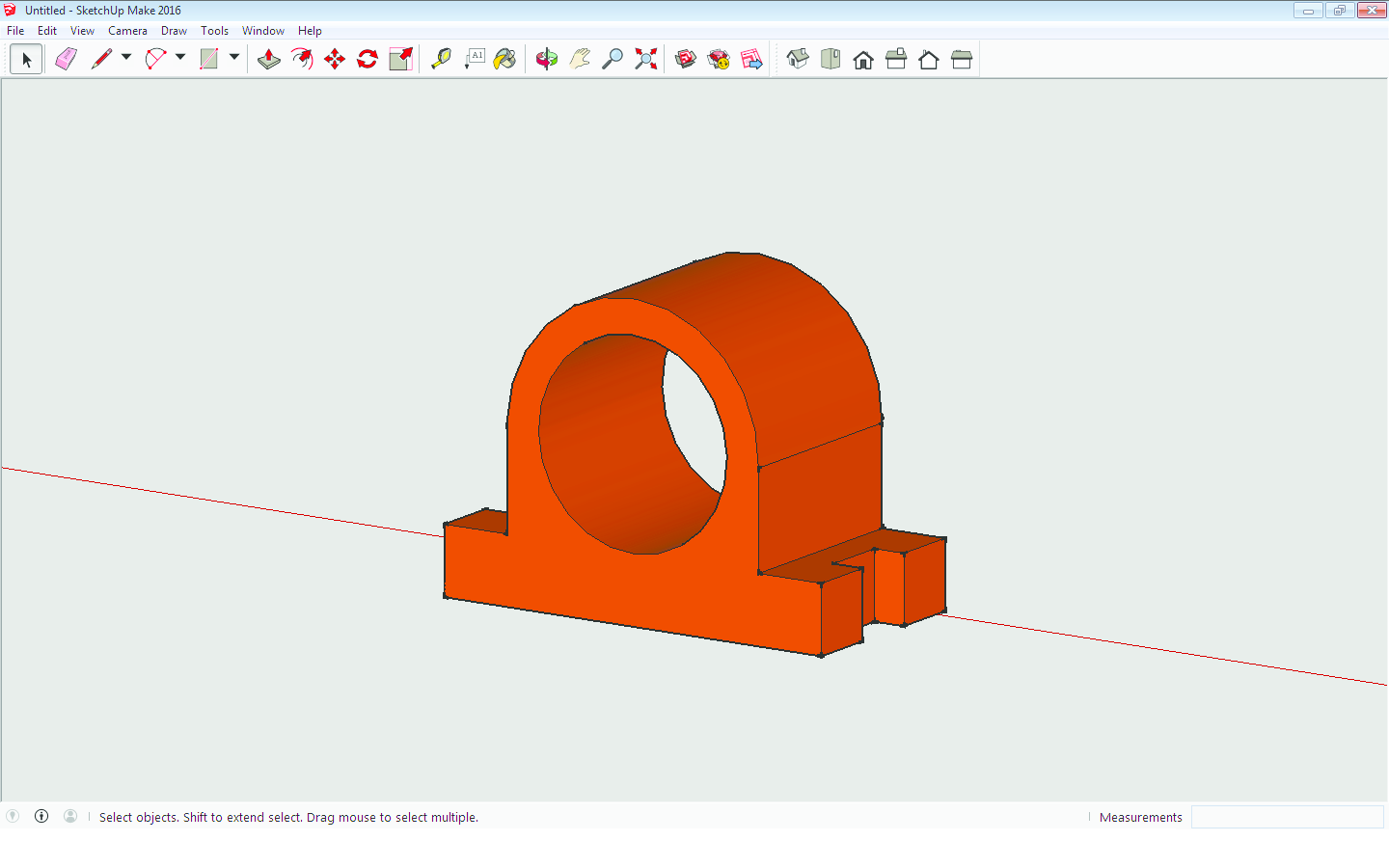
Kako bismo nacrtali isti zadatak u SketchUp-u, izaberemo pogled koji se zove Front i ucrtamo nacrt objekta (Slika 6). Promijenimo pogled iz Front u Iso (Slika 7) te pomoću alata Push/Pull (Slika 8) "povučemo" prema naprijed (ili nazad) za odgovarajuću duljinu te smo odmah iz (dvodimenzionalnog) nacrta dobili trodimenzionalni model. Nakon toga, pomoću istog alata "utisnemo" zadane ureze sa strane (Slika 9). I zadatak je riješen (Slika 10)! Međutim, bez obzira što se malo prije spomenuti pogled zove Iso, što podsjeća na izometriju u kojoj smo i rekli nacrtati ovaj zadatak, slike nisu izrađene u izometriji, nego u perspektivi. Naime, paralelnost nije očuvana kao što je to bio slučaj kod crtanja ručno ili u AutoCAD-u. Dakle rješenje nije onakvo kakvo se tražilo, a postupak nije ni sličan klasičnom crtanju metode kose aksonometrije bilo ručno ili u AutoCAD-u.
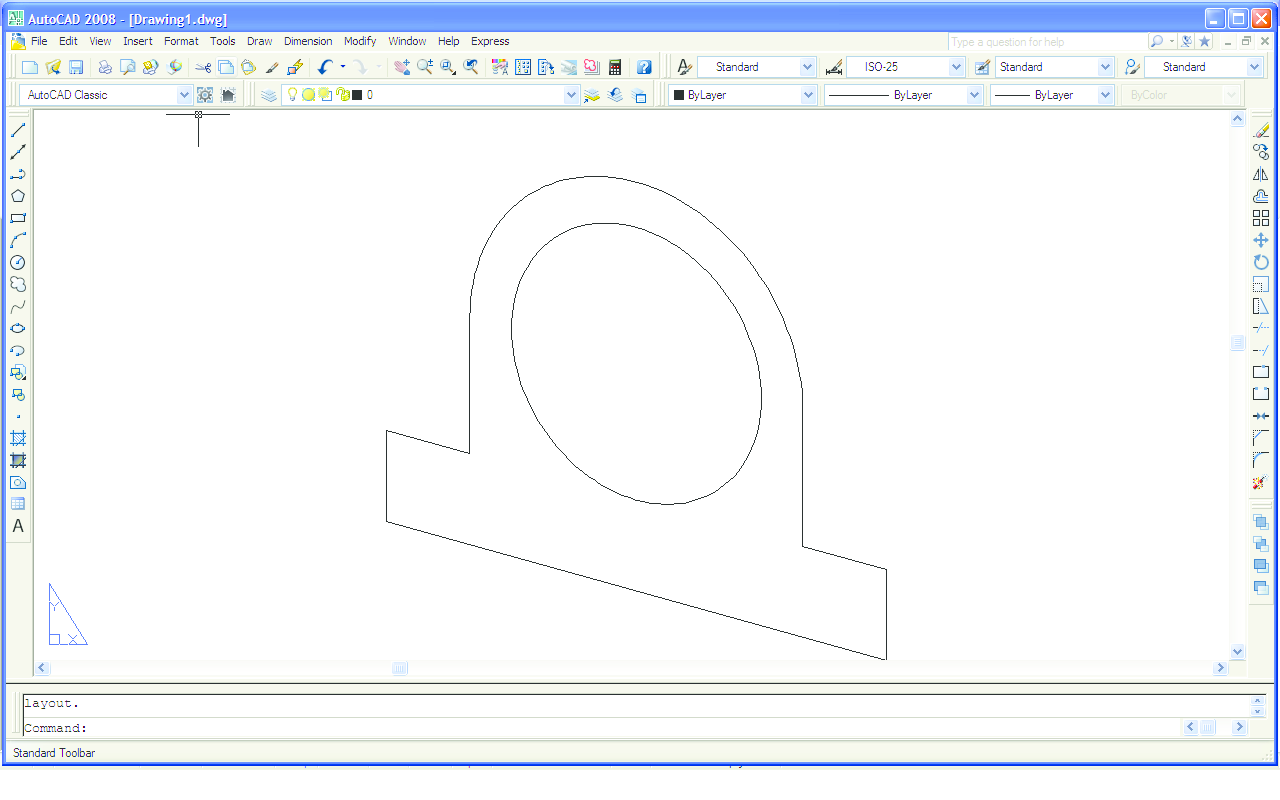
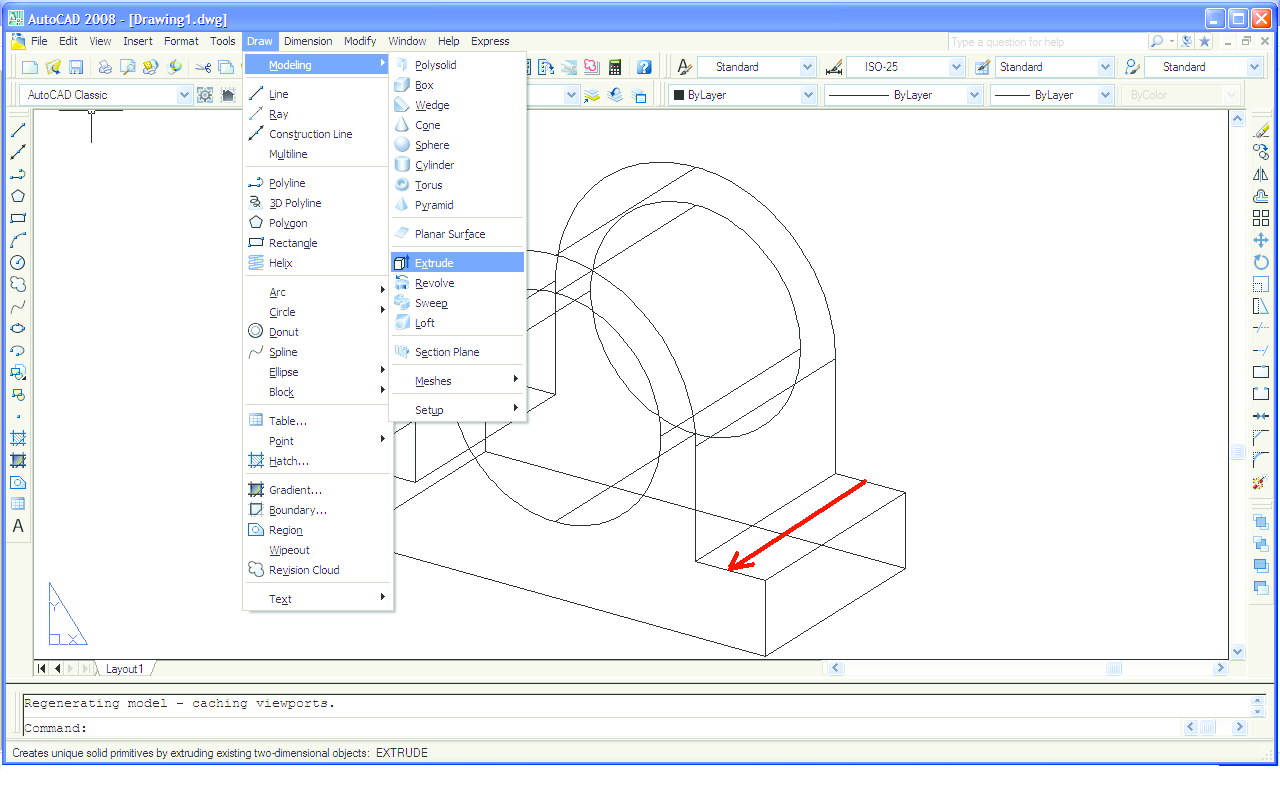
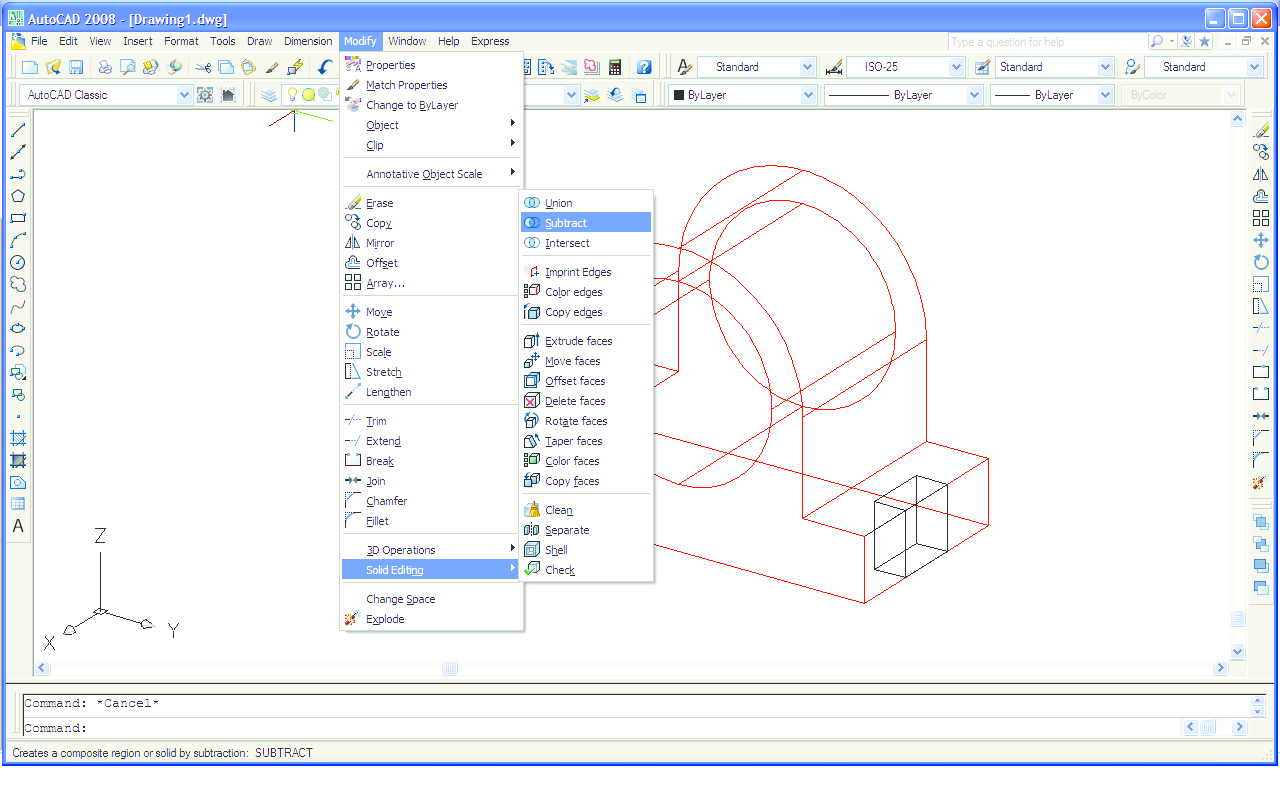
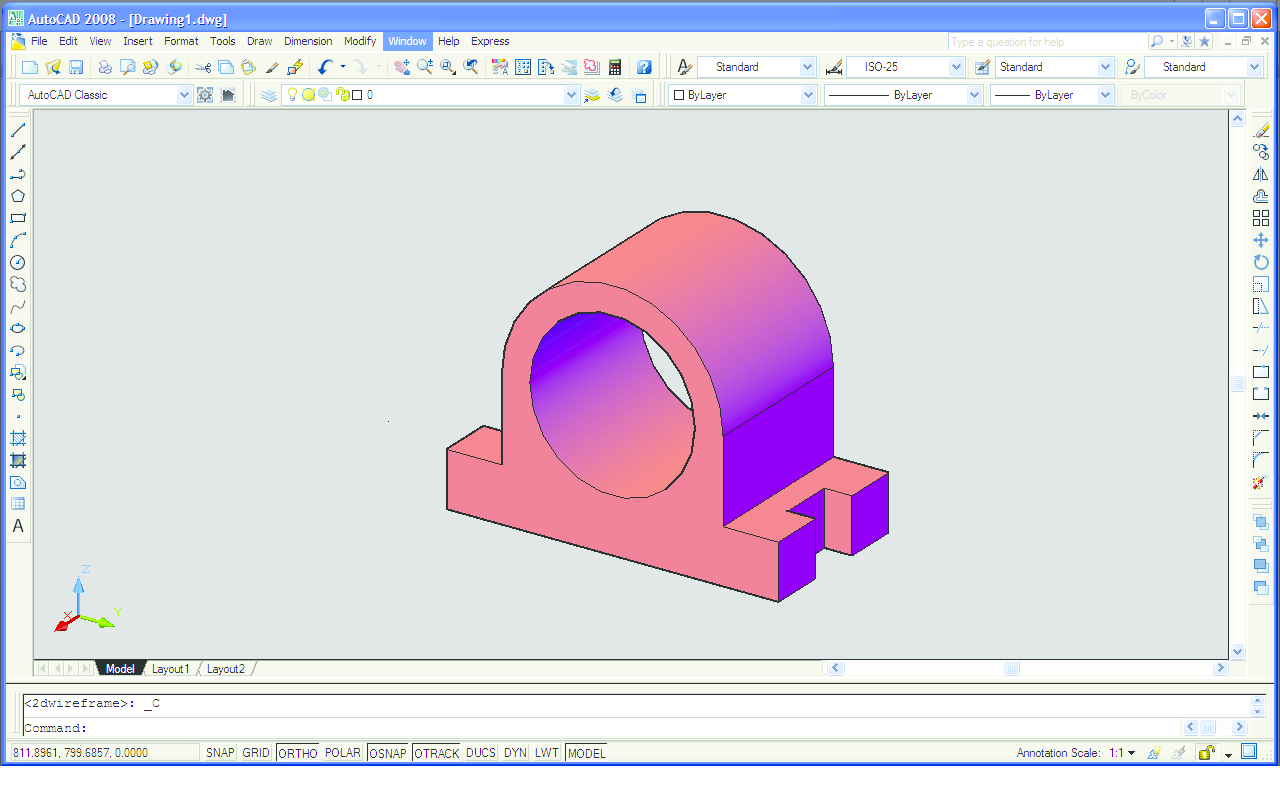
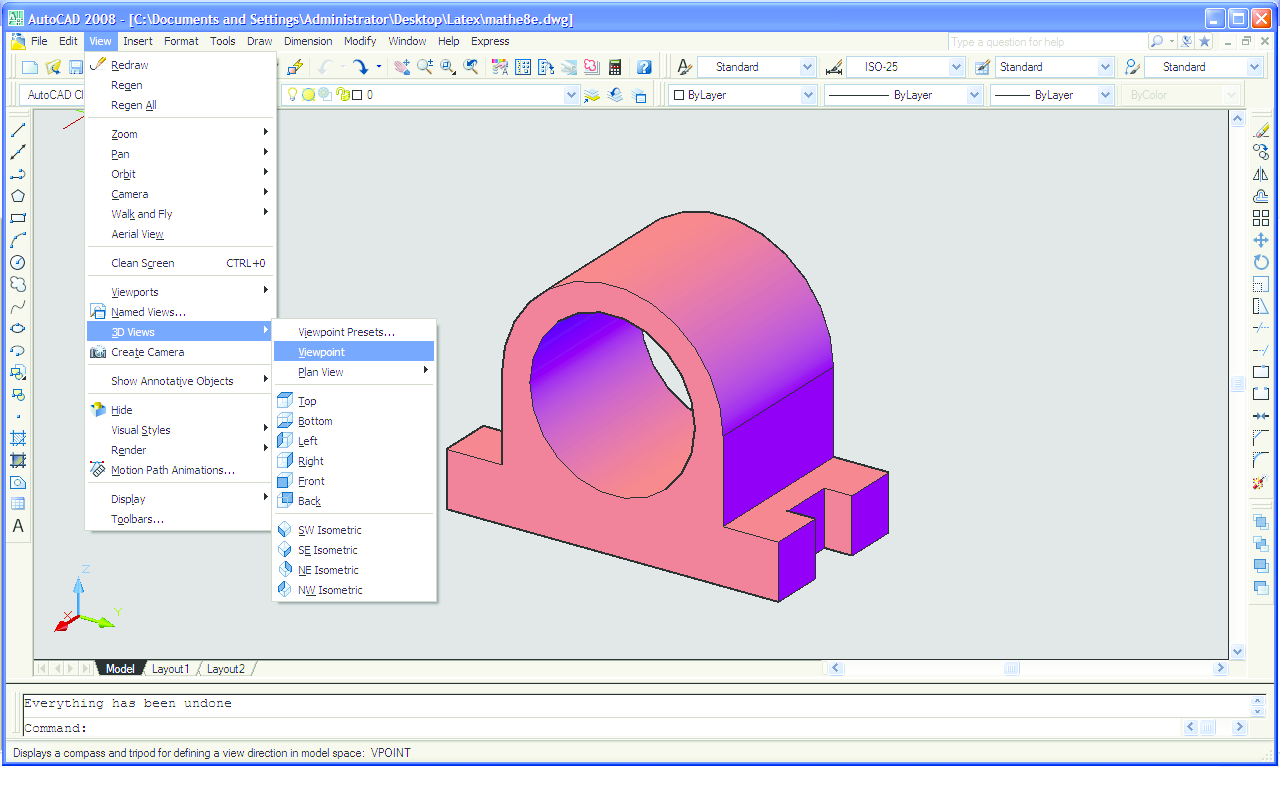
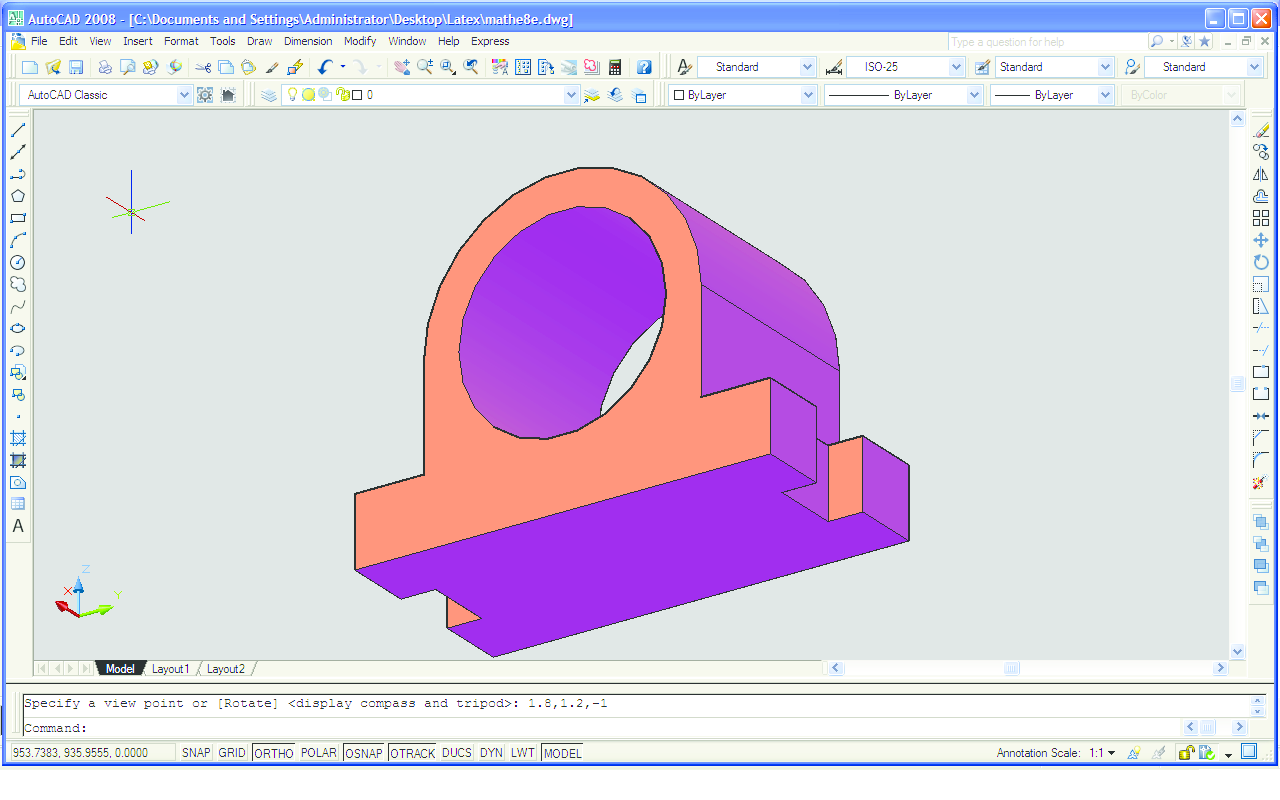
Na vrlo sličan način moguće je virtualni 3D model izraditi u AutoCAD-u. Također krenemo od crtanja nacrta (Slika 11), kojeg zatim pomoću naredbe Extrude "izvučemo" u trodimenzionalni objekt (Slika 12). Ureze sa strane napravimo na taj način da na tim mjestima gdje bi se trebali nalaziti urezi nacrtamo dva kvadra te ih naredbom Solid editing - Subtract "oduzmemo" od cijelog objekta (Slika 13). Na Slici 14 je objekt nacrtan u AutoCAD-u. Paralelnost bridova je očuvana. Objekt na Slici 14 prikazan je iz točke gledišta koja ima koordinate (1.8, 1.2, 1). Pomoću naredbe Viewpoint (Slika 15) možemo promijeniti točku gledišta kako nam god odgovara. Primjerice, isti objekt prikazan je na Slici 16 s pogledom odozdo, iz točke gledišta koja ima koordinate (1.8, 1.2, -1).
5Zaključak
Metoda kose aksonometrije je izuzetno važna i korisna za studente Graditeljskog odjela jer jako doprinosi razvijanju prostornog zora. Od velike je važnosti da studenti nauče iz tlocrta i nacrta "iščitati" kako neki objekt izgleda u prostoru. Iako studenti često ne razumiju čemu služi ručno crtanje programa jer smatraju da danas nitko više ne crta ručno nego isključivo na računalima, njihovi stariji i iskusniji kolege tvrde upravo suprotno. Naime, često su se našli u situaciji da na gradilištu moraju brzinski nešto skicirati kad u blizini nema ni struje, a kamoli računala. Stoga je potrebno znati nešto ručno nacrtati, barem skicirati, a za te skice upravo najbolje odgovara metoda kose aksonometrije. Ručno crtanje također olakšava usvajanje procesa nastajanja crteža, jer je osim krajnjeg rezultata, jako bitan i redoslijed izrade crteža i postupak "stvaranja" završnog objekta. Dakle, iako je ručno crtanje programa iz kose aksonometrije najsporije i najmukotrpnije od svih metoda pokazanih u ovom članku, ipak je ono neobično važno za buduće graditelje.
Bibliografija
|
[1] |
I. Babić, S. Gorjanc, A. Sliepcevic, V. Szirovicza, Nacrtna geometrija - zadaci, HDGG, Zagreb, 2007. |
|
[2] |
I. Babić, S. Gorjanc, A. Sliepcevic, V. Szirovicza, Konstruktivna geometrija - vježbe, HDKGIKG, Zagreb, 2002.
|