Harmonijski brojevi i Euler-Mascheronijeva konstanta
Niz racionalnih brojeva zadan općim članom a_{n}=\frac{1}{n}, n\in\mathbb{N}, zovemo harmonijski niz. Napišimo prvih par članova ovog jednostavnog niza:
Ime mu potječe iz glazbe i teorije valova. Naime, svaki glazbeni ton sastoji se od prostih tonova - harmonika, koji se još nazivaju parcijalni ili alikvotni tonovi. Niz harmonika izgrađen na fundamentalnoj frekvenciji f glasi f, 2f , 3f ,... pri čemu je \lambda, \frac{1}{2} \lambda, \frac{1}{3}\lambda,... niz odgovarajućih valnih duljina harmonika.
U našem članku detaljnije ćemo se pozabaviti zbrojem prvih n članova harmonijskog niza. Takav zbroj nazivamo harmonijski broj i označavamo s H_{n}, odnosno
Očigledno je svaki sljedeći harmonijski broj veći od prethodnog (jer su članovi harmonijskog niza pozitivni brojevi), odnosno niz harmonijskih brojeva je rastući. No taj rast je vrlo polagan, zbroj prvih deset članova harmonijskog niza iznosi približno 2.93, prvih sto 5.19, a zbroj prvih 1000 članova je svega 7.49. Prirodno se nameće pitanje je li rastući niz harmonijskih brojeva omeđen odozgo, odnosno konvergira li prema nekoj vrijednosti. Očito je harmonijski niz \frac{1}{n} padajući i teži k nuli, no pokazat ćemo da usprkos tome niz harmonijskih brojeva divergira.
Grupirajmo pribrojnike n-tog harmonijskog broja na sljedeći način:
Primjećujemo da su u prvoj grupi oba člana veća od \frac{1}{4} pa je stoga njihov zbroj veći od \frac{1}{2}. Slično, u drugoj grupi je svaki od članova veći od \frac{1}{8} pa je i njihov zbroj veći od \frac{1}{2}. Na isti način vidimo da je svaka daljnja grupa od 2^{n} članova veća od \frac{1}{2}. Dakle, ako H_{n} sadrži k takvih grupa, slijedi H_{n} \gt 1+ \frac{k}{2}. S obzirom da k može biti po volji velik, niz harmonijskih brojeva nije omeđen odozgo, odnosno raste prema beskonačnosti.
Kao što smo već opazili, taj rast je vrlo polagan, da bismo došli do sume 10, trebali bismo zbrojiti preko prvih 12000 članova! Zanima nas kako konkretno možemo predočiti taj rast, to jest možemo li taj rast opisati nekom poznatom funkcijom. Time ćemo se baviti u sljedećem poglavlju.
Uz harmonijske brojeve se blisko veže i jedna zagonetna matematička konstantna o kojoj se još uvijek malo toga zna. Radi se o Euler-Macheronijevoj konstanti koju označavamo s \gamma. Njenu vezu s harmonijskim brojevima objasnit ćemo u trećem poglavlju.
Zatim će nas zanimati kako brzo i lako možemo izračunati n-ti harmonijski broj bez uzastopnog zbrajanja članova niza, odnosno njegovu aproksimaciju. U tu svrhu ćemo prikazati zanimljive formule za približno računanje harmonijskih brojeva.
U posljednjem poglavlju navodimo neke popularne probleme u kojima se prirodno pojavljuju harmonijski brojevi.
Zaključili smo da niz harmonijskih brojeva sporo raste i divergentan je. Pokazat ćemo da se ta brzina rasta može dobro opisati logaritamskom funkcijom, naime vrijedi sljedeća ocjena
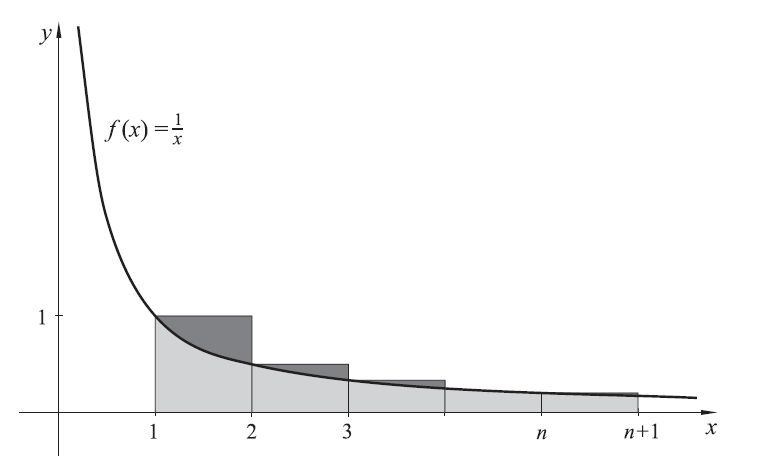
Za dokaz prethodne nejednakosti koristimo se površinom ispod grafa funkcije f(x)=\frac{1}{x} i njenim aproksimacijama danim sumama površina odgovarajućih pravokutnika na segmentu [1, n + 1], odnosno [1, n].
Najprije segment [1, n + 1] podijelimo na n jednakih podsegmenata duljine 1. Površina ipod grafa funkcije f(x) = \frac{1}{x} na segmentu [1, n + 1] manja je od sume površina n pravokutnika čija je širina 1, a visina 1, \frac{1}{2}, \frac{1}{3}, \dots, \frac{1}{n}, redom (vidi Sliku 1). Zaista, budući je funkcija f(x) = \frac{1}{x} padajuća, vrijedi f(x)\le \frac{1}{k} za svaki x\in [k, k + 1], i 1\le k \le n. Još kažemo da smo na ovaj način načinili jednu aproksimaciju odozgo. Suma površina ovih n pravokutnika je jedna gornja Darbouxova suma, a nama je zanimljiva jer upravo predstavlja n-ti harmonijski broj H_{n}. S druge strane površina ispod grafa funkcije f(x) =\frac{1}{x} na segmentu [1, n + 1] jednaka je određenom (ili Riemannovom) integralu funkcije f od 1 do n + 1. Korištenjem Newton-Leibnitzove formule dobivamo
i time smo pokazali nejednakosti \ln(n+1)\lt H_{n} u
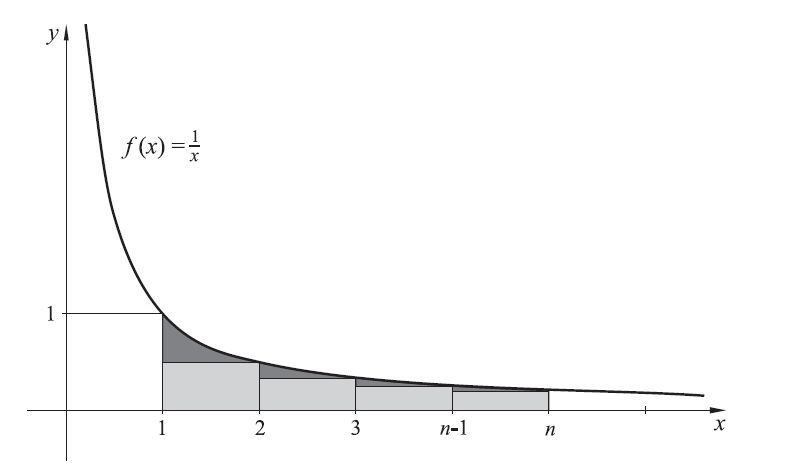
Slično, površinu ipod grafa funkcije f(x) = \frac{1}{x} na segmentu [1, n] aproksimiramo odozdo sumom površina n-1 pravokutnika čija je širina 1, a visina \frac{1}{2}, \frac{1}{3}, \dots, \frac{1}{n}, redom (vidi Sliku 2). Ta suma predstavlja jednu donju Darbouxovu sumu i očito je jednaka H_{n}-1. Vrijedi
pa smo opravdali i drugu nejednakost u
Pogledajmo ponovno Sliku
Pokažimo prvo da je taj niz monoton. Razlika dva susjedna člana toga niza
jednaka je određenom integralu funkcije f(x)=\frac{1}{x}-\frac{1}{n+1} na segmentu [n,n+1], a budući je ta funkcija pozitivna na danom segmentu, njen određeni integral je također pozitivan. Dakle, niz H_{n}-\ln n je padajući. On je i omeđen odozdo s nulom jer vrijedi
Prvo smo koristili da je H_{n}\gt \ln(n+1) prema
Budući je monoton i omeđen niz realnih brojeva konvergentan, definirat ćemo Euler-Mascheronijevu konstantu \gamma kao limes toga niza
Klasifikacija Euler-Mascheronijeve konstante spada među poznatije otvorene probleme u matematici. Naime, još nije pokazano je li \gamma algebarski broj (poput \sqrt{2}, odnosno korijen polinoma s cjelobrojnim koeficijentima) ili transcedentan (poput \pi i e). Štoviše, zanimljivo je da se ne zna ni je li \gamma racionalan ili iracionalan broj! U slučaju da je racionalan, poznato je da bi mu nazivnik bio veći od 10^{242080}, za detalje vidi npr.
Veza
Formula je naravno točnija što je n veći. Primjerice, H_{10}=2.93, a formula nam daje H_{10}\approx 2.88, H_{100}=5.187, a formulom dobijemo H_{100}\approx 5.182, dok je za H_{1000} je još preciznija. No, htjeli bismo ipak bolju točnost, pogotovo za manje harmonijske brojeve. Postoje različita poboljšanja navedene formule, od kojih je najjednostavnija, a pritom i prilično točnija sljedeća:
Još bolja točnost se može dobiti dodavanjem još jednog člana u logaritamsku funkciju
Dokazano je da vrijedi i sljedeća aproksimacija logaritmom kvadratne funkcije
a nedavno su izvedene i aproksimacije logaritmom nekih racionalnih funkcija koje dodatno poboljšavaju točnost, npr.
U sljedećoj tablici ćemo prikazati usporedbu točnosti navedenih formula na deset decimala. Svaki redak odgovora redom gornjim formulama, dok je u zadnjem retku točna vrijednost n-tog harmonijskog broja. U stupcima su različite vrijednosti broja n.
| Formula | n=10 | n=50 | n=100 | n=1000 |
|
|
2.8798007579 | 4.489238670 | 5.182385851 | 7.484970944 |
|
|
2.9285909221 | 4.499189001 | 5.187373392 | 7.485470819 |
|
|
2.9289876687 | 4.499205503 | 5.187377538 | 7.485470861 |
|
|
2.9289687083 | 4.499205339 | 5.187377518 | 7.485470861 |
|
|
2.9289682521 | 4.499205338 | 5.187377518 | 7.485470861 |
| H_{n} | 2.9289682539 | 4.499205338 | 5.187377518 | 7.485470861 |
Za detalje o ovim formulama i njihovim izvodima, kao i ostale najnovije formule za aproksimaciju harmonijskih brojeva, koje zahtijevaju malo složeniju matematičku analizu i poznavanje asimptotike, pogledajte
Za kraj navedimo neke od zanimljivih primjena i problema povezanih s harmonijskim brojevima.
Analiza obaranja rekorda. Primjerice, u meteorologiji nas zanima koliko će puta u nizu od n godina biti oboren temperaturni rekord ili najveća količina padalina. Uz pretpostavku da su vremenski uvjeti slučajni i neovisni o prethodnim godinama, broj oborenih rekorda u n godina je upravo jednak harmonijskom broju H_{n}. Npr. u 100 godina, H_{100}\approx 5.19 puta će biti oboren temperaturni rekord ljeti ili rekordna količina snježnih padalina zimi. Detaljnije o ovom problemu može se saznati u
Problem sakupljanja kupona. Pretpostavimo da želimo sakupiti sve sličice za album Životinjskog carstva ili sve sličice nogometaša za aktualni album svjetskog prvenstva. Definirajmo slučajnu varijablu X kao broj kupljenih kupona kojima smo popunili cijeli album od n sličicu te neka slučajna varijabla X_{i} predstavlja broj kupnji kojima smo dobili novu sličicu nakon što smo već sakupili i-1 sličica, i=1,...n. Budući slučajna varijabla X_{i} mjeri broj ponavljanja slučajnog pokusa do prve realizacije povoljnog događaja, ona ima geometrijsku razdiobu s vjerojatnosti p_{i}=\frac{n-(i-1)}{n} čije je očekivanje E(X_{i})=\frac{1}{p_{i}}, vidi npr.
odnosno očekivani broj kupnji da bismo sakupili sve sličice jednak je n\,H_{n}. Primjerice, za popuniti album od 50 sličica, u prosjeku ćemo morati kupiti 50\, H_{50}\approx 225 kupona ili čokoladica sa sličicama.
Crvić na gumenoj traci. Crvić puzi konstantnom brzinom od 1 centimetar po minuti s jednog kraja trake na drugi, no gumena traka duga 1 metar se svake minute rastegne za još 1 metar. Preciznije, nakon prve minute crvić je prešao 1 cm, tj. 1/100 dio trake, no budući se ona rastegnula na 2 metra, ostalo mu je još 198 cm. U drugoj minuti je prešao 1/200 dio trake, tj. ukupno 3 cm, no nakon rastezanja nalazi se 4.5 cm od početka, odnosno treba puzati još 295.5 cm. Pitanje je hoće li na taj način crvić ikada dopuzati do kraja trake? Crvićev put nakon n minuta jednak je
te zbog neomeđenosti niza harmonijskih brojeva, H_{n} može biti dovoljno velik tako da crvić doista dođe do kraja trake, ali će mu trebati jako puno vremena. Za detalje o ovom zanimljivom problemu pogledajte
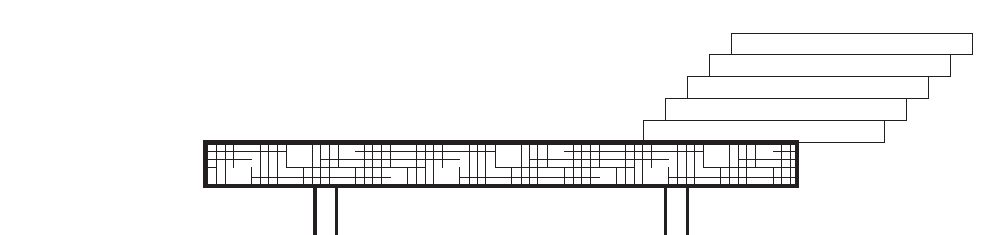
Problem postavljanja pločica. Radi se o matematičko-fizičkom problemu postavljanja n istih pločica (ili n knjiga istih dimenzija i mase) na rub stola na način da je svaka pločica pomaknuta malo dalje preko ruba stola od prethodne, a tako da se cijela konstrukcija ne sruši (vidi Sliku 3). Takva konstrukcija će ostati stabilna ako se težište sistema od n postavljenih pločica nalazi najviše do ruba stola, inače će se srušiti. U