Sažetak
Nekooperativne igre za dva igrača s nenul-sumom tema su koja pripada teoriji igara. Kroz primjere, istaknut ćemo poteškoće kod rješavanja ovakvih matričnih igara te njihovu primjenu u raznim područjima svakodnevnog života.
Ključne riječi: teorija igara, matrične igre, nekooperativne igre s nenul-sumom, Nashova ravnoteža, Pareto optimalnost.
1UVOD
Pod pojmom igra obično mislimo na društvene, kartaške ili računalne igre. Tijekom 20. stoljeća, potaknuta različitim praktičnim problemima, razvila se teorija igara, grana matematičke znanosti koja detaljnije proučava igre uz primjenu teorije vjerojatnosti, linearnog programiranja, kombinatorike i drugih grana matematike. U teoriji igara, igra predstavlja natjecateljsku situaciju u kojoj sudjeluju barem dva igrača, pri čemu svaki ima određenu kontrolu nad ishodom igre. Svaki igrač ima određeni broj mogućih poteza koje može odabrati, a svakom mogućem ishodu igre pridružene su isplate za svakog igrača. Pretpostavljamo da igrači djeluju razumno i žele profitirati.
Proučavat ćemo igre u kojima sudjeluju dva igrača. Nazivamo ih matričnim igrama i prikazujemo matricom isplata P. Redci matrice P označavaju m poteza koje na raspolaganju ima igrač A, a stupci označavaju n mogućih poteza igrača B. Ako igrač A odigra svoj i-ti potez, a igrač B svoj j-ti potez, tada u matrici isplata
(1)
P = \begin{bmatrix} p_{11} & p_{12} & p_{13} & \dots & p_{1n} \\ p_{21} & p_{22} & p_{23} & \dots & p_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ p_{m1} & p_{m2} & p_{m3} & \dots & p_{mn} \end{bmatrix}\in\mathbb{R}^{m\times n},
promatramo element (isplatu) p_{ij}. Kod igara s nula-sumom, igrači imaju strogo konfliktne interese, odnosno dobitak jednoga jednak je gubitku drugoga pa promatramo isplate samo za jednog igrača. Ako je u matrici P vrijednost p_{ij}\gt 0, igrač A dobiva iznos p_{ij} od igrača B, odnosno igrač B gubi iznos p_{ij}. Ako je p_{ij}=0, niti jedan igrač ne dobiva niti gubi. Ako je p_{ij}\lt 0, igrač B dobiva iznos p_{ij} od igrača A, odnosno igrač A gubi iznos p_{ij}. Napomenimo da je situacija kod igara s nenul-sumom nešto složenija, jer igrači nemaju strogo konfliktne interese te stoga na poziciji p_{ij} navodimo isplate za oba igrača.
Primjer 1. Marija i Domagoj igraju igru par-nepar. Ako oboje pokažu paran broj prstiju, Marija dobiva
1 kunu od Domagoja. Ako oboje pokažu neparan broj prstiju, Domagoj dobiva
1 kunu od Marije. Ako su brojevi prstiju koje su pokazali različite parnosti, nitko ne dobiva niti gubi. Martica isplata za ovaj slučaj je
|
|
|
Domagoj |
|
|
|
\begin{matrix} par & nepar \end{matrix} |
|
Marija |
\begin{matrix} par \\ nepar \end{matrix} |
\begin{bmatrix} 1 & 0 \\ 0 &-1 \end{bmatrix}. |
Pravila igre unaprijed su poznata svakom igraču, određuju koje poteze on ima na raspolaganju te koje su posljedice pojedinog poteza. Dobitak na kraju igre ovisi i o potezima suparničkog igrača pa u teoriji igara govorimo o konfliktu ili suradnji. Zbog svega toga, svaki igrač mora imati i primjenjivati određenu strategiju tijekom igre. Sljedeće dvije definicije izričemo iz perspektive prvog igrača u igri (igrača A), a analogno se mogu izreći i iz perspektive drugog igrača.
Definicija 2. Neka igrač
A ima u igri na raspolaganju
m poteza. Strategija igrača
A predstavlja uređenu
m-torku
X=(x_{1},x_{2},...,x_{m}), gdje je
x_{i}\in\mathbb{R},
0\leq x_{i}\leq 1, za
i=1,...,m, vjerojatnost s kojom on bira
i-ti potez u igri te vrijedi
\sum_{i=1}^{m}x_{i}=1.
Definicija 3. Strategiju u kojoj se na
i-tom mjestu u
m-torci
X=(x_{1},x_{2},...,x_{m}), za
i\in\lbrace 1,...,m\rbrace, nalazi vrijednost
1 dok su na svim ostalim mjestima nule nazivamo čistom strategijom
. Strategiju koja nije čista nazivamo mješovita strategija.
Postoji beskonačno mnogo mješovitih strategija za svakog igrača, a glavni cilj teorije igara je svakom igraču pronaći optimalnu strategiju. Kod igara s nula-sumom, optimalne strategije su najopreznije strategije, u kojima igrač A želi osigurati najveći mogući minimalni dobitak, dok će istovremeno za igrača B maksimalan gubitak biti najmanji mogući, bez obzira na to koji potez suparnički igrač odabrao. Ako jedan od igrača ima na raspolaganju samo dva poteza, optimalnu strategiju moguće je odrediti grafički. Kod matrica isplata većih dimenzija u tome pomaže linearno programiranje, a ovakvi se problemi rješavaju korištenjem računala. Traženjem optimalnih strategija ovdje se nećemo baviti (pogledati, na primjer, u [4] i [6]).
Za daljnju analizu matričnih igara potrebno je uključiti i teoriju vjerojatnosti.
Definicija 4. Neka igrač
A i igrač
B igraju igru zadanu matricom isplata (
1), pri čemu koriste mješovite strategije
X=(x_{1},x_{2},...,x_{m}) i
Y=(y_{1},y_{2},...,y_{n}), redom. Očekivani ishod igre (prosječni dobitak nakon više odigranih partija) za igrača
A, s obzirom na strategije
X i
Y, označavamo s
E(X,Y) i računamo po formuli za matematičko očekivanje:
(2)
E(X,Y)=\sum_{i=1}^{m}\sum_{j=1}^{n}p_{ij}x_{i}y_{j}.
Analogno možemo izračunati i prosječni dobitak igrača B, samo što u tom slučaju moramo uzeti u obzir dobitke igrača B.
2NEKOOPERATIVNE IGRE ZA DVA IGRAČA S NENUL-SUMOM
Kod igara s nenul-sumom dobitak jednog igrača ne predstavlja direktni gubitak drugog igrača u svakom od mogućih ishoda igre, odnosno zbroj dobitaka oba igrača nije nužno jednak nuli. Kombiniraju se natjecateljski aspekti s mogućnošću suradnje pa analiza ovakvih igara ovisi o tome jesmo li pretpostavili da igrači komuniciraju tijekom igre ili ne. Razlikujemo kooperativne i nekooperativne igre s nenul-sumom. Mi ćemo pretpostaviti da igrači ne komuniciraju, dakle razmatramo nekooperativne igre. Također, uzet ćemo da istovremeno odabiru svoje strategije i da njihov izbor nije poznat drugom igraču, kao što je to kod igara s nula-sumom. Kod igara s nenul-sumom, elementi matrice isplata su uređeni parovi, pri čemu su prve koordinate vrijednosti isplata za prvog igrača, a druge za drugog.
Primjer 5. Zadana je igra s matricom isplata:
|
|
|
Igrač B |
|
|
|
\begin{matrix} s_{1}\hspace{0,7cm} & s_{2} \end{matrix} |
|
Igrač A |
\begin{matrix} r_{1} \\ r_{2} \end{matrix} |
\begin{bmatrix} (0,0) & (10,-8) \\ (-5,8) & (8,8) \end{bmatrix}. |
U igri iz Primjera 5, na primjer, ako igrač A odabere potez r_{2}, a igrač B potez s_{2}, kao isplatu dobivamo p_{22}=(8,8), kod koje su oba igrača na dobitku.
Kako i u igrama sa sumom nula nije pristuna suradnja, logično je pogledati koji se termini vezani uz igre s nula-sumom mogu proširiti na igre s nenul-sumom. Krenimo s pojmom dominacije.
Definicija 6. Za čistu strategiju
S kažemo da je dominantna u odnosu na čistu strategiju
T ako je svaka isplata pri odabiru strategije
S barem jednako dobra, a barem u jednnom slučaju i strogo bolja od odgovarajuće isplate pri odabiru strategije
T. Za strategiju
T kažemo da je dominirana strategijom
S.
Očekuje se da će razuman igrač uvijek igrati dominantnu strategiju. Kod igara sa sumom nula takva je strategija uvijek optimalna i nazivamo je ravnotežna strategija. U Primjeru 5, za igrača A strategija r_{1} dominantna je u odnosu na strategiju r_{2} jer je 0\gt -5 i 10\gt 8. Za igrača B dominantna je strategija s_{1} u odnosu na strategiju s_{2}, jer je 0\gt -8 i 8=8. Dominantne strategije igrača su X=Y=(1,0), a isplata dobivena primjenom principa dominacije p_{11}=(0,0). No, isplata p_{22}=(8,8) je povoljnija pa zaključujemo da kod nekooperativnih igara s nenul-sumom korištenje dominantnih strategija ne rezultira uvijek najboljim ishodom za igrače. Osim toga, kako kod igara s nula-sumom, tako i kod igara s nenul-sumom, dominantne strategije ne moraju postojati u igri.
Primjer 7. U ovoj igri nema dominantnih strategija:
|
|
|
Igrač B |
|
|
|
\begin{matrix} s_{1}\hspace{0,4cm} & s_{2} \end{matrix} |
|
Igrač A |
\begin{matrix} r_{1} \\ r_{2} \end{matrix} |
\begin{bmatrix} (4,8) & (2,0) \\ (6,2) & (0,8) \end{bmatrix}. |
Postavlja se pitanje možemo li odrediti mješovite strategije za oba igrača, takve da odabirom nekih drugih strategija niti jedan od njih neće profitirati. John Forbes Nash Jr. (1928.-2015.) je 1950. godine dokazao da svaka igra za dva igrača ima barem jedan par ravnotežnih strategija, bilo čistih, bilo mješovith (detaljnije opisano u [3]). Nash je bio američki ekonomist i matematičar, koji je dao veliki doprinos teoriji igara. Njemu u čast, ravnotežu u igrama s nenul-sumom nazivamo Nashova ravnoteža. Nashova ravnoteža imala je veliku primjenu kod donošenja poslovnih strategija te je Nash 1994. godine bio nagrađen Nobelovom nagradom za ekonomiju. Njemu u čast, 2001. godine snimljen je film Genijalni um (engl. A Beautiful Mind).
Definicija 8. U igrama s dva igrača, uređeni par strategija
(X_{0}, Y_{0}) nazivamo Nashova ravnoteža ako igrač
A odabire strategiju
X_{0}, a igrač
B strategiju
Y_{0} te nakon takvog odabira strategija niti jedan od igrača nema poticaj za promjenu svoje strategije, uzimajući u obzir odluke protivnika.
Dakle, ako neki igrač odluči tijekom igre promijeniti svoju strategiju, to mu neće omogućiti veći dobitak, u odnosu na odabir strategije kojom je uspostavljena Nashova ravnoteža, sve dok i drugi igrač ne promijeni svoju strategiju.
Promotrimo li u Primjeru 7 isplate za igrača B kao igru s nula-sumom, kao optimalnu strategiju za igrača A dobit ćemo X_{0}=\big(\frac{3}{7},\frac{4}{7}\big). Zanimljivo je da, bez obzira na to koju strategiju Y odabere igrač B, očekivani ishod igre (2) za njega je E(X_{0},Y)=\frac{32}{7}. Ako promotrimo isplate igrača A kao igru s nula-sumom, kao optimalnu strategiju za igrača B dobit ćemo Y_{0}=\big(\frac{1}{2},\frac{1}{2}\big). Bez obzira na to koju strategiju X odabere igrač A, očekivani ishod igre (2) za njega je E(X,Y_{0})=3. Par ravnotežnih strategija (X_{0},Y_{0}) za uspostavu Nashove ravnoteže pronašli smo tako da je svaki igrač promatrao isplate drugog igrača, a ignorirao svoje. Nashova ravnoteža nije baš u svakoj igri najsretnije rješenje za igrače.
Primjer 9. Promotrimo dominantne strategije u igri zadanoj marticom isplata:
|
|
|
Igrač B |
|
|
|
\begin{matrix} s_{1}\hspace{1cm} & s_{2} \end{matrix} |
|
Igrač A |
\begin{matrix} r_{1} \\ r_{2} \end{matrix} |
\begin{bmatrix} (6,6) & (-2,10) \\ (10,-2) & (0,0) \end{bmatrix}. |
Nashova ravnoteža je uspostavljena ravnotežnim strategijama X_{0}=Y_{0}=(0,1). Dobivamo isplatu p_{22}=(0,0), no isplata p_{11}=(6,6) povoljnija je za igrače. Dakle, opet postoji bolja isplata od one u Nashovoj ravnoteži.
Primjer 10. U ovoj igri postoje dva para ravnotežnih strategija:
|
|
|
Igrač B |
|
|
|
\begin{matrix} s_{1}\hspace{0,5cm} & s_{2} \end{matrix} |
|
Igrač A |
\begin{matrix} r_{1} \\ r_{2} \end{matrix} |
\begin{bmatrix} (5,1) & (0,0) \\ (0,0) & (1,5) \end{bmatrix}. |
Ako igrač A odabere potez r_{1}, za igrača B je bolje odabrati potez s_{1} te igrač A prolazi bolje, s isplatom p_{11}=(5,1). Imamo ravnotežne strategije X_{0}=Y_{0}=(1,0). Ako igrač A odabere potez r_{2}, igrač B odabire potez s_{2} i s isplatom p_{22}=(1,5) on prolazi bolje. Drugi par ravnotežnih strategija je X'_{0}=Y'_{0}=(0,1). Kada bismo igračima dozvolili komunikaciju, mogli bi se dogovoriti da kod višestrukog ponavljanja igre naizmjenično odaberu parove ravnotežnih strategija te tako oba budu na dobitku. No, u nekooperativnim igrama to ne možemo.
Djelomično rješenje problema u kojima postoje povoljnije isplate od onih dobivenih Nashovom ravnotežom, nudi Vilfredo Federico Pareto (1848.-1923.), talijanski sociolog, ekonomist i filozof.
Definicija 11. Isplata u igri nije Pareto optimalna ako postoji isplata koja bi obojici igrača omogućila veći dobitak ili bi jednom od igrača omogućila isti dobitak, a drugom igraču veći dobitak. U protivnom isplata je Pareto optimalna.
Paretov se princip temelji na grupnoj racionalnosti, a princip dominacije na individualnoj. Igre mogu imati više Pareto optimalnih isplata, a riječ optimalna znači da nije lošija od neke druge isplate. Paretov princip glasi: Da bi isplata bila prihvatljiva kao rješenje igre, ona mora biti Pareto optimalna.
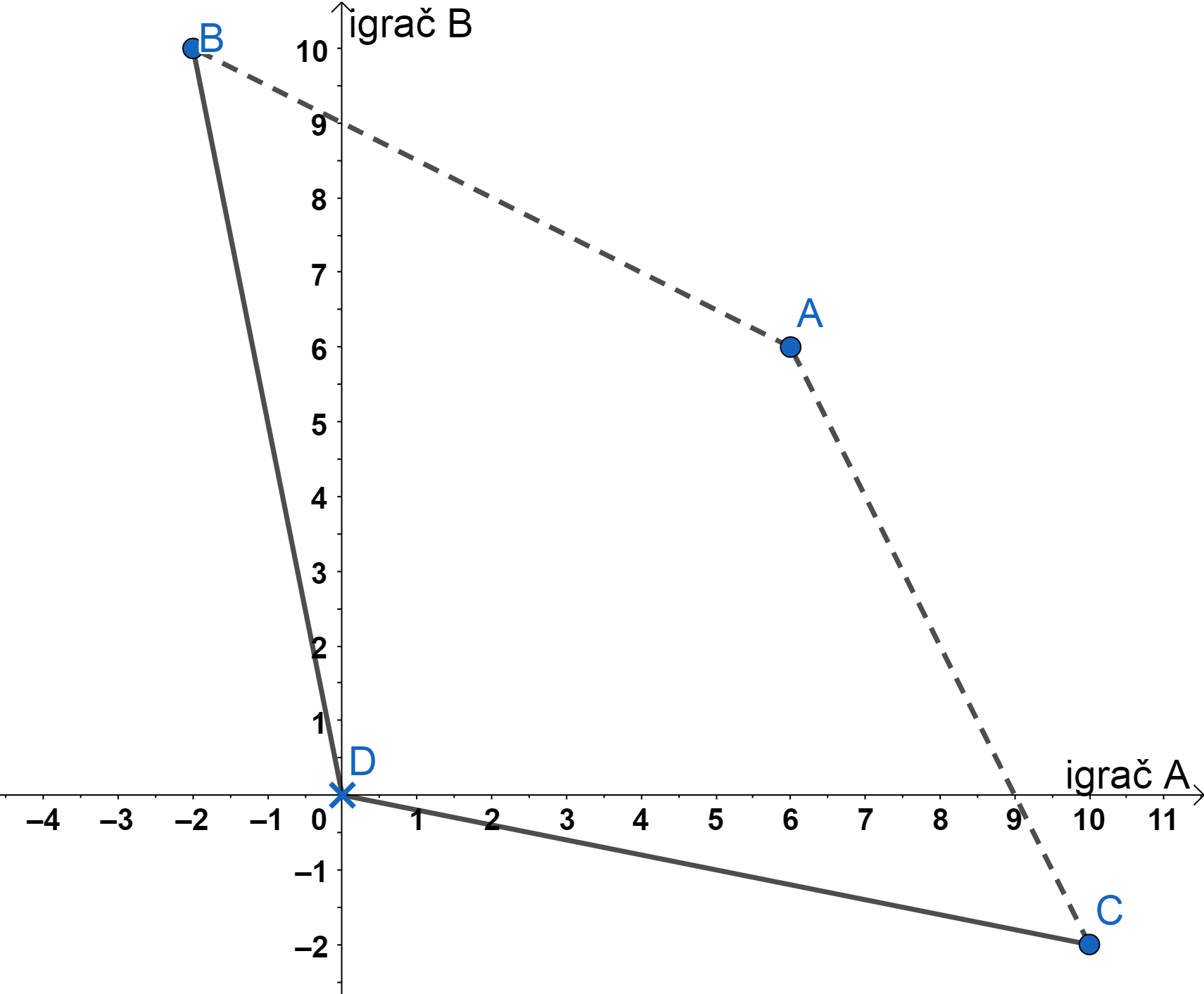
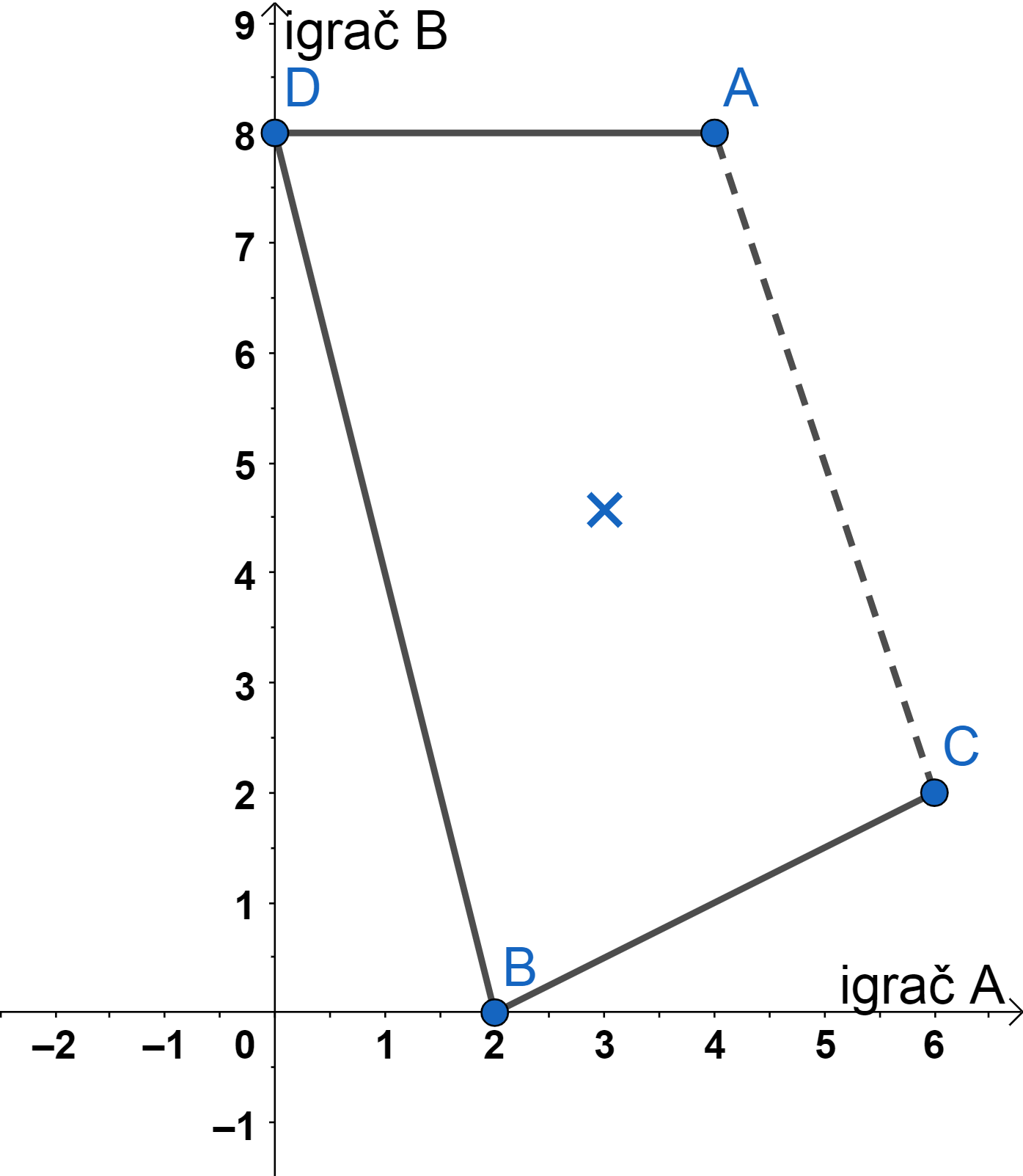
Radi lakšeg razmatranja, problem prikazujemo u koordinatnoj ravnini, s vrijednostima dobitaka za igrača A na osi apscisa te vrijednostima dobitaka za igrača B na osi ordinata. Točke u koordinatnoj ravnini predstavljaju isplate u matrici isplata, a povezane dužinama tvore mnogokut koji se naziva mnogokut isplata. Križić predstavlja isplatu dobivenu uspostavom Nashove ravnoteže, a isprekidane linije povezuju Pareto optimalne isplate.
U Primjeru 9, isplata p_{22}=(0,0) nije Pareto optimalna, jer isplata p_{11}=(6,6) omogućuje bolje dobitke za oba igrača. Tri preostale isplate su Pareto optimalne.
U Primjeru 7, Nashova ravnoteža ne daje dobru isplatu za igrače. Odabirom isplate p_{11}=(4,8), prikazane vrhom A, oba igrača bi se našla u boljoj situaciji.
Ishodi igara dobiveni uspostavom Nashove ravnoteže su poželjni, jer su stabilni i postoje u svakoj igri, ali često dobivene isplate nisu Pareto optimalne. Zato se javlja potreba za drugim idejama. U igrama sa sumom nula optimalne su strategije najopreznije strategije.
Definicija 12. Neka je igra zadana matricom isplata (
1). Označimo s
\min_{j}p_{ij} najmanji element u
i-tom retku, a s
\max_{i}p_{ij} najveći element u
j-tom stupcu. Najveći element među
\min_{j}p_{ij}, za
j\in\lbrace 1,...,n\rbrace, nazivamo maximin. Najmanji element među
\max_{i}p_{ij}, za
i\in\lbrace 1,...,m\rbrace, nazivamo minimax. Ako je vrijednost maximin jednaka vrijednosti minimax, tu vrijednost nazivamo sedlasti element ili sedlo.
Odabirom vrijednosti maximin igrač A nastoji sebi osigurati najveći minimalni dobitak, a igrač B želi sebi osigurati najmanji maksimalni gubitak odabirom ishoda minimax. Ako postoji sedlo, u igri s nula-sumom za oba je igrača najbolje igrati sedlo.
Pogledajmo ponašanje ovakvih strategija u kontekstu igara s nenul-sumom. Za igru iz Primjera 7, potražimo povoljniji ishod od onog dobivenog uspostavom Nashove ravnoteže. Uzmimo da igrač A želi maksimizirati minimalni dobitak. Gledajući njegove isplate, vidimo da je najmanji element u prvom retku 2, a u drugom 0. Kako je 2\gt 0, igrač A će potezom r_{1} osigurati dobitak vrijednosti najmanje 2.
Definicija 13. U igrama s nenul-sumom, optimalna strategija za igrača
A, s obziirom na njegovu igru, naziva se razborita strategija za igrača
A. Ishod igre u tom slučaju naziva se sigurnosni nivo igrača
A.
Dakle, odabirom razborite strategije, igrač A osigurava najmanje onaj dobitak koliko iznosi njegov sigurnosni nivo. U Primjeru 7 razborita strategija igrača A je X=(1,0), a sigurnosni nivo je 2. To je ujedno i sedlo za igru igrača A.
U igri igrača B ne postoji sedlo. Razborita stategija Y=(\frac{4}{7},\frac{3}{7}) za igrača B dobiva se rješavanjem matrične igre s nula-sumom. Njegov sigurnosni nivo iznosi \frac{32}{7}. Ako igrači odigraju svoje razborite strategije, ishod igre (2) je E(X,Y)=\frac{4}{7}(4,8)+\frac{3}{7}(2,0)=(\frac{22}{7},\frac{32}{7}). Taj ishod nije Pareto optimalan, niti dobiven uspostavom Nashove ravnoteže. Isplata p_{11}=(4,8) je bolja za oba igrača. Ukoliko očekuje da će igrač A odigrati svoju razboritu strategiju, igrač B bi odabirom strategije Y=(1,0) sebi osigurao dobit vrijednosti 8. Analogno, ako očekuje da će igrač B odabrati svoju razboritu stretegiju, igrač A odabirom poteza r_{1} dobiva \frac{4}{7}\cdot 4+\frac{3}{7}\cdot 2=\frac{22}{7}, a odabirom poteza r_{2} dobiva \frac{4}{7}\cdot 6+\frac{3}{7}\cdot 0=\frac{24}{7}. Svaki igrač trebao bi potražiti najbolji odgovor na razboritu strategiju drugog igrača.
Definicija 14. U igrama s nenul-sumom, igračeva kontra-razborita strategija je njegov najbolji odgovor na razboritu strategiju protivnika.
|
Strategija igrača A |
Strategija igrača B |
Isplata igrača A |
Isplata igrača B |
|
razborita |
razborita |
3.14 |
4.57 |
|
razborita |
kontra-razborita |
4 |
8 |
|
kontra-razborita |
razborita |
3.42 |
4.57 |
|
kontra-razborita |
kontra-razborita |
6 |
2 |
Tablica 1: Razborite i kontra-razborite strategije u igri iz
Primjera 7
Iz Tablice
1 vidimo da je, u igri iz Primjera
7, za igrača
A najbolje ako oba igrača odaberu kontra-razborite strategije, a za igrača
B ako na razboritu strategiju igrača
A odgovori kontra-razboritom strategijom.
Razmotrimo detaljnije rješivost igre.
Definicija 15. Igra za dva igrača je rješiva u strogom smislu ako vrijedi:
1) postoji barem jedna Nashova ravnoteža koja je Pareto optimalna i
2) ako postoji više Pareto optimalnih Nashovih ravnoteža, one su sve ekvivalnentne
i međusobno razmjenjive
.
Sve do sada prikazane igre s nenul-sumom nisu rješive u strogom smislu.
Primjer 16. Ova je igra rješiva u strogom smislu:
|
|
|
Karolina |
|
|
|
\begin{matrix} s_{1}\hspace{0,5cm} & s_{2} \end{matrix} |
|
Ruža |
\begin{matrix} r_{1} \\ r_{2} \end{matrix} |
\begin{bmatrix} (2,3) & (3,2) \\ (1,0) & (0,1) \end{bmatrix}. |
Za Ružu je strategija X=(1,0) dominantna. Znajući to, Karolina radije igra potez s_{1} nego s_{2}. Ishodom p_{11}=(2,3) postignuta je Nashova ravnoteža u ovoj igri jer niti jedna od igračica nema potrebu promijeniti strategiju. Taj je ishod i Pareto optimalan jer ne postoji drugi koji je za obje bolji ili barem jednako dobar.
3Primjena nekooperativnih igara s nenul-sumom
Nekooperativne igre s nenul-sumom imaju široku primjenu u brojnim situacijama iz svakodnevnog života, na primjer: igra kamen-škare-papir, igra bacanja novčića i šah. Ipak, najpoznatiji primjer nekooperativne igre s nenul-sumom je Dilema zatvorenika. 1950. godine američki matematičari Melvin Dresher i Merrill Flood razvili su igru s nenul-sumom koja ima jedinstvenu Nashovu ravnotežu koja nije Pareto optimalna. Kasnije je kanadski matematičar Albert W. Tucker osmislio priču koja odgovara situaciji u igri te tako doprinio popularizaciji te igre.
Primjer 17. [Dilema zatvorenika]Policija je uhitila dvojicu osumnjičenika za zločin te ih pojedinačno ispitala. Pritom, nisu mogli međusbno komunicirati. Tužitelj je svakom zatvorniku rekao sljedeće:
1.) "Ako jedan od vas prizna sudjelovanje u zločinu, a drugi ne, onda će onaj koji prizna biti nagrađen slobodom, a onaj koji ne prizna dobit će kaznu veću za
3 godine od predviđene."
2.) "Ako obojica priznate sudjelovanje u zločinu, svaki od vas bit će kažnjen propisanom kaznom od
2 godine zatvora."
Postoji i mogućnost da oba osumnjičenika budu oslobođena zbog nedostatka dokaza, ako se obojica odluče za šutnju. Matrica isplata ovog problema je:
|
|
|
Osumničenik B |
|
|
|
\begin{matrix} priznaje\hspace{0,5cm} & ne\ priznaje \end{matrix} |
|
Osumnjičenik A |
\begin{matrix} priznaje \\ ne\ priznaje \end{matrix} |
\begin{bmatrix} (-2,-2) & (0,-5) \\ (-5,0) & (0,0) \end{bmatrix}. |
Ako oba igrača odaberu svoje dominantne strategije X=Y=(1,0), uspostavom Nashove ravnoteže dobivamo isplatu p_{11}=(-2,-2). Ona nije Pareto optimalna, jer je za obojicu bolja isplata p_{22}=(0,0), jedina Pareto optimalna isplata ove igre.
Ovo je tipičan primjer sukoba individualne racionalnosti dominantnih strategija i kolektivne racionalnosti Paretova principa. Oba osumnjičenika slijede vlastite interese, što rezultira lošijim izborom za obojicu. Ovaj bi problem najlakše riješili ako im dopustimo suradnju. Moguće je da oba igrača budu oslobođena i ako postoji mogućnost predviđanja što bi drugi osumnjičenik mogao učiniti. No, teško je predvidjeti što će netko učiniti. Kod Dileme zatvorenika nema pouzdane strategije koja bi uvijek rezultirala najboljim ishodom igre za oba igrača.
Slične igre sa zanimljivim aspektima socijalne interakcije bile su primjenjivane u eksperimentalnom radu iz područja socijalne psihologije. Mnogi su takvi problemi vezani uz ekonomiju, na primjer situacija u kojoj dva trgovačka lanca u svom natjecanju za kupce razmišljaju kako ih zadržati i kako steći nove, a da pritom i dalje budu na dobitku. Ako oba lanca snize cijene kako bi bili konkurentniji, rezultat je podjednak broj kupaca uz niži prihod.
4Zaključak
Promotrili smo različite strategije za rješavanje nekooperativnih igara s nenul-sumom, od jednostavnijih, poput dominacije, do Nashove ravnoteže i Pareto optimalnosti. Riješiti takvu igru nije uvijek moguće, za razliku od igara s nula-sumom. Igre za dva igrača s nenul-sumom često odgovaraju stvarnim situacijama pa je u tome njihova ljepota i intrigantnost, unatoč čestom izostanku rješenja.
Napomena: Članak je nastao iz diplomskog rada studenta Mije Radoša, pod mentorstvom doc. dr. sc. Ane Jurasić, na Diplomskom sveučilišnom studiju Matematika i informatika - smjer nastavnički, Fakulteta za matematiku Sveučilišta u Rijeci.
Bibliografija
|
[1] |
Encyclopedia Britannica: John Nash, https://www.britannica.com/biography/John-Nash |
|
[2] |
Encyclopedia Britannica: Vilfredo Pareto, https://www.britannica.com/biography/Vilfredo-Pareto |
|
[3] |
A. X. Jiang, K. Leyton-Brown: A Tutorial on the Proof of the Existence of Nash Equilibria, https://www.cs.ubc.ca/ jiang/papers/NashReport.pdf |
|
[4] |
G. E. Keough, P. R. Thie: An Introduction to Linear Programming and Game Theory, Wiley, New Jersey, 2008. |
|
[5] |
L. F. Seltzer: The Prisoner's Dilemma and the „Virtues“ of Tic for Tat, Psychology Today, 2016., https://www.psychologytoday.com/us/blog/evolution-theself/201607/the-prisoner-s-dilemma-and-the-virtues-tit-tat |
|
[6] |
P. D. Straphin: Game Theory and Strategy, The Mathematical Association of America, 1993.
|