|
Ivančica Miroševic, Nikola Koceić-Bilan, Josipa Jurko |
1Uvod
Elipsa, hiperbola i parabola su neke od prvo proučavanih krivulja. Pogledamo li "razvoj priče" o njima kroz povijest, vidimo da je "veliki geometar" Apolonije iz Perge još 200-tih godina pr. Kr. napisao o njima opsežnu studiju, i to čisto geometrijskim pristupom. Njegovi su rezultati bili toliko podrobni i potpuni da se današnja euklidska geometrija nije mnogo odmakla od njegovih spoznaja. I kao takvi, bili su dostatna osnova Johannesu Kepleru (1571.-1630.) i Isaacu Newtonu (1643.-1728.) da dođu do svojih izvanrednih otkrića o gibanjima nebeskih tijela.
Međutim, Apolonije nije svojstva čunjosječnica opisivao algebarski, kao što mi to danas u školskom sustavu činimo. Trebalo je proći skoro 2000 godina da bi matematičari postigli veliki pomak u razumijevanju čunjosječnica povezivanjem geometrijskih i algebarskih tehnika.
Ono što nas je ponukalo na pisanje ovoga članka jest dojam da su neki aspekti pri proučavanju tih krivulja kroz srednješkolsku naobrazbu pomalo zanemareni. U nastavnim programima za matematiku u srednjim školama i gimnazijama, krivuljama drugog reda uglavnom se pristupa analitički, preko algebarske jednadžbe tih krivulja, iz čega se onda izvode i njihova svojstva, a mi smo stajališta da se i s pomoću čisto geometrijskog pristupa ove krivulje sasvim lijepo mogu upoznati, i da se na taj način mogu učenicima pokazati neka važna svojstva koja se iz analitičkog pristupa ne vide, npr. njihovo optičko svojstvo refleksije. Time ne želimo umanjiti značaj analitičkog pristupa, već samo ukazati na neke druge pristupe, te ih objediniti u "širu priču" o krivuljama drugoga reda.
U sintetičkom pristupu, u 2. poglavlju uvodimo pojam tangente na najelementarniji način, kao i njezine karakterizacije. Već kod parabole vidimo da je pojam tangente (na način kako ju većina doživljava) vrlo suptilan pojam koji se ne može definirati kao pravac koji siječe krivulju u jednoj točki, a s druge strane želja nam je bila izbjeći bilo koju uporabu infinitezimalnoga računa koji je neprimjeren za učenike prije završnog razreda srednje škole. Nadalje, pojam asimptote hiperbole je, također, uveden ad hoc s ciljem da se izbjegne uobičajeni pristup preko formalnog graničnog procesa. Treba reći da smo, kroz različite pristupe čunjosječnicama, htjeli naglasiti neka njihova važna svojstva koja su nedovoljno istaknuta u analitičkom pristupu, a koja se s lakoćom mogu izvesti bez prevelikog predznanja, i kao takva se mogu obrađivati i prije 3. razreda srednje škole (kad se ove krivulje prvi puta sustavno obrađuju u sklopu analitičke geometrije). Sintetički pristup je pogodan za dokazivanje svojstava tangenata i asimptote i nekih manje poznatih, ali zanimljivih tvrdnja (Ponceletovi teoremi). No, u ovomu pristupu učenik ne može sagledati sličnost i vezu između ovih krivulja. Algebarski pristup pojašnjava zbog čega ove krivulje zajednički nazivamo krivuljama 2. reda. Proučavanje ovih krivulja kao presjeka s konusom (čunjem) opravdava naziv čunjosječnice ili konike, te upućuje kako ih možemo pronaći kao obrise na sjenama što ih ostavlja stožasti izvor svjetlosti sobne svjetiljke, a to otvara zanimljiv prostor za samostalne učeničke pokuse i projektne zadatke. Papus-Boškovićev pristup ovim krivuljama pojašnjava ulogu ravnalice kod elipse i hiperbole, ulogu numeričkog ekscentriciteta \varepsilon (kojeg se najčešće bez neke primjene i svrhe spominje u nastavi) te pokazuje kako se variranjem parametra \varepsilon krivulje mijenjaju od elipse, preko parabole i hiperbole do kružnice.
Slike u članku generirane su uglavnom s pomoću besplatnog programskog paketa Geogebra (https://www.geogebra.org). Iznimno su, zbog ograničenja Geogebre, slike 21, 22 , 23 i 24 izrađene u programu Microsoft Word.
Inače, na internetu se može pronaći velik broj interaktivnih uradaka o čunjosječnicama izrađenih u Geogebri, i mnogi se temelje na sintetičkoj definiciji.
2Sintetički pristup
U ovomu poglavlju, koje se dobrim dijelom temelji na nastavnim materijalima [1], definiramo elipsu, hiperbolu i parabolu, te izvodimo neka njihova svojstva bez uporabe algebarskog alata.
Definicija 1. Neka su
F_{1} i
F_{2} dvije čvrste međusobno različite točke ravnine
\pi i neka je
d\left( F_{1},F_{2}\right) =2e, te neka je
a\gt 0 zadani realni broj,
a\gt e. Skup svih točaka ravnine za koje je zbroj udaljenosti od točaka
F_{1} i
F_{2} konstantan i jednak
2a nazivamo
elipsom, u oznaci
E\left( F_{1},F_{2},a\right). Kraće,
E=\left\lbrace T\in\pi\ :\ \, d(T,F_{1})+d(T,F_{2})=2a\right\rbrace .
Točke F_{1} i F_{2} nazivamo žarištima ili fokusima elipse, a dužine \overline{T F_{1}} i \overline{T F_{2}} radijusvektorima točke T elipse (iako to nisu vektori). Dopustimo li da bude i F_{1}=F_{2}, odnosno e=0, dobivamo skup svih točaka jednako udaljenih od fiksne točke F, kojega nazivamo kružnicom.
Realni broj e nazivamo linearnim ekscentricitetom.
Polovište O dužine \overline{F_{1}F_{2}} nazivamo središtem elipse. Lako se pokaže da pravac F_{1}F_{2} siječe elipsu u dvjema točkama, označimo ih s A i B, i da simetrala dužine \overline{F_{1}F_{2}} također siječe elipsu u dvjema točkama, označimo ih s C i D. Točke A i B, te točke C i D nazivamo tjemenima elipse. Dužinu \overline{A B} nazivamo velikom (glavnom) osi, a dužine \overline{O A} i \overline{O B} velikim poluosima. Dužinu \overline{C D} nazivamo malom (sporednom) osi elipse, a dužine \overline{O C} i \overline{O D} malim poluosima. Duljinu male poluosi označavamo sa b.
Budući da je osna simetrija S_{A B} izometrija, pa čuva i zbroj udaljenosti od točke do fiksnih točaka F_{1} i F_{2} na osi A B, velika os je os simetrije za elipsu. Analogno, budući da je osna simetrija S_{C D} izometrija, pa čuva i zbroj udaljenosti od točke do međusobno simetričnih točaka F_{1} i F_{2} s obzirom na os S_{C D}, mala os je također os simetrije za elipsu.
Sada se lako dokaže da je \left\vert O A\right\vert =a, i da je \left\vert A B\right\vert =2a.
Iz pravokutnoga trokuta \triangle F_{1}O C vidimo da za duljine poluosi a i b, i za linearni ekscentricitet e elipse vrijedi
a^{2}-b^{2}=e^{2}.
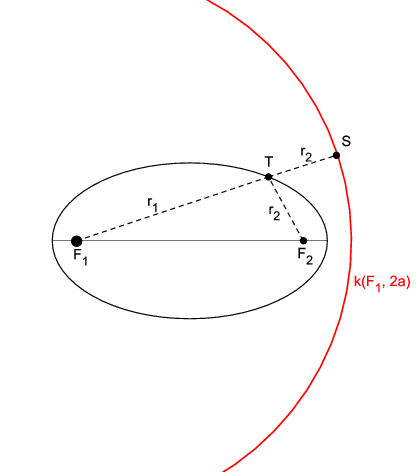
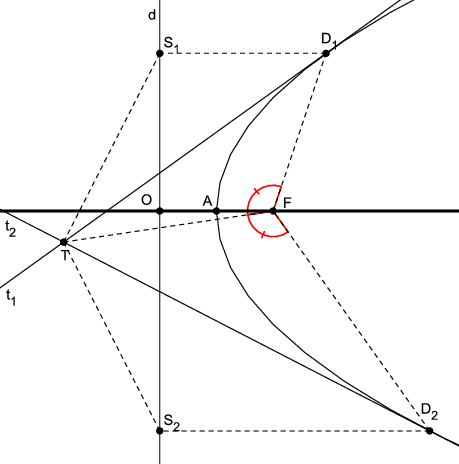
Neka je T bilo koja točka elipse. Produžimo dužinu \overline{F_{1}T} preko točke T za \left|F_{2}T\right|. Tako dobivamo točku S koju nazivamo suprotištem žarišta F_{2} za točku T elipse. Suprotište S je udaljeno od žarišta F_{1} za \left\vert F_{1}S\right\vert =2a. Promjena točke T na elipsi ne utječe na tu udaljenost. Odatle slijedi da, ako točka T varira, onda suprotište S opisuje kružnicu sa središtem u F_{1} i polumjerom 2a. Tu kružnicu nazivamo kružnicom suprotišta žarišta F_{2} (Slika 1). Analogno definiramo i kružnicu suprotišta žarišta F_{1}.
Navest ćemo sada teorem koji opisuje zanimljivo "optičko-geometrijsko" svojstvo elipse: postavimo li izvor svjetlosti u jedno od žarišta elipse, zraka svjetlosti će se odbiti od elipse i proći kroz drugo žarište. To znači da je reflektirani kut zrake u svakoj točki elipse jednak upadnom. Definirajmo najprije tangentu elipse.
Definicija 2. Tangenta elipse je pravac koji s elipsom ima jednu zajedničku (dodirnu) točku.
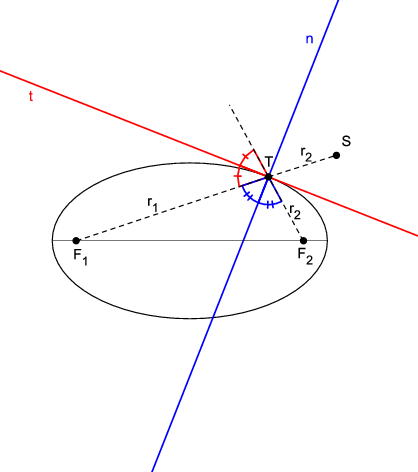
Teorem 3. Tangenta t u točki T elipse je pravac koji raspolavlja vanjski kut što ga tvore dva radijusvektora točke T. Normala n u točki T elipse je pravac koji raspolavlja unutarnji kut što ga tvore dva radijusvektora točke T.
Dokaz. Trokut
F_{2}S T, gdje je
S suprotište žarišta
F_{2} za točku
T elipse, je jednakokračan trokut s osnovicom
F_{2}S (Slika
2). Uz to vrijedi
\left|F_{1}S\right|=\left|F_{1}T\right|+\left|T S\right|=\left|F_{1}T\right|+ \left|F_{2}T\right|=2a.
Neka je pravac
t simetrala dužine
\overline{F_{2}S}, a time i simetrala kuta
\angle F_{2}T S. Dokažimo da je
t ujedno tangenta elipse. Pretpostavimo protivno, tj. da postoji točka
P na pravcu
t koja je ujedno i točka elipse i koja je različita od
T. U trokutu
F_{1}P S vrijedi nejednakost trokuta
\left|F_{1}P\right|+\left|F_{2}P\right|= \left|F_{1}P\right|+\left|P S\right|\gt \left|F_{1}S\right|=2a,
a to se protivi pretpostavci. Dakle, pravac
t je tangenta elipse, čime je dokazana tvrdnja.
Dokažimo sada obrat tvrdnje, odnosno, dokažimo da pravac
p kroz točku
T elipse, koji nije simetrala kuta
\angle F_{2}T S, ne može biti tangenta. U tu svrhu dovoljno je dokazati da pravac
p siječe elipsu u još jednoj točki uz
T. Neka je
F_{2}^{\prime}:=S_{p}(F_{2}) osno simetrična slika žarišta
F_{2} s obzirom na pravac
p i neka je
{Q}=p\cap F_{1}F_{2}^{\prime}. Očito, točka
Q ima svojstvo
\left|F_{1}Q\right|+\left|Q F_{2}\right|\lt \left|F_{1}P\right|+\left|PF_{2}\right|
za svaku točku
P\in p,
P\neq Q, tj. to je točka pravca
p u kojoj je najmanji zbroj udaljenosti od žarišta. Budući da je
Q\neq T jer je
F_{2}'\neq S, to je
\left|F_{1}Q\right|+\left|Q F_{2}\right|\lt \left|F_{1}T\right|+\left|T F_{2}\right|=2a.
Zamijetimo da za dovoljno daleku točku
P polupravca određenog s
p i
Q koji ne sadrži
T vrijedi
\left|F_{1}P\right|+\left|PF_{2}\right|\gt 2a. Sada je intuitivno jasno da na dužini
\overline{Q P} leži točka
T' takva da je
\left|F_{1}T'\right|+\left|T'F_{2}\right|=2a (formalno to slijedi po teoremu o međuvrijednostima). To znači da
p siječe elipsu u još jednoj točki, pa nije tangenta.
\ \blacksquare
Korolar 4. Tangenta t u točki T elipse uvijek postoji i jedinstvena je.
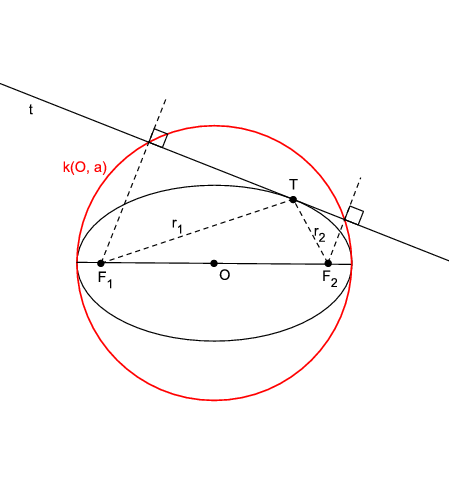
Teorem 5. Nožišta okomica spuštenih iz oba žarišta elipse na tangentu elipse leže na kružnici
k polumjera
a sa središtem u središtu elipse. Tu kružnicu nazivamo
glavnom kružnicom elipse (Slika
3).
Dokaz. Neka je zadana tangenta
t elipse. Označimo s
K nožište okomice spuštene iz
F_{2} na
t, i sa
S suprotište žarišta
F_{2}. Promotrimo trokut
\Delta F_{1}F_{2}S. Dužina
\overline{O K} je srednjica tog trokuta pa vrijedi
\left|O K\right|=\frac{1}{2}\left|F_{1}S\right|=a,
što povlači
K\in k(O,a). Slično se vidi i obratno, tj. da je u točki
K kružnice
k(O,a) okomica na
F_{2}K tangenta elipse.
\ \blacksquare
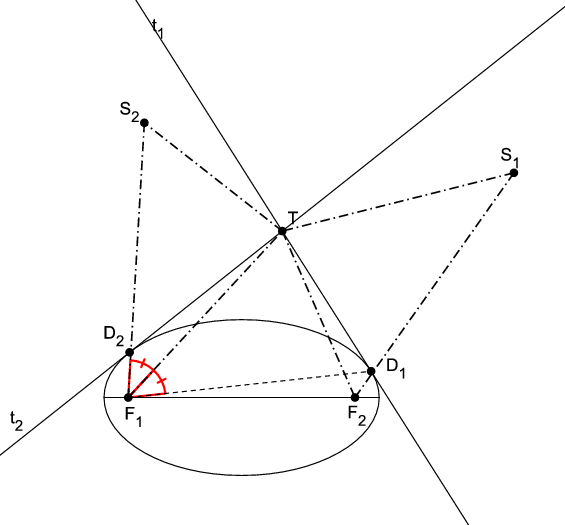
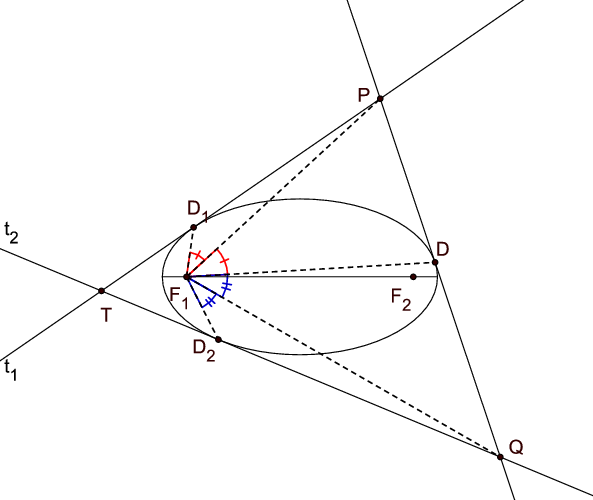
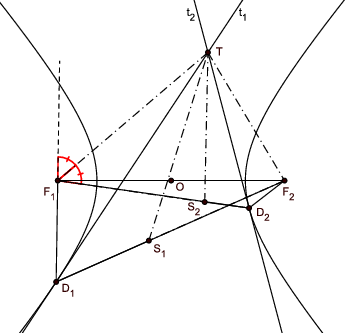
Teorem 6. [Prvi Ponceletov teorem za elipsu] Spojnice žarišta elipse sa sjecištem dviju tangenata simetrale su kutova što ih tvore spojnice žarišta s diralištima tangenata.
Dokaz. Neka je točka
T sjecište tangenata
t_{1} i
t_{2}, neka je
S_{1} suprotište žarišta
F_{1} s obzirom
t_{1} i
S_{2} suprotište žarišta
F_{2} s obzirom na
t_{2} (Slika
4). Tada su
S_{1}, diralište
D_{1} tangente
t_{1} i
F_{2} kolinearne točke. Isto tako,
F_{1}, diralište
D_{2} tangente
t_{2} i
S_{2} su kolinearne točke. Budući da osna simetrija čuva udaljenosti, slijedi
\left|T S_{1}\right|=\left|T F_{1}\right| i
\left|T S_{2}\right|=\left|T F_{2}\right|. Iz
\left|S_{1}F_{2}\right|=2a=\left|S_{2}F_{1}\right| proizlazi
\Delta T F_{2}S_{1} \cong\Delta T F_{1}S_{2}. To povlači
\angle T S_{1}F_{2}=\angle T F_{1}S_{2}. No, budući da je
\angle T S_{1}F_{2}=\angle T S_{1}D_{1}, zbog toga što osna simetrija čuva kutove, slijedi
\angle T S_{1}F_{2}=\angle T F_{1}D_{1}. Time je dokazano da je
\angle T F_{1}D_{1}=\angle T F_{1}D_{2}.
\ \blacksquare
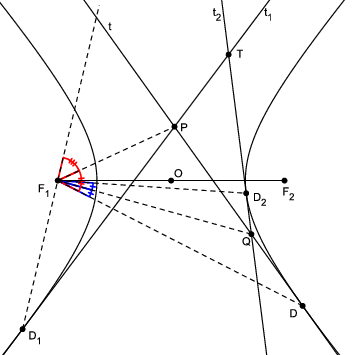
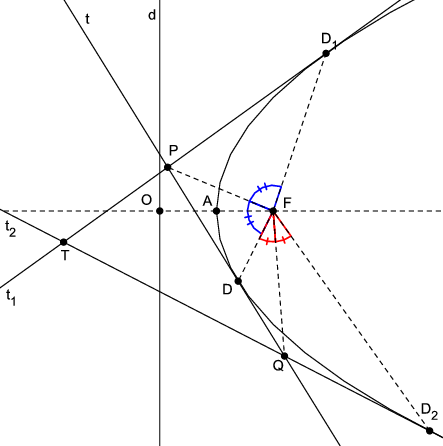
Teorem 7. [Drugi Ponceletov teorem za elipsu] Odsječak varijabilne tangente elipse između dviju fiksnih tangenata vidi se iz žarišta pod stalnim kutom koji je jednak polovini kuta pod kojim se iz žarišta vide dirališta fiksnih tangenata.
Dokaz. Neka su
t_{1} i
t_{2} fiksne tangente, a
t varijabilna tangenta (Slika
5). Neka je
D diralište bilo koje tangente
P Q. Primjenom Teorema
6 na
t i
t_{1} dobivamo da je
\angle D_{1}F_{1}P=\angle PF_{1}D. Isto tako, primjenom na
t i
t_{2} dobivamo da je
\angle DF_{1}Q=\angle D_{2}F_{1}Q. Iz toga slijedi da je
\angle PF_{1}Q=\frac{1}{2}\angle D_{1}F_{1}D_{2}.
\ \blacksquare
Definicija 8. Neka su
F_{1} i
F_{2} dvije međusobno različite čvrste točke ravnine
\pi,
d(F_{1},F_{2})=2e i neka je dan realni broj
a,
0\lt a\lt e. Skup svih točaka za koje je apsolutna vrijednost razlike udaljenosti do danih točaka
F_{1} i
F_{2} konstantna i jednaka
2a, nazivamo
hiperbolom, u oznaci
H\left( F_{1},F_{2},a\right). Kraće,
H=\left\lbrace T\in \pi\ : \ \left\vert d(F_{1},T)-d(F_{2},T)\right\vert =2a\right\rbrace
Točke F_{1} i F_{2} nazivamo žarištima ili fokusima hiperbole, a dužine \overline{\ T F_{1}} i \overline{T F_{2}} radijusvektorima točke T hiperbole. Realni broj e nazivamo linearnim ekscentricitetom. Polovište O dužine \overline{F_{1}F_{2}} nazivamo središtem hiperbole.
Lako se pokaže da pravac F_{1}F_{2} siječe hiperbolu u dvije točke koje leže između F_{1} i F_{2}. Te točke, označimo ih s A i B, nazivamo tjemenima. Dužinu \overline{A B} nazivamo realnom osi, a dužine \overline{O A} i \overline{O B} realnim poluosima.
Točke C i D, koje dobivamo presijecanjem kružnice k(A,e) (ili k(B,e)) i simetrale realne osi, određuju dužinu \overline{C D} koju nazivamo imaginarnom osi hiperbole. Dužine \overline{O C} i \overline{O D} nazivamo imaginarnim poluosima. Duljinu imaginarne poluosi označimo s b.
Budući da je osna simetrija S_{A B} izometrija, pa čuva i razliku udaljenosti točaka od fiksnih točaka F_{1} i F_{2} na osi A B, velika os je os simetrije hiperboli. Analogno, budući da je osna simetrija S_{C D} izometrija, pa čuva i razliku udaljenosti točaka od međusobno simetričnih točaka F_{1} i F_{2} s obzirom na os S_{C D}, mala os je, također, os simetrije hiperboli.
Sada se lako pokaže da je \left\vert O A\right\vert =a, i da je \left\vert A B\right\vert =2a.
Iz pravokutnog trokuta \triangle A O C vidimo da za duljine poluosi a i b, i linearni ekscentricitet e hiperbole vrijedi
a^{2}+b^{2}=e^{2}.
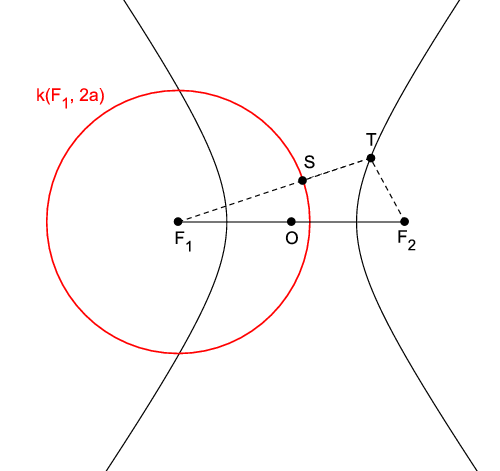
Neka je T\in H, te neka S pripada pravcu F_{1}T tako da je \left\vert F_{2}T\right\vert =\left\vert S T\right\vert i \left\vert F_{1}S\right\vert =\left\vert \left\vert F_{1}T\right\vert -\left\vert S T\right\vert\right\vert. Tada je \left\vert F_{1}S\right\vert =\left\vert \left\vert F_{1}T\right\vert -\left\vert F_{2}T\right\vert\right\vert =2a.
Točku S nazivamo suprotištem žarišta F_{2} (s obzirom na T). Kada točka T varira hiperbolom, pripadna suprotišta variraju kružnicom. Svako suprotište žarišta F_{2} leži na kružnici k\left(F_{1},2a\right) koju nazivamo kružnicom suprotišta žarišta F_{2} (Slika 6). Analogno k\left(F_{2},2a\right) je kružnica suprotišta žarišta F_{1}.
I hiperbola, kao i elipsa, ima "optičko" svojstvo: postavimo li izvor svjetlosti u jedno od žarišta hiperbole, zraka svjetlosti će se odbiti od hiperbole po pravcu koji prolazi kroz drugo žarište. Prije nego navedemo teorem koji opisuje ovo svojstvo, treba nam definicija tangente hiperbole.
Definicija 9. Tangenta hiperbole je pravac koji ima s hiperbolom jednu dodirnu (zajedničku) točku.
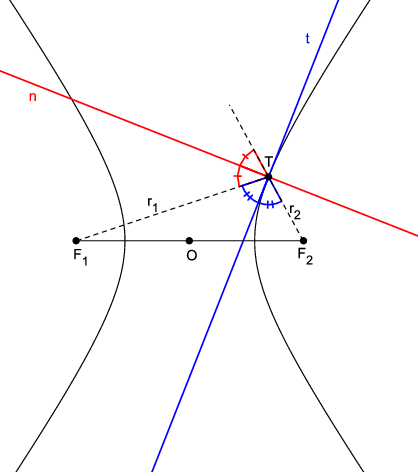
Teorem 10. Tangenta
t u točki
T hiperbole je pravac koji raspolavlja unutrašnji kut, a normala je pravac koji raspolavlja vanjski kut, što ga zatvaraju dva radijusvektora točke
T.
Dokaz ove tvrdnje analogan je onomu za tangentu elipse (Slika 7).
Korolar 11. Tangenta postoji u svakoj točki hiperbole, i jedinstvena je.
Očigledno je da je suprotište S žarišta F_{2} s obzirom na T osno simetrična slika točke F_{2} s obzirom na tangentu na hiperboli u točki T, što opravdava naziv suprotište.
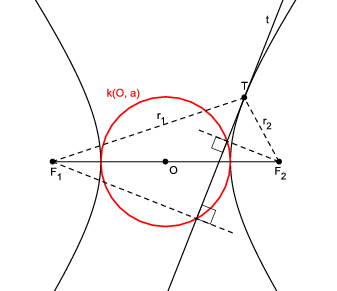
Teorem 12. Nožišta svih okomica spuštenih iz žarišta na tangente hiperbole leže na kružnici
k\left( O,a\right) koju nazivamo
glavnom kružnicom hiperbole.
Dokaz. Analogno dokazu Teorema
5.
\ \blacksquare
Vrijede i analogni Prvi i Drugi Ponceletov teorem za hiperbolu.
Teorem 13. [Prvi Ponceletov teorem za hiperbolu] Spojnica žarišta hiperbole sa sjecištem dviju tangenata simetrala je kuta određenog spojnicama žarišta s diralištima tangenata, kojem pripada sjecište tangenata.
Dokaz. Neka je točka
T sjecište tangenata
t_{1} i
t_{2}, neka je
S_{1} suprotište žarišta
F_{1} s obzirom na
t_{1} i
S_{2} suprotište žarišta
F_{2} s obzirom na
t_{2} (Slika
9). Tada su
S_{1}, diralište
D_{1} tangente
t_{1} i
F_{2} kolinearne točke. Isto tako,
F_{1}, diralište
D_{2} tangente
t_{2} i
S_{2} su kolinearne točke. Budući da osna simetrija čuva udaljenosti, slijedi
\left|T S_{1}\right|=\left|T F_{1}\right| i
\left|T S_{2}\right|=\left|T F_{2}\right|. Iz
\left|S_{1}F_{2}\right|=2a=\left|S_{2}F_{1}\right| proizlazi
\Delta T F_{2}S_{1} \cong\Delta T F_{1}S_{2}. To povlači
\angle T S_{1}F_{2}=\angle T F_{1}S_{2}. No, budući da osna simetrija čuva kutove, slijedi
\angle T S_{1}D_{1}=\angle T F_{1}D_{1}. Time je dokazano da
F_{1}T raspolavlja kut određen spojnicama žarišta s diralištima tangenata, kojem pripada sjecište tangenata.
\ \blacksquare
Teorem 14. [Drugi Ponceletov teorem za hiperbolu] Odsječak varijabilne tangente hiperbole između dviju fiksnih tangenata vidi se iz žarišta pod stalnim kutom koji je jednak polovini kuta određenog spojnicama žarišta s diralištima fiksnih tangenata, kojem pripada sjecište fiksnih tangenata.
Dokaz. Tvrdnju dokazujemo tako da primijenimo Teorem
13, najprije na tangente
t i
t_{1} hiperbole, a zatim na
t i
t_{2} (Slika
10).
\ \blacksquare
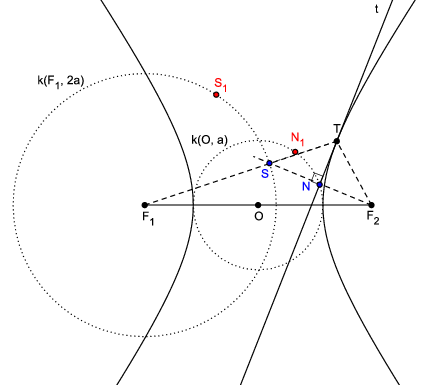
Neka je T po volji odabrana točka hiperbole, t tangenta hiperbole u T i S suprotište, a N ortogonalna projekcija F_{2} na tangentu t (Slika 11).
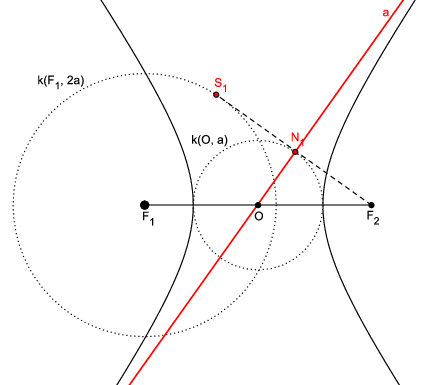
Pretpostavimo da se točka T "giba" po hiperboli tako da se njezina udaljenost od neke fiksne točke povećava prema beskonačnom. Intuitivno možemo zamisliti da točka T ide prema "beskonačno dalekoj točki". Njezina tangenta t past će u tom graničnom procesu u neki pravac a kojeg nazivamo asimptotom (Slika 12). Označimo sa S_{1} točku u koju će u tom graničnom procesu pasti suprotište S žarišta F_{2} s obzirom na T (S\in k(F_{1},2a) \rightarrow S_{1}\in k(F_{1},2a)) i s N_{1} točku u koju će pasti točka N (N\in k\left( O,a\right) \rightarrow N_{1}\in k(O,a)).
Budući da je F_{2}N\perp t, to je i F_{2}N_{1}\perp a. Pri tomu pravac F_{1}T prelazi u F_{1}S_{1}. Budući da je F_{1}T\cap t=\left\lbrace T\right\rbrace, to se F_{1}S_{1} i a "sijeku" u beskonačno dalekoj točki, tj. F_{1}S_{1}\parallel a. Stoga je F_{2}N_{1}\bot F_{1}S_{1}. Budući da je pravac koji prolazi točkama F_{2}, N i S prešao u pravac koji prolazi točkama F_{2}N_{1} i S_{1}, F_{2}S_{1} je tangenta, a F_{1}S_{1} polumjer kružnice suprotišta k(F_{1},2a). Nadalje, iz \left\vert F_{2}N\right\vert =\left\vert NS\right\vert slijedi \left\vert F_{2}N_{1}\right\vert =\left\vert N_{1}S_{1}\right\vert. Asimptota a je simetrala dužine \overline{S_{1}F_{2}}, pa je onda i O\in a. Naravno, analogni zaključci vrijede kad zamijenimo uloge žarišta.
Po tome, smijemo reći ili definirati asimptotu hiperbole kao simetralu dužine \overline{S_{1}F_{2}}, gdje je S_{1}F_{2} tangenta na k(F_{1},2a) iz F_{2}, a S_{1} njezino diralište.
Isto tako, smijemo reći da je asimptota normala na k(O,a) u točki N_{1}, gdje je N_{1} diralište tangente iz F_{2} na k(O,a).
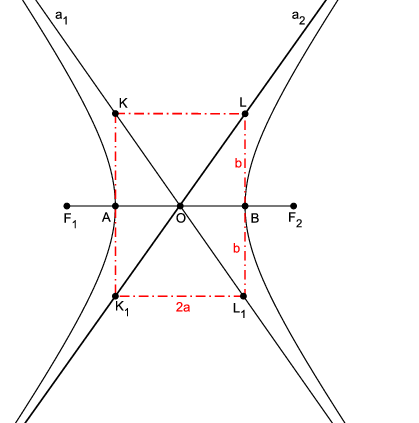
Povucimo u tjemenima A i B okomice na os A B i označimo njihova sjecišta s asimptotama hiperbole s K,L,K_{1} i L_{1}. Tada je
\triangle O A K_{1}\cong\triangle O B L\cong\triangle O F_{2}N_{1}
(trokutima su sukladni jedna stranica \left\vert O B\right\vert =\left\vert ON_{1}\right\vert =a i dva priležeća kuta uz tu stranicu). Također, vrijedi
\left\vert O L\right\vert =\left\vert O F_{2}\right\vert=e\Longrightarrow\left\vert B L\right\vert~=b.
Dakle, asimptote hiprebole leže na dijagonalama pravokutnika sa stranicama 2a i 2b, čije je središte u središtu hiperbole (Slika 13).
U prethodnomu asimptotu smo definirali kao "tangentu u beskonačno dalekoj točki", odnosno kao granični položaj tangente kad se njezino diralište "giba" po neomeđenom dijelu krivulje prema beskonačno dalekoj točki. Uobičajeno je, međutim, da se asimptota definira kao pravac kojemu se krivulja približava kad se točka "giba" po njezinom neomeđenom dijelu prema beskonačno dalekoj točki. Ove dvije definicije su ekvivalentne, ako je krivulja algebarska (hiperbola to jest). Nama je zanimljivija prva definicija, iako manje stroga i formalna, ali vrlo intuitivna, jer s pomoću nje možemo izvesti i neka zanimljiva, netrivijalna svojstva koja nisu očigledna u analitičkom pristupu definiciji.
Definicija 15. Neka je
F točka izvan pravca
d. Skup svih točaka u ravnini
\pi koje su jednako udaljene od točke
F i pravca
d nazivamo
parabolom, u oznaci
P(F,d). Točku
F nazivamo njezinim
žarištem ili
fokusom, a pravac
d ravnalicom ili
direktrisom. Kraće,
P=\left\lbrace T\in\pi\ : \ \frac{d\left( T,F\right) }{d\left( T,d\right) }=1\right\rbrace .
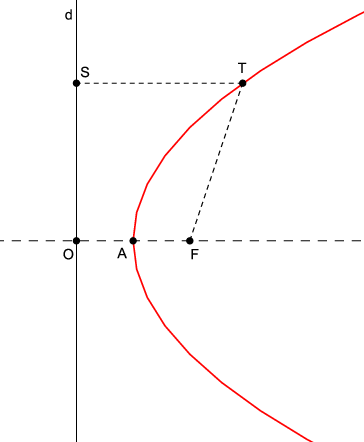
Neka je T točka parabole. Dužinu \overline{T F} nazivamo radijusvektorom točke T parabole, isto kao i dužinu \overline{T S}, gdje je S ortogonalna projekcija točke T na d (Slika 14).
Ako je O ortogonalna projekcija točke F na d, onda polovište A dužine \overline{O F} očigledno pripada paraboli i nazivamo ga tjemenom parabole. Pravac O F nazivamo osi parabole. Parabola je, zbog izometričnih svojstava osne simetrije, simetrična u odnosu na svoju os.
Sada bismo htjeli definirati i tangentu parabole, i to na najjednostavniji mogući način, bez primjene infinitezimalnog računa. Budući da ju ne možemo definirati kao pravac koji s parabolom ima jednu zajedničku točku (npr. os parabole ima to svojstvo, a nije tangenta parabole), motivaciju za definiciju nam daje sljedeći teorem.
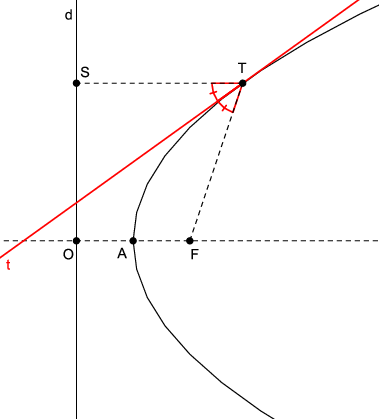
Teorem 16. Simetrala kuta što ga zatvaraju radijusvektori točke
T na paraboli ima s parabolom samo tu jednu zajedničku točku
T. Taj pravac ćemo zvati
tangentom parabole.
Dokaz.
Neka je
T točka parabole i
S ortogonalna projekcija točke
T na ravnalicu
d. Tada je
\left|F T\right|=\left|T S\right|. Neka je
t simetrala kuta
\angle F T S (Slika
15). Pokažimo da parabola i
t imaju samo jednu zajedničku točku, točku
T.
Pretpostavimo protivno, tj. neka postoji još jedna zajednička njima točka
Q,
Q\neq T. Primijetimo da je
t simetrala dužine
\overline{S F}. Po tomu,
\left|Q F\right|=\left|Q S\right|. Neka je
Q_{1} ortogonalna projekcija točke
Q na
d. Budući da je
Q točka parabole, vrijedi da je
\left|QQ_{1}\right|=\left|Q F\right|. Iz toga slijedi da je
\left|QQ_{1}\right|=\left|Q S\right|. S druge strane,
\left|QQ_{1}\right|\lt \left|Q S\right|, čime smo upali u protuslovlje.
\ \blacksquare
Navedeni teorem pojašnjava važno "optičko" svojstvo parabole, da se svjetlost usmjerena iz žarišta parabole odbija od parabole po pravcima paralelnima s osi parabole.
Korolar 17. Tangenta t u točki T parabole uvijek postoji i jedinstvena je.
Ortogonalnu projekciju S točke T na ravnalicu d, budući da je simetrala t kuta \angle F T S ujedno i simetrala dužine \overline{S F}, nazivamo suprotištem žarišta F s obzirom na t.
Korolar 18. Ravnalica je skup svih točaka koje su suprotišta žarišta parabole (točke osno simetrične fokusu s obzirom na tangente parabole).
Teorem 19. Skup svih točaka koje su nožišta okomica iz žarišta parabole na tangente je tjemena (vršna) tangenta parabole.
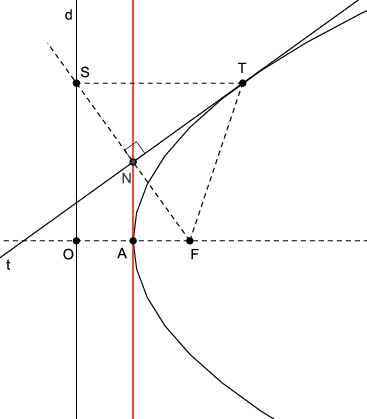
Dokaz. Neka je
N ortogonalna projekcija žarišta
F na tangentu
t s diralištem u točki
T (Slika
16). Budući da je
t simetrala dužine
\overline{S F}, točke
F,
N i
S su kolinearne i
N je polovište dužine
\overline{S F}. Dužina
\overline{N A}, gdje je
A tjeme parabole, je srednjica trokuta
\triangle O F S, pa je
A N\parallel d, tj.
A N\bot O F, što znači da je
A N tjemena tangenta parabole.
Slično se dokaže da je u točki
N tjemene tangente okomica na
F N tangenta parabole.
\ \blacksquare
Teorem 20. [Prvi Ponceletov teorem za parabolu] Spojnica žarišta sa sjecištem dviju tangenata raspolavlja kut što ga tvore radijusvektori dirališta.
Dokaz. Neka je točka
T sjecište tangenti
t_{1} i
t_{2} parabole, i neka su
D_{1} i
D_{2} njihova dirališta (Slika
17). Dokažimo da je
\angle T FD_{1}=\angle T FD_{2}. Budući da je
\left|FD_{2}\right|=\left|S_{2}D_{2}\right| i
\left|T F\right|=\left|T S_{2}\right|, vrijedi
\triangle T FD_{2}\cong \triangle T S_{2}D_{2} i
\angle T FD_{2} =\angle T S_{2}D_{2}. Analogno vrijedi
\angle T FD_{1} =\angle T S_{1}D_{1}.
Nadalje, zbog
\left|T S_{1}\right|=\left|T F\right|=\left|T S_{2}\right| trokut
\triangle S_{1}T S_{2} je jednakokračan, pa je
\angle T S_{2}S_{1}=\angle T S_{1}S_{2}. Po tomu,
\angle T FD_{1}=T FD_{2}.
\ \blacksquare
Teorem 21. [Drugi Ponceletov teorem za parabolu] Odsječak varijabilne tangente parabole između dviju fiksnih tangenata vidi se iz žarišta pod stalnim kutom koji je jednak polovini kuta pod kojim se iz žarišta vide dirališta fiksnih tangenata.
Dokaz.
Tvrdnja se dokazuje tako da se primijeni Teorem
20, najprije na tangente
t i
t_{1} parabole, a zatim na
t i
t_{2} (Slika
18).
\ \blacksquare
3Algebarski pristup
Jednadžbu oblika F(x,y)=0, gdje je F polinom drugog stupnja s realnim varijablama x i y, nazivamo jednadžbom drugog reda. Zbog toga svaku krivulju kojoj je jednadžba F(x,y)=0, gdje je F polinom drugog stupnja s varijablama x i y, nazivamo krivuljom drugog reda. Opći oblik jednadžbe za krivulje drugog reda je, dakle,
a_{1}x^{2}+a_{2}xy+a_{3}y^{2}+a_{4}x+a_{5}y+a_{6}=0,
pri čemu je barem jedan od koeficijenata uz kvadratne članove različit od nule. Pokažimo zašto se elipsa, hiperbola i parabola nazivaju krivuljama drugog reda. Svojstva ovih krivulja koja iz te činjenice proizlaze detaljno su obrađena u [2], pa ih ovdje izostavljamo.
Neka su F_{1} i F_{2} žarišta elipse, te a duljina velike poluosi. Odaberimo pravokutni koordinatni sustav tako da polovište O dužine \overline{F_{1}F_{2}} bude ishodište koordinatnog sustava, pravac F_{1}F_{2} os x, a simetrala dužine \overline{F_{1}F_{2}} os y. Sada se lako iz definicije elipse dobije da za svaku točku T(x,y) na elipsi E\left( F_{1},F_{2},a\right) vrijedi relacija
\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1,
i obratno, da svaka točka T(x,y) za koju vrijedi ova relacija pripada elipsi. Ovu relaciju nazivamo kanonskom jednadžbom elipse.
Analogno dolazimo do kanonske jednadžbe hiperbole H(F_{1},F_{2},a),
\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1.
Da bismo naveli kanonsku jednadžbu parabole, potreban nam je još jedan pojam vezan uz parabolu, poluparametar. Duljinu tetive koja prolazi fokusom i okomita je na os parabole P(F,d) nazivamo parametrom parabole i označavamo s 2p. Poluparametar parabole je duljina p koja je jednaka \left\vert O F\right\vert, gdje je O ortogonalna projekcija točke F na d.
Kanonsku jednadžbu parabole lako izvedemo ako pravokutni koordinatni sustav odaberemo tako da je os x os parabole, i da je ishodište u njezinom tjemenu. Za točku T(x,y) na paraboli tada vrijedi
y^{2}=2px,
gdje je p poluparametar parabole.
Očigledno je da su kanonske jednadžbe elipse, hiperbole i parabole, te kružnice kao specijalnog slučaja elipse, algebarske jednadžbe drugog reda, što znači da su elipsa, hiperbola i parabola krivulje drugog reda. Pokažuje se (ne računajući degenerirane slučajeve) da je svaka krivulja drugog reda neka od ovih krivulja.
U nastavku ćemo pokazati da se svaka čunjosječnica može zadati jednom te istom jednadžbom, čime još jedanput ukazujemo na sličnost naizgled poprilično različitih ravninskih krivulja. Promatrat ćemo krivulje u posebnom položaju u koordinatnom sustavu: kad im je jedno tjeme u ishodištu, a os y tjemena tangenta.
Promotrimo najprije elipsu E(F_{1},F_{2},a) zadanu jednadžbom \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1. Translatiramo li elipsu u pozitivnom smjeru osi x za x_{0}=a, tako da je novi centar elipse u točki S(a,0), dolazimo do jednadžbe elipse
y^{2}=2\frac{b^{2}}{a}x-\frac{b^{2}}{a^{2}}x^{2}.
Isto tako, translatiramo li hiperbolu zadanu jednažbom \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 u negativnom smjeru osi x za x_{0}=-a, tako da je novi centar hiperbole u točki S(-a,0), dolazimo do jednadžbe hiperbole
y^{2}=2\frac{b^{2}}{a}x+\frac{b^{2}}{a^{2}}x^{2}.
Da bismo malo pojednostavnili navedene izraze, definirajmo poluparametar elipse i hiperbole.
Duljinu tetive koja prolazi jednim od žarišta elipse (hiperbole) i okomita je na glavnu os elipse (hiperbole) nazivamo parametrom elipse (hiperbole) i označavamo s 2p. Duljinu p nazivamo poluparametrom elipse (hiperbole).
Označimo li s T sjecište elipse (hiperbole) i tetive elipse (hiperbole) okomite na glavnu os, primjenom Pitagorina poučka na pravokutnom trokutu \Delta F_{1}T F_{2} lako dobivamo da za poluparametar elipse i hiperbole vrijedi p=\frac{b^{2}}{a}.
Sada y^{2}=2\frac{b^{2}}{a}x-\frac{b^{2}}{a^{2}}x^{2} prelazi u
y^{2}=2px-\frac{p}{a}x^{2},
što nazivamo jednadžbom elipse u vršnom ili tjemenom obliku.
Isto tako, y^{2}=2\frac{b^{2}}{a}x+\frac{b^{2}}{a^{2}}x^{2} prelazi u
y^{2}=2px+\frac{p}{a}x^{2},
što nazivamo jednadžbom hiperbole u vršnom ili tjemenom obliku.
Uočimo da se kanonska i vršna jednadžba parabole podudaraju.
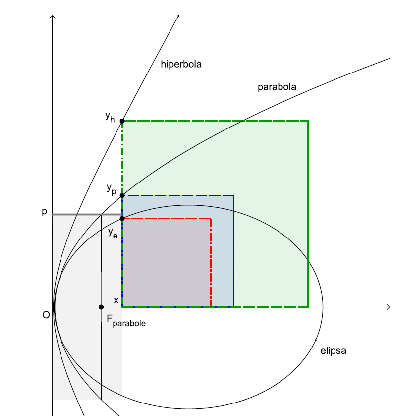
Ako geometrijski interpretiramo ove jednadžbe i usporedimo površinu y^{2} kvadrata određenog točkom T(x,y) na krivulji i površinu pravokutnika 2p\cdot x, jedna stranica kojega je apscisa x točke T, a druga stranica fiksni parametar 2p (Slika 19), vidimo
|
\bullet |
da je za točku na elipsi površina kvadrata manja od površine pravokutnika, |
|
\bullet |
da su za točku na paraboli površine jednake, i |
|
\bullet |
da je za točku na hiperboli površina kvadrata veća od površine pravokutnika, |
što je, po predaji, i navelo Apolonija iz Perge da čunjosječnicama nadjene imena elipsa, hiperbola i parabola. Naime, elipsa na Grčkom znači "manjak", parabola znači "jednakost", a hiperbola znači "višak".
Pogledajmo još jedanput vršne jednadžbe elipse i hiperbole. Uvedemo li oznaku \varepsilon=\frac{e}{a}, za elipsu ćemo dobiti \varepsilon ^{2}=1-\frac{b^{2}}{a^{2}}, pa je \frac{p}{a}=\frac{b^{2}}{a^{2}}=1-\varepsilon^{2}.
Isto tako, za hiperbolu iz \varepsilon=\frac{e}{a} slijedi \varepsilon ^{2}=1+\frac{b^{2}}{a^{2}}, pa je \frac{p}{a}=\frac{b^{2}}{a^{2}}=-(1-\varepsilon^{2}).
Iz ovoga slijedi da je zajednička jednadžba elipse, hiperbole i parabole u vršnom obliku
y^{2}=2px-(1-\varepsilon ^{2})x^{2},
pri čemu je za parabolu \varepsilon =1.
Inače, \varepsilon uobičajeno nazivamo numeričkim ekscentricitetom, a malo više o njemu reći ćemo kad budemo govorili o Boškovićevu pristupu krivuljama drugog reda.
4Krivulja drugoga reda kao presjek stožaste plohe i ravnine
Neka je pravac o os rotacije i neka pravac s koji siječe os o u točki V rotira oko osi o. Pri toj rotaciji pravac s opisuje stožastu plohu. Točku V nazivamo vrhom, pravac o osi, a svaki položaj pravca s izvodnicom te stožaste plohe.
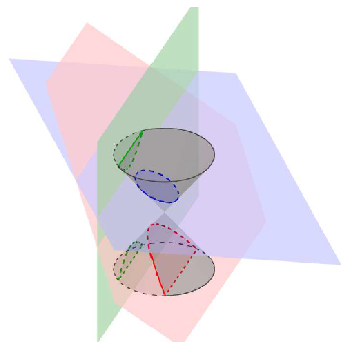
Ovdje ćemo pokazati da se krivulja drugoga reda može okarakterizirati kao presjek stožaste plohe i ravnine (Slika 20). Upravo zbog toga se svaka krivulja drugoga reda naziva čunjosječnicom ili konikom ([2],[4]).
Čunjosječnicama se intenzivno bavio Apolonije iz Perge, starogrčki matematičar koji je o njima napisao osam knjiga, i koji je, uostalom, uveo nazive koje i danas rabimo: elipsa, hiperbola i parabola. On je uočio da vrsta krivulje koju ćemo dobiti presjekom stošca i ravnine ovisi o nagibu ravnine koja presjeca stožac.
Promotrimo najprije elipsu. Definirali smo ju kao krivulju za koju vrijedi da je zbroj udaljenosti svake njezine točke od dvaju žarišta konstantan. Sada tvrdimo da je to krivulja koja se dobije kao presjek stošca ravninom koja nije paralelna ni s jednom od izvodnica i ne prolazi vrhom stošca.
Ove dvije "definicije" elegantno je povezao Germinal Pierre Dandelin (1794. - 1847.), belgijski matematičar i inženjer koji je 1822. otkrio vezu između presjeka stošca i ravnine, zarišta čunjosječnica i kugala upisanih u stožac koje dodiruju ravninu kojom je presječen. Takve kugle, njemu u čast, nazivamo Dandelinovim kuglama.
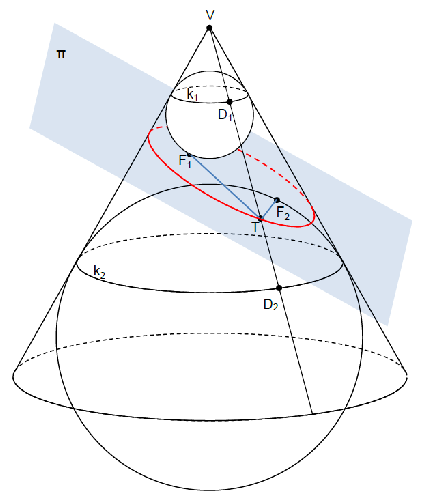
Teorem 22. [Dandelinov teorem za elipsu] Ako stožastu plohu presiječemo ravninom koja ne prolazi vrhom stožaste plohe i siječe sve njezine izvodnice, onda je presječna krivulja ili kružnica (ako je ravnina okomita na os stošca) ili elipsa.
Dokaz.
Na Slici
21 je skiciran presjek stožaste plohe i ravnine
\pi koja ne prolazi vrhom, siječe sve izvodnice stožaste plohe i kosa je prema njezinoj osi. Upišimo u tu stožastu plohu kuglu
K_{1} koja dodiruje ravninu odozgor i kuglu
K_{2} koja dodiruje ravninu odozdol. Neka prva kugla dodiruje ravninu u točki
F_{1}, a druga kugla u točki
F_{2}. Dokazat ćemo da je presječna krivulja elipsa i da su točke
F_{1} i
F_{2} njezina žarišta.
U tu svrhu uzmimo na presječnoj krivulji bilo koju točku
T. Gornja kugla dodiruje stožastu plohu uzduž kružnice
k_{1}, a dolnja kugla uzduž kružnice
k_{2}. Spojimo vrh
V stožaste plohe s točkom
T. Ta izvodnica siječe
k_{1} u točki
D_{1}, a
k_{2} u
D_{2}.
Budući da su duljine tangenata povučenih na kuglinu plohu iz točke izvan nje jednake duljine, to je
\left|T F_{2}\right|=\left|T D_{2}\right| i
\left|T F_{1}\right|=\left|T D_{1}\right|. Zbrajanjem tih jednakosti dobivamo
\left|T F_{1}\right|+\left|T F_{2}\right|=\left|T D_{1}\right|+\left|T D_{2}\right|, dakle
\left|T F_{1}\right|+\left|T F_{2}\right|=\left|D_{1}D_{2}\right|. Dužina
\overline{D_{1}D_{2}} je izvodnica uspravnoga krnjeg stošca kojemu je dolnja osnovica krug omeđen kružnicom
k_{2}, a gornja osnovica krug omeđen kružnicom
k_{1}. Zbog toga je
\left|D_{1}D_{2}\right|=2a, gdje je
a\gt 0 realna konstanta.
Dakle,
\left|T F_{1}\right|+\left|T F_{2}\right|=2a, za svaku točku
T presječne krivulje, pa je ta krivulja elipsa sa žarištima
F_{1} i
F_{2}.
\ \blacksquare
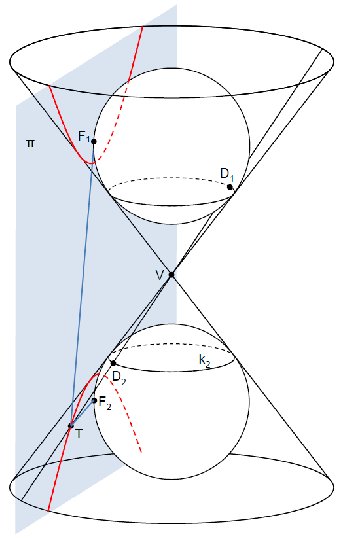
Teorem 23. [Dandelinov teorem za hiperbolu] Ako stožastu plohu presiječemo ravninom koja ne prolazi vrhom stožaste plohe i paralelna je s dvije njezine izvodnice, onda je presječna krivulja hiperbola.
Dokaz. Ako je presječna ravnina
\pi nagnuta prema osi stožaste plohe pod manjim kutom nego izvodnice, ravnina siječe oba dijela plohe po krivulji koja se sastoji od dviju disjunktnih grana (Slika
22).
Upisane kugle dodiruju ravninu s iste strane, u točkama
F_{1} i
F_{2}, a stožastu plohu duž kružnica
k_{1} i
k_{2}. Neka je
T bilo koja točka presječne krivulje. Neka izvodnica kroz točku
T siječe kružnicu
k_{1} u točki
D_{1} i kružnicu
k_{2} u točki
D_{2}. Budući da su pravci
T F_{1} i
T D_{1} tangente povučene iz
T na gornju kuglinu plohu, i da su pravci
T F_{2} i
T D_{2} tangente povučene iz
T na dolnju kuglinu plohu, slijedi
\left|T D_{1}\right|=\left|T F_{1}\right| i
\left|T D_{2}\right|=\left|T F_{2}\right|.
Ravnine u kojima leže kružnice
k_{1} i
k_{2} su paralelne, pa su sve izvodnice krnjega dvostrukog stošca od
k_{1} do
k_{2} jednake duljine. Odatle, i iz
\left|D_{1}D_{2}\right|=\left|T D_{1}\right|-\left|T D_{2}\right|, slijedi da je razlika
\left|T F_{1}\right|-\left|T F_{2}\right| konstantna za svaku točku na presječnoj krivulji.
Dakle, presječna krivulja je skup svih točaka ravnine za koje je razlika udaljenosti od dviju fiksnih točaka
F_{1} i
F_{2} konstantna, što znači da je riječ o hiperboli.
\ \blacksquare
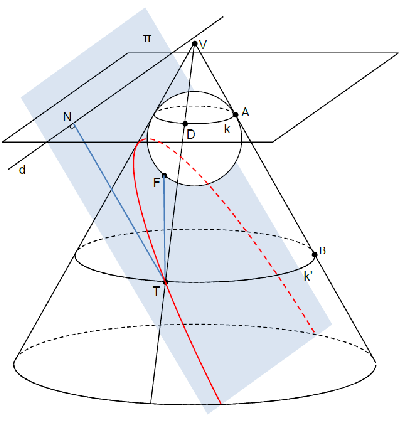
Teorem 24. [Dandelinov teorem za parabolu] Ako stožastu plohu presiječemo ravninom koja ne prolazi vrhom stožaste plohe i paralelna je s jednom njezinom izvodnicom, onda je presječna krivulja parabola.
Dokaz. Ako je presječna ravnina
\pi paralelna s jednom izvodnicom stožaste plohe, označimo ju sa
s, onda u stožastu plohu možemo upisati samo jednu kuglu koja dodiruje ravninu
\pi u točki
F i stožastu plohu uzduž kružnice
k (Slika
23).
Neka je
T bilo koja točka presječne krivulje. Neka izvodnica kroz točku
T siječe kružnicu
k u točki
D. Točka
T leži na kružnici
k' koja je paralelna s ravninom kružnice
k. Dužine
\overline{T F} i
\overline{T D} pripadaju tangentama povučenim iz
T na kuglinu plohu, iz čega slijedi
\left|T D\right|=\left|T F\right|.
Označimo s
A i
B točke u kojima izvodnica
s siječe kružnice
k i
k'. Budući da su ravnine kružnica
k i
k' međusobno paralelne, i okomite na osni presjek kroz izvodnicu
s, a ravnina
\pi je paralelna s dužinom
\overline{A B}, presjek
d ravnine kružnice
k i ravnine
\pi je također okomit na osni presjek stožaste plohe. Zbog toga, za okomicu
T N iz
T na pravac
d vrijedi
\left|T N\right|=\left|A B\right|=\left|T D\right|, odnosno
\left|T N\right|=\left|T F\right|.
Dakle, svaka točka
T na presječnoj krivulji jednako je udaljena od fiksne točke
F i od fiksnog pravca
d, što znači da je presječna krivulja parabola.
\ \blacksquare
Budući da se svaka elipsa, hiperbola ili parabola može dobiti kao presjek ravnine i neke stožaste plohe, to je jasno da je ovakav način uvođenja tih krivulja ekvivalentan sintetičkomu.
Osim opisanih, postoje i degenerirani oblici čunjosječnica, takozvane raspadnute čunjosječnice. Naime, ako se stožasta ploha presiječe ravninom koja prolazi kroz vrh V stožaste plohe, onda je presjek par pravaca koji se sijeku u vrhu V, pa stoga i takav par pravaca smatramo čunjosječnicom, tj. krivuljom drugog reda. Očigledno je da se posebnim odabirom presječnih ravnina dobivaju, k tomu, i jedan pravac ili točka, pa i njih valja smatrati čunjosječnicama.
5Boškovićev pristup
Upravo opisana konstrukcija Dandelinovih kugala, kao što je navedeno u [3], vodi nas do još jednog važnog svojstva čunjosječnica.
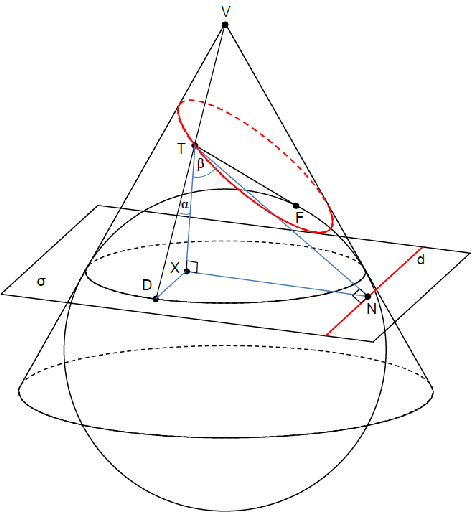
Pretpostavimo da ravnina \pi siječe stožastu plohu i ne prolazi njezinim vrhom V. Promotrimo kuglu upisanu u stožastu plohu, koja dodiruje ravninu \pi u točki F. Kružnicu duž koje kugla dodiruje stožastu plohu označimo s k, a ravninu u kojoj leži kružnica k označimo sa \sigma. Neka se ravnine \pi i \sigma sijeku u pravcu d.
Za bilo koju točku T presječne krivulje ravnine \pi i stožaste plohe, neka je D presjek izvodnice V T i ravnine \sigma, a N projekcija točke T na pravac d. Pokažimo da je omjer udaljenosti \left|T D \right| i \left|T N \right| konstantan, odnosno da ne ovisi o izboru točke T.
Neka je X projekcija točke T na \sigma. Omjer udaljenosti \left|T X \right| i \left|T D \right| ne ovisi o T i jednak je kosinusu kuta između izvodnice stošca i njegove osi o. (označimo ga s \alpha). Omjer udaljenosti \left|T X \right| i \left|T N \right| također ne ovisi o T i jednak je kosinusu kuta između osi o i ravnine \pi (označimo ga s \beta). Iz toga slijedi
\frac{\left| T D\right| }{\left|T N \right| }=\frac{\left| T D\right| }{\left|T X \right| }\frac{\left| T X\right| }{\left|T N \right| }=\frac{\cos\beta}{\cos\alpha}.
Napokon, budući da su \left| T F\right| i \left|T D \right| jednaki (kao tangente na kuglu kroz T), i omjer udaljenosti \left|T F \right| i \left|T N \right| je konstantan.
Dakle, za svaku čunjosječnicu postoji pravac d takav da za je svaku točku na čunjosječnici omjer udaljenosti od žarišta i tog pravca konstantan. Ovaj omjer nazivamo numeričkim ekscentricitetom čunjosječnice i označavamo s \varepsilon, a pravac d nazivamo ravnalicom ili direktrisom. Budući da elipsa i hiperbola imaju dva žarišta, one imaju i dvije ravnalice (po jednu za svako žarište). Broj \varepsilon određuje vrstu i oblik čunjosječnice.
Na ovaj način je naš hrvatski matematičar Ruđer Bošković (1711.-1787.) definirao krivulje drugoga reda, i na osnovi te definicije analitički izveo njihova svojstva. Ta se definicija danas naziva Pappus-Boškovićeva definicija, jer je Pappus iz Aleksandrije (oko 290.-oko 350.) iste rezultate dobio sintetičkom metodom.
Pappus-Boškovićeva definicija čunjosječnice. Neka je F točka izvan pravca d i \varepsilon pozitivni realni broj. Skup svih točaka sa svojstvom
\frac{d\left( T,F\right) }{d\left( T,d\right) }=\varepsilon
je elipsa čim je \varepsilon\lt 1, hiperbola čim je \varepsilon\gt 1, a parabola čim je \varepsilon=1.
Lijep primjer numeričkog ekscentriciteta u prirodi su Mjesečev ekscentricitet i ekscentricitet Halleyeva kometa. Naime, Mjesec se oko Zemlje, te Halleyev komet oko Sunca gibaju po eliptičnim putanjama. Mjesečeva putanja oko Zemlje je skoro kružna i njegov numerički ekscentricitet je 0,055, dok je putanja Halleyeva kometa jako izdužena (Sunce je u jednomu žarištu eliptične putanje) i njegov numerički ekscentricitet je 0.967.
6Projektivni pristup
Čunjosječnice možemo okarakterizirati i kao perspektivno kolinearne slike kružnice. Definirajmo najprije perspektivnu kolineaciju.
Definicija 25.
Perspektivna kolineacija u ravnini je bijekcija na skupu svih točaka i svih pravaca, koja udovoljuje sljedećim uvjetima:
|
(a) |
čuva incidenciju, tj. ako točka A pripada pravcu p, onda slika \overline{A} točke A pripada slici \overline{p} pravca p; |
|
(b) |
sva spojnice pridruženih točaka prolaze istom točkom S ravnine. Točka S je fiksna točka i nazivamo ju središtem kolineacije, a spojnice pridruženih točaka zrakama kolineacije. |
|
(c) |
postoji točno jedan pravac o u ravnini svaka točka kojega je pridružena sama sebi, tj. pravac o je fiksan po točkama. Pravac o nazivamo osi kolineacije. |
Perspektivna kolineacija je posve određena čim je zadana njezina os o, njezino središte S i jedan par pridruženih točaka A i \overline{A}, tako da ni jedna točka tog para ne leži na osi o, niti je njihova spojnica paralelna s osi o.
Sliku \overline{n} "beskonačno dalekog pravca" n kojeg tvore "beskonačno daleke točke", nazivamo nedoglednim pravcem. On je paralelan s osi jer na njemu leži i beskonačno daleka točka osi. Praslika pravca n, tj. pravac m koji se preslikava u "beskonačno daleki pravac" n nazivamo doglednim pravcem.
Perspektivnom kolineacijom kružnica se preslikava u čunjosječnicu, pri čemu o položaju kružnice i doglednog pravca ovisi vrsta čunjosječnice.
Kada dogledni pravac ne siječe kružnicu, sve točke kružnice preslikaju se u realne točke i kolinearna slika kružnice je elipsa.
Ako dogledni pravac dodiruje kružnicu u dvije točke, onda se dvije točke kružnice (sjecišta pravca i kružnice) kolinearno preslikaju u "beskonačno daleke točke" i kolinearna slika kružnice je hiperbola.
Ako dogledni pravac dodiruje kružnicu u jednoj točki, onda se jedna točka kružnice (diralište pravca i kružnice) kolinearno preslika u "beskonačno daleku točku" i kolinearna slika kružnice je parabola.
Zaključak
Donekle je neprimjereno da se u jednoj cjelini, koja je po programu smješ tena u 2. polugodište 3. razreda srednje škole, obrađuju istovremeno dvije važne teme iz elementarne matematike: analitička geometrija i čunjosječnice. Vrlo jak i moćan alat kojega nudi analitička geometrija, s pomoću kojega se mnogi geometrijski problemi svode, nakon koordinatizacije, na algebarske, na prvi pogled ostavlja dojam univerzalnosti. Zapravo, mnogi učenici će rado posegnuti za analiti čkim aparatom pri rješavanju nekoga geometrijskog problema prije nego li čisto geometrijskim, sintetičkim pristupom. To nimalo ne čudi jer sam koncept nastavnog plana i programa predmeće analitič ki pristup geometriji. Osim toga i većina postupaka za rješavanje geometrijskih zadataka na nastavnim satima u višim razredima srednje škole napućuje da je geometrijske zadatke najlakše i najsigurnije rješavati svođenjem na odgovarajuće sustave jednadžbi do kojih dolazimo analitičkim pristupom. I sam Rene Descartes (1596.-1650.), tvorac analiti čke geometrije, se vodio mišlju da ova metoda, ne samo da je najpogodnija za rješavanje geometrijskih problema, već se ona mož e primijeniti i na sve ostale matematičke grane i znanosti. Rezultat njegove filozofske potrage za univerzalnom metodom rješavanja problema je njegovo djelo Praktična i jasna pravila za vođenje uma u istra živanju istine. No, i sam Descartes se uvjerio da univerzalna metoda, koja bi sve probleme svodila na matematičke, a matematičke na rje šavanje odgovarajućih jednadžbi, nije ostvariva. Na sreću, ta metoda nije ostvariva niti unutar matematičke znanosti, jer bi se, u protivnom, širina i ljepota matematičke misli znatno osakatila i vodila bi ka tehnicizmu. Upravo tu zamku treba izbjeći i u nastavi analitičke geometrije. Tehnike analitičke geometrije, koje su bez daljnjega vrlo korisne, često puta sakriju i neka lijepa i zanimljiva svojstva geometrijskih objekata do kojih bismo mogli doći, prirodnijim, sintetičkim putem. Najbolji primjer za to su krivulje elipsa, parabola i hiperbola o kojima učenici, po svršetku srednjoškolske naobrazbe, znaju isključivo u kontekstu njihovih kanonskih jednadž bi. Kružnica je izdvojena iz ove priče, jer se ona obrađuje jo š od nižih razreda osnovne škole. S najljepšim svojstvima kru žnice (obodni kut, pojam tangente...) učenici su već upoznati po svršetku osnovnoškolske naobrazbe, a analitički pristup u 3. razredu srednje škole predstavlja korisnu nadgradnju. A sada zamislimo da kružnicu, poput ostalih čunjosječnica, učenici sustavno obrađuju tek u 3. razredu srednje škole i to uglavnom analitičkim pristupom. Više nego jasno je to da taj objekt ne bi doživjeli na prirodan način. Želja nam je ukazati da bi se i ostale čunjosječnice trebale zasebno obraditi prije 3. razreda srednje škole. Jedan razlog je potreba da se ove krivulje samostalno obrade, neovisno o koordinatizaciji ravnine, budući da se one permanentno javljaju u svijetu koji nas okružuje kao i u koreliranju s drugim nastavnim predmetima još od osnovne škole. Drugi razlog jest što se primjenjujući sintetički ili neki drugi pristup mogu, uz minimalno znanje elementarne geometrije, izvesti neka zanimljiva svojstva ovih krivulja s kojima se učenici po svršetku srednjoškolske naobrazbe (a slično se može dogoditi i po svr šetku nekog matematičkog studija) nisu susreli, a koja ove krivulje čine primijenjivima u mnogim područjima i koja spadaju u opću matematičku kulturu.
Bibliografija
|
[1] |
N. Koceić-Bilan, Nastavni materijali "Konstruktivna geometrija"
|
|
[2] |
B. Pavković, D. Veljan, Elementarna matematika 2, Školska knjiga, Zagreb (1995.)
|
|
[3] |
A. V. Akopyan, A. A. Zaslavsky, Geometry of conics, AMS, Mathematical World, Volume: 26 (2007.)
|
|
[4] |
http://www.nabla.hr/PC-ConicsProperties2.htm
|