Sažetak
Valić transformacija daje sofisticiranu vremensko-frekvencijsku analizu i koristi se u brojnim algoritmima u raznim područjima znanosti. Nakon teorijske pozadine i usporedbe sa frekvencijskom analizom, bit će prezentirane neke primjene u području sažimanja slike i uklanjanju šuma iz signala. Pojašnjen je i algoritam za prepoznavanje osoba pomoću očnog uzorka.
Ključne riječi: wavelet transformacija, valić, vremensko-frekvencijska analiza, sažimanje slike, uklanjanje šuma iz signala, algoritam za prepoznavanje osoba pomoću očiju
1Uvod
Jeste li se zapitali zašto mijenjanjem formata slike iz primjerice bitmap (bmp) u sliku sa ekstenzijom jpeg smanjuje memorija potrebna za pohranu te slike višestruko, a pritom gotovo da ne vidimo razliku u kvaliteti. Zašto audio CD glasi na 80 minuta glazbe, dok na taj isti CD možemo spremiti oko dvije stotine pjesama u formatu sa ekstenzijom mp3. Kako inžinjeri mogu iz signala koji je pod utjecanjem brojnih vanjskih čimbenika koji ga ometaju (šum) razabrati određenu pojavu i u kojem se trenutku dogodila? Kako računalo može na temelju slike prepoznati ili razlikovati objekte, osobe i sl.? Na neka od ovih pitanja odgovorit ćemo u ovom članku. Za početak ćemo postepeno uvesti koncept vremensko-frekvencijske analize krenuvši sa frekvencijskom analizom koja je prezentirana pomoću ideje Fourierove transformacije.
Fourierov red funkciju prikazuje pomoću sinusa i kosinusa. Za funkciju f s periodom T=b-a dan je izrazom:
(1)
f(x) = \frac{a_{0}}{2}+\sum_{n=1}^{\infty} (a_{n} sin(\frac{2n\pi x}{T}) + b_{n} cos(\frac{2n\pi x}{T})),
gdje su izrazi za koeficijente a_{n} i b_{n} dani integralima
a_{0} = \frac{2}{T} \int_{a}^{b} f(x) dx
a_{n} = \frac{2}{T} \int_{a}^{b} f(x) cos\frac{2n\pi x}{T} dx, n\geq 1
b_{n} = \frac{2}{T} \int_{a}^{b} f(x) sin\frac{2n\pi x}{T} dx, n\geq 1.
Ako funkcija nema perioda, odnosno možemo reći da je period beskonačan, trebamo neprekidnu verziju, a to je Fourierova transformacija, koja je dana izrazom:
(2)
F(s) = \int_{-\infty}^{+\infty} f(t)e^{-2\pi i st}dt.
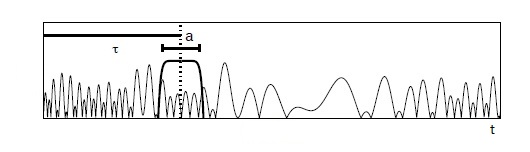
Fourierova transformacija jedan je od najčešće korištenih alata za obradu signala. Ona signal (funkciju u vremenskoj domeni) pretvara u zapis u frekvencijskoj domeni, gdje dobivamo informaciju o zapisu dane funkcije pomoću sinusoida, tj. koje se frekvencije pojavljuju i koliko intenzivno, ali gubimo informaciju o vremenu, tj. kada se koja frekvencija dogodila. Pri analizi signala (funkcije) koji su stacionarni ili periodični, Fourierova transformacija nam je dovoljna za analizu. No, vrlo često nemamo takav signal i potrebne su nam obje informacije, tj. želimo znati kada su se određene frekvencije dogodile. Primjer može biti pjesma koju želimo digitalno analizirati: frekvencije se mijenjaju kako glazba teče i trebamo znati kada se koja od frekvencija odvila. Možemo se zapitati je li moguće imati istovremeno informaciju i o vremenu i o frekvencijama danog signala? Odgovor je potvrdan i takvu vrstu analize nazivamo vremensko-frekvencijska analiza. Prema Heisenbergovu principu neodređenosti ne možemo znati sve frekvencijske i sve vremenske komponente istovremeno, ali možemo znati za određeni vremenski trenutak opseg frekvencija. Jedan od pristupa vremensko-frekvencijskoj analizi je short-time Fourier transformacija (STFT), koja se još naziva i Gaborova transformacija, prema Dennisu Gaboru, koji je dao ideju za ovu transformaciju. Ideja se sastoji u tome da uzmemo prozor (filter) fiksne širine i klizimo njime preko signala radeći Fourierovu transformaciu na tom prozoru. Na taj način žrtvujemo dio frekvencijskih informacija kako bismo dobili informaciju o vremenu kada se neka frekvencija dogodila.
Gaborova transformacija funkcije f dana je izrazom:
(3)
G[f](t, \omega) = \tilde{f}_{g} (t,\omega) = \int_{-\infty}^{+\infty} f(\tau)g(\tau - t) e^{i\omega \tau} d\tau ,
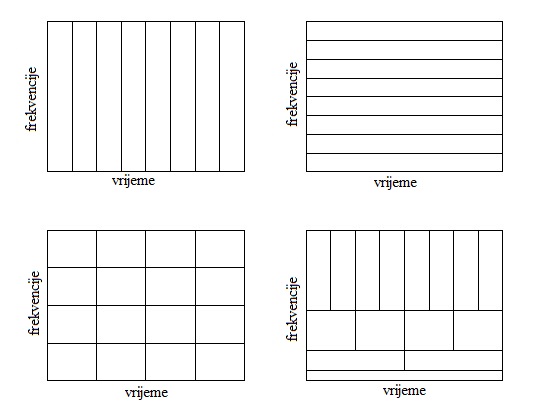
gdje funkcija g definira prozor transformacije i važno je da bude lokalizirana. Uočimo da je ovaj integral konvolucija našeg signala sa prozorom (filterom) i da u slučaju da izostavimo funkciju g iz izraza za transformaciju, imali bismo Fourierovu transformaciju funkcije f. Gaborova transformacija daje informacije o vremenu i frekvencijama, a koliko dobro opisuje vrijeme i frekvencije ovisi o izboru prozora koji pomičemo preko signala. Što je prozor tanji, dobit ćemo manje informacija o frekvencijama, a više o vremenskoj domeni i obratno. Više o Gaborovoj transformaciji možete pronaći u [1, str. 46.-52.] danog izvora (vidi str 271.-277. u cjelovitoj skripti).
1.1Valić transformacija
S obzirom da u Gaborovoj transformaciji imamo ograničenje kvalitete informacija o vremenskoj i frekvencijskoj domeni, javila se potreba za pronalaskom boljih metoda za vremensko-frekvencijsku analizu. Jedna od takvih metoda je valić transformacija (engleski izraz wavelet). Ideja valić transformacije javila se početkom 20. stoljeća s radom Alfreda Haara koji je u svojoj disertaciji istraživao ortogonalne baze funkcija. Haar valić prva je i do danas najjednostavnija familija funkcija koje se koriste za ovu transformaciju.
Intenzivnije se počelo raditi u osamdesetim godinama prošlog stoljeća, a koristi se u mnogim područjima kao što su astronomija, obrada signala i slike, glazba, medicina, optika, predviđanje potresa, rješavanje parcijalnih diferencijalnih jednadžbi itd.
Za razliku od STFT, mijenjat ćemo širinu filtra i tako pokušati dobiti bolje informacije u vremensko-frekvencijskoj analizi. Dakle, zadržavamo ideju superpozicije funkcije sa filtrom, ali sada ćemo mijenjati njegovu širinu. Prozorom male širine prvo ćemo dobiti informacije o visokim frekvencijama u dobroj rezoluciji vremena. Oduzmimo ove informacije iz signala, tako da te informacije ne utječu na rezultate kasnije, a nakon toga ćemo ponoviti analizu signala većim prozorom i dobiti informacije o nižim frekvencijama u lošijoj vremenskoj rezoluciji. Ovaj postupak temelj je valić transformacije i daje odličnu rezoluciju u vremenskoj i frekvencijskoj domeni, a daje i motivaciju za naziv multirezolucijska analiza (MRA). Možemo reći da dijelimo signal od izražajnih lokalnih prema globalnim svojstvima signala (funkcije). Postupak je moguće provoditi i obrnutim redom širine prozora kojim izdvajamo frekvencije iz signala.
Da bismo provodili valić transformaciju potrebna nam je funkcija koju nazivamo korijenski valić:
(4)
\psi _{a,b}=\frac{1}{\sqrt{a}} \psi \left( \frac{t-b}{a} \right),
gdje su a\neq 0 i b realni brojevi. Parametar a skalira funkciju, dok je b translacijski parametar (uloga \tau u Gaborovoj transformaciji). Postoji široki spektar funkcija koje možemo izabrati, a odabir ovisi o problemu kojeg rješavamo. U principu, ova transformacija je razvoj danog signala u nekoj bazi ortogonalnih funkcija koje su određene preko odabranog korijenskog valića.
Korijenski valić za diskretni slučaj transformacije glasi:
(5)
\psi _{m, n} = a_{0}^{m/2} \psi (a_{0}^{-m}x - nb_{0}),
gdje su a_{0}, b_{0} \gt 0, a m,n cijeli brojevi, a diskretna valić transformacija (DWT) dana je izrazom:
(6)
W_{\psi} [f](m,n) = (f, \psi _{m,n})=a_{0}^{m/2} \int_{-\infty}^{+\infty} f(t) \bar{\psi}(a_{0}^{-m}t - nb_{0})dt.
Najčešće želimo signal duljine 2^{j} točaka, jer u tom slučaju možemo dobiti najbolje rezultate pomoću DWT. Napomenimo da u slučaju potpunog prostora čiju bazu čine \psi _{m,n} funkciju f možemo razviti u toj bazi:
(7)
f(t) = \sum_{m,n =-\infty}^{+\infty} (f, \psi_{m,n})\psi_{m,n} (t).
Sve transformacije su dane općenito izrazom:
(8)
(Tf)(\omega, t) = \int_{t} K(t,\omega) f(t) dt,
gdje je K(t, \omega) jezgra transformacije. Za Fourierovu transformaciju jezgra je dana sa e^{i\omega t}, a za valić transformaciju koristit ćemo korijenski valić. Time dobivamo definiciju neprekidne valić transformacije (CWT):
(9)
W_{\psi} [f](a,b)=(f, \psi _{a,b}) = \int_{-\infty}^{+\infty} f(t) \bar{\psi}_{a,b}(t) dt.
Glavno ograničenje na korijenski valić dano je uvjetom na ograničenost konstante C_{\psi} = \int_{-\infty}^{+\infty} \frac{\vert \hat{\psi}(\omega) \vert^{2}} {\vert \omega \vert} d\omega \lt \infty, a zanimljivo je sljedeće svojstvo:
Teorem 1. Ako je \psi valić i \phi ograničena integrabilna funkcija, tada je konvolucija \psi \ast \phi također valić.
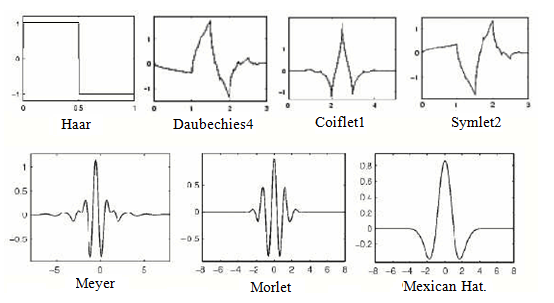
Iz teorema vidimo da postoji beskonačno mnogo mogućnosti za odabir korijenskog valića, ali u praksi koriste se oni za koje su ljudi do sada uočili svojstva koja najbolje odgovaraju rješavanju raznih problema. Za ovu transformaciju vrijede sljedeća svojstva:
|
(1) |
Linearnost: Transformacija je linearna, tj. vrijedi:
(10)
W_{\psi} [\alpha f + \beta g] (a, b) = \alpha W_{\psi} [f](a,b) + \beta W_{\psi} [g](a,b)
|
|
(2) |
Translacija:
(11)
W_{\psi} [T_{c} f](a,b) = W_{\psi} [f] (a, b-c),
gdje je T_{c} = f(t-c). |
|
(3) |
Širenje:
(12)
W_{\psi} [D_{c} f](a,b) = \frac{1}{\sqrt{c}}W_{\psi} [f] (\frac{a}{c},\frac{b}{c}),
gdje je c\gt 0 i D_{c} f(t)=\frac{1}{c} f(t/c). |
|
(4) |
Inverz: Transformaciju možemo invertirati pomoću formule:
(13)
f(t) = \frac{1}{C_{\psi}} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} W_{\psi} [f] (a,b) \psi _{a,b} (t) \frac{dbda}{a^{2}}.
|
2Primjene valić transformacije
U ovom ćemo odjeljku ilustrirati nekoliko primjena valić analize. Između mnogobrojnih primjena odabrao sam sažimanje slike, otklanjanje šuma iz signala i prepoznavanje osoba pomoću slike očiju. Ideje algoritama temelje se na mogućnosti brzog nalaženja koeficijenata DWT pomoću Mallatovog algoritama, što je moguće u najboljem slučaju u vremenu \mathcal{O}(n), a algoritam je definiran za 2^{n} čvorova.
2.1Sažimanje slike
Ideja sažimanja je danu sliku prikazati u valić bazi funkcija i zatim sve koeficijente koji su manji od odabrane granice postaviti na 0, tj. ne koristiti ih. Na taj način koristimo mali broj koeficijenata baze (zanemarujemo "manje" važna svojstva slike) i time pomoću malog broja koeficijenata koje čuvamo možemo rekonstruirati sliku. Ovaj postupak ima svoju cijenu, a to je gubitak "kvalitete". Zato ćemo na nekoliko primjera i algoritama provjeriti učinkovitost ove ideje.
Za početak reći ćemo nešto kratko o digitalnoj interpretaciji slike. Digitalni zapis crno-bijele slike je matrica čije elemente nazivamo pikselima, a vrijednosti svakog elementa mogu biti u rasponu od 0(potpuno crno) do 255(potpuno bijelo). Dakle, elementi matrice daju intenzitet crne ili bijele boje na određenom dijelu slike. Ako imamo sliku u boji, tada radimo sa RGB (crvena, zelena i plava) bojama i digitalna reprezentacija je matrica sa "tri" sloja. Svaki sloj (matrica) sadrži intenzitet određene boje (0-255) za svaki piksel. Budući da su sada slike postale matrice, kvalitetu slike možemo konkretno mjeriti pomoću koeficijenata u matricama.
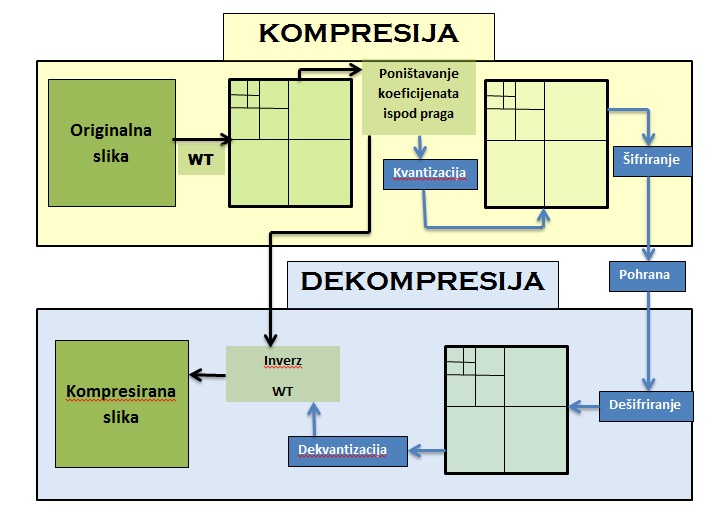
Slika 4 prikazuje proces sažimanja slike, a nakon toga slijedi jednostavni algoritam kojega ćemo implementirati i testirati u Matlabu koristeći Haarovu familiju valić funkcija.Valić dekompozicija slike razlaže sliku na horizintalne, vertikalne i dijagonalne komponente i na nivoe, gdje možemo birati broj nivoa. Ovakav način pruža brojne prednosti i koristi se u sofisticiranim alatima. Prilikom pisanja koda koristit ćemo nekoliko Matlabovih funkcija za rad sa valić analizom slike, tj. 2-D signala.
Napisat ćemo program za jednostavniju verziju algoritama opisanog prema Slici 4 u Matlabu i testirati ga na Haar-ovoj familiji.
%%%%%%%%%%%%%% SAZIMANJE SLIKE %%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;
close all;
A=imread('noised2','jpg'); % ucitavanje slike
Abw2=rgb2gray(A); %pretvaramo sliku u crno-bijelu
Abw=double(Abw2); %za racun trebamo realne brojeve
[nx,ny]=size(Abw); %dimenzije slike (broj piksela)
figure(1), subplot(2,2,1), imshow(Abw2) %crno-bijela verzija
[C,S]=wavedec2(Abw,2,'haar'); %2-D valic transformacija (Haar)
xw=(1:nx*ny)/(nx*ny); %normaliziramo os x
figure(2), subplot(4,1,1),plot(xw,C,'k') %graficki prikaz valic
%koeficijenata originalne crno-bijele slike
th=[25 100 330]; %ograde za rezanje koeficijenta
for j=1:3 %sazimanje po th(j)
count=0; %brojac koeficijenata
C2=C; %koeficijente valic transformacije spremamo u pomocnu
%matricu prije svakog postupka rezanja
for k=1:length(C2); %za svaku od zadanih th(j) gledamo koef.
if abs(C2(k)) < th(j) %provjeravamo je li koeficijent
% manji od dane donje granice (po apsolutnoj vrijednosti)
C2(k)=0; % ako je koef. manji, postavi ga na 0
count=count+1; %ukupni broj trivijalnih koef.
end
end
%odredimo postotak trivijalnih koeficijenata
percent=count/length(C2)*100
%graficki prikaz valic koeficijenata i granice
figure(2),
subplot(4,1,j+1),plot(xw,C2,'k',[0 1],[th(j) th(j)],'r')
%rekonstrukcija slike:
Abw2_sparse=waverec2(C2,S,'haar');
%vracamo koeficijente u raspon 0-255:
Abw2_sparse2=uint8(Abw2_sparse);
%%% racunamo MSE:
D = abs(Abw-double(Abw2_sparse)).^2;
MSE=sum(D(:)) / (nx*ny)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% racunamo PSNR:
PSNR=10* log10(255^2/MSE)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%prikaz komprimirane slike u slijedu
figure(1), subplot(2,2,j+1), imshow(Abw2_sparse2)
end
Koristeći jednostavni algoritam i najjednostavniju familiju (Slika 5) vidimo da originalnu sliku možemo zadržati u stanju gdje je gubitak kvalitete vidljiv, ali nije još u tolikoj mjeri da bismo je odbacili sa samo 5.6% informacija. Napomenimo da je u danom algoritmu granica za rezanje koeficijenata jednaka za svaki nivo. To znači da bi prvo poboljšanje algoritma moglo biti mijenjanje granica za rezanje koeficijenata za svaki nivo. Testirajmo koja poboljšanja nude algoritmi koji koriste i kvantizaciju i šifriranje. U Matlabu ih možemo koristiti unutar skripte pomoću naredbe wcompress() ili pak u novijim verzijama Matlaba otvoriti Wavelet toolbox i odabrati True Compression 2-D. Navedeni alat nudi odabir valić familije, a zatim i način sažimanja i broj koraka šifriranja koji uvelike utječe na rezultat. Alat nudi nekoliko grafičkih prikaza kao i prikaz slike nakon sažimanja. Alat također nudi i nekoliko načina za mjerenje uspješnosti sažimanja. CR (Compression ratio) govori koji postotak informacija koristimo. M.S.E. (Mean Squared Error) govori o udaljenosti između originala i komprimirane slike (što je M.S.E. manji, to je komprimirana slika bolja), a dan je izrazom
(14)
{M}{S}{E}=\frac{1}{mn}\sum_{i=1}^{m}\sum_{j=1}^{n} (X-X_{c})^{2}.
BPP (Bit-Per-Pixel) pokazuje broj bitova potrebnih za pohranu jednog pixela slike. PSNR (The Peak Signal to Noise Ratio) mjeri najveću pogrešku u decibelima i dan je izrazom:
(15)
{P}{S}{N}{R}=10\cdot log_{10} \left( \frac{255^{2}}{{M}{S}{E}}\right).
Što je PSNR veći, to je bolja kvaliteta komprimirane slike. Ako je PSNR iznad 40 dB kaže se da se slike ne razlikuju, a najčešće je dovoljno oko 30 dB da bismo rekli da se radi o dovoljno dobroj kvaliteti.
Uzevši istu sliku kao za testiranje u gore navedenom algoritmu, testirati ćemo nekoliko složenijih metoda sažimanja i rezultate usporediti za familiju Daubechies nivoa 9. Metoda 'wdr' dolazi od Wavelet Difference Reduction, 'spiht' od Set Partitioning In Hierarchical Trees, a 'ezw' od Embedded Zerotree Wavelet, tj. nazivi govore o načinu na koji se provode procesi kvantizacije i šifriranja.
|
Metoda |
Broj koraka šifriranja |
CR |
MSE |
PSNR |
|
WDR |
9 |
0.81 |
251.9 |
24.12 |
|
WDR |
11 |
7.62 |
73.08 |
29.49 |
|
SPIHT |
9 |
0.55 |
264.1 |
23.91 |
|
SPIHT |
11 |
4.76 |
82.3 |
28.98 |
|
SPIHT |
14 |
33.05 |
5.749 |
40.53 |
|
EZW |
11 |
6.81 |
67.81 |
29.82 |
Tablica 1. Prikaz rezultata sofisticiranih metoda dobivenih u Matlabovom alatu True Compression 2-D za sliku koju smo koristili pri testiranju prethodno implementiranog algoritma.
Iz tablice 1 vidimo da porastom broja koraka šifriranja raste broj korištenih informacije, a time i kvaliteta rekonstrukcije. Za danu sliku potrebno je 11 koraka šifriranja da bismo dobili zadovoljavajuće rezultate, a najbolju kompresiju pokazuje metoda 'spiht' koja koristi 4.76% informacija originalne slike i daje dobre rezultate (sažimanje 1:21). Postoje brojni drugi alati za analizu kompresije i signala opcenito. Jedan od njih je i 'Coherence Wavelet Toolbox' koji koristi grafičku interpretaciju, a dostupan je u potpunosti na internet stranici http://www.glaciology.net/wavelet-coherence. Detaljni opis Matlabova alata 'True Compression 2-D', gdje se mogu naći i razne implementacije nalazi se na http://www.mathworks.com/help/pdf_doc/wavelet/wavelet_ug.pdf#page=452&zo...
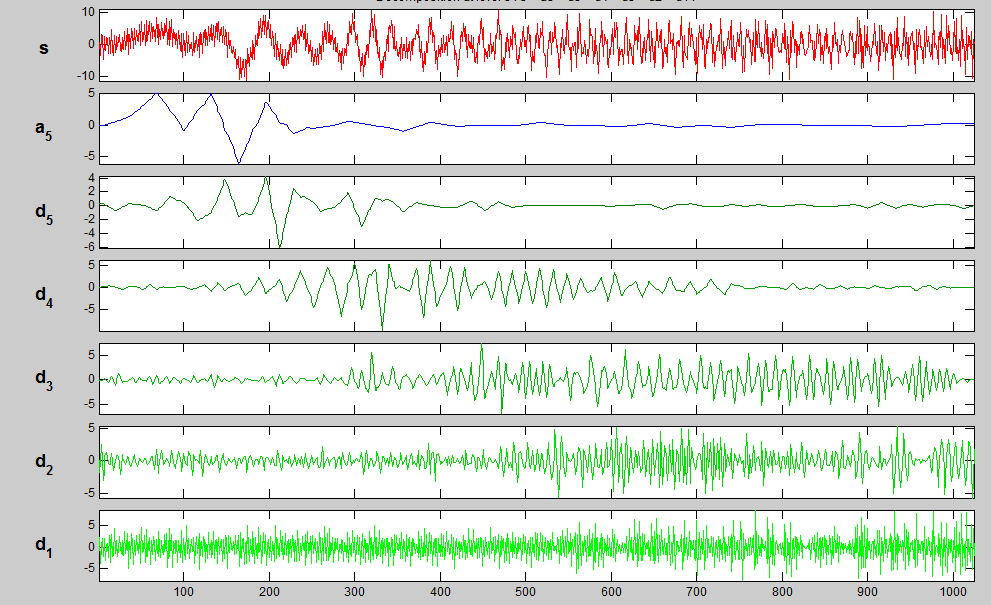
2.2Uklanjanje šuma iz signala
Šum je neželjena smetnja koja se poklapa sa korisnim signalom i može sakriti sadržaj pravog signala. Postoje brojne mogućnosti za pojavu šuma, zbog čega je vrlo važno "očistiti" signal kako ga ne bismo krivo interpretirali ili nam promakle važne informacije unutar signala. Ovisno o vrsti signala, odabiremo pogodni način uklanjanja šuma. Ako je signal stacionaran ili periodičan, dovoljna nam je Fourierova analiza kako bismo uklonili šum. Ali, vrlo često radimo sa nestacionarnim i neperiodičkim signalima. Jedan od pristupa takvim signalima je primjena valić transformacije. Osnovni dio algoritma sličan je kao i kod sažimanja:
|
1. |
Napravi valić transformaciju nad signalom. |
|
2. |
Primijeni rezanje koeficijenata baze s obzirom na odabranu metodu. |
|
3. |
Rekonstruiraj signal pomoću preostalih koeficijenata baze. |
Budući da ne znamo koliko je šuma prisutno, rezanje koeficijenata nije tako jednostavno. Signal je dan izrazom:
(16)
s(t) = x(t) + \epsilon z(t),
gdje je z(t) šum. Da bismo odredili vrijednost rezanja, najčešće se služimo statistikom i pokušavamo odrediti granice pomoću devijacije. Optimalnu granicu rezanja možemo dobiti npr. Monte Carlo simulacijama. Vrlo bitnu ulogu ima odabir familije valića i njezinog nivoa. Najčešće biramo između krutog i mekanog rezanja koeficijenata. Kruto rezanje dano je izrazom
(17)
y_{hard}(t) = \begin{cases} x(t), \vert x(t) \vert \gt \delta \\ 0, \vert x(t) \vert \lt \delta, \end{cases}
a mekano izrazom
(18)
y_{soft}(t)=\begin{cases} sign(x(t))\cdot (\vert x(t) - \delta \vert), \vert x(t) \vert \gt \delta \\ 0, \vert x(t) \vert \lt \delta \end{cases}
Mekano rezanje daje glađe rješenje, što rezultira vizualno ugodnijom slikom, ali kruto rezanje bolje čuva rubove. Razvijeni su brojni algoritmi za rješavanje ovog problema, kao i gotovi alati. Matlabov Wavelet Toolbox ima ugrađen alat za uklanjanje šuma iz signala (1-D, 2-D) pomoću valić analize. Nekoliko implementacija u Matlabu dostupno je na http://www.mathworks.com/help/wavelet/examples/de-noising-signals-and-im....
2.3Prepoznavanje
Pomoću valić analize moguće je dobro prepoznati i naglasiti rubove objekata. Često se ta ideja koristi u algoritmima za prepoznavanje i razdvajanje objekata. Tako primjerice, računalo može naučiti raspoznavati sa slike radi li se o psu ili mački. Koristi se u biometričkom sustavu, gdje se može prepoznati osoba pomoću otiska prsta, očiju, glasa, rukopisu, itd. Opisati ćemo algoritam za prepoznavanje pomoću oka. Koristiti ćemo digitalnu sliku i pokušati naučiti računalo da izdvoji oči kao sredstvo za prepoznavanje.
Za biometrijski sustav važno je da je svojstvo koje promatramo jedinstveno za svaku osobu, jednostavno i brzo za provjeru. Oči su upravo jedan takav alat, koji se zbog svoje jedinstvenosti često naziva "biološka putovnica". U istraživanju koje je provedeno na više od dva milijuna ljudi u Velikoj Britaniji, SAD-u i Japanu pokazalo se da su za sve te osobe uzorci oka bili različiti, čak i u slučaju jednojajčanih blizanaca. Upravo zato, mnogi znanstvenici rade na poboljšanju algoritama koji vrše prepoznavanje osobe pomoću očnog uzorka. Razvijene su brojne metode za ovakvu vrstu prepoznavanja (metoda uzorka, projekcije, infracrvenog svjetla, ...), a mi ćemo opisati metodu koja koristi valić transformaciju kako bi indentificirala dio lica koji sadrži oči na digitalnoj slici.
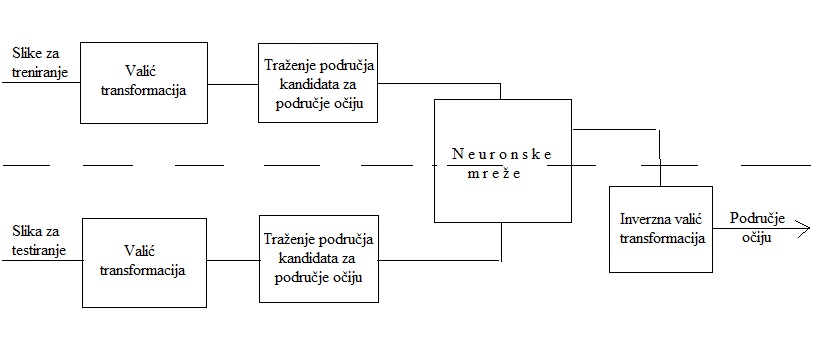
Metoda koja koristi valić transformaciu ima dva glavna dijela, treniranje i prepoznavanje. U prvom dijelu, računalu dajemo slike osoba sa različitim izrazima lica, različitim frizurama, različitih dimenzija, a također možemo uključiti i slike gdje osoba ima zatvorene oči. Slijedi diskretna valić transformacija koja omogućava prepoznavanje rubova i dijela slike koji sadrži oči. Posebno su važne informacije o niskim i visokim frekvencijama. Koeficijenti valić transformacije su izrazito visoki u području oko očiju i na taj način pokušavamo odrediti željeno područje lica. Uzimamo 3\times 3 područja oko visokih frekvencija i te podatke prosljeđujemo algoritmima neuronskih mreža kako bismo dovršili prepoznavanje željenog područja na licu osobe. Algoritmi za rad sa neuronskim mrežama ugrađeni su u Matlabov alatni sustav (Neural Network Toolbox).
Ovaj algoritam daje dobre rezultate (preciznost je iznad 80%), a poteškoće mogu predstavljati slike sa zatvorenim očima i slike koje sadrže vrlo intenzivnu podlogu. Ideja za poboljšanje algoritma ima puno, što dovodi do čestih znanstvenih publikacija upravo na tom području. Detalje implementacije ovakvih algoritama možete pronaći na internet stranicama:
http://matlabsproj.blogspot.hr/2012/06/eye-detection-using-wavelets-and-...,
http://arxiv.org/ftp/arxiv/papers/1401/1401.5108.pdf
3Zaključak
Vremensko-frekvencijska analiza koristi se prilikom rješavanja brojnih problema iz stvarnog svijeta. Jedna od najboljih metoda do sada je valić transformacija koja se još često naziva i multirezolucijska analiza zbog svoje prirode. Za razliku od drugih navedenih metoda nudi nam bolju rezoluciju frekvencija u vremenu, naročito viših frekvencija koje najčešće nose važne informacije. Iako bazu takve transformacije nije uvijek intuitivno lako zamisliti, postoje vrlo sofisticirani alati (npr. Wavelet toolbox) implementirani u Matlabu, ali i drugim programskim jezicima, koji nam pomažu u boljem razumijevanju valić familija, a intenzivna istraživanja u posljednja tri desetljeća na ovom području urodila su vrlo opsežnom i bogatom teorijom koja se izgrađuje i doprinosi poboljšanju algoritama i metoda u brojnim područjima kao što su obrada signala i slike, astronomija, optika, medicina, predviđanje potresa itd. U ovom članku mogli ste upoznati primjenu u sažimanju slike, otklanjanju šuma iz signala i prepoznavanju osobe pomoću očnog uzorka. Bitna prednost DWT je složenost računanja koeficijenata baze koji iznosi \mathcal{O}(n) (Mallatov algoritam), brojne mogućnosti za odabir pogodne familije, nivoa, prikaz signala po nivoima i smjerovima, što dovodi do odlične rekonstrukcije vrlo širokog spektra funkcija, gdje mnoge druge metode ne daju dovoljno dobre rezultate. Možemo istaknuti pouzdanost, prilagodljivost i brzinu kao osnovne karakteristike metoda koje su bazirane na valić analizi, kao i činjenicu da su moguća brojna poboljšanja u budućnosti.{20}