Bojan Basrak i Ivan Varga
PMF-Matematički odsjek, Bijenička 30, 10000 Zagreb
bojan.basrak@math.hr
1Uvod
Prije široke dostupnosti računala i ručnih kalkulatora, znanstvenici su se često oslanjali na tzv. logaritamske tablice. Zahvaljujući njima mnogi su se izračuni mogli pojednostaviti ili barem približno provesti. Posebno su bile važne u astronomiji. Tako je, američki astronom Simon Newcomb, još 1881. godine primjetio da su početne stranice u logaritamskim tablicama istrošenije od ostalih stranica. Kako tablice sadrže logaritme decimalnih brojeva poredanih po prvoj značajnoj znamenki, Newcomb je naslutio da prva značajna znamenka stvarnih podataka nije jednoliko distribuirana. Njegova opažanja ga na kraju dovode do pretpostavke da je vjerojatnost pojave znamenke d kao prve znamenke nekog od podataka, jednaka
\log_{10}(1+d) - \log_{10}(d),
za sve d \in \lbrace 1,2,\ldots ,9 \rbrace. Taj isti fenomen primjećuje i fizičar Frank Benford 1938. godine. On ga detaljnije istražuje i testira na različitim skupovima podataka, kao što su površine rijeka, veličine stanovništva, fizikalne konstante itd., pa se zbog toga otkrivanje ovog zakona pripisuje upravo Benfordu.
U praksi prikupljene numeričke podatke, mi danas matematički modeliramo slučajnim varijablama. Ako slučajnu varijablu označimo sa X, a njenu prvu značajnu znamenku sa D_{1}(X), ove oznake možemo iskoristiti da iskažemo Benfordov zakon. Benford je jednostavno pretpostavio da će vjerojatnost pojavljivanja značajne znamenke d zadovoljavati
(1)
P(D_{1}(X) = d) = \log_{10}\left(1+\frac{1}{d}\right),
za sve d \in \lbrace 1, 2,\ldots,9\rbrace. Upravo kako je naslutio i Newcomb. Za razdiobe za koje vrijedi ova pretpostavka, kažemo da zadovoljavaju {\em Benfordov zakon za prvu značajnu znamenku}.
Lako se uvjeriti da ovaj zakon ipak ne vrijedi za mnoge teorijske i često korištene razdiobe. Ako X npr. uniformno izaberemo iz intervala (0,1), i prva značajna znamenka imat će jednaku vjerojatnost da poprimi vrijednosti od 1 do 9. Ni za najvažniju razdiobu u statistici Benfordov zakon ne vrijedi. Naime, ako je X normalna (ili Gaussova) slučajna varijabla, može se pokazati da (1) ne vrijedi. Unatoč tome Newcombova i Benfordova slutnja potvrđene su empirijski na mnogim skupovima podataka.
U nastavku ćemo detaljnije prikazati Benfordov zakon, kao i neka teorijska opravdanja za njegovo pojavljivanje koje su matematičari (predvođeni T. Hillom) pronašli u zadnjih nekoliko desetljeća.
2Benfordovo svojstvo
Pokazuje se da Benfordov zakon možemo iskazati i preciznije. Takav precizniji zakon određuje razdiobu i za sve ostale značajne znamenke slučajno odabranog broja iz dane razdiobe.
Za svaki realan broj x različit od nule, prvu značajnu znamenku, u oznaci D_{1}(x), formalno definiramo kao jedinstven broj j \in \lbrace 1,2,\ldots,9\rbrace za koji vrijedi
10^{k} j \leq |x| \lt 10^{k} (j+1),
za neki k \in \mathbb{Z}. Jasno je da su brojevi k i j s tim svojstvom jedinstveni. Korisno je definirati i tzv. signifikant (ili mantisu) realnog broja. Za x\not = 0, signifikant je jedinstven broj S(x) iz intervala [1,10) za koji vrijedi \linebreak[4] |x| = 10^{k}S(x) za neki k \in \mathbb{Z}. Funkciju koja svakom realnom broju x pridružuje njegov signifikant
x \mapsto S(x),
nazivamo signifikantna funkcija. Pri tom za x = 0, definiramo S(0) :=0.
Iako nas prije svega zanima Benfordovo svojstvo za slučajne varijable, isto svojstvo mogu imati i nizovi. Označimo sa \# A kardinalitet proizvoljnog skupa A. Niz realnih brojeva (x_{n}) je Benfordov niz, ako
(2)
\lim_{N \rightarrow \infty}\frac{\# \lbrace 1 \leq n \leq N \colon S(x_{n}) \lt t\rbrace }{N} = \log_{10} t \quad \text{ za sve} \ t \in [1, 10).
Benfordovo svojstvo dakle, precizira razdiobu signifikanta takvog niza. Samim tim, uočimo da (2) određuje razdiobu prve, ali i bilo koje druge značajne znamenke u nizu. Posebno npr.
\lim_{N \rightarrow \infty} \frac{\# \lbrace 1 \leq n \leq N \colon D_{1}(x_{n}) = d_{1} \rbrace }{N}
=\lim_{N \rightarrow \infty} \frac{\# \lbrace 1 \leq n \leq N \colon d_{1} \leq S(x_{n}) \lt d_{1}+1 \rbrace }{N}
=\lim_{N \rightarrow \infty} \frac{\# \lbrace 1 \leq n \leq N \colon S(x_{n}) \lt d_{1}+1 \rbrace }{N}
- \lim_{N \rightarrow \infty} \frac{\# \lbrace 1 \leq n \leq N \colon S(x_{n}) \lt d_{1} \rbrace }{N}
= \log \displaystyle \left( d_{1}+1 \right) - \log \displaystyle \left( d_{1} \right) = \log \displaystyle \left( 1 + \frac{1}{d_{1}} \right),
za sve d_{1} \in \lbrace 1, 2,\ldots,9\rbrace. Slično, ako sa D_{2}(x) označimo drugu značajnu znamenku realnog broja x, a niz (x_{n}) je Benfordov, tada
\lim_{N \rightarrow \infty} \frac{\# \lbrace 1 \leq n \leq N \colon D_{1}(x_{n}) = d_{1} \text{ i } \ D_{2}(x_{n}) = d_{2} \rbrace }{N} = \log \displaystyle \left( 1 + \displaystyle \left(10d_{1} + d_{2} \right)^{-1} \right),
za sve d_{1} \in \lbrace 1,2, \ldots,9\rbrace i d_{2} \in \lbrace 0,1,\ldots,9\rbrace.
Poznato je npr. da je niz potencija 2^{n}, n\in \mathbb{N}, Benfordov. Isto vrijedi i za niz faktorijela ili Fibonaccijev niz. S druge strane niz prirodnih odn. prostih brojeva nema ovo svojstvo.
Ako pak slučajna varijabla X zadovoljava
(3)
P(S(X) \lt t ) = \log_{10} t ,
za sve t \in [1,10), kažemo da X (odn. njena razdioba) posjeduje Benfordovo svojstvo. Za sve ovakve X, kao direktnu posljedicu dobivamo Benfordov zakon za prvu značajnu znamenku. Naime, iz (3) slijedi
\displaystyle P(D_{1}(X) = d) = P(d \leq S(X) \lt d+1)
= P(S(X) \lt d+1) - P(S(X) \lt d)
= \log_{10} (d+1) - \log_{10} (d)
za sve d \in \lbrace 1,2,….,9\rbrace, što dokazuje tvrdnju.
3Povezana svojstva
Interesantno je da je Benfordovo svojstvo nizova usko povezano sa tzv. svojstvom uniformnosti modulo 1. Ovo potonje svojstvo je vrlo značajno i podrobno proučavano u teoriji brojeva, npr. označimo sa \lbrace x \rbrace tzv. razlomljeni dio realnog broja x. Preciznije, \lbrace x\rbrace = x - \lfloor x \rfloor, gdje je \lfloor x \rfloor oznaka za najveći cijeli broj manji ili jednak x. Tako, npr. \lbrace 2.71\rbrace = 0.71 i \lbrace -2.71\rbrace = 0.29. Za niz (x_{n}) kažemo da je uniformo distribuiran modulo 1, ako vrijedi
\lim_{N \rightarrow \infty} \frac{\# \lbrace 1 \leq n \leq N \colon \lbrace x_{n} \rbrace \lt s \rbrace }{N} = s, \quad \text{ za svaki} \ s \in [0,1).
Analogno, slučajna varijabla X (odn. njena razdioba) uniformno je distribuirana modulo 1, ako
\mathbb{P}(\lbrace X\rbrace \lt s) = s, \quad \text{ za sve } \ s \in [0,1).
Vezu između ovih svojstava objašnjava idući teorem, koji odmah daje i jedan recept za praktičnu provjeru Benfordovog svojstva. Dokaz teorema se može pronaći u Hill [1].
Theorem 1. Slučajna varijabla je Benfordova ako i samo ako je logaritam po bazi deset njene apsolutne vrijednosti uniformno distribuiran modulo 1.
Analogni teorem vrijedi i za nizove realnih brojeva. Jasno je da stvarni podaci Benfordovo svojstvo mogu imati tek približno. Ipak, u mnogim primjenama razumno je očekivati da podaci (barem približno) zadrže Benfordovo svojstvo i nakon promjene skale. Ako se npr. radi o novčanim iznosima Benfordovo svojstvo bismo mogli očekivati i nakon promjene valute. Slično, Benfordovo svojstvo za duljine rijeka očekivali bismo da vrijedi neovisno o tome da li te duljine izražavamo u miljama ili kilometrima. Izuzetno je zanimljivo da invarijatnost na množenje skalarom daje alternativnu karakterizaciju Benfordovog svojstva.
Theorem 2. Za svaku slučajnu varijablu X, za koju je \mathbb{P}(X = 0) = 0, sljedeće su tvrdnje ekvivalentne:
\bullet
[(i)] X je Benfordova.
\bullet
[(ii)] Postoji znamenka d \in \lbrace 1,2,….,9\rbrace tako da
\mathbb{P}(D_{1}(\alpha X) = d) = \mathbb{P}(D_{1}(X) = d) \quad \text{za svaki} \ \alpha \gt 0,
gdje je \mathbb{P}(D_{1}(X) = d) = \log(1 + d^{-1}).
Dokaz teorema se može vidjeti u Hill [1].
Na sličan način možemo karakterizirati Benfordovo svojstvo i za realne nizove. Navedimo tek da je signifikantna funkcija niza realnih brojeva (x_{n}) invarijantna na množenje skalarom ako za svaki \alpha \gt 0 i t \in [1,10) vrijedi,
(4)
\lim_{N \rightarrow \infty}\frac{\# \lbrace 1 \leq n \leq N \colon S(\alpha x_{n}) \lt t\rbrace }{N} = \lim_{N \rightarrow \infty}\frac{\# \lbrace 1 \leq n \leq N \colon S(x_{n}) \lt t\rbrace }{N}.
Naglasimo još da postoje i razna druga interesantna svojstva Benfordovih razdioba, koja dijelom nadilaze ambicije ovog pregleda, za detalje pogledajte npr. [1].
4Primjeri
Fibonaccijevi brojevi F_{n}, \ n=0,1,2,\ldots, predstavljaju jedan od najzanimljivijih nizova u matematici. Ovaj niz izazivao je fascinaciju još u staroj Indiji, a svojstva mu pročavaju matematičari i danas. Brojevi F_{n} zadovoljavaju jednostavnu rekurziju
F_{n} = F_{n-1}+ F_{n-2}\,,
za sve brojeve n \geq 2, a pri tom je F_{0}=0 i F_{1}=1. Prisjetimo se inicijalni članovi niza su
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, \ldots
Slika 1 donosi usporedbu razdiobe prve značajne znamenke za prvih 1000 članova niza (F_{n}) s Benfordovom razdiobom. Na slici 2 promatramo razdiobu prve značajne znamenke niza (\pi F_{n}). Primjetimo da je i ovdje prisutna vrlo dobra podudarnost s Benfordovim zakonom, baš kako smo mogli očekivati na osnovu razmatranja iz prethodnog odjeljka.
Benfordov zakon možemo ilustrirati i na konkretnim podacima. Promatrat ćemo razdiobu prve značajne znamenke na podacima o broju stanovnika naselja u Hrvatskoj. Podaci su preuzeti iz baze podataka za posljednji popis stanovništva iz 2011. godine, Državnog zavoda za statistiku. Promatrani skup ima oko 6700 podataka. Raspon podataka je reda veličine 10^{5}. Naime, prema popisu stanovnistva iz 2011. godine, Zagreb je imao 686568 stanovnika, dok je najmanje naselje u Hrvatskoj – Špigelski Breg, imalo tek jednog stanovnika. Iz grafa na slici 3 vidimo da i ovaj skup podataka vrlo dobro slijedi Benfordov zakon.
5Benfordov zakon u primjeni
Gotovo od samog otkrivanja Benfordovog zakona postojala su nastojanja da ga se iskoristi u razotkrivanju raznih prevara. Istraživanja Marka Nigrinija pokazuje kako se Benfordov zakon može koristiti kao indikator u financijskim prevarama, npr. analizirajući koliko dobro isplate, uplate, iznosi osiguranja itd. slijede Benfordovu distribuciju (vidi Nigrini [2]). Osim za financijske podatke, zakon se pokazuje koristan i u otkrivanju falsificiranja znanstvenih i makroekonomskih podataka. Tako je npr. Rauch [3] na ovoj osnovi doveo u sumnju makroekonomske podatke koje je Grčka slala prije ulaska u Europsku Uniju. Slični razlozi, nedavno su natjerali ANZ (Australia \& New Zealand Banking Group) da posumnja u kineske ekonomske podatke o godišnjoj bruto domaćoj proizvodnji (BDP), o čemu su izvjestili i mnogi svjetski mediji. Naglasimo ipak, ako podaci ne odgovaraju Benfordovom zakonu, to ne mora značiti da se njima manipuliralo. Unatoč tome, Benfordov zakon se u Americi katkad koristi kao službeni dokaz i u sudskoj praksi.
Osim zbog manipulacije podacima, u praksi, podaci neće slijediti Benfordov zakon ako su ograničeni tako da počinju samo određenim značajnim znamenkama, kao npr. podaci o visini, kvocijentu inteligencije, opsegu glave ili rasponu ruku. Primjetimo, ti podaci su tipično približno normalno distribuirani. Nadalje, ako skupovi podataka imaju raspon kroz samo 1 ili 2 reda veličine (npr. podaci su između 1 i 100), Benfordov zakon isto tako tipično neće vrijediti. Slično, zakon nije primjenjiv za podatke na koje je postavljen maksimum ili minimum. Da smo npr. na skupu podataka o broju stanovnika promatrali samo naselja koja imaju izmedu 500 i 3000 stanovnika, podudarnost podataka s Benfordovim zakonom bila bi puno slabija.
Bibliografija
[1]
Berger, A. i T.P. Hill: A basic theory of Benford’s Law. Probability Surveys, 8:1–126, 2011.
[2]
Nigrini, M.:Benford's Law: Aplications for Forensic Accounting, Auditing and Fraud Detection, svezak 586. Wiley, 2012.
[3]
Rauch, B., M. Goettsche, G. Braehler i S. Engel : Fact and Fiction in EU-Governmental Economic Data. German Economic Review, 12(3):243–255, 2011.
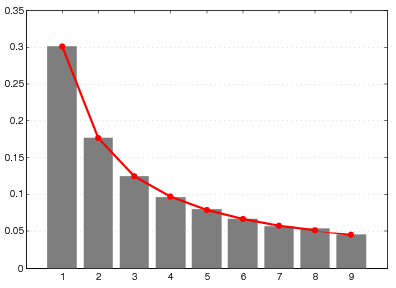
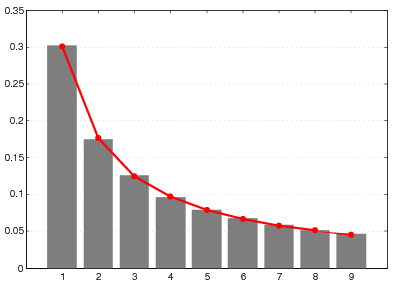
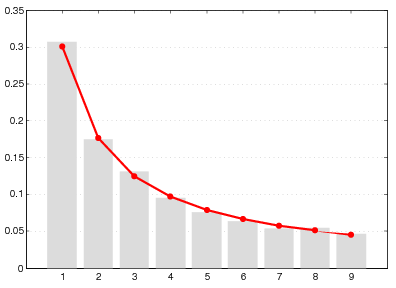Distribucija prve značajne znamenke za 2011. godinu, koja je prikazana svijetlo sivim pravokutnicima, dok je Benfordova distribucija prve značajne znamenke prikazana crvenom linijom.