Vedrana Mikulić Crnković
Ivona Novak |
Sažetak
Nastanak neeuklidske geometrije počinje razmatranjem Euklidovog petoga aksioma (aksioma o paralelama) i zaključkom da on nije zavisan o prethodna četiri. N. I. Lobačevski negirao je Euklidov peti aksiom i sagradio novi geometrijski sustav. Matematičari tadašnjega vremena daljnjim proučavanjem došli su do zaključka da se geometrija Lobačevskog može promatrati na hiperboloidu u
\mathbb{R}^{3}, zbog čega i dobiva naziv hiperbolička geometrija. Osim modela na hiperboloidu, u članku su prikazana još četiri modela hiperboličke ravnine: Kleinov model, model hemisfere, Poincareov model te model gornje poluravnine. U svakom od navedenih modela opisan je međusobni odnos dvaju pravaca. Osim toga, opisana je bijektivna korespondencija između pojedinih modela. Radi lakšeg predočavanja pojedinih modela hiperboličke ravnine, članak je upotpunjen slikama izrađenim u programskom paketu Mathematica (
http://www.wolfram.com/) te programima NonEuclid (
http://www.cs.unm.edu/~joel/NonEuclid/NonEuclid.html) i Interactive Non-Euclidean Geometry (
http://fis.cie.uma.es/~ccriado/Interactive%20Non.htm).
1Povijesni uvod
Iako se pojava geometrije (zemljomjerstva) veže uz stare Egipćane koji su se njome bavili iz potrebe, razvoj geometrije počinje u staroj Grčkoj s Talesom iz Mileta za kojeg se smatra da je znanje Egipćana prenio u Grčku. Uz Talesa, javljaju se Pitagora, Hipokrit, Platon, Aristotel i još brojna velika imena starogrčkih matematičara koji su svojim otkrićima pridonijeli razvoju geometrije. Sva saznanja o geometriji tadašnjeg vremena sistematizirao je Euklid (330.-275. p. n. e.) iz Aleksandrije u svojemu velikom djelu Elementi, u kojem geometriju zasniva deduktivno, odnosno aksiomatski. Euklid je nadmašio svoje prethodnike po sistematičnosti i cjelovitosti, a Elementi su ostali nenadmašeni više od dva tisućljeća. Iako je djelo doživjelo mnoge kritike, ponajviše za definicije koje se smatraju najslabijom točkom Elemenata, matematičarima tadašnjeg doba (a i kasnije) najviše su pažnje privukli Euklidovi postulati:
|
(1) |
neka se postulira da se od svake točke do svake točke povlači dužina, |
|
(2) |
i da se ograničena dužina neprekinuto produžuje u dužinu, |
|
(3) |
i da se svakim središtem i udaljenošću opisuje krug, |
|
(4) |
i da su svi pravi kutovi međusobno jednaki, |
|
(5) |
i da ako dužina koja siječe dvije dužine čini unutarnje kutove s iste strane manjima od pravog kuta, dvije dužine, neograničeno produžene, sastaju se s one strane na kojoj su kutovi manji od dva prava kuta. |
Najviše je kritiziran peti Euklidov postulat (poznat i kao aksiom o paralelama) za koji se smatralo da se može izvesti iz preostalih postulata i aksioma koje je Euklid naveo. Tijekom više od dvije tisuće godina matematičari su pokušavali dokazati peti postulat i pritom su nailazili na razne tvrdnje njemu ekvivalentne. Navedimo neke od njih.
|
\bullet |
[\triangleright] Neka je T točka koja ne pripada pravcu p. Tada postoji jedinstveni pravac q koji sadrži točku T i ima prazan presjek s pravcem p (u euklidskoj ravnini za pravce p i q kažemo da su paralelni). |
|
\bullet |
[\triangleright] Neka su p i q paralelni pravci. Ako pravac p' siječe pravac p onda on siječe i pravac q. |
|
\bullet |
[\triangleright] Neka su R i P dvije poluravnine određene pravcem p. Skup točaka poluravnine R koje su jednako udaljene od pravca p je pravac. |
|
\bullet |
[\triangleright] Zbroj mjera kutova u trokutu jednak je \pi. |
|
\bullet |
[\triangleright] Postoje slični trokuti. |
|
\bullet |
[\triangleright] Pravac koji sadrži unutarnju točku trokuta siječe dvije stranice toga trokuta. |
|
\bullet |
[\triangleright] Svake tri nekolinearne točke određuju jedinstvenu kružnicu. |
|
\bullet |
[\triangleright] Kvadrat dužine hipotenuze pravokutnog trokuta jednak je zbroju kvadrata dužina njegovih kateta (Pitagorin poučak). |
Budući da nikako nije uspijevalo izravno dokazivanje Euklidovog aksioma o paralelama, matematičari 18. stoljeća Saccheri i Lambert pokušali su, nezavisno jedan o drugom, do dokaza doći na indirektan način (metodom kontrapozicije). Saccheri je bio uvjeren da je uspio dokazati peti postulat. Međutim, ono što je konstruirao danas nazivamo Saccherijev četverokut, a Saccherijevo razmatranje petog postulata možemo uzeti za početak hiperboličke geometrije. Mnogo bolje nije prošao ni Lambert, koji je uz pretpostavku da peti postulat ne vrijedi konstruirao Lambertov četverokut kojemu su tri kuta prava, a četvrti je tupi. Također, problem paralela proučava i N. I. Lobačevski, koji dolazi do zaključka da je peti Euklidov postulat nezavisan od ostalih i time dolazi do nove geometrije koju danas nazivamo hiperboličkom geometrijom. Do sličnih zaključaka došao je i Gauss, no iz nepoznatih razloga svoja otkrića nikada nije objavio.
U pokušajima neizravnog dokazivanja aksioma o paralelama matematičari su pretpostavili da on ne vrijedi, odnosno pretpostavili su da vrijedi jedna od sljedećih tvrdnji.
|
(1) |
Neka je T točka koja ne pripada pravcu p. Tada svaki pravac koji sadrži točku T siječe pravac p. |
|
(2) |
Neka je T točka koja ne pripada pravcu p. Tada postoje barem dva pravca koja sadrže točku T i imaju prazan presjek s pravcem p. |
Tek je Hilbert u
19. stoljeću dao potpunu, neproturječnu i konzistentnu aksiomatiku euklidske geometrije, koju i danas koristimo. Prema Hilbertu, aksiomatika ravninske geometrije mora sadržavati osnovne pojmove (točke i pravce), osnovne relacije (”pripadati”, ”biti između” i ”biti kongruentan”), koji se ne definiraju, i konačan broj aksioma (tvrdnji koje se ne dokazuju), koji opisuju osnovne pojmove i relacije te izvedene pojmove (na primjer dužina, polupravac, kut, trokut i sl.).
Ravninska geometrija u kojoj vrijede svi aksiomi euklidske ravnine, osim aksioma o paralelama umjesto koga vrijedi tvrdnja
1., zove se eliptička ravninska geometrija. Ako aksiom o paralelama zamijenimo tvrdnjom
2., dobivamo aksiomatiku ravninske hiperboličke geometrije.
Model pojedine ravninske geometrije je skup objekata (točaka i pravaca) na kojem se mogu definirati relacije ”pripadati”, ”biti između” i ”biti kongruentan” tako da su zadovoljeni aksiomi te geometrije.
1.1Aksiomi euklidske ravninske geometrije
Prije navođenja aksioma navedimo neke izvedene pojmove.
|
\bullet |
[\triangleright] Za dvije različite točke A i B kažemo da tvore dužinu. Točke A i B su krajevi te dužine. Točka C je unutrašnja točka dužine ako je između vrhova te dužine. |
|
\bullet |
[\triangleright] Polupravac s početnom točkom A kojemu pripada točka B je skup svih točaka koje su između točaka A i B i točaka C takvih da je B između točaka A i C. |
|
\bullet |
[\triangleright] Kut je par polupravaca sa zajedničkom početnom točkom. Polupravci se nazivaju krakovi kuta. |
|
\bullet |
[\triangleright] Za tri različite točke A, B i C koje ne pripadaju istom pravcu kažemo da tvore trokut. Točke A, B, C su vrhovi trokuta, a tri dužine određene s po dva vrha stranice trokuta. |
Aksiomi incidencije
|
(1) |
Za svake dvije točke postoji jedinstveni pravac incidentan s njima. |
|
(2) |
Svaki pravac je incidentan s barem dvije točke. |
|
(3) |
Postoje tri točke koje ne pripadaju istom pravcu. |
Aksiomi poretka
|
(1) |
Ako je točka B između točaka A i C, tada su A, B, C tri međusobno različite točke koje pripadaju istom pravcu i točka B je između točaka C i A. |
|
(2) |
Ako su A i B dvije različite točke, tada postoji točka C takva da je točka B između točaka A i C. |
|
(3) |
Od tri različite točke koje pripadaju istom pravcu najviše je jedna točka između preostale dvije. |
|
(4) |
(Paschov aksiom) Ako pravac siječe jednu stranicu trokuta i ne sadrži niti jedan vrh toga trokuta, onda on siječe točno jednu od preostale dvije stranice trokuta. |
Aksiomi kongruentnosti
|
(1) |
Neka je zadana dužina s krajnjim točkama A i B i polupravac s početnom točkom A'. Tada postoji točka B' koja pripada tom polupravcu takva da su dužina s krajnjim točkama A i B i dužina s krajnjim točkama A' i B' kongruentne. |
|
(2) |
Ako je dužina s krajnjim točkama A i B kongruentna dužini s krajnjim točkama A' i B' i kongruentna dužini s krajnjim točkama A” i B”, tada su dužina s krajnjim točkama A' i B' i dužina s krajnjim točkama A” i B” kongruentne. |
|
(3) |
Neka je točka B između točaka A i C, točka B' između točaka A' i C', dužina s krajnjim točkama A i B i dužina s krajnjim točkama A' i B' kongruentne i dužina s krajnjim točkama B i C i dužina s krajnjim točkama B' i C' kongruentne. Tada su dužina s krajnjim točkama A i C i dužina s krajnjim točkama A' i C' kongruentne. |
|
(4) |
Neka je dan kut s krakovima h i k. Neka je a' pravac, O' točka koja pripada pravcu a' i h' polupravac s početnom točkom O' koji pripada pravcu a' te neka je R jedna od dvije poluravnine određene pravcem a'. Tada postoji jedinstveni polupravac k' s početkom u točki O' koji pripada poluravnini R takav da su kut s krakovima h i k i kut s krakovima h' i k' kongruentni. |
|
(5) |
Neka su zadana dva trokuta s jednim parom kongruentnih kutova te neka su stranice trokuta koje pripadaju krakovima kongruentnih kutova kongruentne. Tada postoji još jedan par kongruentnih kutova. |
Aksiom o paralelama
|
(1) |
Neka je p pravac i T točka koja ne pripada pravcu p. Tada postoji točno jedan pravac koji sadrži točku T i ne siječe pravac p. |
Aksiom neprekidnosti
|
(1) |
(Dedekindov aksiom) Neka je zadana dužina s krajnjim točkama A i B, neka su sve točke te dužine podijeljene u dvije klase I i II tako da je A u klasi I i B u klasi II te da je svaka unutrašnja točka te dužina u točno jednoj klasi i neka je svaka točka klase I različita od A između točke A i bilo koje točke klase II. Tada postoji jedinstvena točka C te dužine takva da sve točke između točaka A i C pripadaju jednoj klasi i sve točke između C i B drugoj klasi. |
1.2Aksiomi hiperboličke ravninske geometrije
Lobačevski je novi geometrijski sustav izgradio tako da je peti Euklidov postulat zamijenio novim aksiomom.
|
\bullet |
[\triangleright] (Aksiom hiperboličke geometrije) Točka koja ne pripada pravcu u ravnini sadržana je u barem dva pravca koja ne sijeku dani pravac. |
Iz toga proizlaze sljedeće tvrdnje.
|
\bullet |
[\triangleright] Zbroj mjera kutova u trokutu manji je od zbroja mjera dvaju pravih kutova. |
|
\bullet |
[\triangleright] Trokut je određen svojim kutovima pa zato ne postoje slični nesukladni trokuti. |
|
\bullet |
[\triangleright] Postoji trokut najveće površine. |
|
\bullet |
[\triangleright] Skup točaka jednako udaljenih od pravca nije pravac. |
Aksiomatika hiperboličke ravnine razlikuje se od aksiomatike euklidske ravnine samo u jednom aksiomu, prethodno navedenom.
U nastavku ćemo uvesti pet modela hiperboličke ravnine, prikazati ih grafički i pokazati da pojedini model zadovoljava neke aksiome hiperboličke ravnine.
Iako smo uveli hiperboličku ravninsku geometriju aksiomatski, u daljnjem će tekstu hiperbolička geometrija kroz pojedine modele hiperboličke ravnine bit promatrana analitički.
2Hiperbolička ravnina kao podskup u \mathbb{R}^{3}
2.1Uvod
Definicija 1. Neka je
b bilinearna forma definirana u
\mathbb{R}^{3} na sljedeći način:
b(\vec{x},\vec{y})=x_{1}y_{1}+x_{2}y_{2}-x_{3}y_{3},
gdje je
\vec{x}=(x_{1},x_{2},x_{3}) i
\vec{y}=(y_{1},y_{2},y_{3}).
Definicija 2. Za nenul vektor
\vec{v}\in\mathbb{R}^{3} kažemo da je
|
\bullet |
[i.] prostoroliki vektor ako je b(\vec{v},\vec{v})\gt 0. Posebno, ako je b(\vec{v},\vec{v})=1, kažemo da je \vec{v} jedinični prostoroliki vektor. |
|
\bullet |
[ii.] vremenoliki vektor ako je b(\vec{v},\vec{v})\lt 0. Posebno, ako je b(\vec{v},\vec{v})=-1, kažemo da je \vec{v} jedinični vremenoliki vektor. |
|
\bullet |
[iii.] svjetloliki vektor ako je b(\vec{v},\vec{v})=0. |
Vektor
\vec{v} je normiran s obzirom na formu
b ako je on jedinični prostoroliki ili jedinični vremenoliki vektor. Dva vektora
\vec{x} i
\vec{y} su ortogonalna s obzirom na formu
b ako je
b(\vec{x},\vec{y})=0. S
\vec{x}\times_{b}\vec{y} označavamo vektorski produkt vektora
\vec{x} i
\vec{y} s obzirom na formu
b. Taj produkt je ortogonalan na vektore
\vec{x} i
\vec{y} s obzirom na formu
b. Može se pokazati da svaka ortonormirana baza obzirom na formu
b u
\mathbb{R}^{3} sadrži dva prostorolika i jedan vremenoliki vektor.
2.2Model ravnine
Definicija 3. Hiperbolička ravnina je skup
\mathbb{H}^{2}=\left\lbrace X\in\mathbb{R}^{3}\mid x_{3}\gt 0,\ b(r_{X},r_{X})=-1 \right\rbrace ,
gdje je s
r_{X} označen radijvektor točke
X.
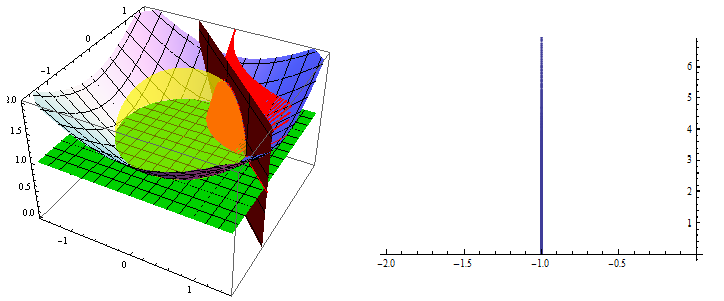
Raspišemo li uvjet iz definicije hiperboličke ravnine
b(r_{X},r_{X})=-1 i uzmemo li u obzir da se promatraju samo točke kojima je treća koordinata pozitivan broj, zaključujemo da hiperboličku ravninu u
\mathbb{R}^{3} možemo prikazati kao gornju polutku hiperboloida zadanog jednadžbom
x_{1}^{2}+x_{2}^{2}-x_{3}^{2}=-1 kojemu je tjeme u točki
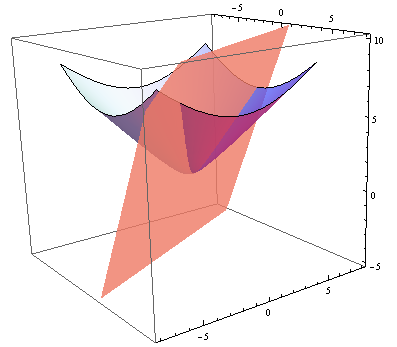
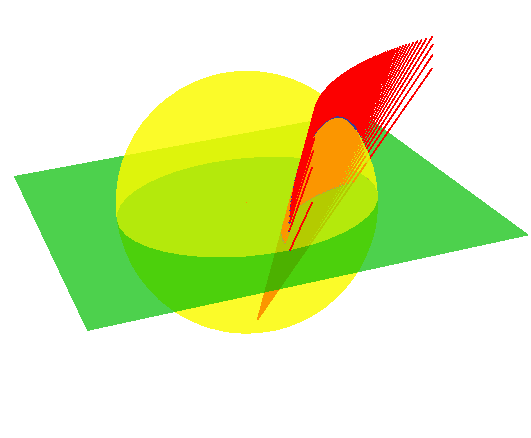
(0,0,1). Pravac u hiperboličkoj ravnini je skup
p=\left\lbrace X\in\mathbb{H}^{2}\mid b(\vec{e},r_{X})=0\right\rbrace ,
gdje je
\vec{e}=(e_{1},e_{2},e_{3}) jedinični prostoroliki vektor. Vektor
\vec{e} zovemo vektorom normale pravca
p. Promatramo li grafički, pravac u hiperboličkoj ravnini je presjek ravnine s vektorom normale
(e_{1},e_{2},-e_{3}) koja sadrži ishodište koordinatnog sustava i gornje polutke hiperboloida, tj. grana hiperbole u
\mathbb{R}^{3} (slika
1).
Teorem 4. Neka su
P i
Q dvije različite točke ravnine
\mathbb{H}^{2}. Tada postoji jedinstveni pravac ravnine
\mathbb{H}^{2} koji sadrži točke
P i
Q.
Dokaz: Neka su
P i
Q različite točke ravnine
\mathbb{H}^{2}. Tada je
b(r_{P},r_{P})=-1 i
b(r_{Q},r_{Q})=-1. Neka je
p=\left\lbrace x\in\mathbb{H}^{2}\mid b(\vec{e},r_{x})=0 \right\rbrace , \ b(\vec{e},\vec{e})=1. Ako točka
P pripada pravcu
p, onda je
b(\vec{e},r_{P})=0. Isto tako, ako točka
Q pripada pravcu
p, onda je
b(\vec{e},r_{Q})=0. Slijedi da je
\vec{e} proporcionalan vektoru
r_{P}\times_{b} r_{Q} i
\vec{e} je jedinični vektor. Treba provjeriti je li
\vec{e} prostoroliki vektor.
Znamo da je
\left\lbrace r_{P},\vec{e}\right\rbrace ortonormirani par vektora i da je
r_{P} vremenoliki vektor. Možemo nadopuniti taj skup do ortonormirane baze od
\mathbb{R}^{3} (s obzirom na formu
b) pa slijedi da je
\vec{e} prostoroliki vektor.
Jedinstvenost je posljedica činjenice da postoji samo jedan jedinični prostoroliki vektor proporcionalan vektoru
r_{P}\times_{b}r_{Q}.
\Box
Ovim smo teoremom pokazali da uvedeni model hiperboličke ravnine zadovoljava prvi aksiom incidencije.
2.3Odnos dvaju pravaca
Definicija 5. Neka su
p i
q pravci ravnine
\mathbb{H}^{2} s jediničnim vektorima normale
\vec{e} i
\vec{f}.
|
\bullet |
[\triangleright] Ako je \vec{e}\times_{b}\vec{f} vremenoliki vektor, kažemo da se pravci p i q sijeku. |
|
\bullet |
[\triangleright] Ako je \vec{e}\times_{b}\vec{f} svjetloliki vektor, kažemo da su pravci p i q paralelni. |
|
\bullet |
[\triangleright] Ako je \vec{e}\times_{b}\vec{f} prostoroliki vektor, kažemo da su pravci p i q ultraparalelni. |
Teorem 6. Ako su
p i
q pravci ravnine
\mathbb{H}^{2} s jediničnim vektorima normale
\vec{e} i
\vec{f} takvim da je
\vec{e}\times_{b}\vec{f} vremenoliki vektor, tada postoji jedinstveno sjecište pravaca
p i
q čiji je radijvektor proporcionalan vektoru
\vec{e}\times_{b}\vec{f}.
Dokaz: Neka su
p=\lbrace x\in\mathbb{H}^{2}\mid b(\vec{e},r_{X})=0\rbrace i
q=\lbrace x\in\mathbb{H}^{2}\mid b(\vec{f},r_{X})=0\rbrace pravci hiperboličke ravnine koji se sijeku. Tada je
b(\vec{e}\times_{b}\vec{f},\vec{e}\times_{b}\vec{f})\lt 0. Označimo točku presjeka sa
S. Točka
S pripada pravcu
p pa je
b(\vec{e},r_{S})=0. Analogno, točka
S pripada pravcu
q pa je
b(\vec{f},r_{S})=0. Slijedi da je
r_{S} proporcionalan vektoru
\vec{e}\times_{b}\vec{f} i jedinični. Kako je
\vec{e}\times_{b}\vec{f} vremenoliki vektor, zaključujemo da je
r_{S} jedinični vremenoliki vektor pa je samim time
S\in\mathbb{H}^{2}.
\Box
Posljedica ovog dokaza je i činjenica da ni paralelni ni ultraparalelni pravci nemaju niti jednu zajedničku točku.
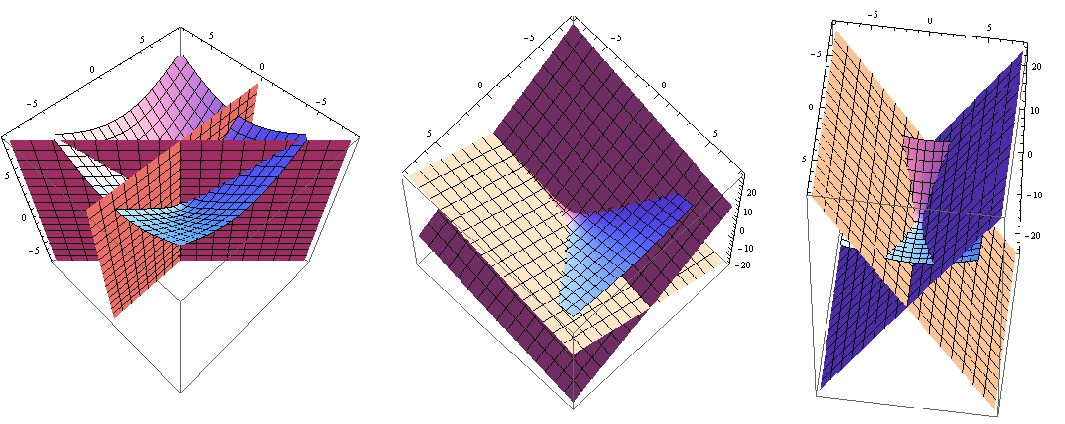
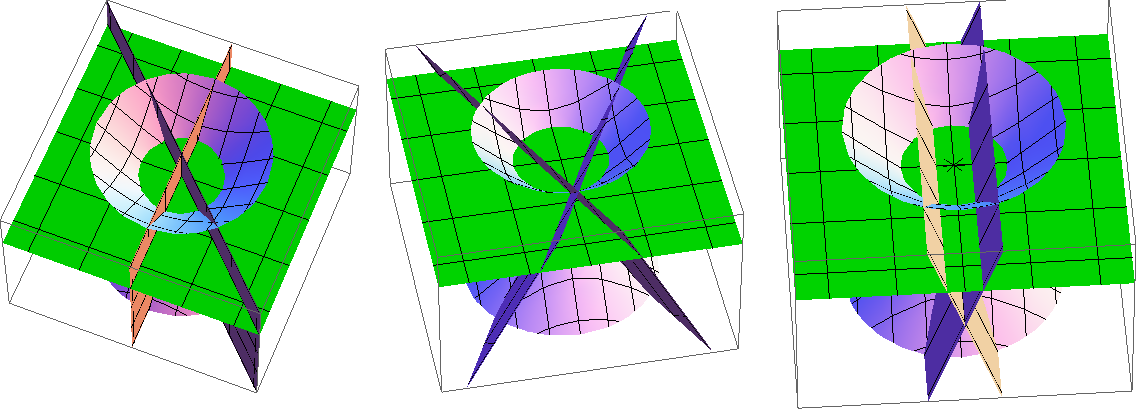
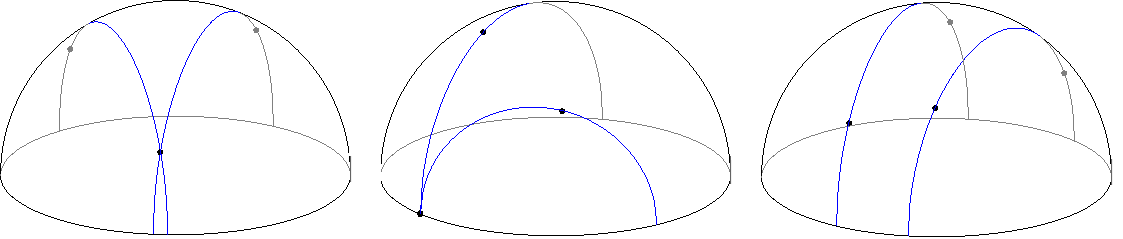
Slika
2 prikazuje moguće odnose dvaju pravaca u modelu hiperboličke ravnine u
\mathbb{R}^{3}.
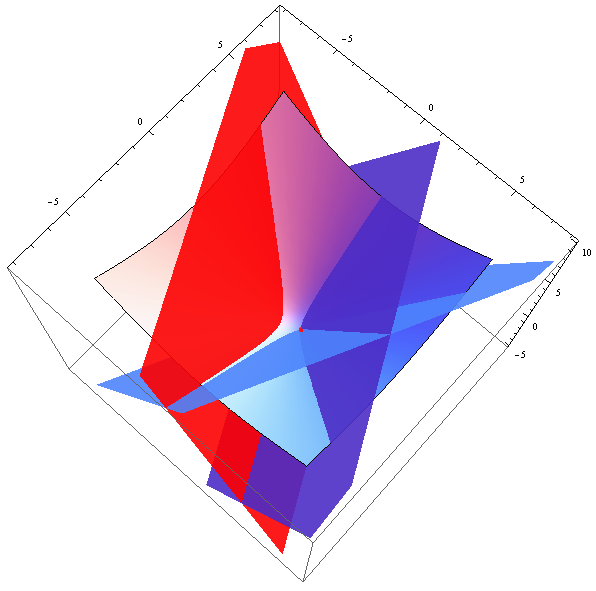
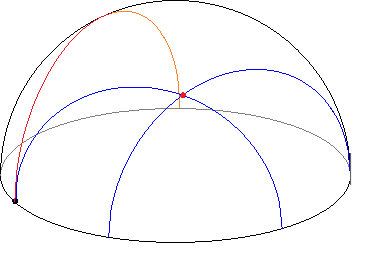
Kao osvrt na aksiomatiku hiperboličke ravnine na Slici
3 prikazani su pravac i točka koja ne pripada tom pravcu, a koju sadrže dva pravca koja ne sijeku taj pravac.
3Kleinov model ravnine
3.1Uvod
Moguće je promatrati hiperboličku ravninu i kao podskup projektivne ravnine. Prije razmatranja Kleinovog modela hiperboličke ravnine uvest ćemo osnovne pojmove iz projektivne ravninske geometrije.
Sfernu ravninsku geometriju možemo proučavati u sljedećem modelu. Točke su točke sfere
\mathbb{S}^{2}=\left\lbrace X\in\mathbb{E}^{3}\mid \left|r_{X}\right|=1\right\rbrace u trodimenzionalnom euklidskom prostoru, a pravci velike kružnice koje pripadaju toj sferi. Točke
P i
Q sferne ravnine
\mathbb{S}^{2} su antipodalne ako je
r_{P}=-r_{Q}.
Skup
\mathbb{P}^{2}=\lbrace \left\lbrace X,-X\right\rbrace \mid X\in\mathbb{S}^{2}\rbrace je model projektivne ravnine.
Označimo s
F:\mathbb{S}^{2}\rightarrow\mathbb{P}^{2} preslikavanje koje točki sferne ravnine pridružuje točku projektivne ravnine definirano s
F(X)=\left\lbrace X,-X\right\rbrace .
Definicija 7. Neka je \left\lbrace \vec{e_{1}},\vec{e_{2}},\vec{e_{3}}\right\rbrace baza od \mathbb{R}^{3}. Tada za svaki \vec{x}\in\mathbb{R}^{3} postoji jedinstvena trojka realnih brojeva (x_{1},x_{2},x_{3}) takva da je \vec{x}=x_{1}\vec{e_{1}}+x_{2}\vec{e_{2}}+x_{3}\vec{e_{3}}. Neka je F(X) točka ravnine \mathbb{P}^{2}, a \lambda proizvoljan realan broj različit od nule i \lambda r_{X}=u_{1}\vec{e_{1}}+u_{2}\vec{e_{2}}+u_{3}\vec{e_{3}}. Trojku (u_{1},u_{2},u_{3}) zovemo homogenim koordinatama točke F(X).
Neka je
bf proizvoljna bilinearna forma. Ako je
\left\lbrace \vec{e_{1}},\vec{e_{2}},\vec{e_{3}}\right\rbrace baza od
\mathbb{R}^{3}, tada je
\begin{align*} bf(r_{X},r_{Y})&=\sum_{i,j=1}^{3}x_{i}y_{j}bf(\vec{e_{i}},\vec{e_{j}})=\sum_{i,j=1}^{3}b_{ij}x_{i}y_{j}=r_{X}\textbf{B}r_{Y}, \end{align*}
gdje su
(x_{1},x_{2},x_{3}) i
(y_{1},y_{2},y_{3}) komponente vektora
r_{X} i
r_{Y}, a
\textbf{B}=\left[b_{ij}\right]=\left[bf(\vec{e_{i}},\vec{e_{j}})\right] matrica kojoj je u
i-tom retku i
j-tom stupcu vrijednost
bf(\vec{e_{i}},\vec{e_{j}}),\ i,j\in\left\lbrace 1,2,3\right\rbrace .
Definicija 8. Neka je bf proizvoljna bilinearna forma, \left\lbrace \vec{e_{1}},\vec{e_{2}},\vec{e_{3}}\right\rbrace baza od \mathbb{R}^{3} i B=[bf(\vec{e_{i}},\vec{e_{j}})],\ i,j\in \lbrace 1,2,3\rbrace . Konika u projektivnoj ravnini je skup \lbrace F(X) \mid bf(r_{X},r_{X})=0\rbrace .
Ako je
bf(r_{X},r_{Y})=b(r_{X},r_{Y})=x_{1}y_{1}+x_{2}y_{2}-x_{3}y_{3}, tada je
\textbf{B}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&-1\end{bmatrix},
a konika je skup točaka
\left\lbrace F( X)\mid b(r_{X},r_{X})=0\right\rbrace =\left\lbrace F(X)\mid x_{1}^{2}+x_{2}^{2}-x_{3}^{2}=0\right\rbrace .
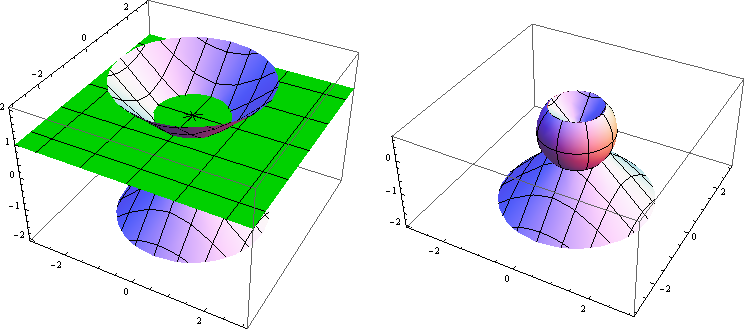
Neka je
\mathbb{D}^{2}=\left\lbrace X\in\mathbb{P}^{2}\mid b(r_{X},r_{X})\lt 0\right\rbrace podskup ravnine
\mathbb{P}^{2}, unutrašnjost konike u ravnini
\mathbb{P}^{2} (slika
4). Točke za koje je
b(r_{X},r_{X})\gt 0 pripadaju vanjštini konike.
Neka je
f:\mathbb{E}^{2}\rightarrow\mathbb{P}^{2} funkcija koja svakoj točki
(\frac{x_{1}}{x_{3}},\frac{x_{2}}{x_{3}},1) ravnine
\mathbb{E}^{2} (koju predstavljamo ravninom
x_{3}=1 u
\mathbb{E}^{3}) pridružuje točku
(x_{1},x_{2},x_{3}) ravnine
\mathbb{P}^{2} s homogenim koordinatama. Preslikavanje
f je bijekcija ako kodomenu od
f restringiramo na
\mathbb{P}^{2}\backslash p_{\infty}.
p_{\infty} označava skup točaka
\mathbb{P}^{2} koje nisu slika niti jedne točke iz
\mathbb{E}^{2}.
p_{\infty} je pravac projektivne ravnine određen jednadžbom
x_{3}=0, odnosno svaka točka koja pripada tom pravcu ima treću koordinatu jednaku
0.
3.2Kleinov model
Disk
\mathbb{D}^{2} možemo promatrati kao skup točaka za koje vrijedi
x_{1}^{2}+x_{2}^{2}\lt 1 u ravnini
x_{3}=1 u
\mathbb{E}^{3}. S obzirom na
f, konika
\left\lbrace F(X)\mid x_{1}^{2}+x_{2}^{2}-x_{3}^{2}=0\right\rbrace projektivne ravnine je slika kružnice
\left\lbrace (x_{1},x_{2})\mid x_{1}^{2}+x_{2}^{2}=1\right\rbrace u
\mathbb{E}^{2}.
Vrijede sljedeće tvrdnje.
|
\bullet |
[\triangleright] Uobičajena projekcija (homogene koordinate) \Pi:\mathbb{R}^{3}\backslash\left\lbrace 0\right\rbrace \rightarrow\mathbb{P}^{2} bijektivno preslikava \mathbb{H}^{2} na \mathbb{D}^{2}. |
|
\bullet |
[\triangleright] Za svaku točku X iz vanjštine konike postoji par jediničnih prostorolikih vektora \left\lbrace r_{Y},-r_{Y}\right\rbrace takav da je F(Y)=F(-Y)=X. Obratno, svaki jednični prostoroliki vektor određuje jednu vanjsku točku konike. |
|
\bullet |
[\triangleright] Točka X pripada konici ako i samo ako je r_{X} svjetloliki vektor. |
|
\bullet |
[\triangleright] Neka je p pravac ravnine \mathbb{H}^{2}. Tada je \Pi p tetiva konike bez krajnjih točaka. |
|
\bullet |
[\triangleright] Ako je p pravac ravnine \mathbb{H}^{2}, onda je \Pi p sadržan u jedinstvenom pravcu \tilde{p} ravnine \mathbb{P}^{2}. Pravci ravnine \mathbb{P}^{2} koji su sekante konike sadrže sliku pravaca ravnine \mathbb{H}^{2}. |
Na taj način dobili smo disk u
\mathbb{P}^{2} (ili
\mathbb{E}^{2}) na kojem možemo promatrati hiperboličku ravninsku geometriju. Hiperboličku geometriju na disku uveo je Klein pa is toga disk definiran na ovaj način zovemo Kleinov disk.
Teorem 9. Svake dvije različite točke Kleinovog modela određuju jedinstveni pravac Kleinovog modela hiperboličke ravnine.
Dokaz: Tvrdnja teorema proizlazi izravno iz prethodno navedenih tvrdnji i Teorema
4.
\Box
3.3Odnos dvaju pravaca
Teorem 10. Neka su
p i
q pravci ravnine
\mathbb{H}^{2} s jediničnim vektorima normale
\vec{e} i
\vec{f} te
\tilde{p} i
\tilde{q} tetive diska
\mathbb{D}^{2} koje su slike pravca
p i
q s obzirom na projekciju
\Pi. Neka su
p' i
q' pravci u
\mathbb{P}^{2} koji sadrže
\tilde{p} i
\tilde{q}. Tada vrijedi:
|
(1) |
Pravci p i q se sijeku ako i samo ako se p' i q' sijeku u unutrašnjosti \mathbb{D}^{2}. |
|
(2) |
Pravci p i q su paralelni ako i samo ako se p' i q' sijeku na rubu od \mathbb{D}^{2}. |
|
(3) |
Pravci p i q su ultraparalelni ako i samo ako se p' i q' sijeku u vanjštini od \mathbb{D}^{2}. |
Dokaz: Svakom pravcu
p ravnine
\mathbb{H}^{2} na jedinstven način pridružen je pravac
\tilde{p} u
\mathbb{D}^{2}, odnosno pravac
p' u
\mathbb{P}^{2}. Dakle, dovoljno je provjeriti sijeku li se pravci
p' i
q' u unutrašnjosti diska. Iz uvjeta da se pravci
p i
q sijeku, prema Teoremu
6 oni se sijeku u jedinstvenoj točki čiji radijvektor je proporcionalan vektoru
\vec{e}\times_{b}\vec{f}. Iz Definicije
5 znamo da je
b(\vec{e}\times_{b}\vec{f},\vec{e}\times_{b}\vec{f})\lt 0, što određuje točku u unutrašnjosti
\mathbb{D}^{2}.
Analogno se dokazuju i ostale tvrdnje.
\Box
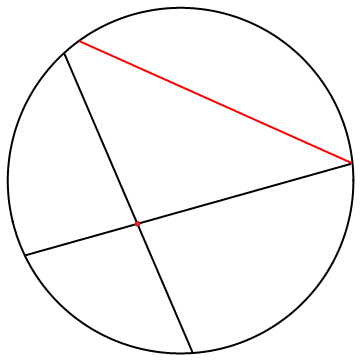
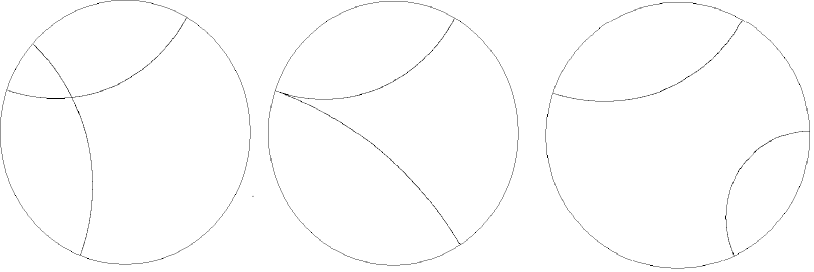
Slika
5 prikazuje moguće odnose dvaju pravaca Kleinovog modela i to redom: pravce koji se sijeku, paralelne pravce te ultraparalelne pravce.
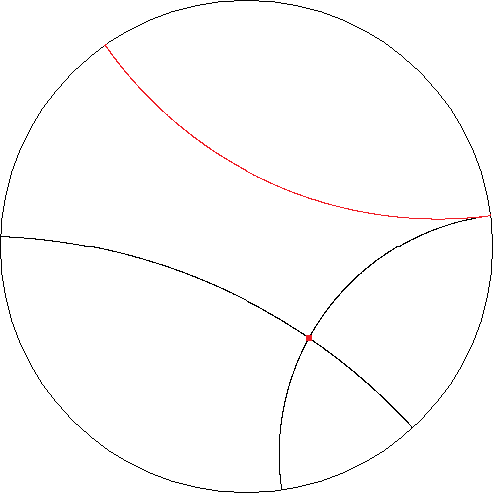
Slika
6 prikazuje aksiom hiperboličke geometrije u Kleinovom modelu hiperboličke ravnine.
4Model hiperboličke ravnine na hemisferi
Uz Kleinov model, predstavit ćemo model hiperboličke ravnine na hemisferi dobiven na sljedeći način.
|
(1) |
Neka je dana sfera čije se središte podudara sa središtem diska \mathbb{D}^{2}, a čiji se ekvator poklapa s rubom diska \mathbb{D}^{2}. |
|
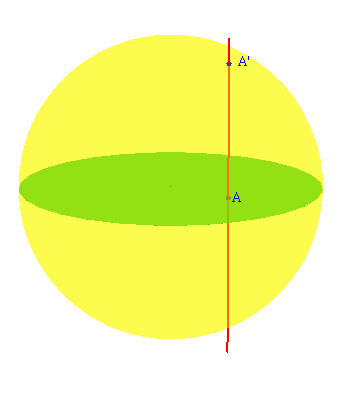
(2) |
Neka je p pravac koji sadrži točku A i okomit je na ekvatorijalnu ravninu. |
|
(3) |
Točku u kojoj pravac p siječe gornju hemisferu označimo s A'. |
Opisani postupak prikazan je na Slici
7.
Pridružujući svakoj točki
A Kleinovog modela točku
A' na opisani način, zaključujemo da se hiperbolička geometrija može promatrati na hemisferi. Kroz navedene korake opisana je bijektivna korespondencija između modela hemisfere i Kleinovog modela hiperboličke ravnine, a s time je uspostavljena i bijektivna korespondencija modela hemisfere i modela hiperboloida.
Pogledajmo sad kako izgledaju pravci u modelu hemisfere. Neka je
\overline{AB} tetiva diska
\mathbb{D}^{2}. Tada
\overline{AB} predstavlja pravac u Kleinovom modelu. Tetivi
\overline{AB} jednoznačno odgovara polukružnica na gornjoj hemisferi dobivena sjecištem ravnine okomite na ekvatorijalnu ravninu koja sadrži tetivu
\overline{AB} i gornje hemisfere. Zaključujemo, pravci hiperboličke ravnine u modelu hemisfere su slike pravaca Kleinovog modela, odnosno polukružnice na gornjoj hemisferi (Slika
8).
Teorem 11. Svake dvije različite točke modela hemisfere hiperboličke ravnine određuju jedinstveni pravac modela hemisfere hiperboličke ravnine.
Dokaz: Neka su
A i
B dvije različite točke modela hemisfere, odnosno dvije točke na gornjoj hemisferi. Tada postoje točke
A' i
B' Kleinovog modela hiperboličke ravnine takve da je
A slika točke
A' i
B slika točke
B'. Prema Teoremu
9, točke
A' i
B' određuju jedinstveni pravac Kleinovog modela. Slika tog pravca bit će pravac modela hemisfere hiperboličke ravnine koji sadrži točke
A i
B.
\Box
4.1Odnos dvaju pravaca
S obzirom na vezu između pravaca Kleinovog modela i pravaca modela hemisfere možemo zaključiti da će se pravci u modelu hemisfere sjeći ako i samo ako su oni slike pravaca koji se sijeku u Kleinovom modelu, a time slike pravca koji se sijeku i u
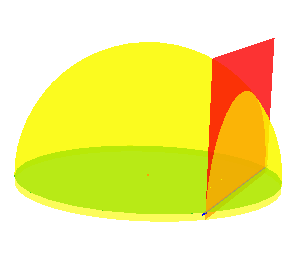
\mathbb{H}^{2}. Analogno, dva pravca modela hemisfere bit će paralelni ako i samo ako su oni slike paralelnih pravaca Kleinovog modela te će biti ultraparalelni ako i samo ako su oni slike ultraparalelnih pravaca. Na Slici
9 prikazani su pravci modela hemisfere koji se sijeku, paralelni pravci te ultraparalelni pravci.
Prikažimo situaciju opisanu aksiomom hiperboličke geometrije i u ovom modelu (Slika
10).
5Poincareov model hiperboličke ravnine
5.1Uvod
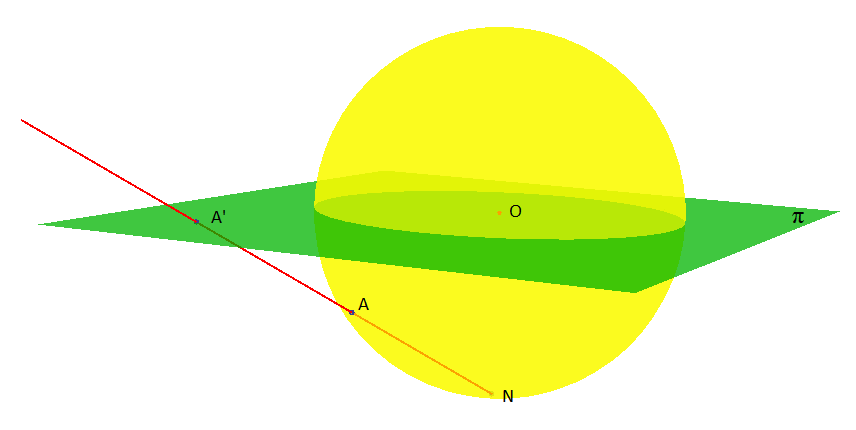
Definicija 12. Neka je S sfera sa središtem u O. Neka je N bilo koja točka sfere i \Pi ravnina koja sadrži točku O i koja je okomita na pravac ON. Stereografska projekcija točke N na ravninu \Pi je preslikavanje koje svaku točku A, koja nije N, sa sfere preslika u točku A' dobivenu kao sjecište ravnine \Pi i pravca NA.
Stereografska projekcija prikazana je na Slici
11.
Napomena: ukoliko promatramo stereografsku projekciju s jedinične sfere čije je središte u ishodištu koordinatnog sustava, uobičajeno je za točku
N uzeti ili točku
(0,0,-1) (južni pol) ili točku
(0,0,1) (sjeverni pol), a za ravninu
\Pi ravninu čija je jednadžba
x_{3}=0 (ekvatorijalna ravnina). Promatrat ćemo stereografsku projekciju s obzirom na južni pol.
Stereografska projekcija transformira pravac i kružnicu u pravac i kružnicu.
5.2Poincareov model
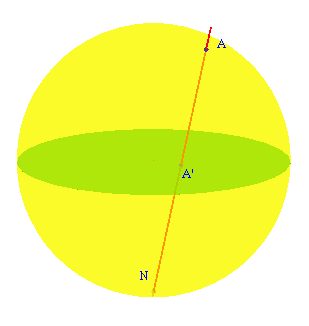
Uz modele koje smo do sada naveli, predstavit ćemo još jedan važan model hiperboličke ravnine ”konstruiran” iz modela hemisfere na sljedeći način. Neka je točka
A točka modela hemisfere (tj. točka na gornjoj polutki sfere čije se središte podudara sa podudara sa središtem diska
\mathbb{D}^{2}, a čiji se ekvator poklapa s rubom diska
\mathbb{D}^{2}). Točki
A na jedinstven je način stereografskom projekcijom pridružena točka
A'. Opisani postupak prikazan je na Slici
12.
Pridružujući svakoj točki
A modela hemisfere točku
A' na opisani način dobivamo transformaciju ekvatorijalnog diska. Model hiperboličke ravnine dobiven na ovaj način zove se Poincareov model diska.
Pogledajmo sad kako izgledaju pravci u Poincareovom modelu hiperboličke ravnine. Neka je
AB polukružnica na gornjoj hemisferi. Tada
AB predstavlja pravac u modelu hemisfere. Stereografska projekcija te polukružnice s obzirom na južni pol sfere na ekvatorijalnu ravninu je luk kružnice okomite na rub diska. Zaključujemo, pravci hiperboličke ravnine u Poincareovom modelu su slike pravaca modela hemisfere, odnosno lukovi kružnica okomitih na rub diska (Slika
13).
Napomenimo, ukoliko je pravac modela hemisfere polukružnica maksimalnog promjera (promjera sfere), tada je njegova slika, pravac u Poincareovom modelu, promjer diska.
Teorem 13. Svake dvije različite točke Poincareovog modela hiperboličke ravnine određuju jedinstveni pravac Poincareovog modela hiperboličke ravnine.
Dokaz: Neka su
A i
B dvije različite točke Poincareovog modela hiperboličke ravnine. Tada postoje točke
A' i
B' modela hemisfere takve da je
A slika točke
A' i
B slika točke
B'. Prema Teoremu
11, točke
A' i
B' određuju jedinstveni pravac modela hemisfere. Slika tog pravca bit će pravac Poincareovog modela hiperboličke ravnine koji sadrži točke
A i
B.
\Box
5.3Odnos dvaju pravaca
S obzirom na stereografsku projekciju i vezu između pravaca modela hemisfere i pravaca Poincareovog modela, možemo zaključiti da će se pravci u Poincareovom modelu hiperboličke ravnine sjeći ako i samo ako su oni slike pravaca koji se sijeku u modelu hemisfere, samim time i slike pravaca koji se sijeku u Kleinovom modelu, a time i slike pravaca koji se sijeku u
\mathbb{H}^{2}. Analogno, dva pravca u Poincareovom modelu bit će paralelni ako i samo ako su oni slike paralelnih pravaca modela hemisfere te će biti ultraparalelni ako i samo ako su oni slike ultraparalelnih pravaca. Na Slici
14 prikazani su pravci u Poincareovom modelu koji se sijeku, paralelni pravci te ultraparalelni pravci.
Prikažimo situaciju opisanu aksiomom hiperboličke geometrije i u Poincareovom modelu (Slika
15).
6Model gornje poluravnine
6.1Uvod
Definicija 14. Preslikavanje
f:\mathbb{C}\rightarrow\mathbb{C} dano formulom
f(z)=\frac{az+b}{cz+d},
gdje su
a, b, c, d\in\mathbb{C} takvi da je
ad-bc\neq0, zovemo linearno-racionalnim preslikavanjem.
Linearno-racionalne transformacije preslikavaju kružnicu ili pravac u kružnicu ili pravac.
6.2Model ravnine
Osim s Kleinovim modelom, modelom hemisfere i Poincareovim modelom, upoznat ćemo se s još jednim modelom hiperboličke ravnine. Poincareov model gornje poluravnine, zvan i samo model gornje poluravnine, može se dobiti pomoću linearno-racionalne transformacije koja preslikava Poincareov disk na gornju poluravninu kompleksne ravnine koja sadrži taj disk:
\mathbb{H}=\left\lbrace x+iy\in\mathbb{C}\mid y\gt 0\right\rbrace .
Preslikavanje
f:\mathbb{C}\mapsto\mathbb{C},\ z\mapsto w=i\frac{1+z}{1-z} zadovoljava navedeno svojstvo.
Zaista,
\text{Im}\ w=\text{Re}\left({\frac{1+z}{1-z}}\right)=\frac{1}{2}\left(\frac{1+z}{1-z}+\frac{1+\overline{z}}{1-\overline{z}}\right)=\frac{1-|z|^{2}}{|1-z|^{2}}.
Stoga je
\text{Im}\ w\gt 0 ako i samo ako je
|z|\lt 1. Za granicu (rub) ovog modela uzimamo pravac
\text{Im}\ w=0.
Znamo da linearno-racionalne transformacije preslikavaju pravac u pravac ili kružnicu pa će pravac u modelu gornje poluravnine biti slika pravca Poincareovog modela (diska).
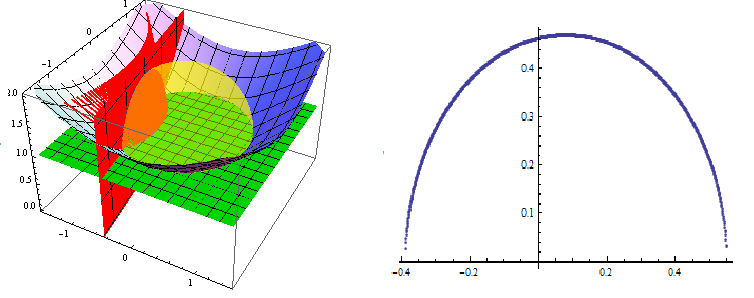
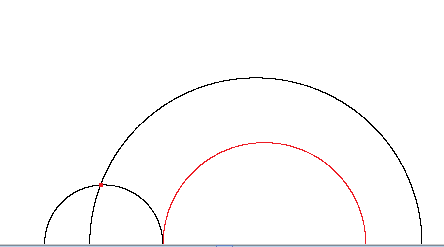
Postoje dva tipa pravca u modelu gornje poluravnine. Prvi je presjek
\mathbb{H} s pravcem kompleksne ravnine okomitim na realnu os u
\mathbb{C}. Drugi tip pravca je presjek
\mathbb{H} s kružnicom kompleksne ravnine kojoj središte pripada realnoj osi. Na slikama
16 i
17 prikazani su pravci Poincareovog modela hiperboličke ravnine (kao slike pravaca modela hemisfere) i njihove slike s obzirom na danu linearno-racionalnu transformaciju, pravci u modelu gornje poluravnine.
Teorem 15. Za svake dvije različite točke P i Q u \mathbb{H} postoji jedinstveni pravac u \mathbb{H} koji ih sadrži.
Dokaz: Dokažimo egzistenciju. Pretpostavimo prvo da je
\text{Re}(P)=\text{Re}(Q). Tada postoji pravac
L kompleksne ravnine definiran kao
L=\left\lbrace z\in\mathbb{C}\mid \text{Re}(P)=\text{Re}(Q)\right\rbrace koji je okomit na realnu os kompleksne ravnine i koji sadrži točke
P i
Q. Tada je
l=\mathbb{H}\cap L pravac u
\mathbb{H} koji sadrži točke
P i
Q. Pretpostavimo sada da je
\text{Re}(P)\neq\text{Re}(Q). Kako pravac kompleksne ravnine koji sadrži
P i
Q nije okomit na realnu os, trebamo konstruirati kružnicu kompleksne ravnine kojoj središte pripada realnoj osi i koja sadrži točke
P i
Q. Neka je
L_{pq} dužina kompleksne ravnine čije su krajnje točke
P i
Q i neka je
k simetrala dužine
L_{pq}. Tada
k sadrži središte svake kružnice kompleksne ravnine koja sadrži točke
P i
Q. Kako
P i
Q imaju različite realne dijelove,
k nije paralelna s realnom osi pa slijedi da
k siječe realnu os u jedinstvenoj točki
C. Neka je
A kružnica kompleksne ravnine čije središte je točka
C, a čiji polumjer je
|P-C|. Tada
A sadrži točku
P. Kako
k sadrži točku
C,
|C-P|=|C-Q| pa slijedi da
A sadrži točku
Q. Tada je
l=A\cap\mathbb{H} pravac modela gornje poluravnine koji sadrži točke
P i
Q. Jedinstvenost pravca
l slijedi iz jedinstvenosti
L i
A u kompleksnoj ravnini. Time je ovaj teorem dokazan.
\Box
6.3Odnos dvaju pravaca
Kao i kod ostalih modela hiperboličke ravnine, postoje tri moguća odnosa dvaju pravaca.
|
\bullet |
[\triangleright] Dva se pravca modela gornje poluravnine sijeku ako se u \mathbb{H} sijeku kružnice (pravci) koji ih predstavljalju. Također, dva pravca modela gornje poluravnine koja se sijeku slika su pravaca Poincareovog modela diska koji se sijeku (a time i slika pravaca koji se sijeku u modelu hemisfere, Kleinovom modelu te u \mathbb{H}^{2}). |
|
\bullet |
[\triangleright] Dva su pravca modela gornje poluravnine paralelna ako se sijeku na rubu od \mathbb{H}. Također, paralelni pravci modela gornje poluravnine slika su paralelnih pravaca Poincareovog modela. |
|
\bullet |
[\triangleright] Dva su pravca modela gornje poluravnine ultraparalelna ako nemaju zajedničkih točaka u \mathbb{H} niti na rubu od \mathbb{H}. Također, ultraparalelni pravci modela gornje poluravnine slika su ultraparalelnih pravaca Poincareovog modela. |
Na Slici
18. prikazani su pravci u modelu gornje poluravnine koji se sijeku, paralelni te ultraparalelni pravci.
Prikažimo aksiom hiperboličke geometrije u modelu gornje poluravnine (Slika
19).
Bibliografija
|
[1] |
Anderson: Hyperbolic Geometry, second edition, Springer-Verlag, London, 2005. |
|
[2] |
Cannon, Floyd, Kenyon, Parry: Hyperbolic Geometry, Volume 31, Flavors of Geometry MSRI Publications |
|
[3] |
Euclides, Elementi 1-6, prevela M. Hudoletnjak Grgić, Kruzak d.o.o., Zagreb, 1999. |
|
[4] |
Prasolov, V. V., Tikhomirov, V. M.: Geometry, Volume 200, American Mathematical Society, 1997. |
|
[5] |
Ryan, P. J.: Euclidean and non-Euclidean Geometry – an Analytic Approach, Cambridge Univ. Press, Cambridge, 1991. |
|
[6] |
Stahl, S: The Poincare Half Plane; a getaway to modern geometry, Jones and Bartlett Publishers International, London, 1993. |