Sažetak
Promatramo elipse i hiperbole koje su definirane s tri ili više fokusa. U prvom dijelu rada pokazat ćemo kako zapisati krivulje s dva i tri fokusa bez korijena samo pomoću standardnih operacija, kvadriranja, etc. Drugi dio rada bit će posvećen podijeli pa vladaj algoritmu kojim crtamo ovakve krivulje direktno po definiciji. U trećem dijelu rada navest ćemo neke primjere krivulja s tri, četiri ili više fokusa te dati njihov grafički prikaz.
1Uvod
Već u našim osnovnoškolskim danima, negdje u davnom petom razredu, susreli smo se s prvom krivuljom drugog reda čiju ćemo definiciju morati znati napamet, za ocjenu. Naš nastavnik je tu krivulju nazvao kružnicom i definirao ju kao skup svih točaka jednako udaljenih od jedne čvrste točke, koju vrlo često i simbolički, nazivamo središte. Nekoliko godina kasnije, dolazimo u srednjoškolske klupe i upoznajemo se s nekim drugim krivuljama drugog reda. Saznajemo što su elipsa, hiperbola i parabola. Znamo, naravno, laički rečeno, te se krivulje nazivaju krivuljama drugog reda upravo zato što je najveća potencija koju njihove varijable sadrže upravo broj dva. No, po čemu su se ipak ove tri krivulje razlikovale od kružnice? Kružnica je, imala samo jedno središte. Elipsa je, kao i hiperbola, definirana pomoću dvije čvrste točke, koje nazivamo fokusi. Parabola je pak bila definirana jednim pravcem i jednim fokusom. Prisjetimo se točnijih definicija. Rekli smo kako je elipsa skup svih točaka ravnine čiji je zbroj udaljenosti od dva fokusa jednak nekom prethodno zadanom broju (kod kružnice bi to bio polumjer). Hiperbola je, pak, skup svih točaka ravnine čija je apsolutna vrijednost razlike udaljenosti od dva fokusa jednaka nekom prethodno zadanom broju. Ovdje je izuzetak parabola jer se ona definira kao skup svih točaka ravnine koje su jednako udaljene od zadanog pravca i fokusa te ju stoga nećemo uključiti u naša razmatranja. Kružnica bi se, naravno, mogla nazvati specijalnim slučajem elipse ukoliko bismo imali zadana dva fokusa jednakih koordinata (ako bi se preklapali). No, mi želimo sada promatrati ovako predstavljenu stvar jedan korak dalje. Što ako bi definirali elipsu i hiperbolu općenitije? Što ako bismo riječ dva u gornjim definicijama elipse zamijenili riječju tri? Što ako bismo htjeli promatrati n fokusa? Definirajmo multifokalnu elipsu.
Definicija 1. Neka je n\in\mathbb{N}, S_{n}=\left\lbrace F_{i}:\ F_{i}\left(x_{i},y_{i}\right)\in\mathbb{R}^{2},\ i=1,\ldots,n\right\rbrace i r\in\mathbb{R}^{+}. Tada multifokalnom elipsom nazivamo skup svih točaka T\left(x,y\right) koje zadovoljavaju jednadžbu
\sum_{i=1}^{n}{d\left(F_{i},T\right)}=r,
tj. skup svih točaka ravnine čiji je zbroj udaljenosti od n unaprijed zadanih točaka (n fokusa) upravo r.
Primjedba 2. Napomenimo samo kako ćemo koristiti skraćeni zapis udaljenosti d\left(T_{1},T_{2}\right) (koja može i ne mora biti euklidska), za točke T_{1}\left(x_{1},y_{1}\right) i T_{2}\left(x_{2},y_{2}\right) u ravnini. Za potrebe našeg rada podrazumijevat ćemo (osim kada je drugačije naznačeno):
d\left(T_{1},T_{2}\right)=\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}.\
Definirajmo i multifokalnu hiperbolu (primijetimo da se definicija multifokalne hiperbole razlikuje od definicije multifokalne elipse po tome što ispred barem jednog člana u jednadžbi imamo negativan predznak).
Definicija 3. Neka je zadan skup S_{n}=\left\lbrace F_{i}:\ F_{i}\left(x_{i},y_{i}\right)\in\mathbb{R}^{2},\ i=1,\ldots,n\right\rbrace, gdje je n\in\mathbb{N}\backslash\left\lbrace 1\right\rbrace i neka je r\in\mathbb{R}^{+}_{0}. Definiramo skupove S^{+} i S^{-} tako da vrijedi S^{+}\cup S^{-}=S_{n}, S^{+}\neq\emptyset, S^{-}\neq\emptyset i S^{+}\cap S^{-}=\emptyset. Tada multifokalnom hiperbolom nazivamo skup svih točaka T\left(x,y\right) koje zadovoljavaju jednadžbu
\left|\sum_{i\in S^{+}}{d\left(F_{i},T\right)}-\sum_{i\in S^{-}}{d\left(F_{i},T\right)}\right|=r,
tj. skup svih točaka ravnine čija je apsolutna vrijednost od zbroja udaljenosti točaka iz S^{+} i razlike udaljenosti točaka iz S^{-} (ukupno n fokusa iz S^{+} i S^{-}) jednaka upravo r.
2Red krivulje
U ovom dijelu rada naš je cilj pokušati standardnim (bolje rečeno srednjoškolskim) metodama riješiti se korijena u gornjim jednadžbama. Dopuštamo samo potenciranje i prebacivanje članova s jedne strane jednakosti na drugu. Pokazat ćemo kako je to moguće napraviti sve do krivulja zadanih pomoću tri fokusa. No, za početak, na jednostavnijim primjerima za kružnicu i elipsu (i hiperbolu) pogledajmo kako naša metoda funkcionira. Zanemarit ćemo sve restrikcije koje se mogu pojaviti kvadriranjem, et similis. Zanima nas samo čista forma algebarskog izraza. Radi lakšeg izvoda, udaljenost d\left(F_{i},T\right), gdje su F_{i}\left(x_{i},y_{i}\right) i T\left(x,y\right) točke u ravnini, kraće ćemo označavati s d_{i}. Uočimo kako d_{i} u sebi sadrži korijen (kako je i prethodno definirana euklidska udaljenost) te kako, ako bi se htjeli riješiti korijena, svaki d_{i} mora biti parne potencije, npr. najmanje d_{i}^{2} (izuzevši trivijalnu d_{i}^{0}=1 koja nam nije od koristi), a to je izraz koji je u stvari jednak
d_{i}^{2}=\left(x-x_{i}\right)^{2}+\left(y-y_{i}\right)^{2}.
Primijetimo kako će, po uzoru na gornji primjer, u kojem je najveća potencija sadržana na x ili y varijabli drugog stupnja (naravno sve potencije moraju biti cjelobrojne), stupanj izraza d_{i}^{2k},\ k\in\mathbb{N} biti 2k-tog reda.
Primjer 4. Kružnica je, mogli bismo sada reći, multifokalna elipsa kada je n=1 (skup S_{1}); zadan je samo jedan fokus (koji nazivamo središte) u točki F_{1}(x_{1},y_{1}) i r\in\mathbb{R}^{+}. Tada je
S_{1}=\left\lbrace T\left(x,y\right):\ d\left(F_{1},T\right)=r\right\rbrace .
Riješimo se korijena u izrazu (moramo dobiti d_{1} parne potencije).
Rješenje. Potrebno je kvadrirati samo jedanput želimo li dobiti izraz bez korijena. Tada je d_{1}^{2}=r^{2}; imamo zadanu krivulju drugog reda jer je najveća potencija nad x ili y varijablom jednaka 2.
Primjer 5. Uobičajenu elipsu i hiperbolu definiramo kao multifokalnu elipsu (hiperbolu) za n=2 (skup S_{2}). Tada, ako imamo zadana dva fokusa F_{1}\left(x_{1},y_{1}\right) i F_{2}\left(x_{2},y_{2}\right) te konstantu r\in\mathbb{R}^{+}, možemo generalizirano uzeti
S_{2}=\lbrace T\left(x,y\right):\ \left|d\left(F_{1},T\right)\pm d\left(F_{2},T\right)\right|=r\rbrace .
Zanima nas oblik jednadžbe \left|d_{1}\pm d_{2}\right|=r bez korijena (i d_{1} i d_{2} moraju biti parne potencije).
Rješenje. Kvadrirajmo cijeli izraz. Kvadratom dobivamo uvijek nenegativne vrijednosti pa nam je apsolutna vrijednost sada nepotrebna. Imamo
d_{1}^{2}\pm2d_{1} d_{2}+d_{2}^{2}=r^{2}.
Članovi d_{1}^{2} i d_{2}^{2} su od sada pa nadalje bez korijena te ih možemo prebaciti na desnu stranu i kvadrirati još jedanput kako bismo se riješili korijena u članu \pm2 d_{1} d_{2}.
\pm2d_{1} d_{2}=r^{2}-\left(d_{1}^{2}+d_{2}^{2}\right).
Nakon kvadriranja dobivamo jednadžbu bez korijena:
4d_{1}^{2} d_{2}^{2}=r^{4}-2r^{2}\left(d_{1}^{2}+d_{2}^{2}\right)+\left(d_{1}^{2}+d_{2}^{2}\right)^{2}.
No, radi potpunosti, riješimo se kvadrata na desnoj strani. Tada je:
4d_{1}^{2} d_{2}^{2}=r^{4}-2r^{2}\left(d_{1}^{2}+d_{2}^{2}\right)+d_{1}^{4}+2d_{1}^{2} d_{2}^{2}+d_{2}^{4}.
Prebacimo li član s lijeve strane na desnu stranu imamo
r^{4}-2r^{2}\left(d_{1}^{2}+d_{2}^{2}\right)+d_{1}^{4}-2d_{1}^{2} d_{2}^{2}+d_{2}^{4}=0.
Zapišemo posljednja tri člana s lijeve strane kao kvadrat binoma:
(1)
r^{4}-2r^{2}\left(d_{1}^{2}+d_{2}^{2}\right)+\left(d_{1}^{2}-d_{2}^{2}\right)^{2}=0.
Promotrimo bolje izraz d_{1}^{2}-d_{2}^{2}:
d_{1}^{2}-d_{2}^{2}=\left(x-x_{2}\right)^{2}+\left(y-y_{2}\right)^{2}-\left(x-x_{2}\right)^{2}-\left(y-y_{2}\right)^{2}.
Lako je uočiti kako će se članovi x^{2} i y^{2} pokratiti te će ostati samo konstante (čije nam potencije nisu bitne) i članovi koji uz sebe sadrže x ili y. Tako je u jednadžbi (1) izraz u zagradi \left(d_{1}^{2}-d_{2}^{2}\right)^{2} prvog reda, a nakon kvadriranja samo drugog reda. Druge dvije najveće potencije su u d_{1}^{2}+d_{2}^{2} i one su također drugog reda. Tako smo pokazali kako su i elipsa i hiperbola krivulje drugog reda. No, tu smo imali sreće upravo zbog pokraćivanja kvadrata u izrazu d_{1}^{2}-d_{2}^{2}. Nažalost, već u elipsi i hiperboli s tri fokusa, takvo nešto se neće dogoditi te izraz postaje iznimno kompliciraniji.
Primjer 6. Promotrimo elipsu s tri fokusa,
S_{3}=\left\lbrace T\in\mathbb{R}^{2}: d\left(F_{1},T\right)+d\left(F_{2},T\right)+d\left(F_{3},T\right)=r\right\rbrace .
Analogno prethodnim primjerima, pokušajmo se riješiti korijena.
Rješenje. Prebacimo d_{3} na desnu stranu i kvadrirajmo izraz d_{1}+d_{2}=r-d_{3}; tako je sada
d_{1}^{2}+2d_{1} d_{2}+d_{2}^{2}=r^{2}-2r d_{3}+d_{3}^{2}.
Preostala su dva člana čijih se korijena moramo riješiti, a to su 2d_{1} d_{2} i -2r d_{3}; prebacimo ih na lijevu stranu, ostale članove na desnu:
2d_{1} d_{2}+2r d_{3}=r^{2}+d_{3}^{2}-d_{1}^{2}-d_{2}^{2}.
Kvadriranjem dobivamo
4d_{1}^{2} d_{2}^{2}+8r d_{1} d_{2} d_{3}+4r^{2} d_{3}^{2}=\left(\left(r^{2}-d_{1}^{2}\right)+\left(d_{3}^{2}-d_{1}^{2}\right)\right)^{2}.
Prebacimo sve članove s lijeve strane na desnu, osim srednjeg člana:
8r d_{1} d_{2} d_{3}=\left(\left(r^{2}-d_{1}^{2}\right)+\left(d_{3}^{2}-d_{1}^{2}\right)\right)^{2}-4\left(r^{2} d_{3}^{2}+d_{1}^{2} d_{2}^{2}\right).
Opet kvadriramo i imamo konačnu jednadžbu
64r^{2} d_{1}^{2} d_{2}^{2} d_{3}^{2}=\left(\left(\left(r^{2}-d_{1}^{2}\right)+\left(d_{3}^{2}-d_{1}^{2}\right)\right)^{2}-4\left(r^{2} d_{3}^{2}+d_{1}^{2} d_{2}^{2}\right)\right)^{2}.
Primijetimo kako s lijeve strane imamo umnožak od tri izraza, a svaki od njih je drugog reda. Tako je ukupan red s lijeve strane šest. S desne strane pak imamo opet pokraćivanje kao kod elipse jer izraz d_{3}^{2}-d_{1}^{2} postaje prvog reda; no, to ipak ne mijenja ništa jer kvadrirajući i r^{2}-d_{1}^{2} dobivamo izraz sa zasad najvećim redom, a to je d_{1}^{4} (izraz četvrtog reda). Drugi član u cijeloj desnoj zagradi je pak isto tako četvrtog reda jer je d_{1}^{2} d_{2}^{2} umnožak dva izraza drugog reda. Stoga, kvadrirajući cjelokupnu desnu zagradu, imamo dva člana najvećeg reda, a to su d_{1}^{8} i d_{1}^{4} d_{2}^{4}; oba člana su osmog reda pa smo pokazali kako je elipsa s tri fokusa krivulja osmog reda. No, što je s hiperbolom definiranom pomoću tri fokusa? Hiperbola naravno mora sadržavati i apsolutnu vrijednost pa je potrebno još jedno kvadriranje. Pokažimo da je ipak i hiperbola definirana pomoću tri fokusa također krivulja osmog reda! Bez smanjenja općenitosti pretpostavimo da je negativan predznak uz d_{2}:
\left|d_{1}-d_{2}+d_{3}\right|=r.
Kvadriranjem bi dobili
d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+2d_{1} d_{3}-2d_{1} d_{2}-2d_{3} d_{2}=r^{2}.
Prebacimo sve članove osim -2d_{1} d_{2}-2d_{3} d_{2} na desnu stranu:
-2d_{1} d_{2}-2d_{3} d_{2}=\left(r^{2}-\left(d_{1}^{2}+d_{2}^{2}+d_{3}^{2}\right)\right)-2d_{1} d_{3}.
Jednostavnosti radi, označimo t_{2}=r^{2}-\left(d_{1}^{2}+d_{2}^{2}+d_{3}^{2}\right) i pamtimo da je t_{2} izraz drugog reda. Kvadriramo opet i sada je
4d_{1}^{2} d_{2}^{2}+8d_{1} d_{2}^{2} d_{3}+4d_{3}^{2} d_{2}^{2}=t_{2}^{2}-4t_{2} d_{1} d_{3}+4d_{1}^{2} d_{3}^{2}.
Prebacimo -4t_{2} d_{1} d_{3} na lijevu stranu, a 4d_{1}^{2} d_{2}^{2}+4d_{3}^{2} d_{2}^{2} na desnu stranu. Imamo
8d_{1} d_{2}^{2} d_{3}+4t_{2} d_{1} d_{3}=t_{2}^{2}+4\left(d_{1}^{2} d_{3}^{2}-d_{1}^{2} d_{2}^{2}-d_{3}^{2} d_{2}^{2}\right).
Kvadriramo.
64d_{1}^{2} d_{2}^{4} d_{3}^{2}+64t_{2} d_{1}^{2} d_{2}^{2} d_{3}^{2}+16t_{2}^{2} d_{1}^{2} d_{3}^{2}=\left(t_{2}^{2}+4\left(d_{1}^{2} d_{3}^{2}-d_{1}^{2} d_{2}^{2}-d_{3}^{2} d_{2}^{2}\right)\right)^{2}.
Prva dva člana s lijeve strane su osmog reda. Kvadriranjem zagrade s desne strane dobivamo izraz najvećeg reda, a to je t_{2}^{4}, koji je, isto tako, osmog reda. Time smo pokazali i da je hiperbola s tri fokusa osmog reda. Možemo li istim postupkom doći i do jednadžbe krivulje definirane s četiri ili više fokusa (tako da ne sadrže korijene)? Taj problem ćemo za sad ostaviti sa strane jer se povećavanjem broja fokusa povećava entropija među članovima jednadžbe, a time se otvaraju i vrata za mnoge druge mogućnosti rješavanja korijena. Za sada, intuitivno, ovakvim gornjim naivnim postupkom, možemo olako reći kako nije moguće. Isto tako, bilo bi krajnje besmisleno pokušati gornji izraz zapisati pomoću x i y varijabli jer je jednadžba jednostavno prekompleksna za takav pothvat, a broj članova je daleko veći nego u slučaju elipse; možemo procijeniti taj broj ako nam je dopušteno ići do osme potencije. Imamo 16 različitih članova za kombinaciju (x,\ldots,x^{8},y,\ldots,y^{8} u parovima), a to je 8\cdot 8=64. Uzmemo li u obzir i slobodan član, to otvara mogućnost za čak 65 članova. Čak i kada bismo zapisali sve te članove, iz njih ne bismo mogli vidjeti ništa što bi nam dalo nekakvu korisnu informaciju o krivulji. Ljepota, čini se, leži u jednostavnosti.
3Algoritam
Cilj ovog rada je zapravo demonstrirati, pokazati primjere krivulja koje možemo dobiti generalizacijom definicija elipse i hiperbole. No, kako ne možemo čak ni za elipsu osmisliti nekakvu jednostavnu jednadžbu za direktno izračunavanje, moramo se poslužiti raznim trikovima koje nam rad na računalu i malo razmišljanja može pružiti. Ideja je ostaviti definicije elipse i hiperbole takve kakve jesu, kao skup točaka čiji je zbroj i/ili razlika udaljenosti od fokusa neki zadan broj i uopće ne pokušavati rješavati se korijena. Ideja je ići od točke do točke na nekom području u ravnini i gledati kolika je vjerojatnost njenog pojavljivanja unutar skupa (elipse, hiperbole ili slično). No, ići od jedne do druge točke, čak i ako je u pitanju prikaz na monitoru rezolucije samo 800\times 600 pixela, je veoma dugotrajan posao. Stoga koristimo drugačiji pristup, podijeli pa vladaj algoritam koji radi na sljedeći način: podijelimo ekran na četiri kvadranta. U svakom od ta četiri kvadranta promatramo samo jednu točku. Računamo udaljenost te točke od fokusa i uz predodređenu preciznost gledamo postoji li mogućnost nalaženja još točki u tom kvadrantu. Ukoliko imamo dovoljan razlog vjerovati kako unutar kvadranta nećemo naći više točki, taj kvadrant zaboravljamo i idemo dalje. Ukoliko mislimo kako bi unutar nekog kvadranta moglo postojati još točki koje zadovoljavaju uvjete skupa tada taj kvadrant dijelimo dalje na četiri kvadranta i postupamo kao i za prošla četiri kvadranta i tako dalje do određene profinjenosti.
Sama struktura algoritma ovdje nije problem. Dijelimo ravninu na četiri dijela i radimo to proizvoljno dugo. Problem je odrediti parametar kojim određujemo udaljenost. Kada imamo euklidsku udaljenost - stvar je jasna. No, kada podijelimo ravninu na četiri dijela, uzmimo za primjer, ravninu veličine 256\times 256. Tada možemo promatrati četiri kvadranta veličine 128\times 128. Imamo četiri točke koje određuju te kvadrante, a to su (0,0), (0,128), (128,0) i (128,128). Treba izračunati zbroj i/ili razliku udaljenosti tih točki od fokusa i vidjeti jesu li one otprilike jednake nekom broju r (iz definicije elipse i hiperbole). Problem je u tome što prelaskom na ovakav diskretan sustav gubimo informacije o udaljenostima. Intuitivno, mogli smo pretpostaviti kako će se još točki nalaziti u kvadrantu (točka T_{i}, gdje je i=1,2,3,4) ako vrijedi \left|\delta\left(T_{i}\right)-r\right|\leq p d\sqrt{2}, gdje je \delta\left(T_{i}\right) funkcija koja vraća zbroj i/ili razliku udaljenosti točke od svih zadanih fokusa. Također, p je parametar kojim određujemo preciznost, a d je dimenzija kvadranta (u našem slučaju 128). Nekako smo smatrali kako ćemo odabirom p=1 pokupiti sve potrebne točke, no ispostavilo se kako to vrijedi samo za mali broj fokusa. Povećanjem broja fokusa, gubimo više točki; stoga intuitivno razmišljamo kako zbog gubitka podataka ne možemo tako olako uspoređivati udaljenosti te moramo uzeti u obzir koliko smo njih zbrojili i/ili oduzeli. Kada je zbrajanje u pitanju, eksperimentalno se pokazalo da je dovoljno uzeti za p broj fokusa ako je u pitanju samo zbrajanje. Ako je u pitanju i oduzimanje neke udaljenosti, sustav postaje kaotičniji i teže je odrediti parametar p (ako nam je optimalnost nužna). Ipak, trivijalno je za vidjeti da, što dublje idemo u rekurziju (što dulje izvršavamo algoritam), to nam p smije biti veći; kupit ćemo više točki pri "silasku", ali ćemo zbog duljine "silaska" poprilično profiniti izbor točki.
4Primjeri
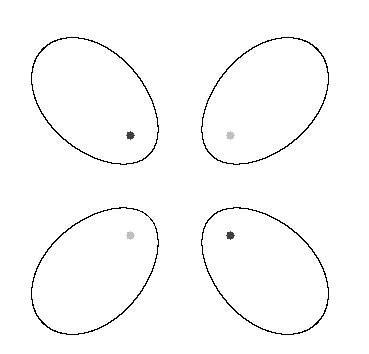
Posljednji dio rada posvećen je isključivo konkretnim primjerima nekih krivulja dobivenih korištenjem definicije multifokalne elipse i hiperbole. U prvom primjeru vidjet ćemo kakve sve krivulje možemo dobiti ako fokusi čine vrhove jednakostraničnog trokuta (ako je udaljenost između svaka dva fokusa jednaka). U drugom primjeru pokazat ćemo primjere krivulja gdje fokusi čine vrhove kvadrata, a u trećem neke "slučajno dobivene" krivulje. Primijetimo kako su fokusi na slikama označeni sivom bojom - tamno sivom ako je uz udaljenost točke do tog fokusa pozitivan predznak, a svijetlo sivom ako je negativan.
Primjer 1. Neka su zadani fokusi sa sljedećim koordinatama:
\bullet
F_{1}\left(200,366.6\right),
\bullet
F_{2}\left(150,250\right),
\bullet
F_{3}\left(250,250\right).
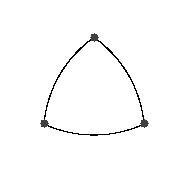
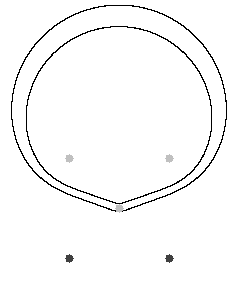
Na Slici 1. prikazani su rezultati dobiveni korištenjem sljedećih jednadžbi (pod (a) i (b) definirane su hiperbole s tri fokusa, a pod (c) i (d) elipse s tri fokusa):
\bullet
[(a)]H_{1}=\left\lbrace T(x,y)\in\mathbb{R}^{2}:\ \left|d\left(T,F_{2}\right)+d\left(T,F_{3}\right)-d\left(T,F_{1}\right)\right|=0\right\rbrace,
\bullet
[(b)]H_{2}=\left\lbrace T(x,y)\in\mathbb{R}^{2}:\ \left|d\left(T,F_{3}\right)-d\left(T,F_{1}\right)-d\left(T,F_{2}\right)\right|=4\right\rbrace,
\bullet
[(c)]E_{1}=\left\lbrace T(x,y)\in\mathbb{R}^{2}:\ d\left(T,F_{1}\right)+d\left(T,F_{2}\right)+d\left(T,F_{3}\right)=200\right\rbrace,
\bullet
[(d)]E_{2}=\left\lbrace T(x,y)\in\mathbb{R}^{2}:\ d\left(T,F_{1}\right)+d\left(T,F_{2}\right)+d\left(T,F_{3}\right)=173.19\right\rbrace.
Ne ulazeći u dublju analizu ovakvih figura, prepuštamo čitatelju za provjeru kako se u krivulji na slici 1. pod (a) zapravo radi o luku trokutu opisane kružnice; zatim, kako se u krivulji pod (c) radi o uniji lukova kružnica povučenih iz svakog pojedinačnog vrha trokuta te kako se u točki pod (d) zapravo radi o središtu trokutu opisane i upisane kružnice (a i o težištu i ortocentru jer imamo vrhove jednakostraničnog trokuta).
Primjer 2. Neka su zadani fokusi sa sljedećim koordinatama:
\bullet
F_{1}\left(150,250\right),
\bullet
F_{2}\left(250,250\right),
\bullet
F_{3}\left(250,350\right),
\bullet
F_{4}\left(150,350\right).
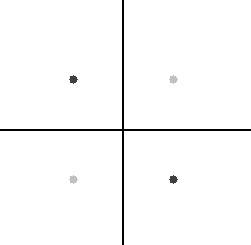
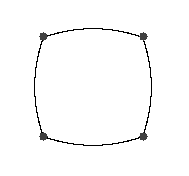
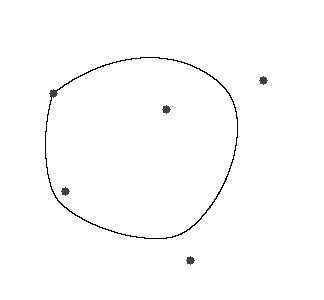
Na Slici 2. prikazani su rezultati dobiveni korištenjem sljedećih jednadžbi (pod (a) i (b) definirane su hiperbole s četiri fokusa, a pod (c) i (d) elipse s četiri fokusa):
\bullet
[(a)]H_{1}=\left\lbrace T(x,y)\in\mathbb{R}^{2}:\ \left|d\left(T,F_{4}\right)+d\left(T,F_{2}\right)-d\left(T,F_{3}\right)-d\left(T,F_{1}\right)\right|=0\right\rbrace,
\bullet
[(b)]H_{2}=\left\lbrace T(x,y)\in\mathbb{R}^{2}:\ \left|d\left(T,F_{4}\right)+d\left(T,F_{2}\right)-d\left(T,F_{3}\right)-d\left(T,F_{1}\right)\right|=25\right\rbrace,
\bullet
[(c)]E_{1}=\left\lbrace T(x,y)\in\mathbb{R}^{2}:\ d\left(T,F_{1}\right)+d\left(T,F_{2}\right)+d\left(T,F_{3}\right)+d\left(T,F_{4}\right)=340\right\rbrace,
\bullet
[(d)]E_{2}=\left\lbrace T(x,y)\in\mathbb{R}^{2}:\ d\left(T,F_{1}\right)+d\left(T,F_{2}\right)+d\left(T,F_{3}\right)+d\left(T,F_{4}\right)=282.84\right\rbrace.
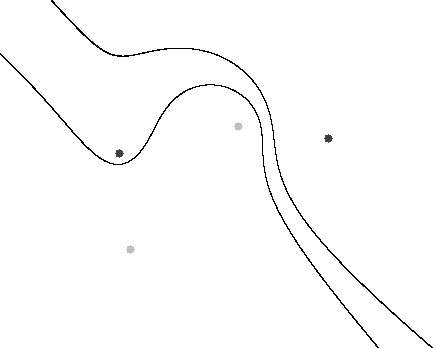
Uzeli smo analogne primjere vrhovima jednakostraničnog trokuta za vrhove kvadrata. Na slici 2. pod (a) možemo primijetiti kako je krivulja sačinjena od dva okomita pravca (polako prelazeći iz stanja u kakvom je pod (b) kada smanjujemo r s 25 na 0); u oba slučaja se radi o hiperboli. Druga dva slučaja su elipse, pod (c) smo uzeli krivulju koja prolazi kroz fokuse, a pod (d) je rezultat jedna točka, a to je sjecište dijagonala (opet prepuštamo čitatelju provjeru o kakvoj se točki radi i kako ona zadovoljava jednadžbu skupa E_{2}). Zanimljivo kako zapravo pod elipsom obično smatramo onu jednu dosadnu krivulju koju radimo kroz srednju školu, ne uzimajući u obzir da elipsa može biti i samo jedna točka ili pak dva okomita pravca! U egzotičnost ovakvih krivulja uvjerit će nas još par idućih primjera multifokalnih elipsi i krivulja prikazanih na slici 3.
5Zaključak
U ovom radu napravili smo kratku obradu općenitijih definicija elipse i hiperbole. Vidjeli smo samo nekoliko primjera od beskonačno mnogo raznih drugačijih postavki, uvjeta i slično. Mogli smo sustave učiniti još kaotičnijim i dodati udaljenosti od nekih pravaca, kružnica, drugih geometrijskih tijela, skupova, funkcija i tako dalje i tako dalje. Također, nije ostavljeno niti dovoljno mjesta u radu za krivulje koje bi mogli dobiti mijenjanjem definicija udaljenosti (mi smo promatrali samo euklidsku udaljenost, a mogli smo dodati u definiciju npr. i trigonometrijske funkcije za eksponencijalno egzotičnije krivulje). No, što više parametara dodajemo, to je teže (i u neku ruku besmislenije) s ovakvim krivuljama raditi, pogotovo algebarski. Stoga smo i koristili numerički algoritam koji divide-and-conquer metodom pronalazi područja u kojima se najvjerojatnije nalaze točke naših krivulja (ovakav algoritam bi se pak mogao bolje iskoristiti u CUDA okružju). Ostaje otvoreno pitanje (što se naših istraživanja tiče), kada i kako se jednadžbe ovakvih krivulja mogu prikazati bez korijena (i ima li to uopće smisla jer se broj članova povećava kvadratno obzirom na red krivulje). Ostaje otvoreno pitanje i kako saznati kojeg će reda biti krivulja bez rješavanja korijena. Ah, bien! Ako dotad autori ovoga rada ne pronađu tražene odgovore, možda se pronađe neki čitatelj koji bi mogao riješiti sve probleme navedene u ovom minijaturnom zaključku! Ako ništa drugo, uvijek je zabavno igrati se sa svim ovim definicijama i promatrati nove rezultate i nove krivulje.{plain}
Bibliografija
[1]
Nie, Jiawang; Parrilo, Pablo A.; and Sturmfels, Bernd. Semidefinite Representation of the k-Ellipse, IMA Volumes in Mathematics and its Applications, Vol. 146, pp. 117-132, 2008
[2]
Cormen, Thomas H.; Leiserson, Charles E. ; Rivest, Ronald L.; and Stein, Clifford. Introduction to Algorithms (Second ed.), MIT Press and McGraw-Hill. pp. 822–848. ISBN 0-262-03293-7, 2001.