O indeksima snage u sustavima glasovanja da-ne
Tomislav Marošević, Marija Šarić
Trg Lj. Gaja 6, HR-31000 Osijek, Hrvatska
Ključne riječi: sustavi glasovanja da-ne, indeksi snage, Shapley-Shubik indeks, Banzhaf indeks, Johnston indeks, Deegan-Packel indeks
Jedan od vrlo važnih pojmova političke znanosti jest snaga. Promotrimo snagu glasovanja u sustavima glasovanja da-ne, gdje glasači (tj. "igrači") imaju određeni utjecaj na donošenje nekih odluka. U smislu formalnog glasovanja, smatra se da je potrebna apsolutna većina za donošenje odluka odnosno određena kvota. Stoga, za prihvaćanje odluka (zakona) treba promatrati pobjedničke koalicije.
Radi kvantitativnog mjerenja snage glasovanja odgovarajućih igrača (primjerice, stranaka u skupštini), predloženi su određeni indeksi glasačke ili političke snage (http://homepages.warwick.ac.uk/~ecaae/links.html, http://powerslave.utu.fi/ ). Neki poznati indeksi snage su Shapley-Shubik indeks, Banzhaf indeks, Johnston indeks, Deegan-Packel indeks (Taylor1995, Cortona1999, Matsui2000, Marosevic2016). Opišimo glavna svojstva ovih indeksa.
Neka je X=\lbrace p_{1}, p_{2}, \ldots, p_{n}\rbrace skup od n igrača u težinskim sustavima glasovanja da-ne, gdje su dane pripadne težine s_{k} igrača p_{k}, k=1,\ldots,n, tako da je s_{k} broj glasova igrača p_{k}. Koalicija C jest bilo koji podskup skupa X. Također, pretpostavimo da je dana kvota q koja je potrebna da bi koalicija pobijedila. Ako je ispunjena nejednakost \sum_{p_{k}\in C} s_{k} \geq q, onda se koalicija C\subseteq X naziva pobjednička koalicija.
Predložen je 1954. god. (
Shapley-Shubik indeks igrača p_{k} jest udio permutacija za koje je p_{k} pivotni igrač (
Primijetimo da je nazivnik u gornjem izrazu jednak n!. Opišimo izračunavanje indeksa SSI jednim primjerom.
Stranka A ne može biti pivotni element kada je u permutacijama na prvom mjestu, jer s_{A}=40\lt 51. Također, A ne može biti pivotni element kada je u permutacijama na četvrtom mjestu, jer s_{B}+s_{C}+s_{D}=60\gt 51. No, stranka A je pivotni element na drugom mjestu u permutacijama oblika: B A . . ; C A . . , kojih ima 2!\cdot 2. Nadalje, stranka A je pivotni element na trećem mjestu u permutacijama oblika: . . A B ; . . A C ; . . A D , kojih ima 2!\cdot 3. Stoga, po izrazu
Za stranku B analogno se zaključuje. Ona također ne može biti pivotni element kada je u permutacijama na prvom mjestu, niti kada je u permutacijama na četvrtom mjestu. B jest pivotni element na drugom mjestu u permutacijama oblika: A B . . , kojih ima 2!\cdot 1, te B jest pivotni element na trećem mjestu u permutacijama oblika: . . B A ; . . B C , kojih ima 2!\cdot 2. Stoga, SSI(B)=\frac{2!\cdot 3}{4!}=\frac{3}{12}.
Za stranku C analogno se zaključuje kao za B i dobiva SSI(C)=\frac{2!\cdot 3}{4!}=\frac{3}{12}.
Stranka D je pivotni element jedino na trećem mjestu u permutacijama oblika: . . D A, pa je SSI(D)=\frac{2!\cdot 1}{4!}=\frac{1}{12}.
Dobivene SSI indekse snage stranaka navodimo i u Tablici 1, a ilustriramo na Slici 1. Vidimo da su vrijednosti tih SSI indeksa stranaka različiti od udjela zastupnika stranaka u skupštini.
Predložen je 1965. god. (
a) p_{k}\in C; b) C je pobjednička koalicija; c) C\setminus\lbrace p_{k}\rbrace nije pobjednička koalicija.
U tom slučaju uklanjanje p_{k} dovodi do toga da koalicija C\setminus \lbrace p_{k}\rbrace nije pobjednička, odnosno kaže se da izlazak p_{k} iz koalicije C jest kritičan (
Kod Banzhaf indeksa snage uzimaju se u obzir kritični izlasci iz pobjedničkih koalicija. Opišimo izračunavanje indeksa BI primjerom.
Tada su pripadne pobjedničke koalicije: \lbrace A,B\rbrace, \lbrace A,C\rbrace, \lbrace A,B,C\rbrace,
\lbrace A,B,D\rbrace, \lbrace A,C,D\rbrace, \lbrace B,C,D\rbrace i \lbrace A,B,C,D\rbrace.
Izlazak stranke A je kritičan iz svih pobjedničkih koalicija kojima ona pripada osim iz koalicije \lbrace A,B,C,D\rbrace, pa je TBP(A)=5.
Izlazak stranke B je kritičan iz pobjedničkih koalicija \lbrace A,B\rbrace, \lbrace A,B,D\rbrace i \lbrace B,C,D\rbrace, pa je TBP(B)=3.
Za stranku C analogno se dobiva da je TBP(C)=3. Izlazak stranke D je kritičan samo iz pobjedničke koalicije \lbrace B,C,D\rbrace, pa je TBP(D)=1.
Stoga, po izrazu
Kod pobjedničkih koalicija može se promatrati ukupan broj igrača čiji izlazak iz dane koalicije je kritičan. Uzimajući to u obzir, Johnston indeks snage definira se ovako (
Pretpostavimo da su C_{1}, \ldots,C_{m} one pobjedničke koalicije kod kojih je igrač p_{k} kritičan. Neka je n_{1} broj onih igrača čiji izlazak iz C_{1} je kritičan, n_{2} je broj onih igrača čiji izlazak iz C_{2} je kritičan, i tako dalje, n_{m} je broj onih igrača čiji izlazak iz C_{m} je kritičan, Tada se definira ukupna Johnston snaga igračap_{k}} ovako:
Prikažimo izračunavanje indeksa JI primjerom.
Za stranku A promatramo pet pobjedničkih koalicija u kojima je njezin izlazak kritičan, pa gledamo za koje je još stranke izlazak iz pojedine koalicije kritičan. U skladu s
Izlazak stranke B kritičan je iz pobjedničkih koalicija \lbrace A,B\rbrace, \lbrace A,B,D\rbrace i \lbrace B,C,D\rbrace, pa je TJP(B)=\frac{1}{2}+\frac{1}{2}+ \frac{1}{3}=\frac{4}{3}.
Za stranku C analogno se dobiva da je TJP(C)=\frac{4}{3}, dok je za stranku D TJP(D)=\frac{1}{3}.
Stoga, po izrazu
Godine 1978. Deegan and Packel (
Neka su C_{1}, \ldots,C_{j} minimalne pobjedničke koalicije kojima pripada igrač p_{k}. Neka je |C_{1}| broj članova C_{1}, |C_{2}| broj članova C_{2}, \ldots ,|C_{j}| broj članova C_{j}. Tada se definira ukupna Deegan-Packel snaga igračap_{k} ovako:
Prikažimo izračunavanje indeksa DPI primjerom.
Za stranku A promatramo minimalne pobjedničke koalicije kojima pripada, \lbrace A,B\rbrace i \lbrace A,C\rbrace, pa se dobiva TDPP(A)=\frac{1}{2}+\frac{1}{2}=1.
Za stranku B gledamo minimalne pobjedničke koalicije kojima pripada, \lbrace A,B\rbrace i \lbrace B,C,D\rbrace, pa je TDPP(B)=\frac{1}{2}+\frac{1}{3}=\frac{5}{6}.
Za stranku C analogno se dobiva da je TDPP(C)=\frac{5}{6}. Za stranku D je TDPP(D)=\frac{1}{3}.
Stoga, po izrazu
| stranka | A | B | C | D |
| s_{k} | 40 | 30 | 20 | 10 |
| SSI | 0.4167 | 0.25 | 0.25 | 0.0833 |
| BI | 0.4167 | 0.25 | 0.25 | 0.0833 |
| JI | 0.50 | 0.2222 | 0.2222 | 0.0555 |
| DPI | 0.3333 | 0.2777 | 0.2777 | 0.1111 |
Iz prethodnih definicija očito jest da indeksi snage imaju vrijednosti između 0 i 1. Te indekse može se izraziti i u postotcima.
Na slici 2 ilustriramo navedene indekse snage u slučaju četiri stranke iz prethodnih Primjera 1 - 4.
Izračunavanje indeksa snage u složenijim slučajevima je komplicirano, što ovdje nećemo razmatrati. Postoje brojne metode za izračunavanje pojedinih indeksa snage, pomoću algoritama prebrojavanja (
U drugom dijelu opisujemo indekse snage još na nekim primjerima i u slučaju Europskog parlamenta.
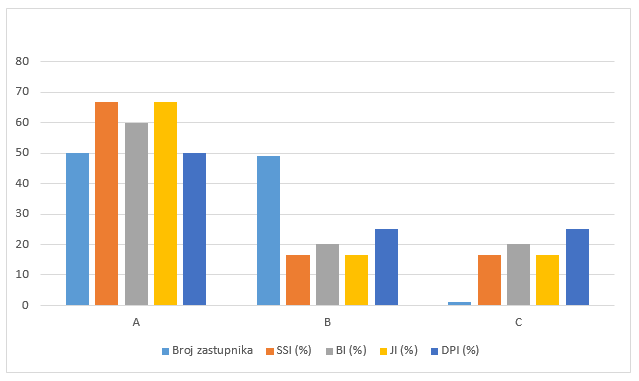
Za ovaj slučaj, u Tablici 2 navedene su pripadne vrijednosti indeksa snage (u postotcima); stranka C (s 1 zastupnikom) ima jednake indekse snage kao stranka B (s 49 zastupnika). Te vrijednosti pokazuju da stranka s vrlo malim brojem zastupnika može imati puno veću političku snagu. Na slici 3 prikazani su navedeni indeksi snage u ovom primjeru.
| stranka | A | B | C |
| s_{k} (\%) | 50 | 49 | 1 |
| SSI (\%) | 66.67 | 16.66 | 16.67 |
| BI (\%) | 60.00 | 20.00 | 20.00 |
| JI (\%) | 66.67 | 16.66 | 16.67 |
| DPI (\%) | 50.00 | 25.00 | 25.00 |
| stranka | A | B | C |
| s_{k} (\%) | 49 | 32 | 19 |
| SSI | 1/3 | 1/3 | 1/3 |
| BI | 1/3 | 1/3 | 1/3 |
| JI | 1/3 | 1/3 | 1/3 |
| DPI | 1/3 | 1/3 | 1/3 |
Na slici 4 prikazani su navedeni indeksi snage u slučaju tri stranke iz Primjera 6.
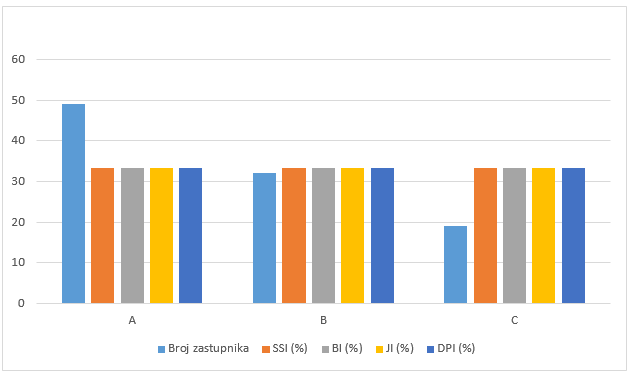
Napomena. Spomenuti indeksi snage stranaka ovise o kvoti q. Primjerice, ako se za podatke iz Primjera 6. definira da je kvota q=67 (to je dvotrećinska većina), dobit će se drugačije vrijednosti indeksa snage, koje navodimo u Tablici 3a.
| stranka | A | B | C |
| s_{k} (\%) | 49 | 32 | 19 |
| SSI | 2/3 | 1/6 | 1/6 |
| BI | 3/5 | 1/5 | 1/5 |
| JI | 2/3 | 1/6 | 1/6 |
| DPI | 1/2 | 1/4 | 1/4 |
Promotrimo osmi saziv Europskog parlamenta, koji se sastoji od 751 članova. Stoga, kvota q=376 predstavlja nadpolovični broj glasova. U ovom primjeru pogledajmo podjelu zastupnika po državama koje predstavljaju, odnosno na n=28 europskih država iz kojih dolaze (
Nadalje, u Tablici 4 navedeni su i pripadni indeksi snage tih država, izračunati pomoću
Tablica 4. Sastav 8. saziva Europskog parlamenta po državama-članicama u 2015. god., te pripadni indeksi snage.
| država | broj zastupnika (\%) | indeks SSI | indeks BI | indeks DPI |
| 1 Njemačka | 96 (12.78\%) | 0.13724 | 0.13656 | 0.03873 |
| 2 Francuska | 74 (9.85\%) | 0.10183 | 0.10017 | 0.03748 |
| 3: Italija | 73 (9.72\%) | 0.10031 | 0.09868 | 0.03746 |
| Velika Britanija | 73 (9.72\%) | 0.10031 | 0.09868 | 0.03746 |
| 4 Španjolska | 54 (7.19\%) | 0.07211 | 0.07132 | 0.03673 |
| 5 Poljska | 51 (6.79\%) | 0.06782 | 0.06709 | 0.03659 |
| 6 Rumunjska | 32 (4.26\%) | 0.04147 | 0.04171 | 0.03607 |
| 7 Nizozemska | 26 (3.46\%) | 0.03343 | 0.03377 | 0.03593 |
| 8: Belgija | 21 (2.80\%) | 0.02683 | 0.02721 | 0.03568 |
| Češka | 21 (2.80\%) | 0.02683 | 0.02721 | 0.03568 |
| Grčka | 21 (2.80\%) | 0.02683 | 0.02721 | 0.03568 |
| Mađarska | 21 (2.80\%) | 0.02683 | 0.02721 | 0.03568 |
| Portugal | 21 (2.80\%) | 0.02683 | 0.02721 | 0.03568 |
| 9 Švedska | 20 (2.66\%) | 0.02553 | 0.02592 | 0.03567 |
| 10 Austrija | 18 (2.40\%) | 0.02293 | 0.02331 | 0.03559 |
| 11 Bugarska | 17 (2.26\%) | 0.02162 | 0.02200 | 0.03553 |
| 12: Finska | 13 (1.73\%) | 0.01645 | 0.01681 | 0.03542 |
| Danska | 13 (1.73\%) | 0.01645 | 0.01681 | 0.03542 |
| Slovačka | 13 (1.73\%) | 0.01645 | 0.01681 | 0.03542 |
| 13: Irska | 11 (1.465\%) | 0.01389 | 0.01422 | 0.03533 |
| Hrvatska | 11 (1.465\%) | 0.01389 | 0.01422 | 0.03533 |
| Litva | 11 (1.465\%) | 0.01389 | 0.01422 | 0.03533 |
| 14: Latvija | 8 (1.065\%) | 0.01006 | 0.01033 | 0.03491 |
| Slovenija | 8 (1.065\%) | 0.01006 | 0.01033 | 0.03491 |
| 15: Cipar | 6 (0.80\%) | 0.00752 | 0.00775 | 0.03406 |
| Estonija | 6 (0.80\%) | 0.00752 | 0.00775 | 0.03406 |
| Luksemburg | 6 (0.80\%) | 0.00752 | 0.00775 | 0.03406 |
| Malta | 6 (0.80\%) | 0.00752 | 0.00775 | 0.03406 |
Na slici 5 prikazana su tri indeksa snage za slučaj 28 država članica u Europskom parlamentu razdijeljenih u 15 skupina po broju svojih zastupnika, iz Primjera 7.
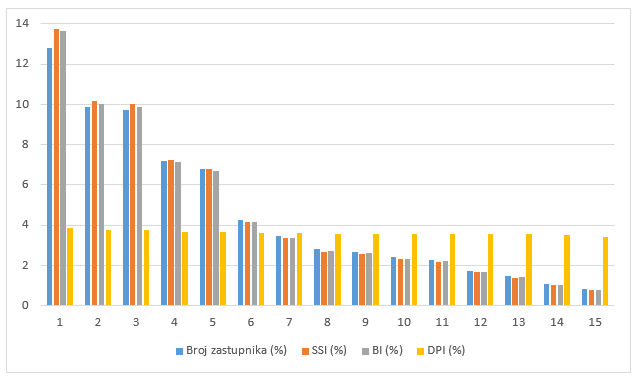
Iz navedenih primjera može se zamijetiti da su Shapley-Shubik indeks (SSI), Banzhaf indeks (BI) i Johnston indeks (JI) monotone funkcije ovisne o broju mjesta (glasova) koje pojedina stranka ima, no nisu linearne funkcije. Napomenimo da Deegan-Packel indeks (DPI) općenito ne mora biti monotona funkcija od broja mjesta, jer kod DPI indeksa uzimaju se u obzir jedino minimalne pobjedničke koalicije.
Spomenimo da se indeksi snage stranaka mogu modificirati, tako da se ne uzimaju u obzir sve pobjedničke koalicije, već samo suženi skup politički mogućih pobjedničkih koalicija (
| [1] | P. G. Cortona, C. Manzi, A. Pennisi, F. Ricca, B. Simeone, Evaluation and optimization of electoral systems, SIAM, Philadelphia, 1999. |
| [2] | D. Leech, Computation of power indices, Department of Economics, University of Warwick, UK, 2002. |
| [3] | D. Leech, R. Leech, Computer algorithms for voting power analysis, http://homepages.warwick.ac.uk/~ecaae/ (ožujak 2019.) |
| [4] | T. Marošević, I. Soldo, Neki kvantitativni (brojčani) pokazatelji političke snage u sustavu glasovanja da-ne, Sveučilišni glasnik, 2016. http://www.glas-slavonije.hr/sglasnik/sveucilisni-glasnik-18.pdf (ožujak 2019.) |
| [5] | T. Matsui, Y. Matsui, A survey of algorithms for calculating power indices of weighted majority games, Journal of the Operations Research Society of Japan 43(2000), No.1, 71–86. |
| [6] | Pajala, A., Meskanen, T. and T. Kause (2002): Powerslave Power Index Calculator: A Voting Body Analyser in the Voting Power and Power Index Website. [online]. Published 22.4.2002. Updated 21.4.2016. University of Turku. http://powerslave.utu.fi/ (ožujak 2019.) |
| [7] | A. D. Taylor, A. M. Pacelli, Mathematics and Politics, Springer, New York, 2008. |
| [8] |
A short guide to European Parliament, EN_EP brochure.pdf (completed in January 2015), http://www.europarl.europa.eu/aboutparliament/en (ožujak 2019.) |

