Neke primjene svojstva konveksnosti i konkavnosti u ekonomiji
Dorian Čudina, Ivana Slamić
1Uvod
Konveksnost je jednostavan matematički pojam kojeg je poznavao još i Arhimed. Naime, Arhimed je ovaj pojam koristio pri odreivanju vrijednosti broja
2Osnovna svojstva
Prvu poznatu definiciju vezanu uz konveksnost napisao je Euklid u svojoj zbirci knjiga Elementi, a doradio ju je Arhimed dajući dvije definicije koje su potom korištene sve do početka
Slika 1: Težište (eng. center of gravity) je pojam koji se odnosi na održavanje statičke ravnoteže. (a) Težište nekih geometrijskih likova i tijela. (b) Održavanje ravnoteže tijela – vertikalna projekcija težišta (prema površini na kojoj stojimo) trebala bi se nalaziti unutar najmanjeg konveksnog skupa koji obuhvaća naša stopala (slika je preuzeta sa: http://thatmanfromsyracuse.weebly.com/contributions/center-of-gravity).
Prisjetimo se, za skup
(1)
(2)
Konveksnost ili konkavnost funkcija jedne varijable koje imaju neprekidnu drugu derivaciju (odnosno funkcije klase
(3)
U primjenama se često pretpostavlja da funkcija korištena u nekom modelu ima dobra analitička svojstva, npr. neprekidnost ili diferencijabilnost. No, uočimo da je uvjet (1) u tom smislu prilično jak. Naime, za funkcije jedne varijable, iz (1) možemo odmah zaključiti da konkavne (odnosno konveksne) funkcije ne mogu imati prekid u unutarnjoj točki domene, te da u svakoj točki postoje lijeva i desna derivacija. Štoviše, skup točaka u kojima derivacija ne postoji je konačan ili prebrojiv, pa su sve konveksne, odnosno konkavne funkcije diferencijabilne gotovo svuda.
Za proizvoljan realan broj
Slika 2: (a) Negativna definitnost Hesseove matrice (u (3 ) vrijede stroge nejednakosti) je dovoljan, ali ne i nužan uvjet za strogu konkavnost. Funkcija
Danski matematičar Johan Jensen karakterizirao je konkavne funkcije
(4)
3Načini optimiziranja poslovanja pri proizvodnji opisanoj konkavnom funkcijom
Proizvodnja dobara i usluga uključuje proces pretvorbe određenih resursa (rad, sirovine itd.) u gotove proizvode. U ovim modelima korisno je imati funkciju kojom bismo opisali vezu između količine proizvedenog (outputa) i količine uloženih faktora (inputa) da bi se proizvodnja ostvarila, kako bismo pomoću nje mogli predvidjeti kako bi se proizvodnja trebala odvijati u budućnosti, odrediti faktore na čiju je promjenu uložene količine najosjetljivija i slično. Funkcije s ovim svojstvom nazivamo funkcijama proizvodnje.
Ekonomisti često pretpostavljaju da je takva funkcija rastuća i konkavna. Činjenica da je rastuća znači da se povećanjem količine uloženog povećava i količina proizvedenog. Konkavnost funkcije odražava se u promjeni količine proizvedenog prilikom povećanja količine uloženog. Promatramo li, naime, koliko se količina proizvedenog promijenila povećavamo li uzastopce količinu uloženog u slučaju funkcije jedne varijable, odnosno količinu jednog inputa u slučaju funkcija više varijabli (recimo, za neku jedinicu), razlika u količini toga što smo proizveli bila bi manja (ili jednaka) pri drugoj promjeni, odnosno pri svakoj sljedećoj promjeni (slika
Godine 1928. Charles Cobb i Paul Douglas objavili su rad u kojim su predstavili model rasta američke ekonomije u razdoblju od 1899. do 1922. Funkcija koju su koristili u tom modelu u općem obliku se zapisuje kao
Slika 3: (a) Graf Cobb-Douglasove funkcije proizvodnje,
U spomenutom modelu
Slika 4: Funkcija
U promatranom obliku Cobb-Douglasove funkcije pretpostavili smo da proizvodnja ovisi samo o dva faktora proizvodnje, odnosno o količini uloženog rada i kapitala, ali promatrana proizvodnja može ovisiti i o više od dva faktora. U idućem primjeru pokazujemo da, uz ove pretpostavke, za svaki faktor proizvodnje možemo relativno jednostavno odrediti točnu količinu koju treba uložiti kako bi se ostvario najveći mogući profit. Želimo li, naime, maksimizirati konkavnu funkciju tada znamo da će ta funkcija poprimati globalni maksimum u unutarnjoj točki domene na čijoj je okolini klase
Slika 5: Za konveksne funkcije jedne varijable, koje su klase 1 )). Ovaj uvjet možemo zapisati kao
Primjer 1. Pretpostavimo da proizvodnja neke tvrtke ovisi o
U prethodnom primjeru profit tvrtke prikazan je kao razlika prihoda i troškova proizvodnje. Ako bismo htjeli minimizirati trošak tvrtke po svim kombinacijama inputa pri kojima je količina proizvedenog barem
Primjer 2. Zamislimo tvrtku koja proizvodi samo jednu vrstu proizvoda i pretpostavimo da je trošak pri proizvodnji
Pretpostavimo da je spomenuta tvrtka izabrala različite godišnje razine outputa,
Pretpostavimo da je spomenuta tvrtka izabrala različite godišnje razine outputa,
4Funkcija korisnosti i odlučivanje u uvjetima nesigurnosti
Osim u poslovanju, pretpostavke konveksnosti i konkavnosti korisne su i u određivanju načina na koji će promatrani pojedinac napraviti racionalan izbor pri odlučivanju u uvjetima nesigurnosti i rizika. U svakodnevnom se životu, od najranije dobi, gotovo neprestano nalazimo pred izborom, češće takvim da ishode pojedinih alternativa ne možemo predvidjeti sa sigurnošću. Tako je uobičajeno da svake godine plaćamo izvjesnu svotu novca za osiguranje automobila, a broj odigranih loto listića značajno se poveća u vrijeme kada je mogući dobitak rekordan, iako znamo da kada bi svi ljudi u svijetu svaki tjedan igrali isti loto, i to u razdoblju od jednog prosječnog životnog vijeka, rijetki bi bili oni sa ostvarenim profitom i da ćemo vjerojatno imati puno više onih godina kada od osiguranja nećemo tražiti nikakvu odštetu, a kamo li onu za koju bismo rekli da se te godine isplatilo platiti ga. Ove i druge svakodnevne, možda nerazumne, ljudske postupke objašnjavamo time da se ljudi razilaze u mišljenju o tome što je vrijedno neke količine rizika. S obzirom da bi većini dobitak na lotu promijenio život, a, ne baš vjerojatna, ali moguća, tužba radi materijalne štete koju smo skrivili u prometu bi bila iznimno neželjen događaj, ranije spomenute investicije se, iz te perspektive, čine vrlo isplative.
U ekonomiji se često sklonost prema riziku prikazuje funkcijom korisnosti novca. Iako bismo korisnost novca na prvi pogled poistovjetili sa vrijednošću, odnosno količinom, novca, to bi općenito bilo pogrešno i to vrlo lako možemo shvatiti razmislimo li koliko bi simboličan iznos od
Pretpostavke za koje se smatra da odgovaraju ponašanju racionalnog pojedinca u stvarnom svijetu su pretpostavke da je funkcija korisnosti novca rastuća, da nema stacionarnih točaka i da je konkavna. To je zato što se pretpostavlja da uvijek želimo imati veću količinu novca, da ne postoji iznos s kojim bismo osjećali potpuno zadovoljstvo i da je većina ljudi nesklona riziku. Možemo uočiti da, ako je
Primjer 3. Pretpostavimo da investitor nesklon riziku želi investirati u projekt od kojeg će ostvariti povrat u iznosu
Iz grafa možemo primijetiti da je korisnost iznosa participacije
Slika 6: (a) Opadajuća granična korisnost. (b) Konkavna funkcija korisnosti koja pokazuje da investitor nije spreman prihvatiti poštenu igru.
Iz grafa možemo primijetiti da je korisnost iznosa participacije
Jensenova nejednakost ima važnu primjenu u teoriji vjerojatnosti. Naime, za sve diskretne slučajne varijable
(5)
Pretpostavimo sada da investitor odabire investiciju u koju želi uložiti. Jasno je da mu je tada u interesu odabrati najisplativiju investiciju, odnosno investiciju koja ima najveću očekivanu korisnost od onih koje su mu ponuđene, a na isti način bi racionalan pojedinac trebao donijeti odluku i u sljedećem primjeru.
Primjer 4. Pretpostavimo da smo u situaciji da moramo izabrati bolju od sljedeće dvije mogućnosti:
| (1) |
Sigurno osvajamo |
| (2) |
Vjerojatnost da osvojimo |
Uočimo da je u (
5Zaključak
Navedeni primjeri samo su neki od razloga zbog kojih se konveksnost smatra jednim od središnjih pojmova u teorijskoj ekonomiji. Proučavanje konveksnosti - od jednostavnog geometrijskog pojma, čija su korisna svojstva uočavali i starogrčki filozofi, a neka od njih gotovo dva tisućljeća kasnije razvojem matematičke analize formalno dokazali matematičari kao što su Cauchy ili Euler, uz primjenu na probleme iz astronomije Keplera ili statike Newtona i Fouriera, dobilo je posebno veliku važnost sredinom 20. stoljeća, paralelno uz razvoj linearnog programiranja, gdje se problemi maksimizacije, odnosno minimizacije rješavaju oslanjajući se na činjenicu da afina funkcija definirana na politopu ima ekstreme i postiže ih u vrhovima tog politopa.
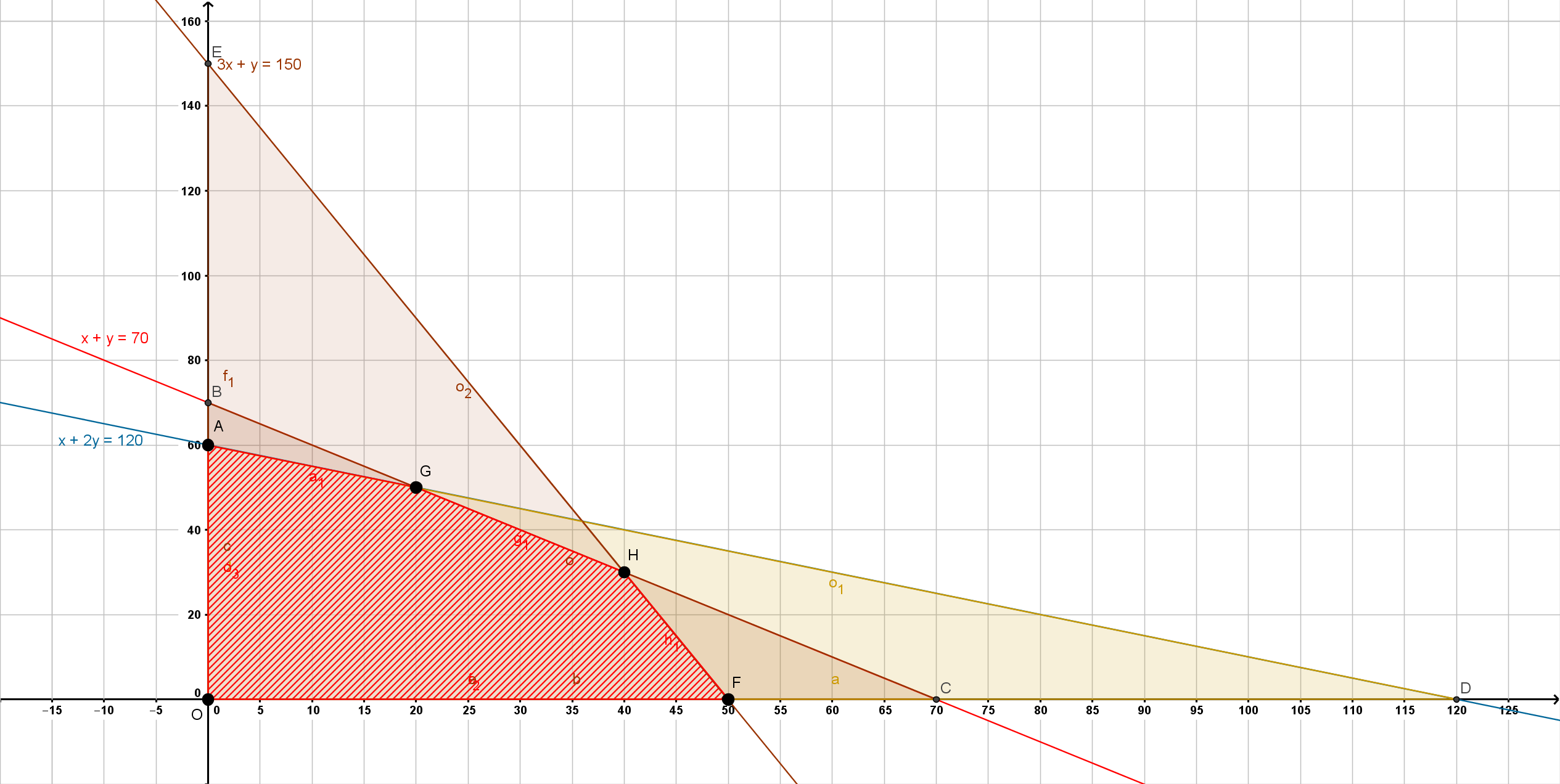
Slika 7: U primjenama često moramo maksimizirati funkciju uz neka ograničenja, a tom kontekstu konveksnost je važna jer znamo da konveksna funkcija definirana na kompaktnom i konveksnom skupu postiže maksimum u rubnoj točki tog skupa. U problemima linearnog programiranja, gdje je funkcija cilja linearna, a skup dopustivih rješenja politop, problem se svodi na ispitivanje vrijednosti funkcije u vrhovima politopa. Na slici je prikazano područje dopustivih rješenja jednog problema linearnog programiranja.
Nije zanemariva ni primjena konveksnosti u nekim drugim teorijama tog vremena, kao što je teorija očekivane korisnosti te u raznim matematičkim teorijama koje ju nadopunjavaju - kao što je teorija igara, ali i na području psihologije i ekonomije - kao što je Kahnemanova i Tverskyjeva teorija očekivanog izbora. Zadnjih nekoliko desetljeća prošlog stoljeća i otkrivanjem da se metodama unutarnjih točaka (koje su zapravo nastale s namjerom da se pomoću njih rješavaju problemi linearnog programiranja) određeni problemi konveksne optimizacije mogu riješiti jednostavno kao i oni linearnog programiranja, ali i tehnološkim napretkom te spoznajom da su problemi konveksne optimizacije u stvarnosti puno rasprostranjeniji nego što se prethodno mislilo, interes za istraživanjem ovog svojstva postaje još veći. Na taj način konveksnost postaje jedan od središnjih pojmova u teoriji optimizacije i na tom području postiže svoju (vjerojatno) najveću primjenu.
U primjerima ovog članka mogli smo koristiti i nešto općenitija svojstva pritom zadržavajući određena načela. Tako, na primjer, u teoriji potrošača ekonomisti o funkciji korisnosti češće razmišljaju kao o sredstvu koje prikazuje prioritete promatranog potrošača nego o brojčanoj vrijednosti njegove dobrobiti, te se u problemima kao što su maksimiziranje korisnosti potrošača više pažnje posvećuje nivo skupovima koje ta funkcija određuje nego vrijednostima koje ona postiže. Zato je za takve probleme prikladnije koristiti pretpostavku kvazikonveksnosti, odnosno kvazikonkavnosti, koja je u matematičkom smislu slabija od konveksnosti, odnosno konkavnosti, ali iz ekonomske perspektive prirodnija, s obzirom da je poželjno da je proizvoljnom transformacijom povećanja vrijednosti koje poprima zadana funkcija korisnosti očuvana ista hijerarhija prioriteta potrošača koja je bila i prije transformacije (a to je svojstvo koje općenito ne vrijedi za konveksne, odnosno konkavne, funkcije).
S obzirom da je teorija konveksnosti teorija koja dotiče gotovo sve grane matematike i mnoga druga područja, ovaj članak zasigurno ne daje pregled svih tema vezanih uz konveksnost, niti svih područja u kojima se konveksnost primjenjuje. Također, jasno je da svaki model, pa tako i oni spomenuti u članku, kojim stvarni problem opisujemo na apstraktan (matematički) način ima mane jer takvim prijelazom neke uvjete nužno moramo idealizirati. Unatoč tome, takvi modeli i njihovi rezultati danas su izrazito važni kod donošenja raznih zaključaka u ekonomiji i omogućuju nam da probleme iskažemo na drugačiji način, sažetim i preciznijim jezikom te tako poboljšamo njegovo razumijevanje i preciznost analize. Napomenimo i da su detalji teorija spomenutih u članku izostavljeni jer bi se o svakoj od njih mogao napisati zaseban članak, ali i zbog toga što je osnovna namjera ovog članka čitatelju predstaviti više zanimljivih načina korištenja ovog svojstva i modeliranja problema koji se pojavljuju u ekonomiji (u problemima proizvodnje, teoriji očekivane korisnosti i sl.) kao i to da je uz takve modele matematički moguće potkrijepiti neke poslovne odluke. Uz to, prikazom uloga ovih pretpostavki i njihovim interpretacijama te naglašavanjem golemog spektra područja u kojima se koriste, ovim člankom čitatelja nastojimo motivirati za uočavanje važnosti i netrivijalnih posljedica ovih naizgled jednostavnih svojstava.
Bibliografija
| [1] | Berger, M.: Convexity, Amer. Math. Mothly, 97, 650-678 (1990) |
| [2] | Kahneman, D - Tversky, A.: Prospect theory, Econometrica, 47(2), 263-291 (1979) |
| [3] | Nicolescu, C. - Persson, L. E.: Convex Functions and Their Applications, Springer, 2006 |
| [4] | Boyd, S. - Vandenberghe, L.: Convex Optimization, Cambridge University Press, 2004 |
| [5] | Johnson T. C. Utility functions. C2922 economics, Heriot Watt University, Edinburgh (2007) |
| [6] | Schoemaker, P.J.H.: The Expected Utility Model: Its Variants, Purposes, Evidence and Limitations, Journal of Economic Literature 20(2),529-563 (1982) |
| [7] | Sydsaeter, K.- Hammond, P. - Seierstad, A. - Strøm A.: Further Mathematics for Economic Analysis, Pearson Education, 2010 |
| [8] | Cobb-Douglas Production Function. URL: http://economicpoint.com/production-function/cobb-douglas . (12.03.2016.) |
| [9] | What is production leveling?. URL: http://www.businessknowledgesource.com/manufacturing/what_is_production_... . (18.03.2016.) |
| [10] | Risk and Certainty Equivalence Applet. URL: http://www.gametheory.net/mike/applets/Risk/ . (26.09.2016.) |
| [11] |
Penati, A. - Pennacchi, G.: Choice Under Uncertainty, Finance 400, URL: http://home.cerge-ei.cz/petrz/FM/notes.html (26.09.2016.) |

