Sokoban je NP --težak
Kod raznih igara često je važno pitanje određivanja pobjedničke strategije. No, vrlo često se razmatraju i problemi računarske složenosti u vezi igara (vidi
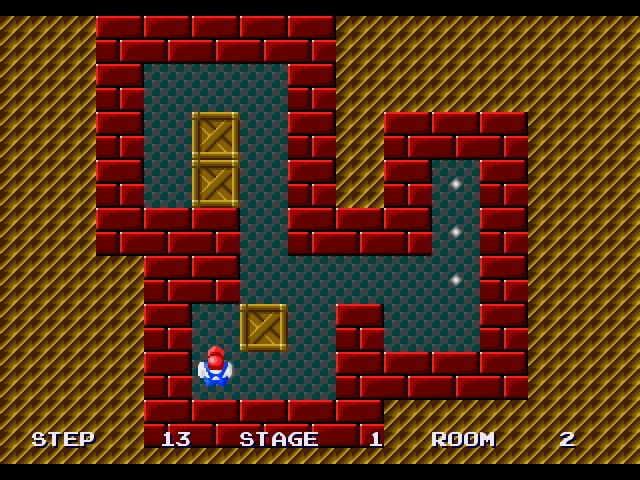
Sokoban je poznata stara računalna igra u kojoj igrač (skladištar) mora odgurati sve kutije u skladištu na odgovarajuće pozicije, s tim da odjednom smije gurati najviše jednu kutiju. Osnovnu verziju igre možete isprobati na sljedećoj poveznici: https://sokoban.info/.
U ovom članku dat ćemo dokaze NP-težine dviju varijanti igre Sokoban. Ti se dokazi svode na to da za svaku instancu 3-SAT problema (ili u drugom slučaju problema P-3-SAT) generiramo početnu konfiguraciju igre koja će biti rješiva ako i samo ako je zadana formula ispunjiva. Većina rezultata u ovom članku dio je članka
Osnovne pojmove teorije složenosti algoritama potrebne za razumijevanje ovog članka predstavit ćemo u točki
U točki
U ovoj točki dati ćemo opise osnovnih pojmova iz teorije složenosti algoritama koje koristimo u ovom članku. Naglašavamo da ćemo dati samo intuitivne opise a ne stroge definicije. Razlog tome je, naravno, veličina teksta članka. Za formalne defincije trebalo bi, primjerice, detaljno definirati Turingove strojeve i sve pojmove u vezi njih. Kolika je to veličina materijala možete vidjeti, primjerice u
U čitavom članku pojam algoritma ćemo koristiti u intutivnom smislu.1
Neka je \Gamma proizvoljan konačan skup. Skup \Gamma ćemo nazivati alfabet. Svaki konačan niz elemenata alfabeta \Gamma nazivamo riječ. Skup svih riječi alfabeta \Gamma označavamo s \Gamma^{*}. Ako je s\in \Gamma^{*} neka riječ tada s |s| označavamo duljinu riječi s. Svaki podskup od \Gamma^{*} nazivamo jezik.
U ovom članku razmatrat ćemo samo algoritme koje imaju jedan ulazni podatak (točnije, za zadani alfabet \Gamma ulazni podatak je neka riječ s\in\Gamma^{*}). Zatim, pretpostavljamo da svaki algoritam za svaki ulazni podatak završi u konačno mnogo koraka te da na kraju kao izlazni podatak daje samo "DA" ili "NE". Razlog takvim ograničenjima je to što promatramo samo tzv. probleme odlučivanja. To su problemi kod kojih nas zanima ima li neki objekt neko zadano svojstvo. Neki primjeri problema odlučivanja su: ispunjivost formula logike sudova, prostost zadanog prirodnog broja i bojanje grafa s tri boje. Problem trgovačkog putnika, problem ruksaka i problem rasporeda su primjeri problema koji nisu problemi odlučivanja. Formalno se problemi odlučivanja definiraju kao odgovarajući jezici. Primjerice, problem PRIMES koji se sastoji od određivanja je li zadani prirodan broj prost, definira se formalno kao \lbrace n\in \mathbb{N}: n je prosti broj\rbrace .
Vremenska složenost nekog algoritma definira se kao funkcija f: \mathbb{N}\to \mathbb{N}, gdje je f(n) maksimalni broj koraka koji algoritam izvrši za svaki ulazni podatak duljine n.2
Sasvim analogno se defnira prostorna složenost nekog algoritma (primijetite da je ovdje nužno imati Turingove strojeve kako bi mogli brojati registre koje algoritam koristi).
Reći ćemo da je neki algoritam vremenski polinoman ili samo kratko da je polinoman, ako je njegova vremenska složenost neki polinom. S P označavamo klasu svih problema odlučivanja za koje postoje polinomni algoritmi koji ih rješavaju. Neki primjeri problema koji pripadaju klasi P su sljedeći: ispitivanje relativne prostosti dva prirodna broja, odre đivanje je li graf povezan i egzistencija rješenja sistema linearnih algebarskih jednad\v zbi. Zanimljivo je da je 2004. godine dokazano da problem PRIMES tako đer pripada klasi P (članak o tome je objavljen u najcjenjenijem matematičkom časopisu Annals of Mathematics).
Sasvim analogno definira se klasa PSPACE koja sadrži sve probleme odlučivanja za koje postoji algoritam koji je polinomno prostorno složen.
Sada ćemo opisati nekoliko pojmova iz logike sudova kako bismo mogli definirati problem SAT. Propozicionalne varijable ovdje označavamo s x_{0}, x_{1}, x_{2}, \ldots Ako je F neka formula logike sudova, tada ćemo s \overline{F} označavati njenu negaciju. Literal je svaka propozicionalna varijabla x_{i} i njena negacija \overline{x}_{i}. Elementarna disjunkcija je disjunkcija literala. Primjerice, x_{2}\vee x_{7} \vee \overline{x}_{33}\vee x_{8} \vee \overline{x}_{201} i x_{4}\vee x_{6} su primjeri elementarnih disjunkcija. Konjunktivna normalna forma (ili kratko: knf) je svaka konjunkcija elementarnih disjunkcija. Neki primjeri knf su (x_{8}\vee \overline{x}_{1}\vee x_{4} \vee x_{5})\wedge (x_{1} \vee x_{2}) i (x_{13}\vee \overline{x}_{23})\wedge x_{33} \wedge (x_{23}\vee \overline{x}_{4} \vee x_{9}). Knf nazivamo 3-knf ako svaka njena elementaran disjunkcija sadrži tri literala. Problem ispunjivosti logike sudova, koji se kratko označava sa SAT, sastoji se određivanja je li zadana knf ispunjiva, tj. postoji li interpretacija propozicionalnih varijabli tako da je za tu interaprtaciju knf istinita, odnosno formalno ovako:
Problem 3-SAT u obzir uzima samo 3-knf. Sasvim analogno se definira problem 2-SAT.
Mi ćemo u ovom članku najviše spominjati klasu problema NP. Jako grubo rečeno klasa NP sadrži sve probleme odlučivanja za koje postoji polinomni algoritam čiji ulazni podatak je par koji uz zadani objekt sadrži i posebni "certifikat". Primjenom "certifikata" algoritam onda odlučuje ima li zadani objekt traženo svojstvo. Pokušat ćemo to objasniti na dva primjera. Problem SAT pripada klasi NP jer očito postoji polinomni algoritam kojemu na ulaz dajemo neku knf F i neku interpretaciju I (to je "certifikat") te onda algoritam određuje vrijedi li I(F)=1 (možete li opisati jedan takav algoritam?). Zatim, problem egzistencije potpuno povezanog podgrafa zadane veličine u nekom grafu također pripada klasi NP. Za taj problem postoji polinomni algoritam koji na ulazu ima zadani graf G, k\in \mathbb{N} i neki podgraf G' od G (ovdje je podgraf "certifikat") te onda algoritam određuje je li G' potpuno povezan i veličine k.
Očito vrijedi P \subseteq NP. Pitanje vrijedi li i obratna inkluzija je centralni problem teorijskog računarstva već više od 50 godina. \v Stovi\v se, problem P vs. NP jedan je od tzv. sedam Milenijskih matemati\v ckih problema.
Neka su \Gamma_{1} i \Gamma_{2} alfabeti. Za neku funkciju g:\Gamma_{1}^{*} \to \Gamma_{2}^{*} kažemo da je vremenski polinomno izračunljiva ako postoji polinom p:\mathbb{N}\to \mathbb{R} i neki algoritam tako da za svaki s\in \Gamma_{1}^{*} algoritam kao izlazni rezulat daje g(s) i za to mu ne treba više od p(|s|) koraka.
Ako imamo dva problema odlučivanja, označimo ih L_{1} i L_{2}, tada je problem L_{1} polinomno reducibilan na problem L_{2} ako možemo svaku instancu problema L_{1} (rješivu i nerješivu) svesti u polinomnom vremenu na neku instancu problema L_{2}. Budući da ovaj pojam polinomne reducibilnosti bitno koristimo u ovom članku, odlučili smo ipak dati nešto formalniju definiciju. Neka su L_{1}\subseteq \Gamma_{1}^{*} i L_{2}\subseteq \Gamma_{2}^{*} dva problema odlučivanja. Kažemo da je problem L_{1} polinomno reducibilan na problem L_{2}, i pišemo L_{1}\leq_{p} L_{2}, ako postoji vremenski polinomno izračunljiva funkcija g tako da za svaki s\in \Gamma_{1}^{*} vrijedi sljedeća ekvivalencija:
U daljnjem tekstu članka dati ćemo primjere polinomne reducibilnosti.
Za neki problem odlučivanja L kažemo da je NP–težak ako za svaki problem L'\in NP vrijedi L'\leq_{p} L. Zatim, govorimo da je neki problem L jedan NP–potpun problem ako je on NP–težak i još vrijedi L\in NP. Cook i Levin su 1970. godine nezavisno dokazali da je SAT jedan NP–potpun problem. Problem 3-SAT je tako đer NP–potpun. (No, vrijedi 2-SAT \in P.)
Označimo s Dif problem odre đivanja ima li zadana diofantska jednadžba cjelobrojnih rješenja. Već smo naveli da za taj problem ne postoji algoritam koji ga rješava. Iz toga posebno slijedi Dif\not\in NP. No, može se pokazati da je Dif jedan NP–težak problem (vidi
U igri Sokoban igrač upravlja skladištarem koji se može kretati u 4 smjera po pravokutnoj mreži. Na slici
U ovom ćemo radu razmatrati još jednu verziju igre. U tom slučaju ćemo pretpostaviti da skladištar istovremeno može gurati do k kutija, gdje je k neki prirodan broj. U toj verziji igre skladišatar smije prema sebi vući najviše jednu kutiju.
Sa Sokoban(k, l) ćemo označiti igru u kojoj skladištar može istovremeno gurati do k kutija i prema sebi vući najviše l kutija, gdje su k i l prirodni brojevi. Tada standardnu verziju igre možemo kratko zapisti kao Sokoban(1, 0), a drugu malo prije opisanu verziju igre možemo kratko označiti sa Sokoban(k, 1), za neki k\geq1.
NP-teški problemi imaju svojstvo da se svaki problem iz klase složenosti NP može polinomno reducirati na njih, dok oni sami ne moraju pripadati klasi NP. Jedan od najpoznatijih načina za dokazivanje da je neki problem NP-težak je polinomno svođenje problema 3-SAT na njega (vidi
Promatrat ćemo problem odlučivanja SOKOBAN u kojem je pitanje ima li igra Sokoban s nekom početnom konfiguracijom rješenje. Preciznije, za problem SOKOBAN(1, 0) zanima nas možemo li za neku početnu konfiguraciju klasične igre sve kutije staviti na željena mjesta. Za verziju igre Sokoban(k, 1) gledat ćemo nešto lakši problem. U problemu SOKOBAN(k, 1) treba za početnu konfiguraciju odrediti može li skladištar doći do neke određene pozicije (neovisno o pozicijama kutija na kraju igre). Želimo samo spomenuti da je u
U ovoj točki dokazat ćemo sljedeći teorem:
Kao što smo već najavili, za dokaz ovog teorema koristit ćemo činjenicu da je problem 3-SAT jedan NP-potpun problem (to je jedna od posljedica Cook, Levinovog teorema; vidi
U tu svrhu koristit ćemo četiri konstrukcijska elementa: usmjerivač, porednik, prekidač i usmjereno raskrižje.
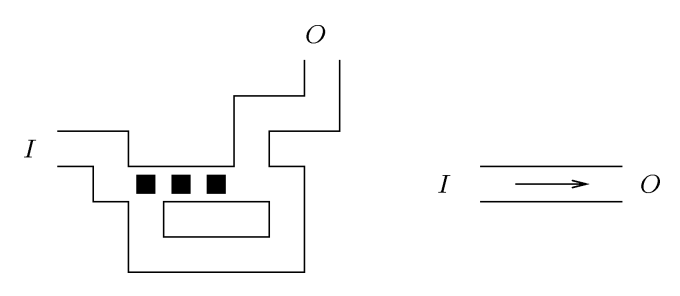
Ako je I oznaka ulaza a O oznaka izlaza u nekom konstrukcijskom elementu, tada s I\rightarrow O označavamo proizvoljni (usmjereni) put od I do O. Sada redom opisujemo svaki od prije navedena četiri konstrukcijska elementa.
| \bullet |
usmjerivač je prikazan na slici Primijetimo da je put I \rightarrow O otvoren jer skladištar mora samo dva puta gurnuti tri uzastopne kutije: prvo udesno, nakon čega mora krenuti donjim puteljkom, te nakon toga ulijevo kako bi oslobodio prolaz koji je zatvorio prethodnim guranjem. Nakon izlaska skladištara, konstrukticijski element izgledat će i kao prije njegovog ulaska u koridor. Primijetimo da skladištar ni na koji način ne može proći putem O \rightarrow I (iz tog razloga ovaj konstrukcijski element nazivamo usmjerivač). |
| \bullet |
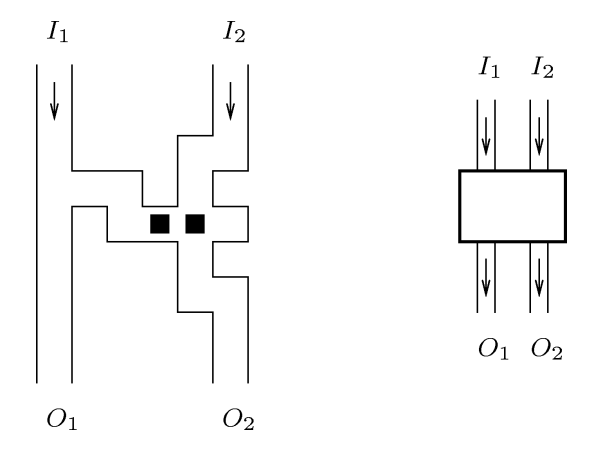
porednik je prikazan na slici Kod ovog konstrukcijskog elementa je na početku put I_{1} \rightarrow O_{1} otvoren, a put I_{2} \rightarrow O_{2} je zatvoren. Kako bi skladištar prošao putem I_{2} \rightarrow O_{2}, prvo mora osloboditi prolaz, a to može samo ako prvo uđe u koridor kroz ulaz I_{1}, obje kutije gurne do zida i zatim bližu kutiju povuće prema sebi. Primijetimo kako je usmjerivač sastavni dio ovog konstrukcijskog elementa. Naime, da njega nema na ulazima I_{1} i I_{2}, skladištar bi mogao ući na ulaz I_{1}, osloboditi prolaz I_{2} \rightarrow O_{2} i izaći iz koridora na mjestu gdje je ušao. |
| \bullet |
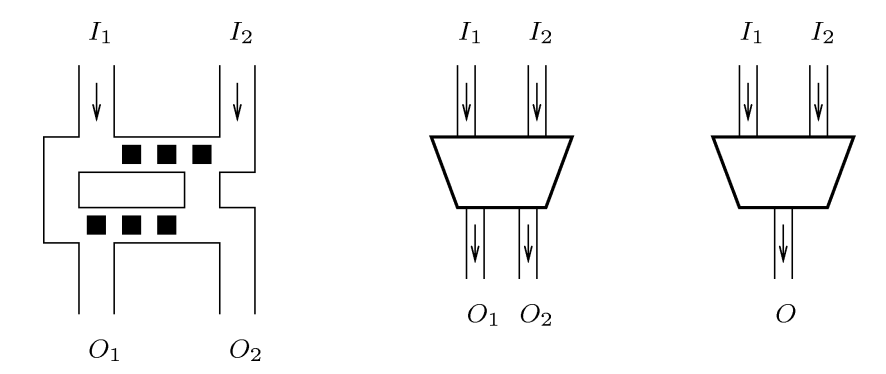
prekidač je prikazan na slici Njegova funkcija je da omogući samo jednu vrstu prolaza. U objašnjenju ćemo se fokusirati na slučaj desnog shematskog prikaza sa slike |
| \bullet |
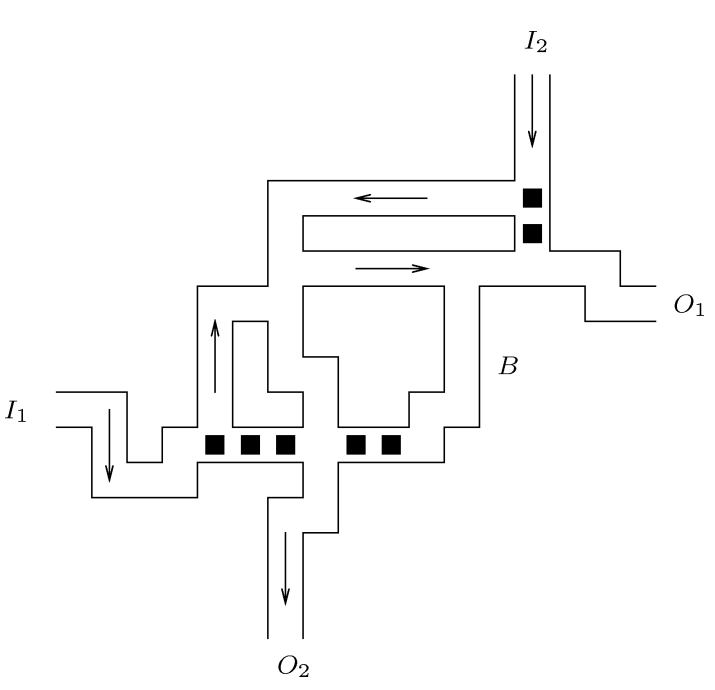
usmjereno raskrižje je prikazano na slici U ovom konstrukcijskom elementu skladištar na početku može proizvoljan broj puta proći putem I_{1} \rightarrow O_{1}. Tijekom jednog od prolazaka putem I_{1} \rightarrow O_{1} skladištar može odlučiti osloboditi prolaz I_{2} \rightarrow O_{2} tako da prođe kroz prolaz označen s B, gurne kutije do zida i zatim najbližu kutiju povuće prema sebi. Nakon što prođe putem I_{2} \rightarrow O_{2}, prolaz I_{1} \rightarrow O_{1} ostat će trajno zatvoren. |
Očito je usmjereno raskrižje najkompliciraniji konstrukcijski element. Kasnije ćemo vidjeti da nam on omogućava da tvrdnju dokažemo i za instance 3-SAT problema čiji inducirani graf nije planaran. O tome ćemo više reći više u dokazu NP-težine standardne verzije igre u kojem nam je planarnost tog grafa ključna.
Sada možemo objasniti i zbog čega je u iskazu teorema uvjet k \geq 5. U usmjerenom raskrižju potrebno je da skladištar u jednom trenutku gura barem 5 kutija u nizu. Kada bismo, primjerice, uspjeli konstruirati usmjereno raskrižje u kojem se guraju najviše 4 kutije, tada bi tvrdnja vrijedila i za k = 4.
Koristeći prethodno opisane konstrukcijske elemente prelazimo na glavni dio dokaza teorema
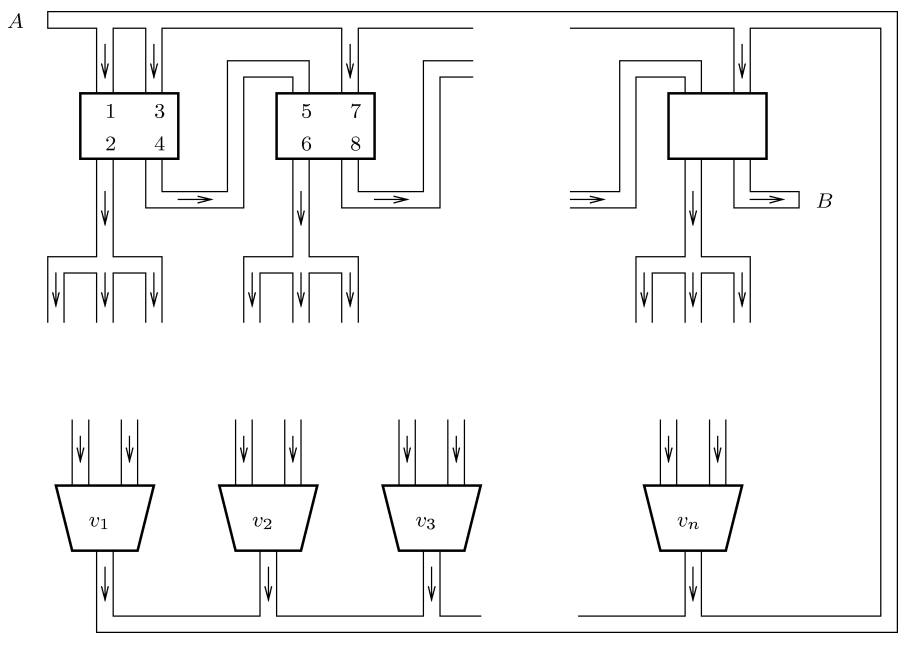
Na slici
Skladištar počinje svoje putovanje na poziciji A i cilj mu je doći do pozicije B. Ovdje je ključno primijetiti da skladištar mora redem proći kroz sve porednike kako bi stigao od ulaza A do izlaza B. Nakon prolaska kroz i-ti porednik skladištar mora barem jednom literalu koji se pojavljuju u elementarnoj disjunkciji C_{i} pridružiti vrijednost "istina". Prekidači skladištaru onemogućuju da istovremeno nekom literalu i njegovoj negaciju pridruži vrijednost "istina". Time smo dokazali da vrijedi sljedeća ekvivalencija:
Time je teorem potpuno dokazan.
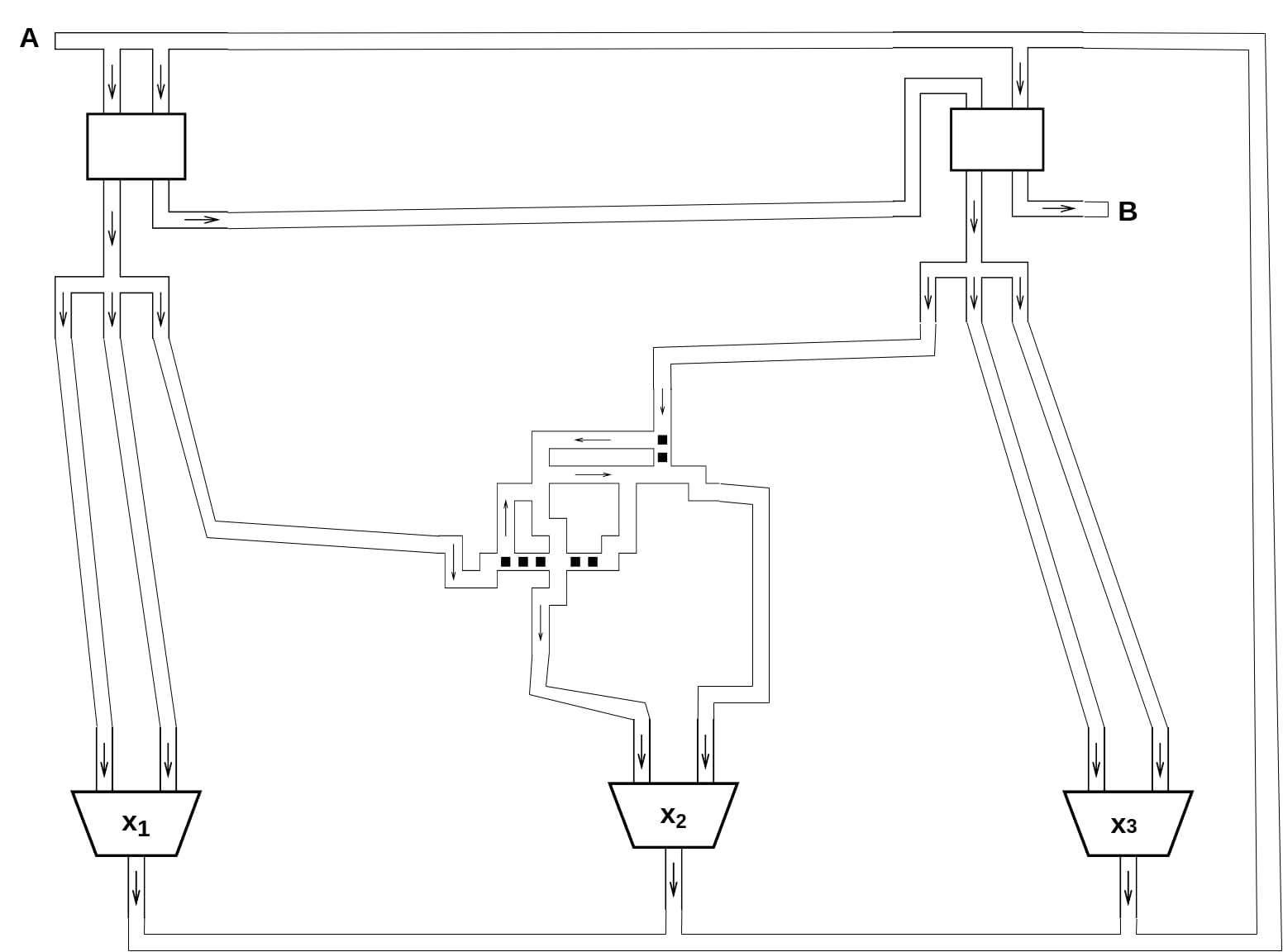
Sada na jednom primjeru želimo ilustrirati neke detalje iz prethodnog dokaza. Na slici
Budući da je prva klauzula od F jednaka x_{1} \lor \bar{x_{1}} \lor \bar{x_{2}} tada prvi izlaz prvog porednika vodi k prvom ulazu prekidača varijable x_{1}, a drugi izlaz tog prekidača k njegovom drugom ulazu jer on odgovara literalu \bar{x_{1}}. Isto je tako treći izlaz spojen s prvim ulazom drugog prekidača jer on odgovara literalu x_{2}, a slično je i za drugi porednik.
Put koji spaja treći izlaz prvog porednika i drugi ulaz drugog prekidača siječe se s putem koji povezuje prvi izlaz drugog porednika i prvi ulaz drugog prekidača pa je neophodno korištenje usmjerenog raskrižja.
U ovom poglavlju dokazujemo NP-težinu standardne verzije igre. To iskazujemo u sljedećem teoremu.
U ovoj verziji igre skladištar smije gurati najviše jednu kutiju i zabranjeno mu je vući kutije prema sebi. U ovom ćemo slučaju zahtijevati da na kraju igre sve kutije budu smještene na predviđenim pozicijama. To je različito od prethodno razmatranog slučaja gdje smo samo promatrali može li skladištar doći do svog cilja.
Slično kao i u prethodnom dokazu, ključnu ulogu igraju konstrukcijski elementi koji će biti korišteni prilikom generiranja početne konfiguracije igre. Koristit ćemo dva konstrukcijska elementa: selektor i klauzulu. Za razliku od otvora konstrukcijskih elemenata iz prijašnjeg dokaza, ovi neće biti usmjereni, već je ulazak i izlazak moguć kroz sve njih. Sada redom opisujemo nove konstrukcijske elemente.
| \bullet |
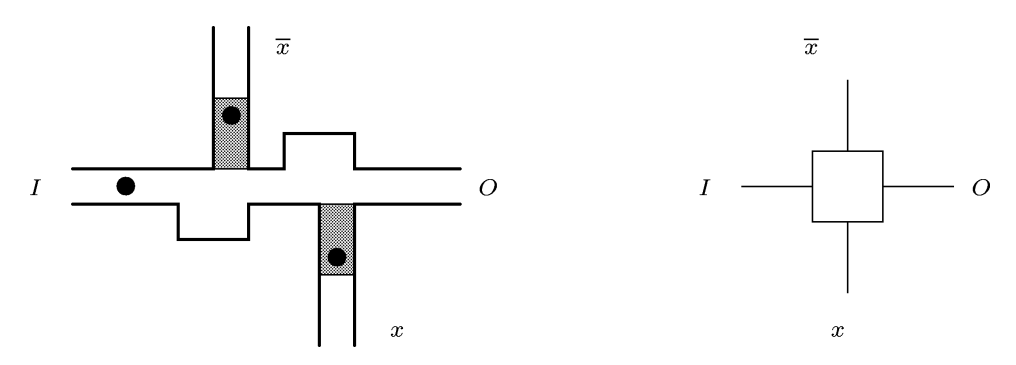
selektor je prikazan na slici U ovom konstrukcijskom elementu nalaze se tri kutije i četri pozicije na kojima se na kraju igre moraju nalaziti kutije. Uz ulazni i izlazni otvor u konstrukcijskom elementu se nalaze još dva otvora označena s x i \bar{x} čiju ćemo funkciju objasniti naknadno. |
| \bullet |
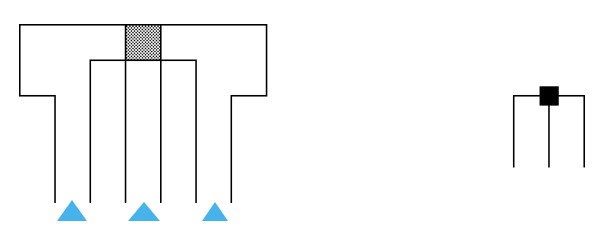
klauzula je prikazana na slici Ovaj konstrukcijski element sadrži tri otvora i jednu poziciju namijenjenu za smještanje kutije. |
Osnovna ideja dokaza teorema
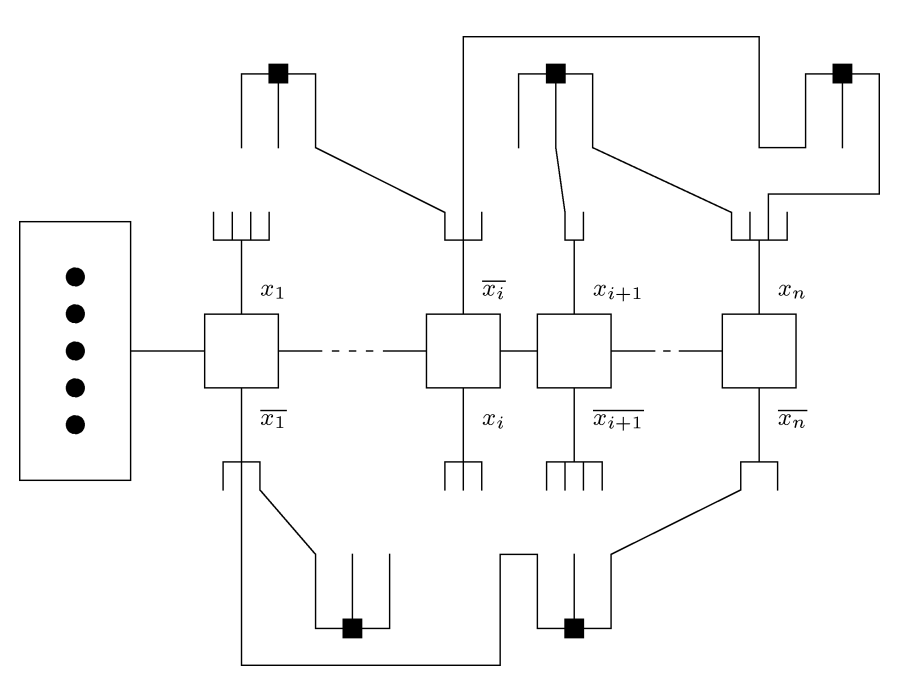
Neka je F \equiv C_{1} \bigwedge...\bigwedge C_{m} neka 3-knf s propozicionalnim varijablama x_{1},..., x_{n}. Neka je skup čvorova grafa G_{F} = (V, E), koji je induciran formulom F, jednak sljedećem skupu:
Zatim, neka je skup bridova grafa G zadan ovako:
Dakle, čvorovi grafa su elementarne disjunkcije C_{i} i varijable formule F. Varijable su bridovima spojene u jedan veliki ciklus, a svaka elementarna disjunkcija C_{i} je spojena s onim varijablama koje se, ili njihova negacija, pojavljuju u njima.
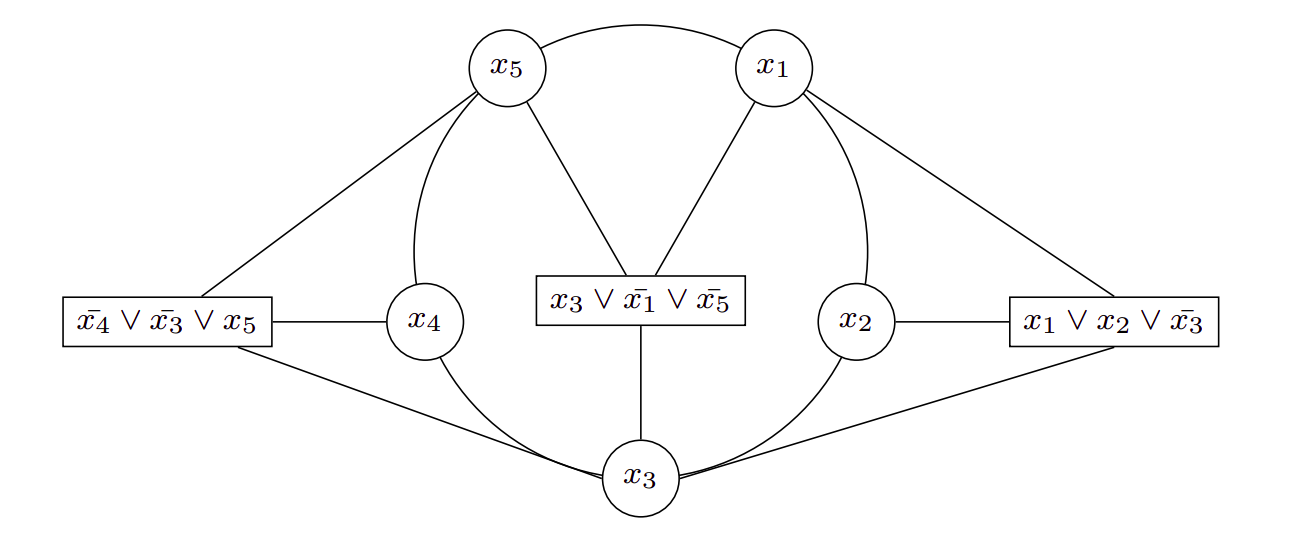
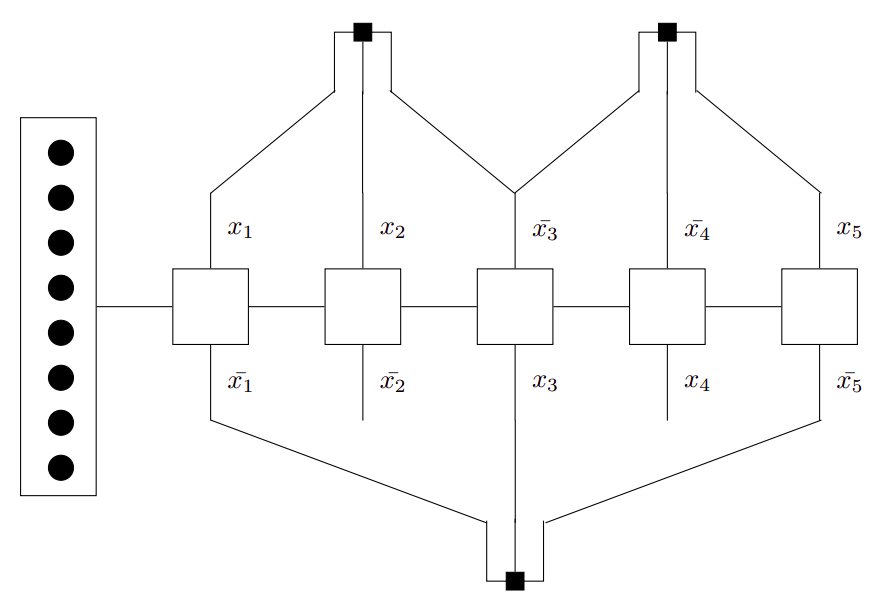
Sada želimo na jednom primjeru ilustrirati kako izgleda graf koji je induciran zadanom formulom. Na slici
Označimo s P-3-SAT problem u kojem se razmatraju samo instance problema 3-SAT za koje je inducirani graf planaran. Ovaj problem je također NP-potpun (vidi
Sada dokazujemo da je problem P-3-SAT polinomno reducibilan na problem SOKOBAN(1, 0). U tu svrhu za proizvoljnu 3-knf F čiji je inducirani graf planaran, konstruiramo početnu konfiguraciju igre kao na slici
Selektori su spojeni onim klauzulama u kojima se pripadne varijable ili njihove negacije nalaze. Preciznije, ako je x_{j} \in C_{i} tada će j-ti selektor biti spojen s klauzulom koja odgovara elementarnoj disjunkciji C_{i} kroz otvor x_{j}, a ako je \bar{x_{j}} \in C_{i} biti će spojen kroz otvor \bar{x_{j}}.
Primijetimo da se u danoj početnoj konfiguraciji nalazi još jedan konstrukcijski element koji do sada nismo opisali. Taj novi konstrukcijski element nazivat ćemo rezervoar. U njemu su na početku smještene kutije. Naime, u svakom od n selektora su na početku tri kutije i četiri mjesta namijenjena za kutije, a u svakoj od m klauzula jedno mjesto namijenjeno za kutije, što znači da fali n+m kutija kako bi na kraju igre svaka kutija bila na točno jednom namijenjenom mjestu.
Preostalo je dokazati da je formula F ispunjiva ako i samo ako za početnu konfiguraciju koju smo iz nje izgradili skladištar može smjestiti sve kutije na zadane pozicije. Neka se na početku skladištar nalazi u rezervoaru.
Pretpostavimo prvo da je F ispunjiva formula. Tada postoji interpretacija I za koju je I(F) = 1. Skladištar kreće iz rezervoara i prolazi redom po selektorima. Svaku kutiju koja mu stoji na putu mora staviti u otvor koji pripada literalu l_{i} za koji je I(l_{i}) = 0. Na taj način blokira taj otvor.
Nakon toga mora dogurati kutije do slobodnih mjesta u svakoj od klauzula. To je moguće zbog toga što su otvori selektora koji pripadaju literalima l_{i} za koje vrijedi I(l_{i}) = 1 ostali otvoreni i zato što, zbog ispunjivosti formule F, za svaku klauzulu postoji barem jedan literal za koji je I(l_{i}) = 1. Nakon što popuni tražena mjesta unutar klauzula, skladištar pomoću preostalih kutija iz rezervoara mora blokirati preostale otvore selektora. Tako je uspio sve kutije dovesti na željene pozicije.
Pretpostavimo sada da igra s početnom konfiguracijom generiranom formulom F rješiva. Cilj nam je pronaći interpretaciju I za koju je I(F) = 1. Kojim god poretkom skladištar smještao kutije na željene pozicije, kroz selektore mora proći redom od prvog do posljednjeg ulazeći u njih kroz glavni ulaz I. Naime, u selektor ne smije ući kroz otvor x_{i} ili \bar{x_{i}} jer bi u tom slučaju kutiju s tog ulaza gurnuo u kut iz kojeg ga više ne može izvaditi. Skladištar također ne smije ući u selektor kroz glavni izlaz O jer bi prije toga morao ući u neki od selektora kroz otvor x_{i} ili \bar{x_{i}}. Prolazeći redom kroz selektore, skladištar mora kutiju koja mu je na putu staviti u neki od otvora x_{i} ili \bar{x_{i}}, jer bi gurajući kutiju prema sljedećem selektoru zablokirao svoj prolaz u trenutku kad kutija koju gura dođe do kutije iz sljedećeg selektora. Ako u i-tom selektoru skladištar prvo blokira otvor x_{i}, definirat ćemo I(x_{i}) = 0, a ako prvo blokira otvor \bar{x_{i}} tada ćemo definirati I(x_{i}) = 1. Očito na taj način dobivamo interpretaciju I za koju je I(F)=1, što smo i trebali pokazati.
Na slici
U ovom članku dani su dokazi NP-težine dviju verzija igre Sokoban.
Culberson je dokazao da je standardna verzija igre Sokoban PSPACE-potpuna (vidi
Za neke druge klasične igre kao što su Minesweeper (vidi
No za razne verzije igre Sokoban je još otvoreno pitanje jesu li NP-potpune.
| [1] |
Čačić, Vedran: Komputonomikon, Izračunljivost za računarce. PMF-Matematički odsjek, 2022. |
| [2] |
Berlekamp, Elwyn R., John H. Conway ,Richard K. Guy:Winning ways for your mathematical plays. Vol. 2. Academic Press , London, 1982 , 0-12-091152-3; 0-12-091102-7 . |
| [3] |
Culberson , Joseph C. Sokoban is PSPACE-complete Sokoban is PSPACE-complete . Proceedings of the International Conference on Fun with Algorithms , 65–76, 1998. |
| [4] |
Demaine , Erik D. , Susan Hohenberger David Liben-Nowell Tetris is hard, even to approximate. Warnow , Tandy Binhai Zhu : Computing and Combinatorics , 351–363, 2003 , 978-3-540-45071-9 . |
| [5] |
Dor , Dorit Uri Zwick Sokoban and other motion planning problems. Computational Geometry , 13(4):215–228, 1999 , 0925-7721 . https://www.sciencedirect.com/science/article/pii/S0925772199000176 . |
| [6] |
Kojić , Vedran Minesweeper problem je NP-potpun. Math.e , 12:0–0, 2007. http://e.math.hr/old/minesweeper/index.html. |
| [7] |
Lichtenstein1982PlanarFA} Lichtenstein , David Planar formulae and their uses. SIAM Journal of Computation , 11:329–343, 1982. |
| [8] |
Lichtenstein , David Michael Sipser Go is polynomial-space hard. Journal of ACM , 27:393–401, 1980. |
| [9] |
Sevenster , Merlijn Battleships as a decision problem. ICGA Journal , 27:142–149, 2004. |
| [10] |
Sevenster , Merlijn The Complexity of Scotland Yard , 209–246. Amsterdam University Press , 2007 , 9789053563564 . http://www.jstor.org/stable/j.ctt45kdbf.12 , 2022-06-24 |
| [11] |
Vuković , Mladen Izračunljivost, predavanja i vježbe . PMF-Matematički odsjek , 2009. |
| [12] |
Vuković , Mladen Složenost algoritama, predavanja i vježbe . PMF-Matematički odsjek , 2019. https://www.pmf.unizg.hr/_download/repository/SA-skripta-2019.pdf . |