Izracunavanje i primjena normalne slučajne varijable u kemiji
Sažetak
Veliki broj pojava u prirodi, kao i mnogi proizvodni procesi, odvijaju se uz bitnu prisutnost raznih slučajnih varijabli. Također, pri analizi in ženjerskih procesa mnoge varijable i inženjerski procesi mogu biti definirani kao slučajne varijable, poglavito u kemiji. Slučajne varijable su funkcije koje imaju realne vrijednosti i koje predstavljaju preslikavanje iz prostora slučajnih vrijednosti S u prostor realnih brojeva \textbf{R}. Slučajne varijable mogu biti diskretne, kao broj sušnih i kišnih dana u nekom periodu, ili kontinuirane, kao što su protok, intenzitet ki še, koncentracija i slično.Diskretne slučajne varijable povezane su s prebrojavanjem u nekom pokusu. One primaju konačan skup vrijednosti (ili možda beskonačan, ali je tada nužno prebrojiv i diskretan). Međutim, u pokusima se prirodno javlja i mjerenje. Skup brojeva kojima se zapisuju rezultati mjerenja nije ni konačan niti diskretan, već neki interval u skupu realnih brojeva. Na primjer slučajna varijabla koja mjeri postotak neke tvari u nekoj smjesi teoretski može primiti svaku vrijednost intervalu [0,100], a slučajna varijabla koja mjeri relativni udio neke tvari u nekoj smjesi može primiti svaku vrijednost u intervalu [0,1]. Takve slučajne varijable, koje poprimaju vrijednosti na nekom intervalu, nazivamo kontinuiranim. Poznavanje niza mogućih vrijednosti slučajne varijable ne daje dovoljnu osnovu za praktički potrebne ocjene. Na primjer, ako treba ocijeniti temperaturu zadane količine plina, a u tu svrhu se nudi samo niz podataka o mogućim brzinama njegovih molekula, tada je naravno, prvo pitanje kako se često javlja svaka od tih brzina. Drugim riječima, treba, što je samo po sebi razumljivo, saznati kolika je vjerojatnost nastupanja svake od mnogih vrijednosti promatrane slučajne varijable. Isto tako, ako su poznate vjerojatnosti raznih mogućih vrijednosti slučajne varijable, znat će se i kako se često očekuje nastupanje njenih povoljnih i nepovoljnih vrijednosti, a to je očigledno dovoljno za ocjenu efikasnosti ili kvalitete kemijskog procesa.
Zbog toga, za slučajnu varijablu vežemo još i pojmove razdioba slučajne varijable, očekivanje slučajne varijable i varijanca. Sve su ovo pojmovi koji su vrlo korisni u inženjerskim procesima, ali s druge strane nekome tko nije primarno matematičar mogu biti teški za izračunati.
Cilj ovoga rada je pokazati primjena kontinuirane slučajne varijable u kemiji i izračun vjerojatnosti iste uporabom dostupnih programskih paketa, čime se računanja višestruko ubrzava i smanjuje se mogućnost pogreške. Za takve izračune se mogu koristiti besplatni programski paketi GeoGebra i Symbolab, koji su vrlo jednostavni za korištenje kad je slučajna varijabla u pitanju. Isto tako ova dva programska paketa omogućavaju provjeru podataka dobivenih izračunom, te detaljnu analizu i međusobnu usporedbu dobivenih rezultata.
Početni dio rada daje čvrstu teorijsku bazu o slučajnoj varijabli. Iskustvo pokazuje da korištenje programske podrške, bez čvrsto utemeljenog znanja statistike i vjerojatnosti, rezultira nekvalitetnim statističkim obradama. Stoga je rad usmjeren na teoriju, konkretnu primjenu i uporabu programskih paketa.
Slučajna varijabla je numerički ishod slučajnog pokusa. Neka je S skup svih ishoda u nekom pokusu. Prema
\int_{x_{1}}^{x_{2}}f(x)dx=P(x_{1}\leq X\leq x_{2}),
odnosno pomoću funkcije gustoće vjerojatnosti, zapravo računamo vjerojatnost da slučajna varijabla X poprimi vrijednost unutar intervala \left[ x_{1},x_{2}\right].
Vjerojatnost da X poprimi vrijednost unutra intervala \left[ x_{1},x_{2}\right] dana je površinom ispod funkcije gustoće vjerojatnosti nad segmentom \left[ x_{1},x_{2}\right].
Pri tom f(x) zadovoljava sljedeća svojstva:
-
[\bullet] f(x)\geq0, za sve realne x,
- [\bullet] \int_{-\infty}^{+\infty}f(x)dx=1
Dakle, svaka ovakva funkcija definira neku razdiobu vjerojatnosti kontinuirane slučajne varijable. Iako ima puno takvih funkcija f, nas u praksi zanima samo nekoliko takvih funkcija.
f(x) = \left\lbrace \begin{array}{l@ {,}l} \cos x & x\in \langle 0, \frac{\pi}{2} ] \\ 0 & x \notin \langle 0, \frac{\pi}{2} ] \end{array} \right.
funkcija gustoće vjerojatnosti neke kontinuirane slučajne varijable X. Odrediti
P(\frac{\pi}{4}\lt X\leq\frac{\pi}{2}).
Iz definicije funkcije f očito je da se radi o nenegativnoj funkciji:
- -
-
na intervalu \langle 0, \frac{\pi}{2} ] je f(x)=\cos x, a funkcija kosinus je na tom intervalu pozitivna
- -
- na \langle -\infty, 0 ] \cup \langle\frac{\pi}{2}\rangle je f(x)=0.
Pokažimo da je funkcija f normirana:
Budući je funkcija f nenegativna i normirana, zaključujemo da može poslužiti kao funkcija gustoće neprekidne slučajne varijable.
Traženu vjerojatnost računamo na sljedeći način:
Vjerojatnost u prethodnom primjeru smo mogli izračunati, jer je pripadna funkcija gustoće f imala primitivnu funkciju, pa se računanje integrala svelo na oduzimanje dviju vrijednosti primitivne funkcije. Zaključujemo da bi nam bilo dobro uvijek znati primitivnu funkciju funkcije f, stoga definirajmo pojam funkcije distribucije.
F(x)\colon=P(X\leq x)=\int_{-\infty}^{x}f(t)dt.
Vrijednost funkcije razdiobe u točki x jednaka je površini ispod krivulje funkcije gustoće do točke x.
Ako znamo F možemo izračunati vjerojatnost da slučajna varijabla pripada pojedinom intervalu. Vrijedi:
=\int_{x_{1}}^{x_{2}}f(x)dx
\dots=P\lbrace x_{1}\leq X \leq x_{2}\rbrace
E(x)=\int_{-\infty}^{+\infty}xf(x)dx,
ukoliko ovaj integral postoji. Očekivanje još označujemo sa \mu.
E(x)=\int_{-\infty}^{+\infty}(x-\mu)^{2}f(x)dx,
ukoliko ovaj integral postoji. Varijancu još označujemo s \sigma^{2}.
\sigma=\sqrt{V(x)}.
To je najvažnija razdioba među svim kontinuiranim razdiobama, ali i među svim razdiobama općenito. To je posljedica spoznaje koja ima fundamentalno značenje u izučavanju slučajnih pojava odnosno fenomena u prirodi. Naime, većina se slučajnih pojava u prirodi odnosno u realnom svijetu koji nas okružuje asimptotski ponaša po normalnoj razdiobi. Tu razdiobu imaju i mnoge slučajne varijable koje nastaju u praksi, primjerice slučajna varijabla koja registrira grešku pri mjerenju, koja registrira rezultat mjerenja (npr. mase, visine, postotka, inteligencije, \dots), koja registrira rezultate pri dobro odmjerenom pismenom ispitu itd. Tako se na temelju teorije koja je razvijena za normalnu razdiobu dobivaju dobre prognoze o ponašanju te slučajne pojave u budućnosti. Prema
f(x))=\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{(x-\mu)^{2}}{2\sigma^{2}}}, x\in\mathbb{R}
kažemo da ima normalnu ili Gaussovu razdiobu s parametrima \mu i \sigma^{2}.
Za normalnu razdiobu koristimo oznaku
Graf funkcije gustoće vjerojatnosti za normalnu razdiobu naziva se normalna ili Gaussova krivulja (Slika 1.).
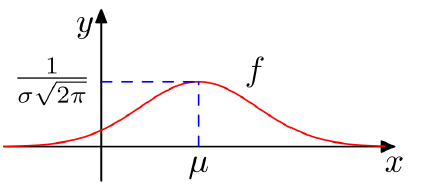
Vidimo da je graf zvonolika krivulja, simetrična obzirom na \mu.
Graf se mijenja u ovisnosti o parametrima \mu i \sigma, gdje \mu određuje središte razdiobe, \sigma koliko su podaci raspršeni (Slika 2.).
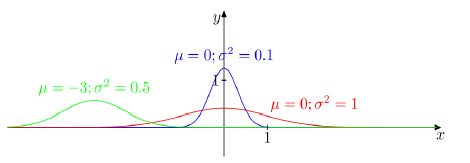
Parametar \mu normalne razdiobe jednak je njenom matematičkom očekivanju E(X), a parametar \sigma ^{2} jednak je njenoj varijanci V(X).
Funkcija razdiobe normalne varijable X\thicksim N(\mu ,\sigma ^{2}) je
Gornji integral se ne može izraziti preko elementarnih funkcija. Stoga se koriste tablice. Vrijednost gornjeg integrala ovisi o parametrima normalne razdiobe, te bi stoga za svaki par parametara trebala posebna tablica.
Međutim dovoljno je gledati samo jedan par parametara.
Uzmimo parametre \mu=0, \sigma=1. Njima je zadana jedinična normalna razdioba Z\thicksim N(0,1) s pripadnom funkcijom gustoće
Primijetimo da se varijabla jedinične normalne razdiobe u pravilu označuje sa z. Funkcija gustoće jedinične normalne razdiobe je parna funkcija, te je njezin graf simetričan obzirom na os y.
Funkcija razdiobe slučajne varijable Z\thicksim N(0,1) se označava sa \Phi
i njene vrijednosti su dane u tablicama (prilog 1.). Zbog simetrije grafa funkcije gustoće imamo da je \Phi(0)=0.5.
što ako slučajna varijabla ima normalnu razdiobu različitu od standardne? Tu nam pomaže sljedeći teorem:
Teorem 1. nam omogućava da računanje normalne razdiobe svedemo na računanje jedinične normalne razdiobe.
Pokažimo sada na primjeru primjenu kontinuirane slučajne varijable u kemiji.
- a)
-
Alkoholiza PVAL-a trajati će točno 1 sat i 45 minuta
- b)
-
Alkoholiza PVAL-a trajati će dulje od 122 minute
- c)
-
Alkoholiza PVAL-a trajati će kraće od 117 minuta
- d)
- Alkoholiza PVAL-a trajati će između 110 i 130 minuta
Rješenje:
1. Primjena programskog paketa GeoGebra
Primjer ćemo prvo riješiti pomoću matematičkog alata GeoGebra. GeoGebra je program kojeg je moguće koristiti bez prethodne instalacije, jednostavnim upisivanjem pojma GeoGebra u Google. Nakon upisivanja, potrebno je kliknuti na Klasična GeoGebra gdje se otvara sučelje koje je prikazano na Slici 3. U izborniku s desne strane kliknuti na Vjerojatnost, a nakon otvaranja novog prozora, u padajućem izborniku potrebno je odabrati opciju Normalna što je vidljivo na Slici 4.
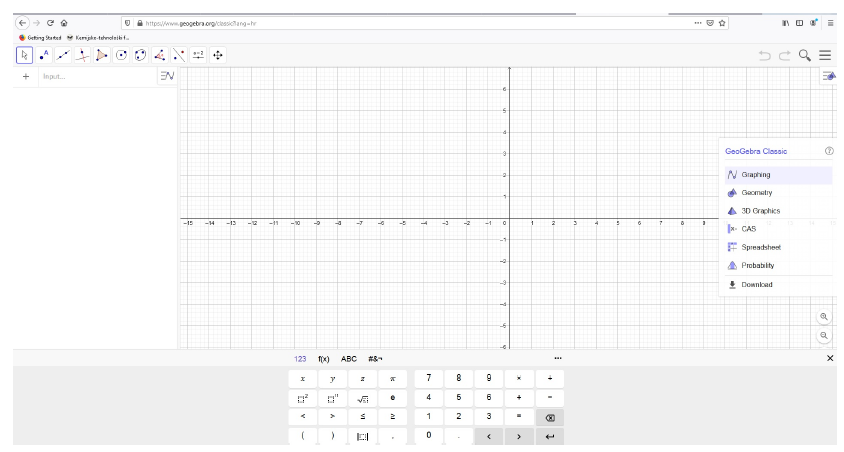
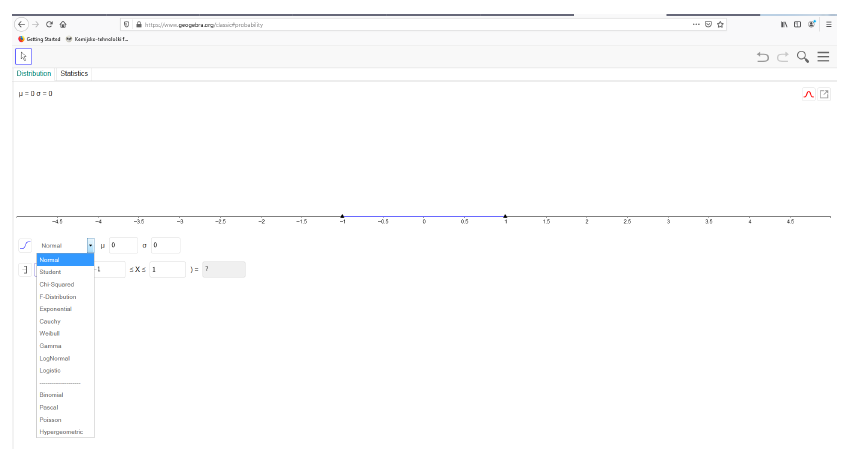
Na Slici 3. vidimo da najprije treba unijeti vrijednost za matematičko očekivanje \mu i standardnu devijaciju \sigma . U našem primjeru je trajanje alkoholize je normalna slučajna varijabla čije je očekivanje 2 sata, pa za \mu stvaljamo 120 (odnosi se na 120 minuta) i standardna devijacija 7 minuta, pa za \sigma stavljamo 7.
U zadatku pod a) pitanje je kolika je vjerojatnost da će alkoholiza PVAL-a trajati će točno 1 sat i 45 minuta, stoga je potrebno izabrati Interval, a potom unijeti vrijednost 105 slijeva i zdesna (Slika 3.).
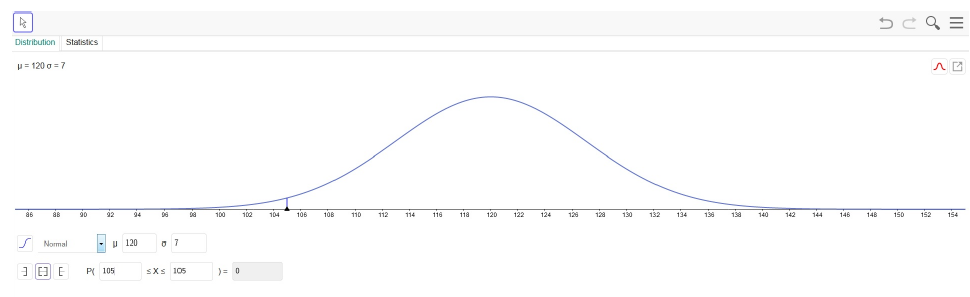
U zadatku pod b) pitanje je kolika je vjerojatnost da će alkoholiza PVAL-a trajati dulje od 122 minute, stoga je potrebno izabrati Jednostrani desni interval, a potom unijeti vrijednost 122 (Slika 5.). Dobivena vjerojatnost iznosi 0.3875.
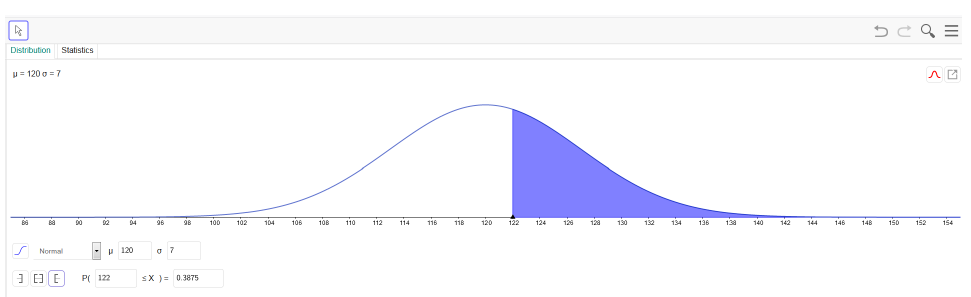
U zadatku pod c) pitanje je kolika je vjerojatnost da će alkoholiza PVAL-a trajati kraće od 117 minuta, stoga je potrebno izabrati Jednostrani lijevi interval, a potom unijeti vrijednost 117 (Slika 7.). Dobivena vjerojatnost iznosi 0.3341.
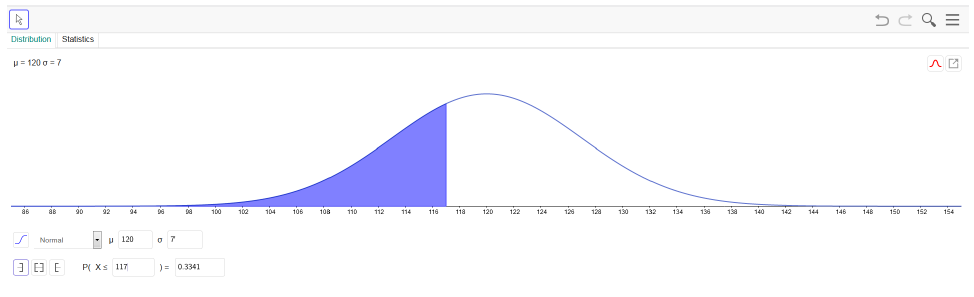
U zadatku pod d) pitanje je kolika je vjerojatnost da će alkoholiza PVAL-a trajati između 110 i 130 minuta, stoga je potrebno izabrati Interval, a potom unijeti vrijednost 110 slijeva i vrijednost 130 zdesna (Slika 8.). Dobivena vjerojatnost iznosi 0.8469.
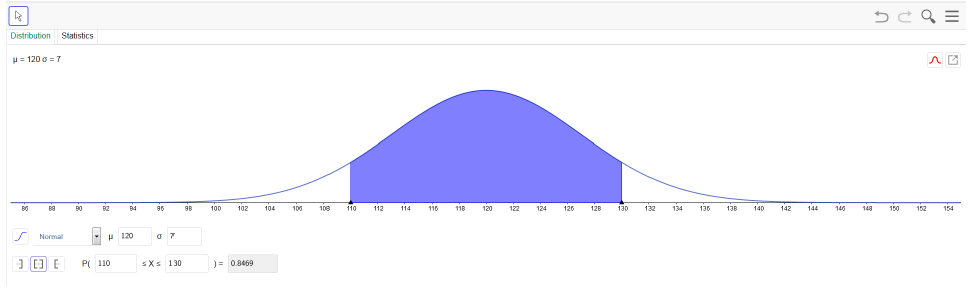
2. Numeričko rješavanje:
a) P(X=105)=0 (pogledati Napomenu 1.)
b)
1-\Phi(\frac{122-120}{7})=1-\Phi(\frac{2}{7})
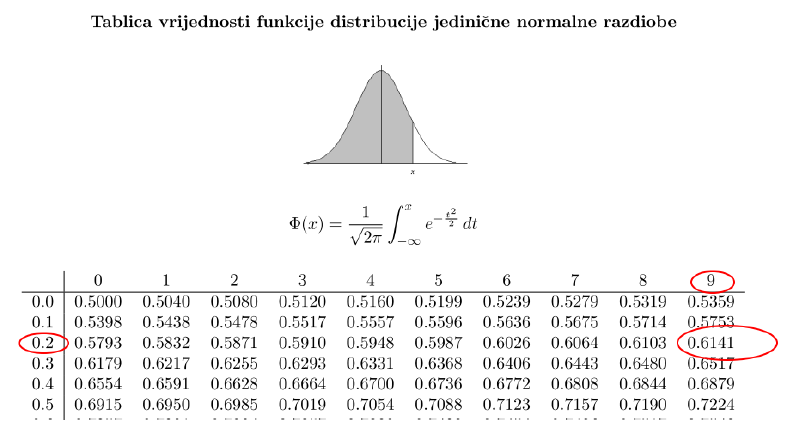
1-\Phi(0.29)=1-0.6141=0.3859
U drugom redu je vidljivo da smo računanje normalne razdiobe sveli na ra čunanje jedinične normalne razdiobe, uvođenjem varijable Z\colon=\frac{X-\mu}{\sigma}. Vrijednost \Phi(0.29) tražimo u tablicama, tako što prvo u prvom stupcu tablice pronadjemo vrijednost 0.2, a zatim u tom retku pronadjemo stupac sa vrijednošću 9 (Slika 9.)
c)
=1-\Phi(3/7)=1-\Phi(0.43)=1-0.664=0.336
d)
\Phi(\frac{10}{7})-\Phi(-\frac{10}{7})=\Phi(1.43)-(1-\Phi(1.43))
=2\cdot 0.9236-1=0.8472.
3. Primjena programskog paketa Symbolab:
a) Obzirom da sami moramo izračunati Z\colon=\frac{X-\mu}{\sigma}, za P(X=105), uopće ne postoji opcija izračuna, nego bi korisnik morao znati činjenicu da se kod kontinuiranih varijabli vjerojatnost pridru žuje intervalima realnih brojeva, a vjerojatnost pridružena pojedina čnim vrijednostima je jednaka 0.
b) Ovdje se mora koristiti formula suprotne vjerojatnosti, odnosno mora se ra čunati po formuli P(X\gt A)=1-P(X\leq A^{C}). I ne samo to, nego se za izračun P(X\gt 122) prvo mora izračunati Z=\frac{122-120}{7}=0.29 i tek onda možemo pristupiti uporabi Symbolaba.
Nakon što smo otvorili Symbolab, u prvom gornjem redu kliknemo na opciju Solutions (Slika 10.).
Na lijevoj strani će nam se pojaviti popis izračuna koje nam nudi Symbolab. Na izborniku biramo Statistics.
Nakon toga nam se pojavi izbornik pod nazivom Statistics Calculator, na kojem se u dnu pojavi mogućnost izračuna Standardne normalne distribucije (Slika 11.).
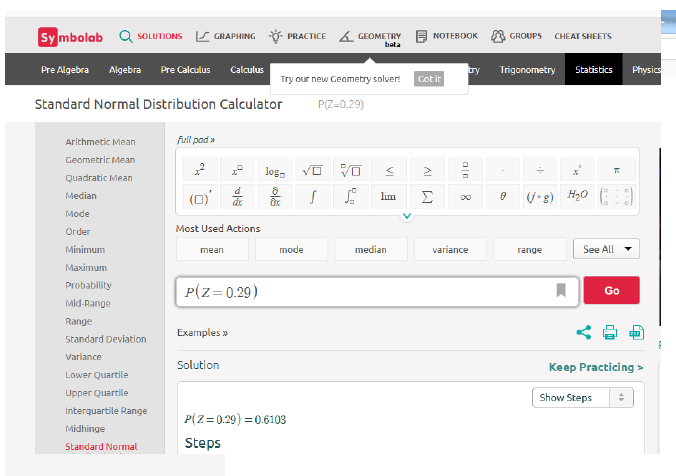
Klikom na Standardnu normalnu distribuciju pojavi se P(Z=), u koji upisemo P(Z=0.29) (Slika 12.). Vidimo da je rješenje P(Z=0.29)=0.6103. Kad smo taj korak napravili možemo izračunati suprotnu vjerojatnost, pa je rješenje
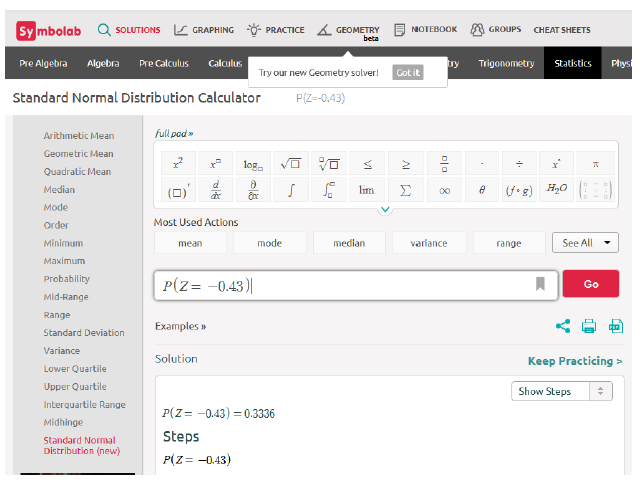
c) Za izračun P(X\lt 117) prvo mora izračunati Z=\frac{117-120}{7} =-0.43. Upisivanjem Z=-0.43 dobijemo (Slika 13.)
d) Za izračun P(110\lt X\lt 130) prvo moramo izračunati Z=\frac{130-120 }{7}=1.43 i Z=\frac{110-120}{7}=-1.43. Na isti način kao u prethodnim primjerima u Symbolabu dobijemo da je P(Z=1.43)=0.9236 i P(Z=-1.43)=0.0764, pa je rješenje
=0.9236-0.0764=0.8472
Iz konkretnog primjera iz kemije je očito da je numeričko rješavanje i postavljanje ovakvih problema složeno. Kod primjene gotovih programskih paketa GeoGebra i Symbolab, se GeoGegebra pokazala boljom opcijom, jer ne zahtjeva nikakve predizračune dok sa Symbolabom nismo u potpunosti izbjegli numeričko rješavanje.
| [1] |
W. Volk: Applied Statistics for Engineers, McGraww-Hill Book Company, Inc., United States of America, 1958. |
| [2] |
https://moodle.srce.hr/2020-2021/enrol/index.php?id=70069; (Datum zadnjeg pristupa: 22.07.2021.) |
| [3] |
B.V. Gnedenko, A.J. Hinčin: Uvod u teoriju vjerojatnosti, Tehnička knjiga, Zagreb, 1995. |
| [4] |
S. Pivac, A. Rozga: Statistika za sociološka istraživanja, Sveučilište u Splitu, Split, 2006. |
| [5] |
http://matematika.fkit.hr/novo/statistika_i_vjerojatnost/predavanja/4-Osnove_teorije_vjerojatnosti_za_inzenjere_3.dio.pdf ; (Datum zadnjeg pristupa: 07.07.2021.) |
| [6] |
N. Koceić Bilan: Primijenjena statistika, Prirodoslovno-matematički fakultet u Splitu, Split, 2011. |
| [7] | https://www.mathos.unios.hr/uvis/poglavlje2.pdf (Datum zadnjeg pristupa: 14.07.2021.) |

