Trisekcija kuta
Marko Srebačić
Trisekcija kuta, još od starih Grka zadavala je glavobolje matematičarima, koji su je pokušavali riješiti samo uz pomoć ravnala i šestara. Takav način rješavanja konstrukcije postavila je Platonova akademija.
Matematičari su dolazili do različitih rješenja ovoga problema, od blago rečeno uzaludnih do poprilično približnih, pa sve do točnih rješenja uz pritom korištenih pomoćnih krivulja ili drugih sredstava. Na posljetku matematičari su došli do zaključka da trisekcija kuta ne može riješiti uz pomoć euklidskih konstrukcija.
Tema je obrađena s povijesnog stajališta i pokazana je nekoliko rješenja dobivenih neeuklidskim metodama do kojih su došli slavni matematičari. Također pokazane su dvije približne konstrukcije trisekcije kuta, do kojih se došlo euklidskim metodama. Uz primjer načina konstrukcija, prikazana su i "rješenja" kojima je prikazano kolika su odstupanja s tim načinom rješavanja navedenog problema.
Povijest trisekcije kuta
Geometrijske konstrukcije predstavljale su značajan dio matematike starih Grka. Oni su konstrukcije vršili isključivo ravnalom i šestarom, pri čemu su ravnalo koristili za spajanje dviju točaka, a šestar za crtanje kružnica, kojima su unaprijed poznati središte i radijus. Akademija koja je postavila takva pravila, bila je Platonova akademija, koja je djelovala od 387. godine prije nove ere, do 529. godine nove ere. Navedeni pristup geometrijskim konstrukcijama doveo je do niza matematičkih problema, među kojima su najpoznatija tri: kvadratura kruga, duplikacija kocke i trisekcija kuta. Važno je napomenuti da su pokušaji rješavanja tih problema doveli do velikog razvoja tadašnje matematike, a matematičarima diljem svijeta ovi su problemi i danas jednako zanimljivi.
Problem trisekcije kuta bio je poznat Grcima još iz doba Antike. Stoljećima su matematičari tražili eukidske konstrukcije, koristeći samo ravnalo i šestar, pa isto tako i druge pristupe: točna rješenja pomoću pomoćnih krivulja i približne vrijednosti euklidskih metoda. Najutjecajniji matematičari koji su se bavili ovim problemom bili su Grci Hipija, Arhimed i Nicomedes. Rani rad na tom problemu pokazuje svaki zamisliv stupanj vještine, u rasponu od najviše uzaludnih,do izvrsnih približnih rješenja, kao i genijalno rješenje koristeći "više" krivulje. Matematičari su na kraju došli do empirijskog zaključka da se problem trisekcije kuta ne može riješiti putem euklidskih konstrukcija, ali to je uzdiglo dublji problem: potreba za dokazom njegove nemogućnosti pod navedenim ograničenjima.
Prema tradicionalnoj klasifikaciji korištenoj u Antici postoje tri vrste problema u geometriji:ravnine, čvrstog tijela i linearan. Problem ravnine je takav problem koji se može riješiti euklidskim metodama, koristeći ravne linije i kružnice. Koristeći jedan ili više dijelova konusa, pod nazivom površina stošca, rješavamo problem čvrstog tijela. Problemi koji uključuju druge linije osim prethodnih navedenih, koje imaju manje prirodne i složenije izvore jer su generirane od više nepravilnih površina ili čisto mehaničkih konstrukcija, zovu se linearni. Rani matematičari su posebno bili zainteresirani za trisekciju kuta uz pomoć metode ravnine. Kako se uspostavilo, trisekcija kuta nije problem ravnine, već problem čvrstog tijela. To je razlog zašto rani matematičari nisu uspjeli pronaći opću konstrukciju trisekcije kuta uz pomoć euklidskih konstrukcija, iako su našli elegantna rješenja temeljena na korištenju konika i drugih sofisticiranih krivulja.
Trisekcija kuta ili općenitije, podjela kuta na bilo koji broj jednakih dijelova, prirodni je nastavak problema bisekcije kuta, koji je riješen u antičko doba. Euklidsko rješenje za problem bisekcije kuta, kao što je navedeno u njegovom djelu "Elementi", je kako slijedi:
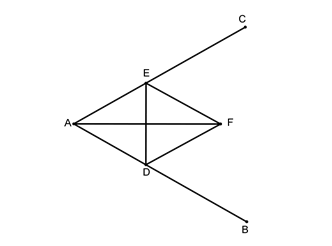
" Napraviti bisekciju pravolinijskog kuta: Neka je kut \(BAC\) zadani pravolinijski kut. Stoga je potrebno da ga prepolovimo. Neka je točka \(D\) nasumično uzeta na \(AB\); neka se na \(AC\) odsiječe \(AE\) koji je jednak \(AD\); spojimo točke \(D\) i \(E\) i neka se na \(DE\) konstruira jednakostraničan trokut \(DEF\); spojimo točke \(A\) i \(F\). Kažemo da je ravna linija \(AF\) prepolovila kut \(BAC\). Jer, budući da je \(AD\) jednaka \(AE\) i \(AF\) im je zajednička, dvije stranice \(DA\) i \(AF\) su jednake dvjema stranica \(EA\) odnosno \(AF\). Baza \(DF\) jednaka je bazi \(EF\); stoga kut \(DAF\) jednak je kutu \(EAF\). Stoga je dani pravolinijski kut \(BAC\) podijeljen na dva jednaka dijela ravnom linijom \(AF\)".
Postoji nekoliko načina po kojima je problem trisekcije kuta različit od preostala dva klasična problema. Prvi je taj da nema stvarnu povijest koja se odnosi na način kojim se ovaj problem prvi put počeo proučavati. Drugo, to je problem sasvim druge vrste. Čovjek ne može kvadrirati krug, niti može duplicirati kocku. Ali, moguće je napraviti trisekciju kuta za određene kutove. Za primjer prilično je jednostavno napraviti trisekciju pravog kuta. Za dani pravi kut \(CAB\) konstruiraj kružnicu takvu da siječe \(AB\) u točki \(E\). Konstruiramo drugu kružnicu jednakog radijusa sa centrom u točki \(E\). Sjecište dviju kružnica je točka \(D\). Tada je trokut \(DAE\) jedankostraničan i stoga je kut \(DAE = 60^{\circ}\) i kut \(DAC = 30^{\circ}\). Time je riješena trisekcija kuta \(CAB\).

Iako je teško dati točan datum kada se problem trisekcije kuta prvi put pojavio, zna se da je Hipokrat, koji je dao prvi veliki doprinos problemu kvadriranju kruga i duplikacije kocke, također proučavao problem trisekcije kuta. Postoji prilično jednostavan način trisekcije kuta koji je poznat Hipokratu.
On funkcionira na sljedeći način. S obzirom na dani kut \(CAB\) konstruiramo okomicu \(CD\) na \(AB\) tako da ju siječe u točki \(D\). Konstruiramo pravokutnik \(CDAF\). Produžimo \(FC\) do točke \(E\) i tada spojimo \(A\) i \(E\) tako da siječe \(CD\) u \(H\). Točka \(E\) je odabrana tako da \(HE=2AC\). Sada je kut \(EAB\) jednak \(\frac{1}{3}\) od kuta \(CAB\).
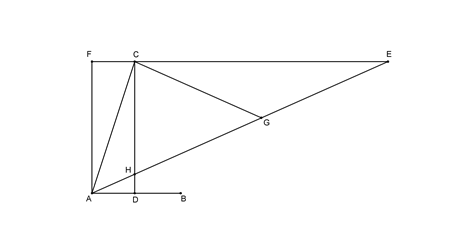
Kako bi se to vidjelo, neka je \(G\) polovište od \(HE\) tako da \(HG=GE=AC\). Kako je \(ECH\) pravi kut, stoga je \(CG=HG=GE\). Sada je \( \measuredangle EAB=\measuredangle CEA=\measuredangle ECG\). Također, budući da je \(AC\)=\(CG\) tada je kut \(CAG\) jednak kutu \(CGA\). Ali \(\measuredangle CGA=\measuredangle GEC+\measuredangle ECG=2CEG=2EAB\) kako je potrebno.
Jedan od razloga zašto je problem trisekcije kuta bio manje privlačan od preostala dva problema kod grčkih matematičara je da iako konstrukcija iznad nije moguća s neoznačenim ravnalom i šestarom, ipak je lako provediva u praksi. Mehanički tip rješenja je lako za naći. Dovoljno je označiti duljinu od \(2AC\) na desnoj strani ravnala, a zatim klizimo ravnalom s jednim označenim krajem po \(CD\) i drugim krajem po polupravcu \(FC\) do te mjere da ravnalom definiramo pravac kroz \(A\). Trisekcija je nađena na prilično jednostavan mehanički način.
Dokaz nerješivosti
Da se dokaže nerješivost ove konstrukcije ravnalom i šestarom, dovoljno je da to dokažemo za jedan posebni kut.
Na temelju Moivreove formule imamo \[(\cos\frac{\varphi }{3}+i\sin\frac{\varphi }{3})^{3}=\cos \varphi +i\sin \varphi \]
\[\scriptsize (\cos^3\frac{\varphi}{3}-3\cos\frac{\varphi}{3}\sin^2\frac{\varphi}{3})+i(3\cos^2\frac{\varphi}{3}\sin\frac{\varphi}{3}-\sin^3\frac{\varphi}{3})=\cos\varphi + i\sin\varphi\]
Odatle slijedi \[\sin\varphi=3\cos^{2}\frac{\varphi }{3}\sin\frac{\varphi }{3}-\sin^{3}\frac{\varphi}{3} \]
ili\[\sin\varphi=3\sin\frac{\varphi }{3}-4\sin^{3}\frac{\varphi }{3}.\]
Neka je uz jediničnu dužinu dan i kut \(\varphi\). Sada možemo smatrati \(\sin\varphi\) kao danu veličinu, a \(\sin\frac{\varphi}{3}\) traženu veličinu. Uvrstimo li sada \[\sin\varphi = a\] \[\sin\frac{\varphi}{3}=x\] u gornju jednadžbu, dobijemo \[4x^3-3x+a=0.\]
Uvrstimo ovdje još \(y=2x\) i dobijemo \[y^3-3y+2a=0.\]
Promotrit ćemo dalje poseban slučaj trisekcije kuta od \(30^{\circ}\). Kako je \(\sin30^{\circ}=\frac{1}{2}\), pa je onda \(a=\frac{1}{2}\), pa je gornja jednadžba oblika \[y^3-3y+1=0.\]
Kad bi ova konstrukcija bila rješiva tada bi gornja jednadžba morala imati jedno iz racionalnih brojeva konstruktibilno rješenje. Prema teoremu
Ako kubna jednadžba \[x^{3}+a_{2}x^{2}+a_{1}x+a_{0}=0\] s racionalnim koeficijentima nema ni jedno racionalno rješenje, onda ni jedno njeno rješenje nije konstruktibilno iz racionalnih brojeva.
bi tada jednadžba \(y^3-3y+1=0\) morala imati barem jedno racionalno rješenje i to bi rješenje prema teoremu
Ako neka kubna jednadžba \[x^{3}+a_{2}x^{2}+a_{1}x+a_{0}=0\] s cjelobrojnim koeficijentima ima racionalno rješenje \(x_1\), tada je taj \(x_1\) cijeli broj i djelitelj od \(a_0\).
moralo biti djelitelj od 1. Kako ni -1 ni +1 nije rješenje od \(y^3-3y+1=0\), to smo time došli do proturječja, odakle vidimo da ova geometrijska konstrukcija nije rješiva ravnalom i šestarom.
Kako možemo neograničeno mnogo vrijednosti od \(a\) navesti za kojih jednadžba \(y^3-3y+2a=0\) vodi opet do nerješivosti odgovarajuće konstrukcije, to očito ima neizmjerno mnogo kutova kod kojih trisekcija nije izvediva ravnalom i šestarom.
Promotrimo kratko još nekoliko slučajeva kada je trisekcija kuta rješiva. Kut od \(90^{\circ}\) očito možemo lako podijeliti na tri dijela. U tom slučaju je \(a=1\), pa jednadžba \(y^3-3y+2a=0\) glasi sada \[y^3-3y+2=0,\] pa se lako provjeri rješivost konstrukcije.
Dalje je očito da ako je za neki kut \(\alpha\) trisekcija rješiva, tada je i za polovicu od \(\alpha\) također trisekcija rješiva. Općenito je za svaki kut oblika \(\frac{\pi }{2^{n}}\), gdje je \(n\) neki pozitivni cijeli broj, trisekcija rješiva.
Osim ovih slučajeva, postoje još i drugi kutovi za koje je trisekcija izvediva. Neka je \(s\) mjerni broj dužine koju smo dobili bilo kojom konstrukcijom iz jedinične dužine. Uvrstimo \[\sin\varphi=a=s^3-3s,\] pa je time moguće konstruirati i kut \(\varphi\). Pripadna jednadžba je sada oblika \[y^3-3y-s^3+3s=0.\] Rješenje ove jednadžbe je \(s\), pa je time i trisekcija ovog kuta izvediva.
Arhimedova konstrukcija - trisekcija kuta pomoću trake papira
Kao što je poznato, ovaj problem se ne može riješiti sa šestarom i ravnalom. Pretpostavimo li uporabu još drugih pomagala, mogu se napraviti takve konstrukcije. Tako ćemo sada prikazati vrlo jednostavno i s teorijskog gledišta vrlo zanimljivo rješenje trisekcije kuta pomoću ravnala, šestara i trake papira.
Ova metoda, to jest konstrukcija je dana u arapskom djelu "Knjiga lema" koja se pripisuje Arhimedu. Sigurno ovo djelo nije samo prijevod arhimedovih radova, jer je Arhimed citiran nekoliko puta u djelu na takav način da si ne može to pripisati za sebe. Međutim većina povjesničara matematike vjeruje da mnogi rezultati u "Knjiga lema" doista dobiveni zbog Arhimeda i rezultat trisekcije kuta je toliko u duhu njegovog rada na spirali da je široko prihvaćeno da je ova metoda doista Arhimedova.
Uzimamo \(S\) kao vrh kuta \(\Phi\) kojega ćemo podijeliti na tri jednaka dijela. Konstruiramo kružnicu radijusa \(r\) koja presijeca krakove kuta \(\Phi\) u točkama \(A\) i \(B\). Nanesemo na rub trake papira točke \(Q\) i \(P\) tako da je \(\left | QP \right |=r\). Položimo tu traku papira na našu ravninu crteža tako da joj točka \(Q\) bude na pravcu \(SA\) i da joj rub prolazi točkom \(B\). tu traku sada pomičemo tako sa točka \(Q\) ostaje na pravcu \(SA\) i da joj rub stalno prolazi kroz \(B\), i to tako dugo dok joj točka \(P\) ne padne u točku na kružnici. Tada \(\measuredangle PQS=\varphi\) je jedna trećina danog kuta \(\Phi\).
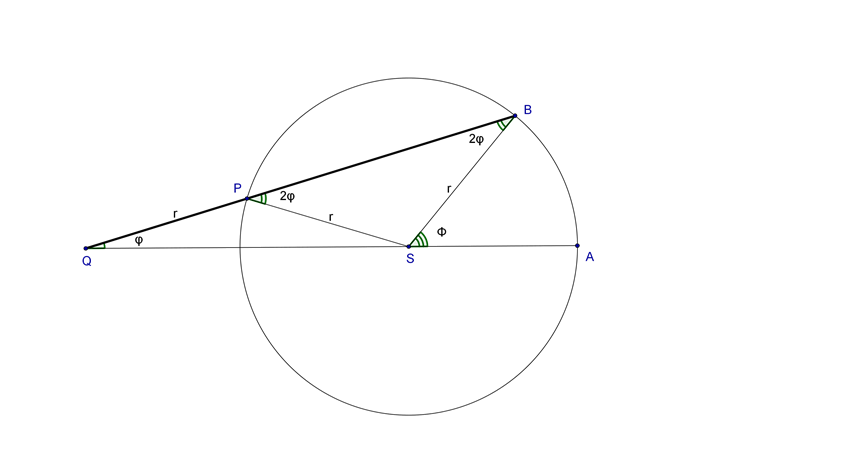
DOKAZ: Kako je \(PS\)=\(PQ\) \(\left ( =r \right )\), \(\bigtriangleup PQS\) je jednakokračan pa je stoga i \(\measuredangle PSQ\) veličine \(\varphi \), dok je vanjski kut \(\measuredangle SPB\) tada jednak \(2\varphi\). Kako je \(\bigtriangleup SPB\) također jednakokračan, \(\measuredangle SBP\) = \(\measuredangle SPB\) = \(2\varphi\). Konačno, kako je vanjski kut \(\Phi\) u vrhu \(S\) trokuta \(\bigtriangleup SBQ\) jednak zbroju dva nesusjedna unutarnja kuta \(\measuredangle SQB\) i \(\measuredangle SBQ\), doznajemo da je \(\Phi =\varphi +2\varphi\) ili \[\varphi =\frac{1}{3}\Phi. \]
Trisekcija kuta pomoću fiksne hiperbole
Problem trisekcije kuta se također može riješiti uz pomoć fiksne hiperbole, kako je grčki matematičar Pappus pokazao u svojem genijalnom remek-djelu \(\Sigma \upsilon \nu \alpha \gamma \omega \gamma \alpha \iota\) \(\mu \alpha \theta \eta \mu \alpha \tau \iota \kappa \alpha \iota\) (Collectiones mathematicae ili matematičke zbirke).
Kako bi razumjeli konstrukciju prvo moramo riješiti sljedeći problem: Pronađi geometrijsko mjesto točaka vrha \(P\) trokuta \(ABP\) sa fiksnom bazom \(AB\) kada su kutovi baze \(\alpha \) i \(\beta\) jedan prema drugome u omjeru 2:1.
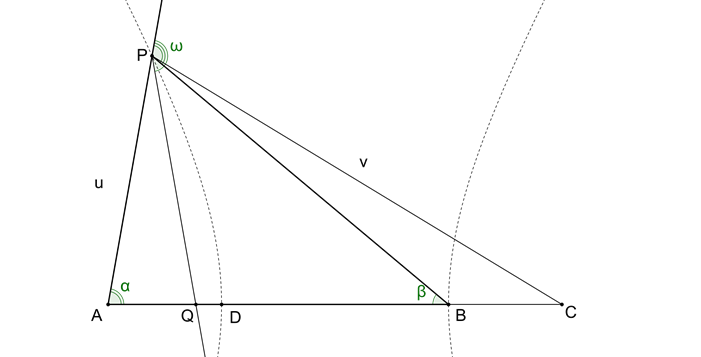
Neka je \(AB = 3k\), \(AP = u\). Položimo kut \(\beta\) u točki \(P\) na dužini \(PB\) i odredimo točku \(Q\) kao mjesto presijecanja kraka kuta \(\beta\) i dužine \(AB\). Trokuti \(BPQ\) i \(APQ\) su jednakokračni ( \(\measuredangle AQP\) je kao vanjski kut od trokuta \(BPQ\) jednak \(2\beta = \alpha\)); stoga slijedi \(AP = QP = BQ = u\). Tada produžimo \(AB\) za \(BC = k\) i postavimo da je \(CP\) jednako \(v\). Iz lika \(AQCP\) slijedi, prema Stewartovom teoremu (vidi http://en.wikipedia.org/wiki/Stewart's_theorem), da je \[v^{2}-u^{2}=CA\cdot CQ=4k(k+u)\] ili \[v^{2}=(u+2k)^{2},\] jednostavnije \[v = u+2k\] ili isto \[v-u = 2k.\]
Ovo je jednadžba geometrijskog mjesta točaka sa kooordinatama \(u , v\).
Geometrijsko mjesto točaka je dakle hiperbola sa žarištima u točkama \(A\) i \(C\) i glavnom osi \(BD = 2k\). ( \(D\) leži između \(A\) i \(B\) tako da prema jednadžbi geometrijskog mjesta točaka \(v-u = 2k, CD = 3k\), i \(AD = k\).
Razmotrimo sada da je hiperbola nacrtana za svaki \(k\). ( Dovoljno je uzeti u obzir polovicu krivulje koja pripada žarištu \(A\) i da je iznad glavne osi.)
Tada nazovimo vanjski kut trokuta \(ABP\) u vrhu \(P\) \(\omega\), to jest \[\measuredangle ABP=\beta =\frac{1}{3}\omega. \]
DOKAZ: Iz \(\measuredangle APB=180^{\circ}-\omega \) zaključujemo da je \(\alpha +\beta =\omega\) i iz toga slijedi ( zato jer je \(\alpha=2\beta\)), \(3\beta=\omega\).
Primjeri "konstrukcija"
- Primjer 1
- Primjer 2
- Primjer 3
- Primjer 4
Literatura
- Dorrie - 100 Great Problems Of Elementary Mathematics
- Palman - Geometrijske konstrukcije
-
http://www.math.rutgers.edu/~
cherlin/History/Papers2000/ jackter.html -
http://www-history.mcs.st-and.
ac.uk/HistTopics/Trisecting_ an_angle.html

