Analiza poginulih u prometu
Sažetak
Koliko puta ste čuli da su žene lošiji vozači od muškaraca ili da su mladi zbog svoje neopreznosti i neiskustva glavni krivci za prometne nesreće? Ovim člankom odlučile smo istražiti govore li i statistički podaci u prilog tim tvrdnjama. Također provjeravamo kakav je utjecaj promjene Zakona o sigurnosti prometa na cestama na broj poginulih, te utječe li obrazovanje vozača na učestalost njihova stradavanja u prometnim nesrećama. Od 2004. do 2008. godine u Hrvatskoj se dogodilo 307 470 prometnih nesreća u kojima je poginulo 3102 ljudi. Ove zastrašujuće brojke dovoljan su razlog da se ovo istraživanje ne shvati olako.
1Uvod
U posljednjih nekoliko godina u Hrvatskoj je sve izraženiji problem nesigurnosti na cestama i velikog broja prometnih nesreća. Svakodnevno smo okruženi lošim vijestima s prometnica te pokušajima da se promjenama zakona i akcijama MUP-a takvo stanje promijeni. Ponukani time, odlučile smo detaljnije istražiti neke od aspekata te crne statistike.
Točnije, ciljevi ovog rada su:
| \bullet | ispitati ovisnost smrtnosti po dobnim skupinama o spolu, dobu dana i danu u tjednu |
| \bullet | ispitati ovisnost smrtnosti o stupnju obrazovanja u svim dobnim skupinama |
| \bullet | odrediti očekivanu dob vozača u trenutku nesreće |
| \bullet | provjeriti utjecaj promjene Zakona o sigurnosti prometa na cestama na smrtnost u dobnoj skupini 20 - 29 |
Prije analize podataka, važno je upoznati se s temeljnim pojmovima korištenima u članku, pa slijedi kratak prikaz glavnih definicija koje se spominju u nastavku.
Statistika je skup ideja i metoda koje se upotrebljavaju za prikupljanje i interpretaciju podataka u nekom području istraživanja te za izvođenje zaključaka u situacijama gdje su prisutne nesigurnosti i varijacije.
Statistička populacija je potpun skup mogućih mjerenja ili podataka o nekom svojstvu koji odgovaraju cijeloj familiji jedinki koju se promatra. U našem slučaju populaciju čine vozači/vozačice koji su poginuli u prometnim nesrećama u razdoblju od srpnja 2004. do lipnja 2009. Podaci su dobiveni iz Državnog zavoda za statistiku, a među ostalim sadržavaju informacije o dobnoj, spolnoj i obrazovnoj strukturi poginulih te o mjesecima, odnosno danima kad su se nesreće dogodile.
Svrha procesa prikupljanja podataka je izvođenje zaključaka o populaciji. Budući da nije uvijek moguće prikupiti sve podatke o području istraživanja, zaključci izvedeni statističkom analizom su nesigurni jer se zasnivaju na promatranju samo manjeg dijela populacije, tj. na nepotpunim podacima. Skup mjerenja na tom dijelu populacije proveden tijekom istraživanja nazivamo uzorak. Naš uzorak čini dio vozača iz već navedene populacije odabranih na slučajan način.
Cilj statističke analize je na osnovi podataka iz uzorka izvesti određene zaključke o populaciji te ocijeniti nesigurnosti koje su obuhvaćene tim zaključivanjem.
Za grafički prikaz podataka, kao i računanje konkretnih vrijednosti pri provođenju statističkih testova koristili smo se programom R
2Opisna statistika
Opisna statistika je grana statistike koja se bavi predočavanjem i opisivanjem glavnih karakteristika prikupljenih podataka.
Za početak, korisno je podatke prikazati grafički, za što smo se koristili histogramima i strukturnim dijagramima.
Općenito, histogram je definiran kao način prikazivanja podataka raspoređenih u određene kategorije ili grupe. Kategorije, u koje smo grupirali podatke, nalaze se na osi apscisa, a prikupljeni podaci koji pripadaju određenoj kategoriji nalaze se na osi ordinata.
Kod strukturnog dijagrama svaka je kategorija ili grupa prikazana kružnim isječkom čija je površina proporcionalna udjelu te kategorije u uzorku.
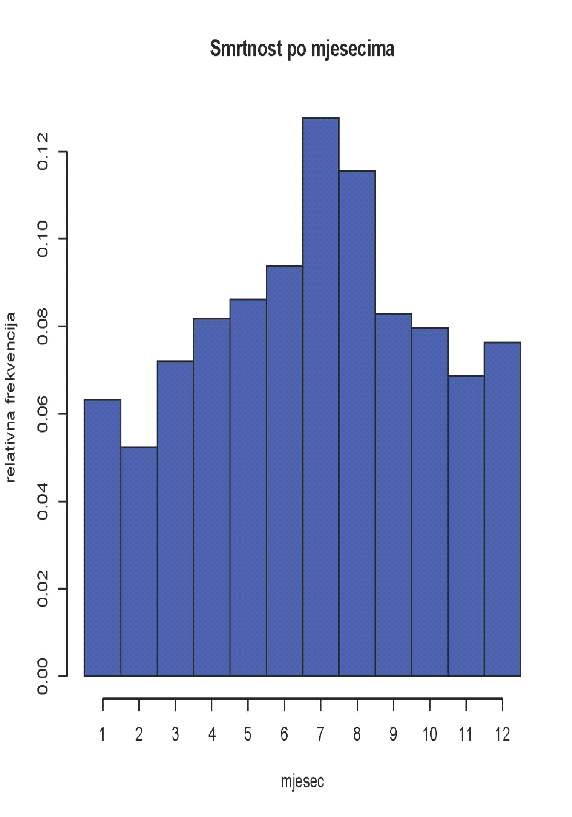
Ovim izborom prikaza podataka dobiven je izvrstan pregled raspoređenosti broja nastradalih kroz mjesece u godini, te dobar uvid u spolnu i dobnu strukturu poginulih u promatranom razdoblju (slika
Iz histograma je očito da najviše ljudi pogine u srpnju, što je vjerojatno posljedica činjenice da tada najviše Hrvata kreće na godišnji odmor. Iako je uvriježeno mišljenje da su zimski mjeseci najopasniji za vozače zbog loših vremenskih uvjeta, iznenađujuće je da je najmanja smrtnost u siječnju i veljači.
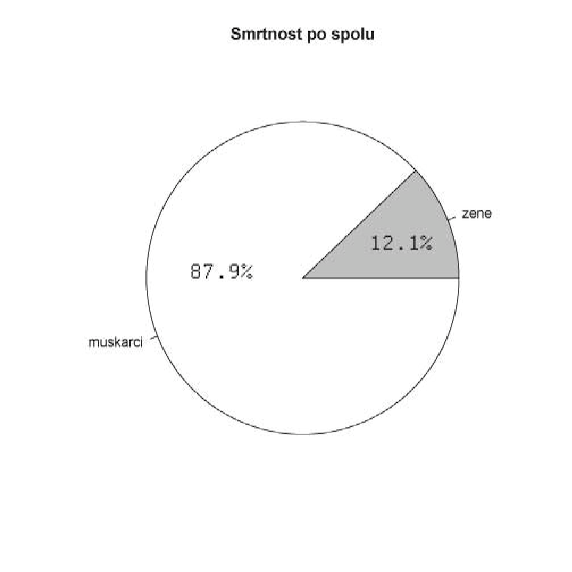
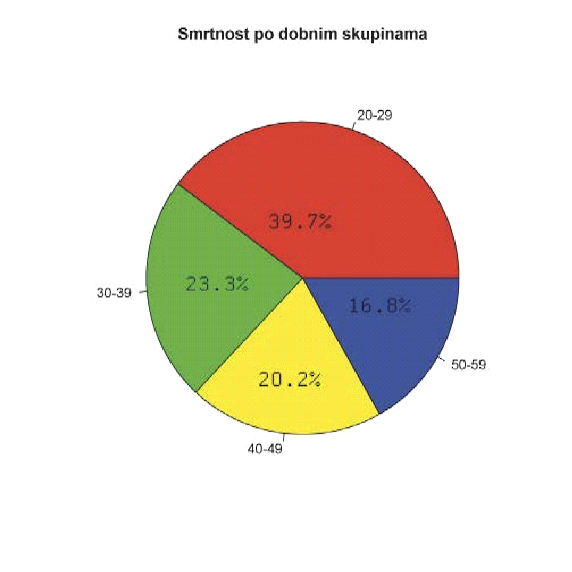
Iz strukturnih dijagrama (slike
Iako se za žene govori da su lošiji vozači od muškaraca, sa strukturnog dijagrama po spolu vidimo da pogine gotovo 7 puta više muškaraca nego žena.
3Testiranje statističkih hipoteza
Tijekom istraživanja mjeri se neko numeričko ili nenumeričko obilježje koje označavamo s X. Rezultat mjerenja obilježja X označavamo s x. Slučajni uzorak tada možemo prikazati kao \left(X_{1} ,\ldots,X_{n} \right), gdje je n duljina uzorka, a s \left(x_{1} ,\ldots,x_{n} \right) označiti jednu realizaciju tog uzorka.
Opažene frekvencije definiramo kao N_{j} =\sum _{i=1}^{n}{\text{1}}_{\left\lbrace X_{i} =a_{j} \right\rbrace }, j=1,\ldots,k, pri čemu izraz {\text{1}}_{\left\lbrace X_{i} =a_{j} \right\rbrace } poprima vrijednost 1 ako je X_{i} =a_{j}, a inače poprima vrijednost 0, gdje je a{}_{j} jedan od rezultata mjerenja obilježja X u uzorku duljine n.
Broj \frac{N_{j} }{n} zove se relativna frekvencija.
Statistička hipoteza je bilo koja pretpostavka o distribuciji obilježja X, tj. pretpostavka da X ima sljedeću distribuciju:
\left(\begin{array}{cccc} {a_{1} } & {a_{2} } & \ldots & {a_{k} } \\ {p_{1} (\theta )} & {p_{2} (\theta )} & {\ldots} & {p_{k} (\theta )} \end{array}\right),
pri čemu \theta označava parametre o kojima ta distribucija može ovisiti, a_{1}, a_{2}, \ldots, a_{k} označavaju rezultate mjerenja, a {p_{1} (\theta )}, {p_{2} (\theta )},\ldots, {p_{k} (\theta )} vjerojatnosti da će se ti rezultati postići. S H_{0} označavamo hipotezu koju želimo dokazati (to je tzv. nul-hipoteza), a s H_{1} njoj alternativnu hipotezu.
Želimo na osnovi realizacije slučajnog uzorka za obilježje X donijeti odluku hoćemo li odbaciti hipotezu H_{0} ili nećemo. Postupak donošenja odluke o odbacivanju ili neodbacivanju te statističke hipoteze zove se testiranje statističkih hipoteza.
Budući da su sve odluke bazirane na uzorcima koji nisu 100% pouzdani, niti zaključak statističkog testa nije 100% pouzdan. Test će biti potpun ako možemo procijeniti vjerojatnosti mogućih pogrešaka u zaključivanju. U većini slučajeva moguće je za zadanu razinu značajnosti testa \alpha, 0 \lt \alpha \lt 1, među testovima kojima vjerojatnost pogreške prve vrste ne prelazi broj \alpha, naći test s najmanjom vjerojatnosti pogreške druge vrste. Pogrešku prve vrste radimo kad odbacujemo hipotezu H_{0} i ona je istinita, a pogrešku druge vrste radimo kad zadržavamo hipotezu H_{0} i ona je pogrešna (tj. hipoteza H_{1} je istinita).
Kako na temelju dobivenih podataka i uz unaprijed određenu razinu značajnosti zaključiti odbacuje li se hipoteza H_{0} i s kojom vjerojatnošću?
Prvo moramo izračunati vrijednost rezultata statističkog testa (test se odabire prema vrsti hipoteza), a zatim tu vrijednost usporediti s graničnom vrijednošću. Granična vrijednost je vrijednost testa za koju se hipoteza H_{0} odbacuje, a ovisi o vrijednostima iz poznate distribucije vjerojatnosti specifične za odabrani test. Područje vrijednosti za koje se H_{0} ne odbacuje nazivamo kritičnim područjem testa.
Jedan od najčešće korištenih testova u statistici je Pearsonov \chi ^{2}-test koji ćemo ovdje navesti, kako bi nam bio matematička podloga za daljnja istraživanja.
Definirajmo prvo očekivane frekvencije kao n_{j} \left(\theta \right)=np_{j} \left(\theta \right),j=1,\ldots,k.
Neka je D\left(\theta \right)=\sum _{i=1}^{k}\frac{\left(N_{j} -n_{j} \left(\theta \right)\right)}{n_{j} \left(\theta \right)} ^{2}. Mi ćemo promatrati jednostavniji slučaj kada je hipotezom H_{0} zadan parametar \theta _{0}, čime je definirana testna statistika H\equiv D\left(\theta _{0} \right).
Također definiramo broj stupnjeva slobode s df=k-1, a ako X ima \chi ^{2}-razdiobu, umjesto X pišemo \chi^{2}(df). \chi ^{2}-razdioba je jedna od najčešćih razdioba u statistici i vrijednosti koje ona poprima zadane su tablično u tzv. tablici kvantila \chi ^{2}-razdiobe.
Sada smo spremni izreći već spomenuti Pearsonov teorem o \chi ^{2}-testu:
Ako je H_{0} točna hipoteza, onda H\stackrel{D}{\longrightarrow} \chi ^{2} \left(k-1\right), kada n\to \infty.
Za zadanu razinu značajnosti \alpha, hipotezu H_{0} odbacujemo ako je opažena vrijednost h\ge \chi _{\alpha }^{2} \left(k-1\right), gdje vrijednost \chi _{\alpha }^{2} \left(k-1\right) čitamo iz tablice kvantila \chi ^{2}-razdiobe.
S \stackrel{D}{\longrightarrow} označavamo konvergenciju po distribuciji, što jednostavnim rječnikom rečeno znači da se razdioba vrijednosti s lijeve strane približava razdiobi s desne strane kada n\to \infty. Često se koristi i oznaka \sim.
Pearsonov \chi ^{2}-test najčešće se upotrebljava ako je riječ o kvalitativnim podacima ili ako tim podacima distribucija značajno odstupa od normalne. Njegova primjena posebno se ističe u slučajevima kada želimo utvrditi odstupaju li dobivene frekvencije (iz slučajnog uzorka) od frekvencija koje bismo očekivali po hipotezi koju ispitujemo. Ovim testom također možemo ispitati povezanost dviju varijabli te vjerojatnost njihove povezanosti.
Općenito, \chi ^{2}-test najpouzdaniji je u sljedećim slučajevima:
| (1) | Kada se ispituju odstupanja frekvencije uzorka od očekivane frekvencije uz zadanu hipotezu. |
| (2) | Kada se uspoređuju dva ili više nezavisnih uzoraka po nekom svojstvu, pri čemu su nam poznate frekvencije svakog od uzoraka. |
3.1Ovisnost smrtnosti u pojedninoj dobnoj skupini o spolu
Jedno od prvih pitanja koje nam se nametnulo pri proučavanju podataka jest jesu li spol vozača i njihova dob zavisna obilježja, tj. možemo li, s određenom sigurnošću, zaključiti da žene, odnosno muškarci imaju jednaku vjerojatnost pogibije u određenoj dobi. Možda naizgled ovo izgleda kao trivijalno, gotovo nevažno pitanje, no u statistici nas odgovori često mogu iznenaditi te ništa ne treba uzimati "zdravo za gotovo".
S obzirom na to da ovo ispitivanje spada u već navedene primjene \chi ^{2}-testa, odlučili smo se za njegovu varijantu \chi ^{2}-test nezavisnosti:
Promatramo dva različita obilježja X i Y. Neka je:
| \bullet | n duljina uzorka, |
| \bullet | r broj različitih vrijednosti koje poprima obilježje X, |
| \bullet | c broj različitih vrijednosti koje poprima obilježje Y. |
Neka je \left(\left(X_{1} ,Y_{1} \right),\ldots,\left(X_{n} ,Y_{n} \right)\right) slučajni uzorak iz dvodimenzionalnog statističkog obilježja \left(X,Y\right), pri čemu X može poprimiti vrijednosti \left\lbrace a_{1} ,\ldots,a_{r} \right\rbrace, a Y vrijednosti \left\lbrace b_{1} ,\ldots,b_{c} \right\rbrace.
\chi ^{2}-test nezavisnosti je statistički test kojim se testiraju hipoteze
H_{0}: X i Y su nezavisna obilježja
H_{1} : X i Y su zavisna obilježja
H_{1} : X i Y su zavisna obilježja
Po Pearsonovu teoremu, uz sitne promjene, možemo zaključiti da je testna statistika dana formulom
H=\sum _{i=1}^{r}\sum _{j=1}^{c}\frac{(N_{ij} -n\hat{p}_{i} \hat{q}_{j} )^{2} }{n\hat{p}_{i} \hat{q}_{j} } \sim\chi ^{2} \left(df\right),
gdje je
| \bullet | N_{ij} opažena frekvencija od \left(a_{i} ,b_{j} \right) u dvodimenzionalnom statističkom uzorku \left(X,Y\right), |
| \bullet | \hat{p}_{i} =\frac{N_{i} }{n}, pri čemu je N_{i} opažena frekvencija od a_{i} u uzorku za X, |
| \bullet | \hat{q}_{j} =\frac{M_{j} }{n}, pri čemu je M_{j} opažena frekvencija od b_{j} u uzorku za Y. |
Područje \left[\chi _{\alpha}^{2}(df) \right. ,\left. +\infty \right\rangle, gdje je df=rc-(r-1)-(c-1)-1, nazivamo kritično područje. Ako je h\in \left[\chi _{\alpha}^{2}(df) \right. ,\left. +\infty \right\rangle, tada odbacujemo hipotezu H_{0}, a ako je h izvan tog intervala, onda je ne odbacujemo. Broj \chi _{\alpha}^{2}(df) čitamo iz tablice kvantila \chi ^{2}-razdiobe.
U našem slučaju obilježje X (= spol) poprima vrijednosti muškarac, žena, a obilježje Y (= dobna skupina) poprima vrijednosti dobnih skupina, tj. 20 - 29, 30 - 39, 40 - 49, 50 - 59.
Podaci su prikazani sljedećom tablicom:
| 20 - 29 | 30 - 39 | 40 - 49 | 50 - 59 | \sum | |
| Muškarac | 327 | 186 | 161 | 131 | 805 |
| Žena | 37 | 28 | 24 | 23 | 112 |
| \sum | 364 | 214 | 185 | 154 | 917 |
\chi ^{2}-testom nezavisnosti koristimo se za testiranje sljedećih hipoteza:
H_{0}: Spol i dobna skupina su nezavisna obilježja
H_{1}: Spol i dobna skupina nisu nezavisna obilježja
H_{1}: Spol i dobna skupina nisu nezavisna obilježja
Test provodimo uz razinu značajnosti \alpha=5%.
Račun provodimo u programu R
> x<-matrix(c(327,186,161,131,37,28,24,23),nrow=2,byrow=T) > x [ [,1] [,2] [,3] [,4]] [[1,] 327 186 161 131] [[2,] 37 28 244 23] > chisq.test(x) Pearson's Chi-squared test data: x X-squared = 2.7395, df = 3, p-value = 0.4336
Odavde dobivamo da je h = 2.7395 i df = 3.
Promatramo u kojem intervalu se nalazi h. Budući da je h\lt \chi _{0.05}^{2}(3) =7.8147, tj. h nije unutar kritičnog područja, ne odbacujemo hipotezu H_{0} i možemo zaključiti da su obilježlja X i Y nezavisna. Dakle, smrtnost u dobnim skupinama ne ovisi o spolu pa muškarci/žene imaju jednaku vjerojatnost da poginu u bilo kojoj starosnoj dobi.
3.2Ovisnost smrtnosti u pojedninoj dobnoj skupini o danima u tjednu
Jeste li se ikada zapitali pogine li više mladih vikendom ili u tjednu? Upravo nas je to potaknulo da provjerimo tvrdnju, često isticanu u medijima ,da najviše mladih nastrada u prometnim nesrećama tijekom vikenda.
Ponovo se koristimo \chi ^{2}-testom nezavisnosti, pri čemu obilježje X poprima vrijednosti dana u tjednu (ponedjeljak, utorak, srijeda, četvrtak, petak, subota i nedjelja), a obilježje Y poprima vrijednosti dobnih skupina, tj. 20 - 29, 30 - 39, 40 - 49, 50 - 59.
Podaci su prikazani sljedećom tablicom:
| 20 - 29 | 30 - 39 | 40 - 49 | 50 - 59 | \sum | |
| Ponedjeljak | 33 | 25 | 19 | 24 | 101 |
| Utorak | 27 | 25 | 35 | 18 | 105 |
| Srijeda | 37 | 25 | 22 | 18 | 102 |
| Četvrtak | 34 | 19 | 20 | 19 | 92 |
| Petak | 51 | 36 | 25 | 26 | 138 |
| Subota | 92 | 40 | 36 | 26 | 194 |
| Nedjelja | 90 | 44 | 28 | 23 | 185 |
| \sum | 364 | 214 | 185 | 154 | 917 |
Koristimo se \chi ^{2}-testom nezavisnosti (vidi
H_{0}: Dan u tjednu i dobna skupina su nezavisna obilježja
H_{1}: Dan u tjednu i dobna skupina nisu nezavisna obilježja
H_{1}: Dan u tjednu i dobna skupina nisu nezavisna obilježja
Test provodimo uz razinu značajnosti \alpha=5%.
Računanjem u R-u
Budući da je h\gt \chi _{0.05}^{2}(18) =28.8693, odbacujemo hipotezu H_{0} (jer se h nalazi u kritičnom području) i možemo zaključiti da obilježja X i Y nisu nezavisna. Dakle, smrtnost u dobnim skupina ovisi o danu u tjednu.
Budući da X i Y nisu nezavisna obilježja, sljedeće što nas zanima jest koliko jedno obilježnje ovisi o drugom. Konkretno, u našem slučaju, koliko su dobne skupine i dani u tjednu međusobno povezani. U statistici se ta povezanost mjeri stupnjem statističke zavisnosti koji je definiran formulom:
o=\frac{f^{2} }{\min \left\lbrace r,c\right\rbrace -1},
gdje je f^{2} =\sum _{i=1}^{r}\sum _{j=1}^{c}\frac{N_{ij} }{N_{i} M_{j} } -1 (za oznake vidi
On je izračunat u R-u
3.3Ovisnost smrtnosti u pojedninoj dobnoj skupini o dobu dana
Sljedeće što ispitujemo jest distribucija smrtnosti po dobnim skupinama u određenom dijelu dana. Dijelove dana možemo promatrati kao nezavisne populacije pa se \chi ^{2}-test nameće kao logičan izbor. Ovu vrstu \chi ^{2}-testa u kojem se ispituje distribucija istog obilježja u više različitih uzoraka nazivamo \chi ^{2}-test homogenosti.
Pretpostavimo da nas zanima distribucija istog diskretnog statističkog obilježja X, koje poprima međusobno različite vrijednosti \left\lbrace a_{1} ,\ldots,a_{k} \right\rbrace, u raznim populacijama.
Želimo na osnovi nezavisnih uzoraka uzetih iz tih populacija testirati nul-hipotezu da su razdiobe od X u tim populacijama jednake, tj. homogene.
Neka je m broj populacija. Iz svake populacije nezavisno odaberemo slučajni uzorak koji predstavlja obilježje X u i-toj populaciji i označimo ga s X_{i}, i=1,\ldots,m.
\chi ^{2}-test homogenosti je statistički test kojim se testiraju hipoteze
H_{0}: X_{1} ,\ldots,X_{m} su jednako distribuirani
H_{1}: postoje i i j takvi da se distribucija od X_{i} razlikuje od distribucije od X_{j}.
H_{1}: postoje i i j takvi da se distribucija od X_{i} razlikuje od distribucije od X_{j}.
Po Pearsonovom teoremu slijedi da je testirana statistika dana formulom
H=\sum _{i=1}^{m}\sum _{j=1}^{k}\frac{(N_{ij} -\hat{n}_{ij} )^{2} }{\hat{n}{}_{ij} } \sim\chi ^{2} \left(df\right),
gdje je
| \bullet | N_{ij} opažena frekvencija od a_{i} u uzorku X_{i}, |
| \bullet | \hat{n}_{ij} =\frac{n_{i} M_{j} }{n}, n_{i} =\sum _{j=1}^{k}N_{ij}, M_{j} =\sum _{i=1}^{m}N_{ij}, n=\sum _{j=1}^{k}M_{j}. |
Područje \left[\chi _{\alpha}^{2}(df) \right. ,\left. +\infty \right\rangle, gdje je df=(m-1)(k-1), je kritično područje. Ako je h\in \left[\chi _{\alpha}^{2}(df) \right. ,\left. +\infty \right\rangle, tada odbacujemo hipotezu H_{0}, a ako je izvan tog intervala, onda je ne odbacujemo. Broj \chi _{\alpha}^{2}(df) čitamo iz tablice kvantila \chi ^{2}-razdiobe.
Podaci su dani sljedećom tablicom:
| 20 - 29 | 30 - 39 | 40 - 49 | 50 - 59 | \sum | |
| \lt0-6] | 133 | 52 | 18 | 17 | 220 |
| \lt6-12] | 44 | 28 | 46 | 44 | 162 |
| \lt12-18] | 68 | 61 | 59 | 55 | 243 |
| \lt18-24] | 119 | 74 | 62 | 37 | 292 |
| \sum | 364 | 215 | 185 | 153 | 917 |
Koristimo se \chi ^{2}-testom homogenosti da bismo testirali hipotezu:
H_{0}: smrtnost u svakom promatranom dijelu dana jednako je distribuirana
Naš test ćemo provesti uz razinu značajnosti \alpha=5%.
Računanjem u R-u
Iz danih podataka vidimo da je h\gt \chi _{0.05}^{2}(9) =16.91898, tj. h je unutar kritičnog područja, odbacujemo hipotezu H_{0} i zaključujemo da smrtnost po dobima dana nije jednako distribuirana.
3.4Utjecaj obrazovanja na smrtnost u svim dobnim skupinama
Proučavanjem podataka, nametnulo nam se pitanje ima li stupanj obrazovanja utjecaj na smrtnost u svim dobnim skupinama, pa smo odlučili provjeriti tu pretpostavku na vozačima sa završenom samo srednjom školom, tj. željeli smo odrediti postotak p takvih vozača u ukupnoj populaciji poginulih.
Za razliku od prijašnjih testova, sada ne uspoređujemo nekoliko populacija, već provjeravamo svoju pretpostavku unutar jedne populacije, pri čemu podatke tumačimo u odnosu na neko zadano obilježje (kod nas: završena samo srednja škola). To, naravno, znači da nam je potrebna drugačija testna statistika koja će nekako "odrediti" očekivani broj poginulih vozača sa završenom samo srednjom školom.
Kao i prije, ideja je pronaći takvu testnu statistiku koja će naše podatke svesti na neku nama poznatu distribuciju iz koje ćemo poslije lako pročitati s kojom vjerojatnošću smo postavili točnu hipotezu. Ovdje smo se poslužili poznavanjem Centralnog graničnog teorema, iz kojeg se odmah nametnula tražena statistika.
Navodimo Centralni granični teorem (CGT), kojim ćemo se poslije nekoliko puta koristiti:
Neka je \left(X_{n} :n\in \mathbb{N}\right) niz nezavisnih, jednako distribuiranih slučajnih varijabli s očekivanjem \mu i varijancom \sigma ^{2}, 0\lt \sigma ^{2} \lt +\infty, te neka je T_{n} =\sum _{k=1}^{n}X_{k}. Tada vrijedi \frac{T_{n} -n\mu }{\sigma \sqrt{n} } \stackrel{D}{\longrightarrow} N\left(0,1\right) kad n\to \infty.
Iako smo CGT naveli u općenitom slučaju, nas zanima nešto jednostavnija situacija. Slučajni uzorak poginulih vozača možemo promatrati kao niz nezavisnih jednako distribuiranih Bernoullijevih slučajnih varijabli koje poprimaju vrijednost 0 ili 1 u ovisnosti o nekom zadanom svojstvu, i to s vjerojatnošću p, odnosno 1-p.
Konkretno, mi ćemo svakog poginulog vozača koji ima završenu najviše srednju školu reprezentirati jedinicom u uzorku, dok će ostali biti reprezentirani nulom. Ovako promatran niz varijabli ima nešto jednostavnije formule varijance \left(\sigma ^{2} =p(1-p)\right) i očekvivanja \left(\mu =p\right), pa je i testna statistika nešto jednostavnija nego u općenitom Centralnom graničnom teoremu. Također, sada je jasno da zapravo tražimo vjerojatnost p, tj. vjerojatnost da je poginuli vozač u uzorku imao završenu samo srednju školu.
Test ovoga oblika, u kojem računamo očekivanje za populaciju reprezentiranu Bernoullijevim varijablama, nazivamo Z-test i definiramo testnu statistiku (s opravdanjem u CGT-u i jer je n\bar{X}_{n} =T_{n}) formulom:
Z=\frac{\bar{X}_{n} -p}{\sqrt{p(1-p)} } \sqrt{n} \sim N(0,1).
Ovo je najjači test za računanje očekivanja uz razinu značajnosti \alpha , gdje je
| \bullet | n duljina uzorka |
| \bullet | \bar{X}_{n} relativna frekvencija vozača sa završenom samo srednjom školom u uzorku. |
Promatrajući svoje podatke, uočili smo da najveći broj poginulih vozača ima završenu samo srednju školu pa smo opisanim Z-testom odlučili provjeriti svoje očekivanje da takvih vozača ima otprilike 70%.
Ovdje je važno napomenuti da je statističko istraživanje često puno pretpostavki dobivenih tzv. "metodom pokušaja i pogrešaka", te često nije moguće iz prve pogoditi koja je hipoteza optimalna.
Dakle, testirat ćemo sljedeće hipoteze:
H_{0}: p=0.70
H_{1}: p\gt 0.70.
H_{1}: p\gt 0.70.
Test ćemo provesti uz razinu značajnosti \alpha=5%.
Za podatke dobivamo \bar{X}_{n} =0.7388.
Uvrštavanjem konkretnih vrijednosti iz uzorka duljine n = 781 dobivamo sljedeće:
z=\frac{0.7388-0.7}{\sqrt{0.7\cdot 0.3} } \sqrt{781} =2.3662\gt z_{0.05} =1.64,
gdje broj z_{0.05} čitamo iz tablice standardne normalne distribucije (z_{0.05} =\Phi (1-0.05)).
Promatramo u kojem intervalu se nalazi z. Ako je z\in \left[z_{0.05} \right. ,\left. +\infty \right\rangle, tada odbacujemo hipotezu H_{0}, u protivnom je ne odbacujemo.
Dobiveni rezultat je iz intervala \left[z_{0.05} \right. ,\left. +\infty \right\rangle pa odbacujemo hipotezu H_{0} u korist hipoteze H_{1} i možemo zaključiti da više od 70% poginulih ima završenu samo srednju školu.
3.5Očekivana dob vozača u trenutku nesreće
Pitanje koje se prirodno nameće je očekivana dob u trenutku nesreće. Točnije, zanima nas možemo li pronaći neki interval godina vozača u kojem je vjerojatnost nesreće najveća. U statistici takav interval nazivamo aproksimativni pouzdani interval.
Prema CGT teoremu znamo da je Z=\frac{\bar{X}_{n} -\mu }{\sigma } \sqrt{n} \sim N(0,1) za velike n.
Po formuli za vjerojatnost vrijedi: \mathbb{P}\left(|Z|\le z_{\frac{\alpha }{2} } \right)=1-\alpha,
što je ekvivaletno s \mathbb{P}\left(z_{\frac{\alpha }{2} } \le \frac{\bar{X}_{n} -\mu }{S_{n} } \sqrt{n} \le z_{\frac{\alpha }{2} } \right)=1-\alpha,
što je ekvivaletno s \mathbb{P}\left(\bar{X}_{n} -z_{\frac{\alpha }{2} } \frac{S_{n} }{\sqrt{n} } \le \mu \le \bar{X}_{n} +z_{\frac{\alpha }{2} } \frac{S_{n} }{\sqrt{n} } \right)=1-\alpha.
Dakle, interval je dan formulom
\left[\bar{X}_{n} -z_{\frac{\alpha }{2} } \cdot \frac{S_{n} }{\sqrt{n} } ,\bar{X}_{n} +z_{\frac{\alpha }{2} } \cdot \frac{S_{n} }{\sqrt{n} } \right],
gdje je
| \bullet | n duljina uzorka, |
| \bullet | x_{i} godine života i-te osobe u trenutku nesreće, |
| \bullet | \bar{X}_{n} =\frac{\sum _{i=1}^{n}x_{i} }{n}, |
| \bullet | S_{n}^{2} =\frac{1}{n-1} \sum _{i=1}^{n}(x_{i} -\bar{X}_{n} )^{2} procjenitelj za varijancu, |
a broj z_{\frac{\alpha }{2} } čitamo iz tablice standardne normalne distribucije.
Iz uzorka duljine n=917 dobivamo \bar{X}_{n} =35.46 i S_{n} =11.72. Dakle, aproksimativni 95% pouzdani interval za očekivanu dob u trenutku pogibije je \left[34.7,36.22\right] pa zaključujemo da je očekivana dob između 34 i 37 godina.
3.6Utjecaj promjene Zakona o sigurnosti prometa na cestama na smrtnost u dobnoj skupini od 20 - 29
Iz strukturnog dijagrama o udjelu pojedinih dobnih skupini u ukupnom broju poginulih, vidjeli smo da je najugroženija skupina u dobi od 20 do 29 godina. S obzirom na to da se i Zakon o sigurnosti prometa na cestama u 2008. bazirao upravo na toj dobnoj skupini, odnosno mladim vozačima, želimo utvrditi je li on uistinu utjecao na smanjenje smrtnosti.
Promatramo podatke o poginulima u toj dobnoj skupini u razdoblju od godine dana nakon donošenja prvog zakona u 2004. godini (prvo razdoblje) te od godinu dana nakon donošenja novog zakona u 2008. godini (peto razdoblje).
Pretpostavljamo da novi zakon ima manji utjecaj na smrtnost u dobnoj skupini od 20 do 29 od starog pa želimo naći neki test kojim bismo mogli usporediti "uspješnost" ovih dvaju zakona. Za početak, tu "uspješnost" zakona definiramo kao udio poginulih vozača u dobi od 20 do 29 godina u cjelokupnom broju poginulih. Sada je još potrebno naći najbolji način da usporedimo omjere prvog i petog razdoblja.
Odabrali smo test omjera proporcija koji se koristi upravo u situacijama kada uspoređujemo "uspješnost" nekog obilježja u nezavisnim populacijama.
Test omjera proporcija provodi se na dvije nezavisne populacije s nekim obilježjem X.
Označimo s X_{1} slučajnu varijablu koja predstavlja obilježje X u prvoj populaciji, a s X_{2} slučajnu varijablu koja predstavlja X u drugoj populaciji.
Neka su p_{1} i p_{2} njihove vjerojatnosti uspjeha u svakoj od populacija.
U osnovnoj nul-hipotezi pretpostavljamo da su vjerojatnosti uspjeha jednake, a druga hipoteza je njena alternativa koja ovisi o zadatku.
Test omjera proporcija definiran je formulom:
Z=\frac{\hat{p}_{2} - \hat{p}_{1} }{\sqrt{\hat{p}(1-\hat{p})} } \frac{1}{\sqrt{\frac{1}{n_{1} } +\frac{1}{n_{2} } } },
gdje su n_{1} i n_{2} dovoljno velike populacije (zbog CGT-a), \hat{p}_{1} procjenitelj za p_{1} (tj. \hat{p}_{1}=p_{1}), \hat{p}_{2} procjenitelj za p_{2} (tj. \hat{p}_{2}=p_{2}) i \hat{p}=\frac{n_{1} \hat{p}_{1} +n_{2} \hat{p}_{2} }{n_{1} +n_{2} } procjenitelj zajedničke vjerojatnosti. U našem slučaju promatrano obilježje je smrtnost, a populacije su poginuli u prvom i petom razdoblju. Označimo vjerojatnosti s
p_{1} = omjer poginulih u dobi od 20 do 29 u prvom razdoblju,
p_{5} = omjer poginulih u dobi od 20 do 29 u petom razdoblju.
Testiramo sljedeće hipoteze uz razinu značajnosti \alpha=5%:
H_{0}: p_{1} =p_{5}
H_{1}: p_{1} \lt p_{5}
H_{1}: p_{1} \lt p_{5}
Koristeći se navedenim formulama, za svoje podatke dobivamo ove rezultate:
| \bullet | n_{1} =157 |
| \bullet | n_{5} =195 |
| \bullet | \hat{p}_{1} =\frac{56}{157} =0.3567 |
| \bullet | \hat{p}_{5} =\frac{74}{195} =0.3795 |
| \bullet | \hat{p}=0.3693 |
| \bullet | Z=0.4406\lt z_{0.05} =1.64, |
gdje broj z_{0.05} čitamo iz tablice standardne normalne distribucije.
Promatramo u kojem intervalu se nalazi z. Ako je z\in \left[z_{0.05} \right. ,\left. +\infty \right\rangle, tada odbacujemo hipotezu H_{0}, u protivnom je ne odbacujemo. Budući da z nije iz tog intervala, ne možemo odbaciti hipotezu H_{0}, odnosno novi i stari zakon imaju jednak utjecaj na smrtnost u dobnoj skupini od 20 do 29.
4Zaključak
Istaknimo na kraju najzanimljivije rezultate rada:
| \bullet | unatoč uvriježenoj pretpostavci, žene nisu lošiji vozači od muškaraca, štoviše, gotovo sedam puta manje žena pogine u prometnim nesrećama |
| \bullet | smrtnost mladih ovisi o danu u tjednu |
| \bullet | više od 70% poginulih ima završenu samo srednju školu |
| \bullet | očekivana dob u trenutku pogibije je između 34 i 37 godina |
| \bullet | promjena Zakona o sigurnosti prometa na cestama nije utjecala na smanjenje smrtnosti mladih. |
5Literatura
Bibliografija
| [1] | M. Huzak - Predavanja iz statisike |
| [2] | N. Sarapa - Teorija vjerojatnosti, Školska knjiga, Zagreb, 1992. |
| [3] | R |
| [4] | Wikipedijini članci o histogramu i Z-testu |
| [5] | MUP |