Statistička obrada podataka
Sažetak
U ovom članku provodimo statističko istraživanje koje se bazira na zavisnosti uspjeha na prijamnom ispitu i prve godine studiranja. U tu svrhu, definiramo i objašnjavamo osnovne statističke pojmove i općeniti tijek statističkog istraživanja. Grafičkim prikazima podataka objašnjavamo što je i čemu služi opisna statistika te zašto ona nije dovoljna za formiranje formalnih zaključaka. Naravno, analiziramo i matematički alat s pomoću kojeg se zaključci mogu smatrati valjanima. Posebnim komentarima ističemo kako interpretirati dobivene rezultate i na što, prilikom toga, treba obratiti posebnu pozornost.Sadržaj
1Uvod
1.1Čime se bavi statistika
Recimo da nam treba prosječna visina svih ljudi na Zemlji. Sasvim je jasno da bi pojedinačnim prikupljanjem podataka taj posao zaista dugo trajao. Zato nećemo mjeriti visinu svih ljudi, već ćemo odabrati neki broj ljudi i s pomoću njihovih visina procijeniti visinu svih. Upravo na taj način počinje svaka statistička analiza – ispitivanjem uzorka procjenjujemo svojstvo cijele populacije.
1.2Što je uzorak i kako ga odabrati?
Naravno, nema smisla mjeriti visinu svih osnovnoškolaca jedne škole na svijetu ili košarkaške reprezentacije i na temelju toga procijenjivati visinu svih ljudi na Zemlji! Uzorak mora biti slučajno odabran. Ljudi ne smiju biti birani npr. prema spolu, boji kose, političkoj opredijeljenosti itd.
1.3Istraživanje
Početak svakog istraživanja je formiranje hipoteza, pretpostavki koje želimo dokazati (ili opovrgnuti). Obradu podataka započinjemo njihovim vizualnim prikazom. Najčešće histogramima i box-plotovima. Na taj način odmah možemo uočiti u kojim granicama se podaci nalaze, kako su raspoređeni te u kojem smjeru uostalom naši zaključci idu. Međutim, vizualna reprezentacija podataka nije dovoljna da bismo neku hipotezu smatrali dokazanom ili opovrgnutom. Tek primjenom različitih statističkih testova možemo s određenom, unaprijed pretpostavljenom vjerojatnošću smatrati da je istraživanje završeno.
2Analiza prikupljenih podataka
2.1Hipoteze
| \bullet | prosjek ocjena ne ovisi o spolu |
| \bullet | prosjek ocjena ne ovisi o godini upisa na fakultet |
| \bullet | prolaznost na 1. godini studija ovisi o mjestu na rang listi prijamnog ispita |
| \bullet | rang i prosjek linearno ovise i moguće je na temelju ranga procijeniti prosjek |
2.2O prikupljanju podataka
Podatke smo prikupljali od studenata s PMF– Matematičkog odjela, prediplomski studij matematike, koji su fakultet upisali 2007. i 2008. godine, a polagali su prijamni ispit. To smo ostvarili s pomoću anonimne ankete u kojoj smo tražili da napišu koje godine su upisali fakultet, kojeg su spola, njihov rang (mjesto) na prijamnom ispitu (uz uvjet da nisu imali izravan upis) te njihove ocjene iz svih kolegija na prvoj godini. Zanima nas njihova prva godina studiranja, pa smo zamolili da napišu i ako su neki predmet pali, s čime ćemo poslije baratati kao s ocjenom 1. Na taj način zaista uočavamo kakav je uspjeh student ostvario godinu dana nakon što se upisao na fakultet i registriramo razliku između studenata koji su neki kolegij položili u roku i onih koji su pali, ali možda položili sljedeće godine s boljom ocjenom.
Ukupna populacija studenata upisanih 2007. i 2008. godine je 500, a mi smo prikupili uzorak od 94, procijenivši da će to biti dovoljno za statističku analizu. Nakon prikupljenih podataka izračunali smo prosjek ocjena svakog studenta (računajući i ocjene 1), te posebno označili je li student prvu godinu prošao ili pao. Zbog anonimnosti, nismo tražili studente da napišu točno mjesto na prijamnom ispitu, nego u razredima od 10. Dakle, ako je netko ostvario npr. 103. mjesto, zapisao je da mu je rang 101– 110. Na taj način anonimnost je sačuvana, a razredi su dovoljno mali da bismo mogli dovoljno dobro provjeriti svoje hipoteze.
2.3O prosjeku ocjena slučajnog uzorka
Promatrano statističko obilježje (spol, prosjek, ...) u idućim analizama označavat ćemo s \textbf{X}, \textbf{Y}, \textbf{Z}, \ldots. Kroz n mjerenja dobivamo niz (tj. uzorak) x_{1},x_{2},\ldots, x_{n} kojim ćemo procijeniti statističko obilježje. U najjednostavnijem slučaju, ako obilježje \textbf{X} poprima samo vrijednost iz nekog diskretnog (konačnog ili prebrojivog) skupa A, onda se kaže da je \textbf{X} diskretno obilježje. U uzorku možemo uočiti ponavljanje nekih veličina. Neka u uzorku x_{1}\ldots,x_{n} ima k ({ k\leq n}) različitih izmjerenih veličina x'_{1},\ldots,x'_{k}. S f_{i} označavamo broj ponavljanja veličine x'_{i} u uzorku, i\in {1,\ldots,k}. Taj broj f_{i} zovemo frekvencija veličine x'_{i}. Još jedna korisna veličina usko vezana uz frekvenciju je relativna frekvencija veličine x'_{i}, koja se jednostavno definira kao p_{i}:=\frac{f_{i}}{n}, i=1,\ldots,k.
Dobivene podatke jednostavnije prikazujemo tablično.
U slučaju da obilježje \textbf{X} ne poprima diskretne vrijednosti, već iz nekog intervala iz \mathbb{R} ne možemo prebrojiti ponavljanja, pa vrijednosti svrstavamo u razrede. Razredi su disjunktni, jednake širine i prekrivaju cijeli interval (biramo ih proizvoljno ovisno o praktičnim potrebama).
Prilikom grupiranja u razrede sve vrijednosti i-tog razreda aproksimiraju se sredinom tog razreda, čime se gubi određeni dio informacija, ali se mogu razlučiti bitna svojstva promatranog kontinuiranog obilježja \textbf{X}.
U ovom slučaju broj veličina unutar nekog razreda predstavlja frekvenciju razreda.
| \bullet | Tablica prosjeka ocjena prikupljenog slučajnog uzorka:
Podsjetimo, prosjek smo računali tako da smo za pad kolegija uzimali ocjenu nedovoljan (1). Zato interval[1.0,2.0\rangle ima smisla.} Napomena 1. Pri tome su F_{i} kumulativne relativne frekvencije definirane rekurzivno, tj:
F_{0} = p_{0}
F_{i} = F_{i-1} + p_{i}, i = 1,2,\ldots, n.
|
|||||||||||||||||||||||||
| \bullet | Histogram prosjeka ocjena slučajnog uzorka: 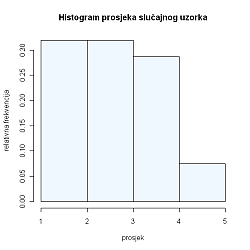 |
Napomena 2. Na osi apscisa nalaze se razredi, dok nam os ordinata predstavlja relativne frekvencije. Primijetimo, ukupna površina dobivenog histograma jednaka je 1. Histogramom relativno jednostavno možemo uočiti distribuciju statističkog obilježja \textbf{X}.
Spomenimo još neke korisne veličine kojima se koristimo u opisnoj statistici. Prije svega poredajmo slučajni uzorak po veličini, tj.:
x_{(1)}\leq x_{(2)}\leq x_{(3)}\leq\ldots,\leq x_{(n)}
| \bullet | Raspon slučajnog uzorka:
d=x_{(n)} - x_{(1)}
|
| \bullet | Medijan slučajnog uzorka je vrijednost koja ima svojstvo da je 50% podataka veće, a 50% manje od nje, tj. uzimamo za medijan:
m = \begin{cases} \frac{1}{2}(x_{ (\frac{n}{2})}+x_{(\frac{n}{2}+1)}) , & \text{ako je }n\text{ paran} \\ x_{(\frac{n+1}{2})}, & \text{ako je }n\text{ neparan} \end{cases}
|
| \bullet | Donji kvartil je vrijednost koja ima svojstvo da je 25% podataka manje od nje, tj. uzimamo:
q_{l} = x_{(\frac{n+1}{4})}
|
| \bullet | Gornji kvartil je vrijednost koja ima svojstvo da je 25% podataka veće od nje, tj. uzimamo:
q_{u}=x_{(\frac{3(n+1)}{4})}
|
| \bullet | Interkvartil: \textbf{IQR} = q_{u} - q_{r} |
Karakteristična petorka uzorka : (x_{(1)}, q_{l}, m, q_{u}, x_{(n)} ).
S pomoću karakteristične petorke uzorka formiramo box–plot (eng. box and whisker plot).
Napomena 3. Outlieri su sve vrijednosti koje su od gornjeg i donjeg kvantila udaljene za više od \frac{3}{2}\textbf{IQR}. Brkovi su najveća i najmanja vrijednost koje nisu outlieri.
Box-plot prosjeka ocjena slučajnog uzorka:
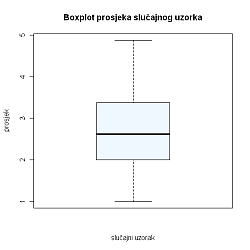
Napomena 4. Budući da je u slučajnom uzorku prosjek ocjena u razredima, ne možemo točno odrediti gornji, donji kvartil i medijan već ih procjenjujemo linearnom interpolacijom iz grafa kumulativnih frekvencija.
"Box" predstavlja podatke koji se po vrijednosti nalaze u rasponu 25\% - 75\% ukupne veličine (tj. donja linija pravokutnika određena je donjim kvartilom, a gornja gornjim). Medijan je u pravokutniku posebno naznačen debljom linijom. Najmanja i najveća vrijednost koje nisu outlieri na grafu su označeni linijom i s pravokutnikom spojeni izlomljenom linijom (zato se i zovu brkovi). Primijetimo da na ovom box-plotu nema outliera (općenito, ako ih ima, posebno se naznače npr. kružićem).
2.4Rang uzorka na prijamnom ispitu
| i | razred | f_{i} | p_{i} | sredina | F_{i} |
| 1 | 1-10 | 5 | 0.0531914893617021 | 5.5 | 0.053191489317021 |
| 2 | 11-20 | 7 | 0.074468085106383 | 15.5 | 0.127659574468085 |
| 3 | 21-30 | 9 | 0.0957446808510638 | 25.5 | 0.223404255319149 |
| 4 | 31-40 | 5 | 0.0531914893617021 | 35.5 | 0.27659595744680851 |
| 5 | 41-50 | 9 | 0.0957446808510638 | 45.5 | 0.372340425531915 |
| 6 | 51-60 | 6 | 0.0638297872340425 | 55.5 | 0.436170212765957 |
| 7 | 61-70 | 2 | 0.0212765957446809 | 65.5 | 0.457446808510638 |
| 8 | 71-80 | 3 | 0.0319148936170213 | 75.5 | 0.489361702127660 |
| 9 | 81-90 | 4 | 0.0425531914893617 | 85.5 | 0.531914893617021 |
| 10 | 91-100 | 7 | 0.074468085106383 | 95.5 | 0.606382978723404 |
| 11 | 101-110 | 2 | 0.0212765957446809 | 105.5 | 0.627659574468085 |
| 12 | 111-120 | 5 | 0.0531914893617021 | 115.5 | 0.680851063829787 |
| 13 | 121-130 | 1 | 0.0106382978723404 | 125.5 | 0.691489361702128 |
| 14 | 131-140 | 1 | 0.0106382978723404 | 135.5 | 0.702127659574468 |
| 15 | 141-150 | 2 | 0.0212765957446809 | 145.5 | 0.723404255319149 |
| 16 | 151-160 | 4 | 0.0425531914893617 | 155.5 | 0.76595744680851 |
| 17 | 161-170 | 2 | 0.0212765957446809 | 165.5 | 0.787234042553192 |
| 18 | 171-180 | 3 | 0.0319148936170213 | 175.5 | 0.819148936170213 |
| 19 | 181-190 | 2 | 0.0212765957446809 | 185.5 | 0.80425531914294 |
| 20 | 191-200 | 2 | 0.0212765957446809 | 195.5 | 0.861702127659575 |
| 21 | 201-210 | 4 | 0.0425531914893617 | 205.5 | 0.904255319148936 |
| 22 | 211-220 | 4 | 0.0425531914893617 | 115.5 | 0.946808510638298 |
| 23 | 221-230 | 1 | 0.0106382978723404 | 225.5 | 0.957446808510638 |
| 24 | 231-240 | 2 | 0.0212765957446809 | 235.5 | 0.978723404255319 |
| 25 | 241-250 | 2 | 0.0212765957446809 | 245.5 | 1 |
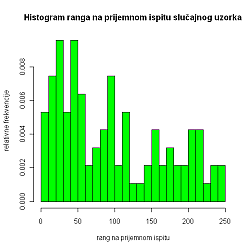
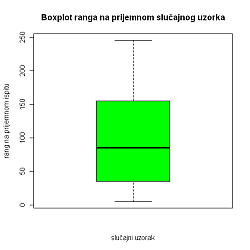
Napomena 5. Primijetimo da podaci nisu jednako raspoređeni, što objašnjavamo činjenicom da dio lošije rangiranih studenata sigurno nije više prisutan na fakultetu. No to nam ne smeta pri obradi, budući da ćemo sve potrebno dobiti linearnom interpolacijom.
3Testiranje nezavisnosti statističkih obilježja
3.1Testiranje hipoteza
Nakon formiranja hipoteze, moramo osmisliti način na koji ćemo je provjeriti, odnosno postupak donošenja odluke o njenom prihvaćanju ili odbacivanju. Taj postupak zove se testiranje. Općenito se problem testiranja sastoji od definiranja područja C \in \mathbb{R}^{n}, koje zovemo kritično područje hipoteze H. Ako se izmjereni uzorak shvati kao (x_{1}, x_{2}, x_{3},\ldots, x_{n}) \in \mathbb{R}^{n} može vrijediti (x_{1}, x_{2}, x_{3},\ldots, x_{n}) \in C ili (x_{1}, x_{2}, x_{3},\ldots, x_{n}) \notin C. Ako vrijedi prvo, hipoteza se odbacuje, a u suprotnom se prihvaća. Ovako definirani postupak zove se statistički test.
U statističkom testu ključnu ulogu ima kritično područje. Njega treba odrediti tako da sadržava one točke (x_{1}, x_{2}, x_{3},\ldots, x_{n}) \in C u kojima dolazi do značajnog odstupanja od hipoteze koju testiramo. Naravno, javlja se problem određivanja što je značajno, a što tolerantno odstupanje.
Neka je {H_{0}} hipoteza koju testiramo. Vidimo da je zapravo riječ o dvije hipoteze, {H_{0}} i {H_{1}} , tj. odbacivanjem hipoteze H_{0} prihvaćamo hipotezu H_{1}, a prihvaćanjem H_{0} odbacujemo H_{1}. H_{0} zove se nul–hipoteza , a H_{1} alternativna hipoteza.
Budući da na temelju uzorka procjenjujemo svojstvo cijele populacije, odbacivanjem hipoteze H_{0} uvijek postoji određeni rizik da je hipoteza odbačena kada je zapravo trebala biti prihvaćena. Taj rizik označava se brojem \alpha\ (0\leq \alpha\leq 1) i kaže se da test ima razinu značajnosti \alpha. Naravno, želimo da \alpha bude što manji, najčešće se uzima 0,05(5\% ). Problem nalaženja najboljeg testa svodi se na određivanje kritičnog područja C tako da razina značajnosti iznosi zadani broj \alpha, te da vjerojatnost prihvaćanja nul–hipoteze kada je stvarno neistinita (pogreška druge vrste) bude minimalna.
3.2Dvodimenzionalna statistička obilježja
Istodobno promatramo više veličina i želimo ustanoviti njihovu ovisnost. Primjerice, promatramo dva statistička obilježja, \textbf{X} i \textbf{Y}. Višestrukim ponavljanjem mjerenja dobiva se niz uređenih parova:
(1)
(x_{1}, y_{1}), (x_{2}, y_{2}), \ldots, (x_{n}, y_{n}).
Neka obilježje \textbf{X} poprima vrijednosti iz nekog diskretnog skupa \textbf{A}=\lbrace a_{1}, a_{2}, \ldots, a_{r}\rbrace, a obilježje \textbf{Y} iz skupa \textbf{B}=\lbrace b_{1}, b_{2}, \ldots, b_{c}\rbrace. Analogno jednodimenzionalnom slučaju, za svaki par (a_{i}, b_{j}), i=1, \ldots, r,\ j=1, \ldots, c, možemo uočiti njegovu frekvenciju u (
Napomena 6. Brojevi f_{i}, i=1, \ldots, r, nazivaju se marginalne frekvencije od a_{i} u (1 ), a brojevi g_{j}, j=1, \ldots, c, marginalne frekvencije od b_{j} u (1 ).
Uz ovisnost dvodimenzionalnih statističkih obilježja usko je vezan tzv. Pearsonov koeficijent korelacije, koji pokazuje stupanj afine povezanosti među podacima u uzorku, a definira se kao:
(2)
r_{\textbf{X}\textbf{Y}}:=\frac{S_{\textbf{X}\textbf{Y}}}{\sqrt{S_{\textbf{X}\textbf{X}}S_{\textbf{Y}\textbf{Y}}}},
(3)
S_{\textbf{X}\textbf{X}}:=\sum_{k=1}^{n}x_{k}^{2}-n{\bar{x}}^{2}, S_{\textbf{Y}\textbf{Y}}:=\sum_{k=1}^{n}y_{k}^{2}-n{\bar{y}}^{2}, S_{\textbf{X}\textbf{Y}}:=\sum_{k=1}^{n}x_{k}y_{k}-n\bar{x}\bar{y}, \bar{x}:=\frac{1}{n}\sum_{k=1}^{n}x_{k}, \bar{y}:=\frac{1}{n}\sum_{k=1}^{n}y_{k}.
Napomena 7. Za Pearsonov koeficijent korelacije vrijedi:
-1 \leq r_{\textbf{X}\textbf{Y}} \leq 1.
Ako vrijedi:
| \bullet | r_{\textbf{X}\textbf{Y}} \lt 0.5, kažemo da su obilježja \textbf{X} i \textbf{Y} slabo korelirana, |
| \bullet | r_{\textbf{X}\textbf{Y}} \geq 0.5, kažemo da su obilježja \textbf{X} i \textbf{Y} značajno korelirana, |
| \bullet | r_{\textbf{X}\textbf{Y}}=1 ili r_{\textbf{X}\textbf{Y}}=-1, kažemo da je veza potpuno linearna, |
| \bullet | r_{\textbf{X}\textbf{Y}}=0, veza nije linearna (to ne mora značiti da ne postoji!). |
Napomena 8. Prethodne definicije i svojstva potpuno vrijede i ako su \textbf{X} i \textbf{Y} neprekidna statistička obilježja. Potrebno je samo napraviti podjelu podataka u razrede.
3.3Pearsonov \chi^{2}-test o nezavisnosti
Neka je (\textbf{X}, \textbf{Y}) dvodimenzionalno statističko obilježje, te neka je (
Prvo moramo definirati veličinu koja će nam predstavljati "udaljenost" od nezavisnosti obilježja na temelju n-članog niza mjerenja, tako da ta "udaljenost" predstavlja značajno odstupanje od hipoteze H_{0}. U tu svrhu definiramo sljedeću veličinu (uz iste oznake kao u Tablici
(4)
H_{n}:=\sum_{i=1}^{r}\sum_{j=1}^{c}\frac{(f_{ij}-n\hat{p_{i}}\hat{q_{j}})^{2}}{n\hat{p_{i}}\hat{q_{j}}},
Također, moramo odrediti kritično područje C, tako da razina značajnosti testa iznosi zadani broj \alpha\in\langle0, 1\rangle. Od sada nadalje, \alpha=0.05=5%. Za C mora vrijediti da ako H_{n} \in C, hipotezu H_{0} odbacujemo u korist H_{1} (s rizikom od 5%). Za rješenje ovog problema koristan je sljedeći teorem:
Teorem 9.[Pearsonov teorem] Ako je H_{0} točna hipoteza, za n\to\infty vrijedi
tj. za velike n, H_{n} ima \chi^{2}-razdiobu1 s (r-1)(c-1) stupnjeva slobode.
(5)
H_{n}\sim\chi^{2}((r-1)(c-1)),
Sada možemo izračunati kritično područje [x_{0}, +\infty\rangle, tj. tražimo točku x_{0}\in\mathbb{R} za koju vrijedi: \mathbb{P}(H_{n}\lt x_{0})\geq0.95, tj. \mathbb{P}(H_{n}\geq x_{0})\leq0.05. Budući da znamo distribuciju H_{n}, vrijednost točke x_{0} iščitavamo iz tablice, a budući da ovisi o \alpha, r i c, označava se s \chi^{2}_{\alpha}((r-1)(c-1)).
Sada lako možemo testirati nezavisnost obilježja \textbf{X} i \textbf{Y}. S pomoću vrijednosti u kontingencijskoj tablici izračunamo H_{n} i ako vrijedi H_{n}\geq\chi^{2}_{\alpha}((r-1)(c-1)), odbacujemo H_{0} u korist H_{1} uz rizik od 5\%. U suprotnom, prihvaćamo H_{0}.
3.4Hipoteza: Prosjek ocjena ne ovisi o spolu
Unaprijed ne očekujemo razliku prosjeka na prvoj godini studiranja između žena i muškaraca. Za početak pogledajmo opisni prikaz odnosa prosjeka slučajnog uzorka obaju spolova.
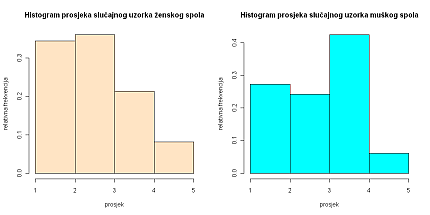
Primijetimo, najveći broj žena iz uzorka ima prosjek između 2.00 i 3.00, dok najveći dio muškaraca iz uzorka ima prosjek između 3.00 i 4.00. Međutim, gotovo dva puta više žena ima prosjek 4.00 do 5.00. Prirodno se pitamo što od toga može utjecati na nezavisnost danih obilježja i na koji način.
Promotrimo box-plot slučajnog uzorka obaju spolova:
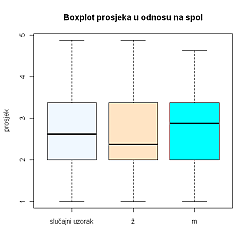
Za razliku od histograma, na box-plotu se ne mogu vidjeti značajne razlike između spolova.
Provedimo Pearsonov \chi^{2}-test o nezavisnosti:
Neka obilježje \textbf{X} poprima vrijednosti u razredima: [1.0, 2.0\rangle, [2.0, 3.0\rangle, [3.0, 4.0\rangle, [4.0, 5.0], a obilježje \textbf{Y} neka poprima vrijednosti: muško, žensko. Testiramo:
H_{0}: \textbf{X} i \textbf{Y} su nezavisna obilježja,
H_{1}: \textbf{X} i \textbf{Y} su zavisna obilježja.
H_{1}: \textbf{X} i \textbf{Y} su zavisna obilježja.
Iz tablice i (
Iako posve neočekivano, provedenim testom zaključujemo da prosjek ocjena na prvoj godini studija ovisi o spolu, na nivou značajnosti od 5%, tj. rizik da je naš zaključak pogrešan je 5%.
3.5Hipoteza: Prosjek ocjena ne ovisi o godini upisa na fakultet
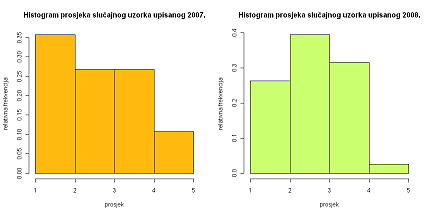
Primijetimo, najveći postotak uzorka upisanog 2007. godine ima prosjek od 1.00 do 2.00, za razliku od uzorka upisanog 2008. godine, gdje se taj prosjek kreće od 2.00 do 3.00. Međutim, relativna frekvencija prosjeka 4.00-5.00 čak je četiri puta veća u korist upisanih 2007. godine. Provedimo \chi^{2}-test o nezavisnosti.
Neka obilježje \textbf{X} poprima vrijednosti u razredima: [1.0, 2.0\rangle, [2.0, 3.0\rangle, [3.0, 4.0\rangle, [4.0, 5.0], a obilježje \textbf{Y} neka poprima vrijednosti godine upisa: 2007., 2008. Testiramo:
H_{0}: \textbf{X} i \textbf{Y} su nezavisna obilježja,
H_{1}: \textbf{X} i \textbf{Y} su zavisna obilježja.
H_{1}: \textbf{X} i \textbf{Y} su zavisna obilježja.
Iz kontingencijske tablice i (
Dakle, \chi^{2}-test potvrdio je naša očekivanja na nivou značajnosti od 5%. Odnosno, zaključujemo da prosjek ocjena na prvoj godini fakulteta na ovisi o godini upisa.
3.6Hipoteza: Prolaznost na prvoj godini studiranja ovisi o mjestu na rang listi prijamnog ispita
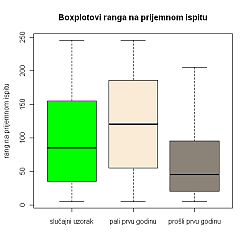
U prethodnim box-plotovima možemo uočiti niz zanimljivih činjenica. Promatrajući studente iz uzorka koji su prošli prvu godinu, uočavamo da nitko nije bio niže od 200. mjesta na rang listi, dok ih je čak 75% bilo rangirano iznad 100. mjesta, te 50% iznad 50. mjesta na prijamnom ispitu. Za razliku od njih, 75% studenata iz uzorka koji su pali prvu godinu bili su rangirani ispod 50. mjesta i čak 25% ispod 170. mjesta na prijamnom ispitu.
Ako studente koji su prošli prvu godinu označimo s 1, a one koji su pali s 0, iz (
Dakle, sve upućuje na zavisnost prolaznosti i ranga na prijamnom ispitu. Provedimo \chi^{2}-test o nezavisnosti:
Neka obilježje \textbf{X} poprima vrijednosti ranga na prijamnom ispitu u razredima: 1-10, 11-20, 21-30,\ldots, 241-250, a obilježje \textbf{Y} neka poprima vrijednosti: prolaz, pad. Testiramo:
H_{0}: \textbf{X} i \textbf{Y} su nezavisna obilježja,
H_{1}: \textbf{X} i \textbf{Y} su zavisna obilježja.
H_{1}: \textbf{X} i \textbf{Y} su zavisna obilježja.
| \textbf{X}\diagdown\textbf{Y} | pad | prolaz | \Sigma |
| 1-10 | 1 | 4 | 5 |
| 11-20 | 1 | 6 | 7 |
| 21-30 | 4 | 5 | 9 |
| 31-40 | 2 | 3 | 5 |
| 41-50 | 6 | 3 | 9 |
| 51-60 | 3 | 3 | 6 |
| 61-70 | 2 | 0 | 2 |
| 71-80 | 1 | 2 | 3 |
| 81-90 | 3 | 1 | 4 |
| 91-100 | 2 | 5 | 7 |
| 101-110 | 0 | 2 | 2 |
| 111-120 | 3 | 2 | 5 |
| 121-130 | 1 | 0 | 1 |
| 131-140 | 1 | 0 | 1 |
| 141-150 | 2 | 0 | 2 |
| 151-160 | 4 | 0 | 4 |
| 161-170 | 2 | 0 | 2 |
| 171-180 | 2 | 1 | 3 |
| 181-190 | 2 | 0 | 2 |
| 191-200 | 1 | 1 | 2 |
| 201-210 | 4 | 0 | 4 |
| 211-220 | 4 | 0 | 4 |
| 221-230 | 1 | 0 | 1 |
| 231-240 | 2 | 0 | 2 |
| 241-250 | 2 | 0 | 2 |
| \Sigma | 56 | 38 | 94 |
Broj stupnjeva slobode je (25-1)(2-1)=24, dakle za kritično područje trebamo odrediti \chi_{0.05}^{2}(24), a tu vrijednost čitamo iz tablice. Dakle, kritično područje je [36.415, +\infty\rangle. Iz kontingencijske tablice (Tablica
Dakle, zaključujemo da su prolaznost na prvoj godini studiranja i mjesto na rang listi prijamnog ispita zavisna obilježja na nivou značajnosti od 5%, kao što smo i očekivali.
4Regresijska analiza
Podsjetimo se, jedna od početnih hipoteza bila je da su prosjek ocjena na prvoj godini i rang na prijamnom ispitu u linearnoj vezi. Zadatak ovog poglavlja je tu hipotezu potvrditi ili opovrgnuti. Provest ćemo vrlo česti statistički model, koji se zove linearni regresijski model.
Na temelju podataka koje smo prikupili, ovaj model provodimo za obilježja koja ćemo označiti na sljedeći način: \textbf{X} predstavlja mjesto na rang listi prijamnog ispita, dok \textbf{Y} predstavlja prosjek ocjena na prvoj godini studiranja.
4.1Metoda najmanjih kvadrata
Prikupljene podatke, (x_{1}, y_{1}), (x_{2}, y_{2}), \ldots, (x_{n}, y_{n}), prvo prikazujemo u koordinatnoj ravnini. Taj prikaz omogućuje nam da zapazimo moguću funkcijsku ovisnost između podataka.
Metoda najmanjih kvadrata unaprijed pretpostavlja linearnu funkcijsku ovisnost te pronalazi pravac y=\hat{a}x+\hat{b} koji najbolje aproksimira vezu između prikupljenih podataka. Procjene \hat{a} i \hat{b} treba odrediti tako da vrijedi:
\min_{(a, b)\in\mathbb{R}^{2}}\sum_{i=1}^{n}(y_{i}-ax_{i}-b)^{2}=\sum_{i=1}^{n}(y_{i}-\hat{a}x_{i}-\hat{b})^{2}.
Pokazuje se da ta jednadžba ima jedinstveno rješenje:
(6)
\hat{a}=\frac{S_{\textbf{}}{XY}}{S_{\textbf{}}{XX}}, \hat{b}=\bar{y}-\hat{a}\bar{x},
Sada kada znamo koji pravac najbolje aproksimira prikupljene podatke, pogledajmo kako izgleda na prikupljenom uzorku. Za početak, pogledajmo kako originalni podaci izgledaju u koordinatnom sustavu:
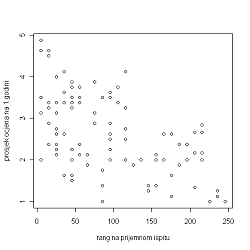
Sa slike možemo uočiti funkcijsku zavisnost ranga na prijamnom ispitu i prosjeka ocjena na prvoj godini. Metodom najmanjih kvadrata odredimo koji pravac najbolje opisuje primijećenu zavisnost. Potrebno je:
n=94, \bar{x}=99.80280264, \bar{y}=2.62235, S_{\textbf{}}{XY}=-3236.216722, S_{\textbf{}}{XX}=425137.155.
Dakle, dobivamo \hat{a}=-0.0076121712, \hat{b}=3.382066, tj. traženi pravac je
y=-0.007621712x+3.382066.
Prikažimo dobiveni pravac i grafički: 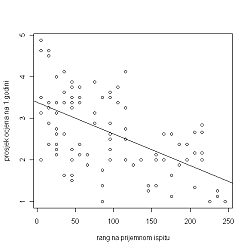
4.2Konstrukcija pouzdanih intervala za parametre linearne regresije
Metodom najmanjih kvadrata odredili smo pravac koji najbolje aproksimira vezu prikupljenih podataka o prosjeku i uspjehu na prijamnom ispitu. Međutim, mi ne želimo odrediti vezu tih 94 parova podataka, već cijele populacije. Tražimo pravac y=ax+b koji najbolje aproksimira vezu ranga na prijamnom ispitu i prosjeka ocjena na prvoj godini cijele populacije. Budući da s pomoću uzorka aproksimiramo populaciju, pravac dobiven metodom najmanjih kvadrata poslužit će nam kao dobra osnova za procjenu parametara a i b. Konstruirat ćemo tzv. pouzdane intervale, tj. s vjerojatnošću od 95\% procijeniti ćemo u kojem se intervalu nalaze vrijednosti paramatara a i b.
Formalno, (1-\alpha)\cdot 100\% pouzdani interval za a je interval [L, D] za koji vrijedi:
\mathbb{P}(L\leq a \leq D)\geq 1-\alpha, \alpha \in\langle0, 1\rangle.
Kao i do sada, uzimamo \alpha=0.05. Potpuno analogno definira se i 95\% pouzdani interval za b. Pri konstrukciji pouzdanih intervala za a i b od iznimne su važnosti sljedeći teoremi:
Teorem 10.Za sve prirodne brojeve n vrijedi:
tj. navedena testna statistika ima Studentovu t-razdiobu2 s n-2 stupnja slobode.
(7)
\frac{\hat{b}-b}{\hat{\sigma}\sqrt{\frac{1}{n}+\frac{\bar{x}}{S_{\textbf{}}{XX}}}}\sim t(n-2),
Teorem 11.Za sve prirodne brojeve n vrijedi:
(8)
\frac{\hat{a}-a}{\hat{\sigma}\sqrt{\frac{1}{S_{\textbf{}}{XX}}}}\sim t(n-2).
Napomena 12. U prethodnim teoremima S_{\textbf{}}{XX} i \bar{x} su kao u (3 ), a \hat{\sigma}:=\sqrt{\frac{SSE}{n-2}}, SSE:=S_{\textbf{}}{YY}-\hat{a}^{2}S_{\textbf{}}{XX}.
Sada lako pronađemo 95\% pouzdane intervale za a i b. Na sljedećoj slici prikazana je Studentova t-distribucija.
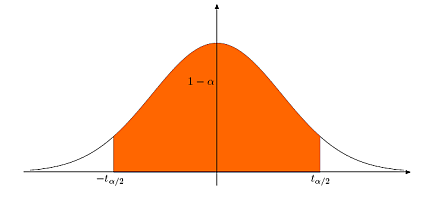
Napomenimo da su vrijednosti t_{\alpha/2}(n-2) tabelirane i u našem slučaju je t_{0.05/2}(92)=1.951. Sada iz (
\mathbb{P}(-t_{0.05/2}(92)\leq\frac{\hat{b}-b}{\hat{\sigma}\sqrt{\frac{1}{n}+\frac{\bar{x}}{S_{\textbf{}}{XX}}}}\leq t_{0.05/2}(92))=0.95,
te iz (\mathbb{P}(-t_{0.05/2}(92)\leq \frac{\hat{a}-a}{\hat{\sigma}\sqrt{\frac{1}{S_{\textbf{}}{XX}}}}\leq t_{0.05/2}(92))=0.95.
Iz tih jednadžbi sad jednostavnim manipulacijama dobivamo 95\% pouzdane intervale za a i b. Napomena 13. Iz prikupljenih podataka dobivamo SSE=71.61195282 i \hat{\sigma}=0.882264581.
Iz prethodnih zaključivanja i vrijednosti SSE i \hat{\sigma} dobivamo da je 95\% pouzdani interval za b[3.06435966, 3.699772334] i za a[-0.010252096, -0.004972246].
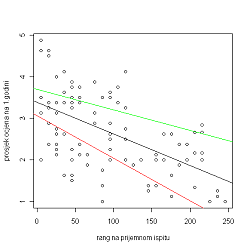
4.3Konstrukcija pouzdanih intervala za očekivani prosjek prve godine studiranja s obzirom na rang na prijamnom ispitu
Prisjetimose, ono što nas je također zanimalo bilo je može li student na temelju svog uspjeha na prijamnom ispitu unaprijed znati koliki je njegov očekivani prosjek na prvoj godini studiranja, pri čemu se pad računa kao ocjena 1. Formalno, želimo procijeniti \mathbb{E}[\textbf{Y}|\textbf{X}=x_{0}].
Budući da smo u prethodnim poglavljima već pretpostavili da je veza obilježja \textbf{X} i \textbf{Y} linearna te procijenili pravac y=ax+b koji tu vezu najbolje aproksimira i pravac y=\hat{a}x+\hat{b} koji najbolje aproksimira vezu podataka iz uzorka, na taj način postupit ćemo i ovdje. Dakle, \mathbb{E}[\textbf{Y}|\textbf{X}=x_{0}]=ax_{0}+b procjenjujemo s \hat{\textbf{Y}}=\hat{a}x_{0}+\hat{b}.
Teorem 14. Za sve prirodne brojeve n vrijedi:
gdje su SSE, S_{\textbf{}}{XX}, \bar{x} kao u napomeni 12 .
(9)
\sqrt{\frac{n-2}{SSE}}\cdot\frac{\hat{a}x+\hat{b}-(ax+b)}{\sqrt{\frac{1}{n}+\frac{(x-\bar{x})^{2}}{S_{\textbf{}}{XX}}}}\sim t(n-2),
Napomena 15. Prethodni teorem kaže da za prirodan broj n dana testna statistika ima Studentovu t-distribuciju s n-2 stupnja slobode. Primijetimo da smo time dobili efektivan način za računanje pouzdanih intervala za \mathbb{E}[\textbf{Y}|\textbf{X}=x_{0}].
Iz (
\mathbb{P}(-t_{0.05/2}(92)\leq \sqrt{\frac{92}{SSE}}\cdot\frac{\hat{a}x_{0}+\hat{b}-(ax_{0}+b)}{\sqrt{\frac{1}{94}+\frac{(x_{0}-\bar{x})^{2}}{S_{\textbf{}}{XX}}}}\leq t_{0.05/2}(92))=0.95,
odnosno procjena 95\% pouzdanog intervala za \mathbb{E}[\textbf{Y}| \textbf{X}=x_{0}]=ax_{0}+b je:
[\hat{a}x_{0}+\hat{b}-t_{0.025}(92)\sqrt{\frac{SSE}{92}}\sqrt{\frac{1}{94}+\frac{(x_{0}-\bar{x})^{2}}{S_{\textbf{}}{XX}}},\hat{a}x_{0}+\hat{b}+ t_{0.025}(92)\sqrt{\frac{SSE}{92}}\sqrt{\frac{1}{94}+\frac{(x_{0}-\bar{x})^{2}}{S_{\textbf{}}{XX}}}].
Pogledajmo koliko to iznosi za konkretne x_{0}. Dobivene rezultate prikazujemo tablicom (Tablica | rang na prijamnom ispitu | 95\% pouzdani interval za očekivani prosjek prve godine studiranja |
| 1-10 | [3.335, 3.345] |
| 11-20 | [3.260, 3.268] |
| 21-30 | [3.184, 3.191] |
| 31-40 | [3.109, 3.115] |
| 41-50 | [3.033, 3.038] |
| 51-60 | [2.957, 2.962] |
| 61-70 | [2.882, 2.885] |
| 71-80 | [2.806, 2.809] |
| 81-90 | [2.731, 2.732] |
| 91-100 | [2.654, 2.655] |
| 101-110 | [2.578, 2.579] |
| 111-120 | [2.502, 2.504] |
| 121-130 | [2.425, 2.428] |
| 131-140 | [2.349, 2.352] |
| 141-150 | [2.272, 2.277] |
| 151-160 | [2.196, 2.201] |
| 161-170 | [2.119, 2.125] |
| 171-180 | [2.043, 2.050] |
| 181-190 | [1.966, 1.974] |
| 191-200 | [1.889, 1.898] |
| 201-210 | [1.813, 1.823] |
| 211-220 | [1.736, 1.747] |
| 221-230 | [1.659, 1.671] |
| 231-240 | [1.583, 1.596] |
| 241-250 | [1.506, 1.520] |
4.4Test značajnosti linearnog regresijskog modela
Primijetimo, u slučaju a=0 dobivamo y=b=const., što nam govori da među promatranim obilježjima nema linearne ovisnosti. Dakle, naša je pretpostavka bila pogrešna. Zato ćemo provjeriti može li se dogoditi ova situacija. Formiramo sljedeće hipoteze:
H_{0}: a=0
H_{1}: a\neq 0
H_{1}: a\neq 0
Testiranje ovih hipoteza zove se test značajnosti linearnog regresijskog modela. Test značajnosti provodimo uz nivo značajnosti \alpha=0.05. Budući da je procjena 95\% pouzdanog intervala za a jednaka [-0.010252096, -0.004972246], a 0\notin[-0.010252096, -0.004972246], odbacujemo H_{0} u korist H_{1} na nivou značajnosti od 0.05, tj. model je značajan.
Dakle, možemo biti 95\% sigurni da je pretpostavka o linearnoj ovisnosti dobra, tj. da su naši rezultati valjani.
5Zaključak
Rezimirajmo dobivene rezultate. Istraživanje smo započeli formiranjem sljedećih hipoteza:
| \bullet | prosjek ocjena prve godine studiranja ne ovisi o spolu |
| \bullet | prosjek ocjena prve godine studiranja ne ovisi o godini upisa na fakultet |
| \bullet | prolaznost na prvoj godini studiranja ovisi o mjestu na rang listi prijamnog ispita |
| \bullet | prosjek ocjena na prvoj godini studiranja i rang na prijamnom ispitu u linearnoj su vezi i na temelju uspjeha na prijamnom ispitu možemo procijeniti prosjek prve godine studiranja |
| \bullet | pomalo neočekivano, prosjek ocjena na 1. godini studiranja ovisi o spolu |
| \bullet | prosjek ocjena ne ovisi o godini upisa na fakultet, tj. ne postoji značajna razlika u prosjeku ocjena generacija upisanih 2007. i 2008. godine |
| \bullet | prolaznost na 1. godini studiranja ovisi o mjestu na rang listi prijamnog ispita, takav rezultat posve je očekivan |
| \bullet | potvrdili smo značajnost provedenog linearnog regresijskog modela, što nam dokazuje da su statistička obilježja rang na prijamnom ispitu i prosjek ocjena na 1. godini u linearnoj vezi y=ax+b, pri čemu je a\in [-0.010252096,-0,004972246] i b\in [3,06435966,3,699772334]. |
1U teoriji vjerojatnosti i statistici, hi-kvadrat razdioba (\chi^{2}-razdioba) jedna je od najčešće korištenih teorijskih razdioba u statistističkim testovima, a ovisi o jednom parametru k (stupnjevi slobode). Ako X ima \chi^{2}-razdiobu s k stupnjeva slobode koristimo oznaku X\sim\chi^{2}(k). Kada je parametar k dovoljno velik, \chi^{2}-razdiobu možemo aproksimirati normalnom razdiobom N(k,2k).
2Studentova t-razdioba (ili samo t-razdioba) je vjerojatnosna razdioba koja se primjenjuje kod procjene srednje vrijednosti normalno distribuirane populacije kada je uzorak mali. Isto tako primjenjuje se za testiranje razlike između dviju srednjih vrijednosti. Studentova razdioba ovisi o jednom parametru k (stupnjevi slobode). Ako X ima t-razdiobu s k stupnjeva slobode, koristimo se oznakom X\sim t(k). Za dovoljno veliku vrijednost parametra k, t-razdioba može se aproksimirati standardnom normalnom razdiobom N(0,1).

