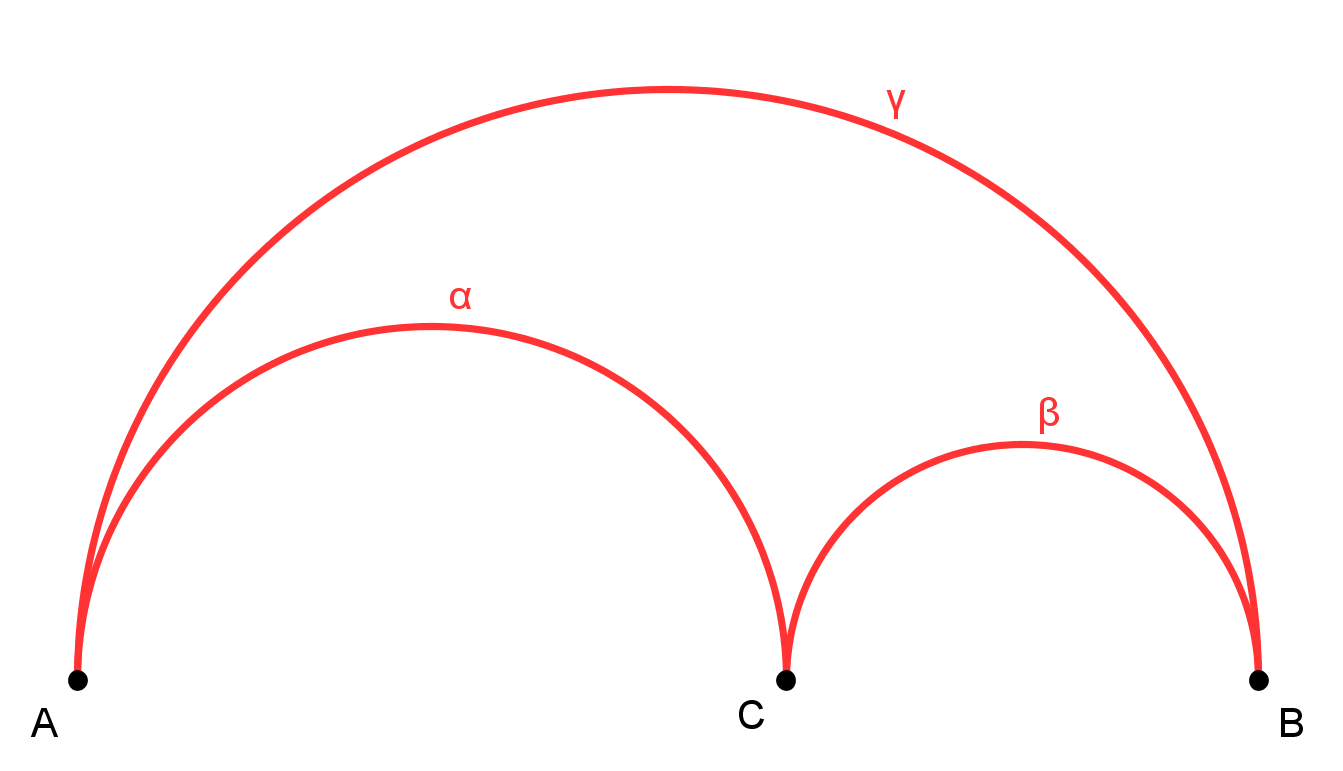
Arbelos
Arbelos ili postolarov nož je lik omeđen trima međusobno tangentnim polukružnicama s kolinearnim središtima. Tim su se likom bavili starogrčki matematičari Arhimed i Pappus Aleksandrijski. Arhimed je unutar arbelosa uočio dvije istaknute kružnice jednakog radijusa, koje je spomenuo i u svojoj ”Knjizi Lema”, dok je Pappus zaključio da je arbelos ispunjen tangentnim kružnicama. Njihov je rad, nakon gotovo dvije tisuće godina, obradio i popularizirao Leon Bankoff, uvodenjem nekoliko novih sličnih kružnica.
U ovom radu opisat ćemo osnovna geometrijska svojstva arbelosa i kružnica koje su proučavali Arhimed i Pappus. Također, iskoristit ćemo prednosti elektroničkog formata tako što ćemo u 4. poglavlju konstrukcije nekih kružnica prikazati dinamički. U tu svrhu bit će potrebno instalirati i pokrenuti programski paket Java 1.4.2. (ili kasniju inačicu).
Započnimo s formalnom definicijom arbelosa.
Polukružnice ćemo označavati s \alpha, \beta i \gamma kao na slici 1, njihove radijuse s r_1, r_2 i r, a dijametre s d_1, d_2 i d. Središta polukružnica \alpha, \beta i \gamma označavat ćemo s O_1, O_2 i O, a pravac na kojem se nalaze središta s AB, gdje je točka A presjecište tog pravca i polukružnice \alpha, a točka B presjecište tog pravca i polukružnice \beta. Točkom C označavat ćemo zajedničko presjecište polukružnica \alpha i \beta i pravca AB.
Često ćemo spominjati različite kružnice pa ćemo u tu svrhu kružnicu sa središtem u točki S označavati sa (S), a kružnicu sa središtem u točki S i radijusom |ST| označavati ćemo sa S(T). Analogno ćemo označavati i različite polukružnice.
Krenimo od osnovnih, ali ne i očiglednih svojstava arbelosa.
b) Ako s D označimo presjecište polukružnice \gamma i okomice na pravac AB u točki C, tada je površina kružnice promjera |CD| jednaka površini arbelosa.
Napomenimo da je tvrdnja b) propozicije 1 poznata kao propozicija 4 u Arhimedovoj "Knjizi Lema".
Uz pomoć arbelosa možemo vizualno predočiti nejednakosti harmonijske, geometrijske, aritmetičke i kvadratne sredine za dvije veličine. U tu svrhu dokazujemo sljedeću propoziciju:
a) duljina dužine CQ je kvadratna sredina M_2(d_1, d_2).
b) duljina dužine OQ i dužine OD je aritmetička sredina M_1(d_1, d_2).
c) duljina dužine CD je geometrijska sredina M_0(d_1, d_2).
d) duljina dužine DD', gdje je D' nožište okomice iz točke C na dužinu OD, je harmonijska sredina M_{-1}(d_1,d_2).
e) Ako je d_1 \geq d_2, onda vrijedi d_1 \geq M_2(d_1, d_2) \geq M_1(d_1, d_2) \geq M_0(d_1, d_2) \geq M_{-1}(d_1, d_2) \geq d_2.
| Slika 2. Pomicanjem klizača d_1 mijenjaju se duljine dužina iz propozicije 2. |
b) Duljina dužina OQ i OD jednaka je \frac{d}{2} pa je očito |OQ|=|OD|=\frac{d_1 + d_2}{2}=M_1(d_1, d_2).
c) Trokut OCD je pravokutan, s pravim kutom u vrhu C. Prema Pitagorinom poučku vrijedi
d) Trokuti DD'C i DCO su slični pa vrijedi \frac{|DD'|}{|CD|} = \frac{|CD|}{|OD|}. Dalje vrijedi |DD'| = \frac{|CD|^2}{|OD|} = \frac{2d_1 d_2}{d_1 + d_2} = M_{-1}(d_1, d_2).
e) Trokut QOC je pravokutan, s pravim kutom u vrhu O. U tom trokutu je |CQ| = M_2(d_1, d_2) hipotenuza, a |OQ| = M_1(d_1, d_2) kateta pa očito vrijedi M_2(d_1, d_2) \geq M_1(d_1, d_2). U pravokutnim trokutima OCD i CD'D analogno pokazujemo M_1(d_1, d_2) \geq M_0(d_1, d_2) \geq M_{-1}(d_1, d_2). Dalje imamo
Prvih nekoliko svojstava pokazuje da je doista riječ o zanimljivom liku, što za američkog matematičara C. Dodgea nije ništa čudno jer je arbelos, pored svega, trokut kojemu su stranice polukružnice ([2]). O još nekim svojstvima arbelosa, koja se mogu dokazati elementarnom geometrijom, možete pročitati u [3]. No ipak, najviše zanimanja za arbelos nisu potaknula ova prethodna svojstva, već svojstva kružnica koje je Arhimed primijetio i zabilježio u svojoj ”Knjizi Lema”. To su tzv. Arhimedove kružnice (u literaturi se ponekad navode i kao ”magične kružnice”).
Vjeruje se da je Arhimed prvi matematičar koji je proučavao arbelos. On je unutar arbelosa prepoznao dvije kružnice koje je smatrao specifičnima zbog toga što uz jednake radijuse, obje diraju dva luka arbelosa i pravac CD. Te dvije spomenute kružnice često se nazivaju Arhimedovim blizancima, očigledno zbog jednakog radijusa, koji ćemo odrediti u sljedećem teoremu.
| Slika 3. Arhimedovi blizanci. Točka C je pomična. |
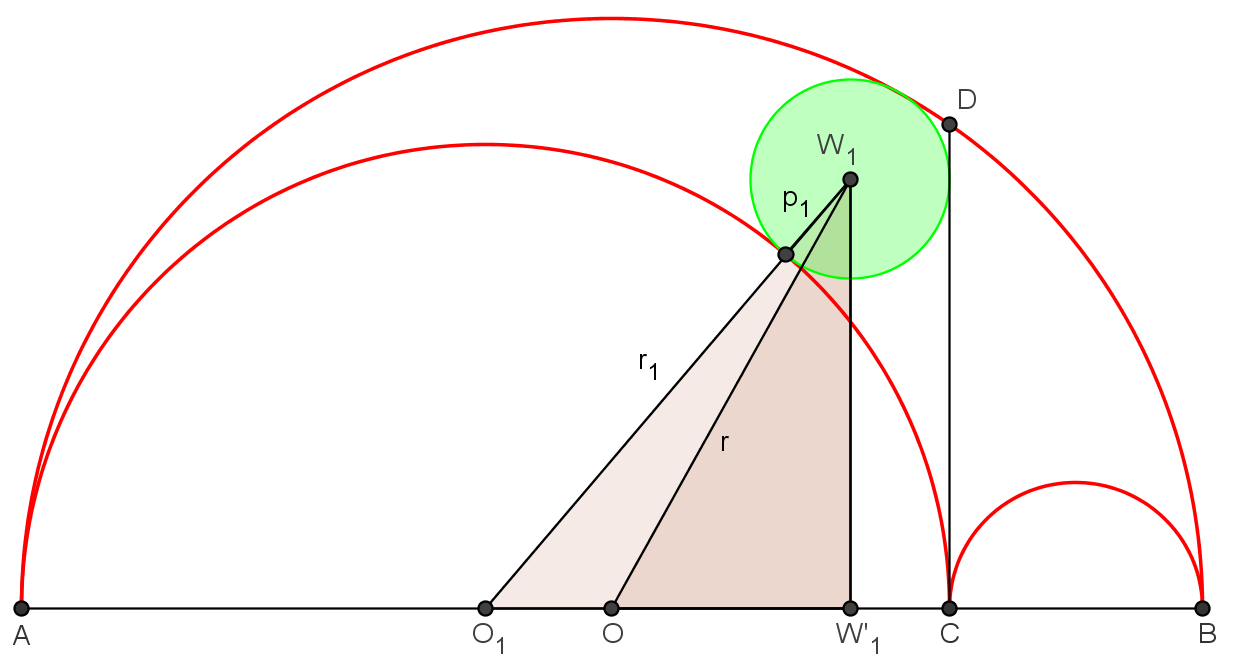
Od vremena Arhimeda pa sve do posljednje četvrtine 20. stoljeća proučavanje Arhimedovih blizanaca nije zaokupljalo pozornost matematičara. Godine 1974. Leon Bankoff, američki zubar i matematičar amater, pokazao je da Arhimedovi blizanci nisu samo blizanci, već da postoji i treća kružnica radijusa \frac{r_1 r_2}{r} koja je nekim karakterističnim svojstvom vezana uz arbelos. Njegov rad potaknuo je niz matematičara, među kojima su Z. Čerin, C. Dodge, F. van Lamoen, H. Okumura, M. Watanabe, P.Y. Woo, P. Yiu i drugi, da pronađu druge kružnice radijusa \frac{r_1 r_2}{r} koje su na neki način vezane uz arbelos. Takve kružnice nazivamo Arhimedovim kružnicama. Definirajmo ih formalnije:
Pored Arhimedovih blizanaca, treća Arhimedova kružnica, koju je otkrio Bankoff, usko je vezana uz kružnicu koja dira sva tri luka arbelosa, tzv. arbelosu upisana kružnica. Arbelosu upisanu kružnicu označavat ćemo s (O_3), a njeno središte s O_3. Treća Arhimedova, odnosno prva Bankoffova kružnica prolazi točkom C i diralištima M i N kružnice (O_3) s lukovima \alpha i \beta (vidi sliku 5.).
| Slika 5. Treća Arhimedova kružnica. Točka C je pomična. |
Dokaz da je zbilja riječ o Arhimedovoj kružnici slijedi iz Pitagorina poučka i Heronove formule, a detalje prepuštamo čitatelju (ili vidi [3]).
Pored prethodne kružnice, Bankoff je otkrio još jednu Arhimedovu kružnicu: označimo s EF zajedničku tangentu polukružnica \alpha i \beta, gdje je točka E diralište polukružnice \alpha i tangente EF, a točka F diralište polukružnice \beta i tangente EF. Tada kružnica, koja iznutra dira polukružnicu \gamma i pravac EF, ima radijus p. Štoviše, ta kružnica dira polukružnicu \gamma u točki D i to je najmanja kružnica koja prolazi kroz točku D i dira pravac EF.
| Slika 6. Četvrta Arhimedova kružnica. Točka C je pomična. |
Dokaz da je riječ o Arhimedovoj kružnici ponovo prepuštamo čitatelju (ili vidi [3]).
Od Bankoffova otkrića treće i četvrte Arhimedove kružnice pa sve do danas otkriveno je više od pedeset novih Arhimedovih kružnica, a H. Okumura i M. Watanabe otkrili su i nekoliko beskonačnih familija Arhimedovih kružnica. O tim kružnicama možete čitati u [2], [3], [4] i [5]. Dostupan je i online katalog Arhimedovih kružnica.
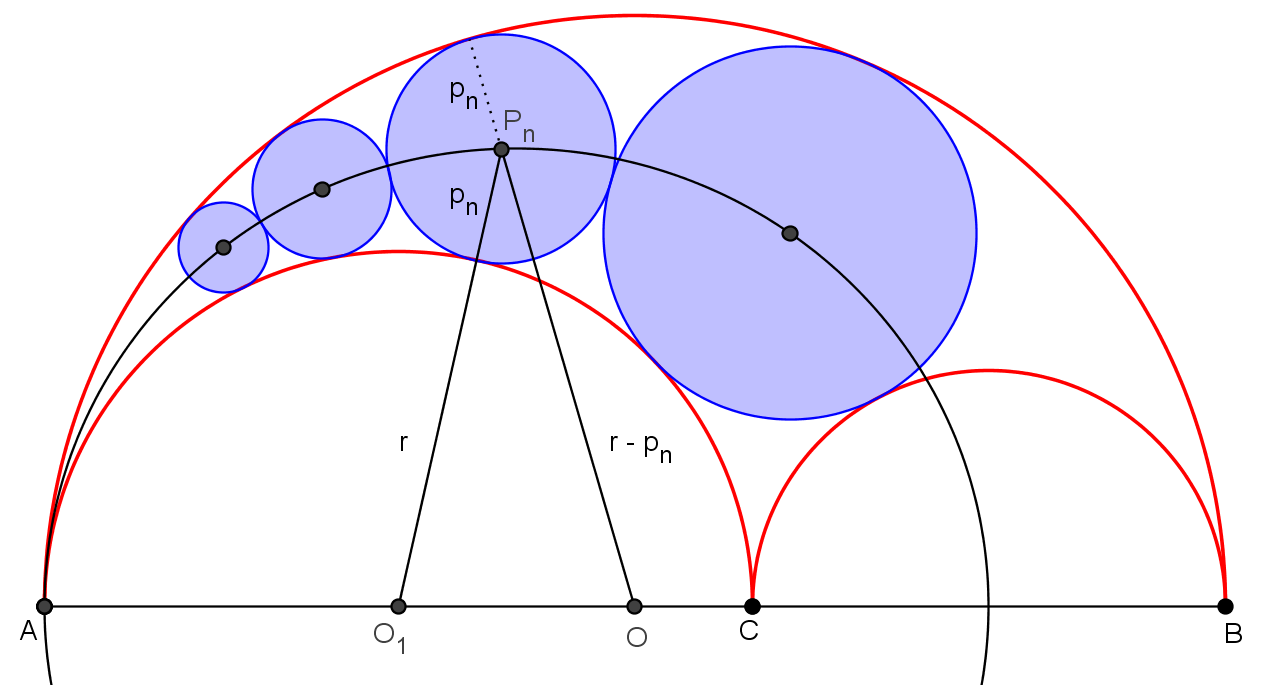
Osim Arhimedovih kružnica uz arbelos vezana je još jedna familija kružnica, tzv. Pappusov lanac kružnica (vidi sliku 7.). Pappusov lanac kružnica formira se na sljedeći način: najprije konstruiramo arbelosu upisanu kružnicu koju ćemo označiti s (P_1). Zatim konstruiramo kružnicu (P_2) koja dira lukove \alpha i \gamma i kružnicu (P_1). Analogno konstruiramo svaku iduću kružnicu (P_n) u lancu.
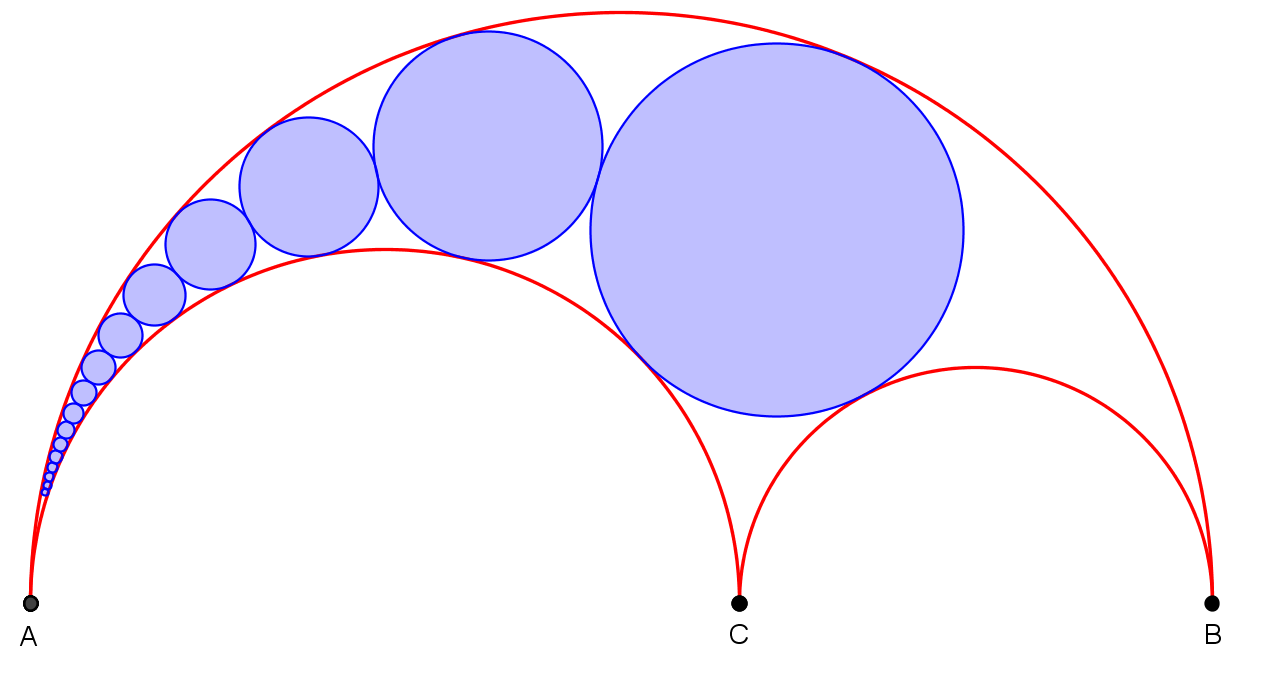
Pappusov lanac kružnica nazvan je prema starogrčkom matematičaru Pappusu Aleksandrijskom. On je dokazao teorem uz pomoć kojeg se može odrediti ordinata središta kružnica u Pappusovu lancu kružnica:
Suvremeni dokaz teorema 2. provodi se inverzijom pa se često postavlja pitanje kako je Pappus dokazao taj teorem kada je tehnika inverzije uvedena tek u 19. stoljeću. Za više informacija i odgovor na to pitanje, korisno je proučiti članak [1]. Dokaz primjenom inverzije možete proučiti u [3].
Pappus je pokazao i da se središta kružnica u lancu nalaze na elipsi.
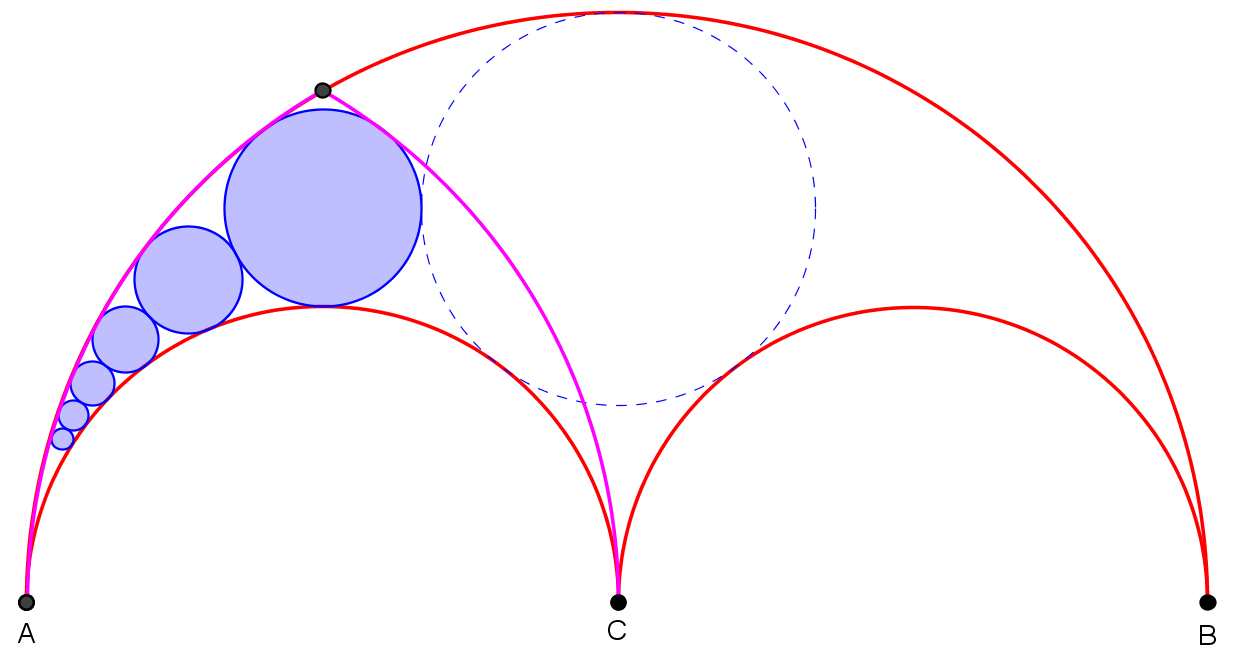
Konstruirajmo arbelos u kojem su radijusi polukružnica \alpha i \beta jednaki i upišimo mu Pappusov lanac kružnica. Konstruirajmo dva kružna luka radijusa |AC| tako da je središte jednog luka u točki A, a središte drugog luka u točki C. Novonastala figura je gotički luk, jedan od motiva u gotičkoj arhitekturi.
U ovom poglavlju opisat ćemo geometrijske konstrukcije Arhimedovih blizanaca, arbelosu upisane kružnice i Pappusova lanca kružnica. Dokaze nećemo provoditi; dokaze čitatelji mogu provesti za vježbu ili pogledati u [3].
- Neka je točka Q_1, odnosno Q_2, presjecište polukružnice \alpha, odnosno \beta i okomice na pravac AB, povučene iz središta polukružnice \alpha, odnosno \beta. Označimo s P presjecište dužina Q_1O_2 i Q_2O_1. To presjecište nalazi se na pravcu CD.
- Konstruirajmo kružnicu (W) sa središtem u točki C i radijusom |CP|. Ta kružnica je Arhimedova.
- Označimo s P_1 i P_2 presjecišta kružnice (W) i pravca AB te povucimo tangente t_1 i t_2 na kružnicu (W) u točkama P_1 i P_2.
- Presjecište tangente t_1 kružnice (W), odnosno t_2 u točki P_1, odnosno P_2 i polukružnice O_1(P_2), odnosno polukružnice O_2(P_1), dat će točku W_1, odnosno W_2, koja je središte kružnice (W_1), odnosno (W_2).
- Konačno, kružnice se središtem u točkama W_1 i W_2 s radijusom |CP| Arhimedovi su blizanci.
| Konstrukcija Arhimedovih blizanaca. Radi jednostavnijeg prikaza, neki su koraci sakriveni. |
- Primjenom konstrukcije 1. konstruirajmo kružnicu (W_3) (to je prva Bankoffova kružnica).
- Neka je točka M presjecište polukružnice \alpha i kružnice (W_3) te neka je točka N presjecište polukružnice \beta i kružnice (W_3). Povucimo pravce O_1M i O_2N i njihovo presjecište označimo s O_3.
- Kružnica sa središtem u točki O_3 i radijusom |O_3M|=|O_3N| je arbelosu upisana kružnica.
| Konstrukcija arbelosu upisane kružnice. Radi jednostavnijeg prikaza, neki su koraci sakriveni. |
- Najprije konstruirajmo okomice na pravac AB u točkama B i C i označimo ih s l i l'. Konstruirajmo zatim kružnicu koja dira polukružnicu \beta i pravce l i l'. Očito se središte te kružnice nalazi na pravcu koji prolazi točkom O_2 i okomit je na pravac AB, a radijus je očito jednak r_2.
- Označimo s Q_2 diralište prethodno konstruirane kružnice s polukružnicom \beta, a s E, odnosno F, označimo diralište s pravcem l, odnosno l'.
- Konstruirajmo pravce AQ_2, AE i AF. Označimo s Q_2' presjecište pravca AQ_2 i polukružnice \beta, s E' presjecište pravca AE i polukružnice \alpha i s F' presjecište pravca AF i polukružnice \gamma. Kružnica određena točkama Q_2, E' i F' je kružnica (P_1).
- Svaku sljedeću kružnicu u lancu konstruiramo analogno.
| Konstrukcija Pappusova lanca kružnica. Radi jednostavnijeg prikaza, neki su koraci sakriveni. |
| [1] | L. Bankoff, How Did Pappus Do It?, Mathematical Gardner (Urednik D. Klarner). Boston, MA: Prindle, Weber, and Schmidt, str. 112.-118., 1981. |
| [2] | C.W. Dodge, T. Schoch, P. Y. Woo, P. Yiu, Those Ubiquitous Archimedean Circles, Math. Mag., 72 (1999), 202.-213. |
| [3] | G. Malić, Arbelos, studentski rad izrađen na PMF-MO, nagrađen Rektorovom nagradom Sveučilišta u Zagrebu za akademsku godinu 2006./2007. |
| [4] | H. Okumura, M. Watanabe, A generalization of Power's Archimedean Circles, Forum Geometricorum 6 (2006), 103.-105. |
| [5] | H. Okumura, M. Watanabe, The Archimedean Circles of Schoch and Woo, Forum Geometricorum 4 (2004), 27.-34. |