Bojan Kovačić,
Tehničko veleučilište u Zagrebu, Zagreb |
Marijana Špoljarić
Visoka škola za menadžment u turizmu i informatici u Virovitici, Virovitica |
Luka Marohnić
Tehničko veleučilište u Zagrebu, Zagreb |
Sažetak
U članku se definira Jacobsthalov niz, te se ukratko opisuje njegova veza s Lucasovim brojevima. Detaljno se izvodi formula za opći član niza, te pripadna funkcija izvodnica. Potom se navode i dokazuju neka osnovna svojstva toga niza, kao i neke jednakosti vezane uz članove niza. Zaključno se opisuje veza Jacobsthalova niza i elementarnih staničnih automata.
1Definicija i osnovna svojstva Jacobsthalova niza
Jacobsthalov niz svoj naziv duguje njemačkom matematičaru Ernstu Jacobsthalu (1882.–1965.). Spomenimo da je, osim po proučavanju ovoga niza, Jacobsthal poznat i po dokazu da se svaki prost broj oblika
4\cdot k+1, pri čemu je
k\in\mathbb{N}, može prikazati kao zbroj kvadrata dvaju prirodnih brojeva. Taj je dokaz Jacobsthal 1906. godine izložio u svojoj doktorskoj disertaciji ,,Primjena jedne formule iz teorije kvadratnih ostataka”.
Jacobsthalov niz definiran je rekurzivno s:
(1)
\begin{cases} J_{n}=J_{n-1}+2\cdot J_{n-2},& n\geq2,\\\ J_{0}=0,\, J_{1}=1. \end{cases}
Iz (
1) se lako dobiva prvih nekoliko članova Jacobsthalova niza: 0, 1, 1, 3, 5, 11, 21, 43, \dots
Osnovna rekurzija reda 2 navedena u (
1) može se pojednostavniti svođenjem na rekurziju reda 1. Točnije, vrijedi sljedeća propozicija:
Propozicija 1. Za svaki prirodan broj
n vrijede jednakosti:
(2)
J_{n+1}=2\cdot J_{n}+(-1)^{n}
i
Dokaz. Obje jednakosti najjednostavnije se dokazuju matematičkom indukcijom. Dokažimo najprije (
2). Za
n=1 dobivamo
J_{2}=2\cdot J_{1}+(-1)^{1}=2\cdot1-1=1
čime smo provjerili valjanost baze indukcije. Pretpostavimo da (
2) vrijedi za neki
n\in\mathbb{N} i sve prirodne brojeve manje od
n, pa pokažimo da je (
2) valjana i za broj
n+1. Koristeći osnovnu rekurziju iz (
1) i izrečenu pretpostavku, dobivamo redom:
J_{n+2}=J_{n+1}+2\cdot J_{n}=J_{n+1}+\left(J_{n+1}-(-1)^{n}\right)=2\cdot J_{n+1}+(-1)^{n+1}
pa (
2) vrijedi i za broj
n+1, a to smo i htjeli pokazati.
Jednakost (
3) se dokazuje potpuno analogno kao i (
2), pa taj dokaz prepuštamo čitatelju.
\ \blacksquare
U nastavku ćemo odrediti zatvorenu formulu za opći član niza, tj. propis realne funkcije
f jedne realne varijable takve da je
J_{n}=f(n) . Vrijedi sljedeća propozicija:
Propozicija 2. Za svaki
n\in\mathbb{N}_{0}:=\left\lbrace 0,1,2,\dots\right\rbrace vrijedi jednakost:
(4)
J_{n}=\frac{2^{n}-\left(-1\right)^{n}}{3}
Dokaz. Pokazali smo da jednakosti (
2) i (
3) vrijede za svaki prirodan broj n. Pomnožimo li jednakost (
3) brojem 2 i zbrojimo dobivenu jednakost s jednakosti (
2), zaključujemo da jednakost
3\cdot J_{n+1}=2^{n+1}+(-1)^{n}
odnosno
(5)
3\cdot J_{n+1}=2^{n+1}-(-1)^{n+1}
vrijedi za svaki
n\in\mathbb{N}. Zamijenimo li
n+1 s
n, vrijednost varijable
n bit će neki cijeli broj iz skupa
\mathbb{N}_{0}. Preostaje jednakost (
5) podijeliti s 3, čime se dobiva jednakost (
4).
\ \blacksquare
Formula (
4) može se izvesti i pomoću funkcije izvodnice za Jacobsthalov niz. Izvedimo najprije zatvorenu formu za tu funkciju. Podsjetimo, funkcija izvodnica za niz
\left(a_{n}\right)_{n\in\mathbb{N}} je izraz
(6)
f(x)=\sum_{n=0}^{\infty}a_{n}\cdot x^{n}.
Desna strana te jednakosti je formalni red potencija. Ako je moguće, treba odrediti zatvoreni oblik funkcije
f , odnosno prikazati je kao izraz koji se sastoji od konačno mnogo članova i faktora. Pritom problem konvergencije desne strane jednakosti (
6) zanemarujemo.
Propozicija 3. Funkcija izvodnica za niz (
1) je
(7)
f(x)=\frac{x}{(x+1)(1-2x)}.
Dokaz. Koristeći osnovnu rekurziju iz (
1) imamo redom:
\begin{aligned} \sum_{n=1}^{\infty}J_{n}x_{n}& = J_{1}x+\sum_{n=2}^{\infty}J_{n}x^{n}=x+\sum_{n=2}^{\infty}\left(J_{n-1}+2J_{n-2}\right)x^{n}=x+\sum_{n=2}^{\infty}J_{n-1}x^{n}+2\sum_{n=2}^{\infty}J_{n-2}x^{n}= \\\& = x+\sum_{n=1}^{\infty}J_{n}x^{n+1}+2\sum_{n=0}^{\infty}J_{n}x^{n+2}=x+x\sum_{n=1}^{\infty}J_{n}x^{n}+2x^{2}\sum_{n=0}^{\infty}J_{n}x^{n}=\\\& = x+x\sum_{n=1}^{\infty}J_{n}x^{n}+2x^{2}\left(J_{0}x^{0}+\sum_{n=1}^{\infty}J_{n}x^{n}\right)=x+x\sum_{n=1}^{\infty}J_{n}x^{n}+2x^{2}\sum_{n=1}^{\infty}J_{n}x^{n}. \end{aligned}
Prema definiciji funkcije izvodnice za Jacobsthalov niz vrijedi
f(x)=\sum_{n=1}^{\infty}J_{n}x^{n}
pa slijedi
f(x)=x+xf(x)+2x^{2}f(x)\quad\Rightarrow\quad f(x)\left(1-x-2x^{2}\right)=x,
odakle je
f(x)=\frac{x}{1-x-2x^{2}}.
Lako se vidi da su
x_{1}=-1 i
x_{2}=\frac{1}{2} nultočke polinoma
p(x)=-2x^{2}-x+1, pa konačno dobivamo
f(x)=\frac{x}{1-x-2x^{2}}=\frac{x}{(-2)(x+1)\left(x-\frac{1}{2}\right)}=\frac{x}{(x+1)(1-2x)}.
\ \blacksquare
Prethodnu propoziciju dokazat ćemo na još jedan način.
Alternativni dokaz propozicije 6. Rastavimo funkciju
f na parcijalne razlomke. Tražimo realne brojeve
A i
B takve da vrijedi
f(x)=\frac{x}{(x+1)(1-2x)}=\frac{A}{x+1}+\frac{B}{1-2x}.
Odavde je
x=\left(\frac{A}{x+1}+\frac{B}{1-2x}\right)\cdot(x+1)(1-2x)
što se nakon kraćenja svodi na
x=A(1-2x)+B(x+1).
Posljednja jednadžba predstavlja jednakost dvaju polinoma. Ona mora vrijediti za svaki
x\in\mathbb{R}. Uvrštavanjem
x=-1 odmah dobivamo
A=-\frac{1}{3}, dok uvrštavanjem
x=\frac{1}{2} slijedi
B=\frac{1}{3}. Stoga vrijedi
(8)
f(x)=\frac{1}{3}\left(\frac{1}{1-2x}-\frac{1}{x+1}\right).
Razvijmo članove unutar zagrade u redove potencija. Primijenit ćemo poznati razvoj
\frac{1}{1-x}=\sum_{n=0}^{\infty}x^{n}.
Uvrstimo li umjesto
x izraz
-x odnosno
2x, dobivamo redom
\frac{1}{1+x}=\sum_{n=0}^{\infty}(-x)^{n}=\sum_{n=0}^{\infty}(-1)^{n}\cdot x{}^{n}\quad\text{i}\quad\frac{1}{1-2x}=\sum_{n=0}^{\infty}(2x)^{n}=\sum_{n=0}^{\infty}2^{n}\cdot x{}^{n}.
Konačno dobivamo
f(x)=\frac{1}{3}\left(\sum_{n=0}^{\infty}2^{n}\cdot x{}^{n}-\sum_{n=0}^{\infty}(-1)^{n}\cdot x{}^{n}\right)=\sum_{n=0}^{\infty}\frac{2^{n}-(-1)^{n}}{3}\cdot x^{n},
odakle, prema (
4), slijedi da je koeficijent uz
x^{n} jednak
J_{n}, čime je dokaz završen.
\ \blacksquare
Napomenimo da je niz (
1) poseban slučaj poopćenoga Lucasova niza
\left(L_{n}\right)_{n\in\mathbb{N}}. Taj se niz zadaje tako da se odaberu
x,y\in\mathbb{Z} sa svojstvom
x^{2}-4y\gt 0, pa se definira redom:
\begin{cases} a=\frac{x+\sqrt{x^{2}-4y}}{2},\, b=\frac{x-\sqrt{x^{2}-4y}}{2},\\\ L_{n}(a,b)=\frac{a^{n}-b^{n}}{a-b},\, n\in\mathbb{N}. \end{cases}
Lako se provjeri da izborom
x=1 i
y=-2 dobivamo Jacobsthalov niz. Detalje ovdje izostavljamo, a mogu se naći u
[1].
2Neke jednakosti vezane uz Jacobsthalov niz
U ovoj ćemo točki dokazati nekoliko zanimljivih jednakosti vezanih uz Jacobsthalov niz. Najprije ćemo izračunati zbroj prvih
n članova toga niza. Vrijedi sljedeća propozicija.
Propozicija 4. Za svaki prirodan broj
n vrijedi jednakost
(9)
\sum_{k=1}^{n}J_{k}=\frac{1}{2}\left(J_{n+2}-1\right).
Dokaz. Jednakost (
9) se „klasično“ može dokazati matematičkom indukcijom, što prepuštamo čitatelju za vježbu. Mi ćemo (
9) dokazati metodom teleskopiranja koristeći jednakost (
3). Napišimo jednakost (
3) za
k=1,2,3,\dots,n:
\begin{gathered}J_{1+1}=2^{1}-J_{1},\\ J_{2+1}=2^{2}-J_{2},\\ J_{3+1}=2^{3}-J_{3},\\ \dots\\ J_{n+1}=2^{n}-J_{n}. \end{gathered}
Zbrajanjem tih
n jednakosti dobivamo
J_{2}+J_{3}+J_{4}+\dots+J_{n+1}=(2+4+8+\dots+2^{n})-(J_{1}+J_{2}+J_{3}+\text{…}+J_{n}).
Lijevoj i desnoj strani ove jednakosti dodajmo broj
J_{1}=1, pa dobivamo
J_{1}+J_{2}+J_{3}+J_{4}+\dots+J_{n+1}=(2+4+8+\dots+2^{n})+1-(J_{1}+J_{2}+J_{3}+\dots+J_{n}).
Odavde slijedi
(10)
\sum_{k=1}^{n}J_{k}=\frac{1}{2}\left[\left(2+4+8+\dots+2^{n}\right)+1-J_{n+1}\right].
U okruglim zagradama napisan je zbroj prvih
n članova geometrijskoga niza kojemu su prvi član i količnik jednaki 2. Taj je zbroj jednak
2+4+8+\dots+2^{n}=2\left(\frac{2^{n}-1}{2-1}\right)=2^{n+1}-2,
pa jednakost (
10) možemo zapisati u obliku
\sum_{k=1}^{n}J_{k}=\frac{1}{2}\left[\left(2^{n+1}-2\right)+1-J_{n+1}\right]=\left(2^{n}-\frac{1}{2}\cdot J_{n+1}\right)-\frac{1}{2}.
Podijelimo li jednakost (
3) s brojem 2, dobit ćemo
\frac{1}{2}\cdot J_{n+1}=2^{n-1}-\frac{1}{2}\cdot J_{n}.
Pišemo li u ovoj jednakosti
n umjesto
n-1,
n+1 umjesto
n i
n+2 umjesto
n+1, dobivamo
2^{n}-\frac{1}{2}\cdot J_{n+1}=\frac{1}{2}\cdot J_{n+2}.
Stoga je
\sum_{k=1}^{n}J_{k}=\frac{1}{2}\cdot J_{n+2}-\frac{1}{2}=\frac{1}{2}\left(J_{n+2}-1\right),
što je i trebalo pokazati.
\ \blacksquare
Poznato je da za niz Fibonaccijevih brojeva
\left(F_{n}\right){}_{n\in\mathbb{N}} definiran s
\begin{cases} F_{n}=F_{n-1}+F_{n-2},& n\geq3,\\\ F_{1}=F_{2}=1 \end{cases}
vrijedi
Cassinijev identitet:
(11)
F_{n+1}\cdot F_{n-1}-F_{n}^{2}=(-1)^{n}.
(Detalji se mogu naći npr. u
[4]). Analogon Cassinijeva identiteta za Jacobsthalov niz izriče sljedeća propozicija.
Propozicija 5. Za svaki prirodan broj
n vrijedi jednakost
(12)
J_{n+1}\cdot J_{n-1}-J_{n}^{2}=(-1)^{n}\cdot2^{n-1}.
Dokaz. Koristeći (
4) imamo redom:
\begin{eqnarray*} J_{n+1}\cdot J_{n-1}-J_{n}^{2}& =& \left(\frac{2^{n+1}-(-1)^{n+1}}{3}\right)\cdot\left(\frac{2^{n-1}-(-1)^{n-1}}{3}\right)-\left(\frac{2^{n}-(-1)^{n}}{3}\right)^{2}=\\\& =& \frac{\left(2^{n+1}+(-1)^{n}\right)\cdot\left(2^{n-1}+(-1)^{n}\right)-\left(2^{n}-(-1)^{n}\right)^{2}}{9}=\\\& =& \frac{2^{2n}+(-1)^{n}\cdot\left(2^{n-1}+2^{n+1}\right)+(-1)^{2n}-2^{2n}+2^{n+1}\cdot(-1)^{n}-(-1)^{2n}}{9}=\\\& =& \frac{(-1)^{n}\cdot\left(2^{n-1}+2\cdot2^{n+1}\right)}{9}=\frac{(-1)^{n}\cdot2^{n-1}\cdot\left(1+2^{3}\right)}{9}=(-1)^{n}\cdot2^{n-1}, \end{eqnarray*}
što je i trebalo pokazati.
\ \blacksquare
Posljednju propoziciju moguće je dokazati i na drugačiji način. Pokazat ćemo najprije da Jacobsthalove brojeve možemo izračunavati pomoću
F-matrice
F=\left(\begin{array}{cc} 1& 2\\\ 1& 0 \end{array}\right),
koja je analogon
Q-matrici
Q=\left(\begin{array}{cc} 1& 1\\\ 1& 0 \end{array}\right) za Fibonaccijeve brojeve. Točnije, vrijedi sljedeća propozicija.
Propozicija 6. Za sve prirodne brojeve
n vrijedi
(13)
F^{n}=\left(\begin{array}{cc} J_{n+1}& 2J_{n}\\\ J_{n}& 2J_{n-1} \end{array}\right).
Dokaz. Tvrdnju ove propozicije jednostavno dokazujemo matematičkom indukcijom koristeći osnovnu rekurziju (
1). Zbog
J_{0}=0 i
J_{1}=J_{2}=1 očito je
F^{1}=F=\left(\begin{array}{cc} 1& 2\\\ 1& 0 \end{array}\right)=\left(\begin{array}{cc} 1& 2\\\ 1& 2\cdot0 \end{array}\right)=\left(\begin{array}{cc} J_{2}& 2J_{1}\\\ J_{1}& 2J_{0} \end{array}\right),
čime smo pokazali valjanost baze indukcije. Pretpostavimo da jednakost (
13) vrijedi za neki
n\in\mathbb{N}. Koristeći (
1), dobivamo:
\begin{eqnarray*} F^{n+1}& =& F^{n}\cdot F=\left(\begin{array}{cc} J_{n+1}& 2J_{n}\\\ J_{n}& 2J_{n-1} \end{array}\right)\cdot\left(\begin{array}{cc} 1& 2\\\ 1& 0 \end{array}\right)=\left(\begin{array}{cc} J_{n+1}+2J_{n}& 2J_{n+1}\\\ J_{n}+2J_{n-1}& 2J_{n} \end{array}\right)=\\\& =& \left(\begin{array}{cc} J_{n+2}& 2J_{n+1}\\\ J_{n+1}& 2J_{n} \end{array}\right), \end{eqnarray*}
čime je dokaz završen.
\ \blacksquare
Alternativni dokaz propozicije~11. Na matrice iz Propozicije
12 primijenimo Binet-Cauchyev
teorem. Determinanta desne strane jednakosti (
13) je
\left|\begin{array}{cc} J_{n+1}& 2J_{n}\\\ J_{n}& 2J_{n-1} \end{array}\right| = 2J_{n+1}\cdot J_{n-1}-2J_{n}^{2},
a determinanta lijeve strane
\det\left(F^{n}\right)=\left(\det F\right)^{n}=\left|\begin{array}{cc} 1& 2\\\ 1& 0 \end{array}\right|^{n}=(-2)^{n}=(-1)^{n}\cdot2^{n},
pa izjednačavanjem tih izraza dobivamo
J_{n+1}\cdot J_{n-1}-2J_{n}^{2}=(-1)^{n}\cdot2^{n-1},
što je upravo jednakost (
12).
\ \blacksquare
U sljedeće dvije propozicije povezat ćemo članove Jacobsthalova niza i binomne koeficijente. Najprije ćemo pokazati da se svaki element Jacobsthalova niza može dobiti kao svojevrsna „linearna kombinacija“ potencija broja 2 s nenegativnim cjelobrojnim eksponentom čiji su „koeficijenti“ određeni binomni koeficijenti.
Propozicija 7. Za svaki prirodan broj
n vrijedi jednakost
\sum_{k\geq0}{n-1-k \choose k}\cdot2^{k}=J_{n}.
Dokaz. Pokazat ćemo da niz
(a_{n})_{n\in\mathbb{N}} čiji je opći član
(14)
a_{n}=\sum_{k\geq0}{n-1-k \choose k}\cdot2^{k}
zadovoljava sve jednakosti u (
1). Znamo da je prva jednakost u (
1) zapravo rekurzija reda 2 koja uz dva zadana početna uvjeta ima jedinstveno rješenje. Prema definiciji, ta rekurzija i početni uvjeti definiraju Jacobsthalov niz. Dokažemo li da ista tri svojstva ima i niz
(a_{n})_{n\in\mathbb{N}}, slijedit će
a_{n}=J_{n}, za svaki
n\in\mathbb{N}.
Koristit ćemo jednakosti
(15)
\binom{0}{0}=1\quad\text{i}\quad\binom{n}{k}=0\quad\text{za }k\gt n\text{ ili }k\lt 0.
Napomenimo da, zbog (
15), ne moramo paziti na gornju granicu indeksa sumacije. Drugim riječima, sve razmatrane sume idu od
k=0 pa „dokle god mogu“ (tj. dok „nazivnik“ binomnoga koeficijenta ne postane strogo veći od „brojnika“). Tako najprije imamo:
\begin{gathered}\begin{gathered}a_{1}=\sum_{k\geq0}\end{gathered} \binom{1-1-k}{k}\cdot2^{k}=\sum_{k\geq0}{0-k \choose k}\cdot2^{k}={0-0 \choose 0}\cdot2^{0}=1,\\\ \begin{gathered}a_{2}=\sum_{k\geq0}\end{gathered} {2-1-k \choose k}\cdot2^{k}=\sum_{k\geq0}{1-k \choose k}\cdot2^{k}={1-0 \choose 0}\cdot2^{0}+{1-1 \choose 1}\cdot2^{1}=1+0=1, \end{gathered}
Dakle, niz (
14) zadovoljava početne uvjete iz (
1). Koristeći poznato svojstvo binomnih koeficijenata
{n \choose k}={n-1 \choose k-1}+{n-1 \choose k-1},
dobivamo redom:
\begin{eqnarray*} a_{n}& =& \sum_{k\geq0}{n-1-k \choose k}\cdot2^{k}=\sum_{k\geq0}\left[{n-2-k \choose k}+{n-2-k \choose k-1}\right]\cdot2^{k}=\\\& =& \sum_{k\geq0}{n-2-k \choose k}\cdot2^{k}+\sum_{k\geq0}{n-2-k \choose k-1}\cdot 2^{k}. \end{eqnarray*}
U posljednjoj sumi zamijenimo
i:=k-1, odnosno
k=i+1. Tada je nejednakost
k\geq0 ekvivalentna nejednakosti
i\geq-1. Međutim, zbog jednakosti
{n-2-(-1+1) \choose -1}={n-2 \choose -1}=0,
najmanja vrijednost indeksa sumacije u drugoj sumi je
i=0. Stoga dobivamo:
\begin{eqnarray*} a_{n}& =& \sum_{k\geq0}{n-2-k \choose k}\cdot2^{k}+\sum_{i\geq0}{n-2-(i+1) \choose i}\cdot2^{i+1}=\\\& =& \sum_{k\geq0}{n-2-k \choose k}\cdot2^{k}+2\sum_{i\geq0}{n-3-i \choose i}\cdot2^{i}=\\\& =& \sum_{k\geq0}{n-2-k \choose k}\cdot2^{k}+2\sum_{k\geq0}{n-3-k \choose k}\cdot2^{k}. \end{eqnarray*}
Iz (
14) slijedi da je prva suma jednaka
a_{n-1}, a druga
a_{n-2}. Stoga je
a_{n}=a_{n-1}+2a_{n-2},
a to je upravo rekurzija iz (
1).
\ \blacksquare
Iz Propozicija
3 i
13 izravno slijedi sljedeći identitet.
Korolar 1. Za sve prirodne brojeve
n vrijedi
\sum_{k\geq0}{n-1-k \choose k}\cdot2^{k}=\frac{2^{n}-(-1)^{n}}{3}.
Promotrimo sada svojevrsni obrat Propozicije
13, tj. „linearnu kombinaciju“ članova Jacobsthalova niza čiji su „koeficijenti“ binomni koeficijenti iz istoga retka Pascalova trokuta. (Detaljnije o binomnim koeficijentima i Pascalovu trokutu može se naći u
[5].) Pomoću takvih „linearnih kombinacija“ mogu se dobiti sve potencije broja 3 kojima je eksponent nenegativan cijeli broj. Točnije, vrijedi sljedeća propozicija.
Propozicija 8. Za svaki prirodan broj
n vrijedi
\sum_{k=0}^{n}{n \choose k}\cdot J_{k}=3^{n-1}.
Dokaz. Primijenit ćemo binomni poučak:
(x+y)^{n}=\sum_{k=0}^{n}{n \choose k}\cdot x^{n-k}\cdot y^{k},\quad n\in\mathbb{N},\, x,y\in\mathbb{C}.
Uvrstimo li u binomni poučak
x=1,
y=2, odnosno
x=1,
y=-1, dobit ćemo:
\begin{gathered}3^{k}=\sum_{k=0}^{n}{n \choose k}\cdot2^{k},\\\ \sum_{k=0}^{n}{n \choose k}(-1)^{k}=0. \end{gathered}
Koristeći jednakost (
4) dobivamo redom:
\begin{eqnarray*} \sum_{k=0}^{n}{n \choose k}\cdot J_{k}& =& \sum_{k=0}^{n}{n \choose k}\cdot\frac{2^{k}-(-1)^{k}}{3}=\frac{1}{3}\left(\sum_{k=0}^{n}{n \choose k}\cdot2^{k}-\sum_{k=0}^{n}{n \choose k}(-1)^{k}\right)=\\\& =& \frac{1}{3}\left(3^{n}-0\right)=3^{n-1}, \end{eqnarray*}
što je i valjalo pokazati.
\ \blacksquare
Posebno je zanimljiva veza članova Jacobsthalova niza s alternirajućim konvergentnim geometrijskim redom. Koristi se jednakost
(16)
\sum_{k=0}^{\infty}\left(-\frac{1}{2}\right)^{k}=\frac{2}{3}
koja se dobiva tako da se u formulu za zbroj konvergentnoga geometrijskoga reda
\sum_{n=0}^{\infty}x^{n}=\frac{1}{1-x},\quad|x|\lt 1,
uvrsti
x=-\frac{1}{2}. Međutim,
n-ti djelomični zbroj reda (
16) definiran s
S_{n}=\sum_{k=0}^{n}\left(-\frac{1}{2}\right)^{k}
usko je povezan s Jacobsthalovim brojevima. O tome govori sljedeća propozicija.
Propozicija 9. Za svaki nenegativan cijeli broj
n vrijedi:
S_{n}=\frac{J_{n+1}}{2^{n}}.
Dokaz. Jednakost se najbrže i najlakše dokazuje matematičkom indukcijom. Za
n=0 imamo:
S_{0}=\sum_{k=0}^{n}\left(-\frac{1}{2}\right)^{k}=\left(-\frac{1}{2}\right)^{0}=1=\frac{1}{2^{0}}=\frac{J_{1}}{2^{0}}
čime smo pokazali valjanost baze indukcije. Pretpostavimo da tvrdnja vrijedi za neki
n\in\mathbb{N}, pa pokažimo da vrijedi za broj
n+1. Koristeći jednakost (
2) dobivamo redom:
\begin{eqnarray*} S_{n+1}& =& \sum_{k=0}^{n+1}\left(-\frac{1}{2}\right)^{k}=\left[\sum_{k=0}^{n}\left(-\frac{1}{2}\right)^{k}\right]+\left(-\frac{1}{2}\right)^{n+1}=S_{n}+\left(-\frac{1}{2}\right)^{n+1}=\\\& =& \frac{J_{n+1}}{2^{n}}+\frac{(-1)^{n+1}}{2^{n+1}}=\frac{2\cdot J_{n+1}+(-1)^{n+1}}{2^{n+1}}=\frac{J_{n+2}}{2^{n+1}}, \end{eqnarray*}
pa tvrdnja propozicije vrijedi i za broj
n+1.
\ \blacksquare
Iz razmatranja ispred Propozicije
16 ili iz Propozicije
3 slijedi
Korolar 2.
\displaystyle\lim_{n\rightarrow\infty}\frac{J_{n+1}}{2^{n}}=\frac{2}{3}.
3Veza Jacobsthalova niza i elementarnih staničnih automata
Grubo rečeno, stanični automat je model dinamičnog fizikalnog sustava u kojem su vrijeme i prostor diskretizirani, a interakcije su samo lokalne. Svaki stanični automat sastoji se od regularne
n-dimenzionalne rešetke, odnosno
n-dimenzionalnog polja stanica (ćelija) od kojih je svaka u jednom od mogućih stanja. Ukupan broj takvih stanja je konačan.
Najjednostavnija klasa jednodimenzionalnih staničnih automata su elementarni stanični automati. Njegove stanice mogu biti u točno dva moguća stanja (0 ili 1). Stanice smještene neposredno lijevo i neposredno desno od promatrane stanice nazivamo susjedne stanice. Stanica i njezine dvije susjedne stanice tvore strukturu koju nazivamo konfiguracija. Svaka konfiguracija može imati ukupno
2^{3}=8 stanja. Za svaku konfiguraciju definiramo pravilo odlučivanja o vrijednostima stanica u sljedećem retku rešetke. To pravilo je funkcija koja svakoj stanici u 2., 3., 4,\dots, retku rešetke pridružuje 0 ili 1 zavisno o konfiguraciji smještenoj neposredno iznad te stanice. Zbog toga postoji ukupno
2^{8}=256 mogućih pravila pridruživanja.
Pravila za izgradnju rešetke elementarnih staničnih automata definirao je i opisao Stephen Wolfram 1983. godine. (Za detalje vidjeti
[3].) Mi ćemo izdvojiti tzv.
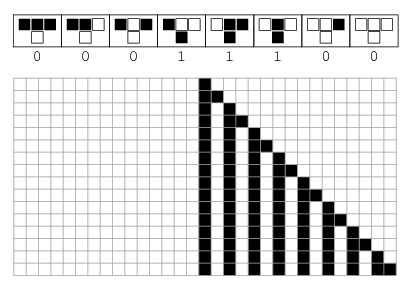
Pravilo 28. Ovo pravilo prikazano je na slici
1 kao i razvoj jedne crne ćelije nakon 15 koraka. Istaknimo da se „izgradnja“ rešetke zasniva na jednakosti
(28)_{10}=(00011100)_{2}.
Formalno gledajući, Pravilo 28 je funkcija
f:\left\lbrace 0,1\right\rbrace ^{3}\rightarrow\left\lbrace 0,1\right\rbrace definirana propisom
f(x,y,z)=(x+y+xz+xyz)\mod2.
(Detaljnije o Pravilu 28 može se naći u [2] ili [3].) Ovo pravilo pregledno možemo zapisati u obliku tablice 1.
\begin{array}{|c|c|}\hline (x,y,z)& f(x,y,z) \\\\\hline \hline (0,0,0)& 0\\\\\hline (0,0,1)& 0\\\\\hline (0,1,0)& 1\\\\\hline (0,1,1)& 1\\\\\hline (1,0,0)& 1\\\\\hline (1,0,1)& 0\\\\\hline (1,1,0)& 0\\\\\hline (1,1,1)& 0\\\\\hline \end{array}
Promotrimo sliku
1, pa zaključimo kako smo na temelju prvoga retka dobili drugi redak. Kao osnovnu stanicu najprije uzimamo jedinu crnu ćeliju u prvom retku. Njezini lijevi i desni susjedi su bijele ćelije, pa imamo konfiguraciju „bijela–crna–bijela“ (vidjeti sliku
2).
Primjenom Pravila 28 na navedenu konfiguraciju kao rezultat dobivamo jednu crnu ćeliju (vidjeti sliku
3).
To znači da će prva ćelija u drugom retku rešetke biti crna (vidjeti sliku
4).
Pomaknimo se za točno jedno mjesto udesno od crne ćelije u prvom retku rešetke. Sada je osnovna stanica bijela ćelija. Njezin lijevi susjed je crna, a desni bijela ćelija, pa imamo konfiguraciju „crna–bijela–bijela“. Primjena Pravila 28 na tu konfiguraciju kao rezultat daje crnu ćeliju (vidjeti sliku
5).
Zbog toga će druga ćelija u drugomu retku rešetke također biti crna (vidjeti sliku
6).
Pomaknimo se za još jedno mjesto udesno. Osnovna stanica je bijela ćelija čiji su i lijevi i desni susjed također bijele ćelije. Stoga imamo konfiguraciju „bijela–bijela–bijela“. Primjena Pravila 28 na ovu konfiguraciju kao rezultat daje bijelu ćeliju (vidjeti sliku
7).
Stoga će treća ćelija u drugom retku rešetke biti bijela (vidjeti sliku
8).
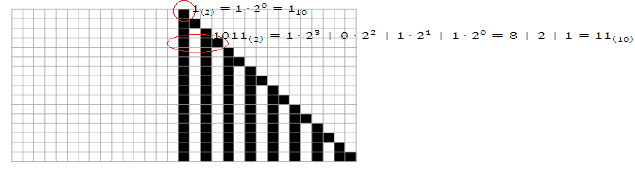
Daljnjim pomicanjem udesno u prvom retku rešetke opet dolazimo na bijelu ćeliju kojoj su susjedi bijele ćelije, pa primjenom Pravila 28 kao rezultat opet dobivamo bijelu ćeliju. Tako zaključujemo da će sve ostale ćelije u drugom retku biti bijele i ne moramo ih dalje promatrati. U svakom retku rešetke uočimo blok ćelija koji počinje i završava crnom ćelijom, te takav da su lijevo i desno od toga bloka isključivo bijele ćelije. Takav blok sigurno postoji jer se u svakom retku rešetke nalazi barem jedna crna ćelija (dobivena primjenom Pravila 28 ili na konfiguraciju „bijela–crna–bijela“ ili „bijela–crna–crna“). Svakoj crnoj ćeliji uočenoga bloka pridružimo broj 1, a svakoj bijeloj broj 0. Na taj način svakom bloku bijektivno pridružujemo binarni broj koji počinje i završava znamenkom 1. Zapišemo li te binarne brojeve u dekadskom zapisu, dobivamo redom:
\begin{gathered}(1)_{2}=(1)_{10}\\\ (11)_{2}=(3)_{10}\\\ (101)_{2}=(5)_{10}\\\ (1011)_{2}=(11)_{10}\\\ (10101)_{2}=(21)_{10}\\\ \dots \end{gathered}
Dobiveni brojevi tvore niz
1,3,5,11,21,\dots Iz ispisa prvih nekoliko članova Jacobsthalova niza naslućujemo da je dobiveni niz zapravo podniz Jacobsthalova niza. Pokazat ćemo da je ova slutnja točna, tj. da rešetka elementarnih staničnih automata dobivena primjenom Pravila 28 na gore opisani način zapravo generira podniz Jacobsthalova niza.
Pogledajmo najprije koje se sve konfiguracije mogu pojaviti unutar jednoga bloka. Pokažimo da se ni u jednom bloku ne mogu pojaviti „jednobojne“ konfiguracije, tj. konfiguracije „bijela–bijela–bijela“ i „crna–crna–crna“, kao ni konfiguracije „bijela–bijela–crna“ i „crna–bijela–bijela“. Najprije dokažimo da se ni u jednom bloku ne može pojaviti konfiguracija „crna–crna–crna“. Radi jednostavnosti, označimo tu konfiguraciju s
C.
Pretpostavimo suprotno, tj. neka je
n prvi redak u kojemu se pojavljuje
C. Pogledajmo kako iz ćelija u
(n-1)-vom retku rešetke može nastati
C. Prema Pravilu 28 postoje tri mogućnosti.
Prva crna ćelija u
C ne može nastati iz konfiguracije „crna–bijela–bijela“. Primjena Pravila 28 na konfiguraciju „bijela–bijela–bijela“, odnosno „bijela–bijela–crna“ kao rezultat daje bijelu, a ne crnu ćeliju. Zbog toga druga ćelija u
C mora biti bijela, što je suprotno pretpostavci da
C sadrži blok od tri crne ćelije.
Prva crna ćelija u
C ne može nastati ni iz konfiguracije „bijela–crna–crna“. Primjena Pravila 28 na konfiguraciju „crna–crna–bijela“ kao rezultat daje bijelu ćeliju. Stoga je drugu crnu ćeliju u
C moguće dobiti isključivo primjenom Pravila 28 na konfiguraciju „crna–crna–crna“. To bi značilo da se
C pojavljuje i u
(n-1)-vom retku, što je suprotno pretpostavci da je
n prvi redak u kojemu se pojavljuje
C.
Prva crna ćelija u
C ne može nastati ni iz konfiguracije „bijela–crna–bijela“. Drugu crnu ćeliju u
C tada bismo mogli dobiti isključivo iz konfiguracije „crna–bijela–bijela“, pa kao u prvoj mogućnosti zaključujemo da iz konfiguracije koja počinje dvjema bijelim ćelijama ni u kojem slučaju ne možemo dobiti treću crnu ćeliju u
C.
Tako smo pokazali da se unutar jednoga bloka ne može pojaviti konfiguracija
C. Potpuno analogno se pokazuje da se unutar jednoga bloka ne mogu pojaviti preostale tri spomenute konfiguracije. Detalje prepuštamo čitatelju.
Označimo s
B_{n} prirodan broj čiji binarni zapis korespondira bloku u
n-tom retku tablice elementarnih staničnih automata. Ne istaknemo li drugačije, pretpostavljamo da je
n bilo koji prirodan broj. Pretpostavljamo i da je
B_{n} zapisan u binarnom, a ne u dekadskom zapisu. Uočimo da je broj
B_{n} neparan jer njegov binarni zapis završava znamenkom 1. (Dokaz tvrdnje da je prirodan broj neparan ako i samo ako njegov binarni zapis završava znamenkom 1 prepuštamo čitatelju.)
Budući da je
B_{1}=1, iz Primjedbe
1 izravno slijedi da broj
B_{n} u svojem zapisu ima točno
n binarnih znamenaka.
Izračunajmo zbroj
Z_{n}:=B_{n}+_{2}B_{n+1}. (S
+_{2} označeno je binarno zbrajanje.) Broj
Z_{n} je zbroj dvaju strogo pozitivnih prirodnih brojeva od kojih prvi ima
n, a drugi
n+1 znamenaka, pa
Z_{n} ima ili
n + 1 ili
n + 2 znamenaka. Tvrdimo da je
Z_{n} ima točno
n + 2 znamenaka i da je jedino vodeća znamenka broja
Z_{n} jednaka 1.
Brojevi
B_{n} i
B_{n+1} imaju posljednju znamenku jednaku 1. Stoga je posljednja znamenka broja
Z_{n} jednaka
1 +_{2} 1 = 0. Navedenim zbrajanjem „nastaje“ jedinica koja se prenosi u zbroj znamenaka na pretposljednjim mjestima brojeva
B_{n} i
B_{n+1}.
Prema konstrukciji brojeva
B_{n} navedenoj u Primjedbi
1, točno jedan od brojeva
B_{n} i
B_{n+1} ima pretposljednju znamenku 1, a drugi pretposljednju znamenku 0. Točnije, ako je
n paran broj, onda je pretposljednja znamenka broja
B_{n} jednaka 1 (jer smo broju
B_{n-1} zdesna nadopisali 1), a pretposljednja znamenka broja
B_{n+1} jednaka je 0 (jer smo između posljednje dvije znamenke broja
B_{n} umetnuli nulu). Ako je
n neparan broj, onda
B_{n} ima pretposljednju znamenku 0, a
B_{n+1} pretposljednju znamenku 1. U svakom je slučaju, dakle, pretposljednja znamenka broja
Z_{n} jednaka
1 +_{2} 1 = 0. I na ovom mjestu opet „nastaje“ jedinica koja se prenosi u zbroj znamenaka na neposredno sljedećoj poziciji.
Neka je
i prva pozicija (gledajući zdesna nalijevo) na kojoj broj
Z_{n} ima znamenku 1. Pretpostavimo da je
i\leq n. (Iz gornjih razmatranja slijedi
i\geq 3.) Na
i-toj poziciji broja
Z_{n} dobit ćemo znamenku 1 ako i samo ako brojevi
B_{n} i
B_{n+1} na
i-toj poziciji imaju jednake znamenke. Naime,
(i-1)-va znamenka broja
Z_{n} jednaka je nuli, pa se
i-ta znamenka broja
Z_{n} dobiva zbrajanjem
i-te znamenke broja
B_{n},
i-te znamenke broja
B_{n+1} i jedinice „nastale“ zbrajanjem kojim je dobivena nula na
(i-1)-voj poziciji. Ako bi brojevi
B_{n} i
B_{n+1} na
i-toj poziciji imali različite znamenke, onda bi
i-ta znamenka broja
Z_{n} bila jednaka nuli, što je suprotno pretpostavci da je
i prva pozicija na kojoj broj
Z_{n} ima znamenku 1.
Uzmimo najprije da brojevi
B_{n} i
B_{n+1} na
i-toj poziciji imaju nule. To znači da je bijela ćelija koja odgovara nuli na
i-toj poziciji broja
B_{n+1} dobivena primjenom Pravila 28 na konfiguraciju koja započinje bijelom ćelijom (koja odgovara nuli na
i-toj poziciji broja
B_{n}). Jedine dvije konfiguracije koje dolaze u obzir su „bijela–bijela–bijela“ i „bijela–bijela–crna“. Ranije smo pokazali da se te konfiguracije ne mogu pojaviti unutar jednoga bloka rešetke. Stoga na
i-toj poziciji u brojevima
B_{n} i
B_{n+1} ne mogu biti nule.
Uzmimo sada da brojevi
B_{n} i
B_{n+1} na
i-toj poziciji imaju jedinice. To znači da je crna ćelija koja odgovara jedinici na
i-toj poziciji broja
B_{n+1} dobivena primjenom Pravila 28 na konfiguraciju koja započinje crnom ćelijom (koja odgovara jedinici na
i-toj poziciji broja
B_{n}). Jedina konfiguracija koja dolazi u obzir je „crna–bijela–bijela“. Ranije smo pokazali da se ta konfiguracija ne može pojaviti unutar jednoga bloka rešetke. Stoga na
i-toj poziciji u brojevima
B_{n} i
B_{n+1} ne mogu biti jedinice.
Time smo iscrpili sve moguće slučajeve, pa zaključujemo da je pretpostavka
i\leq n bila pogrešna. Dakle,
i\geq n+1. Gledajući zdesna nalijevo, znamenka na
(n + 1)-vom mjestu broja
B_{n} jednaka je 0 (jer
B_{n} ima točno
n znamenaka), dok je znamenka na
(n + 1)-vom mjestu broja
B_{n+1} jednaka 1 (to je vodeća znamenka broja
B_{n+1}). Stoga je
(n + 1)-va znamenka broja
Z_{n} jednaka
0 +_{2} 1 +_{2} 1 = 0. (Posljednja jedinica u ovom zbroju „nastaje“ zbrajanjem kojim je dobivena nula na
n-toj poziciji broja
Z_{n}.) Odatle slijedi da broj
Z_{n} ima točno
n + 2 znamenaka, te da vrijedi jednakost:
Z_{n}=(1\underset{n+1\,\text{nula}}{\underbrace{00\dots0}})_{2}=1\cdot2^{n+1}+0\cdot2^{n}+\dots+0\cdot2^{1}+0\cdot2^{0}=2^{n+1},\quad n\in\mathbb{N}.
Tako smo pokazali da niz brojeva
(B_{n})_{n\in\mathbb{N}} zadovoljava sljedeće jednakosti:
(17)
\begin{cases} B_{1}=1,\\\ B_{n}+B_{n+1}=2^{n+1},& \text{za svaki }n\in\mathbb{N}. \end{cases}
Iz (
1), (
3) i (
17) proizlazi da je niz
(B_{n})_{n\in\mathbb{N}} zapravo podniz Jacobsthalova niza čiji je prvi član
J_{2}. Preciznije, zaključujemo da za svaki
n\in\mathbb{N} vrijedi jednakost:
Iz (
4) i (
18) odmah slijedi zatvorena formula za opći član niza
(B_{n})_{n\in\mathbb{N}}:
(19)
B_{n}=\frac{2^{n+1}-(-1)^{n+1}}{3},\quad n\in\mathbb{N}.
Odaberemo li npr.
n=21 i uvrstimo tu vrijednost u (
19), dobit ćemo
B_{21}=\frac{2^{22}-1}{3}=1398101=(101010101010101010101)_{2}.
Stoga će 21. redak rešetke elementarnih staničnih automata izgledati kao na slici
10.
Zaključno napomenimo sljedeće. Budući da nam konfiguracija „crna–crna–crna“ nije bitna u postupku „izgradnje“ rešetke elementarnih staničnih automata, toj konfiguraciji umjesto broja 0 (kao u Pravilu 28) možemo pridružiti broj 1, a da se postupak „izgradnje“ rešetke elementarnih staničnih automata time nimalo ne promijeni. To pridruživanje zapravo znači da broj
(00011100)_{2}=(28)_{10} zamjenjujemo brojem
(10011100)_{2}=(156)_{10}, odnosno umjesto Pravila 28 primjenjujemo Pravilo 156. Tako smo dokazali sljedeću tvrdnju.
Propozicija 10. Pravila 28 i Pravilo 156 generiraju istu rešetku elementarnih staničnih automata, odnosno isti podniz Jacobsthalova niza.
Čitatelja zainteresiranoga za daljnja svojstva i primjene Jacobsthalova niza upućujemo na literaturu navedenu u donjem popisu.
Bibliografija
|
[1] |
Eric W. Weisstein: Jacobsthal Number, javno dostupno na
http://mathworld.wolfram.com/JacobsthalNumber.html (20. 7. 2013.) |
|
[2] |
Eric W. Weisstein: Rule 28, javno dostupno na
http://mathworld.wolfram.com/Rule28.html (20. 7. 2013.) |
|
[3] |
Stephen Wolfram: New Kind of Science, Wolfram Media, Champaign (SAD), 2002. |
|
[4] |
A. Dujella: Fibonaccijevi brojevi, Hrvatsko matematičko društvo, Zagreb, 2000. |
|
[5] |
D. Veljan: Kombinatorna i diskretna matematika, Algoritam, Zagreb, 2001. |
|
[6] |
http://en.wikipedia.org/wiki/Jacobsthal_number (20. 7. 2013.) |
|
[7] |
F. Koken, D. Bozkurt: On the Jacobsthal numbers by matrix methods, International Journal of Contemporary Mathematical Sicences 3(13) (2008.), 605-614. |
|
[8] |
H. W. Gould: A history of the FibonacciQ-matrix and a higher-dimensional problem}, javno dostupno na www.fq.math.ca/Scanned/19-3/gould.pdf (10. 9. 2013.) |