Matej Mihelčić                                Tihomir Lolić

        matmih1@gmail.com                    tihomir.lolic@gmail.com

 

 

 

Sažetak

 

 

U članku definiramo problem ispunjivosti formule logike sudova (SAT) i promatramo neke osnovne rezultate i primjene vezane uz navedeni problem. Opisat ćemo trenutno najvažniji potpuni algoritam za rješavanje problema ispunjivosti logičke formule: Davis-Putnam-Logeman-Loveland algoritam. Čitatelj će moći vizualizirati rad DPLL algoritma koristeći DPvis applet u kojem će moći interaktivno pokušati riješiti problem ispunjivosti nekih složenijih formula. Odjeljak o algoritmima nastavljamo predstavljanjem nekoliko glavnijih skupina heurističkih algoritama za rješavanje problema SAT. Predstavit ćemo prednosti i nedostatke svake skupine algoritama. Na kraju ćemo navesti i kratko opisati neke važnije verzije SAT problema.

 

 

1 Uvod

 

Intuitivno, problem ispunjivosti formule logike sudova, tj. kratko SAT (eng. satisfiability) glasi: za danu formulu logike sudova F, možemo li varijablama te formule pridružiti vrijednosti 0 (laž) ili 1 (istina), tako da F ima logičku vrijednost 1 (istina).

 

Problem SAT intenzivno istražuju znanstvenici iz raznih polja računarstva i šire.

Problem je usko vezan uz teoriju izračunljivosti, složenosti, razvoj i analizu algoritama te strukture podataka. U zadnje vrijeme se problemom sve više bave i znanstvenici na polju kvantne teorije izračunljivosti.

 

Moderni algoritmi za rješavanje problema SAT se mogu podijeliti u dvije velike kategorije:

• moderne varijante Davis-Putnam-Logemann-Loveland algoritma
• stohastičke algoritme lokalnog traženja.

Davis-Putnamov algoritam je algoritam za rješavanje SAT problema baziran na metodi rezolucije. Razvili su ga Martin Davis i Hilary Putnam 1960. godine, a kao njegovo poboljšanje 1962. godine Martin Davis, Hilary Putnam, George Logemann i Donald W. Loveland predstavljaju Davis-Putnam-Logemann-Loveland algoritam. Taj algoritam je potpuni algoritam, baziran na metodi pretraživanja s povratnom korekcijom (eng. backtracking) za rješavanje problema ispunjivosti logičke formule u konjunktivnoj normalnoj formi (KNF).

Algoritmi za rješavanje problema SAT su se razvijali od 1920. godine. Ovdje navodimo neke primjere.

• 1920. metoda traženja rješenja preko tablica istinitosti.
• 1960. klasični SAT solveri bazirani na Davis-Putnamovom algoritmu.
• 1990.-1992. uspješna implementacija stohastičkih algoritama za rješavanje teških SAT formula.
• 1993.-1994. nova hibridna stohastička strategija s poboljšanom robusnosti i performansama.
• 1996.-1997. napredak u stohastičkim algoritmima, randomizirane sistematske metode pretraživanja.
• 1998.-2000. daljnji napredak u stohastičkim algoritmima koristeći GLSM model (generalizirani strojevi lokalnog pretraživanja). Metode pretraživanja raznih algoritama se kombiniraju koristeći određeni mehanizam kontrole.
• 2001.-2004. Algoritmi dinamičkog lokalnog pretraživanja visokih performansi. Primjer takvog algoritma je self-tuning/adaptive WalkSat. (algoritam je sposoban sam odrediti svoje ulazne parametre u ovisnosti o veličini ulazne formule)

 

SAT je jedan NP-potpun problem, tj. SAT \in NP i SAT je NP-težak problem. Formalno, problem spada u klasu složenosti NP ako je rješiv na nedeterminističkom Turingovom stroju u polinomnom vremenu. Bitno je napomenuti da danas nije poznat algoritam koji bi problem SAT riješio u polinomnom vremenu na determinističkom Turingovom stroju. Unatoč tome, ako netko pridruži istinitosne vrijednosti varijablama formule, mi možemo u polinomnom vremenu provjeriti je li to rješenje našega problema, odnosno je li naša konačna formula istinita uz zadane vrijednosti varijabli. Problem SAT je NP-težak: proizvoljni problem iz klase NP se može polinomno reducirati na problem SAT. To znači da možemo svaku instancu nekog problema iz klase NP kodirati kao formulu logike sudova. Kodiranje možemo izvršiti u polinomnom vremenu. Ovo je jedan od glavnih razloga istraživanja tog problema od strane mnogih znanstvenika koji se bave teorijom računarstva.

 

Od industrijskih primjena algoritama za rješavanje problema SAT ističemo razvoj elektronskih sklopova uz pomoć računala, planiranje, vremenske analize elektronskih komponenti, usmjeravanje FPGA  (Field-programmable gate array). SAT- solveri se koriste i u verifikaciji (hardvera i softvera) te optimizaciji.

Već od 1980. godine kompanija Siemens počinje koristiti SAT-solving za verifikaciju svojih proizvoda, a od 1990. godine Stälmarkova metoda za rješavanje problema SAT se koristi za formalnu verifikaciju signalnog sustava na željeznicama. Intel koristi neke od tehnika SAT solvinga za verifikaciju i dizajn svojih procesora.

 

Rad započinjemo uvođenjem osnovnih pojmova logike sudova i definicijom problema. U središnjem djelu članaka navodimo nekoliko potpunih pristupa za rješavanje problema te navodimo neke prednosti i mane takvih pristupa. Uočili smo da samo potpuni algoritmi mogu sa sigurnošću utvrditi da je neka formula neispunjiva, ali i da to ima cijenu u vidu eksponencijalnog porasta vremena izvođenja u odnosu na dimenziju problema.

Porast vremena izvođenja pokušavamo kompenzirati uvođenjem nove klase algoritama, heurističkih algoritama. Ovdje smo uočili da su heuristički algoritmi uglavnom uspješni u praktičnim primjenama, ali imaju i svojih mana. Glavni nedostatak takvog pristupa je nepotpunost, odnosno činjenica da ukoliko takvi algoritmi ne uspiju pronaći rješenje mi ne znamo je li ulazna formula ispunjiva ili nije. Dodatno svojstvo heurističkih algoritama je da ovise o klasi formula, odnosno nisu jednako uspješni na formulama s različitim svojstvima.

Ta činjenica nas je potaknula na stvaranje paralelnog solvera koji bi kombinirao više heurističkih pristupa, što je dovelo do značajnog smanjenja vremena izvođenja i do veće točnosti rješavanja raznih test primjera za problem SAT u odnosu na heurističke algoritme od kojih je solver sastavljen.

Članak nastavljamo predstavljanjem raznih vrsta problema SAT koji se proučavaju ne bi li se bolje razumjela struktura problema i istražio neki specifičniji potproblem. Cilj je pronaći način na koji bi se taj potproblem mogao učinkovitije riješiti te iskoristiti konstruiranu metodu rješavanja u praksi ili možda koristeći tu metodu ubrzati generalni postupak rješavanja problema.  

 

2 Osnovni pojmovi i definicije

Da bi u potpunosti razumjeli i formalno definirali pojmove navedene u uvodu navodimo neke osnovne definicije vezane uz logiku sudova.

 

2.1 Osnovni pojmovi i definicije logike sudova

 

Definicija 1. Alfabet logike sudova je unija skupova A_1, A_2\ i\ A_3 , pri čemu je: $$A_1=\{P_0,\ P_1,\ P_2,\ \dots\}$$ prebrojiv skup čije elemente nazivamo propozicionalne varijable; $$A_2=\{\neg\ ,\wedge\ ,\vee \, \rightarrow\ ,\leftarrow\}$$ skup logičkih veznika; $$A_3=\{(,)\} $$ skup pomoćnih simbola (zagrade);

Definicija 2. Atomarna formula je svaka propozicionalna varijabla. Pojam formule definiramo rekurzivno:

1. svaka atomarna formula je formula;
2. ako su A i B formule tada su i riječi (\neg A),\ (A\wedge B),\ (A\vee B),\ (A\rightarrow B) i (A\leftrightarrow B) također formule
3. riječ alfabeta logike sudova je formula ako je nastala primjenom konačno mnogo koraka 1. i 2.

 

Definicija 3. Svako preslikavanje sa skupa propozicionalnih varijabli u skup \{0,1\} , tj. I\colon \{P_0, P_1 \dots \} \to \{0,1\ \} , nazivamo totalna interpretacija ili kratko interpretacija. Ako je preslikavanje definirano na podskupu skupa propozicionalnih varijabli tada kažemo da je to parcijalna interpretacija. Kažemo da je parcijalna interpretacija I adekvatna za formulu A(P_1, \dots,\ P_n ) ako je funkcija I definirana na P_i za sve i=1, \dots ,n.

 

Definicija 4. Neka je I interpretacija (totalna ili parcijalna). Ako se radi o parcijalnoj interpretaciji I smatramo da je I adekvatna za formule na kojima se definira njena vrijednost. Tada vrijednost interpretacije I na proizvoljnoj formuli definiramo rekurzivno: $$I(\neg A)=1\ \text{ako i samo ako}\ I(A)=0\text{;}$$ $$I(A \wedge B)=1\ \text{ako i samo ako}\ I(A)=1\ \text{i}\ I(B)=1\text{;}$$ $$I(A\vee B)=1\ \text{ako i samo ako}\ I(A)=1\ \text{ili}\ I(B)=1\text{;}$$ $$I(A\rightarrow B)=1\ \text{ako i samo ako}\ I(A)=0\ \text{ili}\ I(B)=1\text{;}$$ $$I(A \leftrightarrow B)=1\ \text{ako i samo ako}\ I(A)=I(B)\text{;}$$  

Ako alfabet sadrži i konstante \top i \bot, tada za svaku interpretaciju I definiramo I(\top)=1 i I(\bot)=0.

 

Definicija 5. Neka je S skup formula, a F neka formula. Kažemo da formula F logički slijedi iz skupa S, u oznaci S\models F, ako za svaku interpretaciju I, za koju je I(S)=1, vrijedi I(F)=1. Relaciju \models nazivamo relacija logičke posljedice. Ako je S jednočlan skup, tj. S=\{A\}, tada činjenicu \{A\}\models\ B zapisujemo i kao A\Rightarrow B.

 

Definicija 6.  Kažemo da su formule A i B\ logički ekvivalentne i označavamo A\Leftrightarrow B, ako za svaku interpretaciju I vrijedi I(A)=I(B).

 

Definicija 7. Za formulu F kažemo da je ispunjiva ako postoji interpretacija I takva da vrijedi I(F)=1. Za formulu F kažemo da je oboriva ako postoji interpretacija I takva da vrijedi I(F)=0. Za formulu F kažemo da je valjana (tautologija, identički istinita) ako je istinita za svaku interpretaciju. Za formulu F kažemo da je antitautologija ili identički neistinita ako je neistinita za svaku interpretaciju.

 

2.2 Normalne forme

Spomenuli smo da naši algoritmi za rješavanje problema SAT rade s formulama koje su u konjunktivnoj normalnoj formi stoga ćemo sada definirati taj pojam i iskazati glavne rezultate vezane uz normalne forme.

 

Definicija 8. Atomarnu formulu i njezinu negaciju nazivamo literal. Formulu oblika A_1\wedge A_2\wedge \dots\wedge A_n nazivamo konjunkcija (A_i su proizvoljne formule). Formulu oblika  A_1\vee A_2\vee \dots\vee A_n nazivamo disjunkcija.
Elementarna konjunkcija je konjunkcija  literala, a elementarna disjunkcija je disjunkcija literala.
Konjunktivna normalna forma je konjunkcija elementarnih disjunkcija. Disjunktivna normalna forma je disjunkcija elementarnih konjunkcija.

Neka je A neka formula, te B konjunktivna normalna forma i C disjunktivna normalna forma. Kažemo da je B konjunktivna normalna forma za A ako vrijedi A \Leftrightarrow B. Kažemo da je C disjunktivna normalna forma za A ako vrijedi A \Leftrightarrow C.
  

Navodimo sljedeći teorem bez dokaza, dokaz se može pogledati u [8].

Teorem 1. Za svaku formulu logike sudova postoji konjunktivna i disjunktivna normalna forma.

Prethodni teorem je jako važan. Garantira nam da možemo svaku formulu pretvoriti u ekvivalentnu konjunktivnu normalnu formu s kojom će naš algoritam raditi, međutim ostavlja nam preveliki izbor zato što mi za svaku formulu možemo generirati beskonačno mnogo konjunktivnih i disjunktivnih normalnih formi. Pošto se radi o algoritmima želimo da nam ulazni podaci (KNF forme) budu donekle jedinstveni stoga ćemo definirati specifičan slučaj konjunktivne normalne forme.

 

Definicija 9. Neka je A(P_1,\dots,P_n) konjunktivna normalna forma. Kažemo da je to savršena konjunktivna normalna forma ako u svakoj njezinoj elementarnoj disjunkciji svaka propozicionalna varijabla P_i nastupa točno jednom (s ili bez negacije), te su sve elementarne disjunkcije međusobno logički neekvivalentne.
Neka je A(P_1,\dots,P_n) disjunktivna normalna forma. Kažemo da je to savršena disjunktivna normalna forma ako u svakoj njezinoj elementarnoj konjunkciji svaka propozicionalna varijabla P_i nastupa točno jednom (s ili bez negacije), te su sve elementarne konjunkcije međusobno logički neekvivalentne.

 

Sljedeći korolar nam garantira da svaku formulu možemo pretvoriti u oblik s kojim će raditi naši algoritmi. Dokaz korolara možete pogledati u [8].

Korolar 1. Za svaku oborivu formulu postoji savršena konjunktivna normalna forma. Za svaku ispunjivu formulu postoji savršena disjunktivna normalna forma. Savršene forme su jedinstvene do na permutaciju varijabli u elementarnim disjunkcijama, odnosno konjunkcijama, te do na permutaciju elementarnih konjunkcija, odnosno disjunkcija.

 

Primijetimo da nam prethodni teorijski rezultati ne daju algoritam kojim ćemo pretvoriti proizvoljnu formulu u pripadnu KNF. Algoritam za prebacivanje proizvoljne formule u KNF ima eksponencijalnu vremensku složenost. Kod pretvaranja formule u KNF možemo se poslužiti trikom i prebaciti malo modificiranu formulu koja je istinitosno ekvivalenta (iako ne logički) s početnom formulom. Za takvo prebacivanje postoji polinoman algoritam. ([6])

 

Formalno, problem SAT glasi: Za proizvoljnu formulu propozicionalne logike F, postoji li interpretacija I\colon \{P_0,P_1,\dots \} \to \{0,1\} takva da I(F)=1.

 

          3 Potpuni algoritmi za rješavanje problema SAT

 

U ovom dijelu navodimo nekoliko potpunih algoritama za rješavanje problema SAT te ističemo neke njihove prednosti i mane.

Kao baza ovog poglavlja je korišten diplomski rad M. Mihelčića [6] koji je dobrim djelom baziran na knjizi W.M.Mareka [5].

Potpuni algoritmi su algoritmi koji za proizvoljnu formulu logike sudova sa 100%-tnom sigurnošću utvrđuju u konačno mnogo koraka je li ta formula ispunjiva.

 

3.1 Istinosne tablice

Istinosne tablice se upotrebljavaju već od 1920. godine i to je najjednostavnija potpuna metoda rješavanja problema SAT.

Algoritam se svodi na provjeru svih mogućih vrijednosti varijabli zadane formule. Odmah uočavamo da je metoda memorijski i vremenski neučinkovita. Za formulu sa n varijabli moramo pamtiti i računati tablicu sa ukupno 2^n redaka.

 

Primjer: Pretpostavimo da želimo ispitati istinitost formule:

F=(A \wedge \neg B) \vee (B\rightarrow C)\vee (A\leftrightarrow C ) koristeći istinitosne tablice.

 

Za riješiti ovaj problem pomoću istinosnih tablica trebamo razmatrati sljedeću tablicu:

 

                                          A     B      C      A \wedge \neg B     B \rightarrow C    A\leftrightarrow C                F

                                          0      0      0           0             1             1                     1

                                          0      0      1           0             1             0                     1

                                          0      1      0           0             0             1                     1

                                          0      1      1           0             1             0                     1

                                          1      0      0           1             1             0                     1

                                          1      0      1           1             1             1                     1

                                          1      1      0           0             0             0                     0

                                          1      1      1           0             1             1                     1                       

 

Na primjeru vidimo da tablica ima točno 8=2^3 redaka.

 

Kada želimo ispitati samo je li formula ispunjiva, možemo stati nakon što pronađemo jedno rješenje. U našem primjeru to je odmah nakon prvog retka. Međutim da smo na ulaz dobili neku formulu koja nije ispunjiva, morali bi pokazati da za sve kombinacije vrijednosti varijabli krajnja formula nije istinita, odnosno ispitati svih 2^n kombinacija.

 

Tablice istinosti se upotrebljavaju većinom u digitalnoj elektronici za specificiranje funkcionalnosti hardverskih preglednih (eng. lookup) tablica te za reduciranje broja logičkih vrata kod digitalnih sklopova.

 

3.2 Davis-Putnamov algoritam

 

U uvodu smo napomenuli da je Davis-Putnamov algoritam jedan potpuni algoritam za rješavanje problema SAT i da je baziran na metodi rezolucije. U nastavku ćemo definirati metodu rezolucije i iznijeti nekoliko osnovnih pojmova vezanih uz tu metodu.

 

3.2.1 Metoda rezolucije

U daljnjem tekstu elementarne disjunkcije ćemo nazivati i klauzule.

 

Definicija 10. Neka je l proizvoljan literal, te C_1 i C_2 klauzule.
Pravilo rezolucije je sljedeće pravilo izvoda:

$$\frac{l\vee C_1 \ \ \ \ \ \ \ \neg l \vee C_2}{C_1 \vee C_2}$$

                                               
Ako su dane klauzule D_1=l \vee C_1 i D_2=\neg l \vee C_2, tada je rezolventa Res(D_1,D_2) definirana i dobiva se eliminacijom l i \neg l iz D_1,D_2 spajanjem preostalih literala u jednu klauzulu. Dakle vrijedi Res(D_1,D_2)=C_1 \vee C_2. Ako u D_1 i D_2 postoji više od jednog para dualnih literala tada je rezultantna klauzula tautologija, jer rezolucijom eliminiramo samo jedan par. Pretpostavljamo da se nakon izvršavanja rezolucije uklanjaju višestruka pojavljivanja nekog literala.

 

Primjer 1. Pretpostavimo da je D_1=p\vee \neg q \vee s i D_2=p \vee q \vee \neg t, tada je Res(D_1,D_2)=p\vee{s}\vee{p}\vee\neg{t}=p\vee{s}\vee\neg{t}

 

Pravilo rezolucije nam omogućava pojednostavljivanje kompliciranih formula eliminiranjem pojedinih varijabli koje se javljaju istovremeno negirane te bez negacije u formuli. Smanjivanjem broja varijabli određene formule smanjuje se i broj koraka koje mora napraviti Davis-Putnamov algoritam pri ispitivanju ispunjivosti određene formule.

 

Za literal l kažemo da je pozitivan za formulu S ako se u S ne javlja negacija literala l.

 

Eliminiranje varijable x iz formule reprezentirane skupom klauzula S se provodi slijedećom operacijom:

Res(S,x):= S-l, ako je l pozitivan za S i l=x,

                \{C_1 \vee C_2: x\vee C_1\in S i \neg x\vee C_2 \in S i C_1\vee C_2 nije tautologija\}\ \bigcup \{ C\in S: x se ne pojavljuje u C\}, inače

 

Sa S-l označavamo skup klauzula dobiven izbacivanjem klauzula koje sadrže literal l iz skup klauzula S. Sa C_i označavamo pojedinu klauzulu iz skupa klauzula S.

 

Primjer 2. Pokažimo računanje skupa Res(S,x) na jednom primjeru:

 

Neka je S=\{x_1,\ \neg x_1 \vee x_2,\ x_1\vee x_2\vee\neg x_3,\ \neg x_1\vee x_3\vee x_4,\ \neg x_4\vee x_5 \} zadani skup klauzula, računajmo Res(S,x_1). U ovom slučaju l, takav da l=x_1, nije pozitivan za S stoga računamo dva skupa:

 

 

1. Za sve klauzule C_i takve da x_1\vee C_i\in S i sve klauzule C_j takve da \neg x_1\vee C_j\in S stavljamo klauzulu C_i\vee C_j u skup Res(S,x_1).

    Dobivamo skup: $$T_1=\{x_2,\ x_2\vee \neg x_3,\ x_3\vee x_4 \}.$$ Primijetimo da smo pri računanju dobili i klauzulu \ x_2\vee \neg x_3 \vee x_3 \vee x_4 no ona je tautologija i ne ubacujemo je u skup T_1.

 

2. Sve klauzule C\in S takve da se x_1 ne pojavljuje u C ubacimo u novi skup: $$T_2=\{\neg x_4\vee x_5 \}.$$ $$Res(S,x_1)=T_1 \cup T_2=\{x_2,\ x_2\vee \neg x_3,\ x_3\vee x_4,\ \neg x_4 \vee x_5 \}$$

 

U nastavku promatramo F kao skup klauzula. F==\emptyset nam označava da formula F ne sadrži više niti jednu klauzulu.

Kažemo da formula F sadrži praznu klauzulu ako sadrži klauzulu koja nema niti jednu varijablu. Ako F sadrži samo jednu klauzulu koja nema niti jednu varijablu tada to označavamo sa F==\{\emptyset\}

Praznu klauzulu možemo dobiti primjenom metode rezolucije na sljedećoj formuli:(\neg p\vee \neg q)\wedge p\wedge q . Primjenom metode rezolucije na klauzule (\neg p\vee \neg q) i p dobivamo klauzulu \neg q, sada primjenom rezolucije na klauzule \neg q i q dobivamo praznu klauzulu (\emptyset).

Sada možemo navesti pseudokod Davis-Putnamovog algoritma za ispitivanje ispunjivosti logičke formule:

 

Ulaz: Konačan skup klauzula F koji sadrži najmanje jednu klauzulu sa barem jednom varijablom.

Izlaz: Odgovor je li F ispunjiva formula.

• Ako je (F==\emptyset) vrati 'formula je ispunjiva'
• Inače ako F sadrži praznu klauzulu (\emptyset) vrati 'formula nije ispunjiva'
• Inače radi
  • Izaberi neku varijablu formule F, označimo ju sa x
  • Izračunaj  F=Res(F,x)
  • pozovi algoritam na formuli F

 

Dokaz korektnosti Davis-Putnamovog algoritma možete pogledati u [6].

 

Davis-Putnamov algoritam u većini slučajeva ne mora ispitivati sve mogućnosti za istinitosne vrijednosti varijabli ulazne formule stoga je brži i memorijski učinkovitiji od istinitosnih tablica. Unatoč mogućnosti smanjivanja broja varijabli formule u svakom koraku Davis-Putnamov algoritam se nije puno koristio u praksi. Računanje skupa Res je memorijski i računarski zahtjevno (veliki broj novonastalih klauzula) stoga Davis-Putnamov algoritam ima u najgorem slučaju eksponencijalnu vremensku složenost. Davis-Putnamov algoritam je baza iz koje je nastao poboljšani Davis-Putnam-Logemann-Loveland algoritam koji je baza većine današnjih potpunih industrijskih SAT solvera. 

 

3.3 Davis-Putnam-Logemann-Loveland algoritam

 

Davis-Putnam-Logemann-Loveland algoritam za razliku od Davis-Putnamovog algoritma provodi ograničeni oblik rezolucije. Računamo skup literala koji se mogu izračunati iz F koristeći rezoluciju gdje je jedna od klauzula na koju primjenjujemo rezoluciju uvijek jedinična klauzula (klauzula koja sadrži samo jedan literal).
Takav ograničeni oblik rezolucije nazivamo jedinična rezolucija. Prednost ovoga pristupa je što nema povećanja u broju nastalih klauzula nakon provođenja svakog koraka rezolucije već se broj klauzula i broj varijabli smanjuje.

Uz primjenu metode jedinične rezolucije DPLL algoritam koristi i redukciju literala.

 

Definicija 11. Pretpostavimo da je S skup klauzula i v parcijalna interpretacija. Tada se redukcija od S u oznaci Red(S,v) računa:

1. Ako za neki l u C, v(l)=1, tada se klauzula C eliminira.
2. U klauzulama C koje su preživjele test (1) eliminiramo sve literale l takve da v(l)=0.

 

Primjer 3.  Neka je F=\{x\vee p\vee q\vee \neg z,p,\neg p\vee z\vee q, p\vee z\} neki skup klauzula. Red(F,p)=\{z\vee q\}.    

 

Da bi objasnili rad DPLL algoritma moramo definirati još jednu operaciju (bcp_F):

 

$$bcp_F(S)=\{l:\ \text{Postoji klauzula } C:\ l_1\vee \dots \vee l_{j-1} \vee l,\ C\in F,\ \bar{l_1},\dots,\bar{l}_{j-1}\in S.\}$$

Po Knaster Tarskijevom teoremu o fiksnoj točci za svaki skup klauzula F operacija bcp_F sadrži najmanju fiksnu točku. Najmanja fiksna točka se označava BCP(F).

Moramo imati na umu da BCP(F) može biti nekonzistentan (sadržavati praznu klauzulu).

 

Primjer 4. Neka je F=\{p, \neg p\vee q, \neg p \vee \neg q\}. Jediničnom rezolucijom možemo dobiti q i \neg q, stoga i praznu klauzulu.

 

Slijedeća propozicija nam daje postupak kojim DPLL algoritam računa ispunjivost logičke formule.

 

Propozicija 1. Neka je F formula u KNF. Tada je F ispunjiva ako i samo ako je BCP(F) konzistentan i redukcija formule F po BCP(F) je ispunjiva.

Dokaz možete pogledati u [6].

 

Definicija 12. Definiramo redukciju formule F po skupu literala S_l na sljedeći način: $$G:=\{C\backslash \{\bar{l_i}\}: C\in F,\text{ za svaki literal $l_i\in S_l$ }, l_i\notin C\}$$

 

U nastavku navodimo DPLL algoritam:

 

Pretpostavljamo da imamo definirane funkcije:

1. Reduce(F,v) koja računa redukciju formule F po skupu literala v.
2. selectLit(F) koja vraća neki literal formule F.
3. BCP(F) koja računa operaciju BCP na zadanoj formuli F.

 

Ulaz: Formula F u KNF

Izlaz: Odgovor je li F ispunjiva formula

• G=F;
• Ako F sadrži praznu klauzulu vrati 'ulazna formula nije ispunjiva'
• v=BCP(G);
• Ako v sadrži par suprotnih literala (l,\ \neg l) vrati 'ulazna formula nije ispunjiva'
• G=reduce(G,v);
• Ako G=\emptyset vrati 'ulazna formula je ispunjiva'
• Inače
  • l=selectLit(G)
  • pozovi algoritam na G\cup{l}
  • pozovi algoritam na G\cup\neg{l}

DPLL algoritam je baza gotovo svih današnjih SAT solvera. To je potpuni algoritam koji sa apsolutnom sigurnošću utvrđuje je li neka formula ispunjiva.

Unatoč navedenim poboljšanjima u najgorem slučaju DPLL algoritam ima još uvijek eksponencijalnu vremensku složenost što je u skladu sa time da je problem SAT u klasi NP potpunih problema.

Dokaz korektnosti algoritma te neka njegova moguća poboljšanja možete pronaći u [6].

 

Jedan zanimljivi online applet autora Carstena Sinza koji vizualizira rad DPLL algoritma i prikazuje zadanu formulu preko grafa međuovisnosti možete pronaći na sljedećem linku: Dpvis.

Detaljnije o aplikaciji možete pogledati na službenoj stranici aplikacije Dpvis home page.

 

 

            4 Heuristički algoritmi za rješavanje problema SAT

 

Za razliku od potpunih algoritama, heuristički algoritmi su uglavnom nepotpuni. To znači da ti algoritmi u nekim slučajevima ne pronađu rješenje niti za neke ispunjive formule. Uz to heuristički algoritmi ne mogu egzaktno dokazati da neka formula nije ispunjiva već to mogu zaključiti s određenom vjerojatnošću.

Heuristički algoritmi su dosta teški za teorijsku analizu, no pokazuju dobre rezultate u praksi, kako na slučajno generiranim formulama tako i na strukturiranim instancama koje su dobivene pretvaranjem raznih problema (kao što su primjerice planiranje ili dizajn mreža) u problem ispunjivosti logičke formule. Teorijsko znanje o ovoj skupini algoritama je maleno i većinom se analizom složenosti dobivaju eksponencijalne gornje ograde izvršavanja.

Heuristički algoritmi mogu biti:

1. Potpuni: Daju rješenje problema s apsolutnom sigurnošću, ako ne uspiju pronaći rješenje za zadani problem tada ono ne postoji.
2. Nepotpuni: Ako nepotpuni algoritam pronađe rješenje ono je sigurno točno, međutim ako naš nepotpuni algoritam ne pronađe rješenje tada ne znamo ništa o rješenju niti o njegovoj egzistenciji.

Primijetimo da nemamo ogradu na vjerojatnost pogreške, stoga ne možemo samo ponavljati algoritam dovoljan broj puta smanjujući vjerojatnost pogreške na neku unaprijed definiranu konstantu.

 

Nepotpuni heuristički algoritmi se mogu podijeliti na:

1. Esencijalno nepotpune: Kod algoritama ove skupine postoje slučajno generirani elementi prostora koji pretražujemo iz kojih algoritam nikako neće poboljšavanjem uspjeti doći do konačnog rješenja. Vjerojatnost da će algoritam uspjeti doći do rješenja iz takvog elementa je strogo manja od 1. Kod esencijalno nepotpunih algoritama se uvode ponovna pokretanja, odnosno restartovi. Ako u određenom broju iteracija ne uspijemo doći do rješenja, na slučajan način generiramo novi početni element kojeg pokušamo dalje poboljšati.
2. Vjerojatnosno aproksimativno potpune: Algoritmi iz ove skupine će bez obzira na element iz kojeg kreću u pretraživanje prostora rješenja doći sigurno do rješenja, ako takvo postoji, u određenom (konačnom) broju koraka.

 

Trenutno poznatiji heuristički algoritmi za rješavanje problema SAT su sljedeći: GSAT, GWSAT, HSAT, HWSAT, SDF, IDB, WalkSAT i njegove podvrste: WalkSAT/Tabu, Novelty, R-Novelty, Novelty+, R-Novelty+. Prisutni su i GA (genetski) algoritmi koji se najčešće kombiniraju s jednim od algoritama lokalnog traženja.

U zadnjih nekoliko godina se radi i na razvijanju algoritama koji bi rješavali problem SAT na kvantnim računalima.

 

4.1 Genetski algoritmi

 

Genetski algoritmi su evolucijske meta-heurstike koje se koriste za rješavanje teških problema. Njihova primjena na kompleksne optimizacijske probleme u nekim slučajevima daje izuzetno dobre rezultate.

Ideja algoritma je bazirana na oponašanju prirodne evolucije. Algoritam kreće od početne populacije koju čine kandidati za rješenja koji predstavljaju jedinke koje će se poboljšavati te na taj način povećavati kvalitetu populacije. Princip samog algoritma se sastoji od niza reprodukcija između jedinki, mutacije jedinke dobivene reprodukcijom te na kraju odabirom bolje jedinke koja će ući u populaciju. Ovaj proces se ponavlja konačan broj puta i cilj je stvaranje što kvalitetnije jedinke.

Genetski algoritam često konvergira što znači da populacija gubi na svojoj raznovrsnosti pa algoritam gubi svoju efikasnost jer mu se može dogoditi da lako zaglavi te na taj način nikada neće pronaći rješenje. Samu konvergenciju ponekad možemo koristiti kao zaustavni kriterij.

Veliki problem predstavlja preuranjena konvergencija koja je svojstvena za klasične genetske algoritme. Ovo svojstvo onemogućava algoritmu pretraživanje većeg dijela domene samog problema.

Križanje i mutacija se mogu izvesti na različite načine, detaljnije pogledajte u ([4]).

Genetski algoritmi su populacijski algoritmi koji omogućavaju rješavanje teških problema, što je jedna od njihovih prednosti. Najveća mana genetskih algoritama je što mogu zaglaviti u lokalnom optimumu.

  

 

4.2 Pohlepni algoritmi

 

Hill climbing je matematička tehnika optimizacije koja pripada u tehnike lokalnog traženja.
To je iterativni algoritam koji počinje pretragu s proizvoljnim rješenjem problema. Algoritam u svakom koraku pokušava pronaći bolje rješenje mijenjajući jedan element trenutnoga rješenja u uzastopnim koracima. Ako promjena stvori bolje rješenje, ono se prihvaća kao trenutno. Postupak se ponavlja sve dok algoritam pronalazi bolja rješenja.

Greedy algoritmi za rješavanje problema SAT u oznaci (GSAT) su slučajni hill-climbing algoritmi. GSAT na slučajan način generira interpretaciju te zatim provodi postupak hill-climbinga. Algoritam mijenja vrijednost interpretacije za onu varijablu za koju se dobije najveće povećanje u broju istinitih klauzula u odnosu na prethodni korak. Ukoliko moramo izabrati između dvije jednako dobre promjene, greedy algoritam na slučajan način izabere jednu od njih. Ako niti jedna promjena ne može popraviti rezultat tada se uzima ona promjena koja najmanje smanjuje broj klauzula koje su istinite za trenutnu interpretaciju. GSAT počinje od slučajne pozicije u prostoru svih rješenja i traži globalno rješenje koristeći samo lokalnu informaciju.

 

Greedy algoritama su najjednostavniji i vrlo brzi algoritmi lokalnog pretraživanja. Najveće mane ove skupine algoritama su što su esencijalno nepotpuni algoritmi i što često zaglave u lokalnom optimumu.

  

 

Za više detalja pogledajte ([4]).

 

4.3 Slučajne šetnje

 

Riječ je o algoritmima lokalnog pretraživanja. Umjesto da pokušavamo pronaći globalno najbolju varijablu, prvo na slučajan način odabiremo nezadovoljenu klauzulu, a potom varijablu unutar te klauzule čiju vrijednost mijenjamo. Zbog toga što slučajna šetnja može previdjeti globalno kretanje onda kažemo da ona izvodi hill-climbing.

Činjenica da je neka klauzula nezadovoljena znači da  vrijednost najmanje jedne varijable mora biti promijenjena da bi dosegnuli globalno rješenje. Označimo s k duljinu najveće klauzule u formuli. Kada je k=2  tada će slučajna šetnja riješiti problem ispunjivosti formule od n varijabli s visokom vjerojatnošću u vremenu O(n^2). Za veće k samo najgori slučajevi garantiraju da je slučajna šetnja eksponencijalna. U praksi se varijable čiju vrijednost mijenjamo biraju na slučajan način iz neke nezadovoljene klauzule koju pak izabiremo koristeći neku pohlepnu heuristiku.

 Originalna heuristika uvodi pojam breakcount, koji predstavlja broj klauzula koje su trenutno zadovoljene, a koje će postati nezadovoljene promjenom vrijednosti varijable. Slično, pojam makecount predstavlja broj klauzula koje su trenutno nezadovoljene, a koje će postati zadovoljene promjenom vrijednosti varijable. Heuristika odabira je sljedeća:

1.     Ako postoje varijable za koje vrijedi breakcount=0, onda na slučajan način odabiremo jednu od njih.
2.     Inače, s nekom fiksnom vjerojatnosti p biramo varijablu s najmanjom vrijednosti breakcount. Ako je takvih više na slučajan način odabiremo jednu.
3.     Inače, biramo varijablu s minimalnom vrijednosti breakcount. Ako je više takvih na slučajan način odabiremo jednu.

Provjera postoje li varijable za koje vrijedi breakcount=0 je ključ za dobre performanse ove heuristike.

Vrijednosti svih breakcount i makecount se mogu održavati u uzastopnim koracima (inkrementalno). Na početku su te vrijednosti inicijalizirane. Kada radimo promjenu vrijednosti varijable x iz istine u laž, tada breakcount možemo ažurirati tako da posjetimo sve klauzule koje sadrže ne negiranu varijablu x, te ako klauzula sadrži samo jedan istinit literal r povećamo breakcount varijable r za jedan. Potrebno je također posjetiti sve klauzule koje sadrže negiranu varijablu x te ako klauzula sadrži samo još jedan istinit literal r potrebno je umanjiti breakcount varijable r za jedan. Sličnu operaciju izvodimo kod promjene vrijednosti neke varijable iz laži u istinu. Odabir vrijednosti za p ovisi o konkretnom problemu. 3-SAT problemi se obično najbrže rješavaju s parametrom p=0.5. Postoji dokaz da je optimalan p približno jednak \mu /\sigma gdje je \mu prosječan broj nezadovoljenih klauzula tijekom izvršavanja algoritma i \sigma je standardna devijacija od ove veličine.

Postoji dosta dobra heuristika za slučajnu šetnju koja se zove Rnovelty. Ideja je pokušati izbjeći mijenjanje malog skupa varijabli. Prilikom svake promijene varijable zabilježimo vremenski žig promjene. Kada je odabrana nezadovoljena klauzula tada Rnovelty radi sljedeće:

1.  Sortira varijable u klauzuli po breakcount i makecount.
2. Ako dvije ili više varijabli daju najbolju vrijednost, odabiremo onu varijablu koja nije iz klauzule koje je nedavno mijenjana što određujemo na temelju vremenskog  žiga.
3. Inače promotri prve dvije najbolje varijable. Ako najbolja varijabla nije nedavno mijenjana tada napravi promjenu varijable u klauzuli.
4. Inače ako je razlika između najbolje i druge najbolje veća od jedan odaberi najbolju inače odaberi drugu najbolju varijablu.

Prednosti slučajnih šetnji su što su to učinkoviti i veoma brzi algoritmi te pretražuju nešto veći prostor od pohlepnih algoritama. Mane ovih algoritama su što mogu zaglaviti u lokalnom optimumu te su esencijalno nepotpuni algoritmi.

 

Za više detalja pogledajte ([4]).

 

4.4 Paralelna heuristika za rješavanje problema SAT

 

U ovom dijelu ćemo dati grubi pregled jedne paralelne heuristike za rješavanje problema SAT razvijene od autora ovoga članka.

 

Za razvijanje heuristike implementiran je jedan genetski algoritam SGAV ([2]), jedan algoritam koji koristi slučajne šetnje i eliminaciju jediničnih klauzula UnitWalk ([3]) i jedan Greedy algoritam za rješavanje problema SAT ([1]). Koristeći ta tri osnovna algoritma stvorena su tri nova hibridna algoritma UnitWalk+SGAV, UnitWalk+Greedy i UnitWalk sa ugrađenim greedy pristupom u heuristici za izbor varijabli.

 

Detalje o svakom od navedenih algoritama možete pogledati u ([4]) stoga u ovom poglavlju nećemo ulaziti u velike detalje.

 

Solver u ovisnosti o broju varijabli ulazne formule određuje koji od tri navedena algoritma se izvršava i broj algoritama koji se izvode paralelno. U ovisnosti o broju n (broju varijabli) to izgleda ovako:

n\leq 100, Osnovni UnitWalk algoritam

100<n\leq 200, UnitWalk+Greedy algoritam

200\leq n, UnitWalk, UnitWalk+SGAV, UnitWalk+Greedy algoritmi

 

Za formule koje sadrže manje od 200 varijabli paralelizacija se ne isplati. Vrijeme trostrukog učitavanja podataka, pokretanja dretvi (eng. threadova), provjere i gašenja dretvi je veće od vremena potrebnog navedenim algoritmima da izračunaju rješenje sekvencijalno.

Za n\geq 200 solver konkurentno izvršava UnitWalk+Greedy, UnitWalk+SGAV i UnitWalk algoritam s dodatno učitanim podacima na tri dretve. Glavna dretva periodički provjerava je li koji od algoritama završio s radom, ako je to slučaj gasi preostale dretve i vraća rješenje.

Vrijeme provjere glavne dretve ovisi o broju varijabli formule, što formula ima više varijabli to su rjeđe provjere jer je vjerojatnost da ćemo pronaći rješenje manja. Stoga više procesorskog vremena trošimo za izvođenje algoritama koji računaju rješenje.

Ovdje navodim vremena čekanja glavne dretve u ovisnosti o veličini problema:

Time_S=

               10 ms, 200 \leq n <225
               30 ms, 225\leq n<240
               40 ms, 240\leq n\leq 250
               200 ms, 250<n<500
               2000 ms, 500\leq{n}

Pošto sva tri navedena algoritma pri računanju interpretacije mijenjaju i ulaznu formulu, učitamo podatke za svaki algoritam posebno te tako dobivamo potpuno konkurentno izvršavanje bez upotrebe tehnika međusobnog isključivanja.

 

Solver je vjerojatnosno aproksimativno potpun, za svaku ispunjivu formulu će pronaći interpretaciju za koju je ona istinita s vjerojatnošću 1 u konačno mnogo koraka. To je napredak u odnosu na esencijalno nepotpune algoritme koji mogu zaglaviti i ne pronaći rješenje iako je zadana formula ispunjiva.

 

Eksperimentalni rezultati pokazuju da tako dobiveni solver dolazi brže do rješenja nego pojedinačni algoritmi od kojih je građen.

 

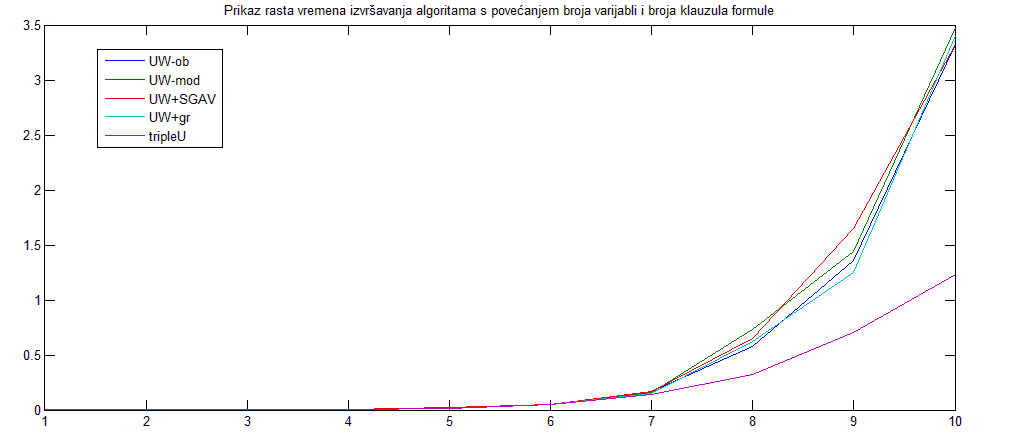
                                                   Slika 1. Vremena izvršavanja algoritama

 

Algoritmi i solver su testirani na standardnim SAT test primjerima. Detaljnije možete pročitati u ([4]).

 

           5 Verzije problema SAT

 

U prethodnim poglavljima smo govorili o nekim algoritmima za rješavanje problema SAT. Zahtijevali smo da formula bude u KNF i da se radi o formuli propozicionalne logike sudova. Kod solvera smo zahtijevali da formula bude u 3-SAT obliku što je jedan specifičniji oblik problema, no opet dovoljno dobar za istraživanje.

 

U ovom poglavlju ćemo definirati neke različite vrste SAT problema i navesti koliko je trenutno teško riješiti svaki od tih problema. Nećemo ulaziti u detalje dokaza složenosti. Detaljnije o svakom od navedenih problema i dokaze pripadnosti problema odgovarajućoj klasi složenosti možete pogledati u ([7]).

 

Definicija 13. Za formulu F logike sudova kažemo da je k-KNF formula, ako je ona u konjunktivnoj normalnoj formi, sadrži više od jedne klauzule i svaka njezina klauzula sadrži točno k literala.

 

Definicija 14. k-SAT= {F|F je ispunjiva k-KNF formula logike sudova}.

 

Jedna dosta zanimljiva stvar vezana uz k-SAT je da probleme 1-SAT i 2-SAT znamo riješiti učinkovito, odnosno znamo u polinomnom vremenu na determinističkom Turingovom stroju ispitati je li formula ispunjiva i za nju u slučaju da je ispunjiva pronaći odgovarajuću interpretaciju za koju je istinita. Već za k=3 to ne znamo napraviti, odnosno 3-SAT je NP potpun problem. Zbog činjenice da je NP potpun problem, ukoliko uspijemo pronaći polinoman algoritam za rješavanje problema 3-SAT na determinističkom Turingovom stroju odmah smo riješili i problem k-SAT.

 

Probajmo istražiti malo izmijenjeni oblik 2-SAT problema.

 

Definicija 15. Za zadanu formulu F u 2-KNF i prirodan broj K, potrebno je ispitati postoji li interpretacija I takva da je za nju istinito barem K elementarnih disjunkcija.

Takvu vrstu SAT problema nazivamo MAX-2-SAT.

 

Pokazuje se da je problem MAX-2-SAT jedan NP potpun problem ([7]).

 

Definicija 16. Kažemo da je neka klauzula Hornova klauzula ako su u njoj svi literali, osim možda jednoga negacije propozicionalnih varijabli. Hornova formula je konjunkcija Hornovih klauzula.

 

Primjer 5. Klauzule (\neg x_2 \vee x_3), (\neg x_1 \vee \neg x_2 \vee \neg x_3 \vee \neg x_4), (x_1) su Hornove klauzule. Prva i treća klauzula sadrže pozitivan literal stoga se one nazivaju implikacije.

 

Klauzule oblika (\neg x_1 \vee \dots \vee \neg x_n \vee y) možemo zapisati u implikacijskom obliku kao ((x_1\wedge\dots\wedge{x_n})\rightarrow{y})

 

Problem HORN-SAT je rješiv u polinomnom vremenu na determinističkom Turingovom stroju, odnosno HORN-SAT \inP ([7]).

 

Definicija 17. Za formulu F kažemo da je pozitivna ako je u konjunktivnoj normalnoj formi i ako su sva pojavljivanja varijabli u klauzulama pozitivna (bez negacija). Analogno definiramo i negativnu formulu ako je u konjunktivnoj normalnoj formi i ako su sva pojavljivanja varijabli u klauzulama negirana.

 

Primjer 6. Formula F=(x_1)\wedge(x_2\vee x_3\vee x_4)\wedge(x_1\vee x_7)\wedge(x_5 \vee x_6\vee x_8\vee x_9) je pozitivna formula.
  

Definicija 18. Definiramo interpretaciju 1_{x_1,\dots,x_n} za koju vrijedi 1(x_i)=1,\forall{i}\in\{1,\dots{n}\}. Očito je da je svaka pozitivna formula istinita za ovakvu interpretaciju definiranu na varijablama te formule.

Analogno definiramo interpretaciju 0_{x_1,\dots,x_n} za koju vrijedi 0(x_i)=0,\forall{i}\in\{1,\dots{n}\}. Očito je da je svaka negativna formula istinita za ovakvu interpretaciju definiranu na varijablama te formule.

 

Problem ispunjivosti pozitivnih i negativnih formula rješiv je u polinomnom vremenu na determinističkom Turingovom stroju.  To možemo u ovom slučaju lako vidjeti, konstruiramo odgovarajuću interpretaciju 1_{x_1,\dots,x_n} ili 0_{x_1,\dots,x_n} za koju naša pozitivna odnosno negativna formula mora nužno biti istinita.

 

Definicija 19. Problem NAESAT (Not-All-Equal satisfiability): Za danu formulu F, postoji li interpretacija I : \{x_1,\dots x_n\}\to\{0,1\} takva da vrijedi I(F)=1 i da je barem jedan literal u svakoj elementarnoj disjunkciji neistinit? Ako takva interpretacija postoji, za formulu F kažemo da je NAE-ispunjiva.

 

Definicija 20. Problem XSAT (Exact satisfiability): Za danu formulu F, postoji li interpretacija I : \{x_1,\dots, x_n\} \to \{0,1\} takva da vrijedi I(F)=1 i da je točno jedan literal u svakoj elementarnoj disjunkciji istinit? Ako takva interpretacija postoji, za formulu F kažemo da je X-ispunjiva.

 

NAESAT i XSAT problemi spadaju u klasu složenosti NP odnosno trenutno nije poznat polinoman algoritam na determinističkom Turingovom stroju za rješavanje ovih problema ([7]).

 

Definicija 21. Booleov krug je graf C = (V,E) u kojem se vrhovi V =\{1,\dots,m\} zovu vrata od C. U grafu C svi bridovi su oblika (i,j) gdje je i < j. Svi vrhovi u grafu imaju ulazni stupanj jednak 0,1 ili 2. Svaka vrata i imaju vrstu s(i), gdje je s(i)\in\{\top,\bot,\wedge,\vee,\neg\}\cup\{x_1,\dots,x_n\}

Ulazni stupanj vrha i, st_{ul}(i), određuje se na sljedeći način:

                   0; ako je s(i)\in\{\top,\bot\}\cup\{x_1,\dots,x_n\}
st_{ul}(i) :=       1; ako je s(i)=\neg
                   2; ako je s(i)=\{\wedge,\vee\}
Vrata bez ulaznih bridova zovu se ulazne vrijednosti od C. Čvor m (koji nema izlaznih bridova) zovemo izlaznim vratima kruga.

 

    

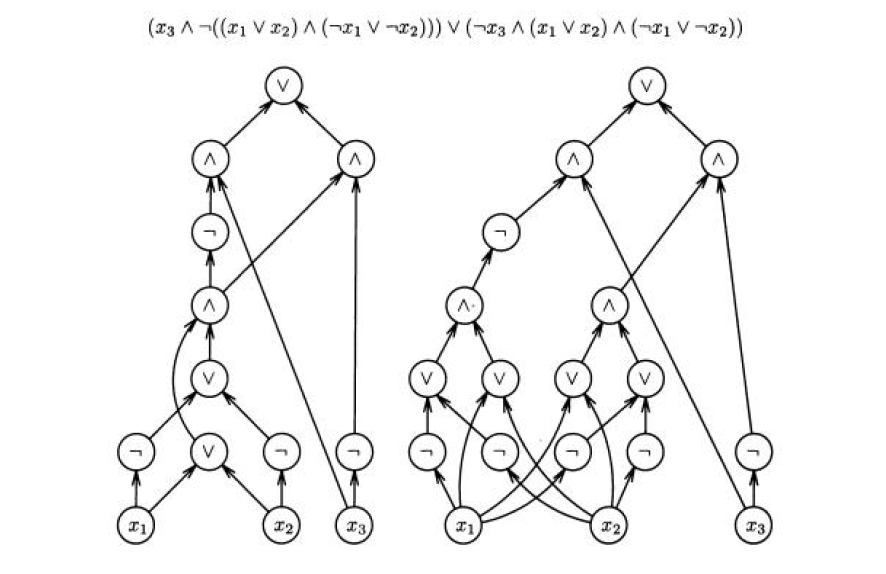
                                               Slika 2. Prikaz booleovog kruga na primjeru       

 

Neka je X(C) skup svih varijabli koje se pojavljuju u krugu C. Interpretacija I je adekvatna za C ako je definirana za svaki x\in X(C).
Za takvu interpretaciju I istinitosna vrijednost vrata i definirana je induktivno:
- ako je s(i)=\top onda je I(i)=1. Ako je s(i)=\bot onda je I(i)=0.
- ako je s(i)\in X, onda je I(i)=I(s(i)).
- ako je s(i)=\neg, onda postoje jedinstvena vrata j < i takva da je (j,i)\in E. I(i)=1 ako I(j)=0 i obrnuto.
- ako je s(i)=\vee, onda postoje dva ulazna brida (j,i) i (k,i). I(i)=1 ako i samo ako I(j)=1 ili I(k)=1.
- ako je s(i)=\wedge , onda postoje dva ulazna brida (j,i) i (k,i).  I(i)=1 ako i samo I(j)=1 i I(k)=1.
- I(C)=I(m), gdje su m izlazna vrata kruga.

 

Definicija 22. Problem CIRCUIT SAT glasi:

Za dani krug C, postoji li interpretacija I adekvatna za C takva da je I(C)=1?

 

Problem CIRCUIT SAT spada u klasu složenosti NP, odnosno još uvijek ne postoji algoritam koji bi ga rješavao u polinomnom vremenu na determinističkom Turingovom stroju ([7]).

 

Sada navodimo jednu modificiranu verziju problema:

 

Definicija 23.  Problem CIRCUIT VALUE:

Za dani krug C koji nema vrata i\in \{1,\dots, m\}, postoji li interpretacija I adekvatna za C takva da je I(C)=1.

 

Vrijedi: Problem CIRCUIT VALUE \in P ([7]).

 

                                               

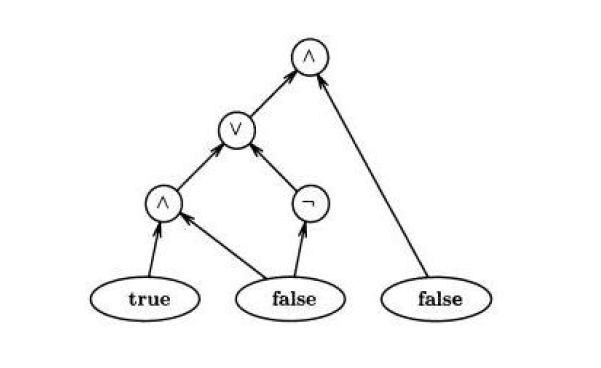
                                                                                      Slika 3. Primjer CIRCUIT VALUE problema

 

Navodimo dvije zanimljive verzije problema SAT.

 

Definicija 24. Problem \#-SAT:
Za danu formulu F, koliko postoji interpretacija I_k takvih da I_k(F)=1?

Problem \#-SAT \in\#P (klasa problema prebrojavanja povezanih s problemima odlučivanja iz klase složenosti NP). Ako je Q neki problem iz klase složenosti NP, tada je problem: za dani x koliko postoji y tako da vrijedi Q(x,y) problem iz klase \#P. ([7]).  

Definicija 25. Problem \oplus-SAT:
Za danu formulu F, je li broj interpretacija I_k takvih da I_k(F)=1 neparan?

Problem \oplus-SAT \in\oplusP. Kažemo da je problem L\in\oplus P ako postoji nedeterministički Turingov stroj M takav da za sve ulazne riječi x vrijedi x\in L ako i samo ako Turingov stroj M s ulazom x ima neparan broj stanja u kojima prihvaća riječ x([7]).  

Sada ćemo definirati klasu složenosti DP i neke verzije problema SAT koje spadaju u tu klasu složenosti.

 

Definicija 26. Problem \xi pripada klasi co-NP ako i samo ako njegov komplement \overline{\xi} pripada klasi NP.

 

Definicija 27. Jezik L pripada klasi DP ako i samo ako postoje dva jezika L_1\in NP i L_2\in co-NP takva da je L=L_1\cap L_2.

 

Navodimo dvije verzije problema SAT koji spadaju u klasu složenosti DP ([7]).

 

Definicija 28. Problem SAT-UNSAT:
Za dane dvije formule F i G, obje u 3-KNF, vrijedi li da je F ispunjiva, a G nije ispunjiva?

 

Definicija 29. Problem CRITICAL-SAT:
Za danu formulu F, vrijedi li da F nije ispunjiva i da brisanjem proizvoljne elementarne disjunkcije ona postaje ispunjiva?

 

Problem SAT nije ograničen samo na propozicionalnu logiku.

 

Definicija 30. Problem FIRST-ORDER SAT:
Je li zadana formula logike prvog reda ispunjiva?

 

Problem FIRST-ORDER SAT je neodlučiv! (Churchov teorem, [8])

 

Činjenica da je FIRST-ORDER SAT neodlučiv znači da ne možemo konstruirati jedan algoritam koji bi za bilo koju formulu logike prvog reda sa sigurnošću utvrdio je li ona ispunjiva.

Ovo svojstvo stvara velike probleme kod formalne verifikacije i kod automatiziranih dokazivača teorema. Upravo zbog neodlučivosti ove vrste problema SAT pokušavaju se konstruirati što bolji programi koji bi služili kao pomoć čovjeku pri dokazivanju teorema. Takvi programi bi trebali pomoći čovjeku izvoditi konzistentne zaključke i skratiti vrijeme izvođenja tih zaključaka.

 

Navest ćemo i jednu podvrstu FIRST-ORDER SAT problema koja je ipak odlučiva, no vrijeme potrebno za pronalaženje rješenja je u najboljem slučaju eksponencijalno.

 

Definicija 31. Formula logike prvog reda je Schönfinkel-Bernaysova formula ako njezin alfabet ima samo relacijske simbole i konstante, bez funkcijskih simbola i jednakosti, te ako je oblika:
$$\phi=\exists x_1\dots \exists x_k\forall y_1\dots\forall y_1 \psi $$
to jest, ako je u preneksnoj formi s nizom egzistencijalnih kvantifikatora nakon kojih slijedi niz univerzalnih kvantifikatora.

 

Definicija 32. Problem Schönfinkel-Bernays-SAT: Je li dana Schönfinkel-Bernaysova formula ispunjiva?

 

Definirani problem spada u klasu složenosti NEXP=\bigcup\limits_{k \in \mathbb{N}}NTIME(2^{n^k}) ([7]).

 

                   6 Zaključak

Problem SAT je jedan od najdetaljnije istraženih problema na polju računarske znanosti. On je ujedno i prvi problem za kojega je dokazano da je NP potpun.  Tu tvrdnju su nezavisno dokazali S. Cook i L. Levin 1971. godine. Brojni pokušaji i razvijene tehnike za rješavanje problema SAT u raznim poljima matematike i računarstva ističu važnost ovoga problema kako u industrijskim primjenama tako i u teoriji.

                   7 Zahvale

Ovim putem zahvaljujemo prof.dr.sc. Mladenu Vukoviću za stručnu pomoć pri pisanju ovoga članka, za buđenje našega interesa za teoriju matematičke logike, teorije izračunljivosti i složenosti algoritama kao i veliku potporu pri našem proučavanju problema ispunjivosti logičke formule.