|
Bojan Kovačić, Renata Opačić i Luka Marohnić
Tehničko veleučilište u Zagrebu, Zagreb, Vrbik 8a,
|
Sažetak
U opisnoj (deskriptivnoj) statistici mjere koncentracije izdvajaju se kao pokazatelji načina razdiobe zbroja svih vrijednosti numeričkoga obilježja, svih vrijednosti konačnoga numeričkog statističkog niza podataka ili neke druge veličine prema elementima statističkoga skupa ili modalitetima statističkoga obilježja. Pritom se razlikuju apsolutne i relativne mjere koncentracije. U apsolutne mjere pripadaju koncentracijski omjer i Herfindahl–Hirschmanov indeks, dok se kao najčešća relativna mjera koncentracije navodi Ginijev koeficijent koncentracije ili Ginijev indeks. U ovome ćemo članku opisati taj koeficijent, te dati statističke interpretacije nekih njegovih konkretnih vrijednosti koje se odnose na Hrvatsku.
Ključne riječi: Ginijev koeficijent koncentracije, Lorenzova krivulja
About Gini concentration coefficient
Sažetak
In descriptive statistics concentration measures stand apart showing distribution of total, all values of finite numerical statistical data sequence or some other statistical value distributed by elements of statistical set or variable modality. There are absolute and relative concentration measures. Absolute measures include concentration ratio and Herfindahl-Hirschman index, while the most frequently used relative measure is Gini coefficient or Gini index. In this article we will describe the latter and give statistical interpretations of its concrete values related to Republic of Croatia.
Keywords: Gini concentration coefficient, Lorenz curve
1.Uvod
Kako je već istaknuto u sažetku, Ginijev koeficijent koncentracije pripada u relativne mjere koncentracije ili mjere nejednakosti (dispariteta) statističkoga niza. Njihova vrijednost može biti bilo koji realan broj iz segmenta [0,1]. Što je ta vrijednost bliža nuli, vrijednosti niza su ravnomjernije raspoređene, tj. na svaki modalitet otpada približno jednak udio u totalu. Obrnuto, što je ta vrijednost bliža jedinici, vrijednosti niza su neravnomjernije raspoređene: slobodno govoreći, većina totala otpada na jedan modalitet.
Okvirno pojasnimo ovu ideju na konkretnom primjeru.
Primjer 1. U tablici 1 zadane su razdiobe uvoza i izvoza Kraljevine Ubananije 2011. godine.
|
Zemlja |
Uvoz (mil. €) |
Izvoz (mil. CHF) |
|
Kraljevina Niškoristija |
0 |
25 |
|
Savezna Republika Vrijedlandija |
100 |
25 |
|
Kneževina Drplandija |
0 |
25 |
|
Republika Ljenčarija |
0 |
25 |
Tablica 1: podaci preuzeti iz Statističkog ljetopisa Kraljevine Ubananije, 2011. (Primjer 1.)
Iz Tablice 1 se vidi da Kraljevina Ubananija uvozi isključivo iz SR Vrijedlandije, pa je pripadna relativna mjera koncentracije u ovom slučaju jednaka 1. Uvoz je ravnomjerno raspoređen prema svim četirima zemljama, pa je relativna mjera koncentracije u ovom slučaju jednaka 0.
2.Lorenzova krivulja
Da bismo precizno definirali Ginijev koeficijent, najprije moramo definirati Lorenzovu krivulju. U tu svrhu pretpostavimo da statistički niz x_{1},x_{2},\dots,x_{n} ima sljedeća svojstva:
-
(S1)
-
x_{i}\geq0, za svaki i\in[n];
-
(S2)
-
Postoji barem jedan i\in[n] takav da je x_{i}\gt 0.
Pritom je standardno:
|
\bullet |
[n]:=\lbrace 1,2,\text{…},n\rbrace tj. skup prvih n prirodnih brojeva, |
|
\bullet |
[n]_{0}:=\lbrace 0,1,2,\dots,n\rbrace. |
Budući da je svaki konačan podskup skupa realnih brojeva moguće uzlazno urediti, tj. poredati elemente toga podskupa od najmanjeg do najvećeg, bez smanjenja općenitosti možemo pretpostaviti da niz x_{1},x_{2},\dots,x_{n} ima svojstvo:
-
(S3)
-
x_{1}\leq x_{2}\leq\dots\leq x_{n},
tj. da je taj niz uzlazno uređen. Tada za svaki i\in[n] definiramo:
(2)
S_{i}:=\sum_{k=1}^{i}x_{k},
(3)
y_{i}:=\frac{S_{i}}{S_{n}}.
Pojasnimo konkretno značenje ovih triju izraza. Izraz (1) definira točke koje dijele segment [0,1] na n jednakih dijelova. Izraz (2) definira i–ti djelomični zbroj članova niza (analogno kao što činimo prigodom definicije numeričkoga reda), pri čemu je S_{n} zbroj svih članova niza. Napokon, izraz (3) definira udio k–toga djelomičnog zbroja u ukupnom zbroju svih članova niza.
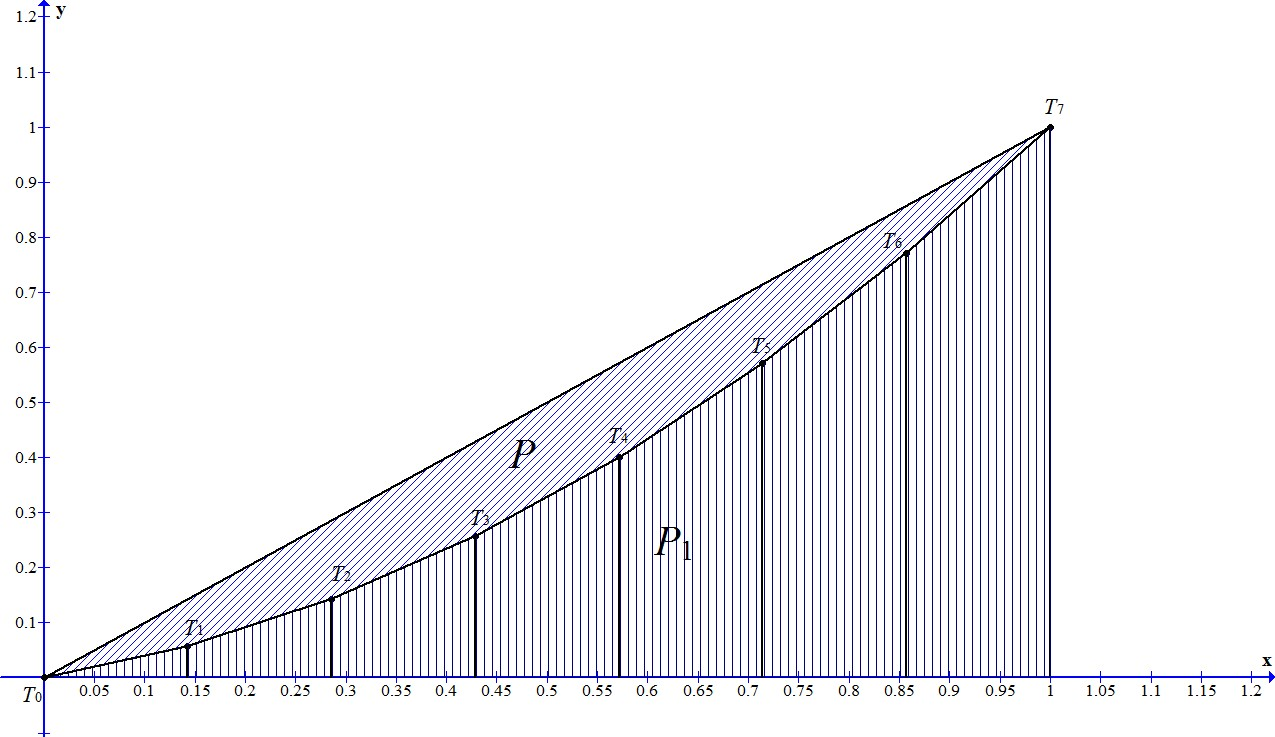
Za netom definirane vrijednosti definiramo niz ravninskih točaka T_{i}, i=[n]_{0} s:
\begin{cases} T_{0} & =(0,0);\\ T_{i} & =\left(p_{i},y_{i}\right),\ \text{za svaki}\ i\in[n]. \end{cases}
Ucrtamo li dobivene točke u pravokutni koordinatni sustav u ravnini, dobit ćemo tzv. izlomljenu poligonalnu liniju L. Ta linija je graf neprekidne, po dijelovima linearne funkcije. Linija L počinje u ishodištu, završava u točki T_{n}=(1,1) i naziva se Lorenzova krivulja. Istaknimo jedno svojstvo Lorenzove krivulje L.
Propozicija 2. Sve točke krivulje L nalaze se ili ispod pravca y=x ili na tom pravcu.
Dokaz. Dovoljno je dokazati da za svaki i\in[n] vrijedi nejednakost:
Definirajmo niz \left(z_{k}\right)_{k\in[n]} na sljedeći način (uz upotrebu (2)):
(5)
z_{i}:=\frac{S_{i}}{i}=\frac{1}{i}\sum_{k=1}^{i}x_{k}.
Tvrdimo da je niz \left(z_{k}\right)_{k\in[n]} monotono rastući. Doista, za svaki i\in[n-1] vrijedi:
(6)
\begin{gathered}z_{i+1}-z_{i}=\frac{1}{i+1}\sum_{k=1}^{i+1}x_{k}-\frac{1}{i}\sum_{k=1}^{i}x_{k}=\\ =\frac{i\sum_{k=1}^{i+1}x_{k}-(i+1)\sum_{k=1}^{i}x_{k}}{i(i+1)}=\frac{i\cdot x_{i+1}-\sum_{k=1}^{i}x_{k}}{i(i+1)}. \end{gathered}
Nazivnik posljednjeg razlomka je očito strogo pozitivan, a nenegativnost brojnika tog razlomka izravno slijedi zbrajanjem nejednakosti
\begin{alignedat}{1}x_{1} & \leq x_{i+1},\\ x_{2} & \leq x_{i+1},\\ & \dots\\ x_{i} & \leq x_{i+1}. \end{alignedat}
koje vrijede prema svojstvu (S3). Stoga iz (6) slijedi
z_{i}\leq z_{n},
odnosno, prema (5),
\frac{1}{i}\sum_{k=1}^{i}x_{k}\leq\frac{1}{n}\sum_{k=1}^{n}x_{k},
odnosno
(7)
\frac{\sum_{k=1}^{i}x_{k}}{\sum_{k=1}^{n}x_{k}}\leq\frac{i}{n}.
Nejednakost (7) je, prema (1), (2) i (3), ekvivalentna nejednakosti
y_{i}\leq p_{i},\ \text{za svaki}\ i\in[n],
koju smo i željeli dokazati.
\ \blacksquare
Neka su
|
\bullet |
P= površina ravninskoga lika koji krivulja L zatvara s pravcem y=x; |
|
\bullet |
P_{1}= površina ravninskoga lika koji krivulja L zatvara s osi x i pravcem x=1; |
|
\bullet |
P_{2}= površina trokuta s vrhovima u točkama T_{0}=(0,0), A=(1,0) i T_{n}=(1,1). |
Očito vrijede jednakosti:
3.Definicija i osnovna svojstva Ginijeva koeficijenta. Izračun Ginijeva koeficijenta u slučaju negrupiranih podataka
Površina P definirana u prethodnom paragrafu u opisnoj se statistici interpretira upravo kao mjera koncentracije, odnosno, grubo rečeno, kao mjera „odstupanja“ Lorenzove krivulje od pravca y=x. Omjer površina P i P_{2} promatra se kao relativna jedinica mjere koncentracije. Taj se omjer naziva Ginijev koeficijent koncentracije. Formalno imamo sljedeću definiciju:
Definicija 3. Ginijev koeficijent koncentracije statističkoga niza \left(x_{i}\right)_{i\in[n]} je nenegativan realan broj G definiran s
(10)
G:=\frac{P}{P_{2}}=2P=1-2P_{1}.
U Definiciji 1 Ginijev koeficijent izrazili smo pomoću površine P_{1} jer je tu površinu lako izračunati koristeći koordinate članova niza točaka \left(T_{i}\right)_{i\in[n]_{0}}. Doista, ravninski lik omeđen izlomljenom linijom L i pravcima x=1 i y=0 sastoji se od jednoga pravokutnoga trokuta i n{–}1 pravokutnih trapeza. Površina pravokutnoga trokuta jednaka je
(11)
P_{\triangle}=\frac{y_{1}}{2n},
dok je površina i-toga trapeza jednaka
(12)
\tilde{P}_{i}=\frac{y_{i}+y_{i+1}}{2n},\ \text{za svaki}\ i=[n-1].
Iz (11) i (12) slijedi:
(13)
P_{1}=P_{\triangle}+\sum_{i=1}^{n-1}\tilde{P}_{i}=\frac{2\sum_{i=1}^{n-1}y_{i}+y_{n}}{2n}=\frac{2\sum_{i=1}^{n-1}y_{i}+1}{2n},
pa uvrštavanjem u (10), koristeći (2) i (3), dobivamo
\begin{alignedat}{1}G & =1-2P_{1}=1-\frac{2\sum_{i=1}^{n-1}y_{i}+1}{n}=1-\frac{2\sum_{i=1}^{n-1}\frac{S_{i}}{S_{n}}+1}{n}=\\ & =1-\frac{2\sum_{i=1}^{n-1}S_{i}+S_{n}}{nS_{n}}=1-\frac{2\sum_{i=1}^{n}S_{i}-S_{n}}{nS_{n}}=\\ & =1-\frac{2\sum_{i=1}^{n}\sum_{k=1}^{i}x_{k}}{nS_{n}}+\frac{1}{n}=1+\frac{1}{n}-\frac{2\sum_{i=1}^{n}(n-i+1)\cdot x_{i}}{nS_{n}}=\\ & =\frac{n+1}{n}-\frac{2(n+1)\sum_{i=1}^{n}x_{i}-2\sum_{i=1}^{n}i\cdot x_{i}}{nS_{n}}=\\ & =\frac{n+1}{n}-\frac{2(n+1)\cdot S_{n}-2\sum_{i=1}^{n}i\cdot x_{i}}{nS_{n}}=\\ & =\frac{2\sum_{i=1}^{n}i\cdot x_{i}}{n\sum_{i=1}^{n}x_{i}}+\frac{n+1}{n}-\frac{2(n+1)}{n}=\frac{2\sum_{i=1}^{n}i\cdot x_{i}}{n\sum_{i=1}^{n}x_{i}}-\frac{n+1}{n}. \end{alignedat}
Dobiveni rezultat iskažimo sljedećom propozicijom.
Propozicija 4. Za numerički niz \left(x_{i}\right)_{i\in[n]} Ginijev koeficijent koncentracije G jednak je
(14)
G=\frac{2\sum_{i=1}^{n}i\cdot x_{i}}{n\sum_{i=1}^{n}x_{i}}-\frac{n+1}{n}.
Navedimo neka svojstva Ginijeva koeficijenta.
Propozicija 5. Za Ginijev koeficijent koncentracije G vrijedi sljedeće:
-
a)
-
G\in[0,1].
-
b)
-
G=0 ako i samo ako je x_{1}=x_{2}=\dots=x_{n}.
-
c)
-
G=1-\frac{1}{n} ako i samo ako je x_{1}=x_{2}=\dots=x_{n-1}=0 i x_{n}\gt 0.
Dokaz. Iz Definicije 1 imamo 0\leq G=1-2P_{1}. Zbog P_{1}\geq0 je G\leq1, odakle slijedi a).
Dokažimo b). Pretpostavimo li da je x_{1}=x_{2}=\dots=x_{n}, iz (14) slijedi G=0. Obrat slijedi iz dokaza Propozicije 1 jer se jednakost u (5) postiže za x_{1}=x_{2}=\dots=x_{n}.
Slično pokazujemo da vrijedi i c). Pretpostavimo li da je x_{1}=x_{2}=\dots=x_{n-1}=0 i x_{n}\gt 0, iz (14) slijedi G=1-\frac{1}{n}. Obrnuto, pretpostavimo da je G=1-\frac{1}{n}. Iz Definicije 1 slijedi
1-2P_{1}=1-\frac{1}{n}
tj.
P_{1}=\frac{1}{2n}.
Iz (13) slijedi
\sum_{i=1}^{n-1}y_{i}=0
pa iz (2), (3) i svojstva (S2) slijedi tvrdnja.
\ \blacksquare
Napomena 6. Budući da za svaki n\in N vrijedi stroga nejednakost
1-\frac{1}{n}\lt 1,
tvrdnju Propozicije 3.a) možemo ,,pooštriti“ na G\in\left[0,1\right\rangle.}
Napomena 7. U slučaju iz Propozicije 3.b) govorimo o savršeno ravnomjernoj koncentraciji. To znači da na svaki pojedini modalitet otpada jednak dio ukupnoga zbroja svih članova niza.
Napomena 8. Radi prirodnoga proširenja na slučaj beskonačnih numeričkih nizova, u slučaju iz Propozicije 3.c) (i samo u tom slučaju!) dogovorno se definira G:=1 i govori o savršeno neravnomjernoj koncentraciji. To znači da ukupan zbroj svih članova niza otpada na točno jedan modalitet.
4.Izračun Ginijeva koeficijenta u slučaju podataka grupiranih u razrede
U gospodarskoj praksi česti su slučajevi kad se numerički podaci, zbog svoje brojnosti i radi preglednosti, grupiraju u prave razrede. Podsjetimo, pravi razredi su (konačni) nizovi intervala \left[x_{0},x_{1}\right\rangle, \left[x_{1},x_{2}\right\rangle, \dots, \left[x_{n-2},x_{n-1}\right\rangle, \left[x_{n{–}1},x_{n}\right], pri čemu je obično x_{0} najmanja vrijednost numeričkog niza podataka, a x_{n} najveća vrijednost tog niza. Razredna sredina i–toga pravog razreda je broj
(\overline{x})_{i}=\frac{x_{i-1}+x_{i}}{2},\ \text{za svaki}\ i\in[n].
Pretpostavimo da je, za svaki i\in[n], i–tom pravom razredu pridružena apsolutna frekvencija f_{i}, što znači da ukupno f_{i} članova numeričkog niza podataka pripada dotičnom razredu. Umjesto apsolutne frekvencije, mogu se razmatrati i relativne frekvencije r_{i} koje označavaju udio broja dotičnog razreda u ukupnom broju svih članova niza.
Uz upravo uvedene oznake, definicijske relacije (1), (2) i (3) prelaze u:
(15)
p_{i}:=\frac{f_{i}}{\sum_{k=1}^{n}f_{k}},
(16)
S_{i}:=\sum_{k=1}^{i}f_{k}\cdot(\overline{x})_{k},
(17)
y_{i}:=\frac{S_{i}}{S_{n}}.
Lorenzova krivulja L ponovno se dobiva iz točaka T_{0}=(0,0) i T_{i}=\left(p_{i},y_{i}\right) za i\in[n]. Definiramo li dogovorno y_{0}:=0, onda iz razmatranja analognoga dokazu Propozicije 2 lako dobivamo:
G=1-\sum_{i=1}^{n}p_{i}\cdot\left(y_{i-1}+y_{i}\right).
5.Normirani Ginijev koeficijent koncentracije
U Napomeni 1 ustvrdili smo da je najveća moguća vrijednost Ginijeva koeficijenta jednaka G_{max}=1-\frac{1}{n}. Stoga se u praksi za „male“ vrijednosti n (obično za n\leq20) dodatno računa omjer vrijednosti G i G_{max}. Taj se omjer naziva normirani Ginijev koeficijent koncentracije. Formalna definicija je:
Definicija 9. Normirani Ginijev koeficijent koncentracije G^{*} za numerički niz \left(x_{i}\right)_{i\in[n]} definiran je s:
(18)
G^{*}=\frac{G}{G_{max}}=\frac{n}{n-1}\cdot G.
Iz (14) i (18) izravno slijedi
G^{*}=\frac{2\sum_{i=1}^{n}i\cdot x_{i}}{(n-1)\sum_{i=1}^{n}x_{i}}-\frac{n+1}{n-1}.
Lako se vidi da za normirani Ginijev koeficijent G^{*} vrijedi sljedeća varijanta Propozicije 3.
Propozicija 10. Za normirani Ginijev koeficijent koncentracije G^{*} vrijedi:
-
a)
-
G^{*}\in[0,1].
-
b)
-
G^{*}=0 ako i samo ako je x_{1}=x_{2}=\dots=x_{n}.
-
c)
-
G^{*}=1 ako i samo ako je x_{1}=x_{2}=\dots=x_{n-1}=0 i x_{n}\gt 0.
Napomena 11. Nejednakost x_{n}\gt 0 u Propozicijama 3.c) i 4.c) slijedi iz uvjeta x_{1}=x_{2}=\dots=x_{n-1}=0 i svojstva (S2), pa je zapravo nismo trebali posebno navoditi. To smo ipak učinili kako bismo opetovano naglasili da niz \left(x_{n}\right)_{n\in[n]} nužno sadrži najmanje jednu strogo pozitivnu vrijednost.
6.Kontinuirana varijanta formule
(10)
Pretpostavimo da se numerički podaci odnose na neko kvantitativno kontinuirano statističko obilježje (npr. visina, masa itd.) i da tvore segment [a,b]. U tom ih slučaju ne možemo poredati u (beskonačan) niz, što znači da pripadnu Lorenzovu krivulju možemo shvatiti kao graf neke realne funkcije f(x) na segmentu [0,1]. Tada definicijska relacija (10) prelazi u:
(19)
G:=1-2\int_{0}^{1}f(x)\,\text{d}x.
Formulu (19), dakako, ima smisla primijeniti znamo li propis funkcije f. Funkcija f ne može biti bilo kakva realna funkcija, nego mora imati sljedeća svojstva:
|
\bullet |
f(0)=0, |
|
\bullet |
f(1)=1, |
|
\bullet |
0\leq f(x)\leq x za svaki x\in[0,1], |
|
\bullet |
f je monotono rastuća i Riemann/Lebesgue integrabilna na segmentu [0,1]. |
Varijanta Propozicije 3 za ovaj slučaj glasi:
Propozicija 12. Za Ginijev koeficijent koncentracije G vrijedi sljedeće:
-
a)
-
G\in[0,1],
-
b)
-
G=0 ako i samo ako je f(x)=x, osim za konačno mnogo x\in[0,1] za koje je 0\lt f(x)\leq x,
-
c)
-
G=1 ako i samo ako je f(x)=0, osim za konačno mnogo x\in[0,1] za koje je 0\lt f(x)\leq x.
Napomena 13. U prvi mah moglo bi se zaključiti da je varijanta Propozicije 3.c) ekvivalencija jednakosti G=1 i jednakosti
f(x)=\begin{cases} 0, & \text{za}\ x\neq1,\\ 1, & \text{za}\ x=1. \end{cases}
No, to je pogrešno. Naime, iz matematičke je analize poznato da je integral nenegativne Riemann/Lebesgue-integrabilne realne funkcije f jednak nuli ako i samo ako je f(x)=0, osim možda za konačno mnogo vrijednosti varijable x. U ovom slučaju postoji jedna takva vrijednost (to je x=1), pa zato u iskazu Propozicije 5.c) treba navesti „osim za konačno mnogo (...)“. Integral u formuli (19) je „obični“ jednostruki Riemannov integral, pa prebrojivost skupa točaka u kojima je f(x)\neq0 povlači da f nije integrabilna u Riemannovom smislu i tada ne možemo primijeniti citiranu formulu.
7.Primjeri
U posljednjem dijelu pokazat ćemo izračun Ginijevog koeficijenta, kao i izradu Lorenzove krivulje na nekoliko jednostavnih primjera. Potrebni podaci dobiveni su korištenjem službeno objavljenih podataka Državnog zavoda za statistiku Republike Hrvatske. Kako je već spomenuto, Ginijev koeficijent je mjera nejednakosti statističkog niza. U svakidašnjem životu vjerojatno je najzanimljivija primjena izračuna Ginijevog koeficijenta te analiza nejednakosti pri raspodjeli dohotka čime ćemo se pozabaviti u prva dva primjera. U Tablici 2 i Tablici 5 dani su podaci prikupljeni Anketom o potrošnji kućanstva iz 2010. godine. Njome se prikupljaju podatci o ukupnom dohotku i različitim oblicima potrošnje kućanstava i ona je glavni izvor podataka za izračune nejednakosti i siromaštva u RH.
Primjer 14. Prvo ćemo se koncentrirati na komponente dohotka: raspoloživi dohodak obuhvaća dohodak od nesamostalnog rada, samostalne djelatnosti, mirovine te transfera i ostalih primitaka. Podaci su navedeni u Tablici 2.
|
|
Dohodak, kune |
|
Dohodak od nesamostalnog rada |
47 346 |
|
Dohodak od samostalne djelatnosti |
12 981 |
|
Dohodak od imovine (nije uključena imputirana najamnina) |
762 |
|
Mirovine |
12 284 |
|
Transferi i ostali primici |
10 474 |
|
Ukupno |
86 847 |
Tablica 2: Raspoloživi dohodak prema izvorima stjecanja, prosjek po kućanstvu u 2009. (Primjer 2.)
Počnimo s konstrukcijom Lorenzove krivulje: statistički niz je očito sastavljen od nenegativnih vrijednosti takvih da je najmanje jedna od njih strogo veća od nule (tj. zadovoljeni su uvjeti (S1) i (S2)). Međutim, trebamo ga još uzlazno urediti (uvjet (S3)), tj. poredati elemente niza od najmanjeg prema najvećem:
(x_{1},x_{2},x_{3},x_{4},x_{5})=(762,10474,12981,15284,47346).
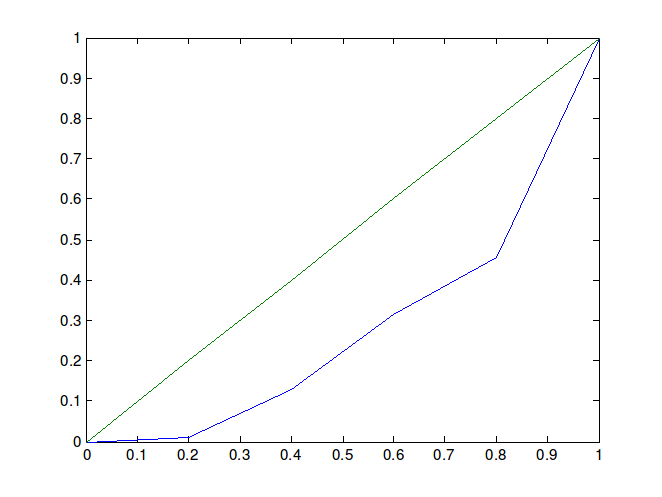
Lorenzovu krivulju dobivamo spajanjem točaka (0,0), \left(p_{1},y_{1}\right), \left(p_{2},y_{2}\right), \dots, \left(p_{5},y_{5}\right)=(1,1). Izračunate vrijednosti p_{i} i y_{i} za i\in[5] nalaze se u Tablici 3, dok je Lorenzova krivulja prikazana na Slici 2.
|
|
dohodak, kn |
kumulativ podtotala |
p_{i} |
y_{i} |
|
Dohodak od nesamostalnog rada |
762 |
762 |
0.2 |
0.0088 |
|
Dohodak od samostalne djelatnosti |
10 474 |
11 236 |
0.4 |
0.1294 |
|
Dohodak od imovine |
12 981 |
24 217 |
0.6 |
0.3134 |
|
Mirovine |
15 284 |
39 501 |
0.8 |
0.4548 |
|
Transferi i ostali primici |
47 346 |
86 847 |
1 |
1 |
|
Ukupno |
86 847 |
- |
- |
- |
Tablica 3: pomoćna tablica za Lorenzovu krivulju (Primjer 2.)
Ginijev koeficijent računamo prema formuli (14), koristeći već izračunate vrijednosti navedene u Tablici 4.
|
|
dohodak, kn |
k |
k\cdot x_{k} |
|
Dohodak od nesamostalnog rada |
762 |
1 |
762 |
|
Dohodak od samostalne djelatnosti |
10 474 |
2 |
20 948 |
|
Dohodak od imovine |
12 981 |
3 |
38 943 |
|
Mirovine |
15 284 |
4 |
236 780 |
|
Transferi i ostali primici |
47 346 |
5 |
358 569 |
|
Ukupno |
86 847 |
- |
- |
Tablica 4: pomoćna tablica za Ginijev koeficijent (Primjer 2.)
Dobivamo:
G=\frac{2\cdot358519}{5\cdot86847}-\frac{6}{5}=0.45.
Sada računamo i normiran Ginijev koeficijent
G^{*}=\frac{n}{n-1}\cdot G=0.45\cdot\frac{5}{4}=0.56.
Iz Lorenzove krivulje i dobivenih vrijednosti Ginijevog koeficijenta, možemo zaključiti da su komponente dohotka neravnomjerno raspoređene. Naime, već Lorenzova krivulja pokazuje da npr. dohodak od imovine čini samo 0.88% ukupnoga raspoloživog dohotka, dok na dohodak od nesamostalnog rada otpada više od 50% ukupnog dohotka. Nadalje, otprije znamo da, što je vrijednost Ginijevog koeficijenta bliža nuli, vrijednosti niza su ravnomjernije raspoređene. Analogno, približavanje jedinici znači i porast nejednakosti među elementima niza, tj. koncentraciju na samo jedan modalitet, što bi u ovom slučaju bio dohodak od nesamostalnog rada.
Primjer 15. U ovome primjeru analizirat ćemo raspodjelu dohotka prema dohodovnim decilima u 2009. godini. Decili se oblikuju podjelom osnovnog skupa na deset jednakih dijelova izračunavanjem prosječnog neto-dohotka po kućanstvu, razvrstavanjem kućanstva prema dohotku od najnižega prema najvišemu te svrstavanjem svakoga pojedinog kućanstva u pripadajući decil. U prvom decilu su kućanstva s najnižim godišnjim neto-dohotkom. U drugom decilu su kućanstva čiji je godišnji neto-dohodak veći od kućanstava iz prvog decila, a manji od kućanstava iz trećeg decila itd. Kućanstva iz 10. decila imaju najviši godišnji neto-dohodak. Podaci su prikazani u Tablici 5.
|
decili |
Izdaci za potrošnju - ukupno, kune |
|
1 |
24 393 |
|
2 |
33 717 |
|
3 |
43 292 |
|
4 |
53 722 |
|
5 |
67 530 |
|
6 |
79 902 |
|
7 |
85 326 |
|
8 |
106 789 |
|
9 |
115 107 |
|
10 |
144 202 |
|
|
Ukupno: 753 980 |
Tablica 5: struktura izdataka za potrošnju prema dohodovnim decilima u 2009. (Primjer 3.)
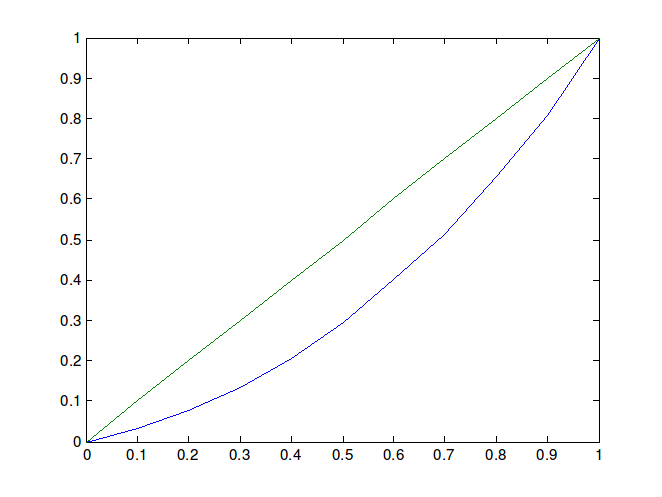
Do rezultata dolazimo na isti način kao u prethodnom primjeru. Najprije pogledajmo Lorenzovu krivulju, prikazanu na Slici 3.
Vidimo da su vrijednosti uglavnom ravnomjerno raspoređene, odnosno niti jedan se modalitet ne ističe, već na svaki od njih otpada približno jednak udio u totalu pa očekujemo da će to potvrditi i sam Ginijev koeficijent. Izračunavanjem Ginijeva koeficijenta dobivamo da je njegova vrijednost jednaka 0.27 (G^{*}=0.31), što potvrđuje zaključak o ravnomjernoj raspodjeli.
Primjer 16. U posljednjem primjeru pogledajmo Tablicu 6 koja sadrži podatke o izvozu/uvozu RH u 2009. godini. (Podatci su preuzeti iz Statističkog ljetopisa 2010.)
|
|
Izvoz, tisuće kuna |
Uvoz, tisuće kuna |
|
Europa |
47 333 172 |
89 601 154 |
|
Azija |
4 070 337 |
16 181 219 |
|
Afrika |
1 951 041 |
661 073 |
|
Sjeverna, Srednja i Južna Amerika |
1 782 383 |
5 244 855 |
|
Australija i Oceanija |
135 266 |
62 797 |
|
Ukupno |
55 242 198 |
111 751 089 |
Tablica 6: Izvoz i uvoz po zemljama namjene/podrijetla (Primjer 4.)
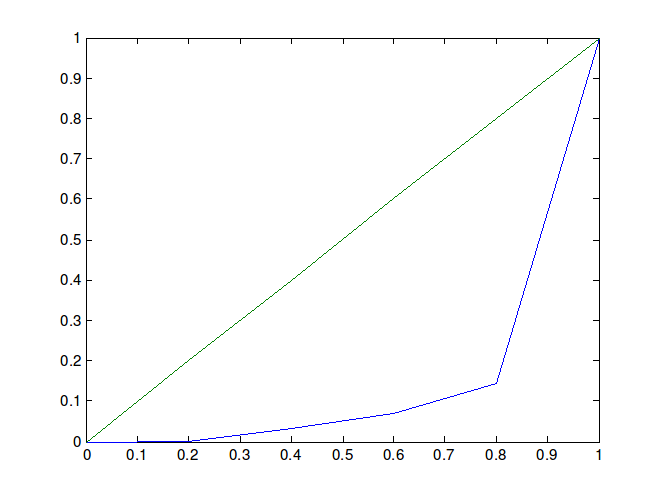
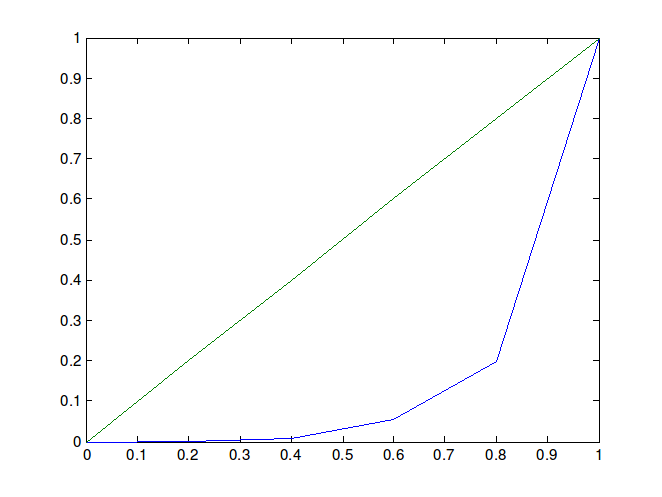
Lorenzova krivulja za izvoz prikazana je na Slici 4.
Primjećujemo da jedan modalitet nosi većinu totala. Vrijednost Ginijevog koeficijenta je 0.70 (G^{*}=0.88), što potvrđuje visok stupanj neravnomjernosti u raspodjeli vrijednosti niza. Konkretno, možemo zaključiti da modalitet „Europa" odnosi većinu totala, odnosno najveći dio ukupnog izvoza odlazi u Europu.
Pogledajmo sada Lorenzovu krivulju za uvoz (Slika 5).
Već je iz slike razvidno da je situacija s uvozom veoma slična. Ginijev koeficijent iznosi 0.71 (G^{*}=0.89), te opet možemo zaključiti da je raspodjela neravnomjerna i da najveći dio uvoza dolazi iz europskih zemalja.
Bibliografija
|
[1] |
I. Šošić, Primijenjena statistika, Školska knjiga, Zagreb, 2004. |
|
[2] |
http://en.wikipedia.org/wiki/Gini_coefficient (15. 9. 2012.) |
|
[3] |
http://en.wikipedia.org/wiki/Lorenz_curve (15. 9. 2012.) |
|
[4] |
S. Kurepa, Matematička analiza 2, Školska knjiga, Zagreb, 1987. |
|
[5] |
Statistički ljetopis Republike Hrvatske za 2009. godinu, Državni zavod za statistiku RH, Zagreb, 2010. |
|
[6] |
Rezultati ankete o potrošnji kućanstava u 2009., statistička izvješća, Državni zavod za statistiku RH, Zagreb, 2011. |