P	U	S	Č	P	S	N
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

geometrija

Inverzija

geometrija

Harun Šiljak

Sadržaj

1 Uvod

Slika 1: Inverzija je bijekcija i involucija.

Slika 2: Ako je

$O$ centar inverzije, pravac

$p$ koji ne prolazi točkom

$O$ preslikava se u kružnicu koja prolazi točkom

$O$ .

2 Primjeri

3 Zadaci za samostalan rad

Sažetak

Ovaj rad nastao je u želji da se mladim natjecateljima srednjoškolcima teorijski i praktično predstavi inverzija u planimetriji. Na samom početku dan je nešto opširniji teorijski uvod u kojem su pored dobro poznatih svojstava inverzije dani i dokazi tih svojstava. U nastavku je na nizu primjera ilustrirana njezina praktična primjena.

1Uvod

Većina transformacija koje se primjenjuju u rješavanju planimetrijskih problema su izometrije. Nešto rjeđe primjenjuju se i homotetivne transformacije – no u svakom od tih preslikvanja pravac se preslikava u pravac, a kružnica u kružnicu (ili u elipsu, u općem slučaju afinih transformacija). No, kod inverzije nije takav slučaj. Inverzija, naime, preslikava pravce i kružnice u pravce i kružnice, ali pri tome može pravac transformirati u kružnicu i obrnuto. Ovo je jedan od razloga zašto inverzija ponekad daje neočekivane i zanimljive rezultate u svojoj primjeni.

Dajmo sada formalnu definiciju inverzije, a zatim protumačimo njezino praktično značenje.

Definicija 1. Neka je

$O$ točka u ravnini

$E$ , a

$r$ pozitivan realan broj. Inverzijom ravnine

$E$ u odnosu na kružnicu

$k(O,r)$ nazivamo preslikavanje koje svaku točku te ravnine

$P$ različitu od

$O$ preslikava u točku

$P'$ na polupravcu

$OP$ tako da vrijedi

$OP\cdot OP'=r^{2}$ . Točka

$O$ se pritom preslikava u točku u beskonačnosti.1

Napomenimo da stariji autori izostavljaju posljednju rečenicu ove definicije, navodeći da se točka

$O$ inverzijom uopće ne preslikava (te, samim tim, osporavaju stajalište da je inverzija geometrijska transformacija u strogom smislu, vidjeti npr. [10]).

Kako su čitatelji upoznati s osnom refleksijom (zrcaljenjem ravnine u odnosu na zadani pravac), pokušat ćemo inverziju objasniti kroz ovo elementarno preslikavanje. Točnije, inverziju možemo smatrati generalizacijom osne refleksije: riječ je, naime, o refleksiji na kružnici. Pravac možemo promatrati kao luk kružnice beskonačnog polumjera, pa ova generalizacija ima smisla.2 Zainteresirani čitatelj može relativno lako pokazati kako se praktično provodi ova generalizacija.

Iz definicije 1 direktno slijedi

Posljedica 2. Inverzija ravnine u odnosu na kružnicu

$k(O,r)$ točke na kružnici

$k$ preslikava u njih same, točke u unutrašnjosti kruga koji omeđuje ta kružnica u njegovu vanjštinu i obrnuto.

Nije se teško uvjeriti da vrijedi i

Posljedica 3. Inverzija je bijekcija i involucija.3

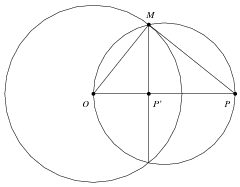
Pokažimo kako konstruirati točku

$P'$ iz definicije 1, tj. kako naći inverz točke u odnosu na kružnicu. Ovim postupkom uvjeriti ćemo se i u istinitost posljedica 2 i 3.

(1)	Neka točka $P$ leži na kružnici $k(O,r)$ . Spojimo li ovu točku sa središtem inverzije $O$ , očito je da na polupravcu $OP$ postoji točno jedna točka $P'$ koja ispunjava jednakost $OP\cdot OP'=r^{2}$ , i to sama točka $P$ . Dakle, $P'= P$ .
(2)	Neka točka $P$ leži izvan kružnice $k(O,r)$ . Povucimo kroz točku $P$ tangentu na kružnicu $k$ (slika 1) i označimo dodirnu točku tangente i kružnice s $M$ . Neka je $MP'$ visina trokuta $OMP$ . Iz sličnosti pravokutnih trokuta $OMP$ i $OP'M$ slijedi $P'O:OM=OM:OP$ , pa je $OP\cdot OP'=r^{2}$ , te je $P'$ slika točke $P$ pri ovoj inverziji.
(3)	Neka točka $P$ leži unutar kružnice $k(O,r)$ . Primijenimo obrnut postupak onom u slučaju (2). Spojimo, dakle, točke $O$ i $P$ i povucimo okomicu na pravac $OP$ kroz točku $P$ . Jedan od presjeka tog pravca s kružnicom $k$ označimo s $M$ , kroz točku $M$ povucimo tangentu na $k$ i presjek te tangente i pravca $OP$ označimo s $P'$ (očito, riječ je o istoj slici kao u slučaju (2), sa zamijenjenim mjestima točaka $P$ i $P'$ ). Iz identičnog razloga sličnosti kao pod (2) slijedi da je $P'$ slika točke $P$ pri ovoj inverziji.

Slika 1: Inverzija je bijekcija i involucija.

Ovim smo direktno dokazali posljedicu 2. Posljedica 3 za točke na kružnici direktno slijedi iz (1), a za ostale slijedi iz činjenica da su točke

$P'$ u (2) i (3) jednoznačno određene (zbog simetrije, svejedno je koju ćemo od dviju mogućih tangenti povući u (2), ili koji ćemo presjek pravca i kružnice odabrati u (3)). Očita je involutivna veza između slučajeva (2) i (3), gdje točka

$P$ iz (2) odogovara točki

$P'$ iz (3) i obrnuto.

Sad ćemo dokazati nekoliko osnovnih svojstava inverzije, koja je čine moćnim sredstvom u modernoj planimetriji.

Teorem 4. Ako je

$O$ centar inverzije, a točke

$A$ i

$B$ tom su inverzijom preslikane u

$A'$ i

$B'$ , tada su trokuti

$OAB$ i

$OB'A'$ slični.

Dokaz. Iz definicije 1 slijedi:

$OA\cdot OA'=OB\cdot OB'$ , pa je

$OA:OB=OB':OA$ , a budući da je

$\angle AOB=\angle B'OA'$ , trokuti

$OAB$ i

$OB'A'$ su slični.

$\ \blacksquare$

Teorem 5. Ako je

$O$ centar inverzije, pravac

$p$ koji prolazi točkom

$O$ preslikava se u samog sebe.4

Dokaz. Prema definiciji 1, svaka točka pravca

$p$ (osim

$O$ ) se preslikava u točku na istom tom pravcu. Budući da je riječ o bijekciji, pravac

$p$ preslikava se u samog sebe.

$\ \blacksquare$

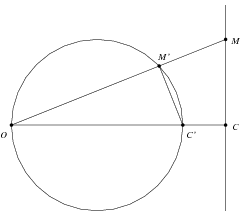
Teorem 6. Ako je

$O$ centar inverzije, pravac

$p$ koji ne prolazi točkom

$O$ preslikava se u kružnicu koja prolazi točkom

$O$ .

Dokaz. Spustimo normalu

$OC$ na pravac

$p$ iz centra inverzije

$O$ (slika 2) te odaberimo proizvoljnu točku

$M$ na

$p$ . Budući da su trokuti

$OCM$ i

$OM'C'$ slični (teorem 4), kut

$\angle OM'C'$ je pravi, pa po Talesovu teoremu točka

$M'$ leži na kružnici

$k$ promjera

$OC'$ . Ako je

$X$ točka kružnice

$k$ različita od

$O$ , tada je ona slika pri inverziji točke

$Y$ koja se nalazi u presjeku polupravca

$OX$ i

$p$ . Dakle, inverzija preslikava pravac

$p$ u kružnicu

$k$ (preciznije,

$k\setminus \lbrace O\rbrace$ ).

$\ \blacksquare$

Slika 2: Ako je

$O$ centar inverzije, pravac

$p$ koji ne prolazi točkom

$O$ preslikava se u kružnicu koja prolazi točkom

$O$ .

Teorem 7. Ako je

$O$ centar inverzije, kružnica koja prolazi točkom

$O$ preslikava se u pravac, a kružnica koja ne prolazi točkom

$O$ u kružnicu.5

Dokaz. Slučaj kružnice koja prolazi točkom

$O$ direktno slijedi iz teorema 6 i svojstva involutivnosti inverzije.

Neka sada

$O$ ne pripada kružnici

$k$ i neka su

$A$ i

$B$ točke presjeka kružnice

$k$ i pravca koji prolazi točkama

$O$ i

$S$ (gdje je

$S$ središte kružnice

$k$ ), a

$M$ proizvoljna točka na

$k$ . Pokažimo da je kružnica

$k'$ promjera

$A'B'$ slika pri inverziji kružnice

$k$ . Za to će, po Talesovu teoremu, biti dovoljno pokazati da je kut

$\angle A'M'B'$ pravi. U daljnjem razmatranju koristit ćemo se orijentiranim kutovima, da ne bismo morali analizirati više slučajeva u ovisnosti o položaju točke

$M$ . Iz teorema 4 imamo sličnost trokuta

$OAM$ i

$OM'A'$ te

$OBM$ i

$OM'B'$ , pa je

$\angle OMA=\angle OA'M'$ i

$\angle OMB=\angle OB'M'$ , tj.

$\angle (OM,MA)=-\angle (OA',M'A')$ i

$\angle (OM,MB)=-\angle (OB',M'B')$ . Zato je

$\angle (A'M',M'B')=\angle (A'M',OA')+\angle (OB',M'B') = \angle (OM,MA)+ \angle (MB,OM)=\angle (MB,MA)=90^{\circ}$ .

$\ \blacksquare$

Teorem 8. Slike pri inverziji kružnice i njezine tangente (ili dviju kružnica koje se dodiruju) dodiruju se ako i samo ako se točka dodira originala ne poklapa s centrom inverzije. U suprotnom, preslikavaju se u paralelne pravce.

Dokaz. Dovoljno je provesti dokaz u jednom smjeru, drugi slijedi iz bijektivnosti i involutivnosti inverzije. Ako se točka dodira ne poklapa sa centrom inverzije, očito će i nakon inverzije postojati zajednička točka među krivuljama, tj. i slike će se dodirivati. S druge strane, ako se dvije kružnice dodiruju u točki

$O$ , tada se preslikavaju u dva pravca okomita na pravac koji povezuje njihova središta. Ako je riječ o pravcu i kružnici koji se dodiruju u točki

$O$ , tada se pravac preslikava u samog sebe, a kružnica u pravac okomit na pravac koji povezuje točku

$O$ i središte kružnice. Očito je da je u oba slučaja riječ o preslikavanju u dva paralelna pravca.

$\ \blacksquare$

Teorem 9. Ako je

$O$ centar inverzije, a točke

$A$ i

$B$ tom su inverzijom preslikane u

$A'$ i

$B'$ , tada vrijedi

$A'B'= \frac{AB\cdot r^{2}}{OA\cdot OB}.$

Dokaz. Iz teorema 4 imamo

$OA:AB=OB':A'B'$ , dok iz definicije 1 imamo

$OB\cdot OB'= r^{2}$ . Iz ove dvije relacije direktno slijedi

$A'B'= AB\cdot r^{2} / (OA\cdot OB)$ .

$\ \blacksquare$

Teorem 10. Inverzija je konformalno preslikavanje, tj. čuva kutove među krivuljama.6

Dokaz. Dokaz ćemo provesti na primjeru dviju kružnica (što ne vodi smanjenju općenitosti, jer je slučaj pravca i kružnice zapravo specijalan slučaj dviju kružnica). Povucimo tangente

$t_{1}$ i

$t_{2}$ kroz točku presjeka kružnica. Prema teoremu 8, kut između slika kružnica jednak je kutu između slika tangenti. Inverzijom s centrom u

$O$ , pravac

$t_{i}$ preslikava se u samog sebe ili u kružnicu čija je tangenta u točki

$O$ paralelna pravcu

$t_{i}$ . Zato je kut između slika pravaca

$t_{1}$ i

$t_{2}$ jednak kutu između originala. Time je tvrdnja dokazana.

$\ \blacksquare$

Navedeni teoremi dovoljni su za uspješno korištenje inverzije u elementarnoj planimetriji (kao što ćemo i vidjeti na primjerima). No, sa znanstvene strane potrebno je na ovom mjestu dati još nekoliko napomena koje inverziju povezuju s modernim tokovima u geometriji.

S analitičke strane, inverziju krivulje možemo promatrati kroz transformaciju koordinata na temelju sljedećih teorema, koje navodimo bez dokaza samo zato što spomenuti teoremi nisu nužni za korištenje inverzije u standardnoj školskoj i natjecateljskoj planimetriji. No, čitatelj s osnovnim poznavanjem analitičke geometrije lako se može uvjeriti da ovi teoremi jednostavno slijede iz definicije 1.

Teorem 11. Ako je polarna jednadžba krivulje

$K$ dana s

$r=r(\theta)$ , tada je polarna jednadžba njoj inverzne krivulje dana jednadžbom

$r=k^{2}/r(\theta)$ , gdje je

$k$ polumjer inverzije.

Teorem 12. Ako je

$O(x_{0},y_{0})$ centar, a

$k$ polumjer inverzije, tada je krivulja inverzna krivulji

$C(f(t),g(t))$ u Kartezijevim pravokutnim koordinatama dana s7

$x=x_{0} + \frac{k^{2} (f-x_{0})}{(f-x_{0})^{2}+(g-y_{0})^{2}}$

$y=y_{0} + \frac{k^{2} (g-y_{0})}{(f-x_{0})^{2}+(g-y_{0})^{2}}.$

Koristeći se ovim teoremima, nije teško pokazati i analitički rezultate koje smo dobili kroz teoreme 4 – 9, kao i nove rezultate, npr. možemo doći do spoznaja u što se inverzijom preslikavaju druge poznate krivulje (konike, spirale

$\ldots$ ). Tako se npr. hiperbola preslikava u lemniskatu (ako se inverzija radi u odnosu na njezino središte), ili parabola u kardioidu (ako se inverzija radi u odnosu na njezin fokus). Više o tome možete naći u [12]. Na kraju, spomenimo i mogućnost generalizacije inverzije na višedimenzionalne prostore, od kojih je za elementarnu geometriju bitna samo sferna (trodimenzionalna) inverzija, o čemu više možete naći u [1].

2Primjeri

Brojni su primjeri korištenja inverzije u planimetrijskim problemima. Kroz većinu primjera provlači se jedna važna činjenica: inverziju primjenjujemo u slučajevima kad se jedna točka na slici zadatka nameće kao centar problema: kroz nju prolazi više kružnica, određuje više važnih kutova i slično.

Ovdje ćemo se ograničiti na primjere iz „natjecateljske prakse”. Naime, iako je jako ilustrativna primjena inverzije na tzv. pramene kružnica i sustave koje čine same kružnice (vidi npr. nešto više o Steinerovoj porizmi, ili o Apolonijevim krugovima u [7] ili [2]), takvi primjeri nisu najpogodniji za upoznavanje mladog natjecatelja s magijom inverzije (kao ni, npr., jako zanimljivi načini primjene inverzije u izvođenju geometrijskih konstrukcija samo s pomoću šestara, vidi [6] ili [10]).

Primjer 13. ([8], Ptolomejev teorem) Za konciklične točke

$A$ ,

$B$ ,

$C$ ,

$D$ vrijedi:

$AB\cdot CD+AD\cdot BC=AC\cdot BD$ .

Rješenje. Promatrajmo inverziju s centrom u

$D$ i proizvoljnim polumjerom

$r$ . Opisana kružnica trokuta

$ABC$ preslikava se u pravac koji prolazi točkama

$A'$ ,

$B'$ i

$C'$ (teorem 7). Budući da je

$A'B'+B'C'=A'C'$ , prema teoremu 9 imamo:

$\frac{AB\cdot r^{2}}{AD\cdot BD}+\frac{BC\cdot r^{2}}{BD\cdot CD} = \frac{AC\cdot r^{2}}{AD\cdot CD}.$ Množenjem posljednje jednakosti s

$(AD\cdot BD\cdot CD)/r^{2}$ dobivamo traženu jednakost. Provedemo li postupak unatrag, nije teško dobiti i obrat ovog teorema.

Primjer 14. ([3]) Dane su kružnice

$k_{1}$ ,

$k_{2}$ ,

$k_{3}$ i

$k_{4}$ takve da svaka od kružnica

$k_{2}$ ,

$k_{4}$ dodiruje kružnice

$k_{1}$ i

$k_{3}$ , pri čemu točke dodira nisu kolinearne. Dokazati da su točke dodira konciklične.

Rješenje. Označimo točke dodira kružnica

$k_{1}$ i

$k_{2}$ ,

$k_{2}$ i

$k_{3}$ ,

$k_{3}$ i

$k_{4}$ te

$k_{4}$ i

$k_{1}$ redom s

$A$ ,

$B$ ,

$C$ i

$D$ . Inverzija s centrom u

$A$ proizvoljnog polumjera preslikava

$k_{1}$ i

$k_{2}$ u paralelne pravce

$k_{1}'$ i

$k_{2}'$ , a

$k_{3}$ i

$k_{4}$ u kružnice

$k_{3}'$ i

$k_{4}'$ koje se dodiruju u točki

$C'$ , a pravce

$k_{2}'$ i

$k_{4}'$ dodiruju redom u

$B'$ i

$D'$ . Očito su

$B'$ ,

$C'$ i

$D'$ kolinearne točke, pa

$B$ ,

$C$ i

$D$ leže na kružnici koja prolazi točkom

$A$ (teorem 6).

Primjer 15. ([8], Iran 1995.) Označimo s

$M$ ,

$N$ i

$P$ točke dodira upisane kružnice trokuta

$ABC$ i stranica

$AB$ ,

$BC$ i

$CA$ , redom. Dokazati da su središte upisane i opisane kružnice trokuta

$ABC$ te ortocentar trokuta

$MNP$ kolinearni.

Rješenje. Središte upisane kružnice trokuta

$ABC$ i ortocentar trokuta

$MNP$ leže na Eulerovom pravcu8 trokuta

$MNP$ . Inverzijom u odnosu na upisanu kružnicu trokuta

$ABC$ točke

$A$ ,

$B$ i

$C$ preslikaju se u

$A'$ ,

$B'$ i

$C'$ koje su redom polovišta dužina

$PM$ ,

$MN$ i

$NP$ . Budući da je središte opisane kružnice trokuta

$A'B'C'$ ujedno i središte kružnice devet točaka9 trokuta

$MNP$ , koji se nalazi na Eulerovom pravcu trokuta

$MNP$ , središte kružnice opisane oko trokuta

$ABC$ također se nalazi na ovom pravcu.

Primjer 16. ([4], IMO 1996.) Neka je

$P$ točka u unutrašnjosti trokuta

$ABC$ takva da vrijedi

$\angle APB - \angle ACB = \angle APC - \angle ABC$ i neka su

$D$ i

$E$ središta upisanih kružnica trokuta

$APB$ i

$APC$ , redom. Pokazati da se

$AP$ ,

$BD$ i

$CE$ sijeku u jednoj točki.

Rješenje. Primijenimo li inverziju s centrom u

$A$ i proizvoljnim polumjerom

$r$ , zadani uvjet pretvara se u

$\angle B'C'P' = \angle C'B'P'$ , tj.

$B'P'=P'C'$ . Budući da je

$P'B'= PB\cdot r^{2}/(AP\cdot AB)$ (teorem 9), vrijedi

$AC/AB=PC/PB$ . Iz posljednje jednakosti slijedi da simetrale

$BD$ i

$CD$ kutova

$\angle ABP$ i

$\angle ACP$ dijele dužinu

$AP$ u istim omjerima, te su konkurentne s

$AP$ .

Primjer 17. ([3], Izrael 1995.) Neka je

$PQ$ promjer polukružnice

$s$ , a kružnica

$k$ iznutra dodiruje

$s$ i dužinu

$PQ$ u točki

$C$ . Neka su

$A$ i

$B$ redom točke na

$s$ i

$PQ$ takve da je

$AB$ tangenta na

$k$ okomita na

$PQ$ . Dokazati da je

$AC$ simetrala kuta

$\angle PAB$ .

Rješenje. Promatrajmo inverziju s centrom u

$C$ , proizvoljnog polumjera. Polukružnica

$s$ preslikava se u polukružnicu

$s'$ promjera

$P'Q'$ , kružnica

$k$ u tangentu

$k'$ polukružnice

$s'$ paralelnu s

$P'Q'$ , a

$AB$ u kružnicu

$l$ čije se središte nalazi na

$P'Q'$ i dodiruje

$k'$ (pa je polumjer kružnice

$l$ jednak polumjeru polukružnice

$s'$ ). Kružnica

$l$ tada siječe

$s'$ i

$P'Q'$ redom u točkama

$A'$ i

$B'$ . Očito je

$P'A'B'$ jednakokračan trokut, pa vrijedi

$\angle PAC = \angle A'P'C = \angle A'B'C = \angle BAC$ (teorem 10).

Primjer 18. ([11], Srbija 2008.) Dan je trokut

$ABC$ . Neka su točke

$D$ i

$E$ na pravcu

$AB$ u redoslijedu

$D$ -

$A$ -

$B$ -

$E$ takve da je

$AD = AC$ i

$BE = BC$ . Simetrale unutarnjih kutova kod tjemena

$A$ i

$B$ sijeku nasuprotne stranice redom u točkama

$P$ i

$Q$ , a kružnicu opisanu trokutu

$ABC$ redom u točkama

$M$ i

$N$ . Pravac koji spaja točku

$A$ sa središtem kružnice opisane trokutu

$BME$ i pravac koji spaja točku

$B$ sa središtem kružnice opisane trokutu

$AND$ sijeku se u točki

$X$ ,

$X \neq C$ . Dokazati da je

$CX \perp PQ$ .

Rješenje. Označimo s

$U$ središte kružnice opisane trokutu

$BME$ . Primijenimo li inverziju s centrom u

$A$ i kvadratom polumjera

$AB\cdot AC$ , točke

$B$ i

$C$ preslikavaju se u točke

$B'$ i

$C'$ simetrične točkama

$C$ i

$B$ u odnosu na

$AP$ , točke

$P$ i

$M$ preslikavaju se jedna u drugu, a

$E$ preslikava se u točku

$E'$ simetričnu

$Q$ u odnosu na

$AP$ . Prema tome, pravac

$AU$ poklapa se s pravcem koji spaja

$A$ sa središtem kružnice

$B'PE'$ .

Vidimo da je taj pravac simetričan pravcu

$AZ$ u odnosu na simetralu kuta

$A$ , gde je

$Z$ središte kružnice opisane trokutu

$CPQ$ . Analogno se dobiva da je pravac

$BZ$ simetričan pravcu koji spaja

$B$ sa središtem

$V$ kružnice

$AND$ u odnosu na simetralu kuta

$B$ . Po Cevinu teoremu u trigonometrijskom obliku, pravci simetrični pravcima

$AU$ ,

$BV$ ,

$CX$ u odnosu na simetrale kutova

$A$ ,

$B$ ,

$C$ redom se također sijeku u jednoj točki, što znači da je pravac

$CZ$ simetričan

$CX$ u odnosu na simetralu kuta

$C$ . No, kako je

$Z$ središte kružnice

$CPQ$ , pravac

$CX$ sadržava visinu trokuta

$CPQ$ , što je trebalo i dokazati.

Analizom ovih primjera čitatelj je mogao doći do zaključka da primjena inverzije često pojednostavljuje inače kompliciran problem (uglavnom je, naime, riječ o problemima koji su i nastali invertiranjem poznatijih, jednostavnih problema). No, to nije uvijek slučaj. Mnoge probleme primjena inverzije može dodatno zakomplicirati – zato oprez!

3Zadaci za samostalan rad

Zadatak 19. ([9], Dunavski kup 2007.) Neka je točka

$E$ polovište dijagonale

$BD$ tetivnog četverokuta

$ABCD$ i neka su

$k_{1}$ ,

$k_{2}$ ,

$k_{3}$ i

$k_{4}$ opisane kružnice trokuta

$AEB$ ,

$BEC$ ,

$CED$ i

$DEA$ , redom. Ako je pravac

$CD$ tangenta na kružnicu

$k_{4}$ , dokazati da su tada pravci

$BC$ ,

$AB$ i

$AD$ redom tangente na kružnice

$k_{1}$ ,

$k_{2}$ i

$k_{3}$ .

Zadatak 20. ([3]) Dokazati Feuerbachov teorem: kružnica devet točaka dodiruje upisanu i sve tri pripisane kružnice trokuta.

Zadatak 21. ([4], IMO Shortlist 2003.) Neka su

$\Gamma_{1}$ ,

$\Gamma_{2}$ ,

$\Gamma_{3}$ ,

$\Gamma_{4}$ nepodudarne kružnice takve da se

$\Gamma_{1}$ i

$\Gamma_{3}$ te

$\Gamma_{2}$ i

$\Gamma_{4}$ dodiruju izvana u točki

$P$ . Neka su

$A$ ,

$B$ ,

$C$ i

$D$ redom točke presjeka

$\Gamma_{1}$ i

$\Gamma_{2}$ ;

$\Gamma_{2}$ i

$\Gamma_{3}$ ;

$\Gamma_{3}$ i

$\Gamma_{4}$ ;

$\Gamma_{4}$ i

$\Gamma_{1}$ , pri čemu su sve te točke različite od

$P$ . Dokazati da vrijedi

$\frac{AB\cdot BC}{AD\cdot DC}=\frac{PB^{2}}{PD^{2}}.$

Zadatak 22. ([7], Rumunjska 1997.) Označimo s

$k$ upisanu kružnicu trokuta

$ABC$ i s

$D$ proizvoljnu točku na stranici

$BC$ tog trokuta. Dokazati da se kružnice koje dodiruju

$k$ ,

$AD$ i

$BD$ te

$k$ ,

$AD$ ,

$DC$ međusobno dodiruju ako i samo ako je

$\angle BAD = \angle CAD$ .

Zadatak 23. ([7], SAD 1993.) Neka je

$ABCD$ četverokut s međusobno okomitim dijagonalama koje se sijeku u

$O$ i neka su točke

$O_{1}$ ,

$O_{2}$ ,

$O_{3}$ i

$O_{4}$ osno simetrične točki

$O$ u odnosu na

$AB$ ,

$BC$ ,

$CD$ i

$DA$ , redom. Dokazati da je četverokut

$O_{1}O_{2}O_{3}O_{4}$ tetivni.

Zadatak 24. ([4], IMO Shortlist 1993.) Neka je točka

$I$ središte upisane, a

$O$ središte opisane kružnice

$k$ trokuta

$ABC$ . Kružnica

$k_{C}$ dodiruje stranice

$CA$ i

$CB$ u točkama

$D$ i

$E$ te iznutra dodiruje kružnicu

$k$ . Dokazati da je točka

$I$ polovište dužine

$DE$ .

Zadatak 25. ([4], IMO Shortlist 2002.) Upisana kružnica

$k$ oštrokutnog trokuta

$ABC$ dodiruje stranicu

$BC$ u točki

$K$ . Točka

$M$ je polovište visine spuštene iz točke

$A$ na

$BC$ , a

$N$ (druga) točka presjeka kružnice

$k$ i

$KM$ . Dokazati da se opisana kružnica trokuta

$BCN$ i kružnica

$k$ dodiruju u točki

$N$ .

Bibliografija

[1]	H. S. M. Coxeter, Introduction to Geometry, Wiley, 1969.
[2]	H. S. M. Coxeter, S.L. Greitzer, Geometry Revisited, Toronto - New York, 1967.
[3]	D. Đukić, Inversion, Olympiad Training Materials (IMO Compendium Group), 2007.
[4]	D. Đukić, V. Janković, I. Matić, N. Petrović, The IMO Compendium, Springer, 2005.
[5]	D. Hilbert, S. Cohn-Fossen, Geometry and the Imagination, Chelsea - New York, 1952.
[6]	I. M. Jaglom, Geometričeskie preobrazovanija II, Moskva, 1956.
[7]	K. S. Kedlaya, Geometry Unbound, 2006.
[8]	K. Y. Li, Inversion, Mathematical Excalibur, Vol. 9., No. 2, May-July 2004.
[9]	MathLinks Forums
[10]	V. V. Praslov, Problems in Plane Geometry (prijevod: D. Leites), 2005.
[11]	Srpska matematička olimpijada 2008 – zadaci i rešenja, Srb. imomath. com., 2008.
[12]	R.C. Yates, A Handbook of Curves and Their Properties, Ann Arbor, 1952.