Frobeniusova metoda

Eulerova diferencijalna jednadžba

 

Ivana Crnjac,
Fakultet primijenjene matematike i informatike, Sveučilište u Osijeku, trg Lj. Gaja 6, 31000 Osijek, Hrvatska; e-mail address: icrnjac@mathos.hr		 Robert Ledenčan
Industrijsko-obrtnička škola Virovitica, Ulica Zbora narodne garde 29, 33000 Virovitica, Hrvatska; e-mail address: robert.ledencan@skole.hr

Sažetak
U ovome radu definirat ćemo Eulerovu diferencijalnu jednadžbu i pokazati na koji način određujemo njezina rješenja. Klasificirat ćemo vrste singularnih točaka te opisati Frobeniusovu metodu za pronalazak rješenja Eulerove diferencijalne jednadžbe u okolini singularnih točaka. Kako se ova jednadžba često pojavljuje u raznim znanstvenim i inženjerskim granama, na kraju ćemo navesti neke od primjena Eulerove diferencijalne jednadžbe u fizici.


Ključne riječi: Eulerova diferencijalna jednadžba, singularne točke, linearna diferencijalna jednadžba drugog reda, Frobeniusova metoda.



1Uvod

Diferencijalna jednadžba je jednadžba koja povezuje i daje odnos između promatrane funkcije i njezinih derivacija. Takvi odnosi su u primjenama iznimno česti pa se diferencijalne jednadžbe prirodno pojavljuju pri matematičkom opisu raznih prirodnih pojava, posebice pri opisivanju velikog broja fizikalnih pojava kao što su električno polje, titranje, provođenje topline, i sl. Osim u fizici, značajna je njihova primjena u inženjerstvu, biologiji, kemiji, medicini i ekonomiji. U ovom velikom području primjena, centralnu ulogu imaju linearne obične diferencijalne jednadžbe, tj. jednadžbe oblika
(1)
y^{(n)} (x)+a_{n-1}(x)y^{(n-1)} (x)+\dots +a_{1}(x)y'(x)+a_{0}(x)y(x)=f(x), \quad x\in I\subseteq \mathbb{R},
pri čemu su funkcije f i a_{i}, i=0,\dots n-1, neprekidne na danom otvorenom intervalu I. Jednadžbu (1) zovemo homogenom ako je f\equiv 0, odnosno nehomogenom ako je f\neq 0. Ukoliko su uz jednadžbu zadani i početni uvjeti
(2)
y(x_{0})=y_{0},\quad y'(x_{0})=y_{1},\quad\dots, \quad y^{(n-1)}(x_{0})=y_{n-1},
tada diferencijalnu jednadžbu (1) zajedno s početnim uvjetima (2) nazivamo Cauchyjeva zadaća. Može se pokazati da Cauchyjeva zadaća na otvorenom intervalu ima jedinstveno rješenje [1, 4].
U nastavku ćemo ukratko objasniti rješavanje diferencijalne jednadžbe (1), a detaljnije informacije mogu se pronaći u [1, 3, 4]. Ukoliko sa y_{p} označimo jedno (partikularno) rješenje diferencijalne jednadžbe (1), onda je opće rješenje spomenute jednadžbe dano s
y(x)=y_{p}(x)+c_{1}y_{1}(x)+c_{2}y_{2}(x)+\dots +c_{n}y_{n}(x),
c_{1},c_{2},\dots ,c_{n}\in \mathbb{R}, pri čemu su y_{1}, y_{2},\dots ,y_{n} linearno nezavisna rješenja pripadne homogene diferencijalne jednadžbe
(3)
y^{(n)}+a_{n-1}(x)y^{n-1}+\dots +a_{1}(x)y'+a_{0}(x)y=0.
Skup \lbrace y_{1},y_{2},\dots , y_{n}\rbrace naziva se fundamentalni skup rješenja. Ukoliko su funkcije a_{i}, i=0,\dots ,n-1, konstantne, tada se fundamentalni skup može vrlo jednostavno odrediti, dok je u suprotnom često potrebno koristiti neke numeričke metode ili redove potencija za pronalazak fundamentalnog rješenja.

Glavni cilj ovog rada je proučavanje jednog predstavnika linearnih diferencijalnih jednadžbi, a to je Eulerova diferencijalna jednadžba. Ova se jednadžba prirodno pojavljuje u rješavanju Laplaceove diferencijalne jednadžbe u polarnim koordinatama, analizi quicksort stabla i stabla pretraživanja, jednadžbama ravnoteže i brojnim drugim znanstvenim i inženjerskim područjima. U drugom poglavlju definirat ćemo Eulerovu diferencijalnu jednadžbu i pokazati metode pronalaska njezinog rješenja. Osim toga, upoznat ćemo se i sa pojmom singularnih točaka koje su od posebnog značaja u primjenama, te ćemo pokazati kako dolazimo do rješenja Eulerove jednadžbe u njihovoj okolini. Treće poglavlje posvećeno je primjenama Eulerove diferencijalne jednadžbe u fizici.


2Eulerova diferencijalna jednadžba

Eulerova diferencijalna jednadžba (poznata u literaturi i pod nazivom Cauchy-Eulerova diferencijalna jednadžba) pripada linearnim običnim diferencijalnim jednadžbama n-tog reda, a definiramo ju na sljedeći način:
Definicija 1. Neka je I\subseteq\mathbb{R} otvoren, te f\in C(I). Diferencijalnu jednadžbu
(4)
a_{n}x^{n}y^{(n)}(x)+ a_{n-1}x^{n-1}y^{(n-1)}(x)+\dots+a_{1}xy'(x)+a_{0}y(x)=f(x),
pri čemu su a_{i}\in\mathbb{R},\, a_{n} \neq 0,\, i=0,\dots,n, nazivamo Eulerova diferencijalna jednadžba n-tog reda.


Ukoliko je f\equiv 0, jednadžbu (4) nazivamo homogenom, u suprotnom jednadžba je nehomogena. Primijetimo da prvi koeficijent a_{n}x^{n} nestane za x=0, što implicira da ćemo rješenje tražiti na intervalima \langle -\infty,0\rangle i \langle 0, \infty\rangle.

Pretpostavimo najprije da je x\in\langle 0,\infty\rangle. Eulerovu jednadžbu rješavat ćemo na način da ju svedemo na linearnu diferencijalnu jednadžbu s konstantnim koeficijentima. Uvedemo li supstituciju x=e^{t}, uzastopnim deriviranjem funkcije y(x)=y(e^{t})=Y(t) dobivamo niz funkcija

\begin{align*} y'(x)&=e^{-t}\frac{d}{dt}Y(t),\\ y''(x)&=e^{-2t}\frac{d}{dt}\left(\frac{d}{dt}-I\right)Y(t),\\ y'''(x)&=e^{-3t}\frac{d}{dt}\left(\frac{d}{dt}-I\right)\left(\frac{d}{dt}-2I\right)Y(t),\\ \vdots& \\ y^{(n)}(x)&=e^{-nt}\frac{d}{dt}\left(\frac{d}{dt}-I\right)\left(\frac{d}{dt}-2I\right)\dots\left(\frac{d}{dt}-(n-1)I\right)Y(t), \end{align*}

gdje je I operator identiteta. Uvrštavanjem supstitucije i gornjih funkcija u homogenu Eulerovu jednadžbu (4), dobivamo jednadžbu

(5)
\begin{align} \begin{split} \Bigg[ a_{n}\frac{d}{dt}\left(\frac{d}{dt}-I\right)\left(\frac{d}{dt}-2I\right)\dots &\left(\frac{d}{dt}-(n-1)I\right)+\dots+ \\ +&a_{2}\frac{d}{dt}\left(\frac{d}{dt}-I\right)+a_{1}\frac{d}{dt}+a_{0}\Bigg] Y(t)=0, \end{split} \end{align}

što je homogena linearna obična diferencijalna jednadžba n-tog reda s konstantnim koeficijentima. Iz teorije linearnih diferencijalnih jednadžbi znamo da je za pronalazak općeg rješenja gornje jednadžbe dovoljno pronaći fundamentalni skup rješenja. Ukoliko za neki \lambda\in\textbf{C} pretpostavimo da je rješenje jednadžbe (5) oblika Y(t)=e^{\lambda t}, uvrštavanjem u jednadžbu slijedi

(6)
P(\lambda)e^{\lambda t}=0,

gdje je

(7)
P(\lambda)= a_{n}\lambda(\lambda-1)(\lambda-2)\dots(\lambda-n+1)+\dots+a_{2}\lambda(\lambda-1)+a_{1}\lambda+a_{0}.

Gornji polinom nazivamo karakterističnim polinomom jednadžbe (5), a često i karakterističnim polinomom homogene Eulerove jednadžbe (4). Nadalje, iz jednadžbe (6) možemo vidjeti da je Y(t)=e^{\lambda t} rješenje jednadžbe (5) ako i samo ako je P(\lambda)=0. Prema tome, određivanjem nultočki karakterističnog polinoma dolazimo do rješenja diferencijalne jednadžbe (5). Može se pokazati da ako je \lambda\in\mathbb{C} nultočka kratnosti m karakterističnog polinoma (7), onda su funkcije

(8)
Y_{i}(t)=t^{i-1}e^{\lambda t},\quad i=1,\dots,m

linearno nezavisne i pripadaju fundamentalnom skupu rješenja jednadžbe (5) [4].

Napomena 1. Kako se u primjenama najčešće pojavljuje Eulerova diferencijalna jednadžba drugog reda,

 

(9)
a_{2}x^{2}y''(x)+a_{1}xy'(x)+ a_{0}y(x)=0,

raspisat ćemo detaljnije postupak rješavanja ove jednadžbe. Pretpostavimo da je x\gt 0 i uvedimo supstituciju x=e^{t}. Tada je

\begin{align*} Y(t)&=y(e^{t})=y(x), \\ \frac{d}{dt}Y(t)&=y'(x)e^{t}, \\ \frac{d^2}{dt^2}Y(t)&=y''(x)e^{2t}+y'(x)e^{t}=y''(x)e^{2t}+ \frac{d}{dt}Y(t), \end{align*}

i jednadžba (9) postaje

(10)
a_{2} \frac{d^{2}}{dt^{2}}Y(t)+(a_{1}-a_{2}) \frac{d}{dt}Y(t)+ a_{0}Y(t)=0.

Karakteristični polinom jednadžbe (10) glasi

(11)
P(\lambda)=a_{2}\lambda^{2}+(a_{1}-a_{2})\lambda+a_{0}.

Neka su \lambda_{1}, \lambda_{2} nultočke karakterističnog polinoma (11). Ovisno o tipu nultočki, razlikujemo tri slučaja fundamentalnog skupa rješenja jednadžbe (10):

\bullet [1)] Ako su \lambda_{1} i \lambda_{2} dvije različite realne nultočke polinoma (11), tada prema (8) slijedi da funkcije Y_{1}(t)=e^{\lambda_{1} t} i Y_{2}(t)=e^{\lambda_{2} t} čine fundamentalan skup rješenja jednadžbe (10).
\bullet [2)] Ako je \lambda_{1}=\lambda_{2} jedna dvostruka realna nultočka polinoma (11), tada (8) implicira da funkcije Y_{1}(t)=e^{\lambda_{1} t} i Y_{2}(t)=te^{\lambda_{1} t} čine fundamentalan skup rješenja jednadžbe (10).
\bullet [3)] Ako je \lambda=\alpha\pm i\beta, \beta\neq 0, kompleksno konjugiran par nultočki polinoma (11), tada je
Y(t)=e^{\lambda t}=e^{\alpha t+i\beta t}=e^{\alpha t}(\cos(\beta t)+i\sin (\beta t))
jedno kompleksno rješenje jednadžbe (10) iz čega slijede dva linearno nezavisna realna rješenja Y_{1}(t)=e^{\alpha t}\cos \left(\beta t\right) i Y_{2}(t)=e^{\alpha t}\sin (\beta t) koja čine fundamentalan skup rješenja jednadžbe (10).

Opće rješenje diferencijalne jednadžbe (10) je linearna kombinacija elemenata fundamentalanog skupa \lbrace Y_{1}(t),\,Y_{2}(t)\rbrace, tj. opće rješenje glasi:

Y(t)=c_{1} Y_{1}(t)+c_{2}Y_{2}(t),\qquad c_{1},\, c_{2}\in \mathbb{R}.

Vraćanjem supstitucije dobivamo opće rješenje Eulerove diferencijalne jednadžbe (9),

y(x)=c_{1} Y_{1}(\ln\, x)+c_{2}Y_{2}(\ln\, x),\qquad c_{1},\, c_{2}\in \mathbb{R}.

 



Pretpostavimo sada da je x\in\langle -\infty, 0\rangle. U tom slučaju x se može zamijeniti sa -x=|x| pa, za \lambda\in\mathbb{C} , dobivamo sljedeći rezultat za rješenje homogene Eulerove diferencijalne jednadžbe [4].

Theorem 2.1 Neka su \lambda_{1} \dots \lambda_{k} različite nultočke karakterističnog polinoma (7) jednadžbe
(12)
a_{n}x^{n}y^{(n)}(x)+ a_{n-1}x^{n-1}y^{(n-1)}(x)+\dots+a_{1}xy'(x)+a_{0}y(x)=0,
te \lambda_{j} kratnosti m_{j}. Tada funkcije p_{ij}, takve da je
(13)
\begin{align} p_{ij}=|x|^{\lambda_{j}}\ln(|x|)^{i-1}, \quad i=1,\dots,m_{j},\quad j=1,\dots,k, \end{align}
čine fundamentalni skup rješenja jednadžbe (12) na svakom intervalu koji ne sadrži x=0.

 



Primijetimo da, ukoliko je x\in\langle 0,\infty\rangle, u slučaju Eulerove diferencijalne jednadžbe drugog reda, fundamentalni skup rješenja iz gornjeg teorema podudara se sa fundamentalnim skupom dobivenim u Napomeni 1. Zaista, ukoliko je, primjerice, \lambda nultočka karakterističnog polinoma jednadžbe (10) kratnosti m=2, tada prema Napomeni 1 funkcije y_{1}(x)=Y_{1}(\ln x)=x^{\lambda} i y_{2}(x)=Y_{2}(\ln x)=x^{\lambda}\ln x čine fundamentalni skup rješenja jednadžbe (9), a to su upravo funkcije oblika (13) iz Teorema 2.1.

 

2.1Singularne točke

Nerijetko je u primjenama potrebno promatrati ponašanje rješenja određene diferencijalne jednadžbe u okolini singularnih točaka što može biti vrlo složen zadatak, u ovisnosti o prirodi singularnih točaka. Rješenja diferencijalne jednadžbe u okolini ovih točaka često postanu vrlo velika ili pak jako brzo osciliraju pa u nekim slučajevima jednadžbu nije moguće riješiti u okolini singularne točke. Kao što smo već ranije napomenuli, mnoge jednadžbe koje se pojavljuju u primjenama su jednadžbe drugog reda, tako da ćemo se u ovom poglavlju fokusirati na singularne točke diferencijalnih jednadžbi drugog reda, a posebno na singularne točke Eulerove diferencijalne jednadžbe.
Definicija 2. Neka su zadani proizvoljni polinomi p, q i r. Za točku x_{0} kažemo da je regularna točka diferencijalne jednadžbe

 

(14)
\begin{align} p(x)y''(x)+q(x)y'(x)+r(x)y(x)=0, \end{align}

ako su funkcije \displaystyle\frac{q(x)}{p(x)} i \displaystyle\frac{r(x)}{p(x)} analitičke u točki x_{0}. Ukoliko točka x_{0} nije regularna, onda kažemo da je x_{0} singularna točka.



Prisjetimo se da je funkcija f:I\subseteq\mathbb{R}\rightarrow\mathbb{R} je analitička u x_{0}\in I ukoliko se može prikazati u obliku reda potencija

 

(15)
\begin{align} f(x)=\sum_{n=0}^{\infty}a_{n}(x-x_{0})^{n} \end{align}

oko točke x_{0} na nekom krugu K(x_{0},R), gdje je R\gt 0 polumjer konvergencije reda potencija (15). Prema tome, funkcije \displaystyle\frac{q(x)}{p(x)} i \displaystyle\frac{r(x)}{p(x)} će biti analitičke u svim točkama, osim u onim za koje je p(x)=0. Takve točke su upravo singularne točke diferencijalne jednadžbe (14).

Definicija 3. Za singularnu točku x_{0} diferencijalne jednadžbe (14) kažemo da je regularna singularna točka ako su funkcije

 

(16)
\begin{align} (x-x_{0})\frac{q(x)}{p(x)} \quad i \quad (x-x_{0})^{2} \frac{r(x)}{p(x)} \end{align}

analitičke u točki x_{0}. Ukoliko barem jedna od prethodnih funkcija nije analitička u točki x_{0}, onda za x_{0} kažemo da je iregularna singularna točka.



U slučaju regularne singularne točke, diferencijalna jednadžba se može transformirati u jednadžbu s regularnim ponašanjem, točnije, rješenje diferencijalne jednadžbe u regularnoj singularnoj točki može se prikazati kao red potencija s konačnim polumjerom konvergencije. S druge strane, ako diferencijalna jednadžba ima iregularnu singularnu točku, rješenje jednadžbe u toj točki ne može se izraziti kao red potencija, nego može uključivati i neke posebne ili neelementarne funkcije. U sljedećem primjeru odredit ćemo singularne točke Eulerove diferencijalne jednadžbe drugog reda.

 

Primjer 1. Neka su a_{2},\,a_{1},\,a_{0}\in\mathbb{R}, i a_{2}\neq 0. Odredimo i klasificirajmo singularne točke obične diferencijalne jednadžbe

 

a_{2}x^{2}y''(x)+a_{1}xy'(x)+ a_{0}y(x)=0.

Kako je p(x)=a_{2}x^{2}, q(x)=a_{1}x, a r(x)=a_{0}, to je

\displaystyle\frac{q(x)}{p(x)}=\frac{a_{1}}{a_{2}x},\quad\displaystyle\frac{r(x)}{p(x)}=\frac{a_{0}}{a_{2}x^{2}},

pa je jedina singularna točka Eulerove diferencijalne jednadžbe jednaka x_{0}=0. Kako je

\begin{align*} (x-0)\frac{q(x)}{p(x)}=\frac{a_{1}}{a_{2}}\quad i \quad(x-0)^{2} \frac{r(x)}{p(x)}=\frac{a_{0}}{a_{2}}, \end{align*}

slijedi da je x_{0}=0 regularna singularna točka.



Ukoliko je točka x_{0} regularna singularna točka diferencijalne jednadžbe (14), onda njena rješenja općenito nisu definirana u točki x_{0}. Međutim, diferencijalna jednadžba (14) ima dva linearno nezavisna rješenja na kružnom vijencu K(x_{0};0,R), R\gt 0 pa je moguće (barem aproksimativno) odrediti rješenje jednadžbe u okolini svake regularne singularne točke. Za pronalazak rješenja koristit ćemo tzv. Frobeniusovu metodu koja kaže da jednadžba (14) uvijek ima barem jedno rješenje oblika

 

y(x)= x^{r} \sum_{n=0}^{\infty}A_{n}|x-x_{0}|^{n},

za pogodno odabrani r i A_{0}\neq 0, koje konvergira na otvorenom kružnom vijencu K(x_{0};0,R), za neki R\gt 0. Ovakvo rješenje nazivamo Frobeniusovim rješenjem.

U nastavku ćemo pretpostaviti da je p(x)=a_{2}x^{2}, q(x)=a_{1}x, i r(x)=a_{0}, tj. rješavat ćemo Eulerovu diferencijalnu jednadžbu

(17)
a_{2}x^{2}y''(x)+a_{1}xy'(x)+ a_{0}y(x)=0

u okolini svoje regularne singularne točke x_{0}=0. Bez smanjenja općenitosti, promatrat ćemo rješenja definirana na \langle 0,\infty \rangle, tj. pretpostavit ćemo da je x\gt 0. Slučaj x\lt 0 je analogan, uz male modifikacije, slično kao u prethodnom poglavlju. Neka je

(18)
y(x)= x^{\lambda} \sum_{n=0}^{\infty}A_{n}x^{n},

Frobeniuosovo rješenje jednadžbe (17) koje konvergira na kružnom vijencu K(0;0,R). Red (18) možemo derivirati član po član pa uvrštavanjem u jednadžbu (17) dobivamo

(19)
\sum_{n=0}^{\infty}\big (a_{2}(\lambda+n)(\lambda+n-1)+a_{1}(\lambda+n)+a_{0}\big )A_{n}x^{\lambda+n}=0.

Da bi gornja jednadžba bila zadovoljena, koeficijent uz svaku potenciju od x mora biti jednak nuli. Kako je po pretpostavci A_{0}\neq 0, a koeficijent uz x^{\lambda}

(a_{2}\lambda(\lambda-1)+a_{1}\lambda+a_{0})A_{0}=0,

to slijedi

(20)
\begin{align} P(\lambda)=a_{2}\lambda(\lambda-1)+a_{1}\lambda+a_{0}=0. \end{align}

Primijetimo da je polinom P(\lambda) karakteristični polinom pridružen diferencijalnoj jednadžbi (17). Prema tome, ukoliko sa \lambda_{1} i \lambda_{2} označimo korijene karakterističnog polinoma (20), i dodatno pretpostavimo da je \text{Re}(\lambda_{1})\geq \text{Re}(\lambda_{2}), tada je jedno Frobeniusovo rješenje diferencijalne jednadžbe (17) oblika

(21)
\begin{align} y_{1}(x)=x^{\lambda_{1}}\sum_{n=0}^{\infty}A_{n}x^{n}, \end{align}

pri čemu gornji red konvergira na kružnom vijencu K(0;0,R), za neki R\gt 0. Za pronalazak fundamentalnog rješenja, potrebno je odrediti još jedno rješenje jednadžbe (17) koje je linearno nezavisno sa rješenjem (21). Njega dobivamo na sljedeći način [3, 5].
1) Ako \lambda_{1}-\lambda_{2} \notin \mathbb{N}_{0}, onda je s

\begin{align*} y_{2}(x)= x^{\lambda_{2}}\sum_{n=0}^{\infty}B_{n}x^{n} \end{align*}

definirano Frobeniusovo rješenje diferencijalne jednadžbe (17) koje je linearno nezavisno s rješenjem (21).
2) Ako je \lambda_{1}=\lambda_{2}, onda je

\begin{align*} y_{2}(x)= y_{1}(x)\ln x+x^{\lambda_{2}}\sum_{n=0}^{\infty}B_{n}x^{n}, \end{align*}

za y_{1} oblika (21), drugo Frobeniusovo rješenje diferencijalne jednadžbe (17) i ta dva rješenja su linearno nezavisna.
3) Ako je \lambda_{1}=\lambda_{2}+m, m\in\mathbb{N}, onda, za rješenje y_{1} oblika (21), slijedi da je

\begin{align*} y_{2}(x)= Cy_{1}(x)\ln x+x^{\lambda_{2}}\sum_{n=0}^{\infty}C_{n}x^{n}, \quad C\in\mathbb{R} \end{align*}

još jedno Frobeniusovo rješenje diferencijalne jednadžbe (17) koje je linearno nezavisno s rješenjem y_{1}.

Koeficijente A_{n}, B_{n}, C_{n} te konstantu C iz gornjih rješenja određujemo uvrštavanjem Frobeniusovih rješenja y_{1} i y_{2} u diferencijalnu jednadžbu (17). Time smo pronašli fundamentalan skup Frobeniusovih rješenja \lbrace y_{1},\,y_{2}\rbrace diferencijalne jednadžbe (17).

Primjer 2. U okolini regularne singularne točke 0 odredimo dva linearno nezavisna Frobeniousova rješenja Eulerove jednadžbe

 

(22)
x^{2}y''(x)+xy'(x)-y(x)=0.

Karakteristični polinom zadane jednadžbe glasi

P(\lambda)=\lambda^{2}-1,

a njegove nultočke su \lambda_{1}=1 i \lambda_{2}=-1. Prema tome, jedno Frobeniusovo rješenje glasi

\begin{align*} y_{1}(x)=x\sum_{n=0}^{\infty}A_{n}x^{n}=\sum_{n=0}^{\infty}A_{n}x^{n+1}, \end{align*}

dok je drugo oblika

\begin{align*} y_{2}(x)= Cy_{1}(x)\ln x+\sum_{n=0}^{\infty}C_{n}x^{n-1}, \end{align*}

jer je \lambda_{1}=\lambda_{2}+2. Odredimo najprije koeficijente A_{n} rješenja y_{1}. Kako je

\begin{align*} y_{1}'(x)&=\sum_{n=0}^{\infty}(n+1)A_{n}x^{n},\\ y_{1}''(x)&=\sum_{n=0}^{\infty}(n+1)nA_{n}x^{n-1}, \end{align*}

uvrštavanjem u jednadžbu (22) dobivamo

\begin{align*} x^{2}\sum_{n=0}^{\infty}(n+1)nA_{n}x^{n-1}+x\sum_{n=0}^{\infty}(n+1)A_{n}x^{n} -\sum_{n=0}^{\infty}A_{n}x^{n+1}=0, \end{align*}

to jest,

\begin{align*} \sum_{n=0}^{\infty}(n^{2}+2n)A_{n}x^{n+1}=0. \end{align*}

Iz gornje jednadžbe slijedi da je A_{n}=0, za svaki n\in\mathbb{N}, pa je

\begin{align*} y_{1}(x)=A_{0}x. \end{align*}

Nadalje, uvrštavanjem

\begin{align*} y_{2}(x)&= CA_{0}x\ln x+\sum_{n=0}^{\infty}C_{n}x^{n-1},\\ y_{2}'(x)&=CA_{0}(\ln x+1)+\sum_{n=0}^{\infty}(n-1)C_{n}x^{n-2},\\ y_{2}''(x)&=CA_{0}\frac{1}{x}+\sum_{n=0}^{\infty}(n-1)(n-2)C_{n}x^{n-3}. \end{align*}

u jednadžbu (22) dobivamo

\begin{align*} 2CA_{0}x+\sum_{n=0}^{\infty}(n-1)(n-2)C_{n}x^{n-1}+\sum_{n=0}^{\infty}(n-1)C_{n}x^{n-1} -\sum_{n=0}^{\infty}C_{n}x^{n-1}=0, \end{align*}

što možemo zapisati kao

\begin{align*} 2CA_{0}x+\sum_{n=0}^{\infty}(n^{2}-2n)C_{n}x^{n-1}=0. \end{align*}

Raspisivanjem koeficijenata uz potencije od x slijedi da su C i svi koeficijenti C_{n}, n\in\mathbb{N}_{0}, jednaki nuli, osim C_{0} i C_{2}. Prema tome,

\begin{align*} y_{2}(x)=C_{0}\frac{1}{x}+C_{2}x. \end{align*}

 



Napomenimo i da jednadžbe oblika

 

(23)
a_{2}(x-a)^{2}y''(x)+a_{1}(x-a)y'(x)+a_{0}y(x)=0,

za neki a\in\mathbb{R}, pripadaju Eulerovim diferencijalnim jednadžbama, s regularnom singularnom točkom x_{0}=a. Ove jednadžbe rješavamo supstitucijom t=x-a, čime se jednadžba (23) svodi na (17).



3Primjene Eulerove diferencijalne jednadžbe

Eulerova diferencijalna jednadžba prirodno se pojavljuje prilikom promatranja mnoštva fizikalnih pojava, a posebice u području elektrostatike i mehaničke otpornosti materijala. U sljedećih nekoliko primjera objasnit ćemo fizikalne probleme u kojima se pojavljuje ova jednadžba, a potom riješiti navedene probleme [2, 6, 7].

 

3.1Stacionarno provođenje topline

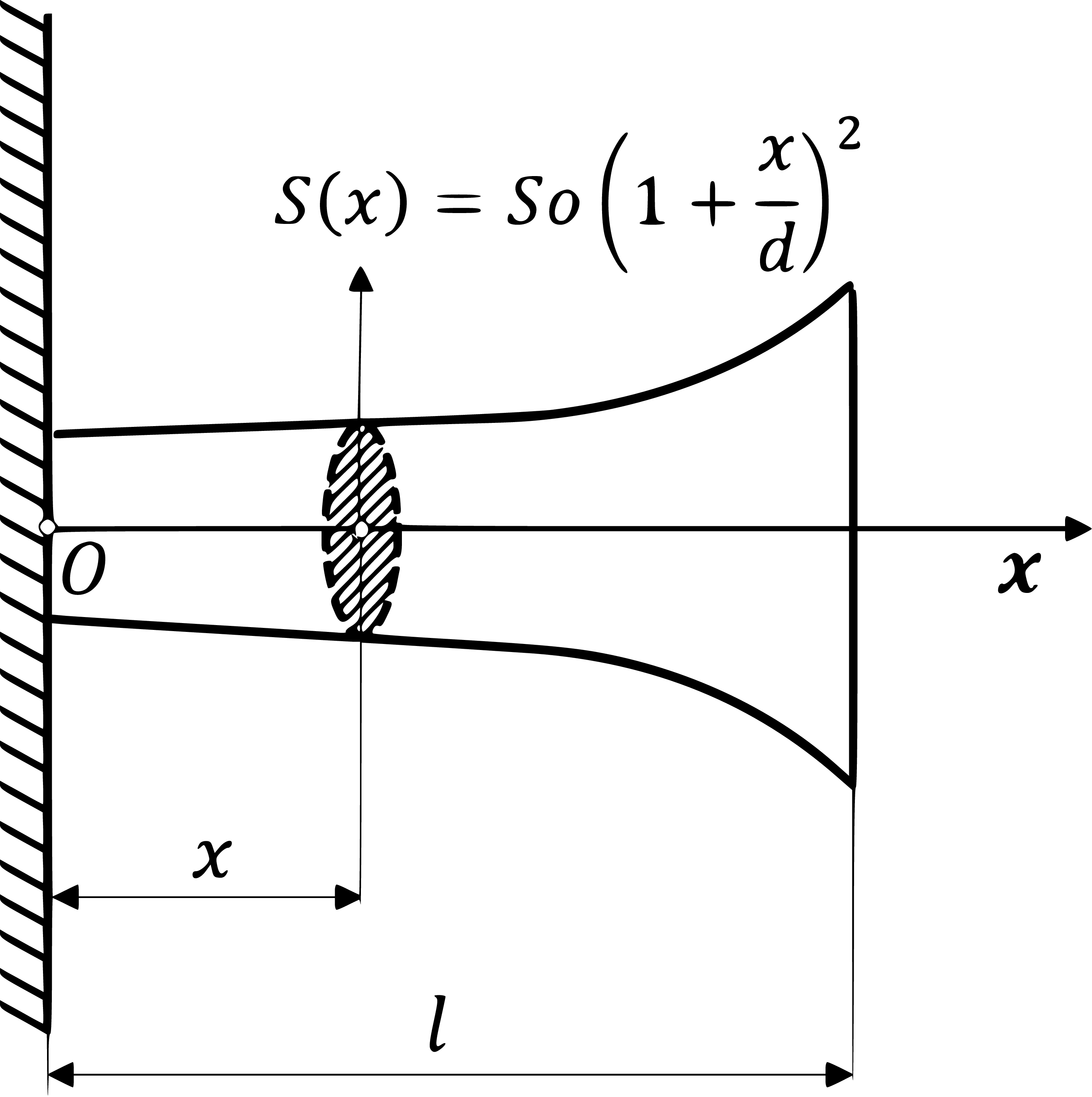
U mehanici se često promatraju štapovi promjenjivog poprečnog presjeka, a jedan takav štap prikazan je na Slici 1. Promjena poprečnog presjeka ovog štapa duljine l ovisi o udaljenosti središta promatranog presjeka štapa od ishodišta, a dana je formulom

 

(24)
S(x)=S_{0}{\left(1+\dfrac{x}{d}\right)}^{2},

pri čemu je S_{0} površina poprečnog presjeka štapa u točki x=0, a d\gt 0 fiksan.

  
Slika 1: Štap promjenjivog poprečnog presjeka.


Ukoliko je uz zadanu vanjsku toplinu f(x) štap u vezi s regulatorom koji na svakom presjeku odvodi iz štapa količinu topline proporcionalne temperaturi u(x) na tom mjestu, onda je prisutan i linijski fluks s gustoćom -b(x)u(x), za b(x)\geq0, i jednadžba stacionarnog provođenja topline glasi

(25)
\left(\kappa S(x)u'(x)\right)'-b(x)u(x)+f(x)=0,

pri čemu je \kappa \gt 0 koeficijent provođenja materijala od kojeg je štap napravljen. Ako pretpostavimo da je f(x)=0 i b(x)= b, jednadžba (25), uz supstituciju t=1+\dfrac{x}{d}, postaje

(26)
\begin{align}\\\\\kappa S_{0}\dfrac{1}{d^{2}}t^{2}U''(t)+\kappa S_{0}\dfrac{2}{d^{2}}tU'(t)-bU(t)=0, \end{align}

gdje je U(t)=U\left(1+\frac{x}{d}\right)=u(x). Jednadžba (26) je upravo Eulerova diferencijalna jednadžba drugog reda (9) s koeficijentima

a_{2}= \kappa S_{0}\dfrac{1}{d^{2}},\, a_{1}=\kappa S_{0}\dfrac{2}{d^{2}},\, a_{0}=-b.

Karakteristični polinom jednadžbe (26) glasi

\begin{align*} \kappa S_{0}\dfrac{1}{d^{2}}\lambda^{2}+\kappa S_{0}\dfrac{1}{d^{2}}\lambda-b=0, \end{align*}

a njegove nultočke su

\lambda_{1,2}=-\dfrac{1}{2}\pm \dfrac{d}{2\kappa S_{0}}\sqrt{\kappa^{2}S_{0}^{2}\dfrac{1}{d^{2}}+4\kappa S_{0} b}.

Radi lakšeg zapisa rješenja, koristimo notaciju

\begin{align*} D&=\kappa^{2}S_{0}^{2}\dfrac{1}{d^{2}}+4\kappa S_{0} b, \\ p_{1}&=1- \dfrac{d\sqrt{D}}{\kappa S_{0}}, \\ p_{2}&=1+ \dfrac{d\sqrt{D}}{\kappa S_{0}}. \end{align*}

Kako je D\gt 0 i t\gt 0, prema Teoremu 11, fundamentalni sustav rješenja jednadžbe (26) čine funkcije

\begin{align*} U_{1}(t)=t^{\lambda_{1} }&=t^{-\frac{p_{1}}{2}}, \\ U_{2}(t)=t^{\lambda_{2} }&=t^{-\frac{p_{2}}{2}}. \end{align*}

Stoga je temperatura u svakoj točki promatranog štapa opisana funkcijom

u(x)=C_{1}\left(1+\dfrac{x}{d} \right)^{-\frac{p_{1}}{2}}+C_{2}\left(1+\dfrac{x}{d} \right)^{-\frac{p_{2}}{2}},\quad C_{1},C_{2}\in \mathbb{R} .

Dodatno, ako pretpostavimo da je lijevi kraj štapa toplinski izoliran, a na desnom kraju štapa se održava temperatura od 1 stupanj, tj. u'(0)=0 i u(l)=1, onda su konstante C_{1} i C_{2} jednake

\begin{align*} C_{1}&=-\dfrac{p_{2}}{p_{1}}\left(-\dfrac{p_{2}}{p_{1}}\left( 1+ \dfrac{l}{d}\right)^{-\frac{p_{1}}{2}}+\left( 1+ \dfrac{l}{d}\right)^{-\frac{p_{2}}{2}}\right)^{-1}, \\ C_{2}&=\left(-\dfrac{p_{2}}{p_{1}}\left( 1+ \dfrac{l}{d}\right)^{-\frac{p_{1}}{2}}+\left( 1+ \dfrac{l}{d}\right)^{-\frac{p_{2}}{2}}\right)^{-1}. \end{align*}

 

3.2Električni potencijal vodljive nabijene sfere

Električni potencijal \varPhi je skalarna fizikalna veličina koja opisuje potencijalnu energiju električki nabijene čestice u statičkom električnom polju. Možemo ga odrediti koristeći Gaussov zakon, zapisan u obliku Poissonove jednadžbe,

 

(27)
\begin{align} \Delta\varPhi=-\dfrac{\rho}{\varepsilon_{0}}, \end{align}

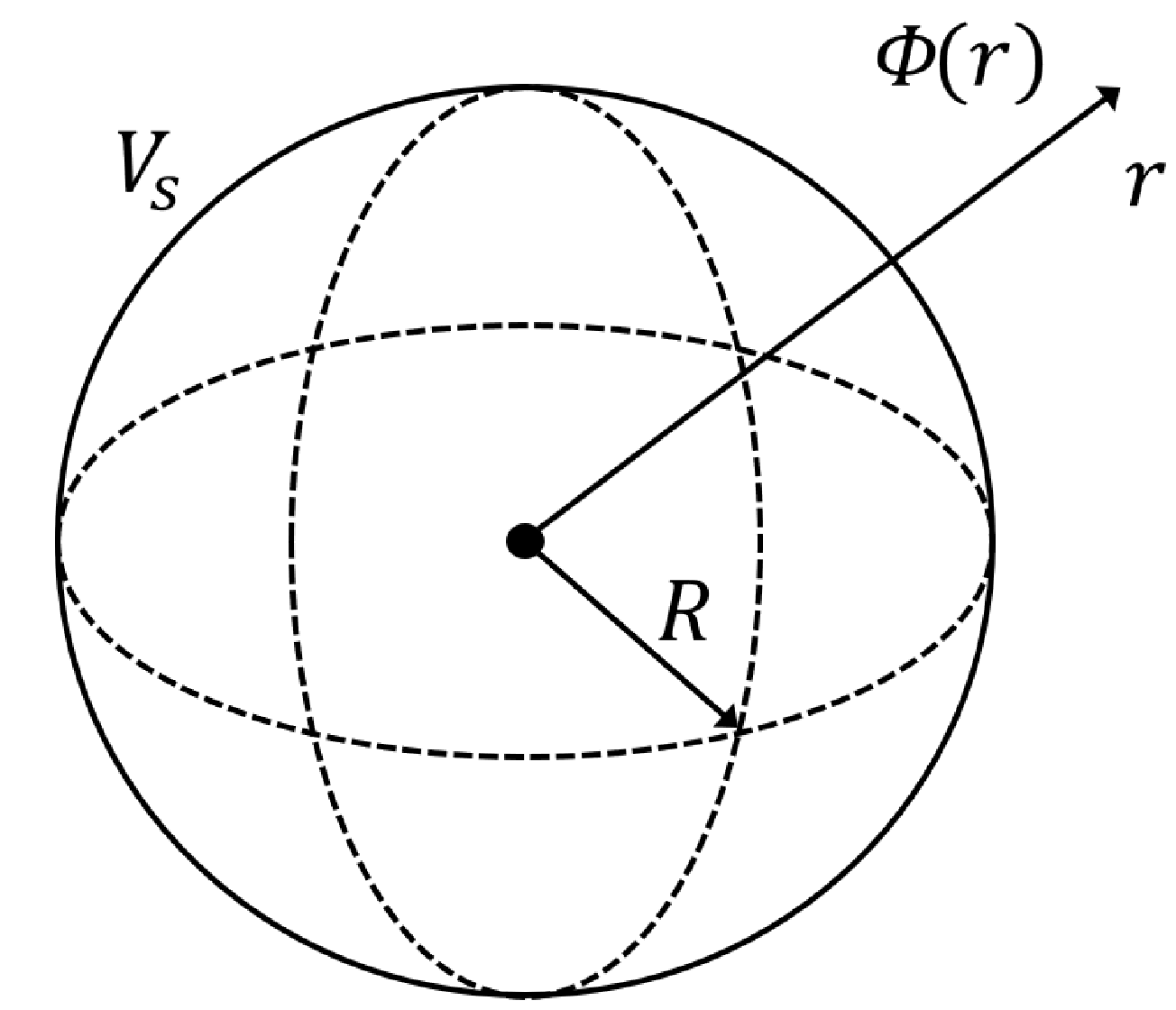
gdje je \rho volumna raspodjela naboja, a \varepsilon_{0} dielektrična konstanta vakuuma. Neka je dana vodljiva nabijena sfera polumjera R čiji je električni potencijal potrebno odrediti na udaljenosti r od površine sfere. Pretpostavimo da se sve točke na površini sfere nalaze na istom potencijalu V_{s}, tj. naboj je simetrično raspoređen. Dodatno, pretpostavimo da se sfera nalazi u velikom mediju bez naboja (što implicira da je \rho=0) te da je električni potencijal u beskonačnosti, \varPhi(\infty), jednak nuli.

 
Slika 2: Vodljiva nabijena sfera.

Kako je naboj simetrično raspoređen, potencijal ovisi isključivo o udaljenosti od površine sfere pa zapisom Laplaceovog diferencijalnog operatora u sfernim koordinatama jednadžba (27) se svodi na jednadžbu

\begin{align*} \left[\dfrac{1}{r^{2}}\dfrac{d}{d r}\left( r^{2} \dfrac{d}{d r} \right)\right] \varPhi(r)=0. \end{align*}

Sređivanjem gornje jednadžbe dobivamo Eulerovu diferencijalnu jednadžbu drugog reda,

(28)
\begin{align} r^{2}\varPhi''(r)+2r\varPhi'(r)&=0. \end{align}

Karakteristični polinom gornje jednadžbe je

\begin{align*} P(\lambda)=\lambda^{2}+\lambda, \end{align*}

a njegove nultočke su \lambda_{1}=0 i \lambda_{2}=-1. Kako je r\gt 0, to je, prema Teorema 11, fundamentalni skup rješenja jednadžbe (28) jednak \left\lbrace 1,\dfrac{1}{r}\right\rbrace, dok je opće rješenje jednadžbe dano s

\begin{align*} \varPhi(r)=C_{1}+C_{2}\dfrac{1}{r},\quad C_{1},C_{2}\in \mathbb{R}. \end{align*}

Iz pretpostavke da je potencijal u beskonačnosti jednak nuli slijedi

\varPhi(\infty)=\lim_{r \to \infty}\left(C_{1}+C_{2}\dfrac{1}{r}\right)=C_{1}=0,

a kako je površina sfere potencijala V_{s}, to je

\varPhi(R)=C_{2}\dfrac{1}{R}=V_{s}.

Dakle, C_{1}=0 i C_{2}=V_{s}R, pa je električni potencijal nabijene vodljive sfere dan formulom

\varPhi(r)=V_{s}R\dfrac{1}{r}.

 

3.3Ravnoteža kružnog diska

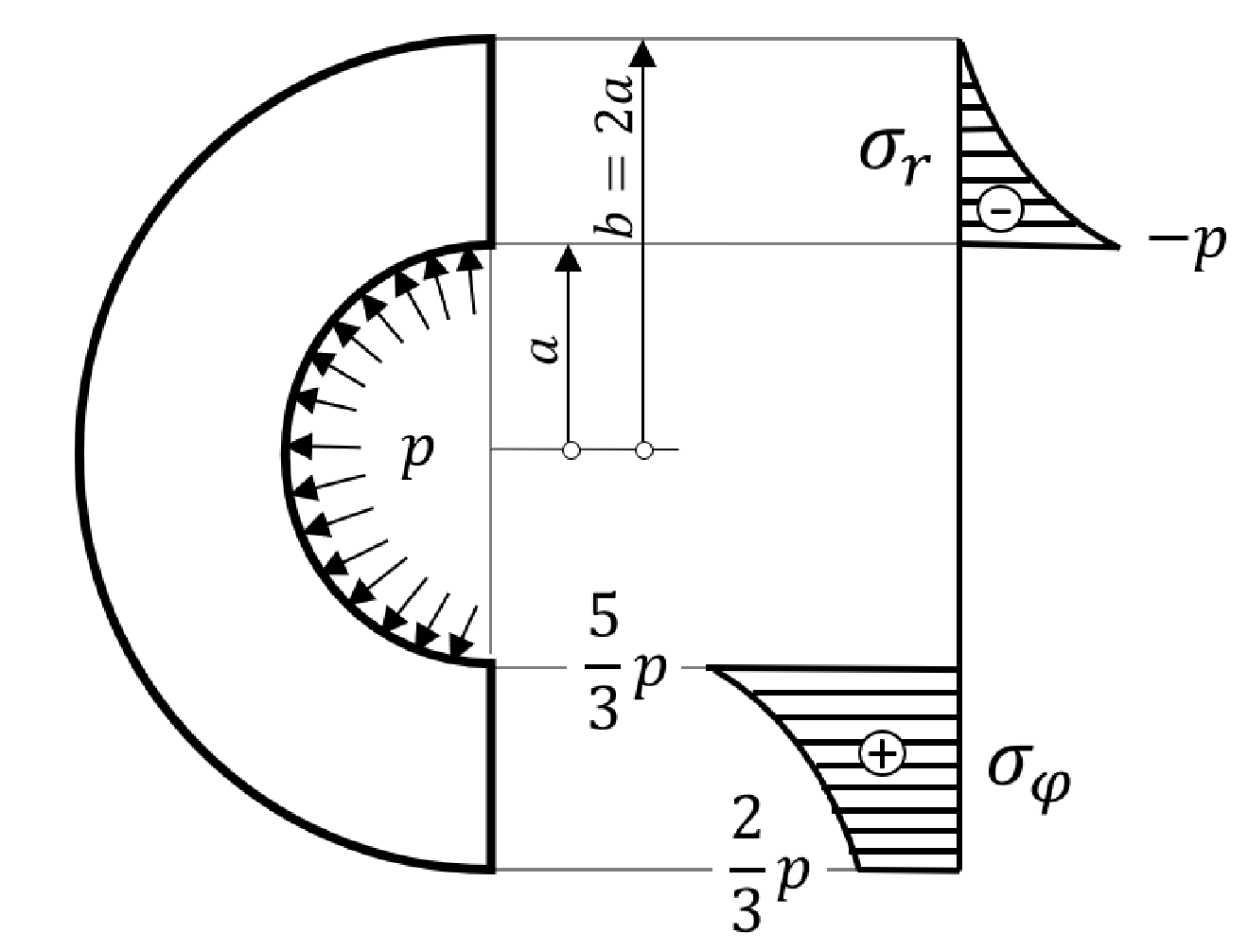
Promotrimo problem određivanja radijalnog pomaka u homogenog diska konstantnog poprečnog presjeka u obliku kružnog vijenca. Pretpostavimo da na disk djelujemo kontinuiranim i radijalno jednoliko raspoređenim opterećenjem p tako da za radijalno naprezanje \sigma_{r} vrijedi \sigma_{r}(a)=-p i \sigma_{r}(b)=0, gdje su a i b=2a polumjeri kružnog vijenca. Dodatno, pretpostavimo da je kutna brzina diska jednaka nuli.

 

 
Slika 3: Poprečni presjek homogenog kružnog diska.


Jednadžba ravnoteže dana je sa

\dfrac{d}{dr}[h(r)r\sigma_{r}]-h(r)\sigma_{\varphi}+h(r)\rho(r)\omega^{2}r^{2}=0,

pri čemu su \sigma_{r} i \sigma_{\varphi} radijalno i kružno naprezanje, h debljina diska, \rho gustoća materijala diska, a \omega kutna brzina diska oko uzdužne osi diska. Kako je disk homogen, konstantnog poprečnog presjeka, te je kutna brzina \omega jednaka nuli, gornja jednadžba postaje

(29)
\dfrac{d}{dr}[r\sigma_{r}]-\sigma_{\varphi}=0.

Nadalje, za radijalno i kružno naprezanje vrijede sljedeći zakoni ponašanja:

(30)
\sigma_{r}=\dfrac{E}{1-\nu^{2}}\left(\dfrac{d u}{d r}+\nu\dfrac{ u}{ r} \right),\, \sigma_{\varphi}=\dfrac{E}{1-\nu^{2}}\left(\dfrac{ u}{ r} +\nu\dfrac{d u}{d r}\right),

gdje je E Youngeov modul elastičnosti materijala, a \nu Poissonov koeficijent koji ovisi o vrsti materijala. Uvrštavanjem zakona ponašanja u jednadžbu (29) dobivamo

(31)
\begin{align} r^{2}\dfrac{d^{2} u}{d r^{2}}+ r\dfrac{d u}{d r}-u=0, \end{align}

što je upravo homogena Eulerova diferencijalna jednadžba drugog reda. Pripadni karakteristični polinom glasi P(\lambda)=\lambda^{2}-1, a nultočke su mu \lambda_{1}=1, i \lambda_{2}=-1. Prema Teoremu 11, rješenje jednadžbe (31) dano je s

\begin{align*} u(r)=C_{1}u_{1}(r)+C_{2}u_{2}(r)&=C_{1}r+C_{2}\dfrac{1}{r},\quad C_{1},C_{2}\in \mathbb{R}. \end{align*}

Konstante C_{1} i C_{2} lako dobivamo iz zakona ponašanja (30) i uvjeta \sigma_{r}(a)=-p i \sigma_{r}(b)=0, i vrijedi

C_{1}=\dfrac{(1-\nu)pa^{2}}{(b^{2}-a^{2})E},\,\, C_{2}=\dfrac{(1+\nu)pa^{2}b^{2}}{(b^{2}-a^{2})E}.

Stoga je radijalni pomak diska dan formulom

\begin{align*} u(r)&=\dfrac{(1-\nu)pa^{2}}{(b^{2}-a^{2})E}r+\dfrac{(1+\nu)pa^{2}b^{2}}{(b^{2}-a^{2})E}\dfrac{1}{r}. \end{align*}

 

3.4Konzola promjenjivog poprečnog presjeka

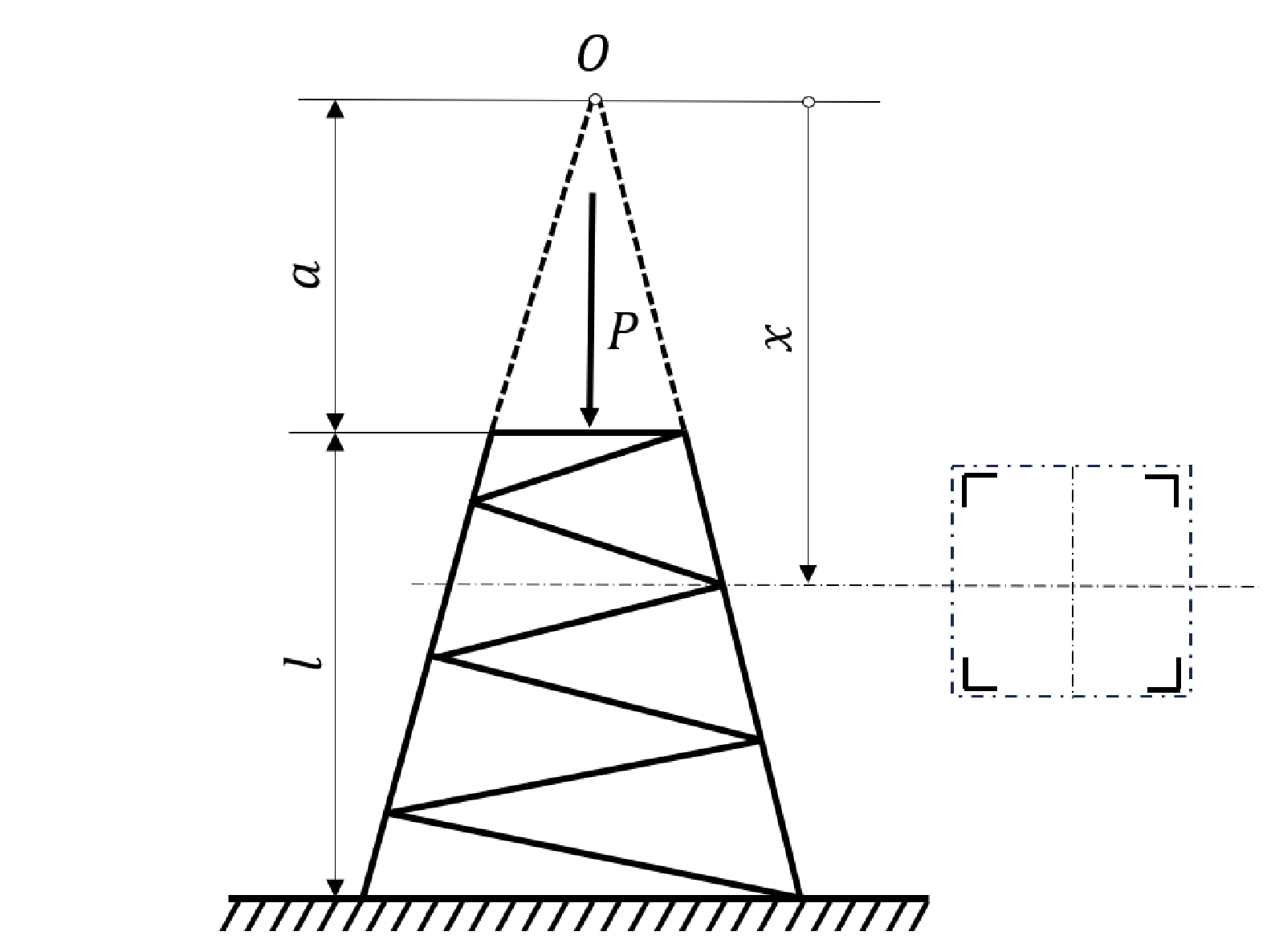
Za kraj, pronađimo kritičnu silu prilikom izvijanja konzole (štap rešetkaste strukture, eng. cantilever) promjenjivog momenta tromosti I_{x}=I_{0}x^{2}a^{-2} opterećene silom P kao na Slici 4.

 

 
Slika 4: Konzola promjenjivog poprečnog presjeka.

Kritična sila je granična vrijednost tlačne sile kod koje dolazi do gubitka stabilnosti ravnoteže, a za konzolu vrijedi

P_{kr}=\dfrac{\pi^{2}EI_{0}}{l_{b}^{2}},

pri čemu je E Youngeov modul elastičnosti materijala konzole, a l_{b} dužina izvijanja štapa. Prilikom promatranja izvijanja, zamišljenu krivulju koja uzdužno prolazi kroz štap i prati deformaciju štapa uzrokovanu tlačnom silom nazivat ćemo elastična krivulja. U slučaju konzole, diferencijalna jednadžba elastične krivulje dana je sa

\begin{align*} EI_{x}\dfrac{d^{2}w}{d x^{2}}+Pw=0, \end{align*}

gdje je w progib konzole. Jedan kraj konzole je učvršen, a drugi slobodan pa su početni uvjeti w(a)=0 i \dfrac{dw}{dx}(a+l)=0. Uzimajući u obzir izraz za I_{x}, diferencijalna jednadžba glasi

(32)
\begin{align} x^{2}\dfrac{d^{2}w}{d x^{2}}+\dfrac{Pa^{2}}{EI_{0}}w=0, \end{align}

što je Eulerova diferencijalna jednadžba drugog reda. Nultočke karakterističnog polinoma P(\lambda)=\lambda^{2}-\lambda+\dfrac{Pa^{2}}{EI_{0}} jednadžbe (32) su

\lambda_{1,2}=\dfrac{1}{2}\pm i\sqrt{\dfrac{Pa^{2}}{EI_{0}}-\dfrac{1}{4}}.

Radi lakšeg zapisa rješenja, koristimo notaciju B=\sqrt{\dfrac{Pa^{2}}{EI_{0}}-\dfrac{1}{4}}. Primjenom Teorema 11, opće rješenje jednadžbe (32) glasi

\begin{align*} w(x)=C_{1}\sqrt{x}\cos(B\ln x)+C_{2}\sqrt{x}\sin(B \ln x),\quad C_{1},C_{2}\in \mathbb{R}. \end{align*}

Može se pokazati da prethodno rješenje ima ekvivalentni zapis oblika

\begin{align*} w(x)&=C_{1}\sqrt{\dfrac{x}{a}}\cos\left(B\ln \dfrac{x}{a}\right)+C_{2}\sqrt{\dfrac{x}{a}}\sin\left(B \ln \dfrac{x}{a}\right),\quad C_{1},C_{2}\in \mathbb{R}, \end{align*}

koji ćemo iskoristiti kako bismo odredili kritičnu silu. Iz uvjeta w(a)=0 slijedi C_{1}=0, dok iz uvjeta w'(a+l)=0 dobivamo

\tan\left(B\ln\left(\dfrac{a+l}{a}\right)\right)C_{2}+2BC_{2}=0.

Kako ne želimo trivijalno rješenje w=0, smatramo da je C_{2}\neq0 pa je

\tan\left(B\ln\left(\dfrac{a+l}{a}\right)\right)+2B=0.

Ukoliko poznajemo vrijednosti l i a, numeričkim metodama možemo odrediti minimalni B što ćemo označiti sa B_{kr}. Tada je

\dfrac{EI_{0}}{a^{2}}\left(B_{kr}^{2}+\dfrac{1}{4}\right)= \dfrac{EI_{0}}{a^{2}}\left(\dfrac{P_{kr}a^{2}}{EI_{0}}-\dfrac{1}{4}+\dfrac{1}{4}\right)=P_{kr},

čime smo odredili kritičnu silu prilikom izvijanja promatrane konzole.
{8}

Bibliografija
[1] M. Alić, Obične diferencijalne jednadžbe, PMF - Matematički odjel, Zagreb, 2001.
[2] I. Alfirević, Nauka o čvrstoći I, Tehnička knjiga Zagreb, Zagreb, 1989.
[3] W.E. Boyce, R.C. DiPrima, Elementary Differential Equations and Boundary Value Problems, Seventh edition, John Wiley and Sons, Inc., New York, 2001.
[4] E.A. Coddington, R. Carlson, Linear ordinary differential equations, Society for Industrial and Applied Mathematics, Philadelphia, 1997.
[5] S. Kalabušić, E. Pilav, Obične diferencijalne jednadžbe, Prvo izdanje, Univerzitet u Sarajevu-PMF, Sarajevo, 2014.
[6] M.N.O. Sadiku, Elements of Electromagnetics, Fourth edition, Oxford University Press, Oxford, 2006.
[7] M.V. Soare, P.P. Teodorescu, I. Toma, Ordinary Differential Equations with Aplications to Mechanics, Springer, Netherlands, 2007.

 

 

  • Share this