Autori zahvaljuju prof. dr. sc. Branimiru Matijaševiću i prof. dr. sc. Zvonimiru Guzoviću na organizaciji i izvođenju eksperimenta čiji su rezultati navedeni u posljednjem odjeljku rada.
1Uvod
Tijela koja rotiraju nalazimo u mnogim mehaničkim uređajima, pa i onima kojima se i sami služimo. Ovdje ćemo se posebno baviti izduženim tijelima koja se rotiraju oko svoje „izdužene” osi. Primjer su svrdla raznih bušilica (klasične ručne ili one za bušenja u geologiji, vađenju nafte), razne osovine (vratila) za prijenos snage, kao kod automobila, brodova ili u primjeru rotora turbina elektrana.
Kod svih ovih primjera mehaničkih sustava tijelo rotira oko svoje osi. Potencijalni problemi dolaze zbog utjecaja centrifugalne sile koja teži izbaciti sustav iz pravilne vrtnje.
Tipično, to se događa za dovoljno velike brzine vrtnje. Posljedice su velike vibracije koje mogu uništiti čitav sustav. Jednom kad izgradimo konkretan sustav, relativno ga je lako eksperimentalno testirati i provjeriti radi li on korektno u radnim uvjetima. No, ako smo ga izgradili „na slijepo”, velike su šanse da nije racionalno izgrađen (ili je predimenzioniran ili iskazuje određene nedostatke, primjerice nestabilnost). Stoga je od interesa modelirati konkretni mehanički sustav da bismo ga lakše projektirali. U našem konkretnom slučaju poželjno je unaprijed znati koje su to brzine koje će producirati nestabilnu vrtnju.
U ovom nam je radu u cilju izložiti čitav proces modeliranja rotirajućih štapova. Počinjemo s opisom teorije i smještanjem problema u okvire te teorije. Zatim tu teoriju primjenjujemo na konkretni problem rotirajućeg štapa. Dobiveni model smještamo u matematički kontekst, te matematički analiziramo problem. Nakon toga određujemo analitička rješenja problema za neke specijalne slučajeve (i jedine kada je to i moguće u našem primjeru), te donosimo numeričke aproksimacije rješenja. Na kraju uspoređujemo dobivene rezultate (analitičke i numeričke) s rezultatima eksperimenta, te time konačno potvrđujemo model.
2Model elastičnog štapa
2.1Geometrija štapa
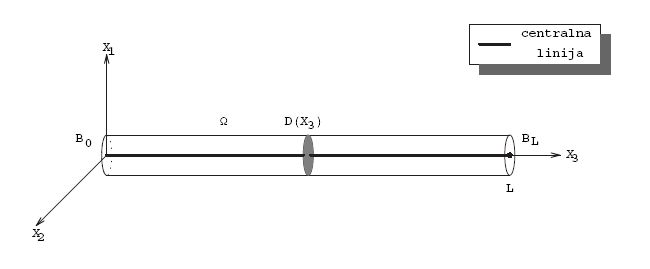
„Izduženo” tijelo koje se rotira u nastavku nazivamo tanki štap. Tanki štap
\Omega \subset \mathbb{R}^{3} opisujemo kao trodimenzionalno tijelo kojem su dvije dimenzije („debljine”) malene u odnosu na treću („duljinu”,
L\gt 0):
u inženjerskoj literaturi tipično se pretpostavlja da je debljina / duljina
\lt 1/ 30. Malo preciznije, neka je dana familija
\lbrace D(x_{3})\subset \mathbb{R}^{2}_{x_{1} x_{2}}: x_{3} \in (0, L)\rbrace. Štap definiramo s
(1)
\Omega = \left\lbrace x=(x_{1}, x_{2}, x_{3}) \in \mathbb{R}^{3} : (x_{1}, x_{2}) \in D(x_{3}), x_{3} \in (0, L)\right\rbrace .
Skupove
D(x_{3}) zovemo poprečni presjeci štapa u točki
x_{3}. Dopuštamo ovisnost o točki poprečnog presjeka jer su nam baš takvi i realni primjeri. Sada tankoću štapa iskazujemo zahtjevom:
\mathop{\rm diam}\nolimits{D(x_{3})}\ll L. Specijalno, od interesa će nam biti samo ravni štap. To je onaj kojemu je centralna linija (linija koja prolazi kroz težišta poprečnih presjeka) ravna. Stoga pretpostavljamo da vrijedi
\mathop{\int\!\!\!\int}\limits_{D(x_{3})} x_{\alpha} \, dx_{1} dx_{2} =0, \quad \alpha=1, 2, \quad x_{3} \in (0, L).
Radi jednostavnosti, ovdje dodatno pretpostavljamo da poprečni presjeci zadovoljavaju dodatni uvjet simetrije
\mathop{\int\!\!\!\int}\limits_{D(x_{3})} x_{1} x_{2} \, dx_{1} dx_{2} = 0, \qquad x_{3} \in (0, L)
(zadovoljen je, naprimjer, za kružni i pravokutni poprečni presjek).
2.2Elastičnost
Djelujući silom naprimjer na tanki čelični štap, on se deformira. Uklonimo li silu kojom smo djelovali, štap se vraća u nedeformirani (prvobitni) položaj. Tipičan primjer takvog ponašanja je opruga. Tijela koja se pri djelovanju sile deformiraju, a nakon uklanjanja sile vraćaju u prvobitni položaj, nazivamo elastičnim tijelima, a teoriju koja se njima bavi teorijom elastičnosti.
Tanki elastični štap je prema prethodnom opisu trodimenzionalno elastično tijelo. Jednadžbe trodimenzionalne teorije elastičnosti, čak i one linearizirane (pojednostavljene uz pretpostavku neznatne deformacije), komplicirane su. No, u slučaju posebnih geometrija tijela, kao u slučaju štapa, moguće je izvesti jednostavnije modele ponašanja (slično je u primjeru opruge, koja je trodimenzionalno elastično tijelo; njeno je ponašanje vrlo kompleksno za precizan opis, ali znamo da je „osnovno” ponašanje modelirano jednadžbom
F=k x;
F je sila koju primjenimo na oprugu,
x pripadno izduženje (skraćenje) opruge, a
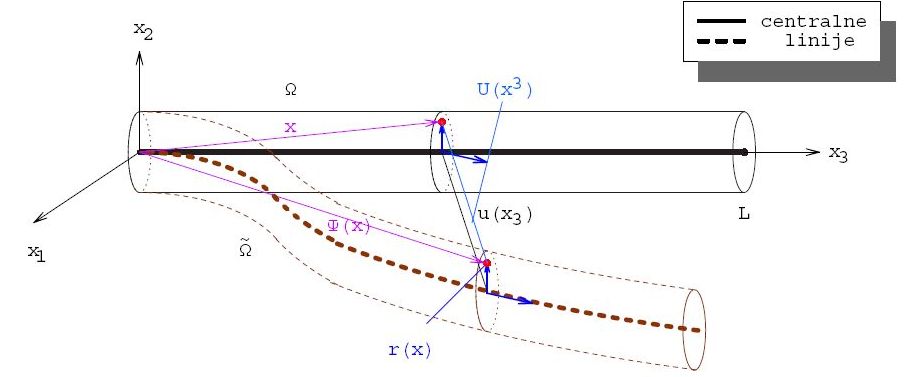
k krutost opruge). Geometrijski tanki štap možemo „dobro” opisati njegovom centralnom krivuljom, parametriziranom s
(0,0,x_{3}),
x_{3}\in (0,L), a „dobro” ovdje znači do na najveći dijametar poprečnih presjeka. Pokazuje se da se i deformacija tankog elastičnog štapa može opisati deformacijom centralne krivulje štapa, parametriziranom s
\mathbf{\Psi}(x_{3}) \in \mathbb{R}^{3},
x_{3}\in (0,L).
I opet je pogreška takvog modela, među ostalim, vezana za najveći dijametar poprečnih presjeka. Izvod takvog modela daje i malo više. Naime, pokazuje se da se deformacija tankog elastičnog štapa može opisati kroz deformaciju centralne linije štapa, te kroz infinitezimalnu krutu deformaciju poprečnih presjeka (infinitezimalna kruta deformacija je translacija i rotacija, s tim da je rotacija aproksimirana sumom matrica
I+A, gdje je
I identiteta, a
A antisimetrična matrica. Naime, može se pokazati da je svaka rotacija
R=e^{A}, za neku antisimetričnu matricu, pa je
I+A zapravo Taylorov polinom 1. stupnja za
R).
Takva deformacija
\mathbf{\Psi}(x),
x \in \Omega s pomoću pomaka
\mathbf{U}(x) = \mathbf{\Psi}(x) - x može se zapisati formulama
(2)
\begin{eqnarray} U_{1} (x) &=& u_{1} (x_{3}) - x_{2} \omega (x_{3}),\\ U_{2} (x) &=& u_{2} (x_{3}) + x_{1} \omega (x_{3}),\\ U_{3} (x) &=& u_{3} (x_{3}) - x_{1} u'_{1} (x_{3}) - x_{2} u'_{2} (x_{3}). \end{eqnarray}
Ovdje je
\mathbf{u}(x_{3})=(u_{1}(x_{3}),u_{2}(x_{3}),u_{3}(x_{3})) pomak točke
(0,0,x_{3}) centralne linije štapa,
u'_{1}(x_{3}) opisuje kut zakreta poprečnog presjeka na mjestu
x_{3} oko osi
\mathbf{e}_{2},
u'_{2}(x_{3}) opisuje kut zakreta poprečnog presjeka na mjestu
x_{3} oko osi
\mathbf{e}_{1}, a
\omega(x_{3}) opisuje kut zakreta poprečnog presjeka na mjestu
x_{3} oko osi
\mathbf{e}_{3} (torziju). Ovakav oblik pomaka naziva se Bernoulli–Navierov (ili Kirchhoff–Love) pomak.
Budući da ćemo promatrati stabilnost rotirajućeg štapa u odnosu na transverzalni pomak (okomit na centralnu liniju), u nastavku pišemo samo jednadžbe koje zadovoljavaju transverzalni pomaci
(u_{1},u_{2}). To su obične diferencijalne jednadžbe četvrtog reda:
(3)
\begin{eqnarray} &&E \left(I_{1} u''_{1}\right)'' - \left(\sigma u_{1}'\right)' - f_{1} + m_{2}' =0,\\ &&E \left(I_{2} u''_{2}\right)'' - \left(\sigma u_{2}'\right)' - f_{2} - m_{1}' =0. \end{eqnarray}
(vidi npr.
[4],
[6]). Ovdje su
(f_{1}, f_{2}) i
(m_{1}, m_{2}), redom, linijska gustoća transverzalne sile i momenta (to znači da je
\int_{a}^{b} f_{1} dx_{3} komponenta ukupne sile u smjeru
\mathbf{e}_{1}=(1,0,0) na komad štapa
\lbrace x\in \mathbb{R}^{3}: (x_{1},x_{2} \in D(x_{3})), x_{3} \in [a,b]\rbrace).
E\gt 0 je Youngov modul elastičnosti materijala (opisuje svojstvo materijala od kojeg je štap napravljen), a
I_{\alpha} (x_{3}),
\alpha=1, 2, su momenti inercije poprečnog presjeka
D(x_{3}) – opisuju geometriju poprečnog presjeka štapa:
I_{\alpha} (x_{3}) = \mathop{\int\!\!\!\int}\limits_{D(x_{3})} x_{\alpha}^{2} \, dx_{1} dx_{2}, \quad \alpha = 1, 2.
Funkcija
\sigma(x_{3}) je longitudinalna napetost štapa (npr. u slučaju bušilice sila kojom je pritišćemo primjerice na zid). Strogi izvod ovog modela može se naći u
[6] i
[7].
3Rotirajući elastični štap
U nastavku ćemo iskoristiti model (
3) za štap koji se rotira konstantnom kutnom brzinom
\gamma, te na njega ne djeluju druge sile osim centrifugalne. Očito je riječ o dinamičkom problemu, što znači da bismo se morali koristiti jednadžbama gibanja, a ne ravnoteže. No, ako odaberemo koordinatni sustav vezan za štap koji se rotira, u tom koordinatnom sustavu štap miruje. U modelu (
3) transverzalni pomak uzrokovan je centrifugalnom silom i njome uzrokovanim momentom. Stoga ih, u koordinatnom sustavu u kojem štap miruje, računamo po formulama
(4a)
\mathbf{f}(x_{3}) = - \varrho \mathop{\int\!\!\!\int}\limits_{D(x_{3})} \gamma \mathbf{e}_{3} \times \left(\gamma \mathbf{e}_{3} \times \left( x + \mathbf{U}(x)\right)\right) \, dx_{1} dx_{2},
(4b)
\mathbf{m}(x_{3}) = - \varrho \mathop{\int\!\!\!\int}\limits_{D(x_{3})} \left(x + \mathbf{U}(x) - (x_{3} \mathbf{e}_{3} + \mathbf{u}(x_{3}))\right) \times\left(\gamma \mathbf{e}_{3} \times \left(\gamma \mathbf{e}_{3} \times \left(x + \mathbf{U}(x)\right)\right)\right) \, dx_{1} dx_{2},
gdje je
\mathbf{e}_{3} =(0, 0, 1);
\varrho \in \mathbb{R}^{+} je linijska gustoća mase (
\rho d je masa komada štapa duljine
d), a
\times označava vektorski produkt (ovo su uobičajene formule za centrifugalnu silu
\mathbf{\gamma} \times (\mathbf{\gamma} \times \mathbf{r}), gdje je
\mathbf{\gamma} vektor kutne brzine, a
\mathbf{r} radij vektor mase; jedini je dodatak integral po svim točkama tijela jer nije riječ o masi u točki).
Koristeći Bernoulli-Navierov oblik pomaka (
2), u stanju smo prikazati silu i moment s pomoću transverzalnog pomaka centralne linije:
(5)
f_{1} = \varrho S \gamma^{2} u_{1}, \quad f_{2} = \varrho S \gamma^{2} u_{2},\quad m_{1} = \varrho I_{2} \gamma^{2} u_{2}', \quad m_{2} = - \varrho I_{1} \gamma^{2} u_{1}';
ovdje je
S(x_{3}) = | D(x_{3})| površina poprečnog presjeka na mjestu
x_{3}.
Uvrštavanjem ovih sila i momenata u jednadžbe modela (
3) dobivamo dvije jednadžbe
\left(I_{\alpha} u''_{\alpha}\right)'' - \frac{1}{E} \left(\sigma u'_{\alpha}\right)' - \lambda \left(\left( I_{\alpha} u'_{\alpha}\right)'+S u_{\alpha} \right) = 0,\qquad \alpha=1,2,
gdje smo uveli konstantu
(6)
\lambda = \frac{\varrho \gamma^{2}}{E}.
Ovo su jednadžbe za transverzalni pomak u oba transverzalna smjera. S obzirom na to da su jednadžbe iste, u nastavku pišemo samo jednu
(7)
\left(I_{\alpha} u''\right)'' - \frac{1}{E} \left(\sigma u'\right)' - \lambda \left(\left( I u'\right)'+S u\right) = 0.
U slučaju kada su oba kraja štapa ukliještena (nije dopušten progib ni rotacija poprečnog presjeka na rubu), uz ovu jednadžbu pridružujemo i rubne uvjete
(8)
u = u' =0 \text{ za } x=0, L.
U slučaju kad su oba kraja učvršćena šarnirom (nije dopušten progib, dok je rotacija slobodna na krajevima), rubni uvjeti su
(9)
u = u'' =0 \text{ za } x=0, L.
4Kritična brzina štapa
Zadaća za pomak štapa pri rotaciji sada glasi: naći funkciju
u koja zadovoljava jednadžbu (
7) te jedan od rubnih uvjeta (
8) ili (
9), ovisno o problemu koji promatramo (čak možemo i kombinirati različite rubne uvjete na oba kraja). Jasno je da za svaki
\lambda \in \mathbb{R} jedno rješenje ovih zadaća funkcija
u=0. Pitanje je postoje li možda i neka druga rješenja za određene
\lambda (možda ne za sve). Stoga je i
\lambda nepoznanica u problemu i on sada glasi: naći sve
\lambda \in \mathbb{R} i funkcije
u koje nisu nul-funkcije za koje vrijedi
(10)
\begin{split} &\left(I u''\right)'' - \frac{1}{E} \left(\sigma u'\right)' = \lambda \left(\left( I u'\right)'+S u\right),\\ & u(0) = u'(0)= u(L) = u'(L) =0, \end{split}
ili u slučaju drugih rubnih uvjeta
(11)
\begin{split} &\left(I u''\right)'' - \frac{1}{E} \left(\sigma u'\right)' = \lambda \left(\left( I u'\right)'+S u\right),\\ & u(0) = u''(0)= u(L) = u''(L) =0. \end{split}
Zadaće ovog tipa nazivaju se svojstvene zadaće (ili spektralne zadaće), a ovo su primjeri svojstvenih zadaća za linearni diferencijalni operator (4. reda). Rješenja su zapravo uređeni parovi
(\lambda, u_{\lambda}) realnog broja
\lambda i nenul-funkcije
u_{\lambda} koja rješava rubnu zadaću za diferencijalnu jednadžbu za dani
\lambda.
\lambda se naziva svojstvena vrijednost, a pripadni
u_{\lambda} svojstveni vektor ili svojstvena funkcija. Za primijetiti je da takav
u_{\lambda} nije jedinstven jer je i svaka funkcija oblika
c u_{\lambda}, za
c\in \mathbb{R} također svojstvena funkcija.
Najjednostavniji primjer svojstvenih zadaća su svojstvene zadaće za linearne operatore na konačnodimenzionalnim vektorskim prostorima koje se reduciraju na matrične svojstvene zadaće (vidi Linearnu algebru).
Matematička teorija ovakvih svojstvenih zadaća bazirana je na spektralnoj teoriji kompaktnih linearnih operatora
[3]. Osnovni je rezultat za našu svojstvenu zadaću da je spektar (skup svih svojstvenih vrijednosti) prebrojiv (ima članova koliko ima i prirodnih brojeva), te da nema konačnog gomilišta. Ovo zajedno daje da je spektar diskretan. Spektar u nastavku označavamo s
\Lambda.
U ovom problemu nenul–rješenja dolaze iz dvaju izvora: rotacije štapa te longitudinalne sile koja djeluje na štap. Naprimjer, pretpostavimo da se štap ne rotira; uzmemo li dovoljno tanki čelični štap i pritisnemo li ga duž osi štapa, doći će do transverzalnog progiba ako smo primijenili dovoljno veliku silu.
Taj slučaj nestabilnosti bez vrtnje (Eulerova nestabilnost, vidi
[4]) ovdje isključujemo zahtjevom (vidi
[1])
\sigma_{\min{}} + E I_{\min{}} \left( \frac{\pi}{L}\right)^{2} \gt 0,
pri čemu je
\sigma_{\min{}} = \min_{x_{3} \in [0, L]}{\sigma(x_{3})}, \quad I_{\min{}} ={\min_{x_{3} \in [0, L]}{I (x_{3})}}.
Zbog definicije broja
\lambda u (
6) i našeg problema jasno je da su nam od interesa samo
\lambda \gt 0. Stoga se ograničavamo na promatranje skupa
\Lambda \cap \mathbb{R}^{+}. Označimo
\lambda_{0} = \min \Lambda \cap \mathbb{R}^{+},
s tim da definiramo
\lambda_{0} = +\infty ako je skup
\Lambda \cap \mathbb{R}^{+} prazan. Sada je štap stabilan za kutne brzine rotacije
\gamma koje zadovoljavaju
0 \lt \gamma \lt \gamma_{\scriptsize{\mbox{kritična}}} = \left( \frac{E\lambda_{0}}{\varrho}\right)^{1/2}.
Kutnu brzinu vrtnje
\gamma_{\scriptsize{\mbox{kritična}}} zovemo kritična brzina. Osim u jednom, dva slučaja kritičnu brzinu nije moguće točno izračunati. Ostaju nam dvije mogućnosti aproksimacije kritične brzine. Jedna je bazirana na analitičkoj ocjeni kritične brzine odozdo i izvedena je u
[1]. Druga je numerička aproksimacija bazirana na metodi konačnih elemenata (Finite Element Method, FEM) i prikazana je u
[5]. Analitičku ocjenu odozdo donosimo sljedećem teoremu
Teorem 1.(
[1]) Neka je
S_{\max} = \max_{x_{3} \in [0, L]}{S(x_{3})}. Tada vrijedi
\begin{eqnarray*} &&S_{\max} \leq \left( \frac{\pi}{L}\right)^{2} I_{\min},\qquad \Rightarrow \qquad \gamma_{\scriptsize{\mbox{crit}}} = \infty,\\ &&S_{\max} \gt \left( \frac{\pi}{L}\right)^{2} I_{\min},\qquad \Rightarrow \qquad \gamma_{\scriptsize{\mbox{crit}}} \geq \overline{\gamma}= \frac{\pi}{L} \varrho^{-1/2} \left( \frac{\sigma_{\min} + E I_{\min} \left( \frac{\pi}{L}\right)^{2}}{S_{\max} - I_{\min} \left( \frac{\pi}{L}\right)^{2}}\right)^{1/2}. \end{eqnarray*}
Ovaj rezultat zapravo kaže: ako je štap dovoljno „debeo” nema nestabilnosti; inače, nestabilnost je moguća samo za brzine rotacije veće od
\overline{\gamma}.
5Primjeri
Ovdje donosimo dva primjera. U prvom primjeru (vjerojatno je i jedini takav) znamo izračunati analitička rješenja našeg problema. U drugom primjeru svedemo određivanje svojstvenih vrijednosti na problem nultočaka nelinearne funkcije. U oba slučaja riječ je o štapu konstantnog poprečnog presjeka te konstantne uzdužne sile
\sigma. Za sve druge slučajeve zadaću moramo numerički rješavati.
Primjer 2.(
[2), str. 116.] Neka je poprečni presjek konstantan. Tada su
I, S konstante. Pretpostavimo nadalje da je
\sigma \geq 0 konstanta. Označimo
\theta = \frac{\sigma}{E I}. Tada zadaća (
11) poprima oblik
(12)
\begin{split} &u'''' - (\theta + \lambda ) u'' - \lambda \frac{S}{I} u = 0,\\ &u(0)=u''(0)=u(L)=u''(L)=0. \end{split}
Ovu diferencijalnu jednadžbu možemo riješiti eksplicitno (naći opće rješenje, tj. odrediti skup svih rješenja), te iskoristiti rubne uvjete da bismo riješili i svojstvenu zadaću (tj. skup nenul–rješenja zadaće). Više o diferencijalnim jednadžbama te rješavanju običnih diferencijalnih jednadžbi možete naći u
[8]. Karakteristična jednadžba pripadna jednadžbi (
12) glasi
k^{4} - (\theta + \lambda) k^{2} - \lambda \frac{S}{I} =0.
Za nultočke ove jednadžbe vrijedi
(k^{2})_{1/2} = \frac{1}{2} (\theta + \lambda) \pm \sqrt{\frac{1}{4} (\theta + \lambda)^{2} + \lambda \frac{S}{I}}.
Budući da tražimo nenegativne svojstvene vrijednosti, označimo li
(13)
\alpha = \left( \frac{1}{2} (\theta + \lambda) + \sqrt{\frac{1}{4} (\theta + \lambda)^{2} + \lambda \frac{S}{I}}\right)^{1/2},\quad \beta = \left( -\frac{1}{2} (\theta + \lambda) + \sqrt{\frac{1}{4} (\theta + \lambda)^{2} + \lambda \frac{S}{I}}\right)^{1/2},
rješenja karakteristične jednadžbe su
\alpha, - \alpha, i \beta, - i \beta, pa je opće rješenje jednadžbe (
12) oblika
u(z) = A \mathop{\rm sh}\nolimits{\alpha z} + B \mathop{\rm ch}\nolimits{\alpha z} + C \sin{\beta z} + D \cos{\beta z},
jer su
\alpha \ne 0 i
\beta \ne 0. Iz rubnih uvjeta (
12) na lijevoj bazi štapa slijedi
B=D=0, dok iz rubnih uvjeta na desnoj bazi slijedi
\begin{eqnarray*} 0 &=& A \mathop{\rm sh}\nolimits{\alpha L} + C \sin{\beta L},\\ 0 &=& A \alpha^{2} \mathop{\rm sh}\nolimits{\alpha L} - C \beta^{2} \sin{\beta L}. \end{eqnarray*}
Ovaj sustav ima netrivijalna rješenja ako je determinanta sustava jednaka nuli:
-(\alpha^{2} + \beta^{2}) \mathop{\rm sh}\nolimits{\alpha L} \sin{\beta L} =0.
Slijedi da svojstvenih vrijednosti
\lambda ima prebrojivo (kao što smo i znali) te da su one određene jednadžbom
\beta_{n} L = n \pi, \quad n \in \mathbb{N}.
Stoga su svojstvene vrijednosti dane s
\lambda_{n} = \left( \frac{n \pi}{L}\right)^{2} \frac{\frac{\sigma}{E I}\left( \frac{n\pi}{L}\right)^{2}}{\frac{S}{I} - \left( \frac{n \pi}{L}\right)^{2}}, \quad n \in \mathbb{N}.
Najmanja svojstvena vrijednost dobiva se za
n=1 te je kritična brzina dana izrazom
\gamma_{\scriptsize{\mbox{kritična}}} = \gamma_{1} = \sqrt{\frac{E \lambda_{1}}{\varrho}} = \frac{\pi}{L} \sqrt{\frac{\frac{\sigma}{I} + E \left( \frac{\pi}{L}\right)^{2}}{\varrho \left( \frac{S}{I} - \left( \frac{\pi}{L}\right)^{2}\right)}}.
Označimo
(14)
c = \frac{\sigma L^{2}}{E I}, \quad d = \frac{I}{S L^{2}}\lt \frac{1}{\pi^{2}}.
Sada kritičnu brzinu možemo zapisati s
(15)
\gamma_{\scriptsize{\mbox{kritična}}} = \frac{1}{L} \left( \frac{E}{\varrho}\right)^{1/2} \gamma_{0}, \qquad \gamma_{0} = \pi \left(d \frac{c + \pi^{2}}{1 - d \pi^{2}}\right)^{1/2}.
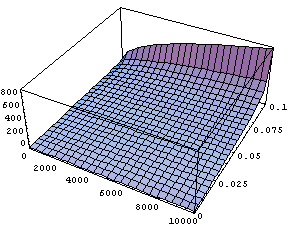
Graf od
\gamma_{0} u ovisnosti o parametrima
c i
d dan je na Slici
10.
Parametar
c možemo interpretirati kao uzdužnu silu i nalazi se na osi
x, dok parametar
d možemo interpretirati kao „debljinu” štapa i nalazi se na osi
y (argument ide do
1/\pi^{2}). Zaključujemo da što je štap deblji, kritična brzina je veća, pa je štap stabilniji. Također, što je uzdužna sila veća, dobivamo stabilniji štap.
U Tablici
1 vrijednosti
\gamma_{\scriptsize{\mbox{kritična}}} za čelični štap duljine
L=1\,{\text{m}} kružnog poprečnog presjeka dane su u ovisnosti o radijusu štapa
R. I ovdje vidimo da „deblji” štap postaje stabilniji. Brzinu
\gamma koja odgovara 2. svojstvenoj vrijednosti nazivamo 2. kritična brzina, te tako redom dalje. I ove su brzine od interesa jer se ponekad radna brzina vrtnje sustava nalazi između 1. i 2. kritične brzine.
| R[m] |
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
0.06 |
0.07 |
0.08 |
0.09 |
0.1 |
| \gamma_{\scriptsize{\mbox{kritična}}}[rpm] |
2440 |
4883 |
7329 |
9781 |
12240 |
14708 |
17187 |
19679 |
22186 |
24711 |
Tablica 1: Kritične brzine u okretajima u minuti za različite radijuse štapa
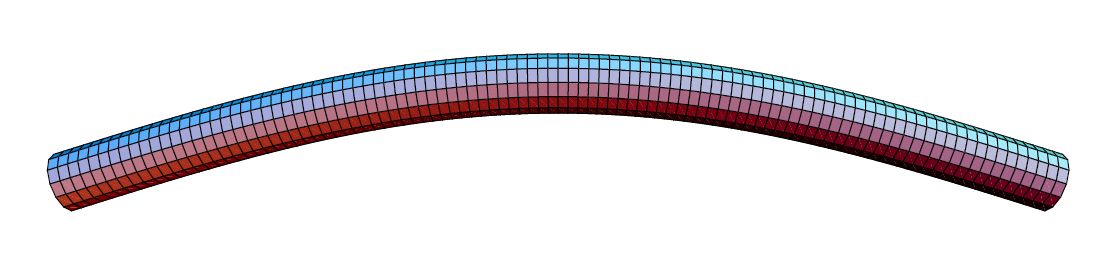
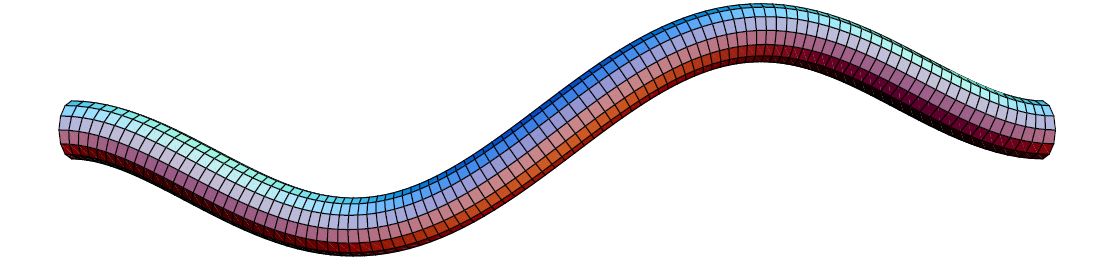
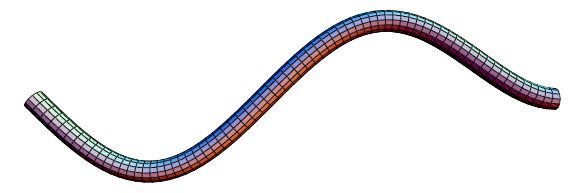
Slike položaja pri prve dvije kritične brzine su na Slikama
11,
12.
Primjer 3.[
[2], str. 116.] Neka je poprečni presjek konstantan. Tada su
I i
S konstante. Uz oznaku
\theta = \frac{\sigma}{E I} i pretpostavku
\sigma\geq 0 jednadžba (
10) poprima oblik
(16)
\begin{split} &u'''' - (\theta + \lambda ) u'' - \lambda \frac{S}{I} u = 0,\\ &u(0)=u'(0)=u(L)=u'(L)=0. \end{split}
U ovom slučju ne možemo izračunati kritičnu brzinu analitički, već je određena najmanjom pozitivnom nultočkom eksplicitno dobivene nelinearne funkcije. Potpuni račun možete naći u
[2].
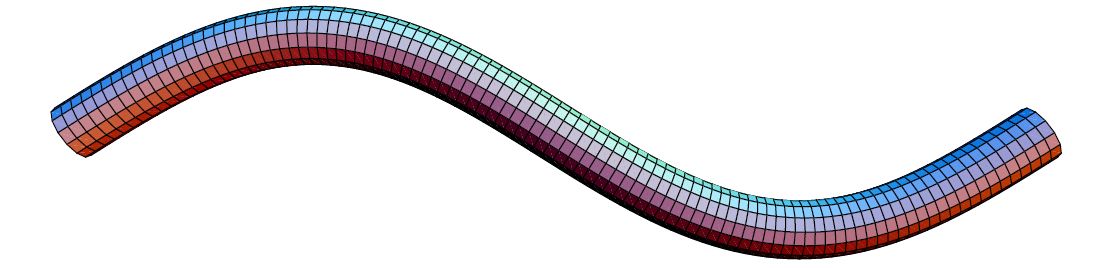
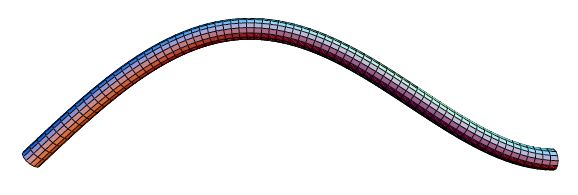
Slike položaja pri prve dvije kritične brzine su na Slikama
13,
14. Obratite pozornost na ponašanje štapa na krajevima.
U Tablici
2 vrijednosti
\gamma_{\scriptsize{\mbox{kritična}}} za ravni čelični štap duljine
L=1m s kružnim poprečnim presjekom dane su u ovisnosti o radijusu
R. Uspoređujući ove vrijednosti s Tablicom
1, vidimo da je u ovom primjeru štap stabilniji, što je i očekivano.
| R[m] |
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
0.06 |
0.07 |
0.08 |
0.09 |
0.1 |
| \gamma_{\scriptsize{\mbox{crit}}}[rpm] |
5533 |
11071 |
16619 |
22183 |
27768 |
33378 |
39020 |
44699 |
50421 |
56192 |
Tablica 2: Kritične brzine u okretajima u minuti u odnosu na radijus
R štapa
6Numerički rezultati
Model rotirajućeg štapa nije moguće analitički riješiti čim neki od koeficijenata nije konstantan (npr. poprečni presjek nije konstantnog radijusa duž štapa). U svim tim slučajevima problem rješavamo numerički, metodom konačnih elemenata, vidi
[5].
Primjer 4.[Varijabilni poprečni presjek] U ovom primjeru promatramo štap duljine
L=1m, radijusa poprečnog presjeka
R(x) = \left\lbrace \begin{array}{ll} 0.01\text{m} & x\in [0, 0.4\rangle \cup \langle 0.6, 1],\\ \tilde{r} & x \in [0.4,0.6], \end{array} \right.
pri čemu ćemo
\tilde{r} \geq 0.01m mijenjati, izrađen od čelika (
\rho=7850{\text{k}g/m^{3}},
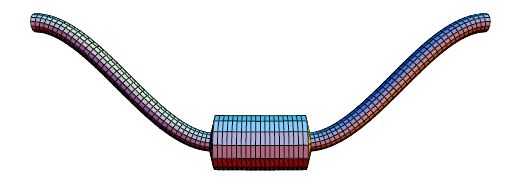
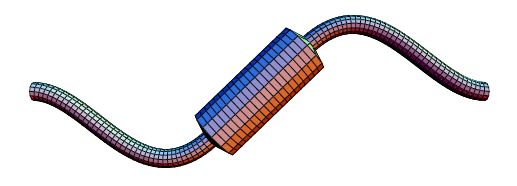
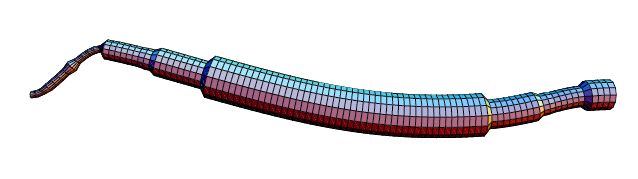
E=2.1\, 10^{11}Pa). Tipični položaj pri prve dvije kritične brzine prikazan je na Slikama
15,
16.
Zanimljivije je pogledati ovisnost (prve) kritične brzine o radijusu zadebljanog dijela
\tilde{r}. Vrijednosti su dane u Tablici
3.
| \tilde{r}[m] |
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
0.06 |
0.07 |
0.08 |
0.09 |
0.1 |
| \gamma_{\scriptsize{\mbox{crit}}}[rpm] |
5533 |
4466 |
3294 |
2560 |
2082 |
1751 |
1509 |
1325 |
1180 |
1064 |
Tablica 3: Kritične brzine u okretajima u minuti u ovisnosti o radijusu
\tilde{r} proširenog dijela štapa
Vidimo da kritična brzina opada s povećanjem radijusa, tj. sustav postaje nestabilniji, kao što je i očekivano.
Primjer 5.[Svrdlo, povećavamo kontaktnu silu] U ovom primjeru analiziramo promjenu kritične brzine pri promjeni kontaktne sile. Pri tome imamo u vidu primjer bušilice. Svrdlo na strani bušilice smatramo ukliještenim, dok na vrhu svrdla postavljamo rubni uvjet šarnira
(17)
u(0)= u''(0)= u(L)= u'(L)=0.
Duljina svrdla u ovom primjeru je
L=0.6m, promjer je
2R=0.01m, dok je svrdlo napravljeno od čelika. I opet je zanimljivo pogledati kako se mijenja kritična brzina, ovaj put u ovisnosti o kontaktnoj sili
\sigma, Tablica
4. Negativan predznak znači da je sila kompresija.
| \sigma[N] |
0 |
-1000 |
-2000 |
-3000 |
-4000 |
-5000 |
-5600 |
-5700 |
-5780 |
-5781 |
| \gamma_{\scriptsize{\mbox{crit}}}[rpm] |
5296 |
4826 |
4301 |
3697 |
2966 |
1970 |
951 |
638 |
86 |
49 |
Tablica 4: Kritične brzine u okretajima u minuti u ovisnosti o kompresivnoj kontaktnoj sili
\sigma
Iz rezultata vidimo da kako povećavamo iznos sile, kritična brzina opada, a rezultati sugeriraju da kritična brzina ide u 0, kako i teorija predviđa, i dovodi do Eulerove nestabilnosti ili bucklinga, tj. nestabilnosti i bez vrtnje. Položaj pri prve dvije kritične brzine dan je na slikama
17 i
18.
Primjer 6.[Svrdlo, mijenjamo duljinu] U ovom primjeru ponovo promatramo svrdlo, pa su nam rubni uvjeti isti kao u (
17). Stoga su položaji pri kritičnim brzinama kao u prethodnom primjeru (slikama
17 i
18). Razlika je u tome da sada analiziramo ovisnost o duljini svrdla. Ovo je posebno važno npr. u geologiji, posebno kod naftnih bušotina. Promjer je i dalje
2R=0.01m, a svrdlo je čelično. Duljinu uzimamo od
1m do
40m. Kritične brzine su u Tablici
5.
| L[m] |
1 |
5 |
10 |
15 |
20 |
40 |
| \gamma_{\scriptsize{\mbox{crit}}}[rpm] |
1906 |
76 |
19 |
8 |
5 |
1 |
Tablica 5: Kritične brzine u okretajima u minuti u ovisnosti o duljini svrdla
Naravno, svrdlo promjera
1cm i duljine
40m nikad nismo vidjeli, a razlog se vidi u ovim rezultatima.
Primjer 7.[Osovina generatora] Jedan mogući izgled osovine generatora dan je na Slici
19.
Duljina osovine je
L=2.165m, presjeci su kružni maksimalnog promjera
2R=0.116m, a za materijal izrade uzet je čelik. Na slikama
20 i
21 su položaji osovine pri prve dvije kritične brzine.
Dobivene kritične brzine nalaze se u Tablici
6.
| kritična brzina |
1 |
2 |
3 |
4 |
| \gamma_{\scriptsize{\mbox{i}}}[rpm] |
492 |
2225 |
5654 |
62075 |
Tablica 6: kritične brzine u okretajima u minutu u ovisnosti o duljini svrdla
Ovi rezultati ipak nisu sasvim realni jer se provodi dodatna stabilizacija osovine koja nije uzeta u obzir u promatranom modelu.
7Eksperiment
Da bismo neki model upotrijebili u praksi, najčešće je nužna verifikacija modela s pomoću eksperimenta. Postavljanje i vođenje eksperimenta iznimno je zahtjevan zadatak te traži puno inženjerskog znanja i iskustva. Fizikalni model izrađen je i ispitivan na Katedri za turbostrojeve Fakulteta strojarstva i brodogradnje Sveučilišta u Zagrebu. Eksperiment su organizirali i vodili prof. dr. sc. Branimir Matijašević i prof. dr. sc. Zvonimir Guzović.
Osnovni podaci eksperimenta su sljedeći:
| \bullet |
duljina štapa: L=0.835m |
| \bullet |
promjer štapa: 2R=0.01m |
| \bullet |
uzdužna napetost: \sigma = 0N |
| \bullet |
materijal štapa: čelik |
| \bullet |
Youngov modul elastičnosti: E=2.1 \, 10^{11}Pa |
| \bullet |
gustoća: \varrho = 7800 \frac{\text{kg}}{\text{m}^{3}} |
Obavljena su dva eksperimenta — jedan za ukliještene krajeve i jedan za krajeve učvršćene šarnirom. Za određivanje kritične brzine korišten je stroboskop (Slika
23),
dok je za rotaciju štapa korišten elektromotor (Slika
24).
Ograničenja korištenih uređaja omogućila su određivanje samo prvih dviju kritičnih brzina.
7.11. eksperiment: šarnir
U slučaju ovih rubnih uvjeta, matematički model te eksperiment daju rezultate u Tablici
7.
| |
\gamma_{1}[rpm] |
\gamma_{1}[rpm] |
\gamma_{1}[rpm] |
\gamma_{1}[rpm] |
| Model |
1754 |
7015 |
15788 |
28076 |
| Eksperiment |
1744 |
6830 |
- |
- |
Tablica 7: Rezultati dobiveni iz matematičkog modela i eksperimenta
Iz rezultata vidimo da je razlika za prvu kritičnu brzinu ispod 1%, a za drugu ispod 3%.
7.22. eksperiment: ukliješteni krajevi
U slučaju ovih rubnih uvjeta, matematički model te eksperiment daju rezultate u Tablici
8.
| |
\gamma_{1}[rpm] |
\gamma_{1}[rpm] |
\gamma_{1}[rpm] |
\gamma_{1}[rpm] |
| Model |
3975 |
10959 |
21490 |
35536 |
| Eksperiment |
1855 |
3480 |
- |
- |
Tablica 8: Rezultati dobiveni iz matematičkog modela i eksperimenta
Rezultati eksperimenta jako odudaraju od onih dobivenih iz modela. Naravno, u ovom slučaju delikatna je implementacija rubnih uvjeta. Za primijetiti je da je 1. kritična brzina zapravo vrlo bliska onoj iz 1. eksperimenta.
Bibliografija
| [1] |
Aganović, I.; Tambača, J.: On the stability of rotating rods and plates, ZAMM 81 (2001), 733. – 742. |
| [2] |
Aganović, I.; Veselić, K.: Jednadžbe matematičke fizike, školska knjiga, Zagreb, 1985. |
| [3] |
Kurepa, S.: Funkcionalna analiza, školska knjiga, Zagreb, 1994. |
| [4] |
Landau, L.; Lifchitz, E.: Theory of Elasticity. Pergamon Press, 1970. |
| [5] |
Tokmačić, J.: Stabilnost rotirajućeg štapa, Diplomski rad, Sveučilište u Zagrebu, PMF-Matematički odjel, Zagreb, prosinac 2005. |
| [6] |
Trabucho, L.; Viaño, J. M.: Mathematical modelling of rods. In: Ciarlet, P. G.; Lions, J. L. (eds.): Handbook of Numerical Analysis, Vol. 4. North–Holland, 1996. |
| [7] |
Tutek, Z.; Aganović, I.: A justification of the one-dimensional linear model of elastic beam, Math. Models Appl. Sci. 8 (1986), 502. – 515. |
| [8] |
Tutek, Z.; Vrdoljak, M: Obične diferencijalne jednadžbe, skripta PMF-Matematički odjel, 2009.
|