Dekompozicija matrice na singularne vrijednosti i primjene
Zagreb, prosinac 2013.
1Uvod
Moderna tehnologija i stalan porast broja stanovnika na Zemlji razlog su velike produkcije podataka. Svaki dan se proizvede ogromna količina novih podataka koje je potrebno spremati, obraditi, a često i slati. Zbog toga je bilo potrebno osmisliti načine za efikasno spremanje podataka kako bi oni zauzimali što je manje moguće prostora, a da glavna informacija bude očuvana.
Lijep primjer toga je kompresija digitalne slike. Uzmimo za primjer sliku dimenzije 3000 \times 2000 piksela. Kako bismo takvu sliku spremili u memoriju potrebno nam je 3000 \cdot 2000 \cdot 24 = 144000000 bitova memorije (za pamćenje jednog piksela koristimo 24 bita) što iznosi 18 megabajta.
U ovom članku bavit ćemo se matričnom dekompozicijom koja nam omogućava da iz nekog skupa podataka, prikazanog pomoću matrice, izdvojimo "najvažniji" dio, a ostatak izostavimo. Koristeći tu tehniku možemo komprimirati slike, razviti algoritme koji klasificiraju rukom pisane znamenke i još mnogo toga. Zamislite sada da ste zaposleni u pošti i da je vaša zadaća sortirati pristigla pisma prema poštanskom broju kako bi ona stigla na pravu adresu. Možda biste radije bili prometni policajac na autocesti koji je zadužen za praćenje brzine automobila koje ulaze u tunel. Vaš posao je snimiti tablice automobila koji ne poštuju ograničenje brzine, a zatim u bazi podataka registracija vozila pronaći tu tablicu te na priloženu adresu vlasnika poslati kaznu za prebrzu vožnju. Biste li svaki dan isti posao radili ručno ili biste radije pokušali taj postupak automatizirati? Srećom, ljudi su se već susreli s ovim problemom i smislili mnogo načina kako taj posao ubrzati i uštediti dragocjeno vrijeme.
Svi navedeni problemi mogu se riješiti upotrebnom jednog moćnog alata numeričke matematike koji ćemo vam pokušati približiti u ostatku ovog članka.
2Dekompozicija matrice na singularne vrijednosti
Dekompozicija matrice na singularne vrijednosti (SVD) je važna dekompozicija matrice bilo s teorijske ili praktične strane. U sljedećem teoremu dana je definicija SVD dekompozicije te tvrdnja o njezinoj egzistenciji za svaku matricu. Navodimo samo tvrdnju teorema, dokaz se može naći u standardnim udžbenicima iz numeričke analize.
Teorem 1. (SVD) Neka su m i n (m \geq n) prirodni brojevi te A proizvoljna m\times n realna matrica. Tada postoji dekompozicija A = U\Sigma V^{\tau}, gdje je U ortonormalna m\times n matrica i V ortogonalna n \times n matrica, a \Sigma = \operatorname{diag}(\sigma_{1}, \sigma_{2}, …, \sigma_{n}), sa \sigma_{1} \geq \sigma_{2} \geq … \geq \sigma_{n} \geq 0.
Definicija 2. Stupce matrice U = [u_{1},…,u_{n}] nazivamo lijevi singularni vektori, a stupce matrice V = [v_{1},…,v_{n}] nazivamo desni singularni vektori. Brojeve \sigma_{i} nazivamo singularne vrijednosti.
Uz uvedene oznake lako se vidi da vrijedi A = U\Sigma V^{\tau} = \sum_{i = 1}^{n} \sigma_{i}u_{i}v_{i}^{\tau}.
Napomena 1. U slučaju kada je m \lt n, SVD definiramo za matricu A^{\tau}.
3Svojstva dekompozicija matrice na singularne vrijednosti
Nakon što smo iskazali teorem koji garantira postojanje dekompozicije, u ovom odjeljku dajemo pregled nekih svojstâva dekompozicije, također bez dokaza. Ali prije iskaza teorema uvodimo još jedan pojam. Do sada smo inverz matrice definirali isključivo za kvadratne matrice, a sada želimo taj pojam proširiti na pravokutne matrice i matrice koje nisu punog ranga. Postoje tri ekvivalentna načina na koji se to može načiniti, u nastavku navodimo samo Penroseovu definiciju.
Definicija 3. Neka je A \in C^{m \times n}, njezin generalizirani inverz je jedinstvena matrica A^{+}, takva da vrijedi
\begin{matrix}{A}{A}^{+}{A}={A},&{A}^{+}{A}{A}^{+}={A}^{+}\\ {(}{A}{A}^{+}{)}^{*}={A}{A}^{+},&{(}{A}^{+}{A}{)}^{*}={A}^{+}{A}. \end{matrix}
Generalizirani inverz ponekad nazivamo i Moore-Penroseov pseudoinverz.
Neka je A=U \Sigma V^{\tau}. Tada Moore-Penrose pseudoinverz za singularnu matricu A možemo izračunati kao A^{+} \equiv V \Sigma^{+} U^{\tau}, gdje je \Sigma^{+}=\begin{bmatrix}\Sigma_{1}&0\\ 0&0 \end{bmatrix}^{+}= \begin{bmatrix}\Sigma_{1}^{-1}&0\\ 0 &0 \end{bmatrix}, a \Sigma_{1} dijagonalna matrica sa ne-nul singularnim vrijednostima na dijagonali.
Teorem 4. (Svojstva SVD-a) Neka je m \geq n te neka je A = U\Sigma V^{\tau} dekompozicija na singularne vrijednosti matrice A.
1.
Neka je A simetrična matrica sa svojstvenim vektorima q_{i}, tj. A = Q\Lambda Q^{\tau}, pri čemu je Q = [q_{1},…,q_{n}] te \Lambda = diag(\lambda_{1},…,\lambda_{n}). Tada je A = U\Sigma V^{\tau} za u_{i} = q_{i}, \sigma_{i} = |\lambda_{i}| i v_{i}=sign(\lambda_{i})q_{i}.
2.
Svojstvene vrijednosti simetrične matrice A^{\tau} A su \sigma_{i}^{2}. Desni singularni vektori v_{i} su pripadni ortonormirani svojstveni vektori.
3.
Svojstvene vrijednosti simetrične matrice A A^{\tau} su \sigma_{i}^{2} te m-n nula. Lijevi singularni vektori u_{i} su pripadni ortonormirani svojstveni vektori za svojstvene vrijednosti \sigma_{i}^{2}.
4.
Ako je A punog ranga, a b proizvoljan vektor, onda je x=A^{+} b =V\Sigma^{-1} U^{\tau} b rješenje problema \min_{x}{\Vert{A}x-b\Vert_{2}}.
5.
Vrijedi \Vert A\Vert_{2} = \sigma_{1}. Ukoliko postoji A^{-1} tada je \Vert A^{-1}\Vert _{2} = 1/{\sigma_{n}}.
6.
Neka je A_{k} = U\Sigma_{k}V^{\tau} = \sum_{i = 1}^{n}\sigma_{i}u_{i}v_{i}^{\tau}, gdje je \Sigma_{k} = diag(\sigma_{1},…\sigma_{k},0,..,0). Tada matrica A_{k} ima rang k te je ona najbliža matrici A među svim matricama ranga k:
\Vert A-A_{k}\Vert_{2}=\min_{rang(B) = k} \Vert A - b\Vert _{2}.
Također je \Vert{A}-A_{k}\Vert_{2}=\sigma_{k+1}.
7.
Pretpostavimo da za singularne vrijednosti matrice A vrijedi \sigma_{1} \geq … \geq \sigma_{r} \gt \sigma_{r+1} = … = \sigma_{n} = 0, tada je rang(A) = r. Nadalje, nul-potprostor od A je razapet stupcima v_{r+1}, …, v_{n} matrice V, a slika operatora A je razapeta stupcima u_{1},…,u_{r} od U.
Napomena 2. Umnožak \Vert A\Vert _{2} \Vert A^{-1}\Vert _{2} iz pete točke nazivamo uvjetovanost matrice A.
U ostatku članka, komentirat ćemo primjenu Teorema 2.
4Neke primjene dekompozicije matrice na singularne vrijednosti
4.1Kompresija slike
Neka je dana m\times n matrica A s elementima a_{i,j} \in [0,1]. Zamislimo da A predstavlja m\times n grayscale sliku gdje broj na (i,j) mjestu u matrici predstavlja svjetlinu piksela na mjestu (i,j) na slici. Ako uzmemo da vrijednost nula predstavlja crno, a jedan bijelo, zanimljivo je pitanje što će se dogoditi kad napravimo A = U\Sigma V^{\tau}, a onda u matrici \Sigma posljednjih nekoliko ne-nul elemenata stavimo na nulu te promotrimo dobivenu sliku A_{k}.
Preciznije, neka je A = U\Sigma V^{\tau}, SVD matrice A. Prema šestoj tvrdnji prethodnog teorema, vrijedi da je A_{k} = \sum_{i=0}^{k}\sigma_{i}u_{i}v_{i}^{\tau} najbolja aproksimacija matrice A matricom ranga k, u smislu \Vert A - A_{k}\Vert _{2} = \sigma_{k+1}. Da bismo spremili podatke u_{1},…u_{k} te \sigma_{1}v_{1},…,\sigma_{k}v_{k} iz kojih možemo dobiti matricu A_{k} potrebno je pamtiti samo (m+n)\cdot k brojeva budući da su u_{i} i v_{j} vektori iz \mathbb{R}^{m} odnosno iz \mathbb{R}^{n}. S druge strane, za spremanje matrice A potrebno je pamtiti svih m \cdot n brojeva. Stoga, koristimo A_{k} kao kompresiju slike A.
Slika 3: Kompresija A_{k} s a) k = 50, b) k = 25, c) k = 15. Omjer kompresije a) 0.275, b) 0.137, c) 0.082, a zauzimaju respektivno 25 KB, 22 KB te 20 KB.
Prethodne simulacije su rađene u programskom paketu Matlab. S obzirom na jednostavnost programske izvedbe u nastavku prilažemo i pojednostavljeni kôd kojim se čitatelj i sam može uvjeriti u korisnost i elegantnost ove primjene.
A = imread('test1.png');
A = A(:,:,1);
A = double(A);
[U,S,V] = svd(A);
k = 25;
Ak = U(:,1:k)*S(1:k,1:k)*V(:,1:k)';
image(Ak) colormap(gray(256));
4.2Osjetljivost sustava linearnih jednadžbi na pogreške u podacima
Neka je dan sustav linearnih jednadžbi u matričnom zapisu Ax = b, gdje je A regularna matrica. Rješenje sustava je tada x = A^{-1}b. Valja se prisjetiti iz linearne algebre da sustavi u kojima je A singularna nemaju rješenje ili ono nije jedinstveno. Prilikom traženja rješenja linearnog sustava jednadžbi u uvjetima konačne aritmetike možemo očekivati poteškoće ako je matrica "blizu" singularne. Upravo Teorem 2 nam kaže da je najbliža singularna matrica od A udaljena za \sigma_{n} stoga je razumno očekivati da će točnost s kojim možemo odrediti rješenje sustava imati neke veze sa \sigma_{k}.
Iako numerički nikako ne želimo računati inverz matrice A, ovakav zapis ima svojih prednosti. Zamislimo primjerice da radimo simulaciju gdje je matrica A fiksna, a jedino što mijenjamo je desna strana sustava. Rješavanje sustava (kad jednom znamo inverz!) se svodi na operaciju množenja matrice vektorom.
Pretpostavimo da smo podatke dobili mjerenjem - što sugerira da oni nisu nužno točni, već sadrže neku grešku. Pretpostavimo da smo umjesto egzaktne vrijednosti b izmjerili vrijednosti b + \delta b na desnoj strani sustava. Rješenje sustava se tada promijenilo iz x u x + \delta x. Zanima nas koliko je velika pogreška u rješenju (\delta x) u odnosu na pogrešku u mjerenju (\delta b). Rješavamo, dakle
x + \delta x = A^{-1}(b + \delta b).
Budući da je x = A^{-1}b slijedi \delta x = A^{-1}\delta b.
Uzimanjem norme slijedi
\Vert \delta x\Vert = \Vert A^{-1}\delta b\Vert \leq \Vert A^{-1}\Vert \Vert \delta b\Vert .
Ako je \Vert A^{-1}\Vert velika lako uviđamo da male greške u podacima b mogu dovesti do velikih grešaka u rješenju.
Dijeljenjem prethodne nejednakosti s \Vert x\Vert i uvažavanjem \frac{\Vert b\Vert }{\Vert A\Vert } \leq \Vert x\Vert na desnoj strani nejednakosti slijedi ocjena
\frac{\Vert \delta x\Vert }{\Vert x\Vert } \leq \Vert A\Vert \Vert A^{-1}\Vert \frac{\Vert \delta b\Vert }{\Vert b\Vert }.
U napomeni 2 već smo spomenuli uvjetovanost matrice k(A) = \sigma_{max}/ \sigma_{min}.
Time smo pokazali da je relativna pogreška u x manja ili jednaka umnošku uvjetovanosti matrice sustava i relativne pogreške u podacima b.
\newpage
4.3Problem najmanjih kvadrata za singularnu matricu A
U ovoj sekciji ne samo da ćemo dokazati tvrdnju 4 iz Teorema 4, već i njeno poopćenje za matrice koje nisu punog ranga. Mnogi problemi iz života mogu se formulirati kao problem najmanih kvadrata što ćemo vidjeti i u sljedećem poglavlju koje se bavi klasifikacijom rukom pisanih znamenki.
Već smo vidjeli da je rješenje problema \min_{x}{\Vert Ax - b\Vert _{2}} za matricu A punog ranga dano sa x = V\Sigma^{-1} U^{\tau} b. Promotrimo sada slučaj kada matrica A nije punog ranga, već ima rang r koji može biti i manji od n. Kako bismo izveli formulu za rješenje takvog problema, prvo valja saznati nešto više o naravi problema.
Propozicija 5. Neka je A matrica dimenzije m \times n gdje je (m \ge n) i rang od A je r, gdje je r \le n. Također, neka je b proizvoljan vektor dimenzije m \times 1. Tada postoji skup dimenzije barem n-r vektora x koji minimiziraju ||Ax - b||_{2}.
Dokaz. Neka je z vektor iz jezgre od A, tj. neka vrijedi Az=0. Tada ako x minimizira ||Ax - b||_{2}, onda i vektor x+z minimizira navedeni izraz jer vrijedi:
||A(x+z) - b||_{2} = ||Ax + Az - b||_{2} \ = ||Ax - b||_{2}.
Time smo, zbog činjenice da je dimenzija jezgre matrice A upravo jednaka n-r, pokazali da je dimenzija skupa rješenja barem n-r.
\ \blacksquare
Iz Propozicije 5 vidimo da izbor vektora x nije jedinstven kada je r\lt n.
Slijedi rezultat koji daje ocjenu na normu vektora rješenja x.
Propozicija 6. Neka je \sigma_{min}, najmanja ne-nul singularna vrijednost matrice A. Ako x minimizira ||Ax - b||_{2}, onda je ||x||_{2} \ge |u_{n}^{\tau}b|/\sigma_{min} gdje je u_{n} zadnji stupac od U u rastavu A=U \Sigma V^{\tau}
Dokaz. Kako je x=A^{+}b=V\Sigma^{-1}U^{\tau}b, slijedi da je ||x||_{2}=||\Sigma^{-1}U^{\tau}b||_{2} \ge |(\Sigma^{-1}U^{\tau}b)_{n}|=|u_{n}^{\tau}b|/\sigma_{min}.
\ \blacksquare
Nakon što smo se uvjerili da norma rješenja ovisi o najmanjoj ne-nul singularnoj vrijednosti matrice A, u sljedećoj propoziciji ćemo dati karakterizaciju vektora x koji minimizira ||Ax-b||_{2} za matricu A koja nije punog ranga.
Propozicija 7. Neka je A = U\Sigma V^{\tau} matrica ranga r\lt n. Tada je možemo zapisati kao
A= \begin{bmatrix}U_{1},&U_{2}\end{bmatrix}\begin{bmatrix}\Sigma_{1}&0 \\ 0&0\end{bmatrix} \begin{bmatrix}V_{1},&V_{2}\end{bmatrix}^{\tau}=U_{1}\Sigma_{1}V_{1}^{\tau}
gdje je \Sigma_{1}r \times r regularna matrica, a U_{1} i V_{1} imaju r stupaca. Neka je \sigma_{min} najmanja singularna vrijednost od A različita od nule. Tada vrijedi:
(1)
Sva rješenja x mogu se zapisati kao x=V_{1} \Sigma_{1}^{-1} U_{1}^{\tau} b + V_{2} z, gdje je z proizvoljan vektor.
(2)
Rješenje x ima minimalnu normu ||x||_{2} kada je z=0, u kojem slučaju x=V_{1} \Sigma_{1}^{-1} U_{1}^{\tau} b i ||x||_{2} \le \frac{||b||_{2}}{\sigma_{min}}.
(3)
Promjenom vektora b u vektor b+\delta b, rješenje x se može promijeniti za najviše \frac{||\delta b||_{2}}{\sigma_{min}}.
Drugim riječima, norma i kondicija rješenja x ovise o najmanjoj ne-nul singularnoj vrijednosti matrice A.
Dokaz. Izaberimo \tilde{U} tako da je [U,\tilde{U}] ortogonalna matrica. Tada
\begin{align*} ||Ax-b||_{2}^{2} = ||[U,\tilde{U}]^{\tau} (Ax-b) ||_{2}^{2}&=||\left[ \begin{array}{c} U^{\tau}\\ \tilde{U}^{\tau}\end{array}\right] (U_{1} \Sigma_{1} V_{1}^{\tau} x - b)||_{2}^{2}\\ &= \left|\left| \left[ \begin{array}{c} \Sigma_{1} V_{1}^{\tau} x - U_{1}^{\tau} b \ U_{2}^{\tau} b \ \tilde{U}^{\tau} b \end{array} \right] \right|\right|_{2}^{2}\\&=||\Sigma_{1} V_{1}^{\tau} x- U_{1}^{\tau} b||_{2}^{2} + ||U_{2}^{\tau} b||_{2}^{2}+||\tilde{U}^{\tau}b||_{2}^{2} \end{align*}
(1)
Budući da zadnja dva pribrojnika u gornjem izrazu ne ovise o x, ||Ax -b||_{2} je minimalna kada je prvi pribrojnik minimalan. Možemo postići da je on jednak nuli ako stavimo \Sigma_{1} V_{1}^{\tau} x = U_{1}^{\tau} b, odnosno x=V_{1} \Sigma_{1}^{-1} U_{1}^{\tau} b + V_{2} z jer je V_{1}^{\tau} V_{2} z = 0 za svaki z.
(2)
Kako su V_{1} i V_{2} ortogonalne, ||x||_{2}^{2}=||V_{1} \Sigma_{1}^{-1} U_{1}^{\tau} b||_{2}^{2} + ||V_{2} z||_{2}^{2}, a ta je norma minimalna za z=0. Ocjena ||x||_{2} \le \frac{||b||_{2}}{\sigma_{min}} slijedi iz nejednakosti ||A \cdot B|| \le ||A|| \cdot ||B|| i definicije matrične 2-norme.
(3)
Promjenom vektora b za \delta b mijenja se x za najviše ||V_{1} \Sigma_{1}^{-1} U_{1}^{\tau} \delta b||_{2} \le ||\Sigma_{1}^{-1}||_{2} ||\delta b||_{2} = \frac{||\delta b||_{2}}{\sigma_{min}}.
\ \blacksquare
Zaključujemo da je, u slučaju kada je matrica A punog ranga, rješenje problema najmanjih kvadrata vektor x=A^{+} b, a kada matrica A nije punog ranga, onda među svim vektorima x koji minimiziraju ||Ax-b||_{2}, vektor x=A^{+} b ima najmanju normu.
4.4Klasifikacija rukom pisanih znamenki
Možda najzanimljivija primjena SVD-a koju ćemo razmatrati u ovom članku je klasifikacija rukom pisanih znamenki. Potreba za algoritmom koji u kratkom vremenu može prepoznati rukom pisane znamenke pojavila se u Američkoj pošti. Budući da pošta dnevno prima velike količine pisama koja je potrebno razvrstati prema poštanskom broju, trebalo je pronaći način da se postupak razvrstavanja automatizira. Razvijeni su brojni algoritmi koji provode klasifikaciju, a u nastavku ovog članka predstavljamo jedan koji se bazira na SVD-u.
4.4.1Prikaz rukom pisanih znamenki u računalu
Prvi problem s kojim se susrećemo u razvoju klasifikacijskog algoritma je način prikaza podataka u računalu. Logičan način unošenja rukom pisanih znamenki u računalo je skeniranje. Na taj način svaku znamenku možemo poistovijetiti sa slikom rezolucije n \times n piksela (u daljnjem tekstu koristit ćemo n=16 jer se pokazalo da je ta rezolucija dovoljna za razlikovanje znamenki). Kako nam boja olovke kojom je znamenka napisana nije bitna, sliku možemo pretvoriti u grayscale format. Na taj način smo postigli da je svaki piksel na slici predstavljen nekom numeričkom vrijednošću koja određuje kojom će nijansom sive boje piksel biti iscrtan na zaslonu računala. Prema tome, svaku znamenku smo poistovjetili s matricom realnih brojeva iz segmenta [0,1] dimenzije 16 \times 16.
4.4.2Opis algoritma
Algoritam bismo mogli ugrubo podijeliti u dvije faze.
\bullet
Prva faza se sastoji od ručnog klasificiranja dovoljno velikog skupa znamenki, tj. stvaranja tzv. "skupa za vježbu". Skup za vježbu se može nadalje podijeliti na deset podskupova, gdje svaki podskup sadrži slike koje predstavljaju jednu od znamenaka 0,1,2,3,\cdots,9.
\bullet
Druga faza se sastoji od odabira neke neklasificirane rukom pisane znamenke (znamenke iz tzv. "skupa za testiranje") i određivanja podskupa skupa za vježbu kojem je ta nepoznata znamenka "najbliža".
Prva faza algoritma nam nije interesantna jer se provodi ručno, odnosno bez upotrebe računala, a drugu fazu ćemo detaljnije proučiti.
Kao što smo već rekli, svaku znamenku u računalu zapisujemo kao matricu dimenzije 16 \times 16. Svaki podskup T_{i}, i=0,\cdots,9 skupa za vježbu sastoji se od k_{i} matrica koje predstavljaju istu znamenku. Kako bismo jedan cijeli podskup T_{i} prikazali kao jednu matricu, a ne njih k_{i} načinit ćemo sljedeće:
(1)
Svaku 16 \times 16 matricu iz podskupa T_{i} pretvorimo u vektor dimenzije 256 tako da prvih 16 elemenata vektora budu elementi prvog stupca matrice, sljedećih 16 elemenata vektora elementi drugog stupca matrice itd. Postupak je lakše prikazati grafički:
\begin{bmatrix}{a}_{1,1}&{a}_{1,2}&\cdots&{a}_{1,16}\\{a}_{2,1}&{a}_{2,2}&\cdots&{a}_{2,16}\\~\vdots&\cdots&\cdots&\vdots\\~{a}_{16,1}&{a}_{16,2}&~\cdots&{a}_{16,16}\end{bmatrix} \rightarrow\begin{bmatrix}{a}_{1,1}\\~{a}_{2,1}\\ \vdots\\~{a}_{16,1}\\~{a}_{1,2}\\~{a}_{2,2}\\~{\vdots}\\~{a}_{16,16}\end{bmatrix}
(2)
Dobivenih k_{i} vektora presložimo tako da tvore stupce matrice A^{(i)} dimenzije 256\times{k}_{i}
Ovim postupkom generirali smo deset matrica A^{(i)} čiji stupci razapinju potprostor od \mathbb{R}^{256} koji sadrži podskup T_{i} skupa za vježbu. Jednostavnije rečeno, svaka rukom pisana znamenka i, i=0,\cdots,9 iz skupa T_{i} odgovara nekom stupcu matrice A^{(i)}. Razumno je očekivati da se svaka znamenka iz skupa za testiranje može prikazati kao linearna kombinacija stupaca matrice A^{(i)}, odnosno da leži u slici te matrice. Valja napomenuti da potprostor razapet stupcima matrice A^{(i)}, za fiksan i, ne bi smio biti velike dimenzije, jer bi inače potprostori koji pripadaju različitim znamenkama i imali presjek velike dimenije, što znači da bi se neka nepoznata znamenka mogla prikazati pomoću stupaca dviju različitih matrica A^{(i_{1})} i A^{(i_{2})} što bi otežalo klasifikaciju.
Sada koristeći SVD dekompoziciju iz:
(1)
A^{(i)}=U^{(i)} \Sigma^{(i)} V^{(i)\tau}=\sum_{j=1}^{256} \sigma_{j}^{(i)} u_{j}^{(i)} v_{j}^{(i)\tau}
slijedi da se svaki stupac a_{l}^{(i)}, l=1,\cdots,k_{i} matrice A^{(i)} može zapisati kao
(2)
a_{l}^{(i)}= A^{(i)}e_{l} =\sum_{j=1}^{256} \left( \sigma_{j}^{(i)} v_{j,l}^{(i)} \right) u_{j}^{(i)}
Iz (2) možemo zaključiti da lijevi singularni vektori u_{j}^{(i)} tvore ortogonalnu bazu za potprostor koji odgovara nekoj znamenci i, a da su koeficijenti u zapisu l-te znamenke iz skupa T_{i} u toj bazi upravo \sigma_{j}^{(i)} v_{j,l}^{(i)}.
Budući da prvi singularni vektor (onaj koji pripada najvećoj singularnoj vrijednosti) određuje "dominantni smjer" matrice A^{(i)}, za očekivati je da će vektor u_{1}^{(i)} prikazan kao slika izgledati kao znamenka i, a vektori u_{2}^{(i)},u_{3}^{(i)},\cdots će predstavljati "dominantne varijacije" u podskupu skupa za vježbu T_{i}.
Neformalno, kažemo da su singularni vektori u_{1}^{(i)},\cdots{,}u_{m}^{(i)} dominantni smjerovi ako su singularne vrijednosti \sigma_{1},\cdots,\sigma_{m} velike u odnosu na \sigma_{m+1},\cdots,\sigma_{n}, odnosno, ako je omjer \frac{\sigma_{1}}{\sigma_{m+1}} \lt \epsilon za neku unaprijed odabranu malenu toleranciju \epsilon. Prema Teoremu 4, to znači da je matrica A_{m}^{(i)} aproksimacija matrice A^{(i)} s pogreškom manjom od \epsilon, te da vektori u_{1}^{(i)},\cdots,u_{m}^{(i)} približno razapinju isti potprostor kao svi stupci matrice A^{(i)}. Stoga očekujemo da ćemo znamenke iz testne skupine moći približno prikazati kao linearnu kombinaciju dominantnih singularnih vektora.
Bitno je naglasiti da se ostatak algoritma zasniva na sljedećim prirodnim pretpostavkama:
(1)
Svaka znamenka (u skupu za vježbu i skupu za testiranje) je dobro karakterizirana s nekoliko dominantnih singularnih vektora u_{1}^{(i)},\cdots,u_{m}^{(i)} za odgovarajuću znamenku i. Drugim riječima, očekujemo da singularne vrijednosti matrice A^{(i)} brzo opadaju, te da je norma ||A^{(i)}-A_{m}^{(i)}||_{2} malena već za malene vrijednosti m.
(2)
Zapis neklasificirane znamenke kao linearne kombinacije nekoliko dominantnih vektora u_{j}^{(i)} se razlikuje značajno za različite vrijednosti i, npr. zapis u bazi trojki se znatno razlikuje od zapisa u bazi petica.
(3)
Ako je nepoznata znamenka bolje aproksimirana u jednoj bazi singularnih vektora (npr. u_{j}^{(5)}), nego u ostalim bazama, tada je nepoznata znamenka vjerojatno znamenka 5.
Jedino što još treba napraviti je na neki način odrediti koliko je dobro nepoznata znamenka opisana u deset različitih baza, odnosno odrediti koeficijente zapisa u bazi u^{(i)} za koje je greška najmanja. To ćemo učiniti tako da izračunamo vektor reziduala kao problem najmanjih kvadrata tipa:
(3)
\text{min}_{\alpha_{i}} \left| \left| z- \sum_{j=1}^{m} \alpha_{j} u_{j}^{(i)} \right| \right|,
gdje je z nepoznata znamenka, u_{j}^{(i)} lijevi singularni vektori koji odgovaraju znamenci i, a m broj koji određuje koliko dominantnih singularnih vektora želimo koristiti za aproksimaciju.
Izraz (3) možemo zapisati i kao \text{min}_{\alpha} \left| \left| z- U_{m}^{(i)}\alpha \right| \right|, gdje je U_{m}^{(i)}=[u_{1}^{(i)}, u_{2}^{(i)},\cdots,u_{m}^{(i)}] matrica čiji su stupci m dominantnih singularnih vektora koji pripadaju znamenci i, a \alpha^{\tau}=[\alpha_{1},\alpha_{2},\cdots, \alpha_{m}]. Budući da su stupci matrice U_{m}^{(i)} ortonormirani, rješenje problema najmanjih kvadrata je dano s \alpha = U_{m}^{(i)\tau} z, pa je norma reziduala je dana s:
(4)
\left| \left| (I-U_{m}^{(i)}U_{m}^{(i)\tau})z \right| \right|_{2}.
Konačno, možemo zapisati pseudokod algoritma:
\bullet
Izračunaj SVD dekompozicije matrica A^{(i)} čiji stupci reprezentiraju znamenke iste vrste iz skupa za vježbu.
\bullet
Za danu znamenku iz skupa za testiranje izračunaj po formuli (4) norme reziduala u svih deset baza. Ako je rezidual u bazi U^{(i)} bitno manji od ostalih, klasificiraj nepoznatu znamenku kao znamenku i.
4.4.3Rezultati testiranja
Algoritam je implementiran u MATLAB-u i testiran na zamenkama iz baze U.S. Postal Service. Baza se sastoji od 9298 klasificiranih rukom pisanih znamenki podijeljenih u dva skupa od 4649 znamenki. Jedan skup je korišten za vježbu, a drugi za testiranje. Za primjer možemo reći da je skup za vježbu sadržavao 786 slika koje odgovaraju znamenci 0, tj. matrica A^{(0)} je imala 786 stupaca. Znamenke korištene prilikom izrade ovog članka mogu se pronaći u formatu pogodnom za MATLAB na adresi:
http://rrr.soundsoftware.ac.uk/rrr/usps-handwritten-digits-dataset .
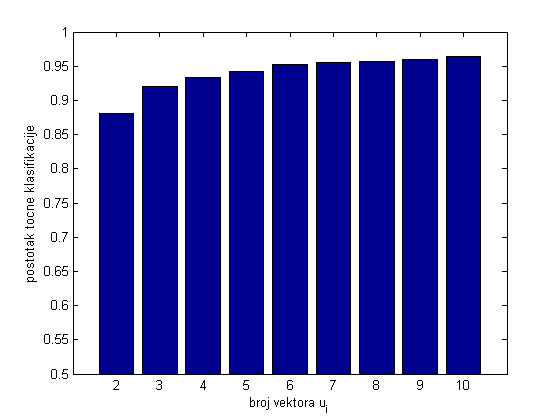
Algoritam je na ovim podacima pokazao zavidne rezultate. Klasifikacija jedne znamenke traje u prosjeku 0.02 sekunde, a uspješnost klasifikacije (broj točno klasificiranih znamenki) ovisi o broju m singularnih vektora korištenih pri računanju reziduala.
Slika 6 prikazuje uspješnost klasifikacije u ovisnosti o broju vektora korištenih pri računanju reziduala. Možemo vidjeti da je za dva korištena singularna vektora uspješnost 88\% dok je za veći broj vektora uspješnost veća te za 10 korištenih vektora iznosi čak 96.5\%.
Za kraj, iz rezultata testiranja možemo izvući dva bitna zaključka koja nam ilustriraju zašto je dekompozicija matrice na singularne vrijednosti iznimno korisna prilikom rješavanja praktičnih problema:
(1)
Algoritam prepoznavanja testne znamenke z kao one koja daje najmanji rezidual kod rješavanja problema najmanjih kvadrata \text{min}_{x} ||z - A^{(i)}x|| ima točnost veću od 95\%.
(2)
Potprostori razapeti stupcima matrice A^{(i)} jako su dobro aproksimirani sa svega nekoliko dominantnih singularnih vektora. Stoga nije potrebno rješavati problem najmanjih kvadrata s potencijalno velikom matricom A^{(i)}, nego s puno manjom matricom čiji su stupci dominantni singularni vektori. Tako proces rješavanja postaje puno efikasniji i brži uz minimalne posljedice na točnost prepoznavanja.
Literatura
(1)
J. Demmel. Applied Numerical Linear Algebra. SIAM. MIT, 1996.
(2)
J. Demmel. Berkeley mathematics: Lecture notes, Volume 1. Center for Pure and Applied Mathematics, University of California, Berkley, California, 1993.
(3)
L. Elden. Matrix Methods in Data Mining and Pattern Recognition. SIAM. Philadelphia, 2007.
(4)
Z. Drmač. Bilješke s predavanja iz kolegija Uvod u složeno pretraživanje podataka, PMF-Matematički odsjek, Zagreb, 2009.
