Primjena linearne algebre na rješavanje običnih linearnih diferencijalnih jednadžbi drugog reda
1Uvod
Obična linearna diferencijalna jednadžba (OLDJ) n-tog reda je svaka diferencijalna jednadžba koja se može zapisati u obliku:
(1)
y^{(n)}(x)+f_{n-1}(x)y^{(n-1)}(x)+\cdots +f_{1}(x)y^{(1)}(x)+f_{0}(x) y(x)=h(x)
pri čemu su {f_{i}} i {h} bilo koje neprekinute funkcije na intervalu I, a y je nepoznata funkcija koja se traži tako da zadovoljava (
2Osnovno o vektorskim prostorima
Prije nego li se krene u razmatranje predmeta članka potrebno je motivirati i definirati osnovne pojmove linearne algebre koji će se koristiti u daljnjem tekstu, a tiču se vektorskih prostora. Najprije će biti definiran pojam (apstraktnog) vektorskog prostora, a zatim će kroz primjer prostora u klasičnoj mehanici ista definicija biti motivirana.
Definicija 1. Neka je V neprazan skup, \mathbb{F} polje2 te neka je V zatvoren s obzirom na operacije zbrajanja i množenja vektora skalarom, tj. +:V\times V \rightarrow{V} i \cdot :\mathbb{F}\times V \rightarrow{V}. Uređena trojka (V,+,\cdot) vektorski je prostor nad poljem \mathbb{F} ako vrijedi:
| (1) | komutativnost zbrajanja vektora: za sve x,y\in{V} vrijedi x+y=y+x; |
| (2) | asocijativnost zbrajanja vektora: za sve x,y,z\in{V} vrijedi (x+y)+z=x+(y+z); |
| (3) | egzistencija neutralnog elementa za zbrajanje: postoji 0\in{V} takav da za sve x\in{V} vrijedi x+0=x; |
| (4) | egzistencija inverza za zbrajanje: za svaki x\in{V} postoji x'\in{V} takav da vrijedi x+x'=0; |
| (5) | usklađenost množenja vektora skalarom: za sve \alpha,\beta\in{\mathbb{F}} i sve x\in{V} vrijedi \alpha(\beta x)=(\alpha \beta)x; |
| (6) | distributivnost množenja skalarom prema zbrajanju vektora: za sve x,y\in{V} i sve \alpha\in{\mathbb{F}} vrijedi \alpha (x+y)=\alpha x + \alpha y; |
| (7) | distributivnost množenja vektorom prema zbrajanju skalara: za sve \alpha,\beta\in{\mathbb{F}} i sve x\in{V} vrijedi (\alpha+\beta) x=\alpha x + \beta x; |
| (8) | egzistencija neutralnog elementa za množenje vektora skalarom: postoji 1\in{\mathbb{F}} takav da za sve x\in{V} vrijedi 1\cdot x=x. |
Kao malu vježbu, dokažimo da uz gornja svojstva za svaki x\in{V} vrijedi 0 \cdot x=0, pri čemu je na lijevoj strani jednakosti 0 neutralni element za zbrajanje u \mathbb{F} (za sve \alpha \in{\mathbb{F}} vrijedi \alpha+0=0+\alpha=0), dok je na desnoj strani 0\in{V} neutralni element za zbrajanje u smislu uvjeta 3. Zaista, kako je 0=0+0, koristeći svojstvo 7 imamo 0\cdot x=(0+0)\cdot x=0\cdot x + 0\cdot x. Sada dodavanjem inverza za zbrajanje elementa 0\cdot x \in{V} (koji postoji po uvjetu 4) na obje strane jednakosti konačno dobivamo 0\cdot x=0. Dodatno, za svaki x\in{V} vrijedi 0=0\cdot x=(1+(-1))\cdot x=1\cdot x + (-1) \cdot x=x+(-x), pri čemu su redom korištene prethodno izvedena relacija, činjenica da je -1 inverzan element elementu 1 za zbrajanje u polju \mathbb{R} ili \mathbb{C} te svojstva 7 i 8. Dakle, suprotni je element za zbrajanje vektora x vektor (-1)\cdot x, a onda je prirodno uvesti i kraću oznaku: -x:=(-1)\cdot x.
Izrečena definicija vektorskog prostora može se motivirati na primjeru prostora u klasičnoj mehanici. Prostor u klasičnoj mehanici jeste skup svih točaka u svemiru. Neka je T točkasto tijelo. Translacija (pomak) tijela T je svaka promjena točke u kojoj se T nalazi. Promatrajmo pomak tijela T iz točke T_{1} u točku T_{2}. Usmjerena dužina od točke T_{1} do točke T_{2} naziva se vektor i označava se s \overrightarrow{T_{1}T_{2}}. Sada promotrimo skup svih vektora pomaka tijela T. Neka su \overrightarrow{x} i \overrightarrow{y} dva takva vektora pomaka. Neovisno o tome pomakne li se tijelo prvo za vektor \overrightarrow{x}, a zatim za vektor \overrightarrow{y} ili obratno, ono će doći u istu točku prostora. To je prvi uvjet iz definicije
Definicija 2. Neka je S=\lbrace x_{1},x_{2},...,x_{n}\rbrace skup vektora iz vektorskog prostora V nad poljem \mathbb{F}. Izraz oblika \sum_{i=1}^{n} \alpha_{i} x_{i}, pri čemu je \alpha_{i}\in{\mathbb{F}} za sve i\in{\lbrace 1,2,...,n\rbrace }, naziva se linearna kombinacija vektora skupa S. Skup vektora S linearno je nezavisan ako vrijedi sljedeće:
\sum_{i=1}^{n} \alpha_{i} x_{i}=0 \iff (\forall {i=1,2,...,n}) \ \alpha_{i}=0.
Definicija 3. Neka je S=\lbrace x_{1},x_{2},...,x_{n}\rbrace skup vektora iz vektorskog prostora V nad poljem \mathbb{F}. Linearna ljuska skupa S definirana je na način:
Skup S je sustav izvodnica za V ako vrijedi \operatorname{span}(S)=V.
\operatorname{span}(S)=\lbrace \sum_{i=1}^{k} \alpha_{i} x_{i} : k\in{\mathbb{N}},\alpha_{i}\in{\mathbb{F}},x_{i}\in{S}\rbrace.
Skup S je sustav izvodnica za V ako vrijedi \operatorname{span}(S)=V.
Zanimljivo je primijetiti da ako je V vektorski prostor nad poljem \mathbb{F} i S\subseteq{V} neki skup vektora, onda je \operatorname{span}(S) vektorski potprostor prostora V nad poljem \mathbb{F}. To se može dokazati direktno iz definicije
Definicija 4. Skup vektora B iz vektorskog prostora V je baza za V ako je B linearno nezavisan sustav izvodnica za V. Kardinalni broj skupa B naziva se dimenzija prostora V i označava se s \operatorname{dim}(V). Prostor V je konačnodimenzionalan ako je broj \operatorname{dim}(V) konačan.
Vektorski prostor svih prostornih pomaka nekog tijela ima dimenziju tri jer postoje najviše tri linearno nezavisna pomaka, a svaki se drugi pomak može prikazati kao linearna kombiancija tih pomaka. Neformalno rečeno, svaki se pomak može rastaviti na pomak po širini, visini i dubini nekog zamišljenog kvadra u prostoru. Ilustracije radi spomenimo kako dva linearno nezavisna vektora pomaka razapinju linearnu ljusku svih vektora pomaka koji leže u istoj ravnini kao i dva zadana vektora.
Sada su definirani osnovni pojmovi vezani uz sve vektorske prostore, međutim, u skupu svih vektorskih prostora postoji posebna klasa vektorskih prostora koji se nazivaju unitarni prostori. Vektorski prostor je unitaran ako je snabdjeven skalarnim produktom. Ispod slijedi definicija skalarnog produkta na vektorskom prostoru.
Definicija 5. Neka je V vektorski prostor nad poljem \mathbb{F} (\mathbb{F}=\mathbb{R} ili \mathbb{F}=\mathbb{C}). Skalarni produkt na V je preslikavanje \langle \cdot,\cdot \rangle : V\times V \rightarrow \mathbb{F} sa sljedećim svojstvima:
| (1) | nenegativnost: za sve x\in{V} vrijedi \langle x,x \rangle \geq0, \langle x,x \rangle \ =0 \iff x=0; |
| (2) | homogenost: za sve x,y\in{V} i sve \lambda \in{\mathbb{F}} vrijedi \langle \lambda x,y \rangle =\lambda \langle x,y \rangle; |
| (3) | hermitska simetričnost: za sve x,y\in{V} vrijedi \langle x,y \rangle =\overline{\langle y,x \rangle}; |
| (4) | linearnost: za sve x,y,z\in{V} vrijedi \langle x+y,z\rangle=\langle x,z\rangle + \langle y,z\rangle. |
U svojstvu 3 potez predstavlja konjugiranje kompleksnog broja. Skalarni produkt omogućuje uvođenje geometrije na vektorskom prostoru. Tako primjerice za dva vektora x,y\in{V} kažemo da su ortogonalni (ili okomiti) ako vrijedi \langle x,y \rangle =0. Uočimo da je nulvektor 0 ortogonalan s obzirom na svaki vektor. Naime, po svojstvu 4 iz definicije
Definicija 6. Neka je V unitaran prostor snabdjeven skalarnim produktom \langle \cdot,\cdot \rangle i S=\lbrace x_{1},x_{2},...,x_{n},...\rbrace bilo koji prebrojiv skup vektora iz V koji ne sadrži nulvektor. Za skup vektora S kažemo da je ortonormiran ako za sve x_{i},x_{j}\in{S} vrijedi \langle x_{i},x_{j} \rangle = \delta_{ij}, pri čemu je \delta_{ij} Kroneckerova delta funkcija:
Ako je ortonormirani skup vektora S iz prostora V baza za V, tada je skup S ortonormirana baza za V.
\delta_{ij}= \begin{cases} 0 & i\neq j \\ 1 & i=j \\ \end{cases}\;.
Ako je ortonormirani skup vektora S iz prostora V baza za V, tada je skup S ortonormirana baza za V.
Dokažimo ovdje da je svaki konačan podskup ortonormiranog skupa linearno nezavisan. Promotrimo proizvoljan konačan podskup vektora x_{1},x_{2},...,x_{n}\in{S} ortonormiranog skupa S. Definicija
\sum_{i=1}^{n} \alpha_{i} x_{i} = 0 \implies \langle \sum_{i=1}^{n} \alpha_{i} x_{i},x_{k} \rangle = \langle 0,x_{k} \rangle.
Prema ranijoj diskusiji znamo da je desna strana jednakosti jednaka 0, dok se lijeva strana prema svojstvima 2 i 4 može raspisati na način:
\sum_{i=1}^{n} \alpha_{i}\langle x_{i},x_{k} \rangle = 0.
Kako je skup S ortonormiran, a x_{1},x_{2},...,x_{n}\in{S}, to prema definiciji
Nadalje, promotrimo kako neki proizvoljan vektor x\in{V} zapisati u ortonormiranoj bazi S=\lbrace e_{1},e_{2},...,e_{n}\rbrace za prostor V. Zahtijeva se da je linearna kombinacija vektora baze jednaka promatranom vektoru x:
\sum_{i=1}^{n} \alpha_{i} x_{i} = x.
Obje strane prethodne jednakosti skalarno pomnožimo s vektorom e_{k}\in{S} za proizvoljni indeks k te uvažimo svojstva 2 i 4 iz definicije
\langle \sum_{i=1}^{n} \alpha_{i} e_{i},e_{k} \rangle = \langle x,e_{k} \rangle \iff \sum_{i=1}^{n} \alpha_{i}\langle e_{i},e_{k} \rangle = \langle x,e_{k} \rangle.
Kako je S=\lbrace e_{1},e_{2},...,e_{n}\rbrace ortonormiran skup vektora, to prema definiciji
x=\sum_{i=1}^{n} \langle x,e_{i} \rangle e_{i}.
Unitarni prostori koji će se promatrati u članku bit će u klasi Hilbertovih prostora. Za definiciju Hilbertovog prostora potrebno je uvesti pojam potpunosti.
Definicija 7. Neka je V normiran prostor i (x_{k},k\in{\mathbb{N}}) niz vektora iz vektorskog prostora V, tj. x_{k}\in{V} za sve k\in{\mathbb{N}}. Ako za svaki \epsilon\gt 0 postoji prirodan broj n=n(\epsilon) takav da za sve prirodne brojeve m,l\geq n vrijedi \left\lVert x_{m}-x_{l} \right\rVert \leq \epsilon, onda je niz vekotra (x_{k}) Cauchyev. Vektorski prostor V je potpun ako svaki Cauchyev niz u V konvergira.
Sljedeći teorem daje karakterizaciju potpunog prostora s apsolutno konvergentnim redovima, a njegov se dokaz može naći u
Teorem 8. Normiran prostor V je potpun ako i samo ako svaki apsolutno konvergentan red vektora iz V konvergira u V, tj. ako i samo ako za svaki niz vektora (x_{n},n\in {\mathbb{N}}) iz V vrijedi sljedeće:
(2)
\sum_{i=1}^{\infty} \lVert x_{i} \rVert \lt \infty \implies (\exists x_{0}\in{V}) \, \lim_{n \to \infty} \: \lVert \sum_{i=1}^{n} x_{i} - x_{0} \rVert =0.
Sada je konačno moguće definirati Hilbertov prostor. To je potpun vektorski prostor snabdjeven skalarnim produktom, odnosno to je potpun unitaran prostor. Za detaljna razmatranja o Hilbertovim prostorima čitatelje se upućuje na
Zanimljivo je ovdje istaknuti da je svaki konačnodimenzionalni unitarni prostor Hilbertov. Jedan konačnodimenzionalni unitarni prostor jeste n-dimenzionalni euklidski prostor \mathbb{R}^{n}:=\underbrace{\mathbb{R}\times \mathbb{R} \times ... \times \mathbb{R}}_{n \text{ puta}}. To je vektorski prostor nad poljem realnih brojeva čiji su elementi uređene n-torke realnih brojeva uz uobičajene operacije zbrajanja i množenja skalarom:
| \bullet | (x_{1},x_{2},...,x_{n})+(y_{1},y_{2},...,y_{n})=(x_{1}+y_{1},x_{2}+y_{2},...,x_{n}+y_{n}) |
| \bullet | \alpha (x_{1},x_{2},...,x_{n})=(\alpha x_{1},\alpha x_{2},...,\alpha x_{n}) |
Kanonski skalarni produkt na \mathbb{R}^{n} dan je s:
\langle (x_{1},x_{2},...,x_{n}),(y_{1},y_{2},...,y_{n}) \rangle = \sum_{i=1}^{n}x_{i}y_{i},
i s njim je dana standardna (euklidska) geometrija na \mathbb{R}^{n}. Ortonormiranu (ili kanonsku) bazu na \mathbb{R}^{n} čine vektori e_{i}=(0,...,0,\underbrace{1,}_{i\text{-ti položaj}} 0,...,0), i\in{\lbrace 1,2,...,n\rbrace }.
Osim konačnodimenzionalnog euklidskog prostora \mathbb{R}^{n}, u članku će biti korišten i beskonačnodimenzionalan Hilbertov prostor svih kvadratno integrabilnih funkcija na zatvorenom intervalu [a,b]. Taj se prostor naziva Lebesgueov prostor kvadratno integrabilnih funkcija i označava se s L^{2}[a,b,r(x)dx] (vidjeti
(3)
\langle f,g\rangle=\int_{a}^{b}f(x)g(x)r(x)dx.
Vektori u prostoru L^{2} [a, b, r(x)dx] su sve funkcije realne varijable f:[a,b]\to \mathbb{R} za koje integral \langle f,f\rangle konvergira. Direktno iz definicije
f(x)=\begin{cases} 0, x\in{[0,1]\setminus \lbrace \frac{1}{2}} \rbrace \\ 1, x=\frac{1}{2} \end{cases}\,.
Naravno, za neprekidne funkcije to se ne može dogoditi, tj. ako je f neprekidna i \langle f,f \rangle =0, onda je f\equiv 0. Kako su rješenja običnih diferencijalnih jednadžbi neprekidne funkcije, čitatelj dalje u članku može uzimati da su elementi prostora L^{2} [a, b, r(x)dx] kvadratno integrabilne funkcije i ne mora voditi računa o tome da se zapravo radi o klasama ekvivalencije funkcija, no radi točnosti i preciznosti to je bilo nužno istaknuti (za više detalja upućujemo na
Čim je uveden skalarni produkt, odmah se može definirati i ortogonalnost dviju funkcija f i g. Za funkcije f,g\in{L^{2} [a, b, r(x)dx]} kažemo da su ortogonalne ako je \langle f,g\rangle=0. Također, prema definiciji
Teorem 9. [Besselova nejednakost] Neka je y_{1},y_{2},...,y_{n},..., n\in{\mathbb{N}}, beskonačan prebrojiv ortonormiran sustav funkcija iz prostora L^{2} [a, b, r(x)dx] i neka je f proizvoljna funkcija iz prostora L^{2} [a, b, r(x)dx]. Tada vrijedi Besselova nejednakost:
Ako se u gornjoj nejednakosti postiže jednakost, onda vrijedi:
\sum_{n=1}^{\infty} {\lvert \langle f,y_{n} \rangle \rvert}^{2} \leq \langle f,f \rangle.
Ako se u gornjoj nejednakosti postiže jednakost, onda vrijedi:
f=\sum_{n=1}^{\infty} \langle f,y_{n} \rangle y_{n}.
Dokaz. Iz svojstva 1 definicije 5 slijedi da za svaki k\in{\mathbb{N}} vrijedi:
Uvažavanjem svojstava 2-4 iz definicije5 desna strana prethodne nejednakosti može se pisati u formi:
8 slijedi da taj red konvergira k nekom vektoru iz L^{2}[a,b,r(x)dx]. Ako se u Besselovoj nejednakosti postiže jednakost, onda po gornjem računu nužno vrijedi 0 = \langle f-\sum_{n=1}^{\infty} \langle f,y_{n} \rangle y_{n}, f-\sum_{n=1}^{\infty} \langle f,y_{n} \rangle y_{n} \rangle. Tada prema svojstvu 1 iz definicije 5 slijedi f-\sum_{n=1}^{\infty} \langle f,y_{n} \rangle y_{n}=0, tj. promatrani red zaista konvergira k funkciji f.
0 \leq \langle f-\sum_{n=1}^{k} \langle f,y_{n} \rangle y_{n}, f-\sum_{n=1}^{k} \langle f,y_{n} \rangle y_{n} \rangle.
Uvažavanjem svojstava 2-4 iz definicije
\begin{align*} \langle f,f\rangle - 2\sum_{n=1}^{k}& \langle f, \langle f,y_{n} \rangle y_{n}\rangle + \sum_{n=1}^{k} {\lvert \langle f,y_{n} \rangle \rvert}^{2} \\ &=\langle f,f\rangle - 2\sum_{n=1}^{k} {\lvert \langle f,y_{n} \rangle \rvert}^{2} + \sum_{n=1}^{k} {\lvert \langle f,y_{n} \rangle \rvert}^{2} \\ &= \langle f,f\rangle - \sum_{n=1}^{k} {\lvert \langle f,y_{n} \rangle \rvert}^{2}. \end{align*}
Iz prethodne nejednakosti sada slijedi da za svaki k\in{\mathbb{N}} vrijedi \sum_{n=1}^{k} {\lvert \langle f,y_{n} \rangle \rvert}^{2} \leq \langle f,f \rangle, a iz toga odmah slijedi i Besselova nejednakost. Promotrimo sada red \sum_{n=1}^{\infty} \langle f,y_{n} \rangle y_{n}. Iz Besselove nejednakosti slijedi da taj red apsolutno konvergira pa iz činjenice da je L^{2}[a,b,r(x)dx] potpun prostor i teorema
\ \blacksquare
Besselova nejednakost vrijedi za svaki ortonormiran sustav funkcija, no zanimljivo je promotriti slučaj kada za svaku funkciju f\in{L^{2} [a, b, r(x)dx]} vrijedi jednakost. Tada po prethodnom teoremu vrijedi:
(4)
f=\sum_{n=1}^{\infty} \langle f,y_{n} \rangle y_{n}=\lim_{k\to\infty} \sum_{n=1}^{k} \langle f,y_{n} \rangle y_{n}.
Kako je \sum_{n=1}^{k} \langle f,y_{n} \rangle y_{n} \in{\operatorname{span}\lbrace y_{i}, i\in{\mathbb{N}} \rbrace }, imamo da se svaka funkcija f\in{L^{2} [a, b, r(x)dx]} može prikazati kao limes niza iz \operatorname{span}\lbrace y_{i}, i\in{\mathbb{N}} \rbrace (odnosno zatvarač skupa \operatorname{span}\lbrace y_{i}, i\in{\mathbb{N}} \rbrace jednak je cijelom prostoru L^{2} [a, b, r(x)dx]). To je ipak slabije svojstvo od onog traženog u definicijama
Posljednja dva pojma koji će biti korišteni u članku, a vezani su uz vekotrske prostore jesu linearni operatori i njihove vlastite (ili svojstvene) vrijednosti. Njihove definicije navedene su u nastavku.
Definicija 10. Neka su V i W vektorski prostori nad istim poljem \mathbb{F}, a L:V\to W preslikavanje iz prostora V u prostor W. Za preslikavanje L kažemo da je linearni operator ako za sve x,y\in{V} i sve \lambda\in{\mathbb{F}} vrijedi:
| (1) | aditivnost: L(x+y)=L(x)+L(y) |
| (2) | homogenost: L(\lambda x)=\lambda L(x). |
Definicija 11. Neka je L:V\to V linearni operator. Vektor x\in{V\setminus \lbrace 0\rbrace } naziva se vlastiti (ili svojstveni) vektor operatora L ako postoji skalar \lambda\in{\mathbb{F}} takav da vrijedi L(x)=\lambda x. Skalar \lambda naziva se vlastita vrijednost operatora L. Ako vrijedi L(x)=\lambda x, kažemo da je vlastiti vektor x operatora L pridružen vlastitoj vrijednosti \lambda operatora L.
3Vektorski prostor rješenja homogene OLDJ drugog reda
Prema (
(5)
y''+f(x) y'+g(x)y=h(x),
gdje su f,g,h neprekinute funkcije. U ovom dijelu promatraju se rješenja homogene jednadžbe koja odgovara općoj formi (
(6)
y''+f(x) y'+g(x)y=0.
Za nastavak razmatranja rješenja jednadžbe (
Da bi neka funkcija y bila rješenje jednadžbe (
Također, da bi rješenje jednadžbe (
Lema 12. Skup svih funkcija y(x) koje na nekom intervalu I zadovoljavaju (3) čini vektorski prostor V nad poljem realnih brojeva s obzirom na uobičajene operacije zbrajanja i množenja.
Dokaz.
Neka je S skup svih funkcija y\in{C^{2}(I)} koje na otvorenom intervalu I zadovoljavaju (6 ). Da bi neka trojka (S,+,\cdot) bila vektorski prostor, moraju vrijediti uvjeti 1-8 iz definicije 1 i zatvorenost na zbrajanje i množenje skalarom. Prvo primijetimo da zbog linearnosti jednadžbe (6 ) vrijedi da ako su y_{1} i y_{2} bilo koja dva rješenja od (6 ), onda je i njihova linearna kombinacija \alpha y_{1} + \beta y_{2} također rješenje od (6 ) za sve realne skalare \alpha, \beta. Stoga uobičajene operacije zbrajanja i množenja zadovoljavaju uvjete zatvorenosti u S. Sada samo preostaje provjeriti jesu li zadovoljeni uvjeti 1-8 iz definicije 1 . Iz činjenice da je C^{2}(I) vektorski prostor slijede sva svojstva 1-8 osim svojstava 3 i 4. Stoga preostaje dokazati da vrijede svojstva 3 i 4. Kako funkcija y=0 zadovoljava (6 ), to slijedi da je 0\in S pa treća tvrdnja zaista vrijedi. Isto tako, ako je y rješenje od (6 ), onda je i y_{0}=-y također rješenje od (6 ) pa vrijedi i četvrto. Dakle, (S,+,\cdot) zaista je vektorski prostor nad poljem realnih brojeva.
Neka je S skup svih funkcija y\in{C^{2}(I)} koje na otvorenom intervalu I zadovoljavaju (
\ \blacksquare
Sad kad je definiran vektorski prostor V, prirodno je zapitati se kolika je njegova dimenzija. O dimenziji vektorskog prostora V govori sljedeći teorem.
Komentar. Kako bi se čitatelju dao određeni uvid u matrice i determinante Wronskog, prvo će biti dokazano da je dimenzija vektorskog prostora V_{n} rješenja homogene OLDJ koja pripada (1), a dobije se uz h(x)=0, manja od n+1, tj. \operatorname{dim}(V_{n})\lt n+1 gdje je n red homogene OLDJ. Zatim je teže dokazati da je \operatorname{dim}(V_{n})\gt n-1 pa će se dokaz tu ograničiti samo na tvrdnju teorema za OLDJ drugog reda.
\ \blacksquare
Dokaz.[Dokaz da je \operatorname{dim}(V_{n})\lt n+1]
Pretpostavimo suprotno, tj. da je \operatorname{dim}(V_{n})\geq n+1. Tada postoji barem n+1 linearno nezavisnih funkcija y_{1},…,y_{n+1} koje zadovoljavaju pripadajuću homogenu jednadžbu od (1 ) na I, a za njih još dodatno vrijedi uvjet linearne nezavisnosti na I:
pri čemu je \alpha_{i} realna konstanta za svaki indeks i. Derivirajmo uvjet (7 ) n puta i zapišimo dobiveni sustav jednadžbi u matričnom obliku:
\begin{bmatrix} y_{1} & \cdots & y_{n} & y_{n+1}\\ y_{1}^{(1)} & \cdots & y_{n}^{(1)} & y_{n+1}^{(1)}\\ \vdots& \cdots &\vdots& \vdots\\ y_{1}^{(n)} & \cdots & y_{n}^{(n)} & y_{n+1}^{(n)}\\ \end{bmatrix} \begin{bmatrix} \alpha_{1} \\ \vdots\\ \alpha_{n} \\ \alpha_{n+1} \\ \end{bmatrix} = \begin{bmatrix} 0\\ \vdots\\ 0\\ 0\\ \end{bmatrix} \iff W \begin{bmatrix} \alpha_{1} \\ \vdots\\ \alpha_{n} \\ \alpha_{n+1} \\ \end{bmatrix} = \begin{bmatrix} 0\\ \vdots\\ 0\\ 0\\ \end{bmatrix},
pri čemu je matrica sustava u izrazu (8 ) označena s W. Ta se matrična funkcija naziva matrica Wronskog, a determinanta te matrice naziva se Wronskijan ili determinanta Wronskog.
Dalje valja iskoristiti uvjet da y_{1},…,y_{n+1} zadovoljavaju pripadnu homogenu jednadžbu od (1 ). To daje sustav jednadžbi:
\begin{bmatrix} y_{1} & y_{1}^{(1)} & \cdots & y_{1}^{(n)}\\ \vdots& \vdots &\vdots& \vdots\\ y_{n} & y_{n}^{(1)} & \cdots & y_{n}^{(n)} \\ y_{n+1} & y_{n+1}^{(1)} & \cdots & y_{n+1}^{(n)} \\ \end{bmatrix} \begin{bmatrix} f_{0} \\ f_{1} \\ \vdots\\ 1\\ \end{bmatrix} = \begin{bmatrix} 0\\ \vdots\\ 0\\ 0\\ \end{bmatrix} \iff W^{T} \begin{bmatrix} f_{0} \\ f_{1}\\ \vdots \\ 1\\ \end{bmatrix} = \begin{bmatrix} 0\\ \vdots\\ 0\\ 0\\ \end{bmatrix},
pri čemu je u (9 ) prepoznata transponirana matrica Wronskog W^{T}. Iz matričnog zapisa (9 ) vidi se da matrica W^{T} ne smije imati inverz niti u jednoj točki intervala I jer bi u suprotnom vrijedilo da je 1=0 (zadnji redak zapisa sustava). Kako za svaku kvadratnu matricu M vrijedi da ima inverz (s obzirom na matrično množenje) ako i samo ako je \operatorname{det}(M) \neq0, to slijedi \operatorname{det}(W^{T})=0 na cijelom I. Za svaku kvadratnu matricu M općenito vrijedi \operatorname{det}(M)=\operatorname{det}(M^{T}) pa je i \operatorname{det}(W^{T} )=\operatorname{det}(W). Stoga je \operatorname{det}(W)=0 na cijelom I pa je matrica W singularna na cijelom I. Neka je x_{0}\in I proizvoljna točka. Kako je W singularna u x_{0} i kako za svaku singularnu kvadratnu matricu M postoji vektor stupac x različit od nulvektora takav da vrijedi Mx=0, sustav (8 ) u točki x_{0} ima netrivijalno rješenje \alpha_{1}^{*},..., \alpha_{n+1}^{*} takvo da je \alpha_{i}^{*} \ne 0 za neki indeks i\in \lbrace 1,...,n+1\rbrace. Promotrimo sada funkciju y^{*}=\sum_{i=1}^{n+1} \alpha_{i}^{*} y_{i}. Ta funkcija očito zadovoljava homogenu OLDJ koja pripada (1 ) i prema (8 ) zadovoljava početne uvjete y^{*}(x_{0})={y^{*}}^{(1)}(x_{0})=...={y^{*}}^{(n-1)}(x_{0})={y^{*}}^{(n)}(x_{0})=0. Time je na intervalu I zadan Cauchyjev problem za homogenu OLDJ koja pripada (1 ) i njegovo je rješenje funkcija y^{*}. Međutim, njegovo je rješenje i funkcija y(x)=0 pa iz jedinstvenosti rješenja Cauchyjevog problema slijedi da su ta dva rješenja identički jednaka na cijelom intervalu I, odnosno da za svaki x\in{I} vrijedi y^{*}(x)=\sum_{i=1}^{n+1} \alpha_{i}^{*} y_{i}(x) = 0. Prisjetimo se da je rješenje \alpha_{1}^{*},..., \alpha_{n+1}^{*} netrivijalno, tj. da postoji indeks i\in \lbrace 1,...,n+1\rbrace takav da je \alpha_{i}^{*} \ne 0. To je kontradikcija s (7 ). Dakle, zaista je \operatorname{dim}(V_{n})\lt n+1.
Pretpostavimo suprotno, tj. da je \operatorname{dim}(V_{n})\geq n+1. Tada postoji barem n+1 linearno nezavisnih funkcija y_{1},…,y_{n+1} koje zadovoljavaju pripadajuću homogenu jednadžbu od (
(7)
\alpha_{1} y_{1}+\cdots +\alpha_{n} y_{n}+\alpha_{n+1} y_{n+1}=0 \Leftrightarrow\alpha=\cdots=\alpha_{n}=\alpha_{n+1}=0,
(8)
\left. \begin{aligned} \alpha_{1} y_{1}+\cdots + \alpha_{n} y_{n}+\alpha_{n+1} y_{n+1}&=&0 \\ \alpha_{1} y_{1}^{(1)}+ \cdots +\alpha_{n} y_{n}^{(1)}+\alpha_{n+1} y_{n+1}^{(1)}&=&0\\ &\vdots&\\ \alpha_{1} y_{1}^{(n)}+ \cdots +\alpha_{n} y_{n}^{(n)}+\alpha_{n+1} y_{n+1}^{(n)}&=&0\\ \end{aligned} \right\rbrace \quad \\ \iff
pri čemu je matrica sustava u izrazu (
Dalje valja iskoristiti uvjet da y_{1},…,y_{n+1} zadovoljavaju pripadnu homogenu jednadžbu od (
(9)
\left. \begin{aligned} y_{1}^{(n)}+f_{n-1}(x)y_{1}^{(n-1)}+ \cdots + f_{1}y_{1}^{(1)}+f_{0}y_{1}&=&0\\ &\vdots&\\ y_{n+1}^{(n)}+f_{n-1}(x)y_{n+1}^{(n-1)}+ \cdots + f_{1}y_{n+1}^{(1)}+f_{0}y_{n+1}&=&0\\ \end{aligned} \right\rbrace \quad \\ \iff
\begin{bmatrix} y_{1} & y_{1}^{(1)} & \cdots & y_{1}^{(n)}\\ \vdots& \vdots &\vdots& \vdots\\ y_{n} & y_{n}^{(1)} & \cdots & y_{n}^{(n)} \\ y_{n+1} & y_{n+1}^{(1)} & \cdots & y_{n+1}^{(n)} \\ \end{bmatrix} \begin{bmatrix} f_{0} \\ f_{1} \\ \vdots\\ 1\\ \end{bmatrix} = \begin{bmatrix} 0\\ \vdots\\ 0\\ 0\\ \end{bmatrix} \iff W^{T} \begin{bmatrix} f_{0} \\ f_{1}\\ \vdots \\ 1\\ \end{bmatrix} = \begin{bmatrix} 0\\ \vdots\\ 0\\ 0\\ \end{bmatrix},
pri čemu je u (
\ \blacksquare
Dovoljno bi još bilo dokazati da je \operatorname{dim}(V_{n})\gt n-1 kako bi se dobila opća tvrdnja \operatorname{dim}(V_{n})=n, no taj je dokaz znatno duži i složeniji (i nije neophodan za nastavak članka) pa ga izostavljamo i prelazimo u ovom dijelu na dokaz isključivo za n=2. Čitatelj može naći potpun dokaz da je \operatorname{dim}(V_{n})=n u
Komentar. Ovdje je zanimljivo uočiti da sustav (8 ) na cijelom I ima jedinstveno rješenje (7 ) ako matrica W ima inverz u barem jednoj točki x_{0}\in I, tj. ako postoji x_{0}\in I takav da je determinanta matrice W različita od 0 (\operatorname{det}(W)\ne 0 u x_{0}\in I). To je teorem o linearnoj nezavisnosti funkcija koji kaže da ako je determinanta Wronskog nekih funkcija u nekoj točki intervala I različita od 0, onda su te funkcije linearno nezavisne na intervalu I. Obrat tog teorema ne vrijedi. Ovdje navodimo Peanov protuprimjer. Na cijelom \mathbb{R} promatraju se funkcije y_{1}(x)=x^{2} i y_{2}(x)=x \lvert x \rvert. Determinanta Wronskog funkcija y_{1},y_{2} jeste 0 na cijelom \mathbb{R}, no te su funkcije linearno nezavisne na \mathbb{R}. Međutim, zanimljivo je spomenuti kako obrat vrijedi uz dodatnu pretpostavku da su promatrane funkcije rješenja homogene OLDJ s koeficijentima neprekinutim na cijelom promatranom intervalu. Dokaz te tvrdnje može se naći u [5] .
\ \blacksquare
Dokaz teorema 3.[Dokaz teorema 3]
Iz prethodnog dokaza specijalno, za n=2, imamo \operatorname{dim}(V)\lt 3. Kako bi se sada dokazala tvrdnja teorema, dovoljno je dokazati da je \operatorname{dim}(V)\gt 1. To će biti dokazano eksplicitnom konstrukcijom dva linearno nezavisna rješenja od (6 ). Neka je y_{1} jedno rješenje od (6 ) takvo da za neki x_{0}\in{I} vrijedi y_{1}(x_{0})\ne 0. Uočimo da takvo rješenje postoji jer u nekoj točki x_{0}\in{I} možemo zadati uvjete y_{1}(x_{0})=1, y_{1}'(x_{0})=1 čime je zadan Cauchyjev problem, a rješenje Cauchyjevog problema postoji. Drugo linearno nezavisno rješenje traži se u obliku y_{2}=C(x)y_{1}. Uvrštavanjem toga u (6 ) dobiva se:
Kako y_{1} zadovoljava (6 ), to slijedi da je član u uglatim zagradama 0 pa (10 ) uz supstituciju u=C' postaje:
Iz (11 ) uvažavajući supstituciju u=C' integracijom slijedi:
Funkcija C(x) dana s (12 ) očito ovisi o x za C_{0}\ne 0, tj. nije konstantna funkcija, pa su y_{1} i y_{2}=C(x) y_{1} sigurno linearno nezavisne na I. Stoga postoje najmanje dva linearno nezavisna rješenja i zato je \operatorname{dim}(V)\gt 1. Sada imamo gornju i donju ogradu 1\lt \operatorname{dim}(V)\lt 3 pa kako je dimenzija vektorskog prostora prirodan broj, zaključujemo \operatorname{dim}(V)=2.
Iz prethodnog dokaza specijalno, za n=2, imamo \operatorname{dim}(V)\lt 3. Kako bi se sada dokazala tvrdnja teorema, dovoljno je dokazati da je \operatorname{dim}(V)\gt 1. To će biti dokazano eksplicitnom konstrukcijom dva linearno nezavisna rješenja od (
(10)
\begin{aligned} C''y_{1}+2C'{y_{1}}'+C{y_{1}}''+f(x)C'y_{1}+f(x)C{y_{1}}'+g(x)Cy_{1}=0 \iff \\ C''y_{1}+2C'{y_{1}}'+f(x)C'y_{1} + C[{y_{1}}''+f(x){y_{1}}'+g(x)y_{1}]=0 \;. \end{aligned}
(11)
\begin{aligned} \frac{du}{dx}y_{1} = -u(2{y_{1}}'+f(x)y_{1})\iff \\ \frac{du}{u}=-\frac{2{y_{1}}'+f(x)y_{1}}{y_{1}}dx\iff u=C_{0}e^{-\int\frac{2{y_{1}}'+f(x)y_{1}}{y_{1}}}dx \;. \end{aligned}
(12)
C(x)=\int(C_{0}e^{-\int\frac{2{y_{1}}'+f(x)y_{1}}{y_{1}}dx})dx=C_{0}\int(\frac{1}{{y_{1}}^{2}}e^{-\int f(x)dx})dx \;.
\ \blacksquare
Iz teorema
(13)
y=C_{1} y_{1}+C_{2} y_{2} \;.
Konstante C_{1} i C_{2} postaju jednoznačno određene ako je zadan Cauchyjev problem, a ne samo jednadžba OLDJ drugog reda. Također, vidi se da je dovoljno poznavati jedno netrivijalno rješenje y_{1} jednadžbe (
4Nehomogena OLDJ drugog reda
U prethodnom dijelu promatran je postupak rješavanja homogene OLDJ drugog reda, a ovdje se promatra nehomogena OLDJ drugog reda čija je opća forma (
(14)
y=C_{1} (x) y_{1}+C_{2} (x) y_{2}.
Jedina razlika između (
(15)
\begin{aligned} {C_{1}}''y_{1}+2{C_{1}}'{y_{1}}'+C_{1} {y_{1}}''+{C_{2}}''y_{2}+2{C_{2}}'{y_{2}}'+C_{2} {y_{2}}''\\ +f(x)[{C_{1}}'y_{1}+C_{1} {y_{1}}'+{C_{2}}'y_{2}+C_{2} {y_{2}}'] +g(x)[C_{1} y_{1}+C_{2} y_{2} ]=h(x) \\ \iff {C_{1}}''y_{1}+2{C_{1}}'{y_{1}}'+C_{1} [{y_{1}}''+f(x) {y_{1}}'+g(x) y_{1} ] +{C_{2}}''y_{2}+2{C_{2}}'{y_{2}}'\\ +C_{2} [{y_{2}}''+f(x) {y_{2}}'+g(x) y_{2} ] +f(x)[{C_{1}}'y_{1}+{C_{2}}'y_{2} ]=h(x) \; .\\ \end{aligned}
Članovi u uglatim zagradama uz C_{1} i C_{2} u (
(16)
{C_{1}}''y_{1}+2{C_{1}}'{y_{1}}'+{C_{2}}''y_{2}+2{C_{2}}'{y_{2}}'+f(x)[{C_{1}}'y_{1}+{C_{2}}'y_{2} ]=h(x) \; .\\
Kako bi se eliminirala f(x) u (
(17)
{C_{1}}'y_{1}+{C_{2}}'y_{2}=0 \iff {C_{2}}'=-{C_{1}}'\frac{y_{1}}{y_{2}} \;.
Uvrštavanjem (
(18)
\begin{aligned} {C_{1}}''y_{1}+2{C_{1}}'{y_{1}}'- {C_{1}}''\frac{y_{1}}{y_{2}} y_{2}-{C_{1}}'\frac{{y_{1}}'y_{2}-{y_{2}}'y_{1}}{{y_{2}}^{2}}y_{2} - 2{C_{1}}'\frac{y_{1}}{y_{2}}{y_{2}}'=h(x)\\ \iff {C_{1}}'({y_{1}}'-\frac{y_{1}}{y_{2}} {y_{2}}')=h(x)\\ \iff {C_{1}}'=\frac{h(x) y_{2}}{{y_{1}}' y_{2}-y_{1} {y_{2}}'} \; .\\ \end{aligned}
Iz (
(19)
{C_{1}}'=-\frac{h(x) y_{2}}{y_{1} {y_{2}}'-{y_{1}}'y_{2}}, \quad {C_{2}}'=\frac{h(x)y_{1}}{y_{1} {y_{2}}'-{y_{1}}' y_{2}} \;.
Neka je W(y_{1},y_{2}) determinanta Wronskog funkcija y_{1} i y_{2}. Tada se može uočiti da su nazivnici u (
(20)
D_{1}= \begin{vmatrix} 0 & y_{2}\\ h(x) & {y_{2}}' \end{vmatrix}, \quad D_{2} = \begin{vmatrix} y_{1} & 0\\ {y_{1}}' & h(x) \end{vmatrix} \; .
Uz determinante definirane u (
(21)
{C_{1}}'=\frac{D_{1}}{W(y_{1},y_{2})}, \quad {C_{2}}'=\frac{D_{2}}{W(y_{1},y_{2})} \; .
Valja uočiti da je (
U sljedećem primjeru pokazano je kako se navedeni općeniti algoritam primjenjuje na rješavanje nehomogenog Cauchyjevog problema.
Primjer 14. Riješimo sljedeći nehomogeni Cauchyjev problem:
y''(x)+\frac{1}{x}y'(x)=x, y(1)=0, y'(1)=0.
Rješenje. Opće rješenje zadane nehomogene OLDJ drugog reda može se zapisati u obliku (14 ), pri čemu su funkcije C_{1} i C_{2} dane u (21 ). Prvo valja pronaći dva linearno nezavisna rješenja y_{1} i y_{2} homogene jednadžbe y''(x)+\frac{1}{x}y'(x)=0, odnosno treba pronaći opće rješenje te homogene jednadžbe u obliku (13 ). Uvođenjem supstitucije u=y' dobiva se u'(x)=-\frac{1}{x}u(x). Direktnom integracijom odavde slijedi u(x)=\frac{C_{1}}{x}, gdje je C_{1}\in{\mathbb{R}} neka konstanta. Kako je u=y', ponovnom integracijom dobiva se y(x)=C_{1} \operatorname{ln}(x)+C_{2}, gdje je C_{2}\in{\mathbb{R}} druga integracijska konstanta. Time je pronađeno opće rješenje pripadajuće homogene OLDJ, a njezina dva linearno nezavisna rješenja su y_{1}(x)=\operatorname{ln}x i y_{2}(x) = 1. Sada se konstante C_{1} i C_{2} zamjenjuju funkcijama C_{1}(x) i C_{2}(x) koje su dane izrazom (21 ). Računamo determinante D_{1} i D_{2} prema izrazu (20 ) uz y_{1}(x)=\operatorname{ln}x, y_{2}(x) = 1, h(x)=x i dobivamo D_{1}=-x, D_{2}=x\operatorname{ln}x. Također, računamo Wronskijan i dobivamo W(y_{1},y_{2})=-\frac{1}{x}. Iz izraza (21 ) sada se dobiva C_{1}'(x)=x^{2} i C_{2}'(x)=-x^{2} \operatorname{ln}x, a odatle direktnom integracijom i C_{1}(x)=\frac{x^{3}}{3}+k_{1}, C_{2}(x)=\frac{x^{3}}{9}(1-3\operatorname{ln}x)+k_{2}, pri čemu su k_{1},k_{2}\in{\mathbb{R}} integracijske konstante. Opće rješenje zadane nehomogene OLDJ dano je izrazom (14 ) i glasi:
Konstante k_{1} i k_{2} određuju se iz uvjeta y(1)=0, y'(1)=0. Uvažavanjem y(1)=0 dobiva se k_{2}=-\frac{1}{9}, a uvažavanjem y'(1)=0 dobiva se k_{1}=-\frac{1}{3} pa je konačno rješenje zadanog Cauchyjevog problema y(x)=-\frac{1}{3}\operatorname{ln}x+\frac{x^{3}}{9}-\frac{1}{9}.
y(x)=(\frac{x^{3}}{3}+k_{1})\operatorname{ln}x+\frac{x^{3}}{9}(1-3\operatorname{ln}x)+k_{2} \iff y(x)=k_{1}\operatorname{ln}x+\frac{x^{3}}{9}+k_{2}.
Konstante k_{1} i k_{2} određuju se iz uvjeta y(1)=0, y'(1)=0. Uvažavanjem y(1)=0 dobiva se k_{2}=-\frac{1}{9}, a uvažavanjem y'(1)=0 dobiva se k_{1}=-\frac{1}{3} pa je konačno rješenje zadanog Cauchyjevog problema y(x)=-\frac{1}{3}\operatorname{ln}x+\frac{x^{3}}{9}-\frac{1}{9}.
\ \blacksquare
5Sturm-Liouvilleov problem
Svaka homogena OLDJ drugog reda (
(22)
\frac{d}{dx}\Big[p(x)\frac{dy}{dx}\Big]+\Big[q(x)+\lambda_{i} r(x)\Big]y=0.
Jednadžba (
(23)
\left. \begin{aligned} k_{1}\frac{dy}{dx}\bigg|_{x=a} + k_{2}y|_{x=a}=0 \\ k_{3}\frac{dy}{dx}\bigg|_{x=b} + k_{4}y|_{x=b}=0 \end{aligned} \right\rbrace \quad \\,
pri čemu su k_{1},k_{2},k_{3},k_{4} realne konstante takve da je k_{1}\neq 0 ili k_{2}\neq 0 i k_{3}\neq 0 ili k_{4}\neq 0. Jednadžba (
(24)
p'(x)y'+p(x)y''+q(x)y=-\lambda_{i}r(x)y\iff -\frac{1}{r}\Big(p'\frac{d}{dx}+p\frac{d^{2}}{dx^{2}}+q\Big)y=\lambda_{i}y.
U jednadžbi (
(25)
Ly=\lambda_{i} y \; .
Iz definicije
Primijetimo da je C^{2}[a,b]\subset{C^{0}[a,b]}, a kako je svaka neprekinuta funkcija na intervalu [a,b] (kvadratno) integrabilna, vrijedi C^{2}[a,b]\subset{C^{0}[a,b]}\subseteq{L^{2}[a, b, r(x)dx]}. Dakle, C^{2}[a,b] jeste potprostor ranije spomenutog Lebesgueovog prostora L^{2}[a, b, r(x)dx]. Kako je prostor L^{2}[a, b, r(x)dx] snabdjeven težinskim skalarnim produktom (
(26)
\langle y_{1},y_{2}\rangle=\int_{a}^{b}y_{1}y_{2}r(x)dx \;.
Sljedeći teorem govori o ortogonalnosti rješenja Sturm-Liouvilleovog problema s obzi\-rom na skalarni produkt (
Teorem 15. [Sturm-Liouville] Neka su y_{m} i y_{n} dva vlastita vektora koji zadovoljavaju (22 ) i (23 ), a odgovaraju dvjema različitim vlastitim vrijednostima \lambda_{m} i \lambda_{n}. Funkcije y_{m} i y_{n} ortogonalne su s obzirom na skalarni produkt (26 ).
Dokaz.
Kako y_{m} i y_{n} zadovoljavaju (22 ), to slijedi:
\frac{d}{dx}\Big[p(x)\frac{dy_{m}}{dx}\Big]+\big[q(x)+\lambda_{m}r(x)\big]y_{m}=0, \quad \frac{d}{dx}\Big[p(x)\frac{dy_{n}}{dx}\Big]+\big[q(x)+\lambda_{n}r(x)\big]y_{n}=0 \;.
Prvu od te dvije jednadžbe valja pomnožiti s y_{n}, a drugu s -y_{m} i zatim ih zbrojiti te algebarski srediti:
Kako bismo producirali član \langle y_{m},y_{n}\rangle, integrirajmo (27 ) na intervalu [a,b]:
Na lijevoj strani (28 ) prepoznaje se skalarni produkt \langle y_{m},y_{n}\rangle, a integrale na desnoj strani valja rastaviti parcijalnom integracijom na način:
Uvrštavanjem toga u (28 ) i sređivanjem dobiva se:
Iz Robinovih uvjeta (23 ) uz uvjet k_{1}\neq 0 i k_{3} \neq 0 mogu se izraziti {y_{m}}'(b), {y_{n}}'(b) te {y_{m}}'(a) i {y_{n}}'(a) preko y_{m}(b), y_{n}(b) te y_{m}(a), y_{n}(a) na način:
Uvrštavanjem toga u (31 ) i sređivanjem dobiva se:
Ako bi bilo k_{1}=0, onda bi iz Robinovih uvjeta uslijedilo y_{n}(a)=y_{m}(a)=0 i druga uglata zagrada u (31 ) bi iščeznula. Ako bi bilo k_{3}=0, onda bi iz Robinovih uvjeta uslijedilo y_{n}(b)=y_{m}(b)=0 i prva uglata zagrada u (31 ) bi iščeznula. Dakle, i u tim bi slučajevima vrijedila jednakost (\lambda_{m}-\lambda_{n})\langle y_{m},y_{n}\rangle=0. Kako je \lambda_{m}\ne\lambda_{n}, to zaista slijedi \langle y_{m},y_{n}\rangle=0, tj. funkcije y_{m} i y_{n} su ortogonalne.
Kako y_{m} i y_{n} zadovoljavaju (
\frac{d}{dx}\Big[p(x)\frac{dy_{m}}{dx}\Big]+\big[q(x)+\lambda_{m}r(x)\big]y_{m}=0, \quad \frac{d}{dx}\Big[p(x)\frac{dy_{n}}{dx}\Big]+\big[q(x)+\lambda_{n}r(x)\big]y_{n}=0 \;.
Prvu od te dvije jednadžbe valja pomnožiti s y_{n}, a drugu s -y_{m} i zatim ih zbrojiti te algebarski srediti:
(27)
y_{n}\frac{d}{dx}\bigg[p(x)\frac{dy_{m}}{dx}\bigg]+(\lambda_{m}-\lambda_{n})r(x)y_{m}y_{n}-y_{m}\frac{d}{dx}\bigg[p(x)\frac{dy_{n}}{dx}\bigg]=0 \;.
(28)
(\lambda_{m}-\lambda_{n})\int_{a}^{b} y_{m}y_{n}r(x)dx=\int_{a}^{b} y_{m}\frac{d}{dx}\bigg[p(x)\frac{dy_{n}}{dx}\bigg]dx-\int_{a}^{b} y_{n}\frac{d}{dx}\bigg[p(x)\frac{dy_{m}}{dx}\bigg]dx \;.
(29)
\int_{a}^{b} y_{m}\frac{d}{dx}\big[p(x)\frac{dy_{n}}{dx}\big]dx=y_{m}p(x)\frac{dy_{n}}{dx}\big|_{a}^{b}-\int_{a}^{b}\frac{dy_{m}}{dx} p(x)\frac{dy_{n}}{dx}dx \; ,
(30)
\int_{a}^{b} y_{n}\frac{d}{dx}\big[p(x)\frac{dy_{m}}{dx}\big]dx=y_{n}p(x)\frac{dy_{m}}{dx}\big|_{a}^{b}-\int_{a}^{b}\frac{dy_{m}}{dx} p(x)\frac{dy_{n}}{dx}dx \; .
(31)
\begin{aligned} (\lambda_{m}-\lambda_{n})\langle y_{m},y_{n}\rangle=y_{m}p(x)\frac{dy_{n}}{dx}\bigg|_{a}^{b} - y_{n}p(x)\frac{dy_{m}}{dx}\bigg|_{a}^{b} \iff (\lambda_{m}-\lambda_{n})\langle y_{m},y_{n}\rangle= \\ =p(b)\Big[y_{m} (b) {y_{n}}'(b)-y_{n} (b) {y_{m}}'(b)\Big]+p(a)\Big[y_{n} (a) {y_{m}}'(a)-y_{m} (a) {y_{n}}'(a)\Big] \; . \end{aligned}
{y_{m}}'(a)=-\frac{k_{2}}{k_{1}}y_{m}(a), \; {y_{n}}'(a)=-\frac{k_{2}}{k_{1}} y_{n} (a), \; {y_{m}}'(b)=-\frac{k_{4}}{k_{3}}y_{m} (b), \; {y_{n}}'(b)=-\frac{k_{4}}{k_{3}}y_{n}(b) .
Uvrštavanjem toga u (
(\lambda_{m}-\lambda_{n})\langle y_{m},y_{n}\rangle=p(b)\Big[-y_{m}(b)\frac{k_{4}}{k_{3}}y_{n}(b)+y_{n}(b)\frac{k_{4}}{k_{3}}y_{m}(a)\Big]+
p(a)\Big[-y_{n}(a)\frac{k_{2}}{k_{1}} y_{m}(a)+y_{m}(a)\frac{k_{2}}{k_{1}}y_{n}(a)\Big]=0\implies (\lambda_{m}-\lambda_{n})\langle y_{m},y_{n}\rangle=0.
p(a)\Big[-y_{n}(a)\frac{k_{2}}{k_{1}} y_{m}(a)+y_{m}(a)\frac{k_{2}}{k_{1}}y_{n}(a)\Big]=0\implies (\lambda_{m}-\lambda_{n})\langle y_{m},y_{n}\rangle=0.
Ako bi bilo k_{1}=0, onda bi iz Robinovih uvjeta uslijedilo y_{n}(a)=y_{m}(a)=0 i druga uglata zagrada u (
\ \blacksquare
Sturm-Liouvilleov teorem našao je najveću primjenu u rješavanju parcijalnih diferencijalnih jednadžbi metodom separacije varijabli, ali to izlazi iz okvira ovog članka. No, ipak će biti pokazana jedna zanimljiva primjena Sturm-Liouvilleovog teorema u sljedećem dijelu. Za to će biti potreban sljedeći teorem čiji dokaz također izlazi iz okvira ovog članka, ali zainteresiranog čitatelja upućuje se na dokaz u
Teorem 16. Neka je {y_{0},y_{1},y_{2},…,y_{n},…} skup vlastitih funkcija koje odgovaraju različitim vlastitim vrijednostima \lambda_{0},\lambda_{1},\lambda_{2},…,\lambda_{n},… jednadžbe (22 ) i koje zadovoljavaju Robinove rubne uvjete (23 ). Tada skup {y_{0},y_{1},y_{2},…,y_{n},…} čini potpunu ortogonalnu bazu na prostoru L^{2}[a, b, r(x)dx].
Ovdje je zanimljivo komentirati kako se uz izbor p(x)=1, q(x)=0 i r(x)=1 u Sturm-Liouvilleovoj jednadžbi uz odgovarajuće Robinove rubne uvjete na rubovima intervala [a,b] koji osiguravaju periodičnost na [a,b] kao rješenja problema vlastitih funkcija (
6Greenove funkcije za OLDJ drugog reda
Jednadžba (
(32)
\left. \begin{aligned} \frac{d}{dx}\Big[p(x)\frac{dy}{dx}\Big]+\big[q(x)+\lambda r(x)\big]y&=f(x)\\ k_{1}\frac{dy}{dx}\Big|_{x=a}+k_{2}y|_{x=a}&=0\\ k_{3}\frac{dy}{dx}\Big|_{x=b}+k_{4} y|_{x=b}&=0, \end{aligned} \right\rbrace \quad \\
uz uvjet \lambda \not \in \lbrace \lambda_{n}: n\in{\mathbb{N}_{0}} \rbrace, tj. \lambda nije svojstvena vrijednost pripadne homogene zadaće (u suprotnom, ako bi rješenje postojalo, ne bi bilo jedinstveno). Ponovno se (
(33)
y=\sum_{n=0}^{\infty}c_{n}y_{n},
pri čemu su c_{i} realne konstante. Nadalje ćemo s ovim izrazom raditi kao da je riječ o konačnoj sumi. Time se izbjegavaju suptilni argumenti potrebni za opravdanje promjene poretka sumacije i derivacije, odnosno sumacije i integracije, što će se javljati u računu. Na taj način moguće je staviti naglasak na sam (formalan) postupak konstrukcije rješenja zadaće (
Uvrštavanjem (
(34)
\begin{aligned} \frac{d}{dx}\Big[ p(x)\frac{d\sum_{n=0}^{\infty}c_{n}y_{n}}{dx}\Big] + \Big[q(x)+\lambda r(x)\Big]\sum_{n=0}^{\infty}c_{n}y_{n}=f(x) \iff \\ \sum_{n=0}^{\infty}c_{n} \Big\lbrace \frac{d}{dx}[p(x)\frac{dy_{n}}{dx}]+[q(x)+\lambda r(x)]y_{n}\Big\rbrace =f(x) \iff \\ \sum_{n=0}^{\infty}c_{n}\bigg\lbrace \Big[ \frac{d}{dx}[p(x)\frac{dy_{n}}{dx}] + q(x)y_{n} + \lambda_{n}r(x)y_{n}\Big] + (\lambda - \lambda_{n})r(x)y_{n} \bigg\rbrace =f(x) \; . \end{aligned}
Član u vanjskoj uglatoj zagradi prethodne jednakosti je 0 jer za svaki n\in N_{0} funkcija y_{n} zajedno sa svojom vlastitom vrijednosti \lambda_{n} zadovoljava homogenu jednadžbu (
(35)
\sum_{n=0}^{\infty}c_{n}(\lambda-\lambda_{n})r(x)y_{n}=f(x) \;.
Da bi se pronašao koeficijent c_{m}, valja pomnožiti (
(36)
\sum_{n=0}^{\infty}c_{n}(\lambda-\lambda_{n})\int_{a}^{b} y_{n} y_{m} r(x)dx=\int_{a}^{b} y_{m}f(x)dx \;.
Uvažavajući teorem
(37)
c_{m}(\lambda-\lambda_{m})\int_{a}^{b} y_{m}^{2} r(x)dx=\int_{a}^{b} y_{m}f(x)dx\iff c_{m}=\frac{1}{\lambda - \lambda_{m}}\frac{\int_{a}^{b} y_{m}f(x)dx}{\int_{a}^{b} y_{m}^{2}r(x)dx} \; .
Ako su {y_{0},y_{1},y_{2},…,y_{n},… } normirane funkcije, tj. ako taj skup nije samo ortogonalna, već i ortonormirana baza, onda je:
(38)
\int_{a}^{b} y_{m}^{2} r(x)dx=\langle y_{m},y_{m}\rangle\equiv \Vert y_{m}\Vert ^{2}=1 ,
pa zbog toga koeficijenti u (
(39)
c_{m}=\frac{\int_{a}^{b} y_{m}f(x)dx}{\lambda - \lambda_{m}} \; .
Uvrštavanjem (
(40)
y(x)=\sum_{n=0}^{\infty} \frac{\int_{a}^{b} y_{n}(z)f(z)dz}{\lambda - \lambda_{n}}y_{n}(x) \iff y(x)=\int_{a}^{b}\Big\lbrace \sum_{n=0}^{\infty}\frac{y_{n}(z)y_{n}(x)}{\lambda - \lambda_{n}}\Big\rbrace f(z)dz \; .
Funkcija u vitičastim zagradama naziva se Greenova funkcija Sturm-Liouvilleovog problema (
(41)
G(x,z)=\sum_{n=0}^{\infty} \frac{y_{n} (z) y_{n} (x)}{\lambda-\lambda_{n}}.
Jasno je da se koristeći Greenovu funkciju rješenje (34) može zapisati u formi:
(42)
y(x)=\int_{a}^{b} G(x,z)f(z)dz.
Posebno, ako je vanjska uzbuda f(z)=\delta(z-x) Diracova delta funkcija s impulsom u z=x, onda je prema (
Primjer 17. Riješimo diferencijalnu jednadžbu u''(x)=-1 s rubnim uvjetima u(0)=u(\pi)=0 metodom Greenovih funkcija.
Rješenje.[Rješenje]
Zadana je jednadžba ekvivalentna nehomogenoj Sturm-Liouvilleovoj zadaći (32 ) uz izbor f(x)=-1, q(x)=0, p(x)=1 i \lambda=0. Pripadni homogeni Sturm-Liouvilleov problem glasi:
pri čemu smo odabrali r\equiv 1. Čitateljima je za vježbu ostavljeno da dokažu kako su netrivijalna (različita od nulfunkcije) rješenja Sturm-Liouvilleovog problema (43 ) dana za \lambda _{n} =n^{2} i jednaka su u_{n}(x)=C\sin(nx), n\in{\mathbb{N}}, gdje je C neka realna konstanta. Funkcija u_{0}=0 također je rješenje, ali nulvektor ne može biti element baze jer svaki neprazan skup vektora koji sadrži nulvektor nije linearno nezavisan. Konstantu C određujemo iz uvjeta normiranosti (38 ):
Konačno rješenje diferencijalne jednadžbe sada se može naći iz (40 ) uz \lambda=0 i f(x)=-1:
Može se pokazati da je rješenje integrala pod sumom 0 za parne n i \frac{2}{n} za neparne n pa je konačno rješenje zadanog problema:
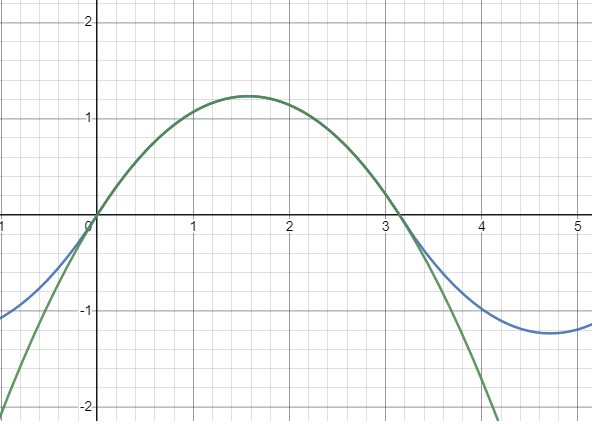
U ovom se primjeru lako možemo uvjeriti da je nađeno rješenje (46 ) točno rješenje usporedbom s rješenjem koje se dobiva integracijom. S obzirom na zadane rubne uvjete, jedinstveno rješenje zadaće dano je s u(x)=-\frac{1}{2}x^{2}+\frac{\pi}{2}x. Na slici 1 zelenom je bojom ucrtan graf funkcije u(x)=-\frac{1}{2}x^{2}+\frac{\pi}{2}x dok je plavom bojom ucrtan graf funkcije u(x)=\frac{4}{\pi}\sum_{n=0}^{1000} \frac{\operatorname{sin}[(2n+1)x]}{(2n+1)^{3}} kao aproksimacija rješenja (46 ). Kako je n-ti sumand u nazivniku (46 ) klase \mathcal{O}(n^{3}), suma prvih 1000 članova reda osigurava točnost do reda veličine 10^{-8}, tj. pogreška je reda veličine 10^{-9}. Na intervalu [0,\pi] može se vidjeti potpuna podudarnost zelenog i plavog grafa, čime je dodatno opravdano da je izrazom (46 ) zaista dano rješenje zadane Sturm-Liouvilleove zadaće.
Zadana je jednadžba ekvivalentna nehomogenoj Sturm-Liouvilleovoj zadaći (
(43)
\left. \begin{aligned} \frac{d^{2}u_{n}}{dx^{2}}+\lambda_{n} u_{n}=0\\ u_{n}(0)=0\\ u_{n}(\pi)=0 \end{aligned} \right\rbrace \quad \\,
(44)
1=\int_{0}^{\pi} u_{n}^{2} dx=C^{2} \int_{0}^{\pi} \sin^{2}(nx) dx=C^{2}\frac{\pi}{2} \implies C=\sqrt{\frac{2}{\pi}}.
(45)
u(x)=\sum_{n=1}^{\infty} \frac{\int_{0}^{\pi} u_{n}(z)dz}{\lambda_{n}}u_{n}(x)=\frac{2}{\pi}\sum_{n=1}^{\infty} \frac{\int_{0}^{\pi} \sin(nz)dz}{n^{2}}\sin(nx).
(46)
u(x)=\frac{4}{\pi}\sum_{n=0}^{\infty} \frac{\sin[(2n+1)x]}{(2n+1)^{3}}.
\ \blacksquare
7Zaključak
Cilj članka bio je pokazati široku primjenu aparata linearne algebre na dokazivanje nekih opće poznatih teorema o običnim linearnim diferencijalnim jednadžbama. Tako je prvo promatran vektorski prostor rješenja OLDJ drugog reda i u nešto manjoj mjeri n-tog reda. Definirana je determinanta Wronskog funkcija i pokazana je njena primjena u ispitivanju linearne nezavisnosti funkcija te u konstrukciji rješenja nehomogene OLDJ drugog reda. Nešto napredniji aparat linearne algebre bio je potreban prilikom razmatranja Sturm-Liouvilleovog problema gdje je ključan bio teorem ortogonalnosti rješenja Sturm-Liouvilleovog problema i potpunost ortogonalne (ortonormirane) baze koju čine vlastite funkcije Sturm-Liouvilleovog problema. Na kraju je pokazano rješavanje nehomogenog Sturm-Liouvilleovog problema metodom Greenovih funkcija te je kao primjer u potpunosti riješena OLDJ drugog reda s konstantim koeficijentima uz Robinove rubne uvjete. Primjene ostalih ovdje pokazanih metoda rješavanja OLDJ drugog reda nisu bile sadržaj i svrha članka, ali ponovno podsjećamo da se konkretne primjene na zadatke ovdje teorijski dokazanih i izvedenih metoda mogu pronaći u kolekcijama zadataka danih u
Bibliografija
2Pojam polja neće biti definiran u članku, no definicija se može naći u [ 1, 2] . Čitatelj može zamisliti da se radi o skupu \mathbb{R} ili \mathbb{C} s uobičajenim operacijama zbrajanja i množenja na tim skupovima.
