Jedna od stilskih figura izražavanja je oksimoron – stilska figura koja objedinjuje dva suprotstavljena pojma. Klasični primjeri oksimorona su drveno željezo, ili pak mudra budala. Naslov ovog teksta svakako pripada toj stilskoj figuri, što potvrđuje i npr. članak Marina Biondića (vidi [1], str. 182) u kojem se upravo izraz „četvrta stranica trokuta“ koristi za opisivanje pojma koji ne postoji.

 

Dapače, matematička definicija trokuta posve je jasna i isključuje mogućnost postojanja „četvrte stranice trokuta“. Naime, ako trokut definiramo kao „najmanji konveksni podskup ravnine koji sadržava tri zadane nekolinearne točke u ravnini“ [2], tada je jasno da bi egzistencija „četvrte stranice“ narušila definiranu minimalnost. Pa ipak, ukoliko pojmu „četvrte stranice trokuta“ pristupimo iz perspektive svojstava stranica trokuta, koncept počinje imati smisla, ili barem, pronalazimo adekvatno opravdanje za takav naziv.

 

U ovom ćemo članku stoga opisati konstrukciju i osnovna svojstva Shermanove dužine. dužine u ravnini koja dijeli neka od svojstava koja su karakteristična za stranice trokuta. Naime, za Shermanovu dužinu vrijedi sljedeće: krajnje joj točke leže na trokutu opisanoj kružnici, polovište joj leži na Eulerovoj kružnici te je Shermanova linija tangenta na trokutu upisanu kružnicu. Pored Shermanove dužine, jedine dužine u ravnini koje dijele ta tri svojstva su upravo tri stranice trokuta.

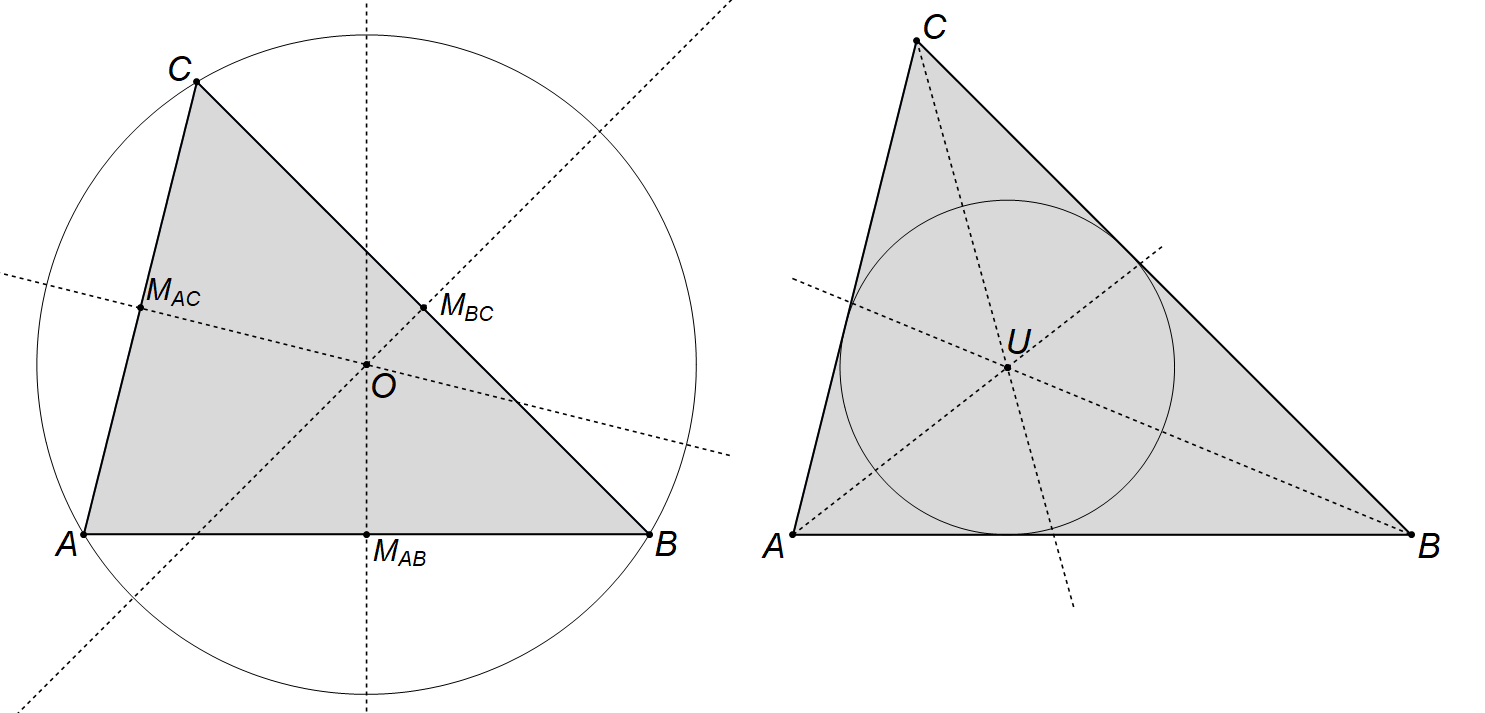
Prije nego li se posvetimo samoj „četvrtoj stranici trokuta“, ponovimo neke od temeljnih pojmova koji će nam biti potrebni. Za početak ćemo istaknuti tri karakteristične kružnice koje se vežu uz trokut. Prvi dvije su široko poznate trokutu opisana i trokutu upisana kružnica (Slika 1).

Slika 1: Prikazi trokutu opisane i trokutu upisane kružnice

Kratko ćemo ponoviti kako se središte trokutu opisane kružnice dobiva kao presjek simetrala stranica trokuta, dok je polumjer te kružnice jednak udaljenosti od tako konstruiranog središta (kojeg ćemo označiti s O) do (bilo kojeg) vrha trokuta.
 

S druge strane, središte trokutu upisane kružnice dobiva se kao presjek simetrala kutova trokuta, dok je polumjer upisane kružnice jednak udaljenosti tako konstruiranog središta (kojeg ćemo označiti s U) od (bilo koje) stranice trokuta.
 

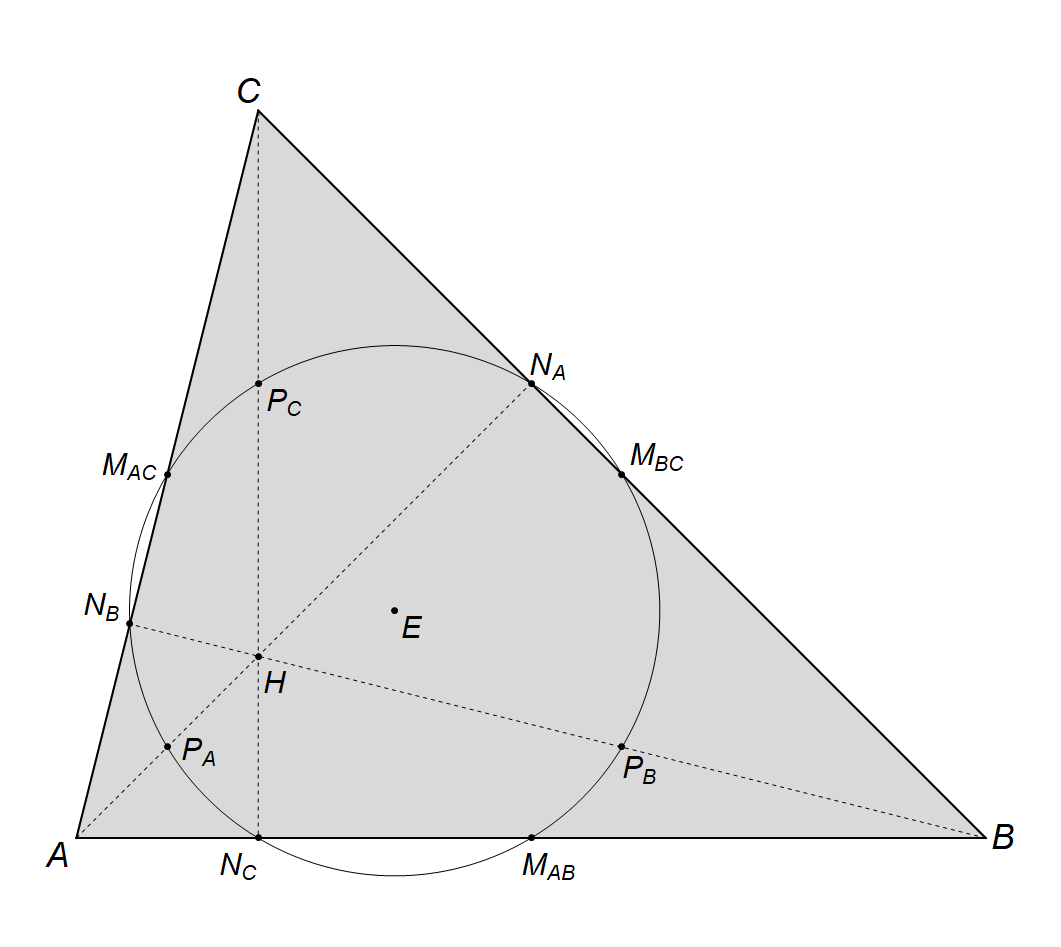
Malo manje poznata kružnica koja se veže uz trokut je Eulerova kružnica, odnosno kružnica devet točaka (Slika 2). Na Eulerovoj kružnici smješteno je devet karakterističnih točaka trokuta: tri polovišta stranica trokuta (na Slici 1 i Slici 2 označena s M_{AC}, M_{BC} i M_{BC}), tri nožišta visina trokuta (na Slici 2 označena s N_{A}, N_{B} i N_{C}), te tri polovišta spojnice ortocentra trokuta (sjecište visina trokuta, točka označena s H na Slici 2) i vrhova trokuta. Ta su polovišta na Slici 2 označena s P_{A}, P_{B} i P_{C}.

Slika 2: Eulerova kružnica

Opisanu kružnicu prvi je nacrtao Leonhard Euler 1765. godine, i dokazao kako se na njoj nalazi šest istaknutih točaka (polovišta stranica i nožišta visina). Polumjer kružnice devet točaka dvostruko je manji od polumjera opisane kružnice [4]. Središte Eulerove kružnice ćemo označiti s E.
 

Navedene karakteristične kružnice trokuta omogućavaju nam iskazivanje sljedećih svojstava stranica trokuta:

(a)

Krajnje točke svake stranice leže na trokutu opisanoj kružnici.

(b)

Polovište svake stranice leži na Eulerovoj kružnici.

(c)

Svaka je stranica tangenta na trokutu upisanu kružnicu.

Upravo u navedenim svojstvima stranica trokuta nalazimo opravdanje za naziv „četvrte stranice trokuta“. Naime, kako je dokazao B.F. Sherman u članku „The fourth side of a triangle“ [4], u ravnini postoje (u općem slučaju) točno četiri dužine koje zadovoljavaju navedena svojstva!

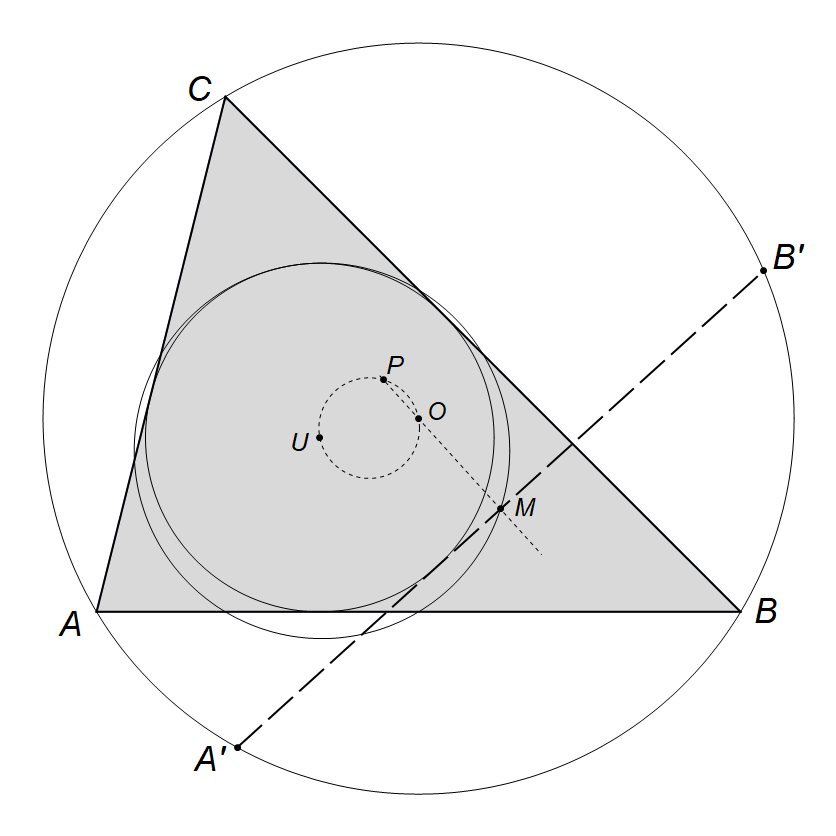
Za potrebe konstrukcije, promotrimo prvo svojstva koja posjeduju polovišta stranica trokuta, pa tako i polovište „četvrte“ stranice. U ovom ćemo radu to polovište označavati s M.
 

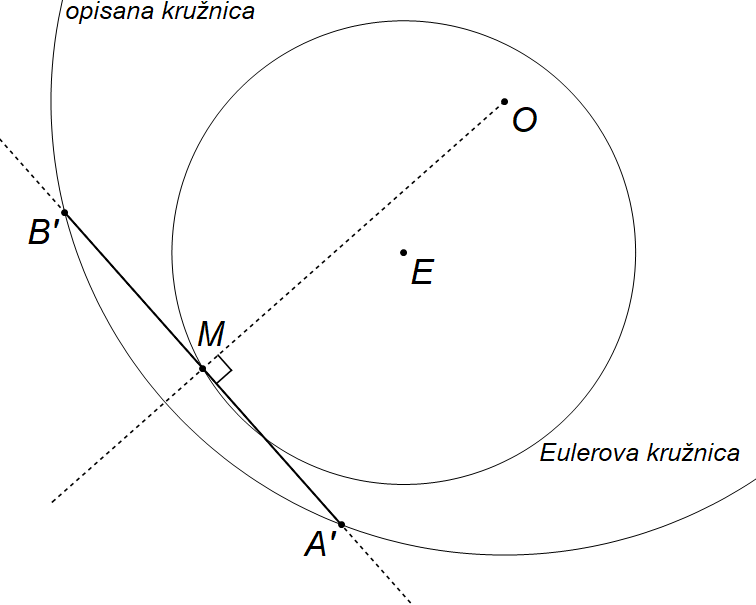
Ukoliko je dana neka točka M na Eulerovoj kružnici (a koja je unutar opisane kružnice), lako je konstruirati dužinu koja zadovoljava uvijete (a) i (b): povučemo pravac kroz točke O i M, te formiramo okomicu na taj pravac kroz točku M. Presjecišta konstruirane okomice i opisane kružnice (točke A' i B') čine dužinu čije je polovište M na Eulerovoj kružnici (Slika 3).1

 

Slika 3: Konstrukcija tetive \overline{A'B'} opisane kružnice s polovištem M na Eulerovoj kružnici

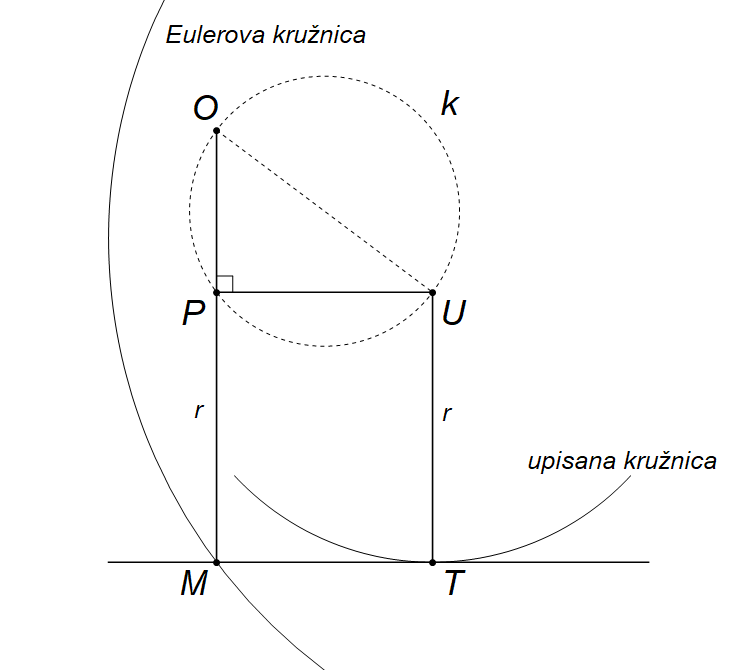
U sljedećem koraku konstrukcije promotrimo pravokutnik čije stranice formiraju simetrala „četvrte“ stranice trokuta, odnosno pravac OM, te spojnica središta upisane kružnice U i diralište tangente T, pravac UT. Oba navedena pravca trebaju biti okomita na „četvrtu“ stranicu trokuta. Stoga su pravci OM i IT paralelni. Vrhove pravokutnika čine točke U, T i M. Četvrti vrh pravokutnika, kojeg dobivamo povlačenjem okomice iz točke U na pravac OM označimo s P. Opisani elementi prikazani su na Slici 4.

 

Slika 4: Konstrukcija točke P

Kako se iz točke P dužina \overline{OU} vidi pod pravim kutom, slijedi da se točka P nalazi na kružnici kojoj je dužina \overline{OU} promjer (kružnica označena s k na Slici 4).
 

Dakle, kako bi konstruirali „četvrtu“ stranicu trokuta, moramo odrediti točku M na Eulerovoj kružnici, takvu da je točka P koja je presjecište pravca OM i kružnice s dijametrom \overline{OU}, udaljena od točke M za polumjer upisane kružnice r.
 

Na ovom mjestu konstrukcija napušta klasičnu metodu konstrukcije pomoću ravnala i šestara. Tehnika koju Sherman opisuje (i dokazuje) glasi:

Kada dođe do tog poklapanja, odredili smo polovište (neke) stranice trokuta. Iz polovišta potom odredimo stranicu na način na koji je to pisano na Slici 3. Tako konstruirana stranica zadovoljava uvjete (a)-(c).
 

No, iznenađujući rezultat jest taj da ćemo prateći gornju proceduru dobiti četiri točke, i četiri tetive trokutu opisane kružnice koje zadovoljavaju ta tri svojstva! Na Slici 5 prikazan je trokut i njegova „četvrta“ stranica koja je konstruirana ovim postupkom. Četvrta stranica je nacrtana isprekidanom linijom i označena s \overline{A'B'}. Slika nam potvrđuje navedena svojstva „četvrte“ stranice trokuta: rubne točke nalaze na opisanoj kružnici (kružnica sa središtem u točki O); polovište se nalazi na Eulerovoj kružnici (točka M); te je stranica \overline{A'B'} tangenta na upisanu kružnicu trokuta (kružnica sa središtem U).

 

Slika 5: Shermanova konstrukcija „četvrte“ stranice trokuta A'B'

Treba napomenuti kako postoje i trokuti koji su izuzetak, tj. trokuti kod kojih opisana procedura rezultira sa samo tri stranice. Radi se o jednakokračnim trokutima, te o trokutima kojima je jedna od stranica paralelna s pravcem OU.

Shermanovu ideju detaljno je u svom radu analizirao Paul Yiu [6]. Za razliku od Shermana, Yiu dužinu sa svojstvima (a)-(c) ne naziva „četvrtom stranicom trokuta“, već Shermanovom dužinom. Svoju analizu Yui temelji na baricentričkim koordinatama, čije predstavljanje izlazi iz okvira ovog teksta. No, zainteresiranim čitateljima preporučamo članak profesora Voleneca [5], nakon kojeg je lakše pratiti rezultate i dokaze koje predstavlja Yui.
 

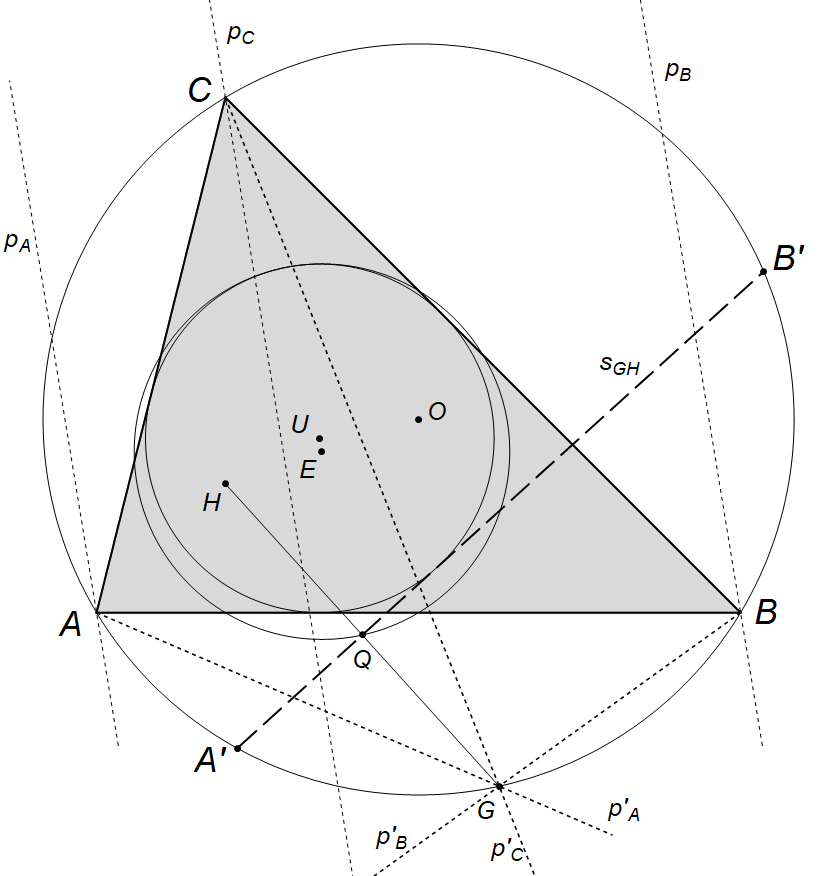
Konstrukcija Shermanove dužine (Slika 7) pomoću ravnala i šestera:

 

Slika 6: Konstrukcija Shermanove dužine pomoću ravnala i šestara

Navedena konstrukcija temelji se na svojstvima MacBeathove upisane ču\-njo\-sječ\-ni\-ce. U ovom slučaju radi se o elipsi, čije su fokalne točke u središtu opisane kružnice O i ortocentra H, dok joj je središte točka E, središte Eulerove kružnice. Konstrukcija slijedi iz poznate činjenice da je MacBeathove upisana čunjosječnica tangencijalna ljuska simetrale dužine \overline{GH}, gdje su točke G točke na trokutu opisanoj kružnici.
 

Pored ove jednostavne konstrukcije Shermanove dužine, Yui u svom radu predstavlja još jednu složeniju konstrukciju koja se temelji na svojstvima Gergonnove točke. Gergonnova točka je presjecište tri pravca koji spajaju točku u kojoj stranica trokuta tangira upisanu kružnicu s nasuprotnim vrhom trokuta. Ta je analiza presložena za ovaj članak, pa zainteresirane čitatelje upućujemo na [6].
 

Konačno, Yui daje i formulu za računanje duljine Shermanove dužine:

gdje je R polumjer opisane kružnice, r polumjer upisane kružnice, a s pola opsega, tj. s=\frac{a+b+c}{2}.

Ovim tekstom smo pokazali kako Shermanov tekst o „četvrtoj“ stranici trokuta ima temelj u svojstvima koja općenito zadovoljavaju stranice trokuta. Egzistencija četvrte dužine, koja pored tri zadane ispunjava tražena svojstva zapravo slijedi iz činjenice da odnosi čunjosječnica (u ovom slučaju zajedničke tangente elipse i kružnice sa istim središtem), zbog kvadratnih izraza koji opisuju te krivulje, (općenito) imaju četiri rješenja. Također, vidjeli smo kako je Shermanov rezultat prihvaćen od strane matematičke zajednice, te kako se Shermanova „četvrta“ stranica trokuta danas naziva Shermanovom dužinom. Za istu su formulirane konstrukcije klasičnom metodom ravnala i šestara, te je dana i formula za određivanje njene dužine.{FLM1}