Guraj-Promijeni visinu algoritam za pronalaženje maksimalnog protoka mreže
Guraj-Promijeni visinu algoritam za pronalaženje maksimalnog protoka mreže
Problem maksimalnog toka i njemu dualan problem, problem minimalnog reza, iznimno su korisni u modeliranju mnogih problema koji sadrže mreže, bilo cestovne, željezničke, računalne ili društvene. Obično modeliramo tok nekog materijala iz jednog dijela mreže u drugi, a tok mogu biti automobili, vlakovi, bitovi, preporuke i mnogi drugi predmeti i koncepti. Zanimljivo je da su se ova dva problema također pokazala korisnima u problemima modeliranja za koje nije očito da uključuju mreže ili protok materijala. Jedan takav primjer izložit ćemo u ovom članku.
U ovom članku izložit ćemo jedan od najefikasnijih poznatih algoritama za rješavanje problema maksimalnog toka, guraj-promijeni visinu algoritam za pronalaženje maksimalnog protoka mreže. Uz teorijsku pozadinu algoritma guraj-promijeni visinu, osvrnut ćemo se i na implementaciju tog algoritma u Javascriptu, kao i neke varijante algoritma koje nude određena poboljšanja.
1 Problem maksimalnog toka
1.1 Općenito o problemu maksimalnog toka
Prije same definicije problema maksimalnog toka, definirat ćemo pojmove iz teorije grafova koji će nam biti korisni u nastavku.
Definicija 1.1. Usmjereni graf je uređeni par \(G=(V, A)\), gdje je \(V\) proizvoljan neprazan konačan skup, a \(A \subseteq V \times V\). Elemente skupa \(V\) nazivamo vrhovi, a skupa \(A\) bridovi.
Kažemo da postoji put između vrhova \(s\) i \(t\) ako postoji konačan niz vrhova \(b_1, \ldots , b_n\) takav da vrijedi \((s, b_1), (b_1, b_2), \ldots , (b_{n-1}, b_n), (b_n, t) \in A\).
Put u kojem se nijedan vrh ne pojavljuje više od jednom nazivamo jednostavnim putem. Put koji počinje i završava u istom vrhu zove se ciklus. Jednostavan ciklus je ciklus u kojem su jedini vrhovi koji se ponavljaju prvi i zadnji.
Definirajmo sada formalno problem maksimalnog toka i pojam toka.
Definicija 1.2. Neka je dan usmjereni graf \(G=(V,A)\) te neka su dani kapaciteti bridova \(u(i,j)\ge 0\) bridova \((i,j)\in A\). s-t tok \(f: A \to \mathbb {R}^{\geq 0}\) je funkcija koja svakom bridu grafa pridružuje nenegativnu vrijednost tako da su sljedeća dva uvjeta zadovoljena:
- za sve bridove \((i, j) \in A\) vrijedi: \begin {equation} \label {uvj1} 0 \leq f(i, j) \leq u(i, j); \end {equation}
- za sve vrhove \(i \in V\backslash \{s, t\}\) vrijedi da je ukupan tok koji ulazi u vrh i jednak ukupnom toku koji izlazi iz vrha i, točnije: \begin {equation} \label {uvj2} \sum _{k:(k, i) \in A} f(k, i) = \sum _{k:(i, k) \in A} f(i, k). \end {equation}
Uz svaki s-t tok \(f\) definiramo vrijednost toka, koju označavamo \(|f|\). To je neto količina toka koja napušta izvor, točnije ukupna količina toka koja izlazi iz izvora smanjena za ukupnu količinu toka koji ulazi u izvor.
Definicija 1.3. Vrijednost s-t toka f dana je s: \begin {equation} |f| = \sum _{k:(s, k) \in A} f(s, k) - \sum _{k:(k, s) \in A} f(k, s). \end {equation}
Definicija 1.4. Problem maksimalnog toka definiramo ovako: na ulazu su nam dani usmjeren graf \(G = (V, A)\) i kapacitet svakog brida \(u(i, j) \geq 0\), \((i, j) \in A\). Uz to su nam dana dva istaknuta vrha \(s, t \in V\), gdje \(s\) nazivamo izvor, a \(t\) ponor. Cilj je pronaći tok koji maksimizira vrijednost s-t toka \(f\), dakle veličinu \(|f|\).
Uvjete \eqref{uvj1} nazivamo ograničenja kapaciteta, a \eqref{uvj2} ograničenja očuvanja toka.
Možemo se pitati zašto se vrijednost toka računa kao neto količina toka koji izlazi iz izvora, a ne kao neto količina toka koji ulazi u ponor, ali može se vidjeti da su te dvije vrijednosti uvijek jednake zbog ograničenja očuvanja toka \eqref{uvj2}.
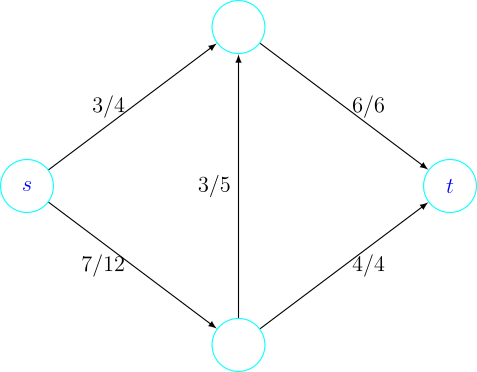
Sada vidimo da je cilj problema maksimalnog toka pronaći s-t tok \(f\) koji maksimizira \(|f|\). Primijetimo da je, zato što su vrijednosti kapaciteta nenegativne, tok \(f\) za kojeg vrijedi \(f(i,j) = 0, \forall (i, j)\in A\) s-t tok. Tada slijedi da je vrijednost maksimalnog toka uvijek nenegativna. Na slici 1 možemo vidjeti jedan primjer maksimalnog toka u grafu.
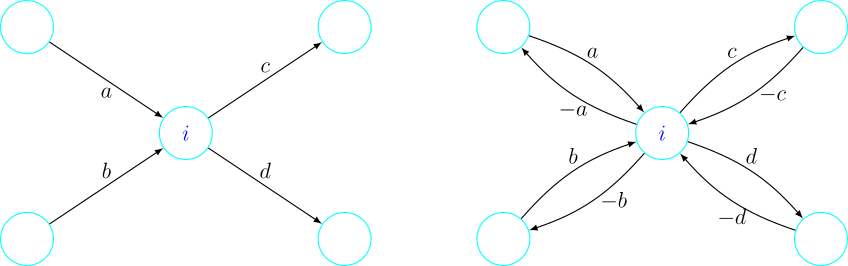
Iako definicija koju smo dali daje dobro postavljen problem, uvodimo novu definiciju pojma toka koja će nam pojednostavniti dokaze. U novoj definiciji uzimamo u obzir samo gornju granicu na vrijednost toka, umjesto gornju i donju kao u definiciji koju smo ranije dali. Svakom bridu \((i, j) \in A\) uvodimo dodatan, njemu suprotan brid \((j, i)\) s uvjetom da ako vrijednost toka na bridu \((i, j)\) iznosi \(f(i, j)\), tada vrijednost toka na bridu \((j, i)\) iznosi \(-f(i, j)\). Formalno, novi graf možemo biti multigraf, graf koji dozvoljava više bridova s istim vrhovima. Ovaj dodatan uvjet nazivamo iskrivljenom simetrijom. Sada se donja ograda \(f(i, j) \geq 0\) može zamijeniti s uvjetom \(u(j, i) = 0\), jer tada \(f(j, i) \leq u(j, i)\) povlači: \(f(i, j) = -f(j, i) \geq -u(j, i) = 0\).
Nadalje, pod novom definicijom, suma vrijednosti svih tokova na bridovima koji izlaze iz vrha \(i\) jednaka je neto vrijednosti toka koji izlazi iz čvora \(i\) po prethodnoj definiciji. Točnije, ako s \(A'\) označimo novi skup bridova (uključujući suprotne bridove), vrijedi: \begin {equation} \sum _{k:(i, k) \in A'} f(i, k) = \sum _{k:(i, k) \in A} f(i, k) - \sum _{k:(k, i) \in A} f(k, i). \end {equation} Tada ograničenje očuvanja toka postaje: \begin {equation} \sum _{k:(i, k) \in A'} f(i, k) = 0, \forall i \in V \backslash \{ s, t \}. \end {equation} Slika 2 prikazuje razliku između ograničenja očuvanja toka po staroj i novoj definiciji. Slično se može vidjeti da vrijednost toka iznosi \[ |f| = \sum _{k:(s, k) \in A'} f(s, k). \] Radi jednostavnosti, od sada ćemo novi skup bridova \(A'\) označavati s \(A\). Definirajmo sada tok formalno:
Definicija 1.5. s-t tok \(f: A \to \mathbb {R}\) je funkcija koja svakom bridu pridružuje vrijednost tako da vrijedi:
- \(f(i, j) \leq u(i, j), \forall (i, j) \in A\);
- za sve \((i, j) \in V \backslash \{ s, t \}\) je ukupna vrijednost toka na bridovima koji izlaze iz vrha \(i\) jednaka 0, točnije \[ \sum _{k:(i, k) \in A} f(i, k) = 0; \]
- \(f(i, j) = -f(j, i), \forall (i, j) \in A \).
1.2 Uvjeti optimalnosti
Nakon što smo definirali tok i problem maksimalnog toka, pitamo se kako odrediti je li dani tok maksimalan ili nije. Promotrimo prvo jedan primjer.
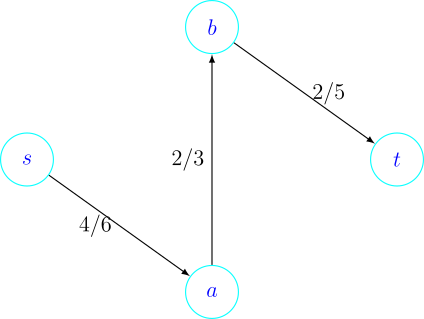
Primjer 1.6. Promotrimo dani graf. Je li označeni tok \(f\) maksimalan?
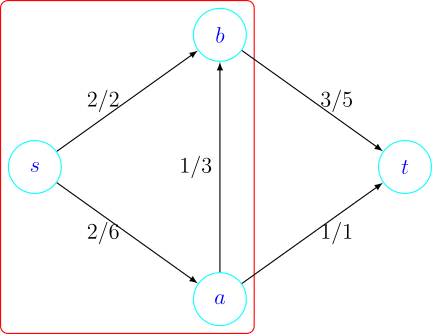
Po definiciji vrijednosti toka vidimo da je \(\left \lvert f \right \rvert = 4\). Također vidimo da svaka jedinica toka koja putuje od vrha \(s\) do vrha \(t\) mora proći bridovima koji idu iz crvenog područja u područje koje nije crveno. Iz toga zaključujemo da maksimalan tok ne može biti veći od \(u(a, t) + u(b, t) = 5 + 1 = 6\). Takvim razmišljanjem dolazimo do ideje minimalnog reza.
Formalizirajmo sada intuiciju iz primjera.
Definicija 1.7. s-t rez je podskup vrhova \(S \subseteq V\) takav da je \(s \in S\) i \(t \notin S\).
Za bridove koji izlaze iz \(S\) kažemo da su u rezu definiranom s \(S\), formalno: \[ \delta ^{+}(S) = \{ (i,j) \in A:i \in S, j \notin S \}. \] Analogno definiramo skup svih bridova koji ulaze u \(S\): \[ \delta ^{-}(S) = \{ (i,j) \in A:i \notin S, j \in S \}. \] Kapacitet s-t reza \(S\) je suma kapaciteta svih bridova koji izlaze iz \(S\), točnije: \[ u(\delta ^{+}(S)) = \sum _{(i,j) \in \delta ^{+}(S)} u(i,j). \]
Sada, kad smo formalno definirali pojam reza, možemo dokazati da za svaki s-t tok \(f\) i s-t rez \(S\) vrijedi da je vrijednost toka \(f\) manja ili jednaka kapacitetu reza \(S\).
Lema 1.8. Za svaki s-t tok \(f\) i s-t rez \(S\) vrijedi: \(\left \lvert f \right \rvert \leq u(\delta ^{+}(S)). \)
Dokaz. Korištenjem definicije vrijednosti foka \(f\) i ograničenja očuvanja toka za sve
\(i \in S \backslash \{ s \}\) (prisjetimo se da vrijedi \(t \notin S\)) imamo: \begin {align*} \left \lvert f \right \rvert &= \sum _{k:(s, k) \in A} f(s, k) = \sum _{k:(s, k) \in A} f(s, k) + 0 \\ &= \sum _{k:(s, k) \in A} f(s, k) + \sum _{i \in S: i \neq s} \left (\sum _{j:(i, j) \in A} f(i, j)\right ) \\ &= \sum _{i \in S} \left (\sum _{j:(i, j) \in A} f(i, j)\right ). \end {align*}
Sada možemo rastaviti sumu na dva dijela ovisno o tome je li početni vrh brida element skupa \(S\) ili nije. Primijetimo da, ako su \(i, j \in S\), suma sadržava \(f(i, j)\) i \(f(j, i) = -f(i, j)\), pa se ta dva sumanda poništavaju. Sada korištenjem ograničenja kapaciteta imamo: \begin {align*} \left \lvert f \right \rvert &= \sum _{i \in S} \left (\sum _{j:(i, j) \in A} f(i, j)\right ) \\ &= \sum _{i \in S} \left ( \sum _{j \in S:(i, j) \in A} f(i, j) + \sum _{j \notin S:(i, j) \in A} f(i, j) \right ) \\ &= \sum _{i \in S, j \notin S, (i, j) \in A} f(i, j) = \sum _{(i, j) \in \delta ^{+}(S)} f(i, j) \\ &\leq \sum _{(i, j) \in \delta ^{+}(S)} u(i, j) = u(\delta ^{+}(S)). \end {align*} □
Korolar 1.9. Neka je \(f\) s-t tok i \(S\) s-t rez. Tada je \(f(i, j) = u(i, j), \forall (i, j) \in \delta ^{+}(S)\) ako i samo ako je \(\left \lvert f \right \rvert = u(\delta ^{+}(S))\).
Dokaz. Ako je \(f(i, j) = u(i, j), \forall (i, j) \in \delta ^{+}(S)\), onda je posljednja nejednakost u prijašnjem dokazu jednakost, pa je time ova implikacija dokazana.
Ako je \(\left \lvert f \right \rvert = u(\delta ^{+}(S))\), onda mora vrijediti \(\sum _{(i, j) \in \delta ^{+}(S)} f(i, j) = \sum _{(i, j) \in \delta ^{+}(S)} u(i, j)\). Međutim, budući da su svi sumandi u obje sume nenegativni i budući da vrijedi \(f(i, j) \leq u(i, j), \forall (i, j) \in A \supseteq \delta ^{+}(S)\), zaključujemo da tada mora vrijediti \(f(i, j) = u(i, j), \forall (i, j) \in \delta ^{+}(S)\). □
Sada možemo vidjeti da dani tok u grafu iz primjera 1.6 nije maksimalan jer je skup \(\{ s, a, b \} \) s-t rez, a ne vrijedi \(f(b, t) = u(b, t)\), što je u kontradikciji s prijašnjim korolarom.
Definicija 1.10. Minimalni s-t rez \(S^*\) je rez s minimalnim kapacitetom, to jest: \[ u(\delta ^{+}(S^*)) = \min _{S \subseteq V, s \in S, t \notin S} u(\delta ^{+}(S))). \]
Po lemi 1.8 zaključujemo da je vrijednost maksimalnog toka manja ili jednaka kapacitetu minimalnog reza. Kada bi u primjeru 1.6 povećali tok na bridovima \((s, a), (a, b)\) i \((b, t)\) za 2, dobili bismo tok čija je vrijednost jednaka kapacitetu minimalnog reza za \(S = \{ s, a, b \}\). To nas dovodi do jednog od najistaknutijih rezultata u teoriji mrežnih tokova.
Teorem 1.11 (Ford, Fulkerson). Vrijednost maksimalnog s-t toka jednaka je vrijednosti minimalnog s-t reza.
Prije navođenja idućeg važnog teorema, definirajmo još nekoliko bitnih pojmova. Ako nam je dan tok \(f\) u grafu \(G = (V, A)\), definiramo rezidualni kapacitet s \( u_f(i, j) = u(i, j) - f(i, j)\). Primijetimo da je rezidualni kapacitet uvijek nenegativan zbog ograničenja kapaciteta. Bridove \((i, j) \in A\) čiji je rezidualni kapacitet 0 nazivamo zasićenim bridovima. Rezidualni graf u odnosu na tok \(f\) definiramo kao graf \(G_f = (V, A_f)\) gdje je \(A_f = \{ (i, j) \in A : u_f(i, j) > 0 \}\).
Primjetimo da za suprotne bridove vrijedi: \[ u_f(j, i) = u(j, i) - f(j, i) = 0 + f(i, j) = f(i, j), \] pa zaključujemo da rezidualni kapacitet suprotnog brida \((j, i)\) odgovara tome koliko maksimalno možemo smanjiti tok na bridu \((i, j)\). Kao primjer rezidualnog grafa dana je slika 3.
Ako postoji put od vrha \(s\) do vrha \(t\) u rezidualnom grafu \(G_f\) takav da su svi bridovi na tom putu elementi skupa \(A_f\), onda takav put nazivamo povećavajući put. Jedan takav put može se vidjeti na slici 3. Kako svi bridovi u povećavajućem putu imaju strogo pozitivan rezidualni kapacitet, zaključujemo da tok \(f\) nije maksimalan. Naime, možemo dobiti tok \(f'\) čija je vrijednost veća od toka \(f\) tako da povećamo tok po bridovima koji se nalaze na povećavajućem putu.
Formalno, neka je \(\delta \) najmanji rezidualni kapacitet na povećavajućem putu \(P\), točnije \(\delta = \min _{(i, j) \in P} u_f(i, j)\). Primjetimo da, jer su rezidualni kapaciteti svih bridova na povećavajućem putu strogo pozitivni, vrijedi \(\delta > 0\). Tada definiramo novi tok \(f'\) ovako: \[ f'(i, j) = \begin {cases} f(i, j) + \delta & \forall (i, j) \in P; \\ f(i, j) - \delta & \forall (j, i) \in P; \\ f(i, j) & \text {inače}. \end {cases} \] Nekada kažemo da gurnemo \(\delta \) jedinica toka po putu \(P\), rezultirajući tokom \(f'\). Također za \(\delta \) nekada kažemo da je rezidualni kapacitet puta \(P\).
Preostalo je još pokazati da je \(f'\) tok. Možemo, bez smanjenja općenitosti, pretpostaviti da je \(P\) jednostavan put. Uvjeti očuvanja i dalje vrijede za sve vrhove izvan puta \(P\). Po definiciji od \(\delta \), za sve \((i, j) \in P\), vrijedi: \[ f'(i, j) = f(i, j) + \delta \leq f(i, j) + u_f(i, j) = f(i, j) + [u(i, j) - f(i, j)] = u(i, j), \] pa je time dokazano da je zadovoljeno ograničenje kapaciteta.
Iskrivljena simetrija očito vrijedi za sve bridove koji nisu u \(P\), a za \((i, j) \in P\) vrijedi: \[ f'(i, j) = f(i, j) + \delta = -[f(j, i) - \delta ] = -f'(j, i). \]
Još je preostalo pokazati da je zadovoljeno ograničenje očuvanja toka. To svojstvo je očito zadovoljeno za sve vrhove \(i\) koji nisu dio puta \(P\). Ako je vrh \(i \neq s, t\) na putu \(P\), onda postoje bridovi \((h, i), (i, j)\) koji su na putu \(P\), pa za njih vrijedi \(f'(i, h) = f(i, h) - \delta \) i \(f'(i, j) = f(i, j) + \delta \). Tada imamo: \[ \sum _{k: (i, k) \in A} f'(i, k) = \sum _{k: (i, k) \in A} f(i, k) + \delta - \delta = 0, \] budući da je \(f\) tok te za njega vrijedi svojstvo ograničenja očuvanja toka. Slično, ako je \((s, j)\) prvi brid na putu \(P\), onda je \(f'(s, j) = f(s, j) + \delta \), pa budući da je \(\delta > 0\) vrijedi: \[ \left \lvert f' \right \rvert = \sum _{k: (s, k) \in A} f'(s, k) = \sum _{k: (s, k) \in A} f(s, k) + \delta = \left \lvert f \right \rvert + \delta > \left \lvert f \right \rvert . \]
Dakle \(f'\) je veći tok od \(f\). Sada možemo dokazati teorem čija je direktna posljedica teorem 1.11.
Teorem 1.12. Iduće 3 tvrdnje ekvivalentne su za svaki s-t tok \(f\):
- \(f\) je maksimalan tok;
- ne postoji povećavajući put u \(A_f\);
- \(\left \lvert f \right \rvert = u(\delta ^{+}(S))\), za neki s-t rez \(S\).
Dokaz. \(1. \Rightarrow 2.\): Ovu implikaciju smo već dokazali, točnije njen obrat po kontrapoziciji, prije navođenja samog teorema kad smo dokazali da ako postoji povećavajući put u \(A_f\), onda \(f\) nije maksimalan.
\(2. \Rightarrow 3.\): Neka je \(S\) skup svih vrhova do kojih postoji put iz vrha \(s\) u \(G_f\) takav da je rezidualan kapacitet svakog brida na tom putu strogo pozitivan. Jer ne postoji povećavajući put u \(A_f\), znamo da vrijedi \(t \notin S\). Također, za svaki brid \((i, j)\) takav da je \(i \in S\) i \(j \notin S\), mora vrijediti da je \(u_f(i, j) = 0\), to jest \(f(i, j) = u(i, j)\). Tada, po korolaru 1.9, zaključujemo da je \(\left \lvert f \right \rvert = u(\delta ^{+}(S))\).
\(3. \Rightarrow 1.\): Po lemi 1.8 znamo da vrijedi \(\left \lvert f \right \rvert \leq u(\delta ^{+}(S))\), za svaki s-t tok \(f\) i s-t rez \(S\). Jer za neki s-t tok \(f\) i s-t rez \(S\) vrijedi \(\left \lvert f \right \rvert = u(\delta ^{+}(S))\), zaključujemo da taj \(f\) mora biti maksimalan tok, a \(S\) minimalan rez. □
Teorem 1.12 daje nam ideju za algoritam za pronalaženje maksimalnog toka: krenemo od toka \(f = 0\), tražimo povećavajući put te ažuriramo tok onako kako smo opisali u dokazu teorema 1.12. Problem ovog algoritma je da, ako ne biramo povećavajuće puteve pažljivo, algoritam nije polinomijalan.
\(f(i, j) \gets 0, \forall (i, j) \in A\)
dok postoji povećavajući put \(P\) u \(A_f\):
Gurni tok u \(P\)
Ažuriraj \(f\)
Vrati \(f\);
dok postoji povećavajući put \(P\) u \(A_f\):
Gurni tok u \(P\)
Ažuriraj \(f\)
Vrati \(f\);
Međutim, ovaj nas algoritam vodi do zanimljivog zaključka: ako su svi kapaciteti \(u(i, j)\) cijeli brojevi, tada postoji maksimalan tok takav da je \(f(i, j) \in \mathbb{Z} , \forall (i, j) \in A\) i algoritam 1 pronalazi jedan takav tok. Ako su sve vrijednosti \(f(i, j)\) cijeli brojevi, tada za tok \(f\) kažemo da je cijeli. Lako je vidjeti da ova tvrdnja vrijedi. Naime, jer su na početku sve vrijednosti \(f(i, j)\) jednake 0 i sve vrijednosti \(u(i, j)\) cijeli brojevi, zaključujemo da su svi rezidualni kapaciteti \(u_f(i, j)\) cijeli brojevi. Tada slijedi da je \(\delta \) cijeli broj, pa onda i za novi tok \(f'\) vrijedi da je svaka vrijednost \(f'(i, j)\) cijeli broj.
Propozicija 1.13 (Svojstvo cijelosti). Ako su svi kapaciteti \(u(i, j)\) cijeli brojevi, tada postoji maksimalan tok \(f\) čija je vrijednost također cijeli broj.
Označimo s \(U\) maksimalan kapacitet, točnije \(U = \max _{(i, j) \in A} u(i, j)\). Tada možemo ograničiti broj iteracija (to jest broj povećavajućih puteva koje moramo pronaći) osnovnog algoritma s \(O(mU)\). Označimo s \(m\) broj bridova, a s \(n\) broj vrhova grafa. Naime, jer je maksimalan tok neto vrijednost toka koji izlazi iz izvora, u najgorem slučaju imamo \(m\) bridova koji izlaze iz izvora takvi da su svi kapaciteta \(U\), tako da je najveća moguća vrijednost maksimalnog toka \(mU\). Ako su kapaciteti cijeli brojevi, tada se vrijednost toka u svakoj iteraciji poveća barem za 1, pa iz toga zaključujemo da je maksimalan broj iteracija \(O(mU)\). Povećavajući put u grafu možemo pronaći u vremenu \(O(m)\), pa je ukupna složenost osnovnog algoritma jednaka \(O(m^2U)\).
Iako je vrijednost \(U\) dio ulaza, ovaj algoritam nije polinomijalan u veličini ulaza problema jer pretpostavljamo da nam je ulaz dan u binarnom zapisu. Broj bitova potreban da bi se zapisao broj \(U\) u binarnom zapisu je najviše \(\left \lceil \log _{2}U\right \rceil + 1\). Tada je \(U\) eksponencijalan u odnosu na veličinu zapisa broja \(U\). Tada za algoritam 1 kažemo da je pseudopolinomijalan. U nastavku ćemo pronaći i analizirati neke polinomijalne algoritme za pronalaženje maksimalnog toka.
1.3 Zajedničko korištenje automobila
Prije nogo što krenemo tražiti polinomijalne algoritme za rješavanje problema maksimalnog toka, promotrimo jedan primjer primjene na problem koji na prvi pogled ne uključuje ni tok ni mrežu.
Primjer koji promatramo uključuje pravednu raspodjelu vozačkih odgovornosti za skupinu ljudi koji zajedno voze. Svaki tjedan ljudi koji se zajedno voze obavijeste ostale kojim danima će koristiti automobil. Oni bi htjeli pravedno rasporediti odgovornost vožnje i tako dolaze do iduće ideje: na dan kada se \(k\) ljudi vozi u automobilu, svaki od njih dobiva \(1/k\) udjela odgovornosti vožnje. Neka je \(r_i\) ukupni udio odgovornosti \(i\)-te osobe za taj tjedan. Onda zaključujemo da bi \(i\)-ta osoba u tom tjednu trebela voziti najviše \(\left \lceil r_i \right \rceil \) dana. U idućoj tablici možemo vidjeti jedan primjer s četvero ljudi.
| Pon | Uto | Sri | Čet | Pet | |
| 1 | X | X | X | ||
| 2 | X | X | X | X | |
| 3 | X | X | |||
| 4 | X | X | X | X | X |
Vidimo da osobe 1, 3 i 4 dobiju \(1/3\) odgovornosti za ponedjeljak, osobe 2 i 4 \(1/2\) odgovornosti za utorak, osobe 1, 2 i 4 \(1/3\) odgovornosti za srijedu i petak te osobe 2, 3 i 4 \(1/3\) odgovornosti za četvrtak. Tada vidimo da vrijedi \(r_1 = \frac {1}{3} + \frac {1}{3} + \frac {1}{3} = 1\), \(r_2 = \frac {1}{2} + \frac {1}{3} + \frac {1}{3} + \frac {1}{3} = \frac {3}{2}\), \(r_3 = \frac {1}{3} + \frac {1}{3} = \frac {2}{3}\) i \(r_4 = \frac {1}{3} + \frac {1}{2} + \frac {1}{3} + \frac {1}{3} + \frac {1}{3} = \frac {11}{6}\). Primijetimo da je \(\sum _{i=1}^{4}r_i = 5\) jer je suma odgovornosti za svaki dan jednaka 1.
Sada ćemo postaviti instancu problema maksimalnog toka čijim rješevanjem ćemo dobiti tko treba voziti koji dan. Da bismo to napravili, treba nam graf čiji skup vrhova sadrži, osim izvora i ponora, po jedan vrh za svaku osobu i po jedan vrh za svaki radni dan u tjednu. Zatim dodamo po jedan brid kapaciteta \(\left \lceil r_i \right \rceil \) od izvora do vrha koji predstavlja osobu \(i\) te po jedan brid kapaciteta 1 od vrha koji predstavlja neki dan u tjednu do ponora. Za kraj dodamo brid kapaciteta 1 od osobe \(i\) do svakog dana u kojem ta osoba koristi automobil.
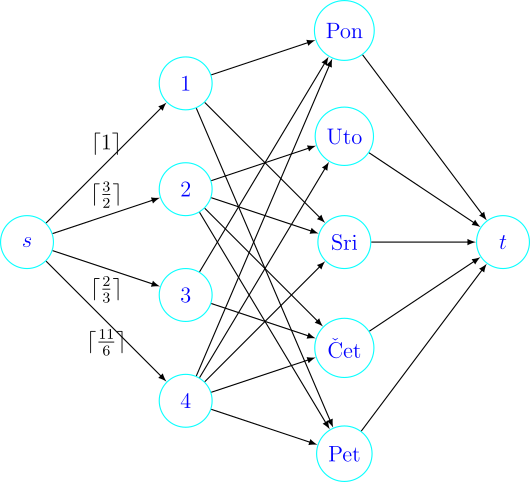
Tvrdimo da ako u mreži postoji cijeli tok \(f\) vrijednosti 5, tada možemo raspodijeliti odgovornosti vožnje osobama. Primijetimo da rez \(S = V \backslash \{ t \}\) ima kapacitet 5 (po jedan brid kapaciteta 1 za svaki radni dan), pa ako takav tok \(f\) postoji, onda je i maksimalan. Zato je svaki brid od nekog dana do ponora zasićen i vrijednost toka na tim bridovima je 1. Za svaki vrh koji predstavlja dan, zbog ograničenja očuvanja toka i činjenice da je \(f\) cijeli, vrijedi da postoji zasićeni brid od vrha koji predstavlja neku osobu do tog dana. Tada odgovornost vožnje za neki dan postavljamo na osobu od koje dolazi brid koji je zasićen. Tada osoba \(i\) može voziti najviše \(\left \lceil r_i \right \rceil \) dana (zbog ograničenja očuvanja toka, ograničenja kapaciteta i činjenice da je kapacitet brida od izvora do čvora \(i\) jednak \(\left \lceil r_i \right \rceil \)), što smo i htjeli.
Sada je još preostalo pokazati da mreža sadrži cijeli tok \(f\) vrijednosti 5. Međutim, zbog svojstva cijelosti, dovoljno je pokazati da postoji bilo kakav tok \(f'\) vrijednosti 5, pa će činjenica da su svi kapaciteti cijeli brojevi povlačiti da postoji cijeli tok \(f\) vrijednosti 5. Tok \(f'\) odgovarat će raspodijeli odgovornosti koju smo opisali na početku: ako u nekom danu \(k\) osoba koristi automobil, svakoj osobi dati ćemo \(\frac {1}{k}\) odgovornosti. To znači da ćemo postaviti tok brida koji spaja osobu s danom na \(\frac {1}{k}\). Jer je suma tokova koji ulaze u vrh koji predstavlja neki dan jednaka 1, a vrijednost toka koji izlazi iz vrha koji predstavlja osobu \(i\) jednak \(r_i\), znamo da smo dobili tok čija je vrijednost \(\sum _{i=1}^{k}r_i = 5\).
Ovaj primjer dobro ilustrira moć svojstva cijelosti. Naime, bilo nam je dovoljno pronaći neki maksimalan tok u grafu čiji su kapaciteti cijeli brojevi da bismo zaključili da postoji cijelobrojan maksimalan tok.
Jedno rješenje problema, dobijeno korištenjem implementacije opisane u sekciji 3, je da vozač 1 vozi petkom, vozač 2 srijedom, vozač 3 ponedjeljkom te vozač 4 utorkom i četvrtkom. Ova raspodjela je pravedna jer \(i\)-ti vozač vozi najviše \(\left \lceil r_i \right \rceil \) dana u tjednu.
2 Guraj-promijeni visinu algoritam
2.1 Opis algoritma
U ovoj sekciji promotrit ćemo algoritam koji je idejno poprilično drugačiji od osnovnog algoritma za pronalaženje maksimalnog toka, ali se u praksi pokazao među najbržim poznatima.
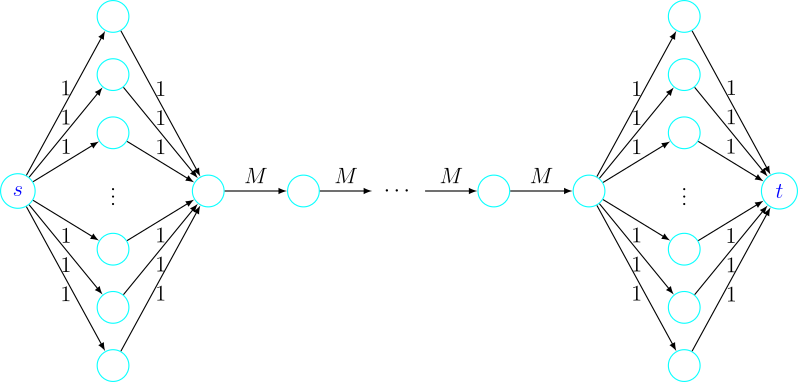
Jedan od problema osnovnog algoritma ilustriran je slikom 5. Taj graf sadrži \(M\) vrhova desno od izvora, \(M\) vrhova lijevo od ponora i jako dugačak put između ta 2 skupa vrhova. Po osnovnom algoritmu, svaki put kada povećamo vrijednost puta, povećamo ju za 1 i to povećanje šaljemo dugim putem. Bilo bi bolje kada bismo nekako mogli povećati put za \(M\) odjednom, stoga bismo onda morali samo jednom slati novi tok po dugačkom putu. Algoritam koji ćemo promatrati u ovoj sekciji, guraj-promijeni visinu algoritam, moći će napraviti upravo to. Dok smo kod osnovnog algoritma održavali tok \(f\) i povećavali ga dok nismo pronašli s-t rez \(S\) kapaciteta jednakog vrijednosti toka \(f\), guraj-promijeni visinu algoritam radi upravo suprotno: u njemu održavamo s-t rez \(S\) sve dok ne dobijemo tok \(f\) vrijednosti jednake kapacitetu s-t reza \(S\).
Guraj-promijeni visinu algoritam održava posebnu vrstu toka koji nema sva svojstva kao i tok kojeg smo definirali. Tu vrstu toka nazivamo predtok. Svojstvo koje predtok ne zadovoljava je svojstvo očuvanja toka: umjesto da zahtijevamo da je neto vrijednost toka za svaki vrh \(i \in V \backslash \{ s, t \}\) jednaka 0, zahtijevamo samo da je nenegativna. Tada neto vrijednost toka u vrhu \(i\) nazivamo višak u vrhu \(i\) i označavamo s \(e_f(i)\).
Definicija 2.1. s-t predtok je funkcija \(f: A \rightarrow \mathbb {R}\) takva da vrijedi:
- \(f(i, j) \leq u(i, j), \forall (i, j) \in A\);
- tok koji ulazi u vrh \(i \neq s\) je nenegativan, točnije \(\sum _{k:(k, i) \in A}f(k, i) \geq 0\);
- \(f(i, j) = -f(j, i), \forall (i, j) \in A\).
Višak od \(i\) za predtok \(f\) definiramo ovako: \(e_f(i) = \sum _{k:(k, i) \in A}f(k, i)\).
Uz održavanje predtoka, guraj-promijeni visinu algoritam održava i oznake visine \(d(i)\) za svaki vrh \(i \in V\). Ako je \(d(i) \leq n\), gdje je \(n\) broj vrhova, onda je oznaka visine \(d(i)\) donja ograda na (netežinsku) udaljenost od vrha \(i\) do ponora po bridovima pozitivnog rezidualnog kapaciteta, tj. po bridovima rezidualnog grafa.
Definicija 2.2. Oznaka visine \(d(i)\) je valjana, za neki \(i \in V\) i predtok \(f\), ako vrijedi:
- \(d(s) = n\);
- \(d(t) = 0\);
- \(d(i) \leq d(j) + 1, \forall (i, j) \in A_f\).
Jedna posljedica postojanja valjane oznake visine je da za svaki predtok \(f\) postoji s-t rez u rezidualnom grafu, to jest ne postoji povećavajući put u rezidualnom grafu. Dokaz je dan sljedećom lemom 2.3
Lema 2.3. Za dani predtok \(f\) i valjanu oznaku visine \(d\) ne postoji povećavajući put u rezidualnom grafu \(G_f\).
Dokaz. Pretpostavimo da postoji jednostavan put \(P\) od vrha \(s\) do vrha \(t\) takav da za svaki brid \((i, j)\) na putu \(P\) vrijedi \((i, j) \in A_f\). Budući da je \(P\) jednostavan put, može sadržavati najviše \(n-1\) bridova, a budući da je \(d\) valjana oznaka visine vrijedi \(d(i) \leq d(j) + 1, \forall (i, j) \in P\). Znamo da vrijedi \(d(t) = 0\), pa budući da je \(d\) valjana oznaka visine mora vrijediti: \(d(s) \leq d(t) + \left \lvert P \right \rvert \leq n-1\), što je kontradikcija s definicijom valjane oznake visine. □
Sada vidimo da je cilj guraj-promijeni visinu algoritma postepeno pretvarati predtok u tok i pri tome održavati valjanu oznaku visine. Jednom kad imamo tok \(f\) i valjanu oznaku visine za \(f\) po lemi 2.3 znamo da ne postoji povećavajući put u rezidualnom grafu \(G_f\), pa je tok \(f\) maksimalan.
Glavna ideja pretvaranja predtoka u tok je postepeno gurati što je više moguće pozitivnog viška prema ponoru. Tok ćemo gurati po bridovima za koje mislimo da su na najkraćem putu do ponora. Ako vrh \(i\) ima pozitivan višak \(e_f(i) > 0\) i postoji brid \((i, j)\) s pozitivnim rezidualnim kapacitetom, možemo dobiti novi predtok ako povećamo tok na bridu \((i, j)\): povećavanje vrijednosti \(f(i, j)\) smanji višak u vrhu \(i\), ali ga poveća u vrhu \(j\). Da bismo osigurali da guramo tok po bridu \((i, j)\) koji je na najkraćem putu od \(i\) do ponora, guramo samo po bridovima za koje vrijedi \(d(i) = d(j) + 1\), to jest \(j\) je bliže ponoru nego \(i\).
Uvodimo terminologiju koju ćemo često koristiti u daljnjim razmatranjima: kažemo da je brid \((i, j)\) dopustiv ako je \((i, j) \in A_f\) i \(d(i) = d(j) + 1\). Tok ćemo povećavati samo po dopustivim bridovima. Kako želimo gurnuti što je više toka moguće po dopustivim bridovima, gurat ćemo minimum između viška \(e_f(i)\) i rezidualnog kapaciteta \(u_f(i, j)\).
Što ako imamo vrh \(i\) sa strogo pozitivnim viškom, ali nemamo dopustivih bridova \((i, j)\), to jest vrijedi \(d(i) < d(j) + 1, \forall j \in V\) takve da vrijedi \((i, j) \in A_f\)? U tom slučaju, intuicija nam govori da nam je oznaka visine za vrh \(i\) preniska. Naime, svi vrhovi \(j \in V\) takvi da postoji dopustiv brid \((i, j)\) imaju oznaku visine barem onoliku koliku ima vrh \(i\), pa onda zaključujemo da \(i\) mora imati veću oznaku visine nego što sad ima. Zato ćemo, u slučaju da ne postoji dopustiv brid iz vrha \(i\) s pozitivnim viškom, promijeniti visinu vrha \(i\): postaviti ćemo \(d(i)\) da bude jednak minimumu vrijednosti \(d(j) + 1\), za sve bridove \((i, j) \in A_f\). Time ćemo dobiti barem jedan dopustiv brid iz vrha \(i\) s pozitivnim viškom, a oznaka visine \(d\) ostat će valjana. Primijetimo da ako vrh \(i\) ima pozitivan višak, onda je \(f(k, i) > 0\), za neki brid \((k, i) \in A\), što onda povlači da postoji barem jedan brid koji izlazi iz \(i\) s pozitivnim rezidualnim kapacitetom (u ovom slučaju brid \((i, k)\)), pa znamo da postoji barem jedan brid koji izlazi iz \(i\) u skupu \(A_f\).
Još nam je preostalo samo vidjeti što napraviti u slučaju kada ne možemo gurnuti višak u ponor. U slučajevima kada se to dogodi, gurnut ćemo tok natrag prema izvoru: ako oznaka visine postane \(n\) ili veća, onda je \(d(i) - n\) donja granica na udaljenost od izvora i višak u vrhu \(i\) ćemo gurnuti prema izvoru.
Sada napokon možemo napisati guraj-promijeni visinu algoritam. Kažemo da je vrh \(i \in V \backslash \{ s, t \}\) aktivan ako ima pozitivan višak, to jest \(e_f(i) > 0\). Ako u grafu postoji aktivan vrh, onda još nemamo tok \(f\), pa tražimo još dopustivih bridova \((i, j)\). Ako postoji dopustiv brid \((i, j)\), gurnemo što više toka možemo po njemu: gurnemo minimum između viška u vrhu \(i\) i rezidualnog kapaciteta brida \((i, j)\). Ukoliko ne postoji dopustiv brid \((i, j)\), promijenimo visinu vrha \(i\).
Guraj\((i, j)\):
\(\delta \leftarrow \min (e_f(i), u_f(i, j))\)
\(f(i, j) \leftarrow f(i, j) + \delta \)
\(f(j, i) \leftarrow f(j, i) - \delta \)
PromijeniVisinu\((i)\):
\(d(i) \leftarrow \min _{(i, j) \in A_f}(d(j) + 1) \)
Guraj-PromijeniVisinu:
\(f(i, j) \leftarrow 0, \forall (i, j) \in A\)
\(f(s, j) \leftarrow u(s, j), f(j, s) \leftarrow -u(j, s), \forall (s, j) \in A\)
\(d(s) \leftarrow n\)
\(d(i) \leftarrow 0, \forall i \in V \backslash \{ s \}\)
dok postoji aktivan vrh \(i\):
ako postoji vrh \(j\) takav da je brid \((i, j)\) dopustiv:
Guraj\((i, j)\)
inače:
PromijeniVisinu\((i)\)
vrati \(f\)
\(\delta \leftarrow \min (e_f(i), u_f(i, j))\)
\(f(i, j) \leftarrow f(i, j) + \delta \)
\(f(j, i) \leftarrow f(j, i) - \delta \)
PromijeniVisinu\((i)\):
\(d(i) \leftarrow \min _{(i, j) \in A_f}(d(j) + 1) \)
Guraj-PromijeniVisinu:
\(f(i, j) \leftarrow 0, \forall (i, j) \in A\)
\(f(s, j) \leftarrow u(s, j), f(j, s) \leftarrow -u(j, s), \forall (s, j) \in A\)
\(d(s) \leftarrow n\)
\(d(i) \leftarrow 0, \forall i \in V \backslash \{ s \}\)
dok postoji aktivan vrh \(i\):
ako postoji vrh \(j\) takav da je brid \((i, j)\) dopustiv:
Guraj\((i, j)\)
inače:
PromijeniVisinu\((i)\)
vrati \(f\)
Prvo ćemo dokazati da algoritam guraj-promijeni visinu pronalazi maksimalan tok za svaku mrežu na ulazu. Započinjemo s dokazivanjem da algoritam održava predtok \(f\) i valjanu oznaku visine \(d\).
Lema 2.4. Guraj-promijeni visinu algoritam održava predtok \(f\).
Dokaz. Prvo moramo pokazati da je \(f\) na početku algoritma stvarno predtok. Za svaki vrh \(k\) takav da postoji brid \((s, k) \in A\) na početku vrijedi \(e_f(k) = u(s, k)\). Za sve ostale vrhove \(i\) vrijedi \(e_f(i) = 0\). Tada je jasno da su ograničenje kapaciteta i svojstvo iskrivljene simetrije ispoštovani, a višak je nenegativan, pa je \(f\) stvarno predtok.
Pretpostavimo sada da u nekoj iteraciji algoritma imamo predtok \(f\) te da smo gurnuli tok u brid \((i, j)\). Neka je \(f'\) vrijednost koju smo dobili time. Iz algoritma je vidljivo da smo gurnuli \(\delta = \min (e_f(i), u_f(i, j))\) jedinica u brid \((i, j)\). Zaključujemo da je ograničenje kapaciteta ispoštovano budući da vrijedi: \(f'(i, j) = f(i, j) + \delta \leq f(i, j) + u_f(i, j) \leq u(i, j)\) i \(f'(j, i) = f(j, i) - \delta \leq u(j, i)\). Svojstvo iskrivljene simetrije je ispunjeno budući da vrijedi: \(f'(i, j) = f(i, j) + \delta = -(f(j, i) - \delta ) = -f'(j, i)\). Konačno, vrhovi imaju nenegativan višak budući da smo gurnuli tok u vrhu \(i \neq s, t\) pa vrijedi \(e_{f'}(i) = e_f(i) - \delta \geq 0\) i \(e_{f'}(j) = e_f(j) + \delta \geq 0\). Time smo dokazali da je \(f'\) predtok. □
Lema 2.5. Guraj-promijeni visinu algoritam održava valjanu oznaku visine \(d\).
Dokaz. Na početku algoritma postavljamo \(d(s) = n\) i \(d(i) = 0, \forall i \in V \backslash \{ s \}\). Jedini bridovi \((i, j)\) za koje je tada moguće da je \(d(i) > d(j) + 1\) su bridovi oblika \((s, k)\) budući da je \(d(s) = n\), a \(d(k) = 0\). Međutim, svi takvi bridovi su na početku zasićeni, pa ne može vrijediti \(d(s) \leq d(k) + 1\) budući da ti bridovi nisu u skupu \(A_f\).
Sada moramo pokazati da \(d\) ostaje valjana oznaka visine tijekom izvođenja algoritma. To slijedi po samoj kostrukciji operacije. Promotrimo sada što se dogodi nakon izvođenja operacije guranja. Povećavanje vrijednosti \(f(i, j)\) može uzrokovati da rezidualni kapacitet brida \((j, i)\) postane pozitivan. Međutim, budući da operaciju guranja izvršavamo samo na bridovima za koje vrijedi \(d(i) = d(j) + 1\), znamo da vrijedi \(d(j) = d(i) - 1 < d(i) + 1\), pa je oznaka visine i dalje valjana. Konačno, nikad nećemo promijeniti oznaku visine vrhovima \(s\) i \(t\) budući da ti vrhovi nikad nisu aktivni, pa je \(d(s) = n\) i \(d(t) = 0\) kroz cijelo izvršavanje algoritma. □
Da bi pokazali da algoritam završi s tokom \(f\), prvo moramo dokazati iduću lemu.
Lema 2.6. Za svaki predtok \(f\) i za svaki vrh \(i\) takav da vrijedi \(e_f(i) > 0\) postoji jednostavan put od \(i\) do izvora takav da svaki brid na tom putu ima pozitivan rezidualni kapacitet.
Dokaz. Neka je \(i\) vrh takav da vrijedi \(e_f(i) > 0\) i neka je \(S\) skup svih vrhova \(j \in V\) takav da postoji put od \(i\) do \(j\) koji sadrži samo bridove s pozitivnim rezidualnim kapacitetom. Pretpostavimo suprotno, to jest da \(s \notin S\).
Primijetimo da je za svaki brid \((j, k)\) takav da je \(j \in S, k \notin S\), \(u_f(j, k) = 0\), pa je \(f(j, k) = u(j, k)\). Tada po iskrivljenoj simetriji vrijedi: \(f(k, j) = -f(j, k) = -u(j, k) \leq 0\). Promotrimo sada \(\sum _{j \in S} e_f(j)\). Po definiciji imamo: \begin {align*} \sum _{j \in S} e_f(j) &= \sum _{j \in S} \sum _{k:(k, j) \in A} f(k, j) \\ &= \sum _{j \in S} \left (\sum _{k \in S:(k, j) \in A} f(k, j) + \sum _{k \notin S:(k, j) \in A} f(k, j) \right ). \end {align*}
Po iskrivljenoj simetriji, elementi sume \(\sum _{j \in S} \sum _{k \in S:(k, j) \in A} f(k, j)\) se svi ponište pa je jednaka 0, dok su elementi sume \(\sum _{j \in S} \sum _{k \notin S:(k, j) \in A} f(k, j)\) svi nepozitivni. Tada zaključujemo da mora vrijediti \(\sum _{j \in S} e_f(j) \leq 0\). Međutim, budući da je \(f\) predtok, mora vrijediti \(e_f(j) \geq 0, \forall j \neq s\), pa imamo da je \(\sum _{j \in S} e_f(j) = 0\), to jest \(e_f(j) = 0, \forall j \in S\). Tako smo došli do kontradikcije budući da je \(i \in S\) i \(e_f(i) > 0\), pa početna tvrdnja vrijedi. □
Iako nam se lema 2.6 na prvi pogled čini nebitna za ovo što radimo, ona je bitna u dokazivanju da su oznake visine odozgo ograničene, što će nam biti bitno u pronalaženju složenosti algoritma.
Lema 2.7. \(d(i) \leq 2n - 1, \forall i \in V\).
Dokaz. Primijetimo da mijenjamo visinu samo vrhovima \(i\) koji imaju pozitivan višak, a po lemi 2.6 znamo da uvijek postoji jednostavan put \(P \subseteq A_f\) od \(i\) do izvora \(s\) koji sadrži samo bridove s pozitivnim rezidualnim kapacitetom. Budući da je \(P\) jednostavan put, vrijedi \(\left \lvert P \right \rvert \leq n-1\), a jer je \(d\) valjana oznaka visine i za sve \((i, j) \in P\) vrijedi \((i, j) \in A_f\), mora vrijediti: \(d(i) \leq d(s) + \left \lvert P \right \rvert = n + \left \lvert P \right \rvert \leq 2n - 1\). □
Koristeći lemu 2.7, lako možemo ograničiti broj operacija promjene visine u algoritmu, a s malo više truda i broj operacija guranja. Krenimo s operacijama promjene visine.
Lema 2.8. Broj operacija promjene visine u algoritmu guraj-promijeni visinu je \(O(n^2)\).
Dokaz. Sve oznake visine za vrhove \(i \neq s\) na početku su postavljene na \(d(i) = 0\), a svaki puta kada izvršimo operaciju promjene visine, za neki vrh se njegova oznaka visine poveća barem za 1. Po lemi 2.7, svaka oznaka visine može biti najviše \(2n-1\), a u grafu imamo \(n-2\) vrhova kojima možemo mijenjati visinu, pa zaključujemo da ukupan broj poziva operacije promjene visine u jednom izvođenju algoritma može biti najviše \((2n-1)(n-1) = O(n^2)\). □
Da bismo mogli ograničiti broj poziva operacija guranja u algoritmu, prvo operacije guranja dijelimo u dvije vrste. Prisjetimo se da u operaciji guranja tok na bridu \((i, j)\) povećavamo za minimum između \(e_f(i)\) i \(u_f(i, j)\). Operaciju guranja u kojoj vrijednost toka \(f(i, j)\) povećamo za \(u_f(i, j)\) nazivamo zasićenom operacijom guranja, dok onu u kojoj \(f(i, j)\) povećamo za \(e_f(i) < u_f(i, j)\) nazivamo nezasićenom operacijom guranja. Osim toga, da bismo mogli ograničiti broj operacija guranja potrebna nam je još jedna propozicija.
Propozicija 2.9. Ako je \(u_f(i, j)\) u trenutačnoj iteraciji algoritma, \(f'\) predtok u idućoj i \(u_{f'}(i, j) > 0\), onda mora vrijediti \(f'(i, j) < f(i, j)\), a time i \(f'(j, i) > f(j, i)\).
Dokaz. Ako je \(u_f(i, j) = 0\) u trenutačnoj iteraciji, a u sljedećoj iteraciji je \(u_{f'}(i, j) > 0\), onda je algoritam između te dvije iteracije morao povećati vrijednost toka na bridu \((j, i)\). Iz toga zaključujemo da je \(f'(j, i) > f(j, i)\), pa iz scojstva iskrivljene simetrije slijedi \(f(i, j) > f'(i, j)\). □
Lema 2.10. Broj zasićenih operacija guranja u algoritmu guraj-promijeni visinu je \(O(mn)\).
Dokaz. Neka je brid \((i, j) \in A\) proizvoljan. Ako smo izvršili zasićenu operaciju guranja na bridu \((i, j)\), onda je taj brid bio dopustiv i \(d(i) = d(j) + 1\). Budući da brid \((i, j)\) tada postane zasićen, njegov rezidualni kapacitet je 0. Iz propozicije 2.9 zaključujemo da tada brid \((i, j)\) može imati rezidualni kapacitet veći od 0 samo ako se u nekoj iteraciji poveća tok na bridu \((j, i)\), što se dogodi ako izvršimo operaciju guranja na bridu \((j, i)\).
Neka je \(d'\) oznaka visine u iteraciji u kojoj je pušten tok u bridu \((j, i)\). Iz toga slijedi da je u toj iteraciji moralo vrijediti \(d'(j) = d'(i) + 1\). Jer su oznake visine nepadajuće tijekom izvođenja algoritma, vrijedi: \(d'(j) = d'(i) + 1 \geq d(i) + 1 = d(j) + 2\). To znači da se oznaka visine vrha \(j\) mora povećati barem za 2 prije nego što brid \((i, j)\) ponovno može imati pozitivan rezidualni kapacitet, a time je moguće i izvršiti novu zasićenu operaciju guranja nad bridom \((i, j)\).
Budući da po lemi 2.7 vrijedi \(d(i) \leq 2n - 1\), zaključujemo da možemo izvršiti najviše \(n\) zasićenih operacija guranja na bridu \((i, j)\) tijekom izvođenja algoritma. Budući da imamo ukupno \(m\) bridova u grafu, broj zasićenih operacija guranja tijekom izvođenja algoritma je najviše \(O(mn)\). □
Ako zamislimo da oznaka visine vrha \(i\) označava na kojoj se visini vrh \(i\) nalazi (što sami naziv ”oznaka visine” sugerira), onda dokaz prijašnje leme sugerira da zasićena operacija guranja gura tok nizvodno, te da bismo mogli gurnuti tok iz \(i\) u \(j\) ponovno, prije toga ga moramo gurnuti iz \(j\) u \(i\). Da bismo mogli gurnuti tok nizvodno, moramo povećati visinu čvora \(j\) barem za 2, a budući da visina vrha \(j\) može biti najviše \(2n-1\), to znači da možemo izvršiti najviše \(n\) zasićenih operacija guranja na bridu \((i, j)\).
Sada ćemo ograničiti broj nezasićenih operacija guranja tijekom izvršavanja algoritma. Da bismo to napravili, koristit ćemo argument potencijalne funkcije. Definirat ćemo potencijaknu funkciju \(\Phi \) koja će kao argumente primati neke parametre algoritma i vrijednost te funkcije će biti nenegativna tijekom izvođenja algoritma. Na početku algoritma, vrijednost funkcije \(\Phi \) biti će neki nenegativan broj \(P\). Svaki korak algoritma koji će nam biti interesantan (primjerice svako izvođenje nezasićene operacije guranja) uzrokovat će smanjenje vrijednosti funkcije \(\Phi \) za barem 1. Ostali koraci, nama nezanimljivi, mogu uzrokovati povećanje vrijednosti funkcije \(\Phi \). Da bismo ograničili broj nama zanimljivih koraka, dovoljno je ograničiti za koliko se vrijednosti funkcije \(\Phi \) poveća tijekom izvođenja algoritma. Naime, broj izvođenja nama zanimljivih koraka može biti najviše \(P\) plus suma svih povećanja vrijednosti funkcije \(\Phi \).
Lema 2.11. Broj nezasićenih operacija guranja u algoritmu guraj-promijeni visinu je \(O(n^2m)\).
Dokaz. Neka je \(\Phi = \sum _{aktivni\; i} d(i)\). Tada je \(\Phi = 0\) na početku i na kraju algoritma jer na početku su oznake visine svih aktivnih vrhova jednake 0, a na kraju algoritma nijedan vrh nije aktivan. Promotrimo sada koje operacije uzrokuju promjene u vrijednosti funkcije \(\Phi \).
Vrijednost fukcije \(\Phi \) se smanjuje nakon svakog izvođenja nezasićene operacije guranja, Budući da izvođenje te operacije pretvori jedan aktivan vrh u neaktivan i time ga miče iz sume. Da bismo izvršili operaciju guranja na bridu \((i, j)\), treba vrijediti \(d(i) = d(j) + 1\), a čak i ako nezasićena operacija guranja pretvori vrh \(j\) u aktivan vrh, ukupna promjena vrijednosti funkcije \(\Phi \) je \(d(j) - d(i) = d(j) - (d(j) + 1) = -1\).
Vrijednost funkcije \(\Phi \) se povećava nakon izvođenja operacije promjene visine i zasićene operacije guranja koja stvara novi aktivan vrh. Operacija promjene visine može povećati vrijednost funkcije \(\Phi \) tako što će povećati oznaku visine, a dodavanje novog aktivnog vrha \(i\) u sumu može povećati vrijednosti funkcije \(\Phi \) za \(d(i) \leq 2n-1\). Tada se \(\Phi \) može ukupno povećati za najviše \(O(n^2)\) zbog operacija promjene visine, a \(O(nm) \dot (2n-1) = O(n^2m)\) zbog zasićenih operacija guranja.
Budući da je na početku izvođenja algoritma \(\Phi = 0\), ukupan broj nezasićenih operacija guranja tijekom izvođenja algoritma je \(O(n^2m)\). □
Sada možemo sve ove rezultate spojiti u jedan i dobiti složenost algoritma guraj-promijeni visinu.
Teorem 2.12. Algoritam guraj-promijeni visinu izračuna maksimalan tok u \(O(n^2m)\) koraka.
Dokaz. Svaka operacija guranja je složenosti \(O(1)\), pa je ukupna složenost svih operacija guranja u algoritmu \(O(n^2m)\). Za svaki vrh \(i\) čuvamo listu bridova koji izlaze iz njega sortiranu po vremenku kada smo zadnji put gurnuli tok po tom bridu. Kada tražimo dopustiv brid koji izlazi iz \(i\), krenemo od posljednjeg brida na kojem je bio gurnut tok; ako taj brid nije dopustiv, prijeđemo na sljedeći. Ako smo došli do kraja liste, ne postoji dopustiv brid iz vrha \(i\), pa možemo izvršiti operaciju promjene visine. Provjeravanje svih bridova koji izlaze iz \(i\) se može napraviti u \(O(\left \lvert \delta ^{+}(\{ i \}) \right \rvert )\) koraka. Po lemi 2.7, operaciju promjene visine napravimo \(O(n)\) puta, tako da je ukupno vrijeme izvođenja svih operacija promjene visine \(O(n\sum _{i \in V}\left \lvert \delta ^{+}(\{ i \}) \right \rvert ) = O(nm)\).
Kada izvršavanje algoritma stane, \(f\) je predtok i \(e_f(i), \forall i \in V\). Tada po lemi 2.3 ne postoji povećavajući put u grafu \(G_f\), pa je \(f\) maksimalan tok. □
3 Implementacija algortima guraj-promijeni visinu
Kao što smo spomenuli u uvodu, za implementiranje svih verzija guraj-promijeni visinu algoritma koristit ćemo programski jezik Javascript, točnije biblioteku React. U ovoj sekciji opisat ćemo implementaciju algoritma guraj-promijeni visinu i struktura koje su nam potrebne. Implementacija algoritma se može naći u GitHub repozitoriju [3].
Osnovna struktura koja nam je potrebna u implementaciji je sam graf. Graf je objekt koji sadrži dva niza podataka: niz vrhova i niz bridova. Svaki vrh je objekt koji sadrži informaciju o vrijednosti oznake visine tog vrha i vrijednosti viška toka u tom vrhu. Svaki brid je objekt koji sadrži oznaku početnog i krajnjeg vrha tog brida, kapacitet i tok. Na početku, niz bridova je prazan, dok niz vrhova sadrži 2 vrha (tako osiguravamo da svaki graf ima izvor i ponor). Početnu vrijednost grafa možemo vidjeti u idućem isječku koda.
1 graph: { 2 nodes: [{ 3 height: 0, 4 excess: 0 5 }, { 6 height: 0, 7 excess: 0 8 }], 9 edges: [] 10 }
Promotrimo sada implementaciju dviju potrebnih operacija: operacije guranja i operacije promjene visine. Operacija guranja danom grafu poveća tok za minimum između vrijednosti viška na početnom vrhu i rezidualnog kapaciteta danog brida. Operacija promjene visine postavi vrijednost oznake visine danog vrha na sljedbenika minimuma visina svih susjednih vrhova koji su spojeni s danim vrhom nezasićenim bridom.
1 const push = (graph, startNodeIndex, admissibleEdgeIndex) => { 2 let delta = Math.min(graph.nodes[startNodeIndex].excess, 3 graph.edges[admissibleEdgeIndex].capacity - 4 graph.edges[admissibleEdgeIndex].flow); 5 graph.edges[admissibleEdgeIndex].flow += delta; 6 graph.edges[admissibleEdgeIndex + 7 (admissibleEdgeIndex % 2 === 0 ? 1 : -1)].flow -= delta; 8 setExcess(graph.nodes, graph.edges); 9 };
1 const relabel = (graph, i) => { 2 let positiveResidualEdges = graph.edges.filter(curr => 3 curr.startNode === i + 1 && curr.flow !== curr.capacity); 4 let neighbourNodesIndexes = positiveResidualEdges.map(elem => 5 elem.startNode === i + 1 ? elem.endNode : elem.startNode); 6 let neighbourNodes = neighbourNodesIndexes.map(elem => 7 graph.nodes[elem - 1].height); 8 graph.nodes[i].height = Math.min(...neighbourNodes) + 1; 9 };
Jednom kada imamo operacije guranja i promjene visine možemo implementirati guraj-promijeni visinu algoritam.
1 const pushRelabel = (graph) => { 2 graph.edges = setInitialFlow(graph.edges); 3 graph.nodes = setInitialHeight(graph.nodes); 4 5 graph.nodes = setExcess(graph.nodes, graph.edges); 6 7 while( help.excessSum(graph.nodes) !== 0 ) { 8 let startNodeIndex = findFirstActive(graph.nodes); 9 let admissibleEdgeIndex = admissibleEdge(startNodeIndex, graph.edges, graph.nodes); 10 if(startNodeIndex !== -1 && admissibleEdgeIndex !== -1) { 11 push(graph, startNodeIndex, admissibleEdgeIndex); 12 } else { 13 relabel(graph, startNodeIndex); 14 } 15 } 16 17 return graph; 18 };
U implementiranim algoritmima koje smo pokazali možemo vidjeti da se koriste dodatne metode. Dvije metode služe nam za postavljanje početnih vrijednosti za neke vrhove i bridove: setInitialFlow i setInitialHeight. Metoda setInitialFlow postavlja vrijednost toka svih bridova koji izlaze iz izvora na kapacitet tog brida, a vrijednost toka svih bridova koji ulaze u izvor na minus kapacitet tog brida. Metoda setInitialHeight postavlja visinu izvora na broj vrhova u grafu.
Preostale dodatne metode korištene u implementaciji algoritma su excessSum,
findFirstActive i admissibleEdge. Metoda excessSum računa sumu viška svih vrhova osim izvora i ponora (u implementaciji se spominje skaliranje u valovima, to će nam biti bitno za jednu varijantu ovog algoritma). Metoda findFirstActive pronalazi prvi aktivan vrh u grafu, a metoda admissibleEdge indeks prvog valjanog brida u grafu.
Metoda setExcess koristi se u implementaciji operacije guranja, prolazi po svim vrhovima grafa te za svakoga računa višak. Implementacije svih ovih metoda možete vidjeti u nastavku.
1 const setInitialFlow = (edges) => { 2 for(let i = 0; i < edges.length; i += 2) { 3 if(edges[i].startNode === 1) { 4 edges[i].flow = edges[i].capacity; 5 edges[i + 1].flow = (-1) * edges[i].capacity; 6 } 7 } 8 return edges; 9 }; 10 11 const setInitialHeight = (nodes) => { 12 nodes[0].height = nodes.length; 13 return nodes; 14 } 15 16 const excessSum = (nodes, isWaveScaling) => nodes.reduce((partialSum, elem) => partialSum + ( isWaveScaling && (elem.label == nodes.length - 1) ? 0 : elem.excess ), -nodes[0].excess); 17 18 const findFirstActive = (nodes) => nodes.findIndex(elem => isNodeActive(nodes.length, elem)); 19 20 const isNodeActive = (numOfNodes, node) => node.label !== 0 && 21 node.label !== numOfNodes - 1 && node.excess > 0; 22 23 const admissibleEdge = (i, edges, nodes, isExcessScaling=false, deltaScale=0) => { 24 for(let edgeInd in edges) { 25 if(edges[edgeInd].startNode === i + 1 26 && nodes[edges[edgeInd].endNode - 1].height 27 === nodes[i].height - 1 28 && edges[edgeInd].flow !== edges[edgeInd].capacity 29 && ( isExcessScaling 30 ? deltaScale > nodes[edges[edgeInd].endNode - 1].excess 31 : true ) ) { 32 return parseInt(edgeInd); 33 } 34 } 35 return -1; 36 }; 37 38 const setExcess = (nodes, edges) => { 39 for(let i = 1; i < nodes.length; i++) { 40 nodes[i - 1].excess = 0; 41 for(let edge of edges) { 42 if(edge.endNode === i) { 43 nodes[i - 1].excess += edge.flow; 44 } 45 } 46 } 47 return nodes; 48 };
Još je samo preostalo komentirati činjenicu da nam u implementaciji algoritam vraća cijeli graf, a ne maksimalan tok. To je napravljeno da bi se omogućio grafički prikaz toka, a iz grafa računamo tok tako da zbrojimo vrijednosti toka u bridovima koji izlaze iz izvora.
1 const calculateMaxFlow = () => 2 pushRelabel(structuredClone(state.graphForAlgs)).edges 3 .reduce((partialSum, elem) => partialSum + 4 (elem.startNode === 1 && elem.endNode !== 1 ? elem.flow : 0) 5 , 0);
4 Varijante algoritma guraj-promijeni visinu
Kod analiziranja osnovne verzije algoritma guraj-promijeni visinu može se vidjeti da je vrijeme izvođenja dominirano operacijama guranja. Guraj-promijeni visinu algoritam vrlo je fleskibilan: imamo dosta slobode u načinu biranja bridova po kojima ćemo gurati tok i vrhova kojima ćemo promijeniti visinu. Iskorištavanjem ova fleksibilnosti možemo ubrzati osnovnu verziju algoritma. Iz teorema 2.12 očito je da je složenost guraj-promijeni visinu algoritma \(O(n^2m)\) zbog nezasićenih operacija guranja. Da bismo smanjili vremensku složenost tog algoritma, uvodimo operaciju ispražnjavanja. Operacija ispražnjavanja uzima neki aktivan vrh \(i\) te izvršava operacije guranja i promjene visine sve dok taj vrh ne postane neaktivan. Primijetimo da se u svakom izvođenju operacije ispražnjavanja nezasićena operacija guranja izvrši samo jednom, jer samo zadnja operacija guranja na aktivnom vrhu može biti nezasićena. U nastavku možete vidjeti implementaciju operacije ispražnjavanja.
1 const discharge = (graph, activeNodes, i) => { 2 while( graph.nodes[i].excess > 0 ) { 3 let nextEdge = admissibleEdge(i, graph.edges, graph.nodes); 4 while( nextEdge !== -1 && graph.nodes[i].excess !== 0 ) { 5 pushWithDischarge(graph, i, nextEdge, activeNodes); 6 nextEdge = admissibleEdge(i, graph.edges, graph.nodes); 7 } 8 if( graph.nodes[i].excess > 0 ) { 9 relabel(graph, i); 10 } 11 } 12 };
Možete vidjeti da se kod implementacije operacije ispražnjavanja ne koristi klasična varijanta operacije guranja, već varijanta operacije guranja kod ispažnjavanja. Naime, kod nekih varijanti algoritma moramo održavati red aktivnih vrhova, pa kod svake operacije guranja moramo provjeriti je li možda krajnji vrh brida po kojem smo gurali tok postao aktivan. Implementaciju nove varijante operacije guranja možete vidjeti u nastavku.
1 const pushWithDischarge = (graph, startNodeIndex, admissibleEdgeIndex, activeNodes) => { 2 let delta = Math.min(graph.nodes[startNodeIndex].excess, 3 graph.edges[admissibleEdgeIndex].capacity 4 - graph.edges[admissibleEdgeIndex].flow); 5 graph.edges[admissibleEdgeIndex].flow += delta; 6 graph.edges[admissibleEdgeIndex + (admissibleEdgeIndex % 2 === 0 ? 1 : -1)].flow -= delta; 7 setExcess(graph.nodes, graph.edges); 8 9 let endNode = graph.nodes 10 [graph.edges[admissibleEdgeIndex].endNode - 1]; 11 if(isNodeActive(graph.nodes.length, endNode) 12 && (!activeNodes.includes(endNode))) { 13 activeNodes.push(endNode); 14 } 15 };
4.1 FIFO guraj-promijeni visinu algoritam
Prva varijanta algoritma guraj-promijeni visinu koju ćemo promatrati zove se FIFO guraj-promijeni visinu algoritam. Ova varijanta održava red aktivnih vrhova: na početku algoritma svi su aktivni vrhovi ubačeni u red. Algoritam uzima vrh \(i\) s početka reda i izrvši operaciju ispražnjavanja nad njim. Ukoliko neki drugi vrh postane aktivan tijekom izvršavanja te operacije, taj vrh se stavlja na kraj reda.
Da bismo odredili vremensku složenost ove varijante guraj-promijeni visinu algoritma, sve što trebamo je odozgo omeđiti broj nezasićenih operacija guranja izvršenih tijekom izvršavanja algoritma. Za to koristimo argument potencijalne funkcije na prolascima po redu. Prvi prolaz po redu završava kada je algoritam izvršio operaciju ispražnjavanja nad svim vrhovima koji su stavljeni u red na početku izvršavanja algoritma. Općenito, \(k\)-ti prolaz po redu završava kada je algoritam izvršio operaciju ispražnjavanja nad svim vrhovima koji su dodani u red u \((k-1)\)-om prolazu po redu.
U razmatranju vremenske složenosti koristi se potencijalna funkcija \(\Phi = \max _{i\; aktivan} d(i)\). Korištenjem te potencijalne fukcije, nije teško vidjeti da se tijekom izvršavanja algoritma odradi \(O(n^2)\) prolaza po redu, a to povlači da je broj izvršavanja nezasićenih operacija guranja u ovoj verziji algoritma \(O(n^3)\). Iz toga slijedi da je vremenska složenosti FIFO guraj-promijeni visinu algoritma \(O(n^3)\).
4.2 Guraj-promijeni visinu algoritam sa skaliranjem viška
Iduća varijanta algoritma guraj-promijeni visinu poznata je pod imenom guraj-promijeni visinu algoritam sa skaliranjem viška. U ovoj varijanti kroz izvođenje algoritma održavamo parametar \(\Delta \) kojeg na početku izvođenja postavljamo na \(2^{\left \lceil \log _{2}U \right \rceil }\). Alogritam se izvršava kao niz faza \(\Delta \)-skaliranja. Parametar \(\Delta \) koristimo u ograničavanju promjene vrijednosti predtoka, točnije održavamo ga \(\Delta \)-optimalnim.
Definicija 4.1. Za predtok \(f\) kažemo da je \(\Delta \)-optimalan ako vrijedi \(e_f(i) \leq \Delta , \forall i \in V \backslash \{ s, t \}\).
U svakoj fazi \(\Delta \)-skaliranja koristimo modificirane verzije operacije guranja i promjene visine da bi predtok ostao \(\Delta \)-optimalan. Korisno će nam biti definirati još jedan pojam.
Definicija 4.2. Za vrh \(i\) kažemo da je \(\Delta \)-aktivan ako vrijedi \(e_f(i) > \frac {\Delta }{2}\).
U ovoj varijanti algoritma, u svakoj fazi \(\Delta \)-skaliranja, odaberemo \(\Delta \)-aktivan vrh s najmanjom visinom \(d(i)\) te tada gurnemo višak po dopustivim bridovima \((i, j)\) (prisjetimo se da je brid \((i, j)\) dopustiv ako ima pozitivan rezidualni kapacitet i ako je \(d(i) = d(j) + 1\)). Nastavljamo gurati po dopustivim bridovima koji izlaze iz vrha \(i\) sve dok višak \(e_f(i)\) ne postane manji ili jednak \(\Delta \) ili dok ne moramo vrhu \(i\) promijeniti visinu. Tada odaberemo idući \(\Delta \)-aktivan vrh s najmanjom visinom. Faza \(\Delta \)-skaliranja završava kada više ne postoji nijedan \(\Delta \)-aktivan vrh. Tada podijelimo \(\Delta \) s 2 i prijeđemo na iduću fazu \(\Delta \)-skaliranja. Primijetimo da, jer na kraju neke faze više nema \(\Delta \)-aktivnih vrhova, predtok je \(\Delta \)-optimalan i za novu vrijednost \(\Delta \).
Može se vidjeti da ovako definiran algoritam staje za \(\Delta < 1\) te da je u toj iteraciji pronađen maksimalan tok. Također, korištenjem potencijalne funkcije \(\Phi = \sum _{i \in V \backslash \{ s, t \} } \frac {e_f(i)d(i)}{\Delta }\) može se dokazati da je broj nezasićenih operacija guranja u svakoj fazi \(\Delta \)-skaliranja odozgo ograničen s \(O(n^2)\), pa iz toga vidimo da je vremenska složenost guraj-promijeni visinu algoritma sa skaliranjem viška \(O(nm + n^2\log (U))\).
4.3 Guraj-promijeni visinu algoritam sa skaliranjem u valovima
Sljedeća varijanta algoritma guraj-promijeni visinu koju ćemo opisati je Guraj-promijeni visinu algoritam sa skaliranjem u valovima. Da bismo mogli implementirati ovu varijantu algoritma, uvodimo novu verziju operacije guranja, takozvana operacija guranja sa stogom. Za svaki vrh \(i\), čuvamo nekako sortiran niz svih bridova koji izlaze iz \(i\). Tijekom izvođenja operacije guranja sa stogom, prolazimo po nizu bridova koji izlaze iz \(i\) i pokušamo gurnuti tok na svakom. Nakon što smo prošli sve bridove koji izlaze iz \(i\), znamo da je vrijeme da promijenimo visinu vrha \(i\).
GurajSaStogom za \(i\):
dodaj \(i\) u prazan stog \(S\)
dok je stog \(S\) neprazan:
neka je \(j\) vrh na vrhu stoga \(S\)
neka je \((j, k)\) trenutni brid čiji je početni vrh \(j\)
ako \((j, k)\) nije dopustiv:
ako je \((j, k)\) zadnji brid iz vrha \(j\):
postavi da je prvi brid iz \(j\) trenutni brid
izbaci \(j\) iz \(S\)
PromijeniVisinu\((j)\)
inače:
postavi da je idući brid iz \(j\) trenutni brid
inače ako je \(e_f(k) \geq \frac {\Delta }{2}\) i \(k \neq t\):
gurni \(k\) na stig \(S\)
inače:
Guraj\((i, j)\)
ako je \(e_f(j) = 0\):
izbaci \(j\) sa stoga \(S\)
dodaj \(i\) u prazan stog \(S\)
dok je stog \(S\) neprazan:
neka je \(j\) vrh na vrhu stoga \(S\)
neka je \((j, k)\) trenutni brid čiji je početni vrh \(j\)
ako \((j, k)\) nije dopustiv:
ako je \((j, k)\) zadnji brid iz vrha \(j\):
postavi da je prvi brid iz \(j\) trenutni brid
izbaci \(j\) iz \(S\)
PromijeniVisinu\((j)\)
inače:
postavi da je idući brid iz \(j\) trenutni brid
inače ako je \(e_f(k) \geq \frac {\Delta }{2}\) i \(k \neq t\):
gurni \(k\) na stig \(S\)
inače:
Guraj\((i, j)\)
ako je \(e_f(j) = 0\):
izbaci \(j\) sa stoga \(S\)
Guraj-promijeni visinu algoritam sa skaliranjem u valovima izvršava se u nizu valova. U svakom valu, prvo sortiramo sve vrhove \(i \in V \backslash \{ s, t \}\) u nerastućem redoslijedu po oznaci visine. Nakon toga prolazimo po sortiranom nizu vrhova te ako je vrh \(i\) aktivan i još mu u ovom valu nismo promijenili visinu, izvršimo operaciju guranja sa stogom na vrhu \(i\).
Definiramo ukupni višak \(E_f\) kao sumu viška svih vrhova \(i\), osim izvora i ponora, točnije \(E_f = \sum _{i \in V \backslash \{ s, t \}} e_f(i)\). Neka je \(l\) parametar čiju ćemo vrijednost definirati kasnije. Algoritam će izvoditi niz valova sve dok je ukupni višak veći ili jednak od \(\frac {n\Delta }{l}\). Onda će se ponašati kao varijanta sa skaliranjem viška i izvršit će operaciju guranja sa stogom nad svim vrhivima \(i\) za koje vrijedi \(e_f(i) > \frac {\Delta }{2}\). To će raditi sve dok postoji vrh čiji je višak veći od \(\frac {\Delta }{2}\), a zatim je trenutna faza \(\Delta \)-skaliranja gotova i tada podijelimo \(\Delta \) s 2. Cijeli algoritam možete vidjeti u nastavku.
\(\Delta \leftarrow 2^{\left \lfloor \log _{2}U \right \rfloor }\)
\(f(i, j) \leftarrow 0, \forall (i, j) \in A\)
\(f(s, j) \leftarrow u(s, j), f(j, s) \leftarrow -u(s, j), \forall (s, j) \in A\)
\(d(i) \leftarrow 0, \forall i \in V\)
\(d(s) \leftarrow n\)
dok je \(\Delta \geq 1\):
dok je \(E_f \geq \frac {n\Delta }{l}\):
neka je \(L\) niz vrhova \(i \in V \backslash \{ s, t \}\) silazno sortiran po \(d(i)\)
za svaki \(i \in L\):
ako je \(e_f(i) > 0\) i vrhu \(i\) još nije promijenjena visina u ovom valu:
GurajSaStogom\((i)\)
dok postoji vrh \(i \in V \backslash \{ t \}\) takav da je \(e_f(i) \geq \frac {\Delta }{2}\):
GurajSaStogom\((i)\)
\(\Delta \leftarrow \frac {\Delta }{2}\)
vrati \(f\)
\(f(i, j) \leftarrow 0, \forall (i, j) \in A\)
\(f(s, j) \leftarrow u(s, j), f(j, s) \leftarrow -u(s, j), \forall (s, j) \in A\)
\(d(i) \leftarrow 0, \forall i \in V\)
\(d(s) \leftarrow n\)
dok je \(\Delta \geq 1\):
dok je \(E_f \geq \frac {n\Delta }{l}\):
neka je \(L\) niz vrhova \(i \in V \backslash \{ s, t \}\) silazno sortiran po \(d(i)\)
za svaki \(i \in L\):
ako je \(e_f(i) > 0\) i vrhu \(i\) još nije promijenjena visina u ovom valu:
GurajSaStogom\((i)\)
dok postoji vrh \(i \in V \backslash \{ t \}\) takav da je \(e_f(i) \geq \frac {\Delta }{2}\):
GurajSaStogom\((i)\)
\(\Delta \leftarrow \frac {\Delta }{2}\)
vrati \(f\)
Kod promatranja vremenske složenosti algoritma, podijelit ćemo operacije guranja u dvije vrste: svaku operaciju guranja koja gurne barem \(\frac {\Delta }{2}\) jedinica toka nazivamo velikom operacijom guranja, a one koje gurnu manje od \(\frac {\Delta }{2}\) jedinica toka malom operacijom guranja.
Može se vidjeti da, svaki put kada je neki vrh \(i\) na stogu tijekom izvršavanja operacije guranja sa stogom, se za taj vrh izvrše najviše dvije nezasićene operacije guranja, takve da je najviše jedna mala. Također, na kraju vala, svakom bridu koji ima pozitivan rezidualni kapacitet je bila promijenjena visina. Koristeći te dvije tvrdnje i potencijalnu funkciju kao u promatranju složenosti varijante s skaliranjem viška, može se dokazati da se tijekom izvršavanja algoritma izvrši najviše \(O(n^2 + \frac {n^2}{l}\log (U))\) nezasićenih velikih operacija guranja i toliko nezasićenih malih operacija guranja plus \(O(n)\) nezasićenih malih operacija guranja po valu.
Može se također vidjeti da, u svim fazama \(\Delta\)-skaliranja osim u zadnjoj, se u svakom valu izvrši \(O(\frac {n}{l})\) operacija promjene visine. Ako se u valu nije izvršila nijedna operacija promjene visine, tada nema vrhova s pozitivnim viškom na kraju vala, pa algoritam staje.
Iz svih ovih tvrdnji može se zaključiti da se tijekom izvršavanja algoritma izvrši
\(O(\min (n^2, nl + \log (U)))\). Tada, uz odabir \(l = \sqrt {\log (U)}\) dobivamo da je složenost guraj-promijeni visinu algoritam sa skaliranjem u valovima \(O(mn + n^2\sqrt {\log (U)})\).
Napomena: Članak je nastao iz diplomskog rada studenta Maria Zečića, pod mentorstvom izv. prof. dr. sc. Ivice Nakića, na Diplomskom sveučilišnom studiju Računarstvo i matematika Matematičkog odsjeka Prirodoslovno-matematičkog fakulteta Sveučilišta u Zagrebu.
Bibliografija
[1] David P. Williamson. Network Flow Algorithms. Cambridge University Press, 2019.
[2] Članak na Wikipediji o Guraj-Promijeni visinu algoritmu Push–relabel maximum flow algorithm .
[3] GitHub repozitorij implementacije https://github.com/Mario173/PushRelabel.
