Turanov teorem
Sažetak Svrha ovoga članka je predstaviti jedan of fundamentalnih rezultata iz teorije grafova poznat pod nazivom Turánov teorem te prezentirati pet dokaza koristeći pritom alate iz različitih grana matematike. Prva tri dokaza se uglavnom oslanjaju na teoriju grafova i metode prebrojavanja, a preostala dva na matematičku analizu, algebru i vjerojatnost.
Ključne riječi multipartitan graf, klika, Turánov graf, Turánov teorem
Turán's theorem
Abstract The purpose of this article is to present one of the fundamental results in graph theory known as Turán's theorem and present five proofs by using tools from various branches of mathematics. First three rely almost exclusively on graph theory and counting methods, while the other two rely on mathematical analysis, algebra, and probability.
Keywords multipartite graph, clique, Turán graph, Turán's theorem
1Uvod
Pál Turán je bio vrsni mađarski matematičar čije su ideje i rezultati znatno utjecali na razvoj teorije grafova, ali i raznih drugih grana matematike. Tome je pridonijela i plodna suradnja s velikim matematičarom Paulom Erdösom: trajala je 46 godina i rezultirala s 28 zajedničkih znanstvenih radova!
Pál Turán je rođen 18. kolovoza 1910. u Budimpešti. Učiteljsku diplomu iz matematike i znanosti dobio je na Sveučilištu u Budimpešti 1933., a doktorirao je pod vodstvom Leopolda Fejéra 1935. godine na Eötvös Loránd Sveučilištu. Skoro trideset godina je radio zajedno s Fejérom, što je vidljivo iz brojnih zajedničkih radova iz matematičke analize, no najviše je bio privučen teoriji brojeva i u tom području je ostvario rezultat međunarodnog značaja. Brojni matematičari iz cijeloga svijeta dolazili su kod Turána pisati disertacije pod njegovim vodstvom. S prijateljima je volio raspravljati o matematici i matematičkim istraživanjima. Govorio je kako napredak u matematici dolazi kroz rješavanje otvorenih problema: ispočetka dokaz može biti vrlo kompliciran, no prije ili kasnije bit će pronađene lakše metode. Metoda i elegancija dokaza su sekundarni.
Ovaj rad je usredotočen na Turánov doprinos teoriji grafova, konkretno na iznimno važan teorem koji danas nosi njegovo ime: Turánov teorem. Radi se o jednom od fundamentalnih rezultata koji služi kao početna točka u istraživanju raznih drugih problema. Navest ćemo dokaze koji su otkriveni i ponovno otkriveni, od kojih se neki ne oslanjaju samo na teoriju grafova, nego i na druge grane matematike poput algebre i vjerojatnosti.
2Osnovni pojmovi i definicije
Broj elemenata danog skupa A označit ćemo s |A| i zvati ga kardinalitetom skupa A. Zatim ćemo s \binom{n}{k} označiti broj svih k-članih podskupova skupa od n elemenata.
Definicija 1. Jednostavan neusmjeren graf je uređen par G=(V,E), gdje je \emptyset\neq V=V(G) konačan skup vrhova, a E=E(G) je konačan skup različitih dvočlanih podskupova skupa V(G) koje zovemo bridovi. Svaki brid e\in E spaja neka dva vrha u,v \in V koje zovemo krajevima od e.
U ovome radu ćemo pod pojmom grafa podrazumijevati jednostavan neusmjereni graf. Neka je G graf sa skupom vrhova V = \lbrace 1,2,\dots,n\rbrace. Za neka dva vrha kažemo da su susjedni ako su krajevi istog brida. U nastavku ćemo s ij ili ji označavati brid kojemu su i i j krajevi.
Za graf G kojemu su svaka dva vrha spojena bridom kažemo da je potpun i označavamo ga s K_{n}, gdje je n broj vrhova. Graf K_{3} se još zove i trokut.
Za graf G'=(V',E') kažemo da je podgraf grafa G ako vrijedi V' \subseteq V i E' \subseteq E, pri čemu krajevi svih bridova u E' moraju biti sadržani u skupu V'. K-klika u G je potpun podgraf od G s k vrhova i označavamo ga s K_{(k)}.
Stupanj d(v) vrha v u grafu G je broj bridova kojima je v jedan od krajeva. Prema definiciji grafa, stupanj vrha jednak je broju njegovih susjeda. Izolirani vrh je vrh stupnja nula. Graf G je {k-regularan} ako su mu svi vrhovi stupnja k. Ukoliko nije potrebno istaknuti koliki je stupanj vrha u takvom grafu, koristit ćemo naziv regularan graf.
Neka je k prirodan broj i neka k \geq 2. Graf G je {k-partitan} ako mu se skup vrhova V mo\v{z}e particionirati u k podskupova tako da nijedan brid nema oba kraja u istom podskupu. Za k=2 takve grafove još zovemo i bipartitnim grafovima. Potpunk-partitan graf} je jednostavan k-partitan graf u kojemu je svaki par vrhova iz različitih skupova k-particije spojen bridom. Ako su V_{1},\ldots,V_{k} skupovi k-particije od V i |V_{i}|=n_{i}, i=1,\ldots,k, tada potpun k-partitan graf označavamo s K_{n_{1},n_{2},\ldots,n_{k}}. Za graf kažemo da je potpun multipartitan ako je potpun k-partitan za neko k\geq 2.
Slijedi tvrdnja koja će nekoliko puta biti korištena u ovom članku.
Teorem 2. [(Cauchyjeva nejednakost)[6] ] Za realne brojeve a_{1}, \dots, a_{n} i b_{1}, \dots, b_{n} vrijedi
Ako je a_{i}\neq 0 za barem jedan i, onda u (2.1 ) stoji znak jednakosti ako i samo ako postoji realan broj \lambda takav da je
(2.1)
\left( \sum_{k=1}^{n} a_{k} b_{k} \right)^{2} \leq \sum_{k=1}^{n} a_{k}^{2} \sum_{k=1}^{n} b_{k}^{2}.
b_{k}=\lambda a_{k},\qquad k=1,\ldots,n.
3Turánov graf i njegova svojstva
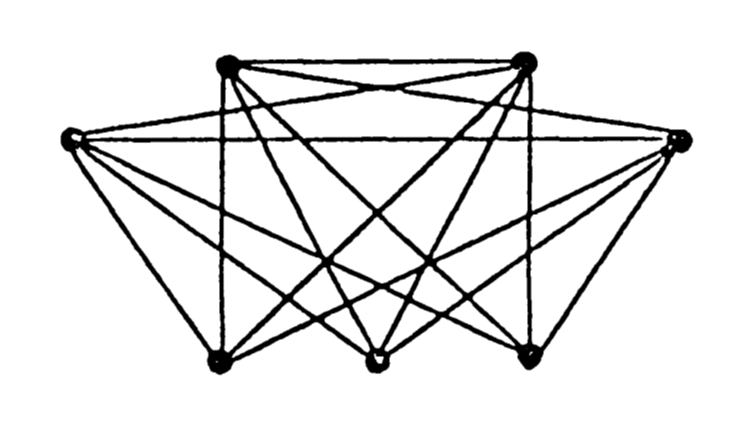
Proučavajući grafove, Turán je tražio odgovor na sljedeće pitanje: koliko najviše bridova može imati graf s n\geq 2 vrhova koji ne sadrži kliku K_{(k)}? Označimo traženi broj s t(n,k). Vrijedi t(n,2) = 0 i t(n,k) je rastuća funkcija po k. Primjer grafa s n vrhova koji sadrži t(n,k) bridova je potpun (k-1)-partitan graf K_{n_{1}, \ldots, n_{k-1}}, n=n_{1}+\cdots+n_{k-1}, pa će formula za t(n,k) biti glavni rezultat kojim ćemo se intenzivno baviti u ovome radu. Na slici 1 prikazan je K_{2,2,3}. Graf K_{n_{1}, \ldots, n_{k-1}} sadrži \displaystyle{ \sum_{i \lt j} n_{i} n_{j}} bridova. Članovi ove sume mogu se dobiti iz jednakosti
(n_{1}+\cdots+n_{k-1})^{2}=\sum_{i=1}^{k-1} n_{i}^{2}+2\sum_{i\lt j}n_{i}n_{j},
odnosno vrijedi
(3.1)
\sum_{i\lt j}n_{i}n_{j}=\frac{1}{2}\left(n^{2}-\sum_{i=1}^{k-1}n_{i}^{2}\right).
\left(\sum_{i=1}^{k-1} n_{i}\cdot 1\right)^{2}\leq \left(\sum_{i=1}^{k-1} n_{i}^{2}\right)\cdot\left(\sum_{i=1}^{k-1} 1^{2}\right),
iz čega proizlazi
\sum_{i=1}^{k-1} n_{i}^{2}\geq \frac{n^{2}}{k-1}.
Jednakost vrijedi ako i samo ako n_{i}=\frac{n}{k-1}, i=1,\ldots,k-1. Zaključujemo da graf K_{n_{1}, \ldots, n_{k-1}} sadrži najveći mogući broj bridova ako i samo ako su mu svi skupovi particije jednakobrojni, odnosno n_{1}=n_{2}=\cdots=n_{k-1}=\frac{n}{k-1}. No, Turánovo pitanje podrazumijeva proizvoljno zadane brojeve n i k pa je jednakobrojnost skupova particije moguća ako i samo ako je n djeljiv s k-1. U suprotnom je dovoljno zahtijevati da kardinaliteti skupova particije budu približno jednaki, odnosno | n_{i} - n_{j} | \leq 1, \forall i,j=1,\ldots,{k-1}, i\neq j.Vratimo se na slučaj kada k-1 dijeli n. Iz (
(3.2)
\sum_{i \lt j}n_{i}n_{j}=\frac{n^{2}}{2}\cdot \frac{k-2}{k-1}
Općenito, grafovi K_{n_{1}, \ldots, n_{k-1}} za koje vrijedi | n_{i} - n_{j} | \leq 1, \forall i,j=1,\ldots,{k-1}, i\neq j, zovu se Turánovi grafovi i označeni su s T(n,k). Sada smo u mogućnosti iskazati Turánov teorem i navesti nekoliko različitih dokaza.
4Turánov teorem
Teorem 3. [(Turánov teorem, 1941.)] Neka je G=(V,E) graf s n vrhova koji ne sadrži kliku K_{(k)}. Tada vrijedi
(4.1)
|E| \leq \frac{(k-2)n^{2}}{2(k-1)}.
Preciznija varijanta ovog teorema sadrži i tvrdnju da je graf K_{n_{1}, \ldots, n_{k-1}} za koji vrijedi | n_{i} - n_{j} | \leq 1, \forall i,j=1,\ldots,{k-1}, i\neq j, jedinstven graf bez klike K_{(k)} s najvećim brojem bridova t(n,k). Otuda i naziv za takav graf: Turánov graf. Mi ćemo se usredotočiti na dokazivanje nejednakosti
Godine 1907. nizozemski matematičar Willem Mantel dokazao je tvrdnju da graf bez trokuta sadrži najviše n^{2}/4 bridova, a graf za koji se postiže gornja granica je K_{n/2,n/2} za n paran, odnosno K_{(n-1)/2,(n+1)/2} za n neparan
(4.2)
\sum_{i=1}^{n}d_{i} = 2 |E|.
U nastavku ćemo navesti pet različitih dokaza Turánovog teorema za proizvoljan k.
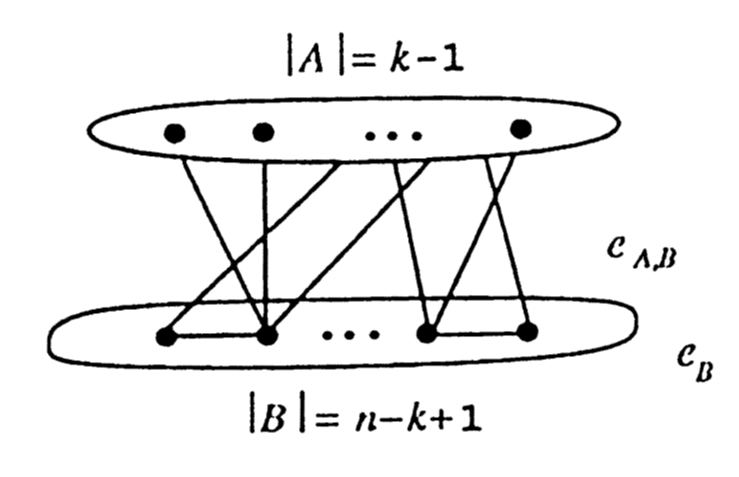
4.1Prvi dokaz: Turán 1941.
Koristimo jaku indukciju po broju n. Ona se od obične indukcije razlikuje jedino u pretpostavci, tj. ako smo u bazi jake indukcije dokazali da tvrdnja vrijedi za k=1, onda pretpostavka jake indukcije glasi da tvrdnja vrijedi za sve k\lt n pa u koraku jake indukcije treba dokazati da tvrdnja vrijedi za k=n.
Nejednakost
e_{B} \leq \frac{(k-2)}{2(k-1)}(n-k+1)^{2}.
S obzirom da G ne sadrži k-klike, svaki j \in B je susjed s najviše k-2 vrhova u A pa dobivamo e_{A,B} \leq (k-2)(n-k+1). Slijedi
|E| \leq \binom{k-1}{2} + \frac{k-2}{2(k-1)}(n-k+1)^{2} + (k-2)(n-k+1)=\frac{k-2}{2(k-1)}n^{2}.
4.2Drugi dokaz: Erdös 1970.
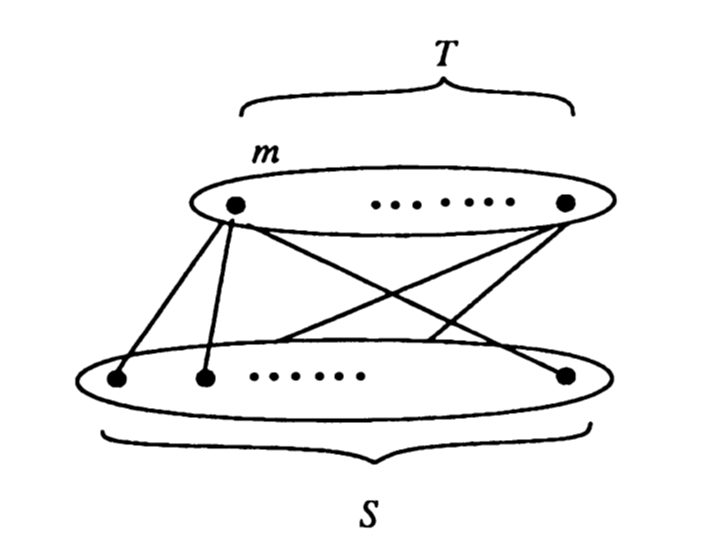
Ovaj dokaz koristi strukturu Turánovih grafova. Neka je m \in V vrh najvećeg stupnja u grafu G, odnosno \displaystyle{d_{m} = \max_{1 \leq j \leq n} d_{j}}. Označimo sa S susjede of m, |S|=d_{m} i stavimo T=V/S. Kako G ne sadrži k-klike i svi vrhovi iz S su susjedi vrhu m, to S ne sadrži (k-1)-klike. Konstruirajmo graf H na skupu V (slika 4). Graf H odgovara grafu G na S i sadrži sve bridove između S i T (dakle, u H je svaki vrh iz S spojen bridom sa svakim vrhom iz T), ali ne i bridove među vrhovima iz T. Skup T je nezavisan u H te H ne sadrži k-klike. Neka je d'_{j} stupanj vrha j u H. Ako je j \in S, tada iz konstrukcije grafa H vrijedi d_{j}' \geq d_{j}. Ako je j \in T, tada imamo d_{j}' = |S| = d_{m} \geq d_{j} prema izboru vrha m. Vidimo da je |E(H)| \geq |E| i zaključujemo da od svih grafova s najvećim brojem bridova, jedan mora biti oblika kakvog je H. Koristeći indukciju na skupu S, zaključujemo da se među grafovima s najvećim brojem bridova nalazi graf K_{n_{1},\ldots,n_{k-1}}. Preciznije, graf H na S ima najviše bridova koliko i Turánov graf K_{n_{1},\ldots,n_{k-2}} na S. Slijedi |E|\leq K_{n_{1},\ldots,n_{k-1}}, pri čemu n_{k-1}=|T|, odnosno \displaystyle{|E|\leq \sum_{i \lt j}n_{i} n_{j}}, što implicira
Navedeni dokaz se odnosi na precizniju varijantu teorema
4.3Treći dokaz: Moon-Moser 1962.
Ovaj dokaz generalizira ideju prvog dokaza za slučaj k=3 i daje procjenu broja h-klika. Neka je G proizvoljan graf sa skupom vrhova V=\lbrace 1,\dots,n\rbrace i označimo s \mathscr{C}_{h} skup h-klika u G, pri čemu |\mathscr{C}_{h}|=C_{h}. Primjerice, imamo C_{1}=n, C_{2}=|E|, a C_{3} je broj trokuta u G. Za A \in \mathscr{C}_{h} označimo s d(A) broj (h+1)-klika koje sadrže A. Brojeći na dva načina, dobivamo
(4.3)
\sum_{A \in \mathscr{C}_{h}}d(A) = (h+1)C_{h+1},\quad h \geq 1
Tvrdnja 4. Vrijedi
(4.4)
\frac{C_{h+1}}{C_{h}} \geq \frac{1}{h^{2}-1} \left( h^{2} \frac{C_{h}}{C_{h-1}}-n \right),\,\, h \geq 2.
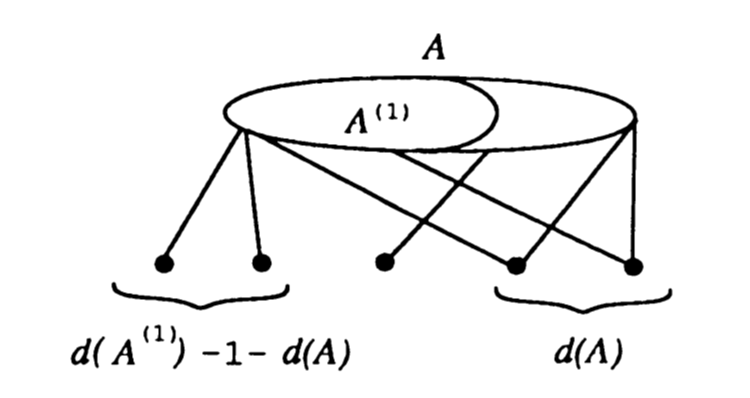
Uzmimo A \in \mathscr{C}_{h}, B=V \backslash A, |B|=n-h. Među vrhovima skupa B postoji točno d(A) vrhova koji su susjedni svim vrhovima u A. Svaki od preostalih vrhova u B je susjed najviše jednoj (h-1)-kliki A^{(i)}, tvoreći h-kliku (slika 5). Dobivamo (primijetimo da se pojavljuje - 1 zbog A^{(i)} \subseteq A)
\sum_{i=1}^{h}(d(A^{(i)})-1-d(A))+d(A) \leq n-h,
odnosno
\sum_{i=1}^{h} d(A^{(i)})-(h-1)d(A) \leq n.
Sumiranjem po svim A \in \mathscr{C}_{h} dobivamo
(4.5)
\sum_{A \in \mathscr{C}_{h}} \sum_{i=1}^{h} d(A^{(i)})-(h-1) \sum_{A \in \mathscr{C}_{h}} d(A) \leq n\, C_{h}.
\sum_{ij\in E(G)}(d(i)+d(j))=\sum_{i=1}^{n} d(i)^{2}\leq n|E(G)|,
zaključujemo
(4.6)
\sum_{A \in \mathscr{C}_{h}} \sum_{i=1}^{h} d(A^{(i)}) = \sum_{B \in \mathscr{C}_{h-1}} d(B)^{2} ,
(4.7)
(h-1) \sum_{A \in \mathscr{C}_{h}} d(A) = (h^{2}-1)C_{h+1}.
(4.8)
\sum_{B \in \mathscr{C}_{h-1}} d(B)^{2} \leq n C_{h} + (h^{2} -1) C_{h+1}.
n C_{h} + (h^{2} -1) C_{h+1} \geq \sum_{B \in \mathscr{C}_{h-1}} d(B)^{2} \geq \frac{1}{C_{h-1}} \left( \sum_{B \in \mathscr{C}_{h-1}} d(B) \right)^{2} = \frac{h^{2} C_{h}^{2}}{C_{h-1}},
što je ekvivalentno Da bismo dokazali
(4.9)
|E|= \left( 1 - \frac{1}{\vartheta} \right) \frac{n^{2}}{2},\,\, \vartheta \in \mathbb{R}.
Tvrdnja 5. Neka je h\geq 1. Vrijedi
(4.10)
\frac{C_{h+1}}{C_{h}} \geq \frac{\vartheta-h}{\vartheta} \cdot\frac{n}{h+1}.
Za h=1 imamo C_{1} = n i C_{2} = |E| pa vrijedi
\frac{C_{h+1}}{C_{h}} \geq \frac{1}{h^{2} -1} \left( h^{2}\cdot \frac{\vartheta-h+1}{\vartheta} \cdot\frac{n}{h} -n \right) = \frac{1}{h^{2} -1} \cdot\frac{(\vartheta-h)(h-1)n}{\vartheta} = \frac{\vartheta-h}{\vartheta} \cdot \frac{n}{h+1},
što je i trebalo dokazati. Ako G ne sadrži k-klike, onda vrijedi C_{k} = 0 i zaključujemo \vartheta \leq k-1 iz
Primjer 6. \normalfont Promotrimo nejednakost (4.4) za h=2. U ovom slučaju za proizvoljan graf s n vrhova vrijedi
C_{3} \geq \frac{|E|}{3}\cdot \left( \frac{4|E|}{n} -n \right) = \frac{|E|}{3n} (4|E| - n^{2}).
Zaključujemo da graf G s parnim brojem vrhova i brojem bridova |E|=n^{2} /4+1 ne sadrži samo jedan trokut (kako vrijedi prema Turánovom teoremu), nego više od n/3 trokuta. Ako dodamo jedan brid u K_{n/2,n/2}, dobivamo n/2 trokuta i onda se lako pokaže da ovo vrijedi za proizvoljan graf s n^{2} /4+1 bridova.Do sada su se dokazi Turánova teorema oslanjali na razne metode prebrojavanja. Sljedeća dva dokaza koriste potpuno drugačije tehnike.
4.4Četvrti dokaz: Motzkin-Straus 1965.
Neka je G proizvoljan graf sa skupom vrhova V = \lbrace 1, \ldots, n \rbrace. S \omega = \omega (G) označimo broj vrhova u najvećoj kliki od G. Nadalje, svakom vrhu i \in V pridružimo realnu varijablu x_{i} i promatramo funkciju f(x_{1}, \dots, x_{n}) =\displaystyle{ 2 \sum_{ij \in E} x_{i} x_{j}}.
Tvrdnja 7. Vrijedi
(4.11)
1- \frac{1}{\omega} = \max \left\lbrace 2 \sum_{ij \in E} x_{i} x_{j} : \sum_{i=1}^{n} x_{i} = 1, x_{i} \geq 0, i=1,\ldots,n\right\rbrace .
S obzirom da je f neprekidna funkcija na kompaktnom skupu K=\lbrace (x_{1},\ldots,x_{n})\in\mathbb{R}^{n}\,:\, \sum_{i=1}^{n} x_{i} = 1, x_{i} \geq 0, i=1,\ldots,n\rbrace (K je tetraedar u \mathbb{R}^{n} omeđen hiperravninom x_{1}+\cdots +x_{n}=1 i koordinatnim osima x_{i}, i=1,\ldots,n), to postoji vektor x=(x_{1},\ldots,x_{n}) u kome f ima najveću vrijednost (vidi
Budući da je
1 = (x_{1} + \dots + x_{n} )^{2} = 2 \sum_{i,j \in C, i\lt j} x_{i} x_{j} + \sum_{i \in C} x_{i}^{2},
zaključujemo da je f(x) najveći ako i samo ako je \displaystyle{\sum_{i \in C} x_{i}^{2}} najmanji, a to je uz pretpostavku \displaystyle{ \sum_{i \in C} x_{i} = 1} onda kada je x_{i} = 1/|C| te dobivamo
f(x)=1- \sum_{i \in C} x_{i}^{2} = 1- \frac{1}{|C|} \leq 1- \frac{1}{\omega},
pri čemu vrijedi jednakost za |C| = \omega, što smo i htjeli dokazati. Nejednakost
\frac{2|E|}{n^{2}} = f(x) \leq 1- \frac{1}{k-1} = \frac{k-2}{k-1}
jer G ne sadrži K_{(k)}.
4.5Peti dokaz: Alon-Spencer 1992.
Zadnji dokaz koristi alate iz područja teorije vjerojatnosti. Neka je G proizvoljan graf sa skupom vrhova V= \lbrace 1, \ldots, n\rbrace.
S jednakom vjerojatnošću 1 / n! biramo permutaciju (\pi_{1}, \dots, \pi_{n}) skupa V i konstruiramo skup C na sljedeći način: stavimo \pi_{i} u C ako i samo ako je \pi_{i} susjedan svim \pi_{j}, \, j\lt i. Prema definiciji C je klika u G. Neka je X=|C| odgovarajuća slučajna varijabla. Imamo X =\displaystyle{ \sum_{i=1}^{n} X_{i} }, gdje je X_{i}=1 ako i \in C, a X_{i}=0 ako i\notin C. Sada zaključujemo da je i \in C s obzirom na permutaciju (\pi_{1}, \dots, \pi_{n}) ako i samo ako se i pojavljuje prije svih n-1-d_{i} ne-susjeda od i, odnosno ako je i prvi među i i njegovim ne-susjedima. Zaključujemo da je očekivanje slučajne varijable X_{i} dano s EX_{i} = 1 / n-d_{i} i nadalje vrijedi
E(|C|) = EX = \sum_{i=1}^{n} EX_{i} = \sum_{i=1}^{n} \frac{1}{n-d_{i}},
zbog linearnosti očekivanja. Posljedično, mora postojati klika C s najmanje E(|C|) vrhova, što je tvrdnja
n^{2} = \left( \sum \sqrt{x_{i}} \sqrt{x_{i}^{-1}} \right)^{2} \leq \sum x_{i} \cdot \sum x_{i}^{-1},
pri čemu x_{i} = n-d_{i}. Uistinu,
(4.13)
\omega (G) \geq \frac{n^{2}}{\displaystyle{\sum_{i=1}^{n} (n-d_{i})}} = \frac{n^{2}}{n^{2} -2 |E|}.
Napomena 9. Nejednakost (4.12) je prvi puta dokazana u [16] uzastopnim uklanjanjem vrhova, slično kao u drugom dokazu.
Bibliografija