Geometrija na grupama
^{\ast}Diplomantica Sveučilišnog studija Diskretna matematika i primjene, Odjel za matematiku Sveučilišta u Rijeci, email: rebeka.gasparic@gmail.com
^{\star}Docentica na Odjelu za matematiku Sveučilišta u Rijeci, email: vera.tonic@math.uniri.hr
Sažetak: U članku uvodimo osnovne koncepte geometrijske teorije grupa: opisujemo kako grupu možemo shvatiti kao geometrijski objekt (Cayleyev graf) te kako na grupi uvodimo metriku. Također definiramo pojam kvazi-izometrije između metričkih prostora, pa ga koristimo između grupa i njihovih Cayleyevih grafova, te između grupa i prostora. Navodimo i vrlo važan rezultat u geometrijskoj teoriji grupa – Švarc-Milnorovu lemu.
Ideja vodilja ovog članka je – kako proučavati grupe kao geometrijske objekte, to jest, kako bazirano na algebarskim svojstvima grupe doći do geometrijskog objekta, točnije Cayleyevog grafa, koji tu grupu predstavlja, te na njemu uvesti metriku. Ujedno ćemo objasniti kako možemo uvesti ekvivalenciju (kvazi-izometriju) između različitih geometrijskih predstavnika iste grupe, te na koji način možemo poistovjetiti određeni metrički prostor s grupom koja na njemu djeluje na ``lijep'' način. Sve je ovo zapravo uvod u područje matematike poznato pod imenom geometrijska teorija grupa.
Od čitatelja očekujemo poznavanje pojmova grupe i metričkog prostora, pa te pojmove u članku ne definiramo.
Za početak ćemo se prisjetiti definicije izometrije i definirati djelovanje grupe izometrijama na metričkom prostoru.
Neka su (X,d_{X}) i (Y,d_{Y}) metrički prostori. Izometrija s prostora X na prostor Y je bijektivno preslikavanje f:X \rightarrow Y za koje vrijedi
tj., to je bijektivno preslikavanje koje čuva udaljenosti. Izometrija prostora X je izometrija :X \rightarrow X. Skup svih izometrija metričkog prostora X s operacijom kompozicije čini grupu koju ćemo označavati s \text{Isom}(X). Na primjer, rotacije oko neke točke u \mathbb{R}^{n} i translacije za neki vektor u \mathbb{R}^{n} primjeri su izometrija od \mathbb{R}^{n} s Euklidskom metrikom.
| (1) | e (x) = x, \forall x \in X, gdje je e neutralni element grupe G, |
| (2) | (g\cdot h) (x)=g (h ( x)), \forall g,h \in G, \forall x \in X, te |
| (3) | d(g (x), g(y)) = d(x,y), \forall g \in G, \forall x,y \in X. |
Prva dva svojstva definiraju djelovanje grupe G na skup X, dok tre\-će svojstvo definira djelovanje izometrijama, tj., možemo poistovjetiti svaki element grupe G s nekom izometrijom iz \text{Isom}(X), čime dobivamo homomorfizam G \rightarrow \text{Isom}(X). Kao primjer ovakvog djelovanja navedimo djelovanje grupe D_{n} izometrijama na pravilan n-terokut u ravnini. Primijetimo da svaka grupa djeluje izometrijama na svaki metrički prostor trivijalnim djelovanjem, to jest djelovanjem u kojem svaki element grupe G fiksira svaku točku metričkog prostora X, no takvo nam djelovanje nije odviše zanimljivo, jer nam ne daje nikakvu informaciju ni o grupi ni o metričkom prostoru. Općenito, možemo očekivati da djelovanje grupe G na X daje više informacija ako je jezgra koja odgovara homomorfizmu G \rightarrow \text{Isom}(X) mala. Time želimo reći da je djelovanje grupe na prostor najznačajnije ako većina elemenata te grupe učini ``nešto'' točkama prostora.
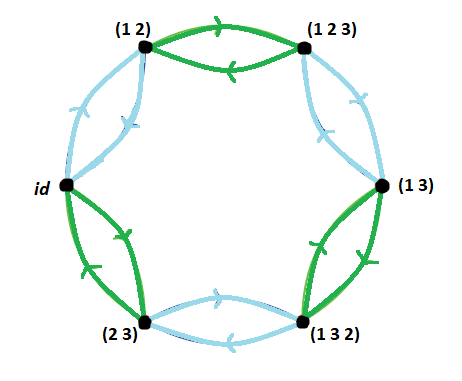
Neka je (G,\cdot) grupa i neka je S njen skup generatora. Zbog jednostavnosti, pretpostavit ćemo da skup S ne sadrži neutralni element e. Cayleyev graf1 grupe G obzirom na skup S je usmjereni, označeni graf \Gamma(G,S) definiran ovako: vrhovi grafa su elementi od G, te postoji usmjereni brid od g prema gs, za svaki g \in G i za svaki s \in S (taj brid označavamo sa s). Ako je skup S malen, bridovi se mogu označiti bojama umjesto elementima iz S. Na slici
Navedimo još jedan primjer Cayleyevog grafa, i to za slobodnu grupu ranga 2, koju ćemo prvo definirati. Za početak definiramo riječ sa slovima a i b kao proizvoljan konačan niz sačinjen od simbola a, b, a^{-1} i b^{-1}. Primjeri riječi su:
Također uvodimo i praznu riječ, odnosno niz koji ne sadrži nijedno slovo iz skupa \lbrace a, b, a^{-1},b^{-1}\rbrace i označimo ga s e. Dvije riječi možemo konkatenirati, tj., nadovezati jednu na drugu, na primjer:
Zatim, definiramo reduciranu riječ kao riječ sa svojstvom da se poslije a ne nalazi a^{-1} (i obrnuto) te da se poslije b ne nalazi b^{-1} (i obrnuto). Ako imamo nereduciranu riječ, možemo je skratiti tako da obrišemo par simbola koji ju ne čine reduciranom. Na primjer:
Ponavljajući takav postupak, u konačnici dolazimo do reducirane riječi. U prethodno navedenom primjeru, reducirana riječ do koje tim postupkom dolazimo je aa. Dodajmo da se npr. riječ aa^{-1} reducira u praznu riječ e. Sada možemo definirati slobodnu grupu ranga 2 kao
zajedno s operacijom koja kombinira konkatenaciju i redukciju.
Izradimo sada Cayleyev graf \Gamma(F_{2},\lbrace a,b\rbrace ) grupe F_{2}. Započinjemo s vrhom koji će predstavljati neutralni element od F_{2}, to jest, praznu riječ e. Četiri brida koja su incidentna s e povezuju vrh e s vrhovima a,b,a^{-1} i b^{-1}. Zatim analogno dodajemo bridove na te nove vrhove. Ovaj postupak ponavljamo i budući da različite reducirane riječi daju različite elemente od F_{2}, nikad nećemo dobiti isti vrh. Dakle, Cayleyev graf grupe F_{2} je stablo i ono je prikazano na slici
Možemo se pitati: ako uzmemo dva različita skupa generatora iste grupe G, u kakvom su odnosu dobiveni Cayleyevi grafovi? Oni ne moraju biti izomorfni, primjerice, ako za istu grupu promatramo skupove generatora različite kardinalnosti. No, postoji način na koji možemo smatrati te grafove ekvivalentnima, a to je preko kvazi-izometrija. Ali vidjet ćemo da se kvazi-izometrije definiraju na metričkim prostorima, pa prvo trebamo naći način za uvođenje metrike na grafu.
Zato krenimo od povezanog grafa \Gamma, to jest grafa u kojem postoji put između svaka dva vrha, pa definirajmo udaljenost između dva vrha grafa kao duljinu najkraćeg puta (puta na grafu koji se sastoji od najmanjeg broja bridova) između ta dva vrha, pri čemu smatramo da je svaki brid duljine 1. Primijetimo da smo na ovaj način zapravo graf geometrijski realizirali, tj., geometrijska realizacija X grafa \Gamma=\Gamma(V,E) je metrički prostor definiran na sljedeći način: svaki vrh iz V predstavimo jednom točkom, svaki brid iz E jednom kopijom jediničnog intervala [0,1], te formiramo X identifikacijom krajnjih točaka svakog intervala s odgovarajućim elementima iz V. Što se tiče metrike na X, već smo objasnili kako se definira udaljenost dvaju vrhova, a ako su x i y dvije točke na istom bridu od X (pod pretpostavkom da krajnje točke brida nisu identificirane), tada, budući da smo brid identificirali sa segmentom [0,1], izraz za Euklidsku udaljenost |x-y| u [0,1] ima smisla i u X pa ga uzmemo za udaljenost između x i y u X. Za x i y na različitim bridovima, njihovu udaljenost definiramo (opet) kao duljinu najkraćeg puta između njih. Metriku koju smo ovdje opisali zovemo metrikom puteva i možemo je promatrati i samo na vrhovima grafa \Gamma.
Neformalno, graf \Gamma i njegovu geometrijsku realizaciju X možemo smatrati jednakima. Intuitivno \Gamma shvaćamo kao listu uputa za izgradnju metričkog prostora i X kao krajnji rezultat tog procesa.
Neka je G grupa i S neki njezin skup generatora. Označimo sa S^{-1} skup inverza svih elemenata iz S. Primijetimo da svaki element grupe G možemo promatrati kao riječ zapisanu u alfabetu S\cup S^{-1}\cup \lbrace e\rbrace (ako operaciju ``\cdot'' na G pišemo tako da se ne vidi). Za g\neq e \in G, definirajmo duljinu od g kao minimalan broj elemenata iz S \cup S^{-1} potrebnih da se g zapiše kao njihov produkt (to zovemo duljinom riječi g), a za duljinu neutralnog elementa e uzima se 0. Definiramo udaljenost između g,h \in G kao duljinu riječi g^{-1}h. Posebno, udaljenost između e i g je duljina riječi g. Ovime smo definirali metriku na grupi G koju ćemo nazivati metrikom riječi, koja se često označava s d_{S}, jer ovisi o izboru skupa generatora S.
Na primjer, u slobodnoj grupi F_{2} generiranoj skupom \lbrace a,b\rbrace, udaljenost između ab i aa je po ovoj definiciji jednaka duljini riječi (ab)^{-1}aa=b^{-1}a^{-1}aa obzirom na \lbrace a,b\rbrace. Riječ b^{-1}a^{-1}aa na najkraći način pomoću elemenata iz \lbrace a,b,a^{-1},b^{-1} \rbrace zapisujemo kao b^{-1}a, odnosno tu smo riječ reducirali. Zaključujemo da je udaljenost između ab i aa jednaka 2.
Dakle, zaključujemo da na svaku grupu možemo gledati kao na metrički prostor (čija metrika ovisi o izboru skupa generatora). Razmišljanje o grupama na takav način središte je geometrijske teorije grupa.
Vidjeli smo da postoji prirodan način na koji se o grupi može razmišljati kao o metričkom prostoru, odnosno, grupu možemo zamijeniti s njezinim Cayleyevim grafom, tj., promatrajući samo vrhove Cayleyevog grafa dobivamo metriku na početnoj grupi. Iako je ova konstrukcija prirodna, ona nije kanonska. Naime, postoji mnogo različitih skupova generatora S za istu grupu i svaki S zadaje svoju metriku d_{S}.
Sada želimo naći dobru definiciju ekvivalencije kojom bismo izjednačili metrike riječi definirane obzirom na različite skupove generatora na istoj grupi. No moramo biti oprezni, želimo da dobivena definicija ekvivalencije bude dovoljno precizna da uoči razliku između bitno različitih grupa. Taj ćemo zadatak riješiti kvazi-izometrijama. Kvazi-izometrija se ponekad naziva i gruba izometrija, budući da je njena definicija vrlo slična klasičnoj definiciji izometrije, no dopušta ograničene multiplikativne i aditivne greške.
Prije ove definicije, pogledajmo na primjeru grupe (\mathbb{Z},+) koje bismo situacije htjeli smatrati ekvivalentnima.
No, grupa \mathbb{Z} može biti generirana i skupom \lbrace 2,3\rbrace. Kako izgleda Cayleyev graf grupe \mathbb{Z} obzirom na taj skup generatora? Vrhovi grafa \Gamma(\mathbb{Z},\lbrace 2,3\rbrace ) su isti kao i kod grafa \Gamma(\mathbb{Z},\lbrace 1\rbrace ), budući da su vrhovi bilo kojeg Cayleyevog grafa grupe \mathbb{Z} upravo njezini elementi. No, u ovom slučaju, umjesto brida koji povezuje n s n+1, postojat će bridovi koji će povezivati n s n+2 i n s n+3, za svaki n \in \mathbb{Z}. Dobiveni graf, koji je prikazan na slici
Kod metrike puteva na Cayleyevim grafovima svaki je brid duljine 1. Radi jednostavnosti crtanja, na skici grafa \Gamma(\mathbb{Z},\lbrace 2,3\rbrace ) ne izgleda kao da su svi bridovi iste duljine, no smatramo da su svi oni duljine 1.
Promotrimo udaljenost između dva vrha, na primjer između vrhova -2 i 5, na prethodno opisanim Cayleyevim grafovima.
| \bullet | Na grafu \Gamma(\mathbb{Z},\lbrace 1\rbrace ), udaljenost između -2 i 5 je 7, jer postoji (jedinstveni) najkraći put između danih vrhova i taj se put sastoji od 7 bridova. |
| \bullet | Na grafu \Gamma(\mathbb{Z},\lbrace 2,3\rbrace ), udaljenost između vrhova -2 i 5 je 3, jer možemo pronaći put između tih vrhova duljine 3 (postoji nekoliko takvih puteva), ali možemo se i uvjeriti se da ne postoji kraći put između njih. |
Sada ćemo definirati pojam kvazi-izometrije i vidjeti da su bilo koja dva Cayleyeva grafa konačno generirane grupe kvazi-izometrična.
Kada je C=0 u nejednakosti
Kvazi-izometričko ulaganje f:X \rightarrow Y naziva se kvazi-izometrička ekvivalencija ili kraće kvazi-izometrija ako postoji konstanta D \geq 0 takva da za svaku točku y \in Y, postoji točka x \in X za koju je d_{Y}(f(x),y) \leq D. Drugim riječima, svaka točka u Y je na udaljenosti manjoj ili jednakoj D od neke točke u slici od f. Ako je D=0, tada je prethodnom definicijom opisana surjektivnost. U ostalim slučajevima f možemo smatrati ``grubo surjektivnom'': slika od f obuhvaća skup točaka čije D-okoline pokrivaju Y. Kažemo da su metrički prostori (X,d_{X}) i (Y,d_{Y}) kvazi-izometrični ako postoji kvazi-izometrija f:X \rightarrow Y. Biti kvazi-izometričan je relacija ekivalencije na familiji svih metričkih prostora.
Spomenimo ovdje da se, kada je f surjektivna i zadovoljava nejednakost
Za identitetu f: (\mathbb{Z}, d_{\lbrace 1\rbrace }) \to (\mathbb{Z}, d_{\lbrace 2,3\rbrace }) iz primjera
No što se događa na bridovima dvaju različitih Cayleyevih grafova za istu grupu? Može se pokazati da su Cayleyevi grafovi \Gamma(\mathbb{Z},\lbrace 1\rbrace ) i \Gamma(\mathbb{Z},\lbrace 2,3\rbrace ) kvazi-izometrični, iako nisu bi-Lipschitz-ekvivalentni. Naime, vrijedi
To znači da kada želimo provjeriti je li Cayleyev graf grupe G (ili njegova geometrijska realizacija) kvazi-izometričan nekom metričkom prostoru X, neće biti bitno koji Cayleyev graf grupe promatramo. A obzirom na primjedbu
Ako primijenimo teorem
| (1) |
Za G=\mathbb{Z}, postoji kvazi-izometrija s Cayleyevog grafa \Gamma(\mathbb{Z},\lbrace 1\rbrace ) na Cayleyev graf \Gamma(\mathbb{Z},\lbrace 2,3\rbrace ). Štoviše, bilo koji Cayleyev graf grupe \mathbb{Z} dobiven od konačnog skupa generatora je kvazi-izometričan grafu \Gamma(\mathbb{Z},\lbrace 1\rbrace ). Također, dodajmo da je (\Gamma(\mathbb{Z},\lbrace 1\rbrace ), d_{\lbrace 1\rbrace }) kvazi-izometričan s (\mathbb{R}, d_{E}), gdje je d_{E}(x,y)=|x-y|, \forall x,y \in \mathbb{R}, uobičajena Euklidska metrika. Dakle, zbog primjedbe |
| (2) |
Za G=F_{2} (slobodna grupa ranga 2), vidjeli smo da je Cayleyev graf ove grupe, dobiven od skupa generatora \lbrace a,b\rbrace, stablo. Iz Teorema |
Bitna posljedica primjedbe
Sad ćemo se dotaknuti fundamentalnog rezultata u geometrijskoj teoriji grupa koji nosi naziv Švarc-Milnorova lema23. Taj nam rezultat omogućava jednostavan prijelaz između grupa i prostora, prenoseći korisna svojstva s jednog na drugo. Ali za taj rezultat nam treba da grupa ``lijepo'' djeluje na ``dobrom'' metričkom prostoru. Uvedimo prvo svojstva za metrički prostor koja ga čine pogodnim za Švarc-Milnorovu lemu.
Za metrički prostor (X,d) kažemo da je geodezijski metrički prostor ako za proizvoljne točke x_{1}\neq x_{2} \in X postoji geodezijski segment što ih povezuje, tj., postoji izometričko ulaganje \gamma : [a,b] \rightarrow X takvo da je \gamma(a)=x_{1} i \gamma(b)=x_{2}. Drugim riječima, metrički je prostor geodezijski ako su bilo koje dvije različite točke tog prostora povezane geodezijskim segmentom koji realizira njihovu udaljenost.
Mnogi važni metrički prostori su geodezijski. Na primjer, ravnina \mathbb{R}^{2} s euklidskom metrikom d_{E} je geodezijski metrički prostor, jer za proizvoljne različite točke iz \mathbb{R}^{2} postoji (jedinstveni) geodezijski segment koji realizira udaljenost između njih. Za primjer metričkog prostora koji nije geodezijski uzmimo ravninu kojoj je maknuto središte, to jest, prostor \mathbb{R}^{2} \setminus \lbrace (0,0)\rbrace s metrikom dobivenom restrikcijom euklidske metrike. Ovo nije geodezijski metrički prostor, jer npr. ne postoji geodezijski segment od točke (1,0) do točke (-1,0).
Za metrički prostor (X,d) kažemo da je pravi ako za svaki x \in X i za svaki r \gt 0, vrijedi da je zatvorena kugla \overline{B}(x,r) kompaktni podskup od X. Uočimo da je prije spomenuti (\mathbb{R}^{2}, d_{E}) ujedno primjer pravog (i geodezijskog) metričkog prostora.
Sada neka je (X,d) pravi geodezijski metrički prostor. Švarc-Milnorova lema govori o grupi G koja ``lijepo'' djeluje na takvom prostoru X. Prvo što zahtijevamo od ``lijepog'' djelovanja grupe G na X je da ono čuva udaljenosti, odnosno da čuva metričku strukturu na X. Opisano djelovanje je djelovanje izometrijama, iz definicije
Zatim, želimo da djelovanje grupe G izometrijama bude pravo diskontinuirano, što znači da je za svaki kompaktan podskup K \subseteq X, skup \lbrace g \in G : g(K) \cap K \neq \emptyset \rbrace konačan. Kako je X pravi metrički prostor, za svaki x \in X i za svaki r \gt 0, postojat će samo konačno mnogo elemenata g \in G takvih da kugla g(\overline{B}(x,r))=\overline{B}(g(x),r) ima neko preklapanje s kuglom \overline{B}(x,r). To jest, neovisno o tome koliko veliki uzmemo r, svi osim konačno mnogo elemenata od G će pomaknuti kuglu \overline{B}(x,r) od same sebe.
Još jedno svojstvo koje želimo od djelovanja grupe G na prostor X je da to djelovanje pokrije cijeli prostor X, umjesto da su G-orbite elemenata od X ograničene na neki manji dio od X. Kažemo da je djelovanje grupe G na X ko-kompaktno ako za bilo koju točku x_{0} \in X postoji R \gt 0, takav da za svaki x \in X, postoji g \in G takav da kugla \overline{B}(g(x_{0}),R) sadrži x. Drugim riječima, zatvorena R-okolina G-orbite točke x_{0} je cijeli X. (Prisjetimo se ovdje da je orbita točke x\in X obzirom na djelovanje grupe G na X skup G x = \lbrace g (x) : g \in G \rbrace.)
Za djelovanje grupe G na X kažemo da je geometrijsko djelovanje ako je ono pravo diskontinuirano, ko-kompaktno djelovanje izometrijama. To je ono ``lijepo'' djelovanje koje nam treba za Švarc-Milnorovu lemu.
Neki primjeri geometrijskih djelovanja su:
| (1) | G=\mathbb{Z}^{2}, X=\mathbb{R}^{2} s euklidskom metrikom, G djeluje na X translacijama. |
| (2) | G je grupa izometrija euklidske ravnine X=\mathbb{R}^{2}, koja je generirana refleksijama preko strana jednakostraničnog trokuta. |
| (3) | G je grupa s konačnim skupom generatora S, X=\Gamma(G,S), G djeluje na X množenjem slijeva. |
Sada možemo izreći tvrdnju Švarc-Milnorove leme.
Dakle, samo iz činjenice da grupa G djeluje geometrijski na (dovoljno dobrom) metričkom prostoru X, izlazi da, po primjedbi
| [1] | Matthew Clay i Dan Margalit,Office Hours with a Geometric Group Theorist, Princeton University Press, 2017. |