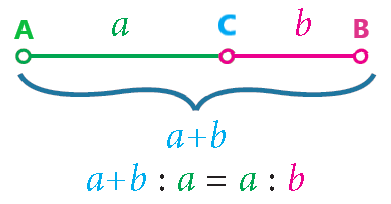Fibonacci, Tribonacci, ... i četiri konstante
Fibonaccijevi brojevi F_{n} definirani su rekurzivnom relacijom
uz početne uvjete F_{0}=0 \text{ i } F_{1}=1. Prvih nekoliko članova Fibonaccijevog niza je
Niz je dobio ime po Leonardu Pisanu Fibonacciju koji je postavio problem razmnožavanja zečeva i time formirao gornji niz.
Fibonaccijev broj F_{n}, odnosno n-ti član Fibonaccijevog niza može se odrediti Binetovom formulom:
Nadalje, Fibonaccijevi brojevi se mogu generirati računanjem potencija matrice Q = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}, tj. vrijedi
Ovo su neke od poznatijih relacija koje zadovoljavaju Fibonaccijevi brojevi:
| (1) | F_{n+m}=F_{m} F_{n+1}+F_{m-1} F_{n} \text{ za sve } m,n\geq 1, |
| (2) | Cassinijev identitet: F_{n+1} F_{n-1}-{F_{n}}^{2}=(-1)^{n}\text{ za } n\geq 2, |
| (3) | Catalanov identitet: F_{n}^{2} - F_{n+r} F_{n-r} = (-1)^{n-r} F_{r}^{2}\text{ za } n\geq r\geq 1, |
| (4) | F_{n}^{2}+F_{n+1}^{2}=F_{2n+1} za n\geq 0, pa slijedi da niz kvadrata Fibonaccijevih brojeva ima svojstvo da sume dva uzastopna člana redom daju Fibonaccijeve brojeve s neparnim indeksima. |
Limes niza kvocijenta dva susjedna Fibonaccijeva broja je
odnosno konstanta naziva zlatni rez. Označavamo ju s
Karakterizacija zlatnog reza, prikazana na Slici
Neka su dane dužina \overline{AB} i točka C na dužini takva da je omjer duljine cijele dužine \overline{AB} i duljine duljeg dijela \overline{AC} jednak omjeru duljine dužine \overline{AC} i duljine dužine \overline{BC}. Taj omjer iznosi
Zlatni rez \varphi zadovoljava identitete:
Neki primjeri Fibonaccijevog niza i zlatnog reza u prirodi
| (1) | Broj ženskih pčela podijeljen s brojem muških pčela, u bilo kojoj košnici u bilo kojem trenutku jednak je \varphi. |
| (2) |
Broj latica u cvijetu dosljedno slijedi Fibonaccijev niz. Primjerice, ljiljan koji ima tri latice, ljutići koji imaju pet, cikorija 21, tratinčica 34, i tako dalje (Slika |
| (3) |
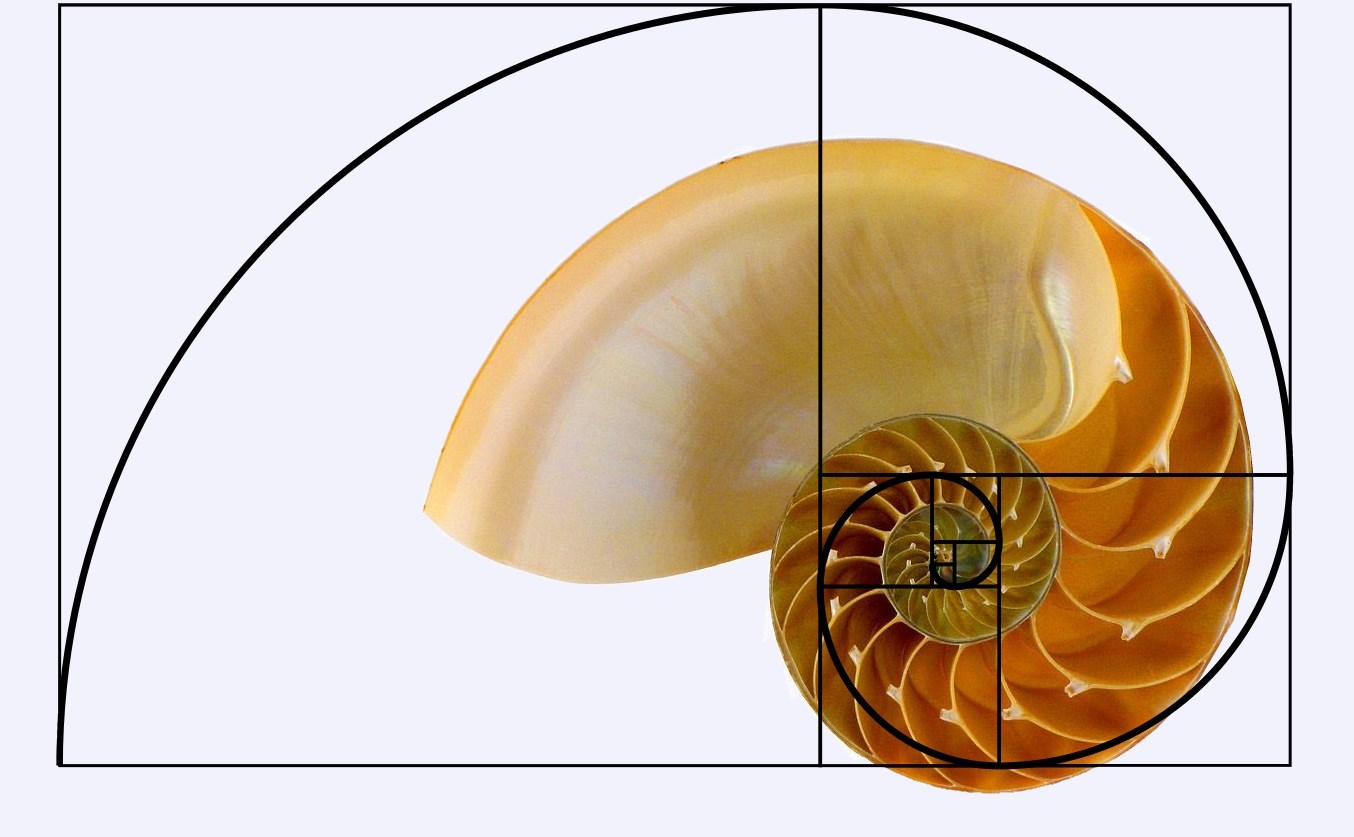
Pravokutnik u kojem je omjer stranica a:b jednak zlatnom rezu \varphi, može rezultirati postupkom gniježđenja koji se može ponoviti u beskonačnost - i koji poprima oblik spirale. U prirodi takav oblik imaju na primjer ljuske puževa i nautilus (Slika |
Kao što je u Fibonaccijevom nizu svaki član počevši od trećeg po redu suma prethodna dva tako je u Tribonaccijevom nizu (
gdje je T_{0}=T_{1}=1 i T_{2}=2 pa je prvih nekoliko članova niza:
Niz je prvi put formalno opisao Agronomof 1914. godine, ali prvu nenamjernu upotrebu u podrijetlu vrsta dao je Charles R. Darwin. U primjeru koji ilustrira rast populacije slonova, oslanjao se na izračune koje je izvršio njegov sin George H. Darwin. Izraz Tribonacci predložio je Feinberg
gdje su \alpha , \text{ } \beta i \gamma korijeni polnoma x^{3}-x^{2}-x-1. Također vrijedi
gdje je \left\lbrack \quad \right\rbrack oznaka za funkciju “najbliže cijelo”. Niz kvocijenta susjednih članova Tribonaccijevog niza konvergira, analogno kao što vrijedi i za Fibonaccijev niz (1).
gdje je
konstanta koja se naziva Tribonaccijeva konstanta. Primijetimo da je Tribonaccijeva konstanta dio brojnika formule (3).
Pellovi brojevi P_{n} i Pell Lucasovi brojevi Q_{n} (
uz početne uvjete P_{0}=0 i P_{1} =1 za Pellove brojeve, odnosno Q_{0}=Q_{1}=2 za Pell Lucasove brojeve. Prvih nekoliko Pellovih brojeva je
a Pell Lucasovih
Pellovi i Pell Lucasovi brojevi povezani su relacijom
Nadalje, ovi brojevi dani su eksplicitno formulama
Q_{n} = (1-\sqrt{2})^{n} + (1+\sqrt{2})^{n}.
Pellovi brojevi se mogu generirati potenciranjem matrice M = \begin{bmatrix} 2 & 1 \\ 1 & 0 \end{bmatrix}, tj. vrijedi
Također, neka je F= \begin{bmatrix} 2 & 2 \\ 2 & -2 \end{bmatrix} tada je (prema
Vrijedi:
| (1) | P_{n+1} P_{n-1} - P_{n}^{2} = (-1)^{n}, analogon Cassinijevog identiteta za Fibonaccijeve brojeve, |
| (2) | P_{m+n} = P_{m} P_{n+1} + P_{m-1} P_{n}, |
| (3) | P_{m+n} = 2 P_{m} Q_{n} - (-1)^{n} P_{m-n}, |
| (4) | Q_{n}^{2} = 4 \big( 2 P_{n}^{2} + (-1)^{n} \big), |
| (5) | Q_{2n} = Q_{n}^{2} - 2 (-1)^{n}. |
| (6) |
Uređena trojka
(2P_{n} P_{n + 1},\, P_{n + 1} ^{2} -P_{n} ^{2}, \,P_{2n + 1})
čini Pitagorinu trojku. Prvih nekoliko takvih trojki je
(4,3,5), (20,21,29), (120,119,169), (696,697,985),…
|
Slično kao što je zlatni rez limes kvocijenta susjednih Fibonaccijevih brojeva, srebreni rez S je limes kvocijenta susjednih Pellovih brojeva, tj. vrijedi
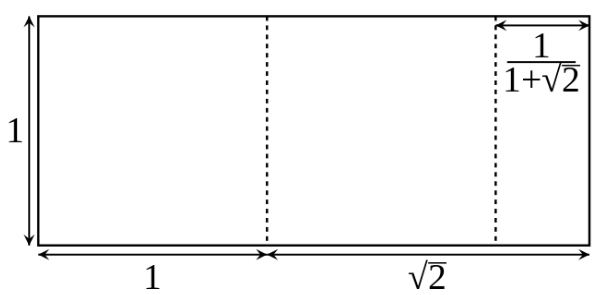
Kažemo da su dvije veličine a i b, a\geq b, u omjeru srebrenog reza (Slika
Uvođenjem supstitucije \displaystyle x=\frac{a}{b} dobiva se kvadratna jednadžba x^{2} - 2x -1=0, a jedno od njenih rješenja je S= 1 + \sqrt{2}.
Padovanovi brojevi D_{n} (
uz početne uvjete D_{0}=D_{1}=D_{2}=1. Prvih nekoliko brojeva Padovanovog niza je
Na Slici
Padovanovi brojevi mogu se generirati pomoću matrice
računanjem njenih pozitivnih potencija, tj. vrijedi
Analogno zlatnom rezu kod Fibonaccijevih brojeva, plastična konstanta P je limes kvocijenta susjednih Padovanovih brojeva, tj. vrijedi
gdje je
Plastična kontanta P
Plastična konstanta P i zlatni rez \varphi su jedini brojevi x za koje postoje prirodni brojevi k i l takvi da vrijedi x+ 1 = x^{k} i x - 1=x^{-l}, tj. oni su takozvani morfni brojevi.
Pisotov broj
Dakle, sve četiri konstante su Pisotovi brojevi, a za njih vrijedi još:
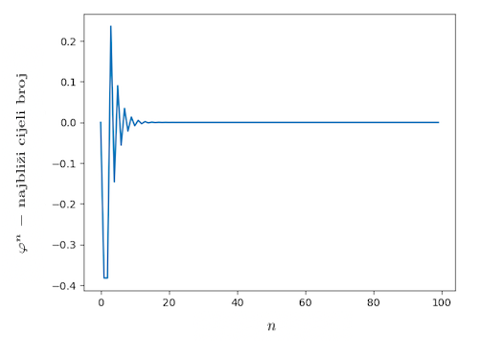
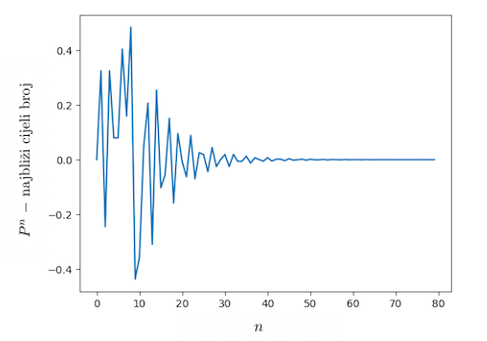
| (1) |
Potencije Pisotovih brojeva se približavaju cijelim brojevima. U Tablici |
| (2) | Ako je \alpha PV broj, onda su \alpha^{n}, n\in \mathbb{N} PV brojevi. |
| (1) |
Sve se mogu prikazati kao beskonačna ugnježđenja
|
||||||||
| (2) |
Zadovoljavaju slične algebarske izraze
\varphi+\frac{1}{\varphi^{2}}=2
\psi+\frac{1}{\psi^{3}}=2.
\frac{1}{\varphi}+1=\varphi
\frac{1}{P}+1=P^{2}
(1-u)^{3}=(2u)^{2} \text{ gdje je } u=\frac{\psi-1}{\psi+1}
(1-v)^{3}=(v)^{2} \text{ gdje je } u=\frac{1}{P+1}
|
||||||||
| (3) |
Sve četiri konstante se mogu izraziti u terminima Dedekind eta funkcije (više o tome u |
| [1] | http://www.britannica.com/eb/article-9034168/Fibonacci-numbers (pristupljeno lipanj, 2021.) |
| [2] | A. Dasdemir, On the Pell, Pell-Lucas and Modified Pell Numbers By Matrix Method, Appl. Math. Sci., 5(64), 3173 - 3181, (2011) |
| [3] | A. Dujella, Fibonaccijevi brojevi, Zagreb, (1999) |
| [4] | M. Feinberg, Fibonacci-Tribonacci, Fibonacci Quarterly 1, 71–74, (1963) |
| [5] | https://www.nationalgeographic.org/media/golden-ratio/(pristupljeno prosinac, 2021.) |
| [6] | https://gizmodo.com/15-uncanny-examples-of-the-golden-ratio-in-nature-59... (pristupljeno lipanj, 2021.) |
| [7] | A. F. Horadam and J. M. Mahon, Pell and Pell-Lucas Polynomials Fi- bonacci Quart., 23(1), 7-20, (1985). |
| [8] | B. Kovačić, L. Marohnić and R. Opačić, O Padovanovu nizu, Osječki matematički list 13, 1-19, (2013). |
| [9] | https://http://www.fibonaccilifechart.com/blog/truth-and-myth-in-the-gol... (pristupljeno prosinac, 2021.) |
| [10] | https://www.johndcook.com/blog/2017/03/26/plastic-powers/(pristupljeno prosinac, 2021.) |
| [11] | https://blogs.scientificamerican.com/roots-of-unity/meet-the-metallic-me... (pristupljeno prosinac, 2021.) |
| [12] | https://sites.google.com/site/tpiezas/0012 (pristupljeno lipanj, 2021.) |
| [13] | https://en.wikipedia.org/wiki/Pell-number (pristupljeno rujan, 2021.) |
| [14] | https://en.wikipedia.org/wiki/Generalizations-of-Fibonacci-numbers (pristupljeno lipanj, 2021.) |
| [15] | https://mathworld.wolfram.com/PadovanSequence.html (pristupljeno rujan, 2021.) |
| [16] | https://mathworld.wolfram.com/PellNumber.html (pristupljeno rujan, 2021.) |
| [17] | https://mathworld.wolfram.com/PisotNumber.html (pristupljeno listopad, 2021.) |
| [18] | https://mathworld.wolfram.com/PlasticConstant.html (pristupljeno rujan, 2021.) |
| [19] |
https://mathworld.wolfram.com/TribonacciNumber.html (pristupljeno lipanj, 2021.) |