Predviđanje tipa osobnosti
U današnje vrijeme, pogotovo zbog izazova u kojima se nalazimo, često je naglašeno pitanje unutarnjeg mira i pronalaska samog sebe. Pojam osobnosti usko je povezan s prethodnim pitanjem i problemom. Što je to osobnost i koja je njegova značajnost? Jedan od glavnih alata i pristupa u psihologiji je analiza osobnosti. Definicija osobnosti glasi: "ukupnost obilježja i ponašanja pojedinca kojima se razlikuje od ostalih pojedinaca". Poznavanje osobnosti može nam pomoći razumjeti bolje samog sebe i svoje postupke, također i psiholozima olakšava da nam bolje pristupe i da nas lakše usmjere. Međutim, psiholozi na razne načine interpretiraju osobnost i pokušavaju ljude klasificirati na temelju sličnosti u osobnostima.
Postoje razni pristupi klasifikaciji osobnosti i sastavljanju samog testa osobnosti. Jedan od trenutno najpoznatijih testova osobnosti je Mayers - Briggs Type Indicator koji osobnost dijeli u 16 kategorija — tipova, primjerice tip INTJ gdje svako slovo označava jednu od karakteristika te kategorije osobnosti, pogledati
Već smo naveli značajnost otkrivanja karakteristika naše osobnosti, a to najbrže možemo rješavajući test osobnosti. Test koji ćemo mi koristiti kako bi ljude klasificirali u neku od kategorija iznijet ćemo u nastavku. Naš je zadatak u ovom radu predstaviti alat kojim na temelju odgovora na test možemo predvidjeti nečiju osobnost. Osim samog opisa testa i analize testnih podataka na kojima smo radili, prikazat ćemo pristup rješavanju zadatka klasifikacije i detaljno opisati metode koje smo pritom koristili. Također, demonstrirat ćemo predviđanje na već postojećim rezultatima testa.
Jedan od često spominjanih modela ličnosti ili osobnosti je Velikih pet tipova (eng. Big five). Taj je model uveden 1980-tih godina i uvelike je olakšao psiholozima rad s ljudima. Prema tom modelu osobnost se svrstava u 5 kategorija:
| (1) | Otvorenost (eng.Openness) |
| (2) | Savjesnost (eng. Conscientiousness) |
| (3) | Ekstrovertiranost (eng. Extraversion) |
| (4) | Srdačnost (eng. Agreeableness) |
| (5) | Neurotičnost (eng. Neuroticsm) |
Promatrajući prva slova engleskog nazivlja, ovaj je model često spominjan pod nazivom OCEAN model. Ukratko ćemo predstaviti svaku od kategorija (prema
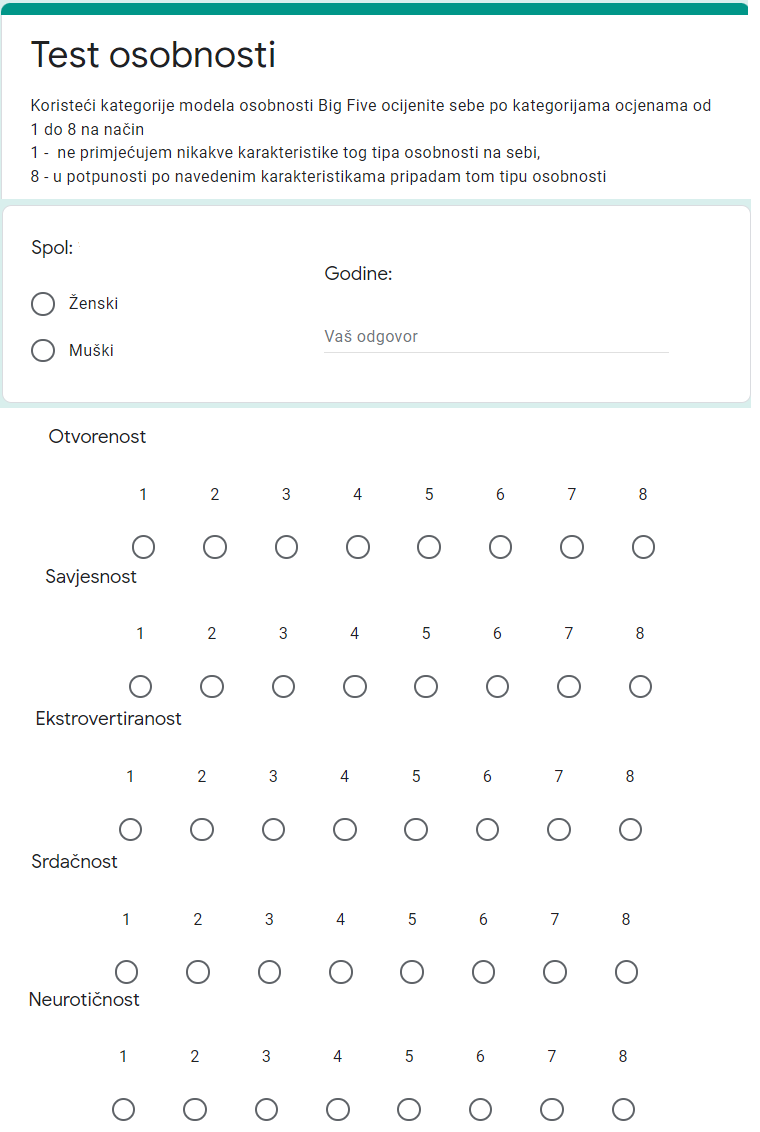
Analizirajući odgovore na testu osobnosti, psiholozi nastoje osobu svrstati u neku od kategorija osobnosti, uzimajući u obzir važnost svakog pojedinog pitanja i odgovor na njega. Mi ćemo analizu malo pojednostaviti budući da se ne bavimo stručnim psihološkim istraživačkim radom nego želimo znanja o umjetnoj inteligenciji demonstrirati na konkretnom primjeru u svakodnevnom životu. Željeli smo da test koji ćemo koristiti bude pristupačan za rješavanje, a da rezultati testa budu jednostavniji za analizu i korištenje. Odlučili smo se koristiti test baziran na obrascu pitanja sa Slike
Na temelju odgovora podnesenih u testu, osobu ćemo svrstati u jednu od ovih kategorija:
| (1) | Ekstrovert (eng. extraverted) |
| (2) | Ozbiljan (eng. serious) |
| (3) | Pouzdan (eng. dependable) |
| (4) | Živahan (eng. lively) |
| (5) | Odgovoran (eng. responsible) |
Obilježja ovih karakteristika slična su gore opisanima. Ekstrovertne osobe karakteriziramo kao društvene, otvorene i primjetljive u društvu. Osobe koje su ozbiljne imaju veoma dobro posložene životne prioritete i ne dopuštaju da im nešto neočekivano stane na zacrtani put, čak i teže otkrivaju svoje emocije. Na pouzdane se osobe možemo osloniti u svakom trenutku, empatične su i ljubazne prema svima. Živahne osobe uvijek su spremne za avanturu, pune su energije i spremne za svaki izazov. Na kraju, odgovorne su osobe uvijek na vrijeme i svoje zadatke ne ostavljaju za zadnji tren. \newpage
Nakon što smo opisali model i test koji smo koristili pri implementaciji programa za predviđanje tipa osobnosti, preostalo nam je nešto reći i o korištenoj bazi podataka. Baza podataka koja odgovara svemu do sad opisanom je
Skup podataka kojim raspolažemo se sastoji od 1024 retka i 8 stupaca, odnosno 1024 popunjenih testova osobnosti. U prvom stupcu nalazi se podatak o spolu (eng. gender) ispitanika s vrijednostima Male i Female za muškarce i žene, redom. U drugom stupcu se nalazi podatak o dobi, primijetili smo da se raspon godina kreće između 15 i 30 godina. Sljedeća četiri stupca sadrže podatke o odgovorima na pitanja o tipu osobnosti. Odgovor na pitanja je broj od 1 do 8, gdje 1 označava da ispitanik ne primjećuje nikakve karakteristike tog tipa osobnosti na sebi, a 8 da u potpunosti po navedenim karakteristikama pripada tom tipu osobnosti. Karakteristike u stupcima su redom: otvorenost (eng. openness), savjesnost (eng. conscientiousness), ekstrovertiranost (eng. extraversion), srdačnost (eng. agreeableness), neurotičnost (eng. neuroticism). U posljednjem stupcu je naziv jedne od pet osobnosti (s kraja točke

Sada kada znamo kojim podacima raspolažemo i kako izgledaju, pristupamo rješavanju zadatka. Prije samog pisanja koda i treniranja modela korisno je analizirati podatke kako bi stekli neki dojam o podacima s kojim radimo. Analizu podataka provodimo koristeći različite alate opisane u nastavku.
Prvo ćemo provjeriti jesu li svi podaci u tablici ispravni, odnosno ispravno zabilježeni/uneseni. Znamo da greške u podacima, poput outliera, mogu kasnije dosta utjecati na korektnost modela. Nepotpune ili pogrešne vrijednosti možemo, prema teoriji, tretirati na više načina. Redak s takvim podacima možemo samo odbaciti, možemo ih zamijeniti nulom ili nekom drugom konstantom (koja je prikladna s obzirom na ostale podatke) ili zamijeniti statističkom vrijednosti, poput srednje vrijednosti ili vrijednosti predviđene na temelju ostalih sličnih podataka.
Pronašli smo jedan test u kojem je oznaka spola označena nekorektno, taj smo dio popravili tako da smo ju zamijenili srednjom vrijednosti ostalih podataka u prvom stupcu. Također, dvije su ocjene greškom bile zapisane kao 9 pa smo ih prepravili na ocjenu 8 koja je maksimalna moguća ocjena. Za kraj, pronašli smo dvije godine upisane kao 5, što pretpostavljamo da je greška s obzirom na druge vrijednosti godina, njih smo zamijenili srednjom vrijednosti godina. Na ovaj smo način pokazali, u praksi, sve ranije navedene mogućnosti rješavanja problema nekorektnih podataka, bez odbacivanja podataka.
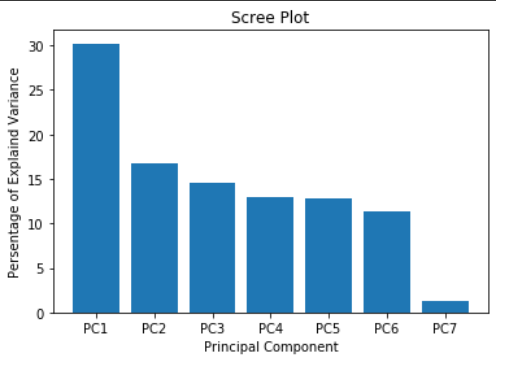
Analiza podataka često je povezana s analizom nekih statističkih elemenata. Koristeći statističke pojmove poput box-plotova, distribucije, koreliranosti ili srednje vrijednosti možemo doći do korisnih svojstava naših podataka. Povezano s time, korisno je takve elemente prikazati grafički, a mi smo se odlučili grafički prikazati analizu glavnih komponenti, primjer box-plotova i ispitati koreliranost pojedinih odgovora.
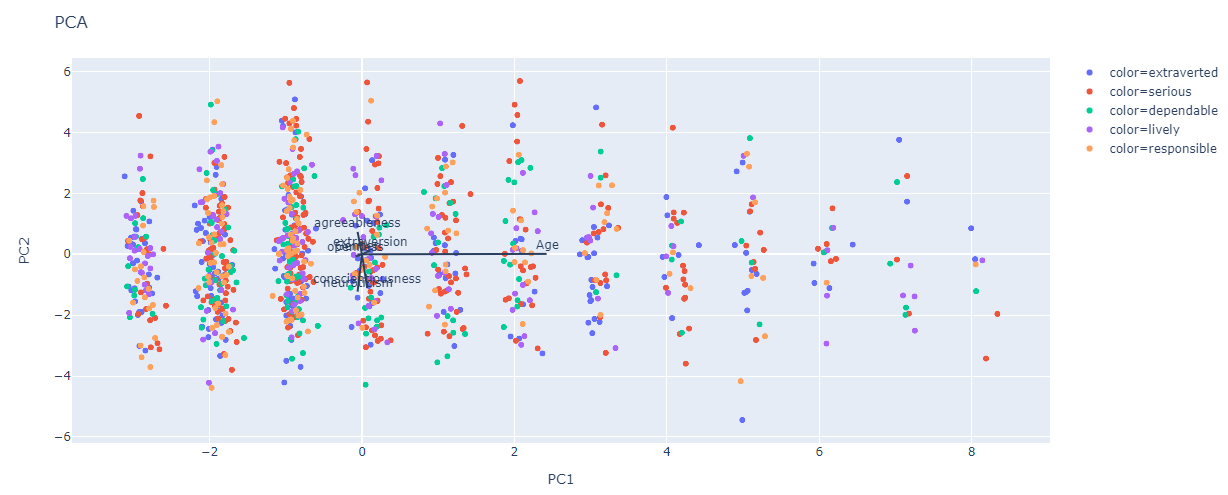
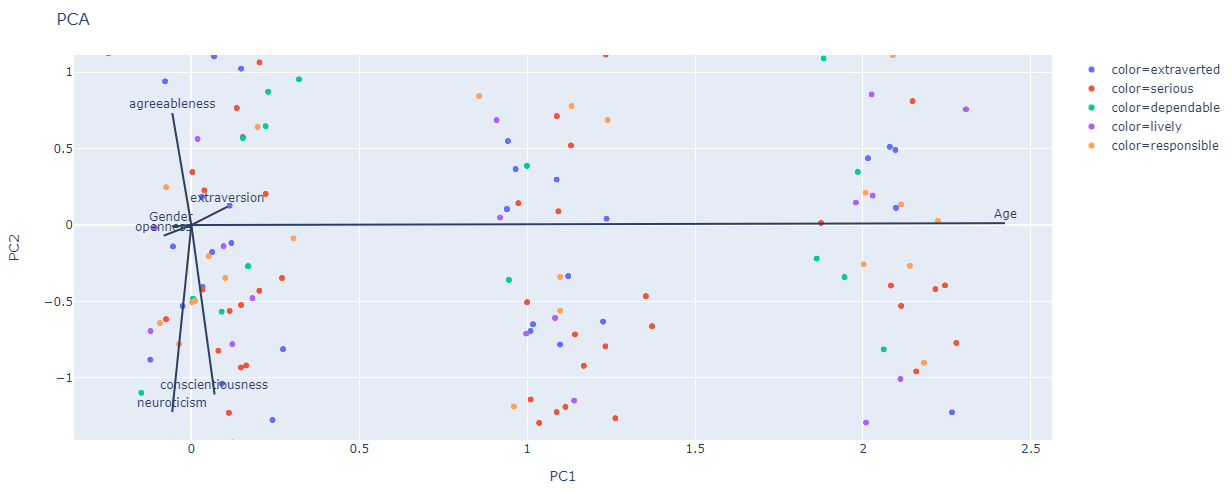
Prikupljene podatke želimo prikazati grafički, no kako imamo osam stupaca za prikaz bi nam trebao graf u osam dimenzija koji intuitivno nije jasan. Da bismo dobili predodžbu kako se naši podaci "ponašaju" koristimo tehniku zvanu Analiza glavnih komponenti (eng. Principal component analysis). Skraćeno PCA je tehnika smanjivanja dimenzije vektora kojeg proučavamo. Korištenjem PCA vektor dimenzije osam ćemo smanjiti na vektor u dvije dimenzije. Način, koji smo mi odabrali za jedan od prikaza, na koji smanjujemo dimenzionalnost podataka gubitkom minimalno informacija je uzimajući u obzir po dva stupca. Na taj način smanjujemo dimenzionalnost na neku koju možemo lakše grafički prikazati.
Na grafu
Na scree plotu
Kao što nam je prethodna analiza sugerirala nemamo vidljivo grupiranje boja. Dužine na grafu
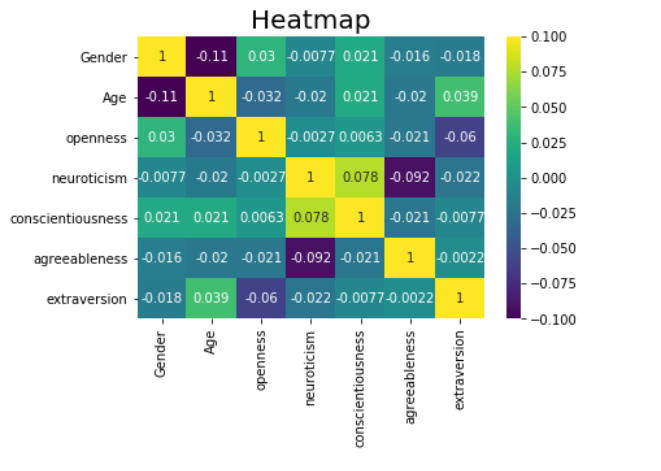
Upravo je koreliranost važan statistički alat, koji bi u našem slučaju mogao biti od velike koristi. Iako već iz grafa
Za dodatnu analizu koreliranosti odlučili smo koristiti heatmap prikaz.
Prema grafu
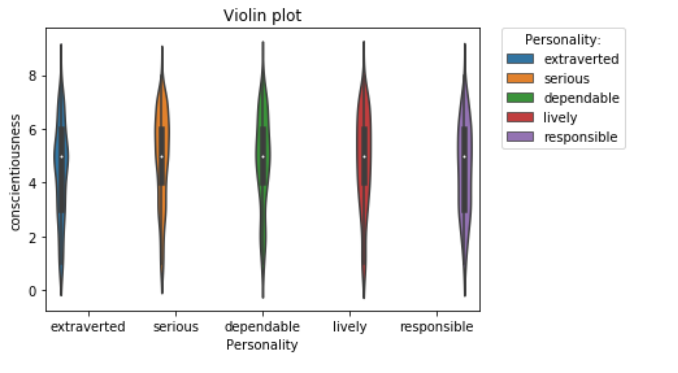
Jedno od svojstva podataka koje još nismo spomenuli je distribucija. Distribucija nam govori koja je vjerojatnost da će neka veličina poprimiti određenu vrijednost. Kako bi nam ta informacija mogla biti korisna prikazat ćemo distribuciju osobina za svaku kategoriju osobnosti. Za prikaz distribucija koristimo violine plot.
Na grafu
Slijedi glavni dio našeg rada, odnosno modeliranje i testiranje modela za predviđanje osobnosti. Veliki skup podataka koji smo do sada skupno analizirali potrebno je podijeliti i jedan dio koristiti za treniranje, dok drugi za testiranje. Omjer u kojem smo mi odlučili dijeliti podatke je 30% za testiranje i 70% za treniranje. Nakon podjele imat ćemo 717 redaka za treniranje modela i 307 za testiranje.
Prije modela i testiranja htjeli bismo ukratko skrenuti pažnju na još dva detalja. Prvi detalj vezan je uz distribuciji. Poželjno je da podaci za treniranje i testiranje imaju istu distribuciju. Modeli umjetne inteligencije bazirani su na pretpostavci da su podaci na kojima treniramo model i oni na kojima ćemo kasnije taj model testirati pa i koristiti jednako distribuirani, jer "vezu" koju pronađu na podacima za treniranje koriste i na onima koje predviđaju.
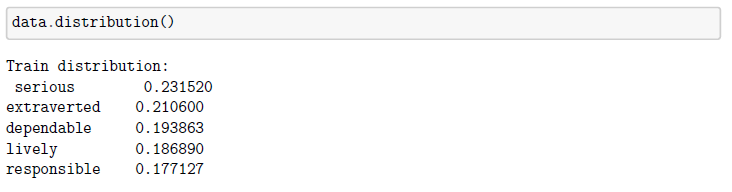
Vidimo da distribucije nisu jednake. U podacima za testiranje broj osoba u klasi ozbiljnih (serious) je tri puta veća od broja osoba odgovornih (responsible), dok je u podacima za treniranje razlika mala. Ta činjenica je malo obeshrabrujući jer nam sugerira da niti jedan model kojeg treniramo na podacima za treniranje neće davati odlične rezultate na podacima za testiranje. Naime, ozbiljna narušenost pretpostavke rezultira slabom točnošću klasifikacije.
Drugi detalj tiče se karakteristika podataka, odnosno tipa kojem pripadaju. Kada ispišemo informacije o samoj bazi (iz točke
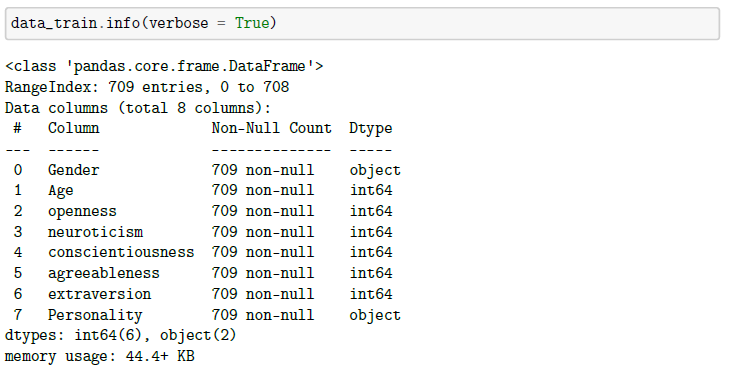
Kako neki modeli i funkcije na podacima rade preciznije ukoliko su podaci svi istog tipa ili samo numeričkog tipa odlučili smo sve podatke pretvoriti u tipove int64. Za tu smo potrebu vrijednosti Female i Male pretvorili redom u 0, 1, a kategorije osobnosti u brojeve od 1 do 5.
U ovoj bi točki kratko htjeli iznijeti teoriju koja stoji iza svih modela i koja prethodi odabiru svakog od njih. Priroda zadatka i podataka na kojima radimo sugerira nam da ćemo naše modele bazirati na učenju s nadzorom. Učenje s nadzorom je vrsta strojnog učenja u kojem se svaki primjer sastoji od ulaznog podatka i željenog izlaza. Model na temelju ulaznih podataka donosi zaključke o izlaznim vrijednostima kako bi mogao dati odgovor na ulaz koji još nije vidio.
Naš zadatak predikcije osobnosti zapravo ima za cilj naučiti podatak svrstati u neku od klasa odnosno kategorija osobnosti. Bitna činjenica je da mi unaprijed znamo klase u koje moramo svrstati podatke.
Kao što na početku poglavlja rekli, na podacima koji služe za treniranje implementirat ćemo model koji će ih fitati u najboljoj mjeri. Nakon toga ćemo taj model testirati na podacima za testiranje i odrediti točnost našeg modela. Ovo je samo jedan od načina validacije odnosno provjere točnosti konačnog modela. Za neke od modela demonstrirat ćemo K-struku unakrsnu validaciju (eng. K-fold cross validation), prema
Isprobavali smo razne modele i mijenjajući njihove parametre pokušali smo dobiti što bolju točnost. Neke od njih ćemo prikazati u nastavku, a za detalje implementacije pogledajte
S obzirom na prirodu zadatka i podatke na kojima radimo prvi model koji smo htjeli implementirati je stablo odluke. Stablo odluke je jedna od najčešće korištenih metoda induktivnog zaključivanja. To je skup više ako-onda pravila koje možemo prikazati grafički, u obliku stabla (na primjer Slika
Važno je dobro odabrati atribute po kojima se stablo grana. Za grananje trenutnog stabla, među preostalim atributima, biramo onaj atribut koji tog trena daje najveći dobitak informacije, a to je onaj s manjom entropijom. Entropija je mjera nečistoće ili nereda u podacima. Pogledati
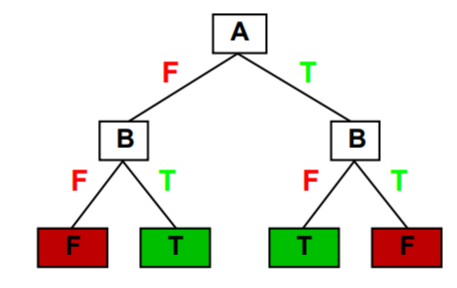
U problemu kojim se bavimo, svaki list stabla je jedan tip osobnosti: extraverted, serious, dependable, lively, responsible. Stablo granamo u ovisnosti o vrijednostima stupaca: gender, age, openness, neuroticism, conscientiousness, agreeableness, extraversion. Naše stablo nema puno različitih atributa, no imat će dosta grananja za svaki atribut (osim spola) zbog raspona odgovora.
Za implementiranje stabla odluke koristili smo funkciju sklearn.tree.DecisionTreeClassifier(). Njome stvorimo model s unaprijed zadanim kriterijem entropy, čime označavamo da ćemo koristiti mjeru entropije u modelu. Ostale parametre spremimo u listu koju zatim prosljeđujemo funkciji best_hyperparameters() da nam vrati najbolje parametre za naše podatke. Nakon toga moramo fitati model na podacima za treniranje i radi predostrožnosti ispišemo točnost. Isto to napravimo i za test podatke. Mjera točnosti modela koju također koristimo je i funkcija k_validation() koja i grafički prikazuje točnost.
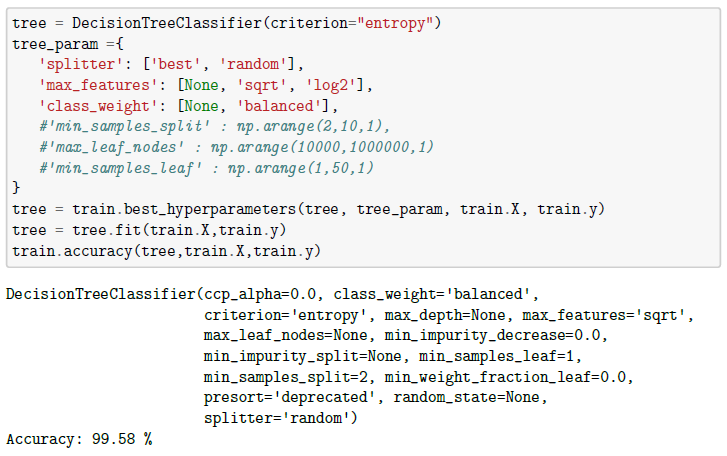
Pomoću ispisa možemo vidjeti koliku je točnost model postigao na podacima za treniranje, kao i parametre koje je izabrao kao najbolje. Vidimo da je točnost na train podacima preko 99%, s čime smo bili veoma zadovoljni.

Nakon toga potrebno je koristiti model kako bi predvidjeli rezultate na test podacima. Na test podacima je točnost ispod 30% što nije puno, pogotovo ako uzmemo u obzir da bi nasumičnim pogađanjem točnost bila 20%. Razlog tako male točnosti je upravo razlika u distribuciji između podataka za treniranje i testiranje te slaba veza između podataka o kojoj smo govorili u točki

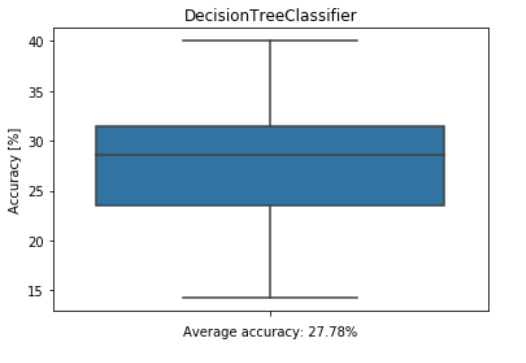
Navest ćemo neke od tehnika kojima smo pokušali poboljšati rješenja. Prvi je promjena baze podataka na način da svaki stupac sadrži samo nule ili jedinice, čime povećavamo broj stupaca, a smanjujemo broj vrijednosti na 0 i 1. U nekim slučajevima ovaj način modificiranja podataka dovodi do poboljšanja rezultata, no u našem slučaju nije. Također, vizualizacijom stabla odluke možemo pažljivije odabrati parametre i time poboljšati točnost, iako je nismo prikazali u radu, obratili smo pažnju na njen izgled i time pokušali odabrati prikladne parametre za model.
Dodatna tehnika je proučavanje matrica zabune. Matrica zabune je matrica u kojoj su zapisane vrijednosti koje se računaju analizirajući stvarne i predviđene vrijednosti u modelu, a zapisane su redom kao na Slici
a pomoću nje zaključujemo da su najčešće tipovi ekstrovert i ozbiljan bili zamjenjeni u predikciji, dok su najmanje zamjenjeni bili živahan i pouzdan.
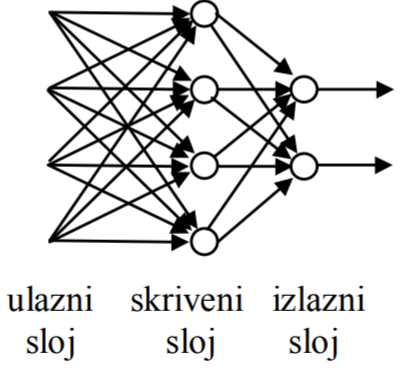
Sljedeći pristup koji smo odabrali za rješavanje problema bio je treniranje neuronske mreže. Razlog zbog kojeg smo se odlučili njih koristiti je njihova efikasnost pri rješavanju višedimenzionalnih problema, no one su zato i teoretski složenije i mogu dovesti do overfittinga. Također, važno svojstvo je i što podržavaju učenje s nadzorom i problem klasifikacije s kojim se mi susrećemo.
Neuronska mreža je računalni sustav koji oponaša živčani sustav ljudi i životinja. Izgrađena je od jednostavnih elemenata zvanih neuroni. Neuron je jednostavna funkcija f koja transformira određen broj ulaznih varijabli x_{1},x_{2},\ldots s pripadnim težinama w_{1},w_{2},\ldots u jednu izlaznu varijablu y = f(x_{1},x_{2},\ldots), pojednostavljeno objašnjenje po
Stvorili smo model koristeći funkciju sklearn.neural_network.MLPClassifier() koji ćemo fitati na podacima za treniranje. Dodatni parametri koje pozivamo u funkciji su povezani s karakteristikama neuronske mreže, pogledati u
Struktura neuronske mreže koju mi koristimo opisana je kroz parametar hidden_layer_sizes i zaključujemo da se naša mreža sastoji od 3 skrivena sloja, svaki sadrži 600 neurona.

U ovome načinu pokretanja, koristeći najbolje parametre koje smo dobili pomoćnom funkcijom, dolazimo do točnosti na podacima za treniranje od 99%, dok je točnost na podacima za testiranje bila 26%.
Istu funkciju smo pokrenuli i sa standardnim (defaultnim) parametrima.

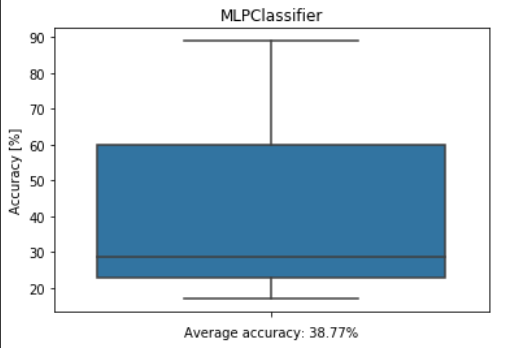
U ovoj situaciji je točnost na train podacima nešto niža, 32%, dok je točnost na test podacima viša od prethodne. Također, upotrijebili smo i k_validation() koji nam je pokazao da je ponašanje ovog modela prividno bolje od prošlog. Prvi poziv ovog modela nam daje lijepi primjer overfittinga na podacima. Overfitting je fenomen ili pojava kod kojeg model jako dobro opisuje train podatke, ali na test podacima daje loše rezultate.
Stablo odluke smo prethodno opisali u točki

U funkciji random_forest() koristili smo metodu sklearn.ensemble.RandomForestClassifier() koju smo pozvali s najboljim parametrima, čija su objašnjenja slična kao kod stabla odluke. Ispisana vrijednost je točnost na test podacima. Slučajne šume stabla odluke pokazale su znatno bolji rezultat od modela stabla odluke. Vrijeme izvršavanja RandomForestClassifier() znatno je dulje nego kod ostalih metoda jer se više puta radi stablo odluke s različitim parametrima i ulazim podacima.
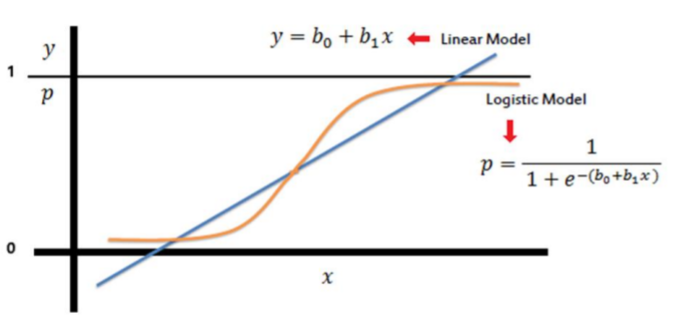
Jedna od dodatnih metoda koju smo htjeli istražiti je i logistička regresija. Zbog loših rezultata predviđanja, razmišljali smo kako na neki drugačiji način poboljšati točnost. Razlog zbog kojeg nam se ova metoda činila zanimljivom je njezina povezanost s linearnom regresijom koja je svima dobro poznata.
Logistička regresija pripada familiji generaliziranih linearnih modela. Kako je teorija koja stoji iza generalizacije i samog modela zahtjevnija napomenut ćemo samo neka bitna svojstva (iz
Međutim, postoje modifikacije modela u kojima je moguće koristiti logističku regresiju za klasificiranje u više klasa. Naravno, postoji više načina na koji se može napraviti modifikacija, no nećemo opisivati svaki od njih. Mi smo koristili multinomijalnu vjerojatnosnu distribuciju(
Funkcija koju pozivamo je sklearn.linear_model.LogisticRegression() uz parametre koji su pronađeni kao najbolji i multiclass='multinomial', koji je od velike važnosti jer imamo više klasa.
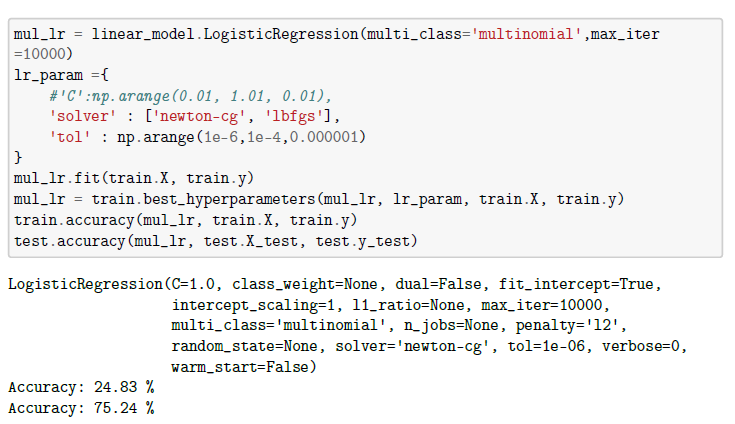
Iako je točnost na podacima za treniranje svega 25%, vidimo da je na test podacima točnost puno bolja i iznosi 75%. Ovaj je rezultat najbolji od svih modela koje smo koristili. Stoga, njime završavamo naše izlaganje o modelima umjetne inteligencije koje smo koristili u ovome radu.
Kao što smo rekli na početku, smatramo da je zadatak predikcije osobnosti dobar i koristan primjer korištenja umjetne inteligencije. Koristan je iz razloga što postoji potreba za analiziranjem rezultata testova osobnosti, ovog i ostalih koji postoje. Primjer je dobar jer smo na njemu mogli prikazati tijek jednog projekta čiji je zadatak predvidjeti konačni rezultat.
Na početku smo htjeli dati motivaciju i pregled u projekt kako bi bilo lakše razumjeti daljnji rad. Nadalje, smatramo da je analiziranje podataka i bavljenje s njim prije samog pisanja koda od velike važnosti, jer "priprema je pola posla". U tom dijelu rada mogu se otkriti zanimljive i korisne informacije koje kasnije mogu biti od velike koristi, kao i u našem slučaju. Analizom koreliranosti i prikazom distribucija, došli smo do zaključka da bi točnost modela koje ćemo raditi na našim podacima mogla biti loša. Tada je slijedilo pisanje koda i testiranje modela koje smatramo najvažnijima. Zbog lošijih rezultata predikcija koji su nas malo obeshrabrili, pokušali smo više pristupa kako bi probali doći do preciznijeg modela. Prikazali smo modele koje smatramo bitnima, uz detaljne rezultate testiranja. Kao što smo rekli najbolje nam se pokazao model logističke regresije.
Zaključno, smatramo da su podaci koje smo koristili zaslužni (odnosno "krivci") za loše rezultate predviđanja. S obzirom na ograničenu i malu količinu podataka u bazi, korišteni modeli nisu davali veliku točnost predviđanja na testnim podacima, ali demonstriraju njihovo korištenje na konkretnom primjeru i važnost poznavanja svojstva podataka prije modeliranja.
7Literatura
[1] I. Bistrovi´c. Logistička regresija u analizi smrtnosti. Zadnje pristupljeno: prosinac 2021. URL:
https://repozitorij.pmf.unizg.hr/islandora/object/pmf%3A5812/datastream/
PDF/view.
[2] D. H. Saklofske C. Coulacoglou. Psychometrics and Psychological Assessment. 2017.
[3] M. Cular. Modeli slučajnih šuma i primjene. Zadnje pristupljeno: prosinac 2021. URL: https://repozitorij.pmf.unizg.hr/islandora/object/pmf%3A9099/datastream/....
[4] B. Gavranovic. Primjena modela dubokog uˇcenja na analizu sentimenata.
[5] S. Lončarič. Neuronske mreže: Uvod. Zadnje pristupljeno: prosinac 2021. URL: https://www.fer.unizg.hr/_download/repository/01-Uvod-1s.pdf.
[6] Kaggle baza podataka. Zadnje pristupljeno: prosinac 2021. URL: https://www.kaggle.com/
pavlorymarchuk/test3434.
[7] O. P. John R. R. McCrae. An Introduction to the Five-Factor Model and Its Applications. Zadnje pristupljeno: prosinac 2021. URL: https://www.workplacebullying.org/multi/pdf/
5factor-theory.pdf.
[8] Git repozitorij. URL: https://github.com/Krcivoj/Personality-prediction.
[9] S. Singer. Provjera (validacija) modela. Zadnje pristupljeno: prosinac 2021. URL: http://degiorgi.math.hr/~singer/ui/ui_1415/ch_18c.pdf
[10] S. Singer. Učenje na primjerima. Zadnje pristupljeno: prosinac 2021. URL: http://degiorgi.math.hr/~singer/ui/ui_1415/ch_18b.pdf.
[11] S. Singer. Učenje na primjerima(promatranjem). Zadnje pristupljeno prosinac 2021. URL: http://degiorgi.math.hr/~singer/ui/ui_1415/ch_18.pdf.
[12] J. Šnajder. Strojno učenje. Zadnje pristupljeno: prosinac 2021. URL: https://www.fer.unizg.hr/_download/repository/SU-2015-Vrednovanje_modela....
[13] J. Šnajder. Strojno učenje: 7. Logistička regresija II. Zadnje pristupljeno: prosinac 2021.
URL: https://www.fer.unizg.hr/_download/repository/SU-2019-07-LogistickaRegre....



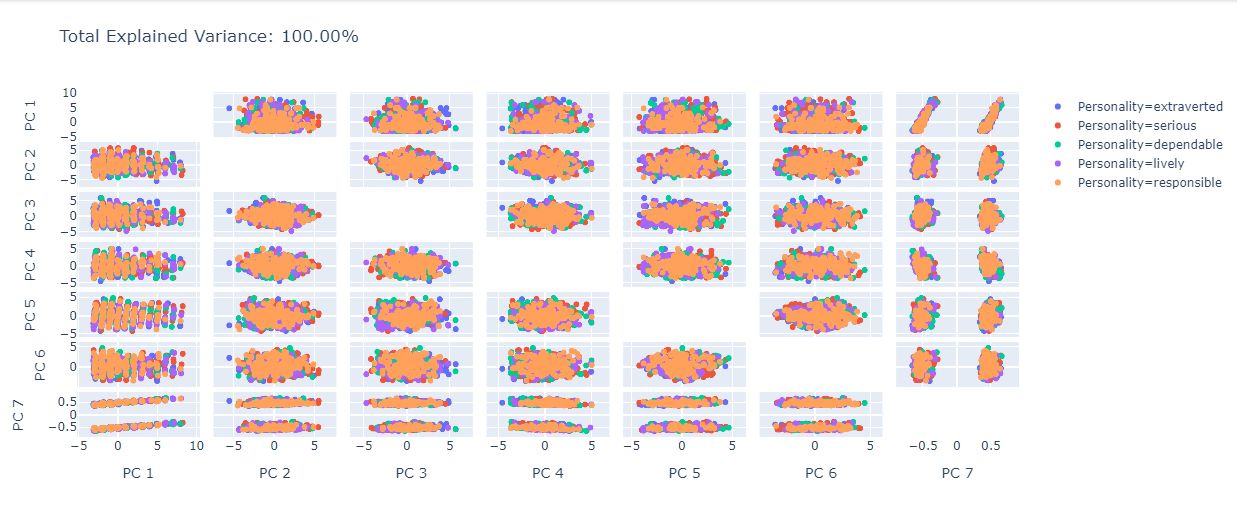 Slika 2: PCA s dva stupca
Slika 2: PCA s dva stupca