P	U	S	Č	P	S	N
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	31

Primjene Fourierove analize na konačnim komutativnim grupama

Vjekoslav Kovač2

Ljudevit Palle3

Sažetak. U ovom članku izlažu se osnove Fourierove analize na konačnim Abelovim grupama. Potom se dobiveni rezultati primjenjuju na raznovrsne zadatke u različitim matematičkim granama: (linearnoj) algebri, geometriji ravnine, elementarnoj teoriji brojeva i (aditivnoj) kombinatorici.

1Fourierova transformacija

Fourierova analiza je opsežna matematička disciplina koja se razvila iz razmatranja J.-B. J. Fouriera (1768–1830) o razvojima u redove sastavljene od trigonometrijskih funkcija, inicijalno u kontekstu proučavanja jednadžbe provođenja topline. Već oko dvije stotine godina njezina mnogobrojna pitanja intrigiraju poznate matematičare, a i danas se nalaze nove zanimljive primjene teorijskih rezultata. Svrha ovog članka je čitatelju približiti jedan aspekt Fourierove analize na konačnim strukturama, koji ne iziskuje neko posebno predznanje, za razliku od općenite teorije. Tako se već čitatelj sa znanjem srednjoškolske matematike može uvesti u ovo područje, a natjecatelji mogu naučiti poneki trik za rješavanje prilično teških zadataka.

Za prirodni broj $d$ označimo sa $ℤ_{d}$ skup ostataka pri dijeljenju s $d$ , tj.

ℤ_{d} : = {0, 1, 2, 3, \dots, d - 2, d - 1} .

Na skupu $ℤ_{d}$ se podrazumijevaju operacije zbrajanja i množenja modulo $d$ , tj. nakon izvršenog zbrajanja ili množenja još podijelimo rezultat s $d$ i uzmemo samo ostatak pri dijeljenju. Tako npr. na $ℤ_{4}$ imamo sljedeće tablice zbrajanja i množenja.

$+$	0	1	2	3
0	0	1	2	3
1	1	2	3	0
2	2	3	0	1
3	3	0	1	2

$\cdot$	1	2	3
0	0	0	0
1	1	2	3
2	2	0	2
3	3	2	1

Fiksirajmo sada $n \in ℕ$ i brojeve $d_{1}, \dots, d_{n} \in ℕ ∖ {1}$ . Kada pišemo

(1)

A = ℤ_{d_{1}} \oplus ℤ_{d_{2}} \oplus \dots \oplus ℤ_{d_{n}},

tada smatramo da je $A$ Kartezijev produkt skupova $ℤ_{d_{1}}, \dots, ℤ_{d_{n}}$ na kojem se promatra zbrajanje po koordinatama. Drugim riječima, elementi od $A$ su $n$ -torke $x = (x_{1}, x_{2}, \dots, x_{n})$ koje se zbrajaju kao:

(x_{1}, x_{2}, \dots, x_{n}) + (y_{1}, y_{2}, \dots, y_{n}) : = (x_{1} + y_{1}, x_{2} + y_{2}, \dots, x_{n} + y_{n}) .

Često pišemo samo $0$ umjesto $n$ -torke samih nula, $(0, 0, \dots, 0)$ . Tako je npr. operacija zbrajanja na $ℤ_{2} \oplus ℤ_{2}$ opisana sljedećom tablicom.

$+$	(0,0)	(0,1)	(1,0)	(1,1)
(0,0)	(0,0)	(0,1)	(1,0)	(1,1)
(0,1)	(0,1)	(0,0)	(1,1)	(1,0)
(1,0)	(1,0)	(1,1)	(0,0)	(0,1)
(1,1)	(1,1)	(1,0)	(0,1)	(0,0)

Čitatelj upoznat s pojmom grupe odmah će prepoznati da je gore opisana struktura $(A, +)$ primjer konačne komutativne (ili Abelove) grupe. Obratno, poznato je da svaka konačna komutativna grupa ima strukturu (1) za određene parametre $n$ i $d_{1}, \dots, d_{n}$ . Zato mi i ne moramo raditi s općenitim grupama, veće upravo s grupama $A$ danima formulom (1).

Definirajmo preslikavanje $E : A \times A \to ℂ$ formulom

E (x, ξ) : = (e^{2 π i / d_{1}})^{x_{1} ξ_{1}} (e^{2 π i / d_{2}})^{x_{2} ξ_{2}} \dots (e^{2 π i / d_{n}})^{x_{n} ξ_{n}}

za svake $n$ -torke $x = (x_{1}, x_{2}, \dots, x_{n})$ i $ξ = (ξ_{1}, ξ_{2}, \dots, ξ_{n})$ iz $A$ . Primijetimo da $E$ poprima vrijednosti u kompleksnim brojevima modula $1$ . Jedini razlog zašto lijevi argument pišemo latiničnim slovom $x$ , a desni grčkim slovom $ξ$ , je kako bismo naglasili da se oni nalaze u dvije različite kopije od $A$ , povezane preslikavanjem $E$ .

Propozicija 1. Preslikavanje

E

ima sljedeća svojstva (za svaki izbor od

x, y, ξ, ζ \in A

E (x + y, ξ) = E (x, ξ) E (y, ξ), E (x, ξ + ζ) = E (x, ξ) E (x, ζ),

E (0, ξ) = 1, E (x, 0) = 1, E (- x, ξ) = \bar{E (x, ξ)}, E (x, - ξ) = \bar{E (x, ξ)},

\sum_{x \in A} E (x, ξ) = \{\begin{cases} | A | & ako je ξ = 0, \\ 0 & ako je ξ \neq 0, \end{cases} \sum_{ξ \in A} E (x, ξ) = \{\begin{cases} | A | & ako je x = 0, \\ 0 & ako je x \neq 0 . \end{cases}

Napomenimo da sa $| S |$ označavamo broj elemenata konačnog skupa $S$ .

Proof. Prvih šest formula su direktne posljedice definicije od

E

, dok su posljednje dvije ekvivalentne radi simetričnosti iste definicije obzirom na

x

ξ

. Dokažimo zadnju navedenu formulu.

Za fiksirani

x = (x_{1}, x_{2}, \dots, x_{n})

sumiranjem po svim mogućnostima koordinata od

ξ = (ξ_{1}, ξ_{2}, \dots, ξ_{n})

dobivamo

(2)

\sum_{ξ \in A} E (x, ξ) = (\sum_{ξ_{1} = 0}^{d_{1} - 1} (e^{2 π i x_{1} / d_{1}})^{ξ_{1}}) \dots (\sum_{ξ_{n} = 0}^{d_{n} - 1} (e^{2 π i x_{n} / d_{n}})^{ξ_{n}}) .

Preostaje primijetiti da za

x_{j} \neq 0

vrijedi

e^{2 π i x_{j} / d_{j}} \neq 1

pa formula za parcijalnu sumu geometrijskog reda daje

\sum_{ξ_{j} = 0}^{d_{j} - 1} (e^{2 π i x_{j} / d_{j}})^{ξ_{j}} = \frac{1 - e^{2 π i x_{j}}}{1 - e^{2 π i x_{j} / d_{j}}} = \frac{1 - 1}{1 - e^{2 π i x_{j} / d_{j}}} = 0,

dok za

x_{j} = 0

imamo

\sum_{ξ_{j} = 0}^{d_{j} - 1} (e^{2 π i x_{j} / d_{j}})^{ξ_{j}} = \sum_{ξ_{j} = 0}^{d_{j} - 1} 1 = d_{j} .

Produkt iz (2) nije jednak

0

samo kada je

x_{1} = \dots = x_{n} = 0

i tada je jednak

d_{1} \dots d_{n} = | A |

Definicija 2. Fourierova transformacija funkcije

f : A \to ℂ

je nova funkcija

\hat{f} : A \to ℂ

definirana formulom

\hat{f} (ξ) : = \sum_{x \in A} f (x) E (x, ξ) za svaki ξ \in A .

Primjer 3. (a) Ako je

A = ℤ_{4}

i ako funkcije na

A

pišemo kao uređene četvorke

f = (f_{0}, f_{1}, f_{2}, f_{3}),

tada je

\hat{f} = (f_{0} + f_{1} + f_{2} + f_{3}, f_{0} + i f_{1} - f_{2} - i f_{3}, f_{0} - f_{1} + f_{2} - f_{3}, f_{0} - i f_{1} - f_{2} + i f_{3}) .

(b) Ako je

A = ℤ_{2} \oplus ℤ_{2}

i ako funkcije na

A

pišemo kao uređene četvorke

f = (f_{0, 0}, f_{0, 1}, f_{1, 0}, f_{1, 1}),

tada je

\hat{f} = (f_{0, 0} + f_{0, 1} + f_{1, 0} + f_{1, 1}, f_{0, 0} - f_{0, 1} + f_{1, 0} - f_{1, 1}, f_{0, 0} + f_{0, 1} - f_{1, 0} - f_{1, 1}, f_{0, 0} - f_{0, 1} - f_{1, 0} + f_{1, 1}) .

Osnovna svojstva Fourierove transformacije dana su u sljedećem teoremu.

Teorem 4.

$∙$	[(a)] Vrijedi tzv. formula inverzije: $f (x) = \frac{1}{\| A \|} \sum_{ξ \in A} \hat{f} (ξ) \bar{E (x, ξ)} za svaki x \in A .$ Njom se polazna funkcija $f : A \to ℂ$ može rekonstruirati iz svoje Fourierove transformacije. Posebno, Fourierova transformacija je injektivna, tj. $\hat{f} = \hat{g}$ implicira $f = g$ .
$∙$	[(b)] Vrijedi Plancherelov identitet: $\sum_{ξ \in A} \| \hat{f} (ξ) \|^{2} = \| A \| \sum_{x \in A} \| f (x) \|^{2}$ i općenitije: $\sum_{ξ \in A} \hat{f} (ξ) \bar{\hat{g} (ξ)} = \| A \| \sum_{x \in A} f (x) \bar{g (x)}$ za proizvoljne funkcije $f, g : A \to ℂ$ .
$∙$	[(c)] Ako je funkcija $h : A \to ℂ$ definirana kao tzv. konvolucija funkcija $f, g : A \to ℂ$ , $h (x) : = \sum_{\binom{y, z \in A}{y + z = x}} f (y) g (z) za svaki x \in A,$ što pišemo $h = f * g$ , tada vrijedi $\hat{h} (ξ) = \hat{f} (ξ) \hat{g} (ξ) za svaki ξ \in A .$ Drugim riječima, Fourierova transformacija prevodi konvoluciju u obični produkt.
$∙$	[(d)] Za funkciju $f : A \to ℂ$ te za $y, ζ \in A$ definiramo nove funkcije $T_{y} f, M_{ζ} f : A \to ℂ$ formulama $(T_{y} f) (x) : = f (x - y), (M_{ζ} f) (x) : = E (x, ζ) f (x) za svaki x \in A .$ Njihove Fourierove transformacije su dane sa $(\hat{T_{y} f}) (ξ) = E (y, ξ) \hat{f} (ξ), (\hat{M_{ζ} f}) (ξ) = \hat{f} (ξ + ζ) za svaki ξ \in A .$ Slova $T$ i $M$ dolaze od riječi translacije i modulacije.
$∙$	[(e)] Fourierova transformacija je linearna, tj. $\hat{α f + β g} = α \hat{f} + β \hat{g} .$

Proof. (a) Navedena formula je naprosto posljedica zamjene poretka u dvostrukoj sumaciji i svojstava od

E

iz propozicije 1:

\begin{matrix} \sum_{ξ \in A} \hat{f} (ξ) \bar{E (x, ξ)} & = \sum_{ξ \in A} \sum_{y \in A} f (y) E (y, ξ) \bar{E (x, ξ)} \\ = \sum_{y \in A} f (y) \sum_{ξ \in A} E (y - x, ξ) = | A | f (x) . \end{matrix}

(b) Slično kao i u prethodnom dijelu, zamjena redoslijeda sumiranja daje:

\begin{matrix} \sum_{ξ \in A} \hat{f} (ξ) \bar{\hat{g} (ξ)} & = \sum_{ξ \in A} \sum_{x, y \in A} f (x) \bar{g (y)} E (x, ξ) \bar{E (y, ξ)} \\ = \sum_{x, y \in A} f (x) \bar{g (y)} \sum_{ξ \in A} E (x - y, ξ) = | A | \sum_{x \in A} f (x) \bar{g (x)} . \end{matrix}

x

i rastavljanjem

E (x, ξ) = E (y, ξ) E (z, ξ)

dobivamo:

\begin{matrix} \hat{h} (ξ) & = \sum_{x \in A} (\sum_{\binom{y, z \in A}{y + z = x}} f (y) g (z)) E (x, ξ) = \sum_{y, z \in A} f (y) E (y, ξ) g (z) E (z, ξ) \\ = (\sum_{y \in A} f (y) E (y, ξ)) (\sum_{z \in A} g (z) E (z, ξ)) = \hat{f} (ξ) \hat{g} (ξ) . \end{matrix}

(d) Ovo su također direktne posljedice definicija i propozicije 1:

\begin{matrix} (\hat{T_{y} f}) (ξ) & = \sum_{x \in A} f (x - y) E (x, ξ) = \sum_{x \in A} f (x) E (x + y, ξ) \\ = \sum_{x \in A} f (x) E (x, ξ) E (y, ξ) = E (y, ξ) \hat{f} (ξ), \\ (\hat{M_{ζ} f}) (ξ) & = \sum_{x \in A} f (x) E (x, ζ) E (x, ξ) = \sum_{x \in A} f (x) E (x, ζ + ξ) = \hat{f} (ζ + ξ) . \end{matrix}

(e) Ovdje jedino treba rastaviti konačnu sumu na dijelove koji se tiču funkcija

f

g

redom:

\begin{matrix} (\hat{α f + β g}) (ξ) & = \sum_{x \in A} (α f (x) + β g (x)) E (x, ξ) \\ = α \sum_{x \in A} f (x) E (x, ξ) + β \sum_{x \in A} g (x) E (x, ξ) = α \hat{f} (ξ) + β \hat{g} (ξ) . \end{matrix}

2Primjene u algebri

Već i dosad navedeni koncepti dovoljni su za maštovite primjene na raznolike probleme. Započinjemo s nekoliko jednostavnijih primjera iz linearne algebre ili algebre polinoma.

Zadatak 5. Koliko se najviše može odabrati međusobno ortogonalnih vektora iz

ℝ^{1024}

čije su sve koordinate iz skupa

{- 1, 1}

Napomenimo da su vektori $u, v \in ℝ^{n}$ , $u = (u_{1}, \dots, u_{n})$ , $v = (v_{1}, \dots, v_{n})$ ortogonalni ili okomiti ako i samo ako je njihov skalarni produkt jednak $0$ , tj. vrijedi $u \cdot v = \sum_{j = 1}^{n} u_{j} v_{j} = 0$ . Za kompleksne vektore $u, v \in ℂ^{n}$ definicija ortogonalnosti ostaje ista, osim što skalarni produkt postaje $u \cdot v = \sum_{j = 1}^{n} u_{j} \bar{v_{j}}$ .

Rješenje.. U euklidskom prostoru

ℝ^{n}

može postojati najviše

n

u parovima ortogonalnih ne-nul vektora. Zato će u našem zadatku odgovor biti

1024

ako još pronađemo primjer koji ima točno

1024

vektora.

Promotrimo grupu

A = ℤ_{2}^{10} = \underset{10}{\underset{︸}{ℤ_{2} \oplus \dots \oplus ℤ_{2}}}

; ona očigledno ima

2^{10} = 1024

elemenata. Za svaki

x \in A

promotrimo vektor

(3)

u^{x} : = (E (x, ξ) : ξ \in A)

duljine

| A | = 1024

. Kako se u formuli za

E

sada pojavljuju samo drugi korijeni iz jedinice (tj. samo potencije od

- 1

), zaključujemo da sve koordinate tog vektora pripadaju skupu

{- 1, 1}

. Primjenom propozicije 1 odmah se vidi da su vektori

u^{x}

međusobno ortogonalni:

(4)

u^{x} \cdot u^{y} = \sum_{ξ \in A} E (x, ξ) \bar{E (y, ξ)} = \sum_{ξ \in A} E (x - y, ξ) = 0

ako je

x \neq y

Slika 1: Međusobno ortogonalni

\pm 1

vektori iz

ℝ^{8}

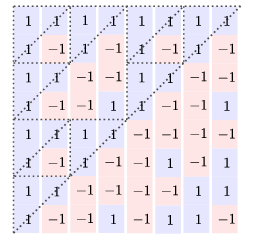
Pogledajte sliku 1 za analogni primjer u $2^{3}$ -dimenzionalnom euklidskom prostoru; vektori su ovdje zapisani kao stupci. Naziru se fraktalni uzorci, koji nisu slučajni, već su posljedica rekurzivnih relacija što ih zadovoljava preslikavanje $E$ za grupe $A = ℤ_{2}^{n}$ .

Zadatak 6. Neka je

v = (v_{0}, v_{1}, . . ., v_{m - 1}) \in ℂ^{m}

vektor kojeg možemo shvatiti kao funkciju na

ℤ_{m}

i pretpostavimo da vrijedi

\hat{v} (ξ) \neq 0

za svaki

ξ = 0, 1, \dots, m - 1

. Dokažite da je sistem cikličkih permutacija od

v

linearno nezavisan.

Pod cikličkim permutacijama od $v$ smatramo vektore

(v_{j}, v_{j + 1}, \dots, v_{m - 1}, v_{0}, v_{1}, \dots, v_{j - 1})

za $j = 0, 1, \dots, m - 1$ . Prisjetimo se i da je sistem vektora $w_{1}, w_{2}, \dots, w_{n}$ linearno nezavisan ako činjenica $\sum_{k = 1}^{n} α_{k} w_{k} = 0$ za neke skalare $α_{1}, α_{2}, \dots, α_{n}$ implicira da svi ti skalari moraju biti jednaki $0$ . Pritom $0$ označava nul-vektor u odgovarajućem vektorskom prostoru.

Rješenje.. Ovog puta radimo s kompleksnim funkcijama na grupi

A = ℤ_{m}

. Uočimo da je gornji ciklički permutirani vektor upravo

T_{- j} v

, pri čemu opet koristimo notaciju iz (d) dijela teorema 4. Prema tome, trebamo pokazati da su funkcije

T_{0} v

T_{1} v

, \ldots,

T_{m - 1} v

linearno nezavisne. Pretpostavimo da su

α_{0}, α_{1}, \dots, α_{m - 1} \in ℂ

skalari takvi da je

\sum_{j = 0}^{m - 1} α_{j} T_{j} v = 0

. Zbog linearnosti Fourierove transformacije i (d) dijela teorema 4, za svaki

ξ = 0, 1, \dots, m - 1

vrijedi

0 = \sum_{j = 0}^{m - 1} α_{j} (\hat{T_{j} v}) (ξ) = (\sum_{j = 0}^{m - 1} α_{j} E (j, ξ)) \hat{v} (ξ)

pa po pretpostavci mora biti

\sum_{j = 0}^{m - 1} α_{j} E (j, ξ) = 0, tj. \sum_{x \in A} α_{x} u^{x} = 0,

pri čemu su

u^{x} : A \to ℂ

u^{x} (ξ) : = E (x, ξ)

funkcije koje poistovjećujemo s vektorima danima formulom (3). Istim računom (4) kao u prethodnom zadatku provjeri se da su ti vektori u parovima ortogonalni. Zato su oni pogotovo i linearno nezavisni pa je

α_{0} = α_{1} = \dots = α_{m - 1} = 0

, čime je dokazana tražena tvrdnja.

Čitatelju ostavljamo dva zadatka za vježbu.

Zadatak 7. Promotrite sve matrice tipa

2^{n} \times 2^{n}

(gdje je

n

prirodan broj) s elementima iz skupa

{- 1, 1}

. Pronađite najveću moguću vrijednost determinante jedne od takvih matrica.

Uputa.. Potražite Hadamardovu nejednakost [5], koja će vam dati gornju ogradu za takve matrice

A

reda

N = 2^{n}

\det A ⩽ N^{N / 2} = 2^{n 2^{n - 1}} .

Sada konstruirajte primjer kada se postiže jednakost koristeći račun iz zadatka 5.
Analogni problem je uvelike otvoren za matrice reda

N

koji nije potencija broja

2

i zove se Hadamardov problem.

Zadatak 8. Faktorizirajte polinom

5

varijabli,

\begin{matrix} P (x_{0}, x_{1}, x_{2}, x_{3}, x_{4}) & = \sum_{j = 0}^{4} x_{j}^{5} + 5 \sum_{j = 0}^{4} x_{j - 1} x_{j} x_{j + 1} (x_{j - 1} x_{j + 1} - x_{j}^{2}) \\ + 5 \sum_{j = 0}^{4} x_{j - 2} x_{j} x_{j + 2} (x_{j - 2} x_{j + 2} - x_{j}^{2}) - 5 x_{0} x_{1} x_{2} x_{3} x_{4}, \end{matrix}

na faktore s koeficijentima iz prstena

ℤ [e^{2 π i / 5}] = {\sum_{j = 0}^{4} α_{j} e^{2 π i j / 5} : α_{0}, α_{1}, α_{2}, α_{3}, α_{4} \in ℤ} .

Napomenimo da se zbrajanje i oduzimanje indeksâ u formuli za $P$ shvaćaju modulo $5$ .

Uputa.. Označite kratko

ε = e^{2 π i / 5}

i shvatite vektor varijabli

x = (x_{0}, x_{1}, x_{2}, x_{3}, x_{4})

kao funkciju na

ℤ_{5}

. Korištenjem formule inverzije nakon duljeg računa dobiva se

P (x_{0}, x_{1}, x_{2}, x_{3}, x_{4}) = \prod_{j = 0}^{4} \hat{x} (j) = \prod_{j = 0}^{4} (x_{0} + ε^{j} x_{1} + ε^{2 j} x_{2} + ε^{3 j} x_{3} + ε^{4 j} x_{4}) .

3Primjene u geometriji

U ovom odjeljku bavimo se primjenama u planimetriji, tj. geometriji ravnine. Autor sljedećeg zadatka je M. Roseman, a dolje opisano elegantno rješenje korištenjem Fourierove analize predložio je I. J. Schoenberg [8].

Zadatak 9. Neka je

n \in ℕ

n ⩾ 3

. Definiramo niz

n

-terokuta

(M^{k})_{k = 0}^{\infty}

M^{k} = A_{0}^{k} A_{1}^{k} \dots A_{n - 1}^{k},

u ravnini na sljedeći način. Neka je

M^{0}

proizvoljan. Za

k ⩾ 1

vrhovi

A_{0}^{k}, A_{1}^{k}, \dots, A_{n - 2}^{k}, A_{n - 1}^{k}

mnogokuta

M^{k}

rekurzivno su definirani kao polovišta stranica

\bar{A_{0}^{k - 1} A_{1}^{k - 1}}, \bar{A_{1}^{k - 1} A_{2}^{k - 1}}, \dots, \bar{A_{n - 2}^{k - 1} A_{n - 1}^{k - 1}}, \bar{A_{n - 1}^{k - 1} A_{0}^{k - 1}}

mnogokuta

M^{k - 1}

. Dokažite da se mnogokuti

(M^{k})_{k = 0}^{\infty}

“stišču” prema točki, tj. preciznije, da vrijedi

\lim_{k \to \infty} A_{j}^{k} = T

j = 0, 1, \dots, n - 1

, pri čemu je

T

težište od

M^{0}

Slika 2: Niz peterokuta koji se stišče prema zajedničkom težištu.

Rješenje.. Pogledajte sliku 2 za ilustraciju nekoliko iteracija u slučaju

n = 5

.

Uvedimo kompleksni koordinatni sustav u ravnini s ishodištem u točki

T

i neka je

z_{j}^{(k)} \in ℂ

koordinata točke

A_{j}^{k}

. Shvatimo vektor

f_{k} = (z_{0}^{(k)}, z_{1}^{(k)}, \dots, z_{n - 2}^{(k)}, z_{n - 1}^{(k)})

kao kompleksnu funkciju na grupi

A = ℤ_{n}

. Rekurzivnu relaciju možemo zapisati

z_{j}^{(k)} = \frac{1}{2} z_{j}^{(k - 1)} + \frac{1}{2} z_{j + 1}^{(k - 1)} za j = 0, 1, \dots, n - 1,

pri čemu indekse zbrajamo modulo

n

, što se još kompaktnije zapisuje

f_{k} = \frac{1}{2} f_{k - 1} + \frac{1}{2} T_{- 1} f_{k - 1},

uz notaciju iz (d) dijela teorema 4. Korištenjem tog istog teorema dobivamo relaciju između Fourierovih transformacija:

\begin{matrix} \hat{f}_{k} (ξ) & = \frac{1}{2} \hat{f}_{k - 1} (ξ) + \frac{1}{2} E (- 1, ξ) \hat{f}_{k - 1} (ξ) = \frac{1}{2} (1 + e^{- 2 π i ξ / n}) \hat{f}_{k - 1} (ξ) \\ = e^{- π i ξ / n} \frac{1}{2} (e^{π i ξ / n} + e^{- π i ξ / n}) \hat{f}_{k - 1} (ξ) = e^{- π i ξ / n} \cos \frac{π ξ}{n} \hat{f}_{k - 1} (ξ), \end{matrix}

odakle je

| \hat{f}_{k} (ξ) | = | \cos \frac{π ξ}{n} | | \hat{f}_{k - 1} (ξ) |

pa iteriranjem dobivamo

(5)

| \hat{f}_{k} (ξ) | = | \cos \frac{π ξ}{n} |^{k} | \hat{f}_{0} (ξ) | .

Po konstrukciji je

\hat{f}_{0} (0) = z_{0}^{(0)} + z_{1}^{(0)} + \dots + z_{n - 2}^{(0)} + z_{n - 1}^{(0)} = 0

pa prema (5) slijedi

\hat{f}_{k} (0) = 0

za svaki

k ⩾ 0

. S druge strane, za

ξ = 1, 2, \dots, n - 1

imamo

| \cos \frac{π ξ}{n} | < 1

te radi (5) postoji limes

\lim_{k \to \infty} | \hat{f}_{k} (ξ) |

i iznosi

0

. Konačno, Plancherelov identitet iz teorema 4 daje

\lim_{k \to \infty} \sum_{j \in ℤ_{n}} | z_{j}^{(k)} |^{2} = \frac{1}{n} \lim_{k \to \infty} \sum_{ξ \in ℤ_{n}} | \hat{f}_{k} (ξ) |^{2} = 0,

što znači

\lim_{k \to \infty} z_{j}^{(k)} = 0

j = 0, 1, \dots, n - 1

Zadatak kojeg ostavljamo za vježbu čitatelju prilično je težak pa dajemo i detaljnu uputu. Kao problem ga je postavio A. Björner, a riješili su ga D. Svrtan, D. Šterc i I. Urbiha u članku [9], odakle je zadatak i preuzet.

Zadatak 10. Neka su

z_{0}, z_{1}, z_{2}, z_{3}, z_{4}

kompleksni brojevi za koje vrijedi

$∙$	[(i)] $\| z_{0} \| = \| z_{1} \| = \| z_{2} \| = \| z_{3} \| = \| z_{4} \| = 1$ ,
$∙$	[(ii)] $z_{0} + z_{1} + z_{2} + z_{3} + z_{4} = 0$ ,
$∙$	[(iii)] $z_{0} z_{1} + z_{1} z_{2} + z_{2} z_{3} + z_{3} z_{4} + z_{4} z_{0} = 0$ .

Dokažite da oni leže u vrhovima pravilnog peterokuta.

Uputa.. Petorku kompleksnih brojeva

(z_{0}, z_{1}, z_{2}, z_{3}, z_{4})

shvatite kao funkciju

f

na grupi

ℤ_{5}

i neka je njena Fourierova transformacija

\hat{f} = (w_{0}, w_{1}, w_{2}, w_{3}, w_{4})

. Iz drugog uvjeta zaključite

w_{0} = \hat{f} (0) = 0

te potom iz prvog uvjeta i svojstava Fourierove transformacije izvedite

w_{2} \bar{w_{1}} + w_{3} \bar{w_{2}} + w_{4} \bar{w_{3}} = 0, w_{3} \bar{w_{1}} + w_{4} \bar{w_{2}} + w_{1} \bar{w_{4}} = 0 .

Treći uvjet u zadatku se pak primjenom formule inverzije i

w_{0} = 0

transformira u

w_{1} w_{4} \cos \frac{2 π}{5} + w_{2} w_{3} \cos \ t e x t s t y l e \frac{4 π}{5} = 0, tj. (\sqrt{5} - 1) w_{1} w_{4} = (\sqrt{5} + 1) w_{2} w_{3} .

Iz dobivenih jednakosti lako slijedi

| w_{2} | ((\sqrt{5} - 1) | w_{1} |^{2} + (\sqrt{5} + 1) | w_{3} |^{2}) = (\sqrt{5} - 1) | w_{1} | | w_{2} | | w_{3} | .

Diskutiranjem slučajeva zaključite da je najviše jedan od brojeva

w_{1}, w_{2}, w_{3}, w_{4}

različit od

0

. Preostat će iskoristiti formulu inverzije.

4Primjene u teoriji brojeva

Autor sljedećeg rezultata je J. Bourgain [1], a njegov dokaz je preuzet iz knjige [11].

Zadatak 11. Neka je

p

prost broj i

S \subseteq {1, 2, 3, \dots, p - 1}

skup takav da je

| S | > p^{3 / 4}

. Dokažite da za svaki cijeli broj

m

postoje

a_{1}, a_{2}, b_{1}, b_{2}, c_{1}, c_{2} \in S

takvi da vrijedi

m \equiv a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} (mod \(p\)) .

Rješenje.. Koristeći operacije modulo

p

vidimo da zapravo treba svaki

x \in ℤ_{p}

prikazati kao

x = a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2}

za neke

a_{1}, a_{2}, b_{1}, b_{2}, c_{1}, c_{2} \in S \subseteq ℤ_{p}

. Zbog činjenice da je

p

prost, za svake

s, y \in ℤ_{p}

s \neq 0

jednadžba

s x = y

ima jedinstveno rješenje

x \in ℤ_{p}

. Drugim riječima, za svaki

s \in ℤ_{p} ∖ {0}

funkcija

ℤ_{p} \to ℤ_{p}

x \mapsto s x

je bijekcija. Tu ćemo tvrdnju višestruko koristiti kod zamjene indeksa sumacije.

Promotrimo funkciju

f : ℤ_{p} \to ℂ

f : = \sum_{s \in S} χ_{s \cdot S}

, gdje

χ_{T}

označava karakterističnu funkciju skupa

T

te pišemo

s \cdot S = {s x : x \in S}

. Najprije primijetimo da je

\begin{matrix} (f * f * f) (x) & = \sum_{\binom{a, b, c \in ℤ_{p}}{a + b + c = x}} f (a) f (b) f (c) = \sum_{\binom{\binom{a_{1}, b_{1}, c_{1} \in S}{a, b, c \in ℤ_{p}}}{a + b + c = x}} χ_{a_{1} \cdot S} (a) χ_{b_{1} \cdot S} (b) χ_{c_{1} \cdot S} (c) \\ = [\begin{matrix} a = a_{1} a_{2} \\ b = b_{1} b_{2} \\ c = c_{1} c_{2} \end{matrix}] = \sum_{\binom{\binom{a_{1}, b_{1}, c_{1} \in S}{a_{2}, b_{2}, c_{2} \in S}}{a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = x}} 1 = broj traženih prikaza od x \end{matrix}

pa zapravo trebamo dokazati da je

(f * f * f) (x) > 0

za svaki

x \in ℤ_{p}

.

Fourierova transformacija od

f

\hat{f} (ξ) = \sum_{s \in S} \sum_{x \in ℤ_{p}} χ_{s \cdot S} (x) e^{2 π i x ξ / p} = [x = s y] = \sum_{s \in S} \sum_{y \in S} e^{2 π i s y ξ / p} = \sum_{s \in S} \hat{χ}_{S} (s ξ) .

Imamo

\hat{f} (0) = | S | \hat{χ}_{S} (0) = | S |^{2}

. Za

ξ \neq 0

su elementi

s ξ

svi međusobno različiti kako

s

varira pa aritmetičko-kvadratna nejednakost i Plancherelov identitet daju

\begin{matrix} | \hat{f} (ξ) | & ⩽ | S |^{1 / 2} (\sum_{s \in S} | \hat{χ}_{S} (s ξ) |^{2})^{1 / 2} ⩽ | S |^{1 / 2} (\sum_{ξ \in ℤ_{p}} | \hat{χ}_{S} (ξ) |^{2})^{1 / 2} \\ = | S |^{1 / 2} (p \sum_{x \in ℤ_{p}} | χ_{S} (x) |^{2})^{1 / 2} = | S |^{1 / 2} p^{1 / 2} | S |^{1 / 2} = p^{1 / 2} | S | . \end{matrix}

Zbog nejednakosti Minkowskog (tj. nejednakosti trokuta u euklidskom prostoru

ℂ^{ℤ_{p}} ≅ ℂ^{p} ≅ ℝ^{2 p}

) imamo

\begin{matrix} (\sum_{ξ \in ℤ_{p}} | \hat{f} (ξ) |^{2})^{1 / 2} ⩽ \sum_{s \in S} (\sum_{ξ \in ℤ_{p}} | \hat{χ}_{s \cdot S} (ξ) |^{2})^{1 / 2} \\ = \sum_{s \in S} p^{1 / 2} (\sum_{x \in ℤ_{p}} | χ_{s \cdot S} (x) |^{2})^{1 / 2} = | S | p^{1 / 2} | S |^{1 / 2} = p^{1 / 2} | S |^{3 / 2} . \end{matrix}

Posljednje dvije ocjene se mogu kombinirati u

(6)

\sum_{ξ \in ℤ_{p} ∖ {0}} | \hat{f} (ξ) |^{3} ⩽ p^{1 / 2} | S | \sum_{ξ \in ℤ_{p} ∖ {0}} | \hat{f} (ξ) |^{2} ⩽ p^{1 / 2} | S | (p^{1 / 2} | S |^{3 / 2})^{2} = p^{3 / 2} | S |^{4} .

Konačno, zbog (c) dijela teorema 4 imamo

(\hat{f * f * f}) (ξ) = \hat{f} (ξ)^{3}

pa formula inverzije i (6) daju {\allowdisplaybreaks

\begin{matrix} (f * f * f) (x) & = p^{- 1} \sum_{ξ \in ℤ_{p}} \hat{f} (ξ)^{3} e^{- 2 π i x ξ / p} ⩾ p^{- 1} \hat{f} (0)^{3} - p^{- 1} \sum_{ξ \in ℤ_{p} ∖ {0}} | \hat{f} (ξ) |^{3} \\ ⩾ p^{- 1} | S |^{6} - p^{1 / 2} | S |^{4} = p^{- 1} | S |^{4} (| S |^{2} - p^{3 / 2}) . \end{matrix}

} Preostaje iskoristiti pretpostavku zadatka

| S | > p^{3 / 4}

, tj.

| S |^{2} - p^{3 / 2} > 0

Postoje i složenije primjene Fourierove analize na konačnim grupama u teoriji brojeva. Zainteresirani čitatelj može pogledati dokaz tzv. Gaussovog zakona kvadratnog reciprociteta izložen u knjizi [2].

5Primjene u kombinatorici

Fourierova analiza svoje najzanimljivije primjene nalazi u kombinatorici i to posebno u području tzv. aditivne kombinatorike, koja se bavi kombinatornim aspektima operacije zbrajanja. O tome svjedoči cijelo jedno poglavlje opsežne knjige [11]. Kako bismo mogli riješiti neke zahtjevnije zadatke, trebamo naučiti još jedan rezultat, koji se popularno naziva princip neodređenosti, po uzoru na formalno slične rezultate iz kvantne mehanike.

Za funkciju $f : A \to ℂ$ na konačnoj komutativnoj grupi $A$ označimo

supp (f) : = {x \in A : f (x) \neq 0},

a promatrat ćemo i

supp (\hat{f}) = {ξ \in A : \hat{f} (ξ) \neq 0} .

Kratica “supp” dolazi od engleske riječi support, koja se na hrvatski prevodi kao nosač funkcije.

Teorem 12. [Princip neodređenosti]

$∙$	[(a)] Neka je $A$ grupa dana s (1). Za svaku funkciju $f : A \to ℂ$ koja nije identički jednaka konstanti $0$ vrijedi $\| supp (f) \| \| supp (\hat{f}) \| ⩾ \| A \| .$
$∙$	[(b)] Za svaku funkciju $f : ℤ_{p} \to ℂ$ , gdje je $p$ prost broj, koja nije identički jednaka konstanti $0$ vrijedi $\| supp (f) \| + \| supp (\hat{f}) \| ⩾ p + 1 .$ Obratno, za svaka dva skupa $A, B \subseteq ℤ_{p}$ koji zadovoljavaju $\| A \| + \| B \| ⩾ p + 1$ postoji funkcija $f : ℤ_{p} \to ℂ$ takva da je $supp (f) = A$ i $supp (\hat{f}) = B$ .

Proof. Dokažimo samo (a) dio teorema. Korištenjem nejednakosti trokuta, aritmetičko-kvadratne nejednakosti i Plancherelovog identiteta redom dobivamo {\allowdisplaybreaks

\begin{matrix} \max_{ξ \in A} | \hat{f} (ξ) | & = \max_{ξ \in A} | \sum_{x \in A} f (x) E (x, ξ) | ⩽ \sum_{x \in A} | f (x) | = \sum_{x \in supp (f)} | f (x) | \\ ⩽ | supp (f) |^{1 / 2} (\sum_{x \in supp (f)} | f (x) |^{2})^{1 / 2} = | supp (f) |^{1 / 2} (| A |^{- 1} \sum_{ξ \in A} | \hat{f} (ξ) |^{2})^{1 / 2} \\ = | A |^{- 1 / 2} | supp (f) |^{1 / 2} (\sum_{ξ \in supp (\hat{f})} | \hat{f} (ξ) |^{2})^{1 / 2} \\ ⩽ | A |^{- 1 / 2} | supp (f) |^{1 / 2} | supp (\hat{f}) |^{1 / 2} \max_{ξ \in A} | \hat{f} (ξ) | . \end{matrix}

} Ako

f

nije identički jednaka

0

, tada ni

\hat{f}

nije identički jednaka

0

pa je

\max_{ξ \in A} | \hat{f} (ξ) | > 0

. Dijeljenjem s tim faktorom dobivamo traženu nejednakost.

Dio (b) je mnogo složeniji i zasniva se na teoremu Čebotareva o korijenima iz jedinice, koji govori da za

1 ⩽ m ⩽ p

, za različite

x_{1}, \dots, x_{m} \in ℤ_{p}

i za različite

ξ_{1}, \dots, ξ_{m} \in ℤ_{p}

vrijedi

\det [e^{2 π i x_{j} ξ_{k} / p}]_{\binom{j = 1, \dots, m}{k = 1, \dots, m}} \neq 0 .

Jedan elementaran (ali još uvijek prilično tehnički) dokaz dao je T. Tao [10].

Dio (a) teorema 12 daje ocjenu za proizvoljnu konačnu komutativnu grupu $A$ , dok njegov (b) dio govori o pojačanju te ocjene u slučaju grupe $ℤ_{p}$ . R. Meshulam je u članku [6] dao analogno pojačanje i za općenitu grupu $A$ , koje ovdje nećemo diskutirati.

Zadatak 13. Neka je

n

prirodan broj. Označimo s

℘_{n}

familiju svih

2^{n}

podskupova skupa

{1, 2, \dots, n}

. Za svaki

S \in ℘_{n}

dan je realni broj

a_{S}

i pretpostavimo da je točno

k ⩾ 1

od tih brojeva

a_{S}

različito od

0

. Dokažite da jednadžba

\sum_{S \in ℘_{n}} a_{S} \prod_{j \in S} x_{j} = 0

ima najviše

2^{n} (1 - 1 / k)

rješenja u skupu

{- 1, 1}^{n}

, tj. ima najviše toliko

n

-torki

(x_{1}, x_{2}, \dots, x_{n})

koje zadovoljavaju jednadžbu i za svaki indeks

j

je ili

x_{j} = - 1

ili

x_{j} = 1

Napomenimo da za $S = \emptyset$ produkt $\prod_{j \in S} x_{j}$ uvijek interpretiramo kao broj $1$ . Naprimjer, za $n = 2$ jednadžba glasi

a_{\emptyset} + a_{{1}} x_{1} + a_{{2}} x_{2} + a_{{1, 2}} x_{1} x_{2} = 0 .

Rješenje.. Promotrimo grupu

A = ℤ_{2}^{n} = \underset{n}{\underset{︸}{ℤ_{2} \oplus \dots \oplus ℤ_{2}}} = {0, 1}^{n}

i uspostavimo bijektivnu korespondenciju

℘_{n} \to A, S \mapsto karakteristična funkcija skupa S

s inverzom

A \to ℘_{n}, (z_{1}, \dots, z_{n}) \mapsto {j \in {1, 2, \dots, n} : z_{j} = 1} .

Dakle, skupu

S \in ℘_{n}

odgovara

n

-torka

z = (z_{1}, \dots, z_{n})

takva da je

z_{j} = 1

j \in S

z_{j} = 0

j \in S^{c}

. Tada umjesto

a_{S}

pišemo

a_{z}

.

Definiramo funkciju

f : A \to ℂ

f (y_{1}, \dots, y_{n}) : = \sum_{S \in ℘_{n}} a_{S} \prod_{j \in S} (- 1)^{y_{j}} = \sum_{z = (z_{1}, \dots, z_{n}) \in A} a_{z} \prod_{j = 1}^{n} (- 1)^{y_{j} z_{j}},

tj.

f (y) : = \sum_{z \in A} a_{z} E (y, z) .

Primijetimo da zapravo želimo pobrojati rješenja

(y_{1}, \dots, y_{n}) \in A

jednadžbe

f (y_{1}, \dots, y_{n}) = 0

, jer su ona putem

x_{j} = (- 1)^{y_{j}}

u korespondenciji s rješenjima

(x_{1}, \dots, x_{n}) \in {- 1, 1}^{n}

polazne jednadžbe. Trebamo dokazati da je

| supp (f) | ⩾ 2^{n} / k

, jer će tada broj rješenja biti najviše

2^{n} - 2^{n} / k

.

Zbog

E (y, z) \in {- 1, 1} \subset ℝ

i propozicije 1 imamo

\hat{f} (ξ) = \sum_{y \in A} (\sum_{z \in A} a_{z} \bar{E (y, z)}) E (y, ξ) = \sum_{z \in A} a_{z} \sum_{y \in A} E (y, ξ - z) = 2^{n} a_{ξ} .

Po pretpostavci zadatka je

| supp (\hat{f}) | = k

. Zato (a) dio teorema 12 primijenjen na grupu

A

daje

| supp (f) | ⩾ \frac{| A |}{| supp (\hat{f}) |} = \frac{2^{n}}{k} .

Naredni rezultat zove se Cauchy-Davenportov teorem. Elegantni dokaz koji slijedi osmislio je R. Chapman, a mi ga preuzimamo iz članka [10].

Zadatak 14. Ako je

p

prost broj i ako su

A, B \subseteq ℤ_{p}

neprazni, dokažite da tada vrijedi

| A + B | ⩾ \min {| A | + | B | - 1, p},

pri čemu označavamo

A + B : = {a + b : a \in A, b \in B} .

Rješenje.. Najprije tvrdimo da možemo naći skupove

X, Y \subseteq ℤ_{p}

takve da je

| X | = p + 1 - | A |, | Y | = p + 1 - | B |, | X \cap Y | = \max {p + 2 - | A | - | B |, 1} .

Razlikujemo dva slučaja. Ako je

| A | + | B | ⩽ p + 1

, tada možemo uzeti

X = {0, 1, \dots, p - | A |}, Y = {| B | - 1, | B |, \dots, p - 1} .

Ako je pak

| A | + | B | ⩾ p + 2

, tada možemo uzeti

X = {0, 1, \dots, p - | A |}, Y = {p - | A |, p - | A | + 1, \dots, 2 p - | A | - | B |} .

Prema (b) dijelu principa neodređenosti postoje funkcije

f, g : ℤ_{p} \to ℂ

takve da je

supp (f) = A, supp (\hat{f}) = X, supp (g) = B, supp (\hat{g}) = Y .

Promotrimo funkciju

f * g

. Iz definicije konvolucije odmah se vidi

supp (f * g) \subseteq supp (f) + supp (g) = A + B,

dok iz svojstva

(\hat{f * g}) (ξ) = \hat{f} (ξ) \hat{g} (ξ)

slijedi

supp (\hat{f * g}) = supp (\hat{f}) \cap supp (\hat{g}) = X \cap Y .

Konačno, ponovnim korištenjem (b) dijela teorema 12 dobivamo

| A + B | + | X \cap Y | ⩾ | supp (f * g) | + | supp (\hat{f * g}) | ⩾ p + 1,

što je upravo

| A + B | ⩾ p + 1 - \max {p + 2 - | A | - | B |, 1} = \min {| A | + | B | - 1, p} .

Za vježbu ostavljamo još jedan zadatak iz članka [10].

Zadatak 15. Neka je

p

prost broj i neka je

S : = {z \in ℂ : z^{p} = 1}

skup

p

-tih korijena iz jedinice. Nadalje, neka su

c_{0}, c_{1}, c_{2}, \dots, c_{p - 1} \in ℂ

, među kojima je točno

k ⩾ 1

brojeva različito od

0

. Dokažite da je moguće odabrati podskup

T \subseteq S

koji ima

| T | = p - k + 1

elemenata i takav je da za svaki

z \in T

vrijedi

\sum_{j = 0}^{p - 1} c_{j} z^{j} \neq 0

Uputa.. Promotrite funkciju

f : ℤ_{p} \to ℂ, f (x) : = \sum_{j = 0}^{p - 1} c_{j} e^{- 2 π i j x / p},

tako da treba pokazati

| supp (f) | ⩾ p - k + 1

. Primijetite da je

\hat{f} (ξ) = p c_{ξ}

| supp (\hat{f}) | = k

pa se pozovite na (b) dio teorema 12.

U ovom radu odlučili smo promatrati samo konačne komutativne grupe. Naravno da se bogatija teorija dobiva razmatrajući općenitije komutativne grupe i njih proučava tzv. harmonijska analiza, čije osnove zainteresirani čitatelj može naučiti iz knjige [3] ili diplomskog rada [7]. Nekomutativnim grupama bavi se teorija reprezentacija i opet je najelementarnije krenuti od konačnih grupa, kao npr. u knjizi [4]. {10}

Bibliografija

[1]	J. Bourgain, Mordell's exponential sum estimate revisited, J. Amer. Math. Soc. 18 (2005), 477–499.
[2]	H. Dym, H. P. McKean, Fourier Series and Integrals, Probability and Mathematical Statistics 14, Academic Press, New York-London, 1972.
[3]	G. B. Folland, A Course in Abstract Harmonic Analysis, drugo izdanje, Textbooks in Mathematics, CRC Press, Boca Raton, 2016.
[4]	W. Fulton, J. Harris, Representation Theory: A First Course, Graduate Texts in Mathematics 129, Springer-Verlag, New York, 1991.
[5]	S. Kurepa, Konačno dimenzionalni vektorski prostori i primjene, Tehnička knjiga, Zagreb, 1967.
[6]	R. Meshulam, An uncertainty inequality for finite abelian groups, European J. Combin. 27 (2006), 63–67.
[7]	Lj. Palle, Fourierova analiza na lokalno kompaktnim, Abelovim grupama i neke primjene, diplomski rad, Sveučilište u Zagrebu, 2015.
[8]	I. J. Schoenberg, The finite Fourier series and elementary geometry, Amer. Math. Monthly 57 (1950), 390–404.
[9]	D. Svrtan, D. Šterc, I. Urbiha, On cyclic characterizations of regular pentagons and heptagons: two approaches, Math. Commun. 7 (2002), 71–89.
[10]	T. Tao, An uncertainty principle for cyclic groups of prime order, Math. Res. Lett. 12 (2005), 121–127.
[11]	T. Tao, V. Vu, Additive Combinatorics, Cambridge Studies in Advanced Mathematics 105, Cambridge University Press, Cambridge, 2006.

1Osnove za gradivo ovog članka čine izlaganja prvog autora na pripremama za Međunarodnu matematičku olimpijadu i kolegiju Studentska natjecanja iz matematike na Matematičkom odsjeku PMF-a te diplomski rad drugog autora [7].

2Matematički odsjek, Prirodoslovno-matematički fakultet, Sveučilište u Zagrebu, Bijenička cesta 30, 10000 Zagreb, vjekovac@math.hr

3Matematički odsjek, Prirodoslovno-matematički fakultet, Sveučilište u Zagrebu, Bijenička cesta 30, 10000 Zagreb, ljpalle@math.hr

math.e

Secondary links

Novi brojevi časopisa math.e

Kalendar

Prosinac

Matematički blogovi

Sponzori

Primjene Fourierove analize na konačnim komutativnim grupama