Landauova igra
Sažetak
U ovom radu dan je pregled pravila Landauove igre s automobilskim tablicama, kao i postojećih općih rješenja. Predstavljeno je jedno moguće novo rješenje, kao i računalna verzija ove igre. Također je upozoreno na vezu Landauove igre s jednim zadatkom s natjecanja. Natjecatelji su se možda već susreli sa sljedećim problemom:
Zadatak 1 (USAMO 1995/2, [1] ) Na pokvarenom džepnom kalkulatoru funkcioniraju samo tipke koje odgovaraju sinusu, kosinusu, tangensu i njima inverznim operacijama. Na zaslonu kalkulatora u početnom se trenutku nalazi 0. Pokazati da se pritiskom na tipke kalkulatora konačan broj puta može dobiti bilo koji pozitivan racionalan broj (Argumenti funkcija su u radijanima, pretpostavka je da kalkulator računa s beskonačnom preciznošću).
S rješenjem zadatka ćemo pričekati - slijedi uvod u Landauovu igru.

Slika 1: Lav Davidovič Landau
1Uvod
Slavni ruski nobelovac Lav Davidovič Landau ostao je upamćen po svom doprinosu znanosti, seriji ispita poznatoj kao „Teorijski minumum”, ali i po anegdotama iz života. Boris S. Gorobec tako u
Naime, u to vrijeme automobilske su tablice u Sovjetskom Savezu imale formu ab-cd, gdje su a,b,c,d cifre od 0 do 9. Zadatak u Landauovoj igri bio je jednostavan - primjenom elementarnih matematičkih funkcija poznatih svakom srednjoškolcu nad znamenkama s obje strane crtice na tablicama postići jednakost između lijeve i desne polovine (bez dodavanja novih znamenki!). U primjeru sa slike, jedno moguće rješenje bi bilo 0+0=3!-6, a drugo 0!+0=3!/6.

Slika 2: Registracijske tablice u Sovjetskom savezu
Istina, vremenom se mijenjao skup dopuštenih matematičkih funkcija i operacija nad znamenkama, kako se mijenjao plan i program u srednjim školama - na tu temu ćemo se vratiti malo poslije.
2Opća rješenja
Prirodno pitanje koje se nameće nakon upoznavanja s ovom igrom je sljedeće: je li moguće uspješno riješiti svaku kombinaciju znamenki? Kada je M. I. Kaganov postavio to pitanje Lavu Landauu (vidjeti
Budući da je \operatorname{tg}^{2}x+1=\frac{\sin^{2}x+\cos^{2}x}{\cos^{2}x}=\frac{1}{\cos^{2}x}=\sec^{2}x, možemo načiniti funkciju f(n)=n+1 koristeći se izvedenim identitetom: f(n)=n+1=\sec^{2}\operatorname{arctg}\sqrt{n}. Jedino što nam smeta da ovakvu funkciju primijenimo u igri Landaua jest kvadrat sekansa, pa obje strane korjenujemo i dobivamo konačno
\sqrt{n+1}=\sec\operatorname{arctg}\sqrt{n}.
Primjenom ove formule više puta jednostavno manji od dva dvoznamenkasta broja na tablicama pretvorimo u onaj veći, čime je Landauova igra riješena. Upozorimo na vezu između Zadatka 1 i dobivenog općeg rješenja, koja će biti jasnija ako malo preuredimo formulu i dobijemo
\cos\operatorname{arctg}\sqrt{n-1}=\sqrt{\frac{1}{n}}
odnosno
\cos\operatorname{arctg}\sqrt{n}=\sqrt{\frac{1}{n+1}}
Primijetimo li zatim da je \cos\operatorname{arctg} x=\sin\operatorname{arctg}(1/x) dobivamo formulu \operatorname{tg}\arcsin\cos\operatorname{arctg}\sqrt{1/n}=\sqrt{n}, pa smo ostvarili mogućnost da od broja \sqrt{n-1} dobijemo broj \sqrt{n} u konačno mnogo koraka korištenjem samo šest dostupnih tipki na kalkulatoru. Zamijenimo li n racionalnim brojem a/b, gdje su a i b uzajamno prosti nenegativni brojevi i b\gt 0, tada imamo mogućnost da od broja \sqrt{(a-b)/b} dobijemo broj \sqrt{a/b}. Pokažimo da ta činjenica implicira mogućnost dobivanja bilo kojeg broja oblika \sqrt{a/b} od polaznog stanja na zaslonu, tj. od 0. Dokaz se izvodi jakom indukcijom po b:
| (1) | Slučaj b=1 odgovara već prikazanom (tj a/b=n). | ||||
| (2) | Pretpostavimo da je moguće ovim postupkom dobiti sve brojeve \sqrt{c/d} (za prirodne c i d) kod kojih je d\lt b. Pokažimo da se tada i \sqrt{a/b} može dobiti ovim postupkom.
|
Kako Gorobec primjećuje, funkcija sekans više nije u redovnom planu i programu srednjih škola u Rusiji, pa je upitna validnost ovakvog rješenja po strogim pravilima Landauove igre. U
Opće rješenje koje je ponudio S. N. Fedin prati ideju prvog općeg rješenja kroz ekvivalentnu formulu
\sqrt{n+1}=\operatorname{tg}\operatorname{arcctg}\cos\operatorname{arctg}\sqrt{n}
koja u obzir uzima činjenicu da je \operatorname{tg}\operatorname{arcctg}\ x=\frac{1}{x}, čime se izbjegava korištenje sekansa.
Treće opće rješenje je dao Gorobec i ono se zasniva na činjenici da je 6!=720=2\cdot360, jer na temelju te vrijednosti znamo da je \sin\ n!^{\circ}=0 za n\gt 5. Ako s obje strane crtice imamo dvoznamenkaste brojeve čija prva znamenka nije nula, na ovaj način lako dobivamo nulu s obje strane, a ako je prva znamenka nekog od brojeva nula, trivijalno - množenjem - dobijamo nulu i jednakost 0=0.
Čemu služe ova opća rješenja, zar ne ubijaju čar igre? Objektivno govoreći, traženje općeg rješenja ima svoj poseban čar, baš kao i traženje neobičnih rješenja za teške primjere tablica. Time igra dobiva dvostruki smisao. Naravno, postoje i trivijalna opća rješenja - ako bismo se koristili funkcijama [x] i \lbrace x\rbrace (cijeli i razlomljeni dio broja, redom) vrlo lako bismo mogli doći do trivijalnih jednakosti 0=0. Diferenciranje obiju strana jednakosti također bi učinilo igru trivijalnom, kao i korištenje nekih neelementarnih funkcija.
3Novo opće rješenje
U ovom članku predstaviti će se (koliko je nama poznato) novo, dosad neobjavljeno opće rješenje Landauove igre, zasnovano na binarnom logaritmu, \mathop{\text{lb}}x.
Riječ je jednostavno o logaritmu po bazi 2, tj \mathop{\text{lb}}x=\log_{2}x. Baš kao logaritmi po bazama e i 10 čije je široko područje primjene uvjetovalo pojavu posebnih oznaka za ove logaritme, \ln i \lg, redom, tako je i binarni logaritam, nezamjenjiv u teorijskom računarstvu i teoriji informacija, zaslužio zasebnu oznaku. Istina, svijet se još nije usuglasio koja bi to oznaka bila: na Zapadu se često koristi oznaka \lg za ovaj logaritam, što izaziva zabunu zbog činjenice da se u ruskoj i njemačkoj literaturi oznaka \lg koristi za dekadski logaritam. ISO standard propisuje oznaku \text{lb} za binarni i \lg za dekadski logaritam, čega se u ovom članku i mi držimo.
Rješenje se zasniva na sljedećem lancu jednakosti: \mathop{\text{lb}}4=2, \mathop{\text{lb}}2=1, \mathop{\text{lb}}1=0 (naravno, binarni logaritam je nuždan samo za prelazak iz 2 u 1, ostala dva prijelaza mogu se izvesti i drugačije, onaj iz 4 u 2 korjenovanjem, a onaj iz 1 u 0 logaritmiranjem po bilo kojoj drugoj bazi). Prema ovom lancu zaključujemo da se svaki par znamenki u kojem je bar jedna znamenka iz skupa \lbrace 0,1,2,4\rbrace ili čija je razlika/zbroj iz tog skupa može svesti na nulu primjenom binarnog logaritma, što vodi ka jednakosti 0=0. Što je s ostalim parovima? Brzi račun pokazuje nam da su jedini preostali parovi znamenaka (poredak nije bitan) 36, 38, 39, 58, 69. Budući da je 3!-6=0, 3-\mathop{\text{lb}}8=0, 3-\sqrt{9}=0, 5-\mathop{\text{lb}}8=2, 6-(\sqrt{9})!=0, i ovi se preostali slučajevi svode na već riješene, čime kompletiramo rješenje.
4Računalna realizacija
U igri nazvanoj Dau, prema nadimku koji je Lav Davidovič nosio, korisnik ima priliku isprobati svoje vještine brzog kombiniranja na nasumice izabranim tablicama putem sučelja kao na slici 3. Moguće je igrati sam, ali i s prijateljem putem mreže, i to na različitim razinama težine - u zavisnosti o skupu funkcija i operacija koje su dopuštene - na najlakšem nivou dopuštene su gotovo sve elementarne funkcije i operacije, na težem nivou onemogućene su one koje mogu poslužiti za gore pobrojena opća rješenja, dok na nivou nazvanom Teorminimum (po već spomenutom kvalifikacijskom testu - Teorijskom minimumu) igrač ne može ni zbrajati, ni množiti ni dijeliti - stoga se mora 'igrati' logaritmima.
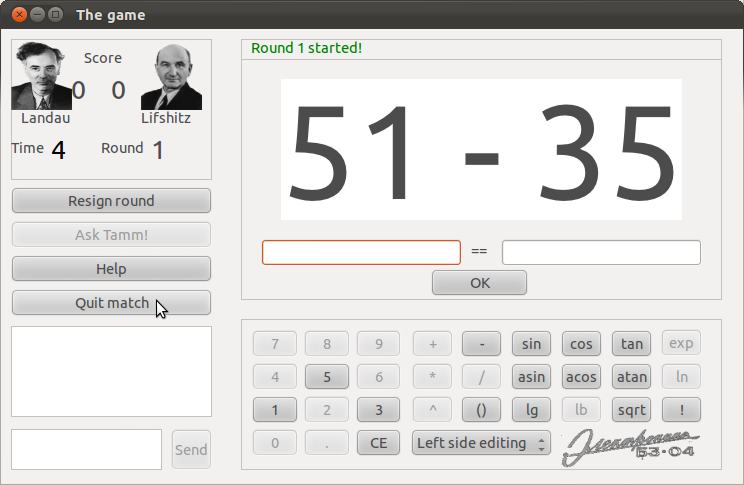
Slika 3: Izgled korisničkog sučelja
Na web siteu
Bibliografija
| [1] | „24th United States of America Mathematical Olympiad”, AMC MAA, 1995. |
| [2] | B. S. Gorobec, „Krug Landau”, Letnij sad, Moskva, 2006 |
| [3] | M. I. Kaganov, „Landau's license plate game”, Quantum, Vol. 3 No. 4 (1993) |
| [4] | H. Šiljak, Dau - the game, http://dau.etf.ba |

