O spektru nelinearnih operatora
Sažetak
U ovom radu pokazujemo da preslikavajući spektar nelinearnih operatora ne zadržava neke bitne osobine koje ima spektar linearnih operatora. To ilustriramo nizom primjera. Ključne riječi: spektar, nelinearni operator, bijekcija
1Uvod
Dobro je poznata važnost spektralne teorije za linearne operatore. Podsjetimo se nekih najznačajnijih osobina spektra linearnih operatora. Neka je X Banachov prostor nad poljem \mathbb{K} realnih ili kompleksnih brojeva.
Definicija 1. Spektar ograničenog linearnog operatora L:X\rightarrow X je skup
(1)
\sigma(L)=\lbrace \lambda\in \mathbb{K}:\lambda I- L\text{ nije bijekcija}\rbrace .
Za svako \lambda \in \mathbb{K}\setminus \sigma (L) postoji rezolventni operator (\lambda I- L)^{-1} koji je ograničen.
Definicija 2. Neka je X kompleksan Banachov prostor, \sigma(L) spektar ograničenog linearnog operatora L i \lambda\in \sigma(L).
1) Kažemo da \lambda pripada točkovnom spektru ako \lambda I-L nije injekcija. Skup svih takvih \lambda označavamo sa \sigma_{p}(L) i nazivamo točkovnim spektrom operatora L.
2) \lambda je element neprekidnog spektra ako je \lambda I-L injekcija i (\lambda I-L) (X) gust potprostor od X. Skup svih takvih \lambda označavamo sa \sigma_{c}(L) i nazivamo neprekidnim spektrom operatora L.
3) \lambda je element rezidualnog spektra ako je \lambda I-L injekcija, ali (\lambda I-L) (X) nije gust potprostor od X. Skup svih takvih \lambda označavamo sa \sigma_{r}(L) i nazivamo rezidualnim spektrom operatora L.
1) Kažemo da \lambda pripada točkovnom spektru ako \lambda I-L nije injekcija. Skup svih takvih \lambda označavamo sa \sigma_{p}(L) i nazivamo točkovnim spektrom operatora L.
2) \lambda je element neprekidnog spektra ako je \lambda I-L injekcija i (\lambda I-L) (X) gust potprostor od X. Skup svih takvih \lambda označavamo sa \sigma_{c}(L) i nazivamo neprekidnim spektrom operatora L.
3) \lambda je element rezidualnog spektra ako je \lambda I-L injekcija, ali (\lambda I-L) (X) nije gust potprostor od X. Skup svih takvih \lambda označavamo sa \sigma_{r}(L) i nazivamo rezidualnim spektrom operatora L.
U slučaju da dim X\lt \infty onda je \sigma(L)=\sigma_{p}(L). Primijetimo da \lambda_{0}\in \sigma_{c}(L) povlači da operator (\lambda_{0} I-L) ima inverzni operator (\lambda_{0} I- L)^{-1} ali da taj nije ograničen. Situacija \lambda_{0}\in \sigma_{r}(L) znači da rezolventni operator postoji, ali njegovo područje definicije nije gusto u X; u tom slučaju rezolventni operator može biti ograničen ili neograničen.
Slobodno govoreći, elementi \lambda u subspektru \sigma_{p}(L) karakteriziraju neki gubitak injektivnosti, oni iz \sigma_{r}(L) neki gubitak surjektivnosti, a oni iz \sigma_{c}(L) neki gubitak stabilnosti operatora \lambda I-L.
Ovi dijelovi spektra formiraju disjunktnu podjelu spektra
\sigma (L)=\sigma_{p}(L)\cup \sigma_{c}(L)\cup \sigma_{r}(L).
Vrijedi i sljedeći teorem koji daje tzv. formulu spektralnog preslikavanja polinoma.
Teorem 3. Neka je L linearan operator u Banachovu prostoru X nad poljem \mathbb{K }. Za svaki polinom p:\mathbb{K}\rightarrow \mathbb{K}, p(\lambda)=a_{n}\lambda^{n}+a_{n-1} \lambda^{n-1}+\cdots +a_{1}\lambda+a_{0} vrijedi
gdje je p(L)=a_{n}L^{n}+\cdots +a_{1}L+a_{0} I i p(\sigma(L))=\lbrace p(\lambda):\lambda\in\sigma(L)\rbrace.
(2)
\sigma(p(L))=p (\sigma(L)),
Spektar linearnog operatora \sigma (L) ima sljedeće važne osobine:
| \bullet | zatvoren je i ograničen skup (dakle kompaktan) |
| \bullet | neprazan je skup kad je \mathbb{K} polje kompleksnih brojeva |
| \bullet | vrijedi formula spektralnog preslikavanja |
2Preslikavajući spektar
Kod definiranja spektra nelinearnih operatora, cilj je, po mogućnosti:
| \bullet | u slučaju linearnog operatora da se svodi na poznati spektar ( |
| \bullet | da ima bar neke zajedničke osobine s linearnim spektrom (npr. zatvorenost, kompaktnost), |
| \bullet | da sadrži svojstvene vrijednosti operatora. |
(3)
\Sigma(F):=\lbrace \lambda\in \mathbb{K}:\lambda I- F \text{ nije bijekcija}\rbrace .
(4)
\Sigma_{i}(F):=\lbrace \lambda\in \mathbb{K}:\lambda I- F \text{ nije injekcija}\rbrace
(5)
\Sigma_{s}(F)=\lbrace \lambda\in \mathbb{K}:\lambda I- F \text{ nije surjekcija}\rbrace ,
Pokazat ćemo primjerima da preslikavajući spektar (
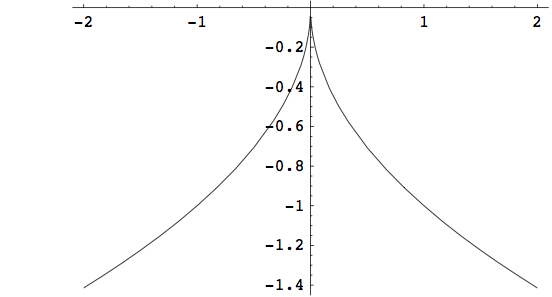
Primjer 2.1 Neka je operator F:\mathbb{R}\rightarrow \mathbb{R} definiran s
F(x)=\sqrt{|x|}.
Odredimo spektre injektivnosti i surjektivnosti, odnosno preslikavajući spektar operatora F. Označimo G(x)=(\lambda I-F)(x)=\lambda x-\sqrt{|x|}.
a) Ispitajmo kad je ovo preslikavanje injektivno.
Za \lambda =0 je G(x)=-\sqrt{|x|}, a to nije injekcija (jer za x\neq 0 vrijedi G(x)=G(-x)). Prema tome, 0 \in \Sigma_{i}(F).
Neka je sada \lambda \neq 0 i promatrajmo jednakosti
G(x_{1})= \lambda x_{1}-\sqrt{|x_{1}|}=\lambda x_{2}-\sqrt{|x_{2}|}=G(x_{2})
\lambda (x_{1}-x_{2})=\sqrt{|x_{1}|}-\sqrt{|x_{2}|}.
U slučaju da su x_{1} i x_{2} pozitivni i x_{1}\neq x_{2}, vrijedi
\lambda (\sqrt{x_{1}}-\sqrt{x_{2}})(\sqrt{x_{1}}+\sqrt{x_{2}})=\sqrt{x_{1}}-\sqrt{x_{2}}
\lambda (\sqrt{x_{1}}+\sqrt{x_{2}})=1 \Rightarrow \sqrt{x_{2}}=\frac{1}{\lambda}-\sqrt{x_{1}}.
Iz uvjeta \frac{1}{\lambda}-\sqrt{x_{1}}\gt 0 dobivamo \lambda \gt 0 i x_{1} \in (0,\frac{1}{\lambda^{2}}).
U slučaju da su x_{1} i x_{2} negativni i x_{1}\neq x_{2}, vrijedi
\lambda (-\sqrt{|x_{1}|}+\sqrt{|x_{2}|})(\sqrt{|x_{1}|}+\sqrt{|x_{2}|})=\sqrt{|x_{1}|}-\sqrt{|x_{2}|}
\lambda (\sqrt{|x_{1}|}+\sqrt{|x_{2}|})=-1 \Rightarrow \sqrt{|x_{2}|}=-\frac{1}{\lambda}-\sqrt{|x_{1}|}.
Rješavanjem nejednakosti -\frac{1}{\lambda}-\sqrt{|x_{1}|}\gt 0 dobivamo \lambda \lt 0 i x_{1} \in (-\frac{1}{\lambda^{2}},0). Ovim smo pokazali da za proizvoljno \lambda \gt 0, ako uzmemo x_{1} \in (0,\frac{1}{\lambda^{2}}) i
x_{2}=(\frac{1}{\lambda}-\sqrt{x_{1}})^{2}, onda dobivamo G(x_{1})=G(x_{2}). To znači da za \lambda \in (0,\infty) preslikavanje G nije injektivno, odnosno (0,\infty)\subseteq \Sigma_{i}(F). S druge strane, za proizvoljno \lambda \lt 0, ako uzmemo x_{1} \in (-\frac{1}{\lambda^{2}},0) i x_{2}=-(\frac{1}{\lambda}+\sqrt{|x_{1}|})^{2}, onda opet dobivamo G(x_{1})=G(x_{2}). Dakle, (-\infty,0)\subseteq \Sigma_{i}(F). Sveukupno, našli smo spektar injektivnosti
\Sigma_{i}(F)=(-\infty,0)\cup \lbrace 0\rbrace \cup (0,\infty)=\mathbb{R}
b) Ispitajmo kad je G surjektivno preslikavanje.
Za \lambda =0 je G(x)=-\sqrt{|x|}, a ovo nije surjekcija jer je G(\mathbb{R})=(-\infty,0]. Prema tome, 0\in \Sigma_{s}(F). Neka je sad \lambda \neq 0 i y \in \mathbb{R} proizvoljno. Ispitajmo rješenja jednadžbe
\lambda x-\sqrt{|x|}=y.
Nalazimo: za \lambda \gt 0 je
x=\begin{cases} \frac{1+2\lambda y + \sqrt{1+4\lambda y}}{2\lambda ^{2}} & y \in [-\frac{1}{4\lambda},\infty) \\ \frac{1+2\lambda y - \sqrt{1+4\lambda y}}{2\lambda ^{2}} & y \in [-\frac{1}{4\lambda},0] \\ \frac{-1+2\lambda y+ \sqrt{1-4\lambda y}}{2\lambda ^{2}} & y \in (-\infty,0] \\ \end{cases},
a za \lambda \lt 0 je
x= \begin{cases} \frac{1+2\lambda y - \sqrt{1+4\lambda y}}{2\lambda ^{2}} & y \in (-\infty,0] \\ \frac{-1+2\lambda y + \sqrt{1-4\lambda y}}{2\lambda ^{2}} & y \in [\frac{1}{4\lambda},0] \\ \frac{-1+2\lambda y - \sqrt{1-4\lambda y}}{2\lambda ^{2}} & y \in [\frac{1}{4\lambda}, \infty) \\ \end{cases}.
Tako da za \lambda \neq 0 i proizvoljno y, postoji x \in \mathbb{R} takav da je G(x)=y; odnosno G je surjekcija. Ostaje samo \Sigma_{s}(F)=\lbrace 0\rbrace . Preslikavajući spektar je
\Sigma (F)=\Sigma_{i}(F)\cup \Sigma_{s}(F)=\mathbb{R},
pa vidimo da nije ograničen skup.
Primjer 2.2 Neka je F:\mathbb{R}\rightarrow \mathbb{R} definiran s
(6)
F(x)= \left\lbrace \begin{array}{ll} x & \text{ako je }|x|\gt 1\text{}, \\ x^{2} & \text{ako je }0\leq x\leq 1\text{}, \\ -x^{2} & \text{ako je }-1\leq x\leq 0.\text{} \end{array} \right.
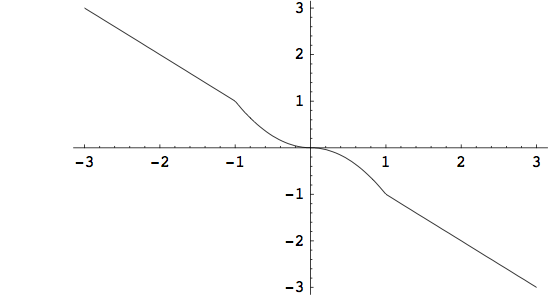
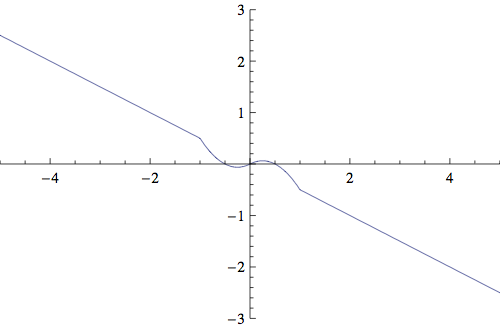
G(x)=-F(x)=\begin{cases} -x & \text{ ako je } |x|\gt 1,\\ -x^{2} & \text{ ako je } 0\leq x\leq 1,\\ x^{2} & \text{ ako je } -1\leq x\leq 0 \end{cases}
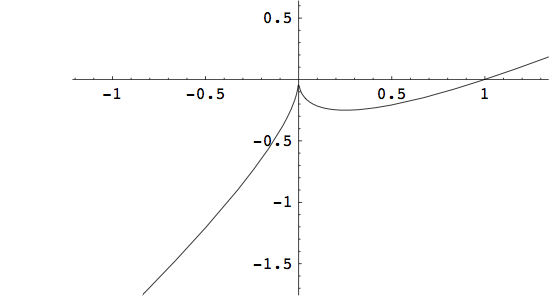
i pokažimo da je u pitanju bijekcija (vidi sliku Za y\in (-\infty, -1)\cup (1,\infty),\quad \exists x=-y, tako da G(x)=y. Za y\in [-1,0],\quad \exists x=\sqrt{-y}, tako da G(x)=y. I za y\in [0,1], \exists x=-\sqrt{y},\quad G(x)=y. Dakle, G(\mathbb{R})=\mathbb{R}, pa je G surjekcija i 0\notin \Sigma_{s}(F). Jasno je i da je injekcija jer iz svake jednadžbe G(x_{1})=G(x_{2}) slijedi da je x_{1}=x_{2}. Injektivnost se može dokazati i činjenicom da je G neprekidna i stalno opadajuća funkcija od +\infty do -\infty na čitavoj realnoj osi. Dakle, 0\notin \Sigma_{i}(F). Kad je \lambda =1 imamo:
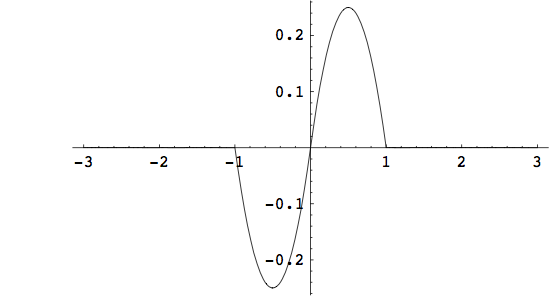
G(x)=\begin{cases} 0 & \text{ ako je } |x|\gt 1,\\ x-x^{2} & \text{ ako je } 0\leq x\leq 1,\\ x+x^{2} & \text{ ako je } -1\leq x\leq 0. \end{cases}
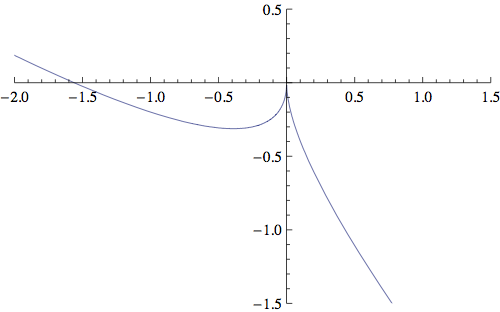
G_{max}=G(\frac{1}{2})=\frac{1}{4}, a G_{min}=G(-\frac{1}{2})=-\frac{1}{4} (vidi sliku Budući da je G neprekidna funkcija, vrijedi G(\mathbb{R})=[-\frac{1}{4}, \frac{1}{4}], pa nije surjekcija i 1\in \Sigma_{s}(F). Jasno je da G nije ni injekcija jer npr. G(2)=G(3)=0. Prema tome, 1\in \Sigma_{i}(F). Neka je \lambda \in (0,1) (vidi sliku
(7)
G(x)=\begin{cases} x(\lambda-1) & \text{ ako je } |x|\gt 1,\\ \lambda x-x^{2} & \text{ ako je } 0\leq x\leq 1,\\ \lambda x+x^{2} & \text{ ako je } -1\leq x\leq 0. \end{cases} G^{\prime} (x)= \begin{cases} \lambda-1 & \text{ ako je } |x|\gt 1,\\ \lambda -2x & \text{ ako je } 0\leq x\leq 1,\\ \lambda +2x & \text{ ako je } -1\leq x\leq 0. \end{cases}.
| x | (-\infty,-1) | (-1,-\lambda/2) | (-\lambda/2,0) | (0,\lambda/2) | (\lambda/2,1) | (1,\infty) |
| G'(x) | - | - | + | + | - | - |
| G(x) | \searrow | \searrow | \nearrow | \nearrow | \searrow | \searrow |
Budući da je G neprekidna funkcija na \mathbb{R} i dostiže lokalni minimum za x=-\frac{\lambda}{2}, a lokalni maksimum za x=\frac{\lambda}{2}, slijedi da nije injekcija. Tako npr. za x_{1}\in (0,\frac{\lambda}{2}) i x_{2}\in (\frac{\lambda}{2}, 1), iz jednadžbe G(x_{1})=G(x_{2}) dobivamo x_{2}=\lambda -x_{1}. Ovim smo pokazali (0,1)\subseteq \Sigma_{i}(F).
Jasno je da je G surjekcija jer je neprekidna funkcija i
\lim_{x \to -\infty} G(x)= + \infty,\quad \lim_{x \to +\infty} G(x)= - \infty.
U slučaju \lambda \in (1,2) je
| x | (-\infty,-1) | (-1,-\lambda/2) | (-\lambda/2,0) | (0,\lambda/2) | (\lambda/2,1) | (1,\infty) |
| G`(x) | + | - | + | + | - | + |
| G(x) | \nearrow | \searrow | \nearrow | \nearrow | \searrow | \nearrow |
tako da opet nemamo injekciju, pa (1,2)\subseteq \Sigma_{i}(F). Sada je
\lim_{x \to -\infty} G(x)= - \infty,\quad \lim_{x \to +\infty} G(x)= +\infty
pa G jest surjekcija. Iz (\Sigma_{i}(F)=\Sigma (F)=(0,2), \qquad \Sigma_{s}(F)=\lbrace 1\rbrace .
Dakle, \Sigma (F) nije zatvoren skup.
Jedna od najvažnijih osobina linearnog spektra je ta da je on uvijek neprazan u slučaju kad je \mathbb{K} polje kompleksnih brojeva. Međutim, pokazuje se da ovo više ne vrijedi kad je riječ o nelinearnom operatoru.
Primjer 2.3 Neka je operator F:\mathbb{C}^{2}\rightarrow \mathbb{C}^{2} definiran s
(8)
F(z,w)=(\overline{w},i\overline{z}).
(\lambda I-F)^{-1} (\zeta,\omega)= \left( \frac{\overline{\lambda}\zeta + \overline{\omega}}{i + |\lambda |^{2}}, -\frac{\overline{\lambda}\omega + i \overline{\zeta}}{i - |\lambda |^{2}} \right).
Slijedi da je:
\Sigma_{i}(F)= \Sigma_{s}(F)=\Sigma(F)=\emptyset.
Prema tome preslikavajući spektar ovog nelinearnog operatora (9) je prazan skup.
Primjer 2.4 Neka je operator F:\mathbb{R}\rightarrow \mathbb{R} definiran s
(9)
F(x)= \begin{cases} 0 & \text{ ako je } x\leq 1, \\ x-1 & \text{ ako je } 1 \lt x \lt 2, \\ 1 & \text{ ako je } x \geq 2. \end{cases}
Spektar injektivnosti
\sigma_{p} (F):=\lbrace \lambda \in \mathbb{K}: F(x)= \lambda x \text{ za neko } x\neq 0\rbrace .
Kao i u linearnom slučaju, elemente \lambda \in \sigma_{p} (F) nazivat ćemo svojstvenim vrijednostima operatora F. U slučaju da je F(0)=0, vrijedi inkluzija
\sigma_{p} (F)\subseteq \Sigma_{i} (F)
koja može biti i stroga. U Primjeru 2.1 imamo da je \sigma_{p} (F)=\mathbb{R}\setminus \lbrace 0\rbrace \subset \mathbb{R}= \Sigma_{i}(F). Naravno, za linearne operatore L uvijek vrijedi da je \sigma_{p} (L)=\sigma_{i} (L), po definiciji.
Pogledajmo sad spektar surjektivnosti
(10)
F_{z}(x)=F(x)+z
Propozicija 4. Za neprekidan operator F:X \to X vrijedi jednakost
(11)
\mathbb{K}\setminus \Sigma_{s}(F)=\bigcap_{z\in X \setminus \lbrace -F(0)\rbrace } \sigma_{p}(F_{z}).
Dokaz.
Na osnovi pokazanog u (i) i (ii) slijedi tražena jednakost.
| (i) | Pokažimo najprije da
\bigcap_{z\in X \setminus \lbrace -F(0)\rbrace } \sigma_{p}(F_{z})\subseteq \mathbb{K}\setminus \Sigma_{s}(F).
Neka za svako z\neq -F(0) vrijedi \lambda \in \sigma_{p}(F_{z}). Tada:
(\exists x_{z}\neq 0) \lambda x_{z}=F_{z} (x_{z})=F(x_{z})+z \Rightarrow (\lambda I-F)(x_{z})=z,
što znači da z \in R(\lambda I-F). Dakle, \forall z \in X \setminus {-F(0)}, z \in R(\lambda I-F), pa R(\lambda I-F)\supseteq X \setminus {-F(0)}. Budući da još, očito, vrijedi i -F(0) \in R(\lambda I-F), imamo: R(\lambda I-F)\supseteq X. Svakako je R(\lambda I-F)\subseteq X, pa R(\lambda I-F)=X. Dakle \lambda I-F je surjektivno preslikavanje, tj. \lambda \in \mathbb{K}\setminus \Sigma_{s}(F). |
| (ii) | Neka je sada \lambda \in \mathbb{K}\setminus \Sigma_{s}(F), tj. \lambda I-F je surjektivno, te vrijedi:
(\forall z \in X) (\exists x_{z} \in X) \lambda x_{z}-F(x_{z})=z. Ako z\neq -F(0), onda x_{z}\neq 0, a to znači da je x=x_{z} netrivijalno rješenje jednadžbe F_{z}(x)=\lambda x. Prema tome, \lambda \in \sigma_{p}(F_{z}). Budući da ovo vrijedi \forall z \in X \setminus {-F(0)}, onda je \lambda \in \bigcap_{z\in X \setminus \lbrace -F(0)\rbrace } \sigma_{p}(F_{z}).
Dakle,
\mathbb{K}\setminus \Sigma_{s}(F)\subseteq \bigcap_{z\in X \setminus \lbrace -F(0)\rbrace } \sigma_{p}(F_{z}).
|
\ \blacksquare
Za F(x)=\sqrt{|x|} iz Primjera 2.1, translatirana funkcija je F_{z}(x)=\sqrt{|x|}+z. Budući da je za svako z\in \mathbb{R} točkovni spektar \sigma_{p}(F_{z})=\mathbb{R}\setminus \lbrace 0\rbrace, na osnovi
Primjer 2.5 U prostoru neprekidnih funkcija C[0,1] dan je Hammersteinov integralni operator
H(x)(s)=s^{\beta +1} \int_{0}^{1}t^{\beta} \sin x(t)dt \qquad (0\leq s\leq 1, \beta \geq 0).
Operator H je kompozicija H=KF, nelinearnog operatora F definiranog s
F(x)(t)=\sin x(t)
i linearnog Fredholmova integralnog operatora
Ky(s)=\int_{0}^{1} s^{\beta +1}t^{\beta}y(t)dt.
Odredimo točkovni spektar \sigma_{p}(H). Operator H je kompaktan. Za neprekidnu funkciju x_{n}(t)\equiv n\pi\equiv 0, pa H(x_{n})=0=0x_{n}. To znači da 0 \in \sigma_{p}(H). Razmotrimo sad jednadžbu H(x)=\lambda x, za \lambda \neq 0. Imamo
H(x)(s)=s^{\beta +1} \int_{0}^{1}t^{\beta} \sin x(t)dt=\lambda x(s)
x(s)=cs^{\beta +1} \text{ za neko } c\neq 0.
(12)
\lambda =\frac{1}{c}\int_{0}^{1}t^{\beta} \sin (ct^{\beta +1})dt=:\psi (c).
\sigma_{p}(H)=\lbrace \psi(c):c \in \mathbb{R}\setminus \lbrace 0\rbrace \rbrace .
Uvedimo u \lambda =\psi (c)=\frac{1}{(\beta +1) c^{2}}\int_{0}^{c} \sin \tau d\tau =\frac{1-\cos c}{(\beta +1) c^{2}} \quad (c\neq 0).
Sada je
\lim_{c \rightarrow 0} \psi (c)=\lim_{c \rightarrow 0}\frac{1-\cos c}{(\beta +1) c^{2}}= \lim_{c \rightarrow 0}\quad \frac{\sin c}{2(\beta +1) c}=\frac{1}{2(\beta +1)}.
Možemo dodefinirati funkciju \psi u točki 0 tako da bude neprekidna na \mathbb{R}:
\widetilde{\psi}(c)= \begin{cases} \frac{1-\cos c}{(\beta +1) c^{2}} & c\neq 0, \\ \frac{1}{2(\beta +1)} & c =0. \end{cases}
Budući da je funkcija \widetilde{\psi} neprekidna, vrijedi
0\leq \widetilde{\psi}(c) \leq \frac{1}{2(\beta +1)}, \quad (-\infty \lt c\lt \infty),
pri čemu se dostižu sve vrijednosti između lijeve i desne granice. Lijeva strana nejednakosti dostiže se u točkama c=2k \pi, k \in \mathbb{Z}, tj. \psi(2k\pi)= 0. Desna strana nejednakosti ne dobiva se ni za jedno c\neq 0, jer iz \psi (c)=\frac{1}{2(\beta +1)} slijedi
\frac{1}{2(\beta +1)}=\frac{1-\cos c}{(\beta +1) c^{2}}=\frac{2\sin^{2}(\frac{c}{2})}{(\beta +1) c^{2}}= \frac{1}{2(\beta +1)}\Big (\frac{\sin \frac{c}{2}}{\frac{c}{2}}\Big )^{2},
\sin \frac{c}{2}=\frac{c}{2}\Rightarrow c = 0.
Prema tome \sigma_{p} (H)=\Big [0,\frac{1}{2(\beta +1)}\Big ).
3Zaključak
Ovim primjerima pokazali smo da nam treba drugačiji pristup pri definiranju spektra nelinearnih operatora. Za nelinearni neprekidni operator F i neku klasu neprekidnih operatora \mathcal{M}(X) koja sadržava F možemo definirati rezolventni skup
\rho (F)=\Big \lbrace \lambda \in \mathbb{K}: \lambda I-F \text{ je bijekcija i } (\lambda I-F)^{-1} \in \mathcal{M}(X)\Big \rbrace
i spektar
\sigma (F)=\mathbb{K} \setminus \rho (F).
Ovisno o tome što uzmemo za klasu \mathcal{M}(X) (npr. neprekidno diferencijabilni, Lipschitz neprekidni, stabilno rješivi ili epi operatori) dobivamo razne spektre. Nazive su dobivali po matematičarima koji su ih prvi uveli: Rhodius, Neuberger, Kachurovski, Feng, itd. Na ovaj način dobivaju se spektri koji imaju samo neke dobre osobine koje imaju spektri linearnog operatora. Nelinearne spektralne teorije i dalje su u razvoju, a opseg njihove primjene vrlo je širok.