Fourierov red i Fourierova transformacija
Sažetak
U ovom radu objasniti ćemo kako svaku periodičku funkciju možemo napisati kao sumu (ne nužno konačnu) sinusa različitih amplituda, faza i frekvencija – Fourierov red. U drugom dijelu rada motivirati ćemo formulu za Fourierovu transformaciju preko Fourierova reda te objasniti formulu za diskretnu Fourierovu transformaciju.
1Uvod
U današnjoj se literaturi Fourierova transformacija najčešće prezentira čitatelju kao cjelovit samostalan izraz te se rijetko motivira čitatelja da shvati kako je sam izraz nastao (vidi
Fourierova analiza proizlazi iz glavne ideje da svaku periodičku funkciju možemo zapisati kao sumu (ne nužno konačnu) sinusa različitih amplituda, faza i frekvencija. Takva suma naziva se Fourierov red (vidi npr.
Sama motivacija koju je Jean Baptiste Joseph Fourier (Slika
Iako je Fourierova transformacija proizašla kao rezultat proučavanja Fourierova reda, u današnjoj literaturi često se servira kao „gotov alat” i vrlo je teško shvatiti iz same formule Fourierove transformacije motivaciju za njeno nastajanje.
Struktura ovog rada sastoji se od dvaju osnovnih poglavlja. U
2Fourierov red
Pri razvoju funkcije u Fourierov red, uvjet je da je funkcija periodična. Prvo pitanje koje se postavlja - možemo li to napraviti i za neperiodične funkcije na nekom intervalu? Odgovor je: da, ako ih učinimo periodičnima! Tada taj interval postaje period te funkcije i ponavlja se beskonačno mnogo puta. Iako sva razmatranja koja ćemo ovdje iznijeti vrijede za periodične funkcije nekog općenitog perioda [-L/2, L/2 ], u ostatku teksta ćemo zbog jednostavnosti pretpostaviti da je promatrana funkcija periodična na nekom intervalu [-\pi, \pi ]. Dakle, za danu funkciju (ili signal, ako je funkcija ovisna o vremenu) f:\mathbb{R}\rightarrow\mathbb{R}, periodičnu na [-\pi,\pi], želimo pronaći brojeve a_{0}, a_{k}, \phi_{k}\in\mathbb{R}, za k=1,\ldots,n tako da vrijedi
f(x)=\frac{a_{0}}{2}+\sum_{k=1}^{n}{a_{k}\sin{(k x+\phi_{k})}}, \quad n\ge 0.
U ovom izrazu a_{k} ima ulogu amplitude, a \phi_{k} ulogu faze za sinus funkciju frekvencije k. Član \frac{a_{0}}{2} je poseban i on služi za translaciju funkcije duž y-osi (često se naziva „DC komponenta”). Ako u gornjem izrazu primijenimo adicijsku formulu za sinus funkciju,
\sin{(\alpha+\beta)}=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta},
vidimo da možemo zapisati Fourierov red i drugačije:
f(x)=\frac{a_{0}}{2}+\sum_{k=1}^{n}{(a_{k}\sin{(k x)}\cos{\phi_{k}}+a_{k}\cos{(k x)}\sin{\phi_{k}})}.
Primijetimo da u ovoj formuli \sin{\phi_{k}} i \cos{\phi_{k}} ne ovise ni o varijabli x ni o k - to su brojevi koji su dio koeficijenata uz \sin{(k x)} i uz \cos{(k x)}. Stoga, možemo definirati nove koeficijente a_{k}, b_{k}\in\mathbb{R} u kojima će implicitno biti uključeni i \phi_{k}. Tako da nova formula izgleda ovako:
(1)
f(x)=\frac{a_{0}}{2}+\sum_{k=1}^{n}{(a_{k}\sin{(k x)}+b_{k}\cos{(k x)})}, \quad n\ge 0.
Traženje Fourierova reda sada se svodi na traženje koeficijenata a_{k} i b_{k}. Primijetite da više eksplicitno ne moramo promatrati fazu pojedine sinus funkcije, već je dovoljno tražiti koeficijente (amplitude) uz sinus i kosinus.
2.1Uvjeti na funkciju f(x)
Vrijedi li jednakost (
No, stvar prima drugačiju perspektivu kada iskoristimo činjenicu da veće frekvencije sinusa i kosinusa u sumi (
f(x)= \begin{cases} 1, & x\in(-1,1), \\ 0, & \text{inače.} \\ \end{cases}.

Slika 2: Na slici je prikazana aproksimacija tzv. rectangle funkcije na intervalu [-2,2] s pomoću Fourierova reda za: a) n=2; b) n=4; c) n=8; d) n=16.
Stoga, kada bismo dodavali sve više i više funkcija, brojač k bio bi sve veći i veći i naša rezultatna krivulja sve bi bolje aproksimirala vrhove u kojima funkcija nije derivabilna. Ovaj argument iskoristiti ćrmo za motivaciju da sumu (
(2)
f(x)=\frac{a_{0}}{2}+\sum_{k=1}^{\infty}{(a_{k}\sin{(k x)}+b_{k}\cos{(k x)})}.
I ova se suma može bolje zapisati, prisjetimo li se Eulerove formule
r e^{i\phi}=r(\cos{\phi}+i\sin{\phi}).
Formulu (
c_{k} e^{ikx} + \overline{ c_{k}e^{ikx}} = a_{k} \sin(kx) + b_{k} \cos(kx),
što je ekvivalentno
(\cos{(k x)}-i\sin{(k x)})\overline{c_{k}}+(\cos{(k x)}+i\sin{(k x)})c_{k}=a_{k}\sin{(k x)}+b_{k}\cos{(k x)}.
Nadalje, vrijedi
\cos{(k x)}(\overline{c_{k}}+c_{k})+\sin{(k x)}(c_{k} i-\overline{c_{k}} i)=a_{k}\sin{(k x)}+b_{k}\cos{(k x)}.
Primijetimo da je c_{k} i-\overline{c_{k}}i=-2Im(c_{k}). Sada iz gornjeg izraza dobivamo sljedeće dvije jednadžbe:
\begin{eqnarray*} a_{k}&=&-2Im(c_{k}),\\ b_{k}&=&2Re(c_{k}). \end{eqnarray*}
Ako prvu jednadžbu pomnožimo s imaginarnom jedinicom i, tj. a_{k} i=-2Im(c_{k})i te joj pribrojimo drugu jednadžbu, dobivamo
\begin{eqnarray*} b_{k}+a_{k} i&=&2Re(c_{k})-2Im(c_{k})i,\\ \overline{c_{k}}&=&\frac{1}{2}(b_{k}+i a_{k}). \end{eqnarray*}
Primijetite da smo se gore koristili jednakošću Re(c_{k})-Im(c_{k})i=\overline{c_{k}}. Nadalje, sada je lako dobiti samu vrijednost c_{k}.Ako uvedemo oznaku c_{-k}=\overline{c_{k}}, općenitiji razvoj u Fourierov red možemo zapisati sljedećom formulom
f(x)=\sum_{k=-\infty}^{\infty}{c_{k} e^{i k x}},
gdje je c_{-k}=\frac{1}{2}(b_{k}+i a_{k}) i c_{k}=\frac{1}{2}(b_{k}-i a_{k}). Nulti član, „DC komponenta”, u ovom je slučaju c_{0}=\overline{c_{0}}=\frac{a_{0}}{2}.
2.2Određivanje Fourierovih koeficijenata c_{k}
U ovom poglavlju pokazat ćemo kako za danu periodičku funkciju f(x) izračunati k-ti koeficijent c_{k}. Budući da je
f(x)=\ldots+c_{k-1}e^{(k-1)x i}+c_{k} e^{k x i}+c_{k+1}e^{(k+1)x i}+\ldots,
dijeleći ovu jednadžbu s e^{k x i} (koji je uvijek različit od nule) dobivamo
\begin{eqnarray*} c_{k}&=&\frac{f(x)}{e^{k x i}}-(\ldots+c_{k-1}e^{-x i}+c_{k+1}e^{x i}+\ldots)\\ &=&f(x)e^{-k x i}-\sum_{j=-\infty,j\neq k}^{\infty}{c_{j}e^{(j-k) x i}}, \end{eqnarray*}
za k\in\mathbb{Z}. Sada iskoristimo činjenicu da je c_{k} konstanta, tako da integrirajući obje strane po varijabli x na [-\pi,\pi] dobivamo
\begin{eqnarray*} \int_{-\pi}^{\pi}{c_{k} dx}&=&\int_{-\pi}^{\pi}{f(x)e^{-k x i}dx}-\int_{-\pi}^{\pi}{\sum_{j=-\infty,j\neq k}^{\infty}{c_{j}e^{(j-k) x i}}dx},\\ c_{k}\pi-(-c_{k}\pi)&=&\int_{-\pi}^{\pi}{f(x)e^{-k x i}dx}-\sum_{j=-\infty,j\neq k}^{\infty}{\int_{-\pi}^{\pi}{c_{j}e^{(j-k) x i}dx}},\\ 2\pi c_{k}&=&\int_{-\pi}^{\pi}{f(x)e^{-k x i}dx}-\sum_{j=-\infty,j\neq k}^{\infty}{\frac{1}{(j-k)i}c_{j}(e^{(j-k) \pi i}-e^{-(j-k) \pi i})}, \end{eqnarray*}
za k\in\mathbb{Z}. Čini se da smo dobili još kompliciraniji izraz za c_{k}, ali ako primijetimo da je, po Eulerovoj formuli, te jer je (j-k)\in\mathbb{Z},
e^{(j-k)\pi i}-e^{-(j-k)\pi i}=i\sin{(j-k)\pi}=0,
vidimo da se cijela suma poništava. Dijeleći jednadžbu s 2\pi dobivamo formulu za k-ti koeficijent Fourierova reda:
c_{k}=\frac{1}{2\pi}\int_{-\pi}^{\pi}{f(x)e^{-k x i}dx}.
Slično se može pokazati da vrijedi i za općenitiji interval, odnosno period, [-L/2,L/2], te da tada Fourierov red glasi
(3)
f(x)=\sum_{k=-\infty}^{\infty}{c_{k} e^{(2\pi i k x)/L}},
s pridruženim koeficijentima
(4)
c_{k}=\frac{1}{L}\int_{-L/2}^{L/2}{f(x)e^{-(2\pi k x i)/L}dx},
gdje je k\in\mathbb{Z}. Primijetimo da koeficijent \frac{2\pi}{L} služi da bismo sveli sinus i kosinus funkcije na interval [0, L] s periodom L. Time je možemo promatrati i na [-L/2, L/2] s periodom L.
2.3Konvergencija Fourierovog reda
Ostaje nam samo pitanje konvergencije, koje je stoljećima predstavljalo poveći problem. Razlog tomu je alternirajuća priroda sinus i kosinus funkcije; tim svojstvom znatno je otežano promatranje konvergencije ovako definiranog reda. No, stvar otežava i promatranje Fourierove tvrdnje - da se ovako može razviti svaka, pa i nederivabilna funkcija! Rezultati promatranja ovog reda govore da je najvažniji uvjet zapravo integrabilnost funkcije koju razvijamo u Fourierov red. Što se tiče konvergencije, navest ćemo jedan važniji rezultat, a to je teorem koji govori o konvergenciji po L^{2} normi:
Teorem 1. [Riesz-Fischer] Funkcija f\in L^{2}([-P/2,P/2]) s periodom P je L^{2}-integrabilna, tj. vrijedi
ako i samo ako je Fourierov red te funkcije L^{2}-konvergentan, tj. ako
kada n\rightarrow\infty.
\int_{-P/2}^{P/2}{|f(x)|^{2}dx}\lt \infty,
ako i samo ako je Fourierov red te funkcije L^{2}-konvergentan, tj. ako
\int_{-P/2}^{P/2}{|f(x)-\sum_{k=-n}^{n}{c_{k} e^{(2\pi i k x)/P}}|^{2}}dx\rightarrow 0,
kada n\rightarrow\infty.
Dakle, kvadrat razlike funkcije f(x) i njene konačne aproksimacije na nekom intervalu teži u nulu. Ovakve rezultate o konvergenciji Fourierova reda dobivamo ako se koristimo općenitijim, odnosno Lebesgueovim integralom. U analizi signala L^{2} integral funkcije, odnosno signala, predstavlja energiju signala. Ako je taj integral konačan, kaže se da signal ima konačnu energiju. Ovo rješenje postignuto je tek 1907. godine, što je cijelo stoljeće od prvotnog utemeljenja Fourierove analize. Ovaj teorem usko je vezan s Parsevalovim teoremom, pa se nerijetko tako i naziva.
3Fourierova transformacija
Promatrali smo kako razviti periodičnu funkciju perioda L definiranu na intervalu [-L/2,L/2] u Fourierov red. No, ako pokušamo pustiti da L teži u beskonačnost, tada je funkcija periodična na intervalu (-\infty,\infty) s beskonačno velikim periodom (pretpostavljamo da je funkcija definirana svugdje). Ovakvim razmišljanjem čini se da možemo dobiti koeficijente i za funkciju koja je potpuno neperiodična te na taj način proširiti teoriju koja vrijedi za Fourierov red i na neperiodične funkcije. Međutim, ima li to smisla? Primijetimo da ako postavimo L\rightarrow\infty, ako integral ima konačnu vrijednost na (-\infty,\infty), izraz (
Međutim, ovakvo razmišljanje vodit će nas prema transformaciji izraza (
Kao prvi korak u toj transformaciji zapisat ćemo formulu (
(5)
F\left(\frac{k}{L}\right)=\int_{-L/2}^{L/2}{f(x)e^{-(2\pi k x i)/L}dx}.
Tada nova formula za Fourierov red glasi:
(6)
f(x)=\sum_{k=-\infty}^{\infty}{\frac{1}{L}F\left(\frac{k}{L}\right) e^{(2\pi i k x)/L}}.
Sada pustimo da L\rightarrow\infty. Primijetimo da sada varijabla k/L, koja je bila diskretna, prelazi u kontinuiranu. Iako bismo prvo mislili da za fiksni k ovaj izraz prelazi u nulu, ideja je da je -\infty\lt k\lt \infty. Stoga se povećavanjem broja L zapravo samo smanjuje „razmak” između vrijednosti koje varijabla prima. Drugim riječima, varijabla k/L prelazi iz diskretne u kontinuiranu varijablu s. Sada zapišemo (
F(s)=\int_{-\infty}^{\infty}{f(x)e^{-2\pi s x i}dx}.
Dobivena funkcija F:\mathbb{C}\rightarrow\mathbb{C} naziva se Fourierovom transformacijom funkcije f:\mathbb{C}\rightarrow\mathbb{C}; budući da izrazi za F i f sadržavaju kompleksne brojeve, i jedan i drugi daju kompleksne vrijednosti, a samim time i primaju. Promotrimo što se dogodi s formulom za Fourierov red. Budući da smo stavili L\rightarrow\infty, možemo primijetiti da suma u (
f(x)=\int_{-\infty}^{\infty}{F(s) e^{2\pi i s x}ds}.
U ovom izrazu f(x) predstavlja inverznu Fourierovu transformaciju - transformaciju koja temeljeno na koeficijentima F(s) za svaki s\in\mathbb{R} vraća originalnu funkciju.
Bitno je primijetiti da smo Fourierovu transformaciju dobili iz jednadžbe za koeficijente Fourierova reda, dok smo inverznu Fourierovu transformaciju dobili iz same jednadžbe Fourierova reda. U sljedećem primjeru pokazat ćemo Fourierovu transformaciju za rectangle funkciju.
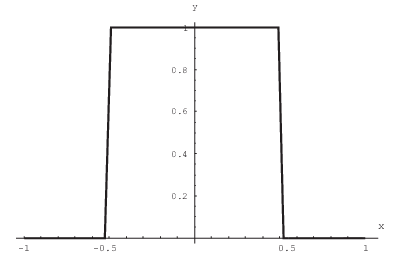
Primjer 2. Neka je zadana funkcija izrazom
Ovakva se funkcija, kao što je prije napomenuto, često naziva rectangle funkcija (vidi sliku3 ) i ima bitnu primjenu pri obradi signala. Nekada se definira i vrijednost od \frac{1}{2} u točkama \frac{1}{2} i -\frac{1}{2}, ali račun ostaje isti. Na\dj imo Fourierovu transformaciju ove funkcije.
f(x)=\left\lbrace \begin{array}{ll} 1, & \text{}x\in(-\frac{1}{2},\frac{1}{2})\text{;} \\ 0, & \text{inače.} \\ \end{array} \right.
Ovakva se funkcija, kao što je prije napomenuto, često naziva rectangle funkcija (vidi sliku
Rješenje 3. Fourierova transformacija ove funkcije dobiva se preko već opisane formule:
Da bismo mogli izračunati ovaj integral za zadani f(x), moramo ga rastaviti na tri dijela i uvrstiti odgovarajuće slučajeve za f(x) na sljedeći način:
Iz gornjeg izraza vidimo da iščezavaju svi integrali osim srednjeg te je dovoljno pronaći:
Tada po Eulerovoj formuli slijedi:
Koristeći se svojstvom parnosti funkcije kosinus i neparnosti funkcije sinus dobivamo
Gornjim izrazom dana je Fourierova transformacija tražene funkcije.
F(s)=\int_{-\infty}^{\infty}{f(x)e^{-2\pi s x i}dx}.
Da bismo mogli izračunati ovaj integral za zadani f(x), moramo ga rastaviti na tri dijela i uvrstiti odgovarajuće slučajeve za f(x) na sljedeći način:
F(s)=\int_{-\infty}^{-\frac{1}{2}}{0\cdot e^{-2\pi s x i}dx}+\int_{-\frac{1}{2}}^{\frac{1}{2}}{1\cdot e^{-2\pi s x i}dx}+\int_{\frac{1}{2}}^{\infty}{0\cdot e^{-2\pi s x i}dx}.
Iz gornjeg izraza vidimo da iščezavaju svi integrali osim srednjeg te je dovoljno pronaći:
F(s)=\int_{-\frac{1}{2}}^{\frac{1}{2}}{e^{-2\pi s x i}dx}.
Tada po Eulerovoj formuli slijedi:
\begin{eqnarray*} F(s)&=&\int_{-\frac{1}{2}}^{\frac{1}{2}}{(\cos{(-2\pi s x)}+i \sin{(-2\pi s x)})dx}\\ &=&\int_{-\frac{1}{2}}^{\frac{1}{2}}{\cos{(-2\pi s x)}dx}+i \int_{-\frac{1}{2}}^{\frac{1}{2}}{\sin{(-2\pi s x)}dx}\\ &=&-\frac{1}{2\pi s}\left(\sin{\left(-2\pi s\cdot \frac{1}{2}\right)}-\sin{\left(-2\pi s\cdot\left(-\frac{1}{2}\right)\right)}\right)\\ &&-\frac{i}{2\pi s}\left(\cos{\left(-2\pi s \cdot \frac{1}{2}\right)}-\cos{\left(-2\pi s \cdot\left(-\frac{1}{2}\right)\right)}\right). \end{eqnarray*}
Koristeći se svojstvom parnosti funkcije kosinus i neparnosti funkcije sinus dobivamo
\begin{eqnarray*} F(s)&=&-\frac{1}{2\pi s}(-\sin{(\pi s)}-\sin{(\pi s)})-\frac{i}{2\pi s}(\cos{(\pi s)}-\cos{(\pi s)})\\ &=&-\frac{1}{2\pi s}(-2\sin{(\pi s)})\\ &=&\frac{\sin{(\pi s)}}{\pi s}. \end{eqnarray*}
Gornjim izrazom dana je Fourierova transformacija tražene funkcije.
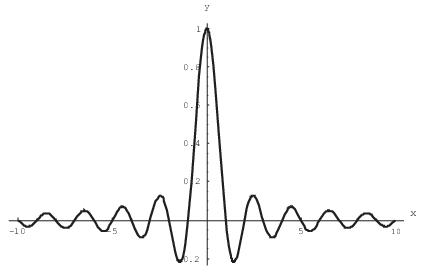
{\bf Napomena.} Funkcija dobivena Fourierovom transformacijom rectangle funkcije često se u analizi signala naziva sinc funkcija (vidi sliku
\text{sinc}(x)=\frac{\sin{(\pi x)}}{\pi x}.
3.1Diskretna Fourierova transformacija (DFT)
Ako imamo diskretan skup kompleksnih brojeva (koji smo mogli dobiti i uzorkovanjem funkcije na nekom intervalu), Fourierova transformacija koja je definirana za kontinuiran skup nam ne odgovara. Tada definiramo DFT na sljedeći način:
(7)
F_{j} = \sum_{k=0}^{n-1} f_{k} e^{\frac{2\pi ikj}{n}},
(8)
f_{k} =\frac{1}{n}\sum_{j=0}^{n-1}F_{j} e^{\frac{-2\pi ikj}{n}},
Primijetite da su u izrazima (
n\cdot \frac{1}{B} = L \text{ tj. } n\cdot \frac{1}{L} = B.
Budući da su ovako definirane dvije Fourierove transformacije inverz jedna drugoj, nije nam nužno strogo definirati jednu od tih transformacija izričito kao inverz. Stoga se u literaturi (kao i za općenitu Fourierovu transformaciju), uglavnom radi jednostavnosti, inverzi označavaju različito. Tako se (
4Zaključak i diskusija
Fourierov red, a posebice Fourierova transformacija u današnje su vrijeme jedan od najčešće korištenih matematičkih alata, a time i predmet brojnih šala na račun matematičara i inženjera (vidi sliku
Značenje Fourierove transformacije je višestruko i ovisno o primjeni. Česta je primjena kada se funkcija - signal, koja je definirana na cijelom realnom pravcu, pretvara u funkciju koja za određenu frekvenciju k vraća F(s), vrijednost iz koje možemo saznati informacije o amplitudi i fazi za frekvenciju s. Mnogo je operacija lakše obavljati preko Fourierove transformacije funkcije, među njima je najbitnija konvolucija. Jednako tako, Fourierova transformacija ima puno svojstava koja olakšavaju analiziranje funkcije - signala (vidi
Ovaj rad je rezultat uvodne diskusije diplomskog rada „Brza Fourierova transformacija i primjene” studenta S. Poljaka napisanog pod mentorstvom D. Matijevića.
Bibliografija
| [1] | Brigham, E. Oran. The fast Fourier transform and its applications, Englewood Cliffs, N.J.: Prentice Hall. ISBN 0-13-307505-2, 1988 |
| [2] | Cormen, Thomas H.; Leiserson, Charles E. ; Rivest, Ronald L.; and Stein, Clifford. "Chapter 30: Polynomials and the FFT". Introduction to Algorithms (Second ed.), MIT Press and McGraw-Hill. pp. 822–848 ISBN 0-262-03293-7, 2001 |
| [3] | Oppenheim, Alan V.; Schafer, R. W.; and Buck, J. R., Discrete-time signal processing, Upper Saddle River, N.J.: Prentice Hall. ISBN 0-13-754920-2, 1999 |
| [4] | Osgood, Brad G. The Fourier Transform and its Applications, on-line lectures by Stanford School of Engineering, at http://academicearth.org/courses/the-fourier-transform-and-its-applications. |
| [5] | Poljak, Stjepan. Brza Fourierova transformacija i primjene, diplomski rad, Odjel za matematiku Sveučilište J.J. Strossmayer u Osijeku, Java implementacija: http://www.mathos.hr/FFT/fourier.html, 2010. |
| [6] | Tolstov, Georgi P. Fourier Series. Courier-Dover. ISBN 0486633179, 1976 |