Banach-Tarskijev paradoks
Sažetak
Banach–Tarskijev paradoks je teorem koji kaže da su bilo koje dvije kugle u \mathbb{R}^{3} jednakorastavljive, u smislu da postoje particije tih kugli u jednak broj respektivno izometričnih dijelova. Tekst prezentira dokaz Banach–Tarskijeva teorema korak po korak i prilagođen je studentima matematike i tehničkih znanosti.
1Uvod - paradoksi u teoriji skupova
U matematici ponekad nailazimo na tvrdnje koje se kose s našom početnom slikom o proučavanim objektima. Razvoj teorije skupova temelji se dobrim dijelom na borbi s takvim tvrdnjama. Paradoksi su logički izvedene tvrdnje koje upućuju na kontradikciju unutar sustava zaključivanja ili koje se kose s našom intuicijom. Naprimjer, Russelov paradoks ili paradoks brijača pripada prvoj skupini. Možemo ga iskazati na sljedeći način:
Ako je \mathcal{S} skup svih skupova koji ne sadržavaju sami sebe, je li \mathcal{S}\in \mathcal{S}?
Taj paradoks nazivamo i paradoks brijača jer ga možemo preformulirati kao "Ako u nekom selu brijač brije svakog tko ne brije sam sebe i nikog drugog, tko brije brijača?" Ovaj paradoks istaknuo je kontradiktornost teorije skupova u 19. stoljeću i doveo do uvođenja Zermelo-Fraenkelove (ZF) aksiomatike teorije skupova u kojoj ovakve konstrukcije nisu dopustive.
U drugu skupinu paradoksa pripadaju teoremi koji se kose s našom svakodnevnom intuicijom. Znamo da su skup svih parnih i skup svih prirodnih brojeva ekvipotentni (jednakobrojni) jer postoji bijekcija između njih, iako bi osnovnoškolac možda želio ustrajati "Pa svih prirodnih ima dvostruko više nego parnih!"
Ovaj tekst posvećen je Banach–Tarskijevom paradoksu koji također spada u tu drugu vrstu paradoksa. Banach–Tarskijev paradoks je teorem koji, laičkim jezikom, kaže da kuglu u \mathbb{R}^{3} možemo razrezati na konačno mnogo disjunktnih dijelova od kojih možemo sastaviti dvije kugle identične početnoj kugli. Slična tvrdnja, izrečena još više poetski, kaže da od zrna graška možemo napraviti Sunce, a to se svakako kosi s našom intuicijom! Zato je važno istaknuti još jednom da se ne radi ni o čemu mističnom, ali niti kontradiktornom. Važnu ulogu u dokazu ima konstrukcija paradoksalne dekompozicije kugle u kojoj se koristimo skupovima koji su vrlo neobični i koje je nemoguće predočiti. Dekompozicija kugle nije rezanje limuna kuhinjskim nožem u 5 dijelova, već seciranje vrlo preciznim "skupovnim" skalpelom. Ono što činimo na apstraktnoj razini točaka nemoguće je izvesti u stvarnosti.
Čitatelj koji ima neka osnovna znanja iz teorije mjere i algebre lakše će pratiti dokazivanje, ali tekst je pisan i za one koji će prvi put vidjeti dokaz koji povezuje više područja matematike (geometrijske i algebarske aspekte transformacija prostora). Izostavljeni su dokazi poznatijih tvrdnji i tehničkih lema, s referencom gdje se dokaz može pronaći.
Aksiom izbora jedan je od bitnih sastojaka u dokazu Banach–Tarskijeva teorema. Kontroverznost ovog aksioma sastoji se u tome da je ponekad korišten u konstrukciji manje intuitivnih rezultata, ali neupitno je da bez njega ne bismo imali mnoge važne rezultate u modernoj matematici. Gödel je dokazao da ako je ZF teorija konzistentna, onda ona ostaje konzistentna i nakon dodavanja tog aksioma. U ovom tekstu podrazumijevamo aksiom izbora kao dio proširene ZF teorije skupova.
Aksiom. (AI) Neka je I skup i \lbrace A_{i}, i\in I\rbrace familija nepraznih skupova koji su u parovima disjunktni. Tada postoji skup B takav da je za sve i\in I presjek B \bigcap A_{i} jednočlani skup.
U
2Pitanje invarijantne mjere
U osnovnoj i srednjoj školi naučili smo računati površine raznih geometrijskih likova i volumene geometrijskih tijela. Uočimo da su površina i volumen funkcije koje nekim podskupovima od \mathbb{R}^{2} ili \mathbb{R}^{3} pridružuju realne brojeve. Također, jasno je da proizvoljnom segmentu [a,b]\subseteq \mathbb{R}, a\leq b možemo dodijeliti broj b-a\in \mathbb{R} kao njegovu duljinu. No, pitanje je imaju li svi podskupovi skupa \mathbb{R} duljinu, imaju li svi podskupovi od \mathbb{R}^{3} volumen? Koja su svojstva tih veličina? Odgovor dajemo uvođenjem pojma mjere.
Neka je 2^{X} oznaka za partitivni skup skupa X. Mjeru na \mathbb{R} željeli bismo definirati kao funkciju \mu:2^{\mathbb{}}{R}\rightarrow \overline{\mathbb{R}}=\mathbb{R} \cup \lbrace \infty\rbrace koja zadovoljava sljedeća svojstva:
| (i) | za A\subseteq \mathbb{R}, \mu(A)\geq 0. |
| (ii) | \mu(\emptyset)=0. |
| (iii) | za disjunktne A_{i}\subseteq \mathbb{R}, i\in \mathbb{N}, \mu(\bigcup_{i\in \mathbb{N}} A_{i})=\sum_{i\in\mathbb{N}}\mu(A_{i}). |
| (iv) | za A\subseteq \mathbb{R}, c\in \mathbb{R}, \mu(c+A)=\mu(A),\mu(-A)=\mu(A). |
| (v) | za a,b\in \mathbb{R}, a\leq b, \mu([a,b])=b-a. |
Svojstvo (iii) zovemo \sigma-aditivnost, a njemu analogno svojstvo, ali s konačno mnogo disjunktnih podskupova A_{i}, nazivamo konačna aditivnost. Svojstvo (iv) zovemo invarijantnost s obzirom na translacije i zrcaljenja (izometrije).
Zbog svojstva (v) vidimo da se ovakva definicija poklapa s našim predodžbama o duljini segmenta. Može se pokazati da iz svojstava (i)-(v) slijedi da je npr. \mu(\mathbb{Q})=0, pa kažemo da je skup racionalnih brojeva skup mjere nula.
Problem invarijantne mjere zapravo je problem egzistencije takve funkcije. Odgovor je dan sljedećim teoremom.
Teorem 1. Ne postoji funkcija \mu:2^{\mathbb{}}{R}\rightarrow \overline{\mathbb{R}} koja bi zadovoljavala svojstva (i)-(v).
Dokaz ovog teorema (v.
Ako ne želimo da se ovakav rezultat pojavljuje u našoj teoriji, moramo odustati od jedne od ovih triju pretpostavki:
| (1) | aksiom izbora; |
| (2) | \sigma-aditivnost; |
| (3) | funkcija \mu može se definirati na svim podskupovima skupa \mathbb{R}. |
Razmotrimo li još neke rezultate koji se postižu u drugim matematičkim teorijama, vidimo da je zapravo najlakše odustati od treće pretpostavke, te mjeru definirati na manjem skupu podskupova od \mathbb{R} koje onda nazivamo izmjerivim skupovima.
Na \mathbb{R} i \mathbb{R}^{2} moguće je definirati mjeru koja je konačno aditivna (to su donekle duljina i površina na kakve smo naviknuli). Felix Hausdorff dokazao je 1914. da u \mathbb{R}^{3} ne postoji čak niti konačno aditivna mjera koja bi bila invarijantna prema izometrijama u \mathbb{R}^{3}. Metode koje je uveo Hausdorff koriste se i u dokazu Banach–Tarskijeva teorema.
3Jednakorastavljivost i paradoksalne dekompozicije
Kako bismo razumjeli zašto Banach–Tarskijev paradoks zaista vrijedi, moramo razumjeti pojam paradoksalne dekompozicije. Pri tome je ključna veza geometrijskih i algebarskih aspekata. Naime, transformacije prostora (npr. izometrije, ili samo rotacije) imaju strukturu grupe. Grupa transformacija djeluje na prostoru i poznavanjem strukture te grupe vidimo može li se neki objekt paradoksalno dekomponirati te možemo li od dijelova te dekompozicije sastaviti neki drugi objekt.
Definicija 2. Neka je \Vert \cdot\Vert norma na vektorskom prostoru \mathbb{R}^{n}. Bijekciju \phi:U\subseteq\mathbb{R}^{n}\rightarrow V \subseteq\mathbb{R}^{n} zovemo izometrija ako za svake x,y\in U vrijedi
\Vert \phi(x)-\phi(y)\Vert =\Vert x-y\Vert .
Primijetimo da su rotacije i translacije izometrije. Označimo s G_{n} grupu svih izometrija prostora \mathbb{R}^{n}, a sa {S}{O}(n) podgrupu grupe G_{n} koja se sastoji samo od rotacija. Općenito, izometrije koje su ujedno i linearna preslikavanja reprezentirane su ortogonalnim matricama (A\in M_{n}(\mathbb{R}) t.d. {A}{A}^{t}=I) i čine grupu O(n). Tada je {S}{O}(n)=\lbrace \phi\in O(n): \det \phi=1\rbrace.
Definicija 3. Za dva podskupa U,V\subseteq \mathbb{R}^{n} kažemo da su kongruentni, te pišemo U\simeq V, ako postoji izometrija \phi:U\rightarrow V.
Definicija 4. Neka su X,Y\subseteq \mathbb{R}^{n}, te pretpostavimo da postoje particije
Tada kažemo da su X i Y jednakorastavljivi u m dijelova (ili kraće m-jednakorastavljivi) i pišemo X \equiv _{m} Y.
X=X_{1}\cup X_{2}\cup ... \cup X_{m}, \quad Y=Y_{1}\cup Y_{2}\cup ... \cup Y_{m}
takve da je X_{i} \simeq Y_{i} za svaki i=1,2,...,m.Tada kažemo da su X i Y jednakorastavljivi u m dijelova (ili kraće m-jednakorastavljivi) i pišemo X \equiv _{m} Y.
Teorem 5.[Banach–Schröder–Bernstein] Neka su X i Y podskupovi od \mathbb{R}^{n} i U\subseteq X, V \subseteq Y. Ako je X\equiv_{k} V i Y\equiv_{m} U, onda je X\equiv_{k+m} Y.
Dokaz ovog teorema je tehnički, a svodi se na konstrukciju injekcija s X u Y i s Y u X, analogno Cantor–Schröder–Bernsteinovom teoremu.
Definicija 6. Neka je G grupa i X skup. Za preslikavanje \mu:G\times X\rightarrow X (uz oznaku \mu(g,x)=g(x)) kažemo da je djelovanje ako vrijedi
(g_{1}g_{2})(x)=g_{1}(g_{2}(x)), \quad \forall g_{1},g_{2}\in G, x\in X.
Tada kažemo da grupa G djeluje na skup X ili da je X G-skup.
Definicija 7. Neka je X G-skup i E\subseteq X. Kažemo da E ima G-paradoksalnu dekompoziciju ako postoje prirodni brojevi m i n, elementi g_{1},\ldots,g_{n},h_{1},\ldots,h_{m}\in G i u parovima disjunktni podskupovi A_{1},...,A_{n}, B_{1},..., B_{m}\subseteq E takvi da je
pri čemu za g\in G, A\subseteq E, oznaka g(A) označava skup \lbrace g(a): a\in A\rbrace.
E=\cup_{i=1}^{n} g_{i}(A_{i})=\cup_{j=1}^{m} h_{j}(B_{j}),
pri čemu za g\in G, A\subseteq E, oznaka g(A) označava skup \lbrace g(a): a\in A\rbrace.
Banach–Tarskijev paradoks kaže da svaka kugla u \mathbb{R}^{3} ima paradoksalnu dekompoziciju s obzirom na grupu izometrija.
Paradoksalne grupe. Svaka grupa djeluje sama na sebe množenjem slijeva. Paradoksalne grupe definiramo kao grupe koje su paradoksalne s obzirom na takvo djelovanje na samima sebi. Najvažniji primjer paradoksalne grupe je slobodna grupa s dva generatora (slobodna grupa ranga 2), koju ćemo označavati s F_{2}.
Slobodna grupa ranga 2. Elementi grupe F_{2} su riječi sastavljene u alfabetu \lbrace a,b,a^{-1},b^{-1}\rbrace, pri čemu nije dopušteno da bilo koja dva susjedna slova čine par inverznih slova (a i a^{-1} ili b i b^{-1}). Grupovna operacija na riječima je konkatenacija, tj. spajanje dviju riječi (nizova slova) u jednu tako da drugu riječ napišemo iza prve, izostavljajući eventualne parove susjednih inverznih slova. Neutralni element je prazna riječ i označavamo ga s e. Uočite da F_{2} ima prebrojivo mnogo elemenata.
Za x\in \lbrace a,b,a^{-1},b^{-1}\rbrace označimo sa S(x) skup svih riječi F_{2} koje počinju s x.
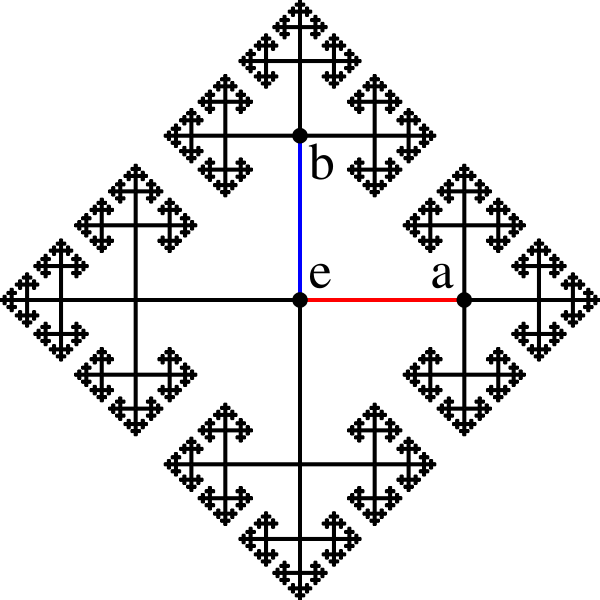
Fraktalnost. Riječi koje počinju slovom a možemo podijeliti u 4 skupa – riječ a i tri skupa određena drugim slovom u riječi. Pogledamo li skup čijim elementima je i drugo slovo a, vidimo da je taj skup zapravo "sličan" skupu S(a). Skupovi S(x), x\in \lbrace a,b,a^{-1},b^{-1}\rbrace su fraktali, objekti čiji su podskupovi kopije čitave cjeline (v. sliku 1).
Teorem 8. Grupa F_{2} je paradoksalna.
Uz oznake koje smo uveli vrijedi:
F_{2}=\lbrace e\rbrace \cup S(a^{-1})\cup S(a)\cup S(b^{-1}) \cup S(b)
F_{2}=aS(a^{-1})\cup S(a)=bS(b^{-1})\cup S(b).
Ove relacije zapravo opisuju da grupu F_{2} možemo rastaviti na 5 dijelova, te od njih sastaviti dvije kopije grupe F_{2}. Ovo paradoksalno svojstvo grupe F_{2} ćemo iskoristiti kako bismo pokazali da od jedne kugle možemo "napraviti" dvije identične kugle polumjera jednakog polumjeru početne kugle.
4Paradoksalna dekompozicija sfere
Ključni korak u dokazu Banach–Tarskijeva teorema je dobivanje paradoksalne dekompozicije sfere u \mathbb{R}^{3}, što se temelji na tome da grupa rotacija {S}{O}(3) ima podgrupu izomorfnu paradoksalnoj grupi F_{2}. Naime, možemo odabrati dvije rotacije koje neće komutirati tako da grupa, generirana tim dvijemama rotacijama, bude izomorfna grupi F_{2}.
Teorem 9. Neka su \alpha i \beta rotacije oko x-, odnosno z-osi za kut \theta takav da je \cos \theta racionalan i različit od 0,\pm\frac{1}{2},\pm1. Tada je podgrupa \Gamma grupe {S}{O}(3) generirana elementima \alpha i \beta izomorfna slobodnoj grupi ranga 2.
Dokaz ovog teorema zainteresirani čitatelj može pronaći u
Definicija 10. Neka je P\subseteq \mathcal{P}(S) i Z\subseteq S. Kažemo da su elementi skupa P kongruentne kopije skupa Z ako je za svaki X\in P, X kongruentan Z.
Teorem 11. Neka je S^{2} sfera u \mathbb{R}^{3} sa središtem u ishodištu. Postoji skup M\subseteq S^{2} takav da
| (i) | S^2 sadržava beskonačno mnogo u parovima disjunktnih kongruentnih kopija od M i |
| (ii) | S^2 se može pokriti s 4 kongruentne kopije od M. |
Dokaz. Particija na orbite. Definirajmo na S^2 relaciju \sim, tako da je x\sim y ako postoji rotacija u \Gamma koja prevodi točku x u točku y. Budući da \Gamma djeluje na S^2, lako je vidjeti da je \sim relacija ekvivalencije.
Fiksne točke. Neka je C skup točaka iz S^{2} koje se pri nekoj rotaciji iz \Gamma (različitoj od identitete \mathcal{E}) preslikavaju u same sebe. Svaka rotacija u {S}{O}(3) , osim \mathcal{E}, ima točno dvije fiksne točke na S^{2}. Zato prebrojivost skupa \Gamma povlači da je skup C prebrojiv.
Neka je x\in C, te y\in S^{2} takav da je x\sim y. Tada postoje \phi, \psi\in \Gamma takvi da je \phi(x)=x i \psi(x)=y. Tada je (\psi \circ \phi \circ \psi ^{-1})(y)=y, te \phi\neq \mathcal{E} povlači \psi \circ \phi \circ \psi ^{-1}\neq \mathcal{E}. Dakle, x\in C, x\sim y \Rightarrow y\in C. Zato je C unija čitavih klasa ekvivalencije, a onda je to i S^{2}\setminus C.
Konstrukcija skupaM.} Koristeći se aksiomom izbora, iz svake klase ekvivalencije u S^{2}\setminus C odaberemo po jednu točku i tako dobivamo skup H. Sada možemo definirati M kao
Svojstvo (i). Promotrimo skupove \beta^{n}(M), n\in\mathbb{N} \cup \lbrace 0\rbrace. Jasno je da su svi oni međusobno kongruentni jer je \beta izometrija. Pokažimo da su i u parovima disjunktni.
Pretpostavimo suprotno da je \beta^{n}(M)\cap \beta^{m}(M) \neq \emptyset za n\lt m. Neka je y\in \beta^{n}(M)\cap \beta^{m}(M). Tada postoje x_{1}, x_{2}\in H i \phi_{1}, \phi_{2} \in S(\alpha) takve da je \beta^{n} \phi_{1} (x_{1})=y=\beta^{m} \phi_{2} (x_{2}). To povlači da je x_{1}=(\phi_{1}^{-1} \circ \beta^{m-n} \circ \phi_{2})(x_{2}). Dakle, x_{1} \sim x_{2}. Budući da je H takav da sadržava točno jedan element iz svake klase ekvivalencije relacije \sim, to je x_{1}=x_{2}. Zato je x_{1} fiksna točka rotacije \phi_{1}^{-1} \circ \beta^{m-n} \circ \phi_{2}\in \Gamma (koja nije identiteta!), odnosno x_{1}\in C, što je kontradikcija s x_{1}\in H\subseteq S^{2}\setminus C. Ovo pokazuje da M ima svojstvo (i).
Svojstvo (ii). Ostaje pokazati da S^{2} možemo pokriti s 4 kongruentne kopije skupa M. Prvo ćemo pokazati da je S^{2}\setminus C\subseteq M \cup \alpha(M). Neka je x\in S^{2}\setminus C. Tada postoji y\in H takav da je x\sim y, odnosno postoji \psi \in \Gamma takav da je \psi(y)=x. Ako je \psi\in S(\alpha), onda je x\in M. Ako pak \psi\not\in S(\alpha), onda je \alpha^{-1}\psi \in S(\alpha^{-1}), pa je x=\alpha(\alpha^{-1}\psi(y))\in \alpha(M).
Budući da je C prebrojiv, mora postojati \rho \in {S}{O}(3) takav da je C\cap \rho(C)=\emptyset. Naime, mora postojati pravac p koji prolazi ishodištem, a ne sadržava niti jednu točku iz C. Rotaciju \rho možemo odabrati kao rotaciju oko pravca p za odgovarajući kut.
Tada je \rho(C)\subseteq S^{2}\setminus C\subseteq M \cup \alpha(M), što povlači C\subseteq \rho^{-1}(M) \cup \rho^{-1}\alpha(M). Dakle, S^{2}=(S^{2}\setminus C )\cup C\subseteq M \cup \alpha(M) \cup \rho^{-1}(M) \cup \rho^{-1}\alpha(M), što pokazuje da M ima svojstvo (ii).
Fiksne točke. Neka je C skup točaka iz S^{2} koje se pri nekoj rotaciji iz \Gamma (različitoj od identitete \mathcal{E}) preslikavaju u same sebe. Svaka rotacija u {S}{O}(3) , osim \mathcal{E}, ima točno dvije fiksne točke na S^{2}. Zato prebrojivost skupa \Gamma povlači da je skup C prebrojiv.
Neka je x\in C, te y\in S^{2} takav da je x\sim y. Tada postoje \phi, \psi\in \Gamma takvi da je \phi(x)=x i \psi(x)=y. Tada je (\psi \circ \phi \circ \psi ^{-1})(y)=y, te \phi\neq \mathcal{E} povlači \psi \circ \phi \circ \psi ^{-1}\neq \mathcal{E}. Dakle, x\in C, x\sim y \Rightarrow y\in C. Zato je C unija čitavih klasa ekvivalencije, a onda je to i S^{2}\setminus C.
Konstrukcija skupaM.} Koristeći se aksiomom izbora, iz svake klase ekvivalencije u S^{2}\setminus C odaberemo po jednu točku i tako dobivamo skup H. Sada možemo definirati M kao
M=\lbrace \phi(x); \phi\in S(\alpha), x\in H\rbrace \cup \lbrace \phi(x); \phi\in S(\alpha^{-1}), x\in H\rbrace .
Svojstvo (i). Promotrimo skupove \beta^{n}(M), n\in\mathbb{N} \cup \lbrace 0\rbrace. Jasno je da su svi oni međusobno kongruentni jer je \beta izometrija. Pokažimo da su i u parovima disjunktni.
Pretpostavimo suprotno da je \beta^{n}(M)\cap \beta^{m}(M) \neq \emptyset za n\lt m. Neka je y\in \beta^{n}(M)\cap \beta^{m}(M). Tada postoje x_{1}, x_{2}\in H i \phi_{1}, \phi_{2} \in S(\alpha) takve da je \beta^{n} \phi_{1} (x_{1})=y=\beta^{m} \phi_{2} (x_{2}). To povlači da je x_{1}=(\phi_{1}^{-1} \circ \beta^{m-n} \circ \phi_{2})(x_{2}). Dakle, x_{1} \sim x_{2}. Budući da je H takav da sadržava točno jedan element iz svake klase ekvivalencije relacije \sim, to je x_{1}=x_{2}. Zato je x_{1} fiksna točka rotacije \phi_{1}^{-1} \circ \beta^{m-n} \circ \phi_{2}\in \Gamma (koja nije identiteta!), odnosno x_{1}\in C, što je kontradikcija s x_{1}\in H\subseteq S^{2}\setminus C. Ovo pokazuje da M ima svojstvo (i).
Svojstvo (ii). Ostaje pokazati da S^{2} možemo pokriti s 4 kongruentne kopije skupa M. Prvo ćemo pokazati da je S^{2}\setminus C\subseteq M \cup \alpha(M). Neka je x\in S^{2}\setminus C. Tada postoji y\in H takav da je x\sim y, odnosno postoji \psi \in \Gamma takav da je \psi(y)=x. Ako je \psi\in S(\alpha), onda je x\in M. Ako pak \psi\not\in S(\alpha), onda je \alpha^{-1}\psi \in S(\alpha^{-1}), pa je x=\alpha(\alpha^{-1}\psi(y))\in \alpha(M).
Budući da je C prebrojiv, mora postojati \rho \in {S}{O}(3) takav da je C\cap \rho(C)=\emptyset. Naime, mora postojati pravac p koji prolazi ishodištem, a ne sadržava niti jednu točku iz C. Rotaciju \rho možemo odabrati kao rotaciju oko pravca p za odgovarajući kut.
Tada je \rho(C)\subseteq S^{2}\setminus C\subseteq M \cup \alpha(M), što povlači C\subseteq \rho^{-1}(M) \cup \rho^{-1}\alpha(M). Dakle, S^{2}=(S^{2}\setminus C )\cup C\subseteq M \cup \alpha(M) \cup \rho^{-1}(M) \cup \rho^{-1}\alpha(M), što pokazuje da M ima svojstvo (ii).
\ \blacksquare
5Banach–Tarskijev paradoks
Ostalo je konačno pokazati najavljivanu tvrdnju. Sljedeći teorem dokazali su S. Banach i A. Tarski 1924. godine. Napominjemo da tvrdnja pokazuje kako u \mathbb{R}^{3} ne postoji invarijantna konačno aditivna mjera.
Teorem 12.[Banach–Tarski] Neka su B_{1}, B_{2} disjunktne trodimenzionalne kugle istog radijusa. Tada je B_{1}\equiv _{10} B_{1}\cup B_{2}.
Dokaz. Tvrdnja slijedi primjenom Banach–Schröder–Bernsteinova teorema (BSB).
Neka je O središte, a S rub kugle B_{1}. Za x\in S s r_{x} označimo dužinu koja spaja x i O. Prema prethodnom teoremu, sfera S se može dekomponirati na četiri dijela. Naime, prema teoremu, sferu možemo pokriti s kongruentna četiri dijela, nazovimo ih M_{1}, M_{2}, M_{3}, M_{4}, a disjunktnost možemo postići tako da stavimo C_{1}=A_{1}, C_{i}=M_{i}\setminus \bigcup_{j=1}^{i-1} M_{j}, i=2,3,4. Tada je S=C_{1} \cup C_{2} \cup C_{3} \cup C_{4}.
Probušenu kuglu B_{1}\setminus \lbrace O\rbrace rastavimo na C^{*}_{i}=\bigcup_{x\in C_{i}} (r_{x} \setminus \lbrace 0\rbrace ), i=1,2,3,4. Središte ćemo dodati skupu C^{*}_{1}. Nadalje, neka je t translacija koja prevodi kuglu B_{1} na B_{2}. Tada primjenom te translacije dobivamo dekompoziciju od B_{2}\setminus \lbrace 0\rbrace.
Da bismo došli do pretpostavki teorema BSB, primijenimo još jednom prethodni teorem, ali ovaj put svojstvo (i). Neka su D_{i}, i\in \mathbb{N} skupovi iz prethodnog teorema takvi da je D_{i}\simeq M za svako i\in \mathbb{N}. Tada je C_{1}^{*} \cup \lbrace O\rbrace kongruentan podskupu skupa D_{1}^{*} \cup \lbrace O\rbrace, te su C_{i}^{*} kongruentni podskupovima od D_{i}^{*}, za i=2,3,4.
Analogno su t(C_{i}^{*}) kongruentni podskupovima D_{i+4}^{*}, i=1,2,3,4, a točka t(O) nekoj točki skupa D_{9}^{*}. Budući da je \bigcup_{i=1}^{9} D_{i}^{*} \subseteq B_{1}, slijedi da je
Dakle, postoji V\subseteq B_{1} takav da je B_{1} \cup B_{2} \equiv _{9} V.
Trivijalno je primijetiti B_{1} \equiv _{1} B_{1} \subseteq B_{1} \cup B_{2}.
Sada primjenom teorema BSB slijedi traženi zaključak
Neka je O središte, a S rub kugle B_{1}. Za x\in S s r_{x} označimo dužinu koja spaja x i O. Prema prethodnom teoremu, sfera S se može dekomponirati na četiri dijela. Naime, prema teoremu, sferu možemo pokriti s kongruentna četiri dijela, nazovimo ih M_{1}, M_{2}, M_{3}, M_{4}, a disjunktnost možemo postići tako da stavimo C_{1}=A_{1}, C_{i}=M_{i}\setminus \bigcup_{j=1}^{i-1} M_{j}, i=2,3,4. Tada je S=C_{1} \cup C_{2} \cup C_{3} \cup C_{4}.
Probušenu kuglu B_{1}\setminus \lbrace O\rbrace rastavimo na C^{*}_{i}=\bigcup_{x\in C_{i}} (r_{x} \setminus \lbrace 0\rbrace ), i=1,2,3,4. Središte ćemo dodati skupu C^{*}_{1}. Nadalje, neka je t translacija koja prevodi kuglu B_{1} na B_{2}. Tada primjenom te translacije dobivamo dekompoziciju od B_{2}\setminus \lbrace 0\rbrace.
Da bismo došli do pretpostavki teorema BSB, primijenimo još jednom prethodni teorem, ali ovaj put svojstvo (i). Neka su D_{i}, i\in \mathbb{N} skupovi iz prethodnog teorema takvi da je D_{i}\simeq M za svako i\in \mathbb{N}. Tada je C_{1}^{*} \cup \lbrace O\rbrace kongruentan podskupu skupa D_{1}^{*} \cup \lbrace O\rbrace, te su C_{i}^{*} kongruentni podskupovima od D_{i}^{*}, za i=2,3,4.
Analogno su t(C_{i}^{*}) kongruentni podskupovima D_{i+4}^{*}, i=1,2,3,4, a točka t(O) nekoj točki skupa D_{9}^{*}. Budući da je \bigcup_{i=1}^{9} D_{i}^{*} \subseteq B_{1}, slijedi da je
B_{1} \cup B_{2}=[C_{1}^{*} \cup \lbrace O\rbrace ] \cup \bigcup_{i=2}^{4} C_{i}^{*} \cup \bigcup_{i=1}^{4} t(C_{i}^{*}) \cup \lbrace t(O)\rbrace \subseteq B_{1}.
Dakle, postoji V\subseteq B_{1} takav da je B_{1} \cup B_{2} \equiv _{9} V.
Trivijalno je primijetiti B_{1} \equiv _{1} B_{1} \subseteq B_{1} \cup B_{2}.
Sada primjenom teorema BSB slijedi traženi zaključak
B_{1}\equiv _{10} B_{1}\cup B_{2}.
\ \blacksquare
Korolar 13.[Banach–Tarski, jaka forma] Neka su A i B ograničeni podskupovi u \mathbb{R}^{3}, nepraznog interiora. Tada su A i B jednakorastavljivi.
Dokaz. Neka su K i L kugle takve da K sadržava A (K postoji zbog ograničenosti skupa A) i B sadrži L (L postoji jer je B nepraznog interiora). Tada postoji prirodan broj n takav da je K sadržano unutar n kopija od L. Dakle,
Time smo pokazali da je A jednakorastavljivo s nekim podskupom od B. Analogno, zamjenom uloga A i B pokazujemo da je B jednakorastavljiv s nekim podskupom od A, te tvrdnja slijedi korištenjem teorema BSB.
A\subseteq K\subseteq (n \text{ kopija od } L)\equiv L\subseteq B,
pri čemu (n \text{ kopija od } L)\equiv L dobivamo indukcijom koristeći se Banach–Tarskijevim teoremom.Time smo pokazali da je A jednakorastavljivo s nekim podskupom od B. Analogno, zamjenom uloga A i B pokazujemo da je B jednakorastavljiv s nekim podskupom od A, te tvrdnja slijedi korištenjem teorema BSB.
\ \blacksquare
6Generalizacije
Problem postojanja paradoksalnih dekompozicija usko je povezan s postojanjem konačno-aditivnih mjera i ta veza opisana je na raznim primjerima u
Pozorno čitanje dokaza Banach–Tarskijeva teorema otkriva da smo konstruirali paradoksalnu dekompoziciju na 10 dijelova. Može se pokazati da je minimalan broj dijelova potreban za paradoksalnu dekompoziciju četiri.
Usko vezan uz Banach–Tarskijev paradoks je Hausdorffov paradoks koji kaže da na sferi S^{2} postoji prebrojiv podskup D takav da je S^{2}\setminus D {S}{O}(3) -paradoksalan. To povlači da na partitivnom skupu sfere S^{2} ne postoji konačno aditivna mjera \mu koja bi bila rotacijski invarijantna i zadovoljavala \mu(S^{2})=1. Dakle, dijelovi paradoksalne dekompozicije sfere ne mogu biti Lebesgue izmjerivi skupovi. Naravno, ograničimo li se samo na izmjerive podskupove, tada postoji takva mjera – Lebesgueova mjera.
Slična svojstva kao izmjerivi skupovi imaju Baireovi skupovi. Baireovi skupovi su podskupovi topološkog prostora koji se od Borelovih razlikuju za uniju nigdje gustih skupova, a izmjerivi skupovi od Borelovih se razlikuju za skup mjere nula. No, pojam Baireova i izmjeriva skupa se ne podudaraju. Otvoreno je pitanje postoji li konačno aditivna mjera ograničimo li se na Baireove skupove. Postojanje takve mjere impliciralo bi negativan odgovor na sljedeće pitanje.
Marczewskijev problem. Postoji li paradoksalna dekompozicija sfere S^{2} (invarijantna s obzirom na rotacije) tako da su svi dijelovi u dekompoziciji Baireovi skupovi?
Moguća je i generalizacija ovih rezultata na neeuklidske prostore. Tako u hiperboličkoj ravnini postoji analogon Hausdorffova paradoksa, pri čemu dijelovi u paradoksalnoj dekompoziciji mogu biti Borelovi!
Centralni teorem koji povezuje paradoksalne dekompozicije i konačno aditivne mjere je Tarskijev teorem.
Teorem 14.[Tarski] Neka grupa G djeluje na skupu X i neka je E\subseteq X. Tada na X postoji konačno aditivna, G-invarijantna mjera \mu: \mathcal{P}(X)\to [0,+\infty] takva da je \mu(E)=1 ako i samo ako E nije G-paradoksalan.
Pokazati da paradoksalna dekompozicija ne postoji moguće je unutar teorije mjerljivih (engl. amenable - pokoran, povodljiv) grupa. Kažemo da je grupa G mjerljiva ako postoji lijevo-invarijantna konačno aditivna vjerojatnosna mjera na svim podskupovima od G.
Teorem 15. Ako je G mjerljiva grupa izometrija od \mathbb{R}^{n}, onda ne postoji ograničen podskup od \mathbb{R}^{n} nepraznog interiora koji je G-paradoksalan. Posebno, Banach–Tarskijev paradoks ne postoji u \mathbb{R} i \mathbb{R}^{2}.
Bibliografija
| [1] | M. Laczkovich, Conjecture and Proof, MAA, Washington, 2001. |
| [2] | S. Mardešić, Matematička analiza, drugi dio, Školska knjiga, Zagreb, 1989. |
| [3] | F. E. Su, The Banach–Tarski Paradox, Minor Thesis, Harvard University, 1990. http://www.math.hmc.edu/ su/papers.html |
| [4] | M. Vuković, Teorija skupova, skripta, Zagreb, 2006. |
| [5] | S. Wagon, The Banach–Tarski Paradox, University Press, Cambridge, 1985. |
| [6] | http://en.wikipedia.org/wiki/Banach–Tarski, zadnja promjena 11. kolovova 2010. |
| [7] |
http://en.wikipedia.org/wiki/Cayley graph, zadnja promjena 22. travnja 2010. |