Kochova pahuljica

Kochova krivulja i Kochova pahuljica jedne su od prvih opisanih fraktalnih krivulja. Predstavio ju je švedski matematičar Niels Fabian Helge von Koch (1870. - 1924.) 1904. godine u radu “On a continuous curve without tangents, constructible from elementary geometry" (originalni francuski naslov: Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire).

To je jedan od najpoznatijih fraktala koji se često koristi kao reprezentativni primjer. Razlika između krivulje i pahuljice je u tome što se kod krivulje počinje s dužinom, a kod pahuljice s jednakostraničnim trokutom.

Možemo je nacrtati tako da počnemo od jednakostraničnog trokuta i rekurzivno mijenjamo svaku stranicu na sljedeći način:

1. Podijelimo dužinu na tri dužine jednake duljine.
2. Nacrtamo jednakostraničan trokut, tako da mu je osnovica srednja dužina dobivena u 1. koraku, a vrh gleda prema van
3. Uklonimo dužinu koja je osnovica trokuta iz 2. koraka

U Lindenmayerovu sustavu konstrukcija izgleda ovako:

• Početak: F + + F + + F
• Pravilo: F → F - F + + F - F
• Značenje:
  • F = "crtaj naprijed"
  • + = "zakreni u smjeru kazaljke na satu za 60°"
  • - = "zakreni u smjeru suprotnom od smjera kazaljke na satu za 60°"

Dakle,

• nulta iteracija: F + + F + + F
• prva iteracija: F - F + + F - F + + F - F + + F - F + + F - F + + F - F
• druga iteracija: F - F + + F - F - F - F + + F - F + + F - F + + F - F - F - F + + F - F + + F - F + + F - F - F - F + + F - F + + F - F + + F - F - F - F + + F - F + + F - F + + F - F - F - F + + F - F + + F - F + + F - F - F - F + + F – F …

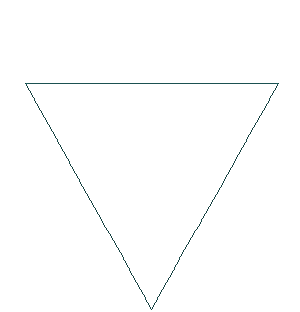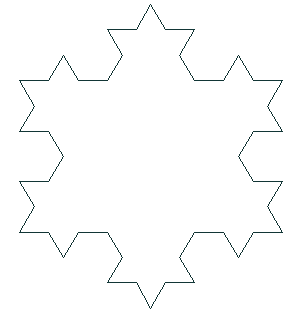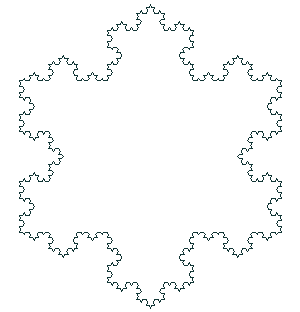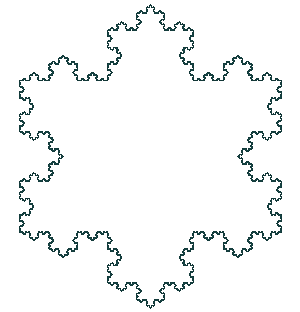
Duljina

Recimo da je duljina početne dužine 1 m. Nakon prve iteracije, duljina krivulje je 4/3 m jer imamo četiri dužine duljine 1/3 m. Nakon druge iteracije, duljina je 16/9 m. Matematičkom indukcijom lako dolazimo do opće formule L = (4/3)ⁿ, n je broj iteracija. Vidimo da duljina raste eksponencijalno te zaključujemo da duljina teži u beskonačno, ako broj iteracija teži u beskonačno.

Površina

Budući da je duljina Kochove krivulje beskonačna (odnosno, teži u beskonačno), i duljina Kochove pahuljice je beskonačna. No, njena je površina konačna.

Uzmimo da je površina osnovnog trokuta 1. Jednostavnom podjelom trokuta vidimo da će manji trokuti u sljedećoj iteraciji imati devet puta manju površinu. Površina svih triju trokuta u prvoj iteraciji tada je 1/3 površine početnog trokuta. U sljedećoj iteraciji imamo 12 trokuta ukupne površine 4/27, a površina svih trokuta u sljedećoj iteraciji jest 16/243. Uočavamo da svi navedeni članovi osim prvog tvore geometrijski niz kvocijenta 4/9, čiji je zbroj:

Dodamo li još površinu početnog trokuta (koja nije dio geometrijskog niza), dobivamo ukupnu površinu \frac{8}{5} površine početnog trokuta.