Gabrielov rog
Gabrielov rog
Gabrielov rog (ili Torricellijeva truba) je figura koju je otkrio Evangelista Torricelli, koja ima beskonačnu površinu, ali konačan volumen. Toricelli (1608. - 1647.) je bio talijanski fizičar i matematičar, najpoznatiji po svom izumu barometra. Paradoks je dobio ime po anđelu Gabrijelu koji svirajući trubu najavljuje Sudnji dan.
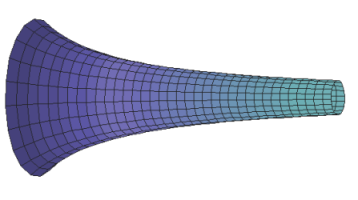
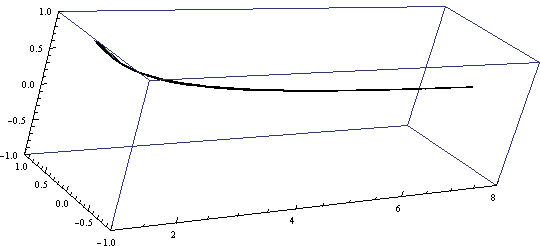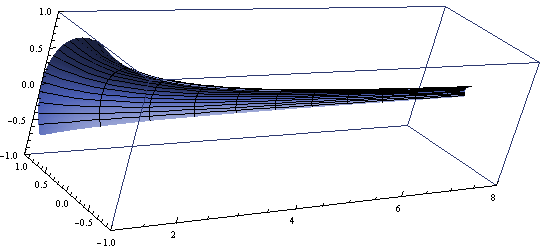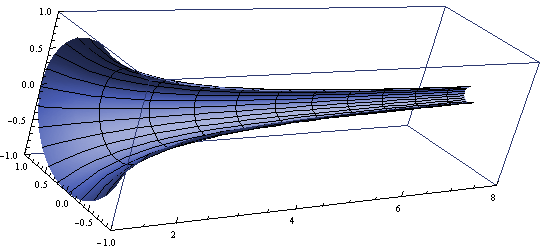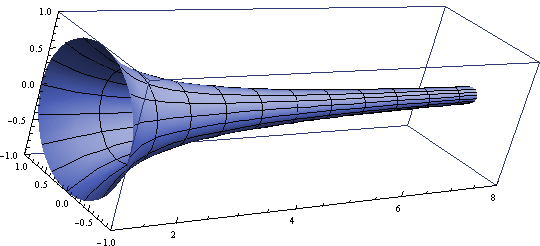
Gabrielov rog dobijemo tako da uzmemo graf funkcije y=\frac{1}{x} na domeni x \geq 1 i rotiramo ga u tri dimenzije oko x-osi. S pomoću integrala možemo odrediti volumen V i površinu A:
Iako a može biti proizvoljno velik, volumen nikad neće preći \pi, ali će se približavati \pi kad a teži u beskonačno:
Općenito, ako rotiramo krivulju y=f(x) za 2 π oko x-osi između granica x = a i y = b, površina dobivene figure je dana formulom
U slučaju Gabrielova roga imamo:
Površina će biti veća od 2\pi \ln a. Budući da \ln a nema gornju među kad a teži u beskonačno, rog će imati beskonačnu površinu:
U vrijeme kad je ovo otkriveno (prije otkrića integralnog računa) bilo je smatrano paradoksalnim. Torricellijev zaključak bazirao se na Cavalierievoj metodi uspoređivanja volumena područja među paralelnim ravninama.
Paradoksalna posljedica dobivenog rezultata je da Gabrielov rog možemo napuniti s π kubičnih jedinica boje, ali je beskonačan broj kvadratnih jedinica boje potreban za obojiti cijelu površinu. Jedno jednostavno rješenje je bojiti rog s unutarnje strane. Budući da stvarna boja ima volumen, rog će u jednom trenutku postati preuzak, pa će biti pokriven samo konačan dio površine.