Cantorov teorem

Za bilo koji skup A, partitivni skup od A ima strogo veći kardinalni broj od samog A.

Dokaz.

Promotrimo skup A. Postoji bar jedan skup podskupova od A iste kardinalnosti kao A. To može biti skup koji sadržava sve takve skupove da je u svakom od njih točno jedan element iz A. Naprimjer, za skup {1, 2, 3} to je skup {{1},{2},{3}}.

Neka je S partitivni skup od A.

Budući da pravila koja vrijede za konačne skupove ne moraju vrijediti za beskonačne, pretpostavimo da S ima isti kardinalni broj kao A. Pokazat ćemo da je postojanje bijekcije između A i S u kontradikciji s definicijom skupa S kao partitivnog skupa od A. Zasad pretpostavimo da su obje tvrdnje istinite.

Tada svakom elementu iz S možemo pridružiti jedan element iz A. Neka je Q neki element iz S, to jest, podskup od A. Skupu Q pridružili smo neki element iz A. Taj element može se i sam nalaziti u Q, ali i ne mora.

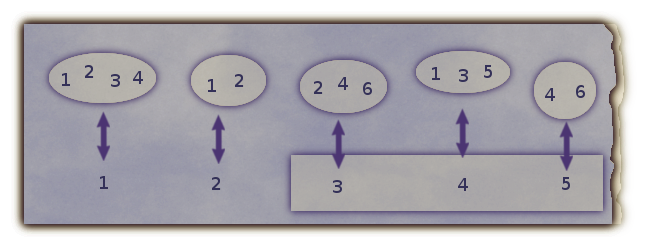Primjer: Brojevi 3, 4 i 5 pridruženi su skupovima u kojima se sami ne nalaze.

Neka je a element iz A koji je pridružen nekom skupu iz S tako da se sam a ne nalazi u njemu pridruženom skupu. Neka je T skup svih takvih elemenata iz A. Skup T očito je podskup od A. No, tada po definiciji skupa S, skup T mora biti element od S, te mu zato mora biti pridružen neki element iz A, nazovimo ga t. Nalazi li se t u skupu T ili ne?

Primjer: Skupu koji sadržava sve brojeve koji su pridruženi skupovima u kojima se sami ne nalaze pridružili smo broj t

Po definiciji T, ako je t iz A pridružen skupu T, onda se sam ne smije nalaziti u T. Ali, ako t nije u T, onda sam mora biti element skupa kojem je pridružen. Došli smo do kontradikcije. Zaključujemo da ne postoji bijekcija između A i partitivnog skupa od A.