Proučavanje srodnosti različitih organizama jedan je od temeljnih interesa biologije. Obično tvrdnje o srodnosti među različitim biljnim ili životinjskim vrstama, kao i među ljudima zasnivamo na njihovim fizičkim sličnostima. No srodnost se ne mora uvijek manifestirati kroz zajedničke fizičke osobine, a ne vrijedi ni obrnuto – velike fizičke sličnosti ne moraju nužno značiti vrlo blisko zajedničko podrijetlo. Tragove zajedničkih korijena danas tražimo na molekularnom nivou, odnosno proučavajući promjene u DNK nizovima, tj. mutacije. DNK niz na apstraktnom nivou možemo shvatiti kao niz nukleotida tipova adenin, citozin, timin, gvanin ili, još jednostavnije, kao dugački niz sastavljen od slova A, C, T, G. Kroz generacije, određeni niz mutira i sve se više razlikuje od polaznog niza, primjerice
 
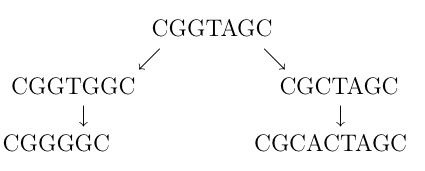
prikazuje dva niza nastala od istog određenim brojem promjena. U prvoj generaciji od originalnog niza jednom promjenom slova (A u C, odn. G u C) dobili smo dva nova niza. Takva promjena naziva se supstitucija. Poslije su oba ova niza doživjela dodatne mutacije – lijevom je obrisano slovo T, dok je desnom umetnut par CA. Ove mutacije nazivamo delecija odnosno insercija. Insercija, delecija i supstitucija (umetanje, brisanje i zamjena) nukleotidnih baza jedini su tipovi mutacija koje susrećemo na molekularnom nivou. Postavlja se pitanje kako za dva određena niza, bez poznavanja evolucijskih događaja, odrediti imaju li oni zajedničko podrijetlo, odnosno imaju li organizmi čiji su to nizovi zajedničkog pretka.

Pretpostavimo da smo izdvojili nizove ATAAGC i AAAAAC. Želimo li te nizove usporediti i utvrditi njihovu sličnost, napisat ćemo ih jedan ispod drugog, tako da je svaki znak drugog niza potpisan točno ispod jednog znaka prvog niza, kao što je vidljivo na primjeru: Ovaj postupak naziva se poravnanje nizova, a za odgovarajuće parove znakova kažemo da su poravnati. Jednakost dvaju poravnatih slova zovemo podudaranjem, različitost promašajem. Poravnanje nizova zapravo slikovito prikazuje moguću evoluciju nizova, stoga bi velik broj podudarajućih znakova mogao sugerirati evolucijsku vezu. U slučaju nizova različitih duljina, kao što su npr. CGGGGC i CGCACTAGC čiju smo evoluciju ilustrirali na početku, na odgovarajuća mjesta u nizovima umetnut ćemo znakove "-" i time dobiti nizove jednakih duljina koje možemo poravnati. Time zapravo pretpostavljamo da je u (mogućoj) evoluciji došlo do insercije ili delecije pa za poravnanje tog znaka s bilo kojim drugim znakom upotrebljavamo riječ indel, nastalu spajanjem riječi insercija i delecija. Gornje nizove primjerice možemo poravnati na sljedeća 2 načina: ali to, naravno, nisu jedine mogućnosti. Uočimo da je broj mogućih poravnanja jako velik, no nas ne zanimaju sva poravnanja, već samo ono koje izražava najveću sličnost među nizovima.
Kako bismo poravnanja mogli uspoređivati, uvest ćemo veličinu koju ćemo zvati ocjena poravnanja ili score. Ta bi veličina trebala nagraditi sličnosti (podudaranja), a kazniti različitosti (promašaje i indele). Optimalno poravnanje bit će ono s najvećom ocjenom. Zbog velike duljine nizova, velikog broja mogućih poravnanja, optimalno poravnanje nije lako naći. Postoje razni algoritmi vezani uz taj problem, a najpoznatiji su Needleman-Wunsch algoritam za globalno i Smith-Waterman algoritam za lokalno poravnanje.

Globalno poravnanje je poravnanje prilikom kojeg su iskorištena sva slova u oba niza. Kod lokalnog poravnanja poravnavamo samo dijelove niza, pa se to poravnanje npr. svodi na traženje najduljeg podudarajućeg segmenta. Nadalje, prilikom lokalnog poravnanja možemo ili ne moramo dopustiti indele. Postoje i tzv. višestruka poravnanja kada, kako sama riječ kaže, poravnavamo više nizova odjednom.

Kao što je već rečeno, sličnost nizova izražena je preko veličine koju smo nazvali ocjenom poravnanja. Međutim, pitanje je koliko velika mora biti ta veličina da bismo nizove proglasili sličnima. Odgovor na to pitanje dat će teorija vjerojatnosti i statistika. Za početak, DNK nizove shvatit ćemo kao realizaciju niza nezavisnih slučajnih varijabli A_{1},\ldots ,A_{n} s vrijednostima u skupu \mathcal{A}=\lbrace \text{A,C,T,G}\rbrace. Pretpostavit ćemo zbog jednostavnosti da indeli ne postoje, odnosno da smo ih uklonili nakon poravnanja nekim od algoritama. Tako ćemo uspoređivati poravnate nizove jednake duljine, npr. \textbf{A}=A_{1},\ldots ,A_{n} i \textbf{B}=B_{1},\ldots ,B_{n}.

Sada možemo postaviti statističke hipoteze: Dakle, polazimo od nulhipoteze da među nizovima nema izrazite sličnosti, odnosno da je uočena „sličnost” (mjerena ocjenom poravnanja) posljedica slučajnosti. Jedan od načina testiranja ovakvih hipoteza svodi se na izračun tzv. testne statistike, što je u našem slučaju ocjena poravnanja, te na određivanje tzv. p-vrijednosti te ocjene. Kao što ćemo ilustrirati, p-vrijednost dobivamo korištenjem teorije vjerojatnosti, a grubo govoreći ona predstavlja vjerojatnost da, ako vrijedi nulhipoteza (o nezavisnosti nizova) vidimo dobivenu ili još bolju ocjenu poravnanja. Ako pokažemo kako je vjerojatnost da se tako dobro poravnanje dogodi „sasvim slučajno” velika, ostajemo pri polaznoj pretpostavci, u suprotnom se priklanjamo alternativi.

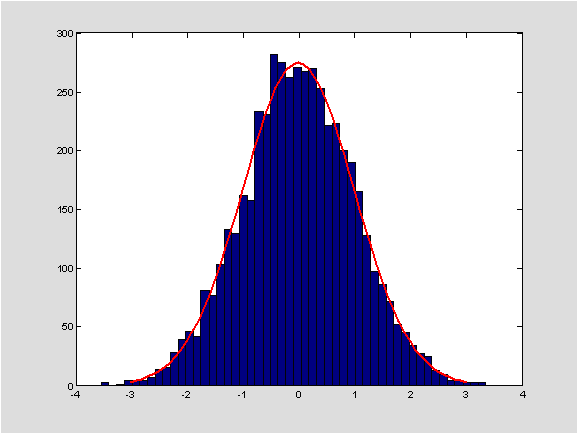
Jedan od najpoznatijih rezultata teorije vjerojatnosti je tzv. centralni granični teorem. On kaže da ako zbrojimo niz nezavisnih, jednako distribuiranih slučajnih varijabli koje imaju očekivanje \mu i varijancu (odn. srednjekvadratno odstupanje) \sigma^{2}\lt \infty, tada će za njihovu sumu S_{n} vrijediti da ima približno jediničnu normalnu ili Gaussovu razdiobu za velike n. Prisjetimo se da ovu razdiobu karakterizira gustoća koja se naziva i Gaussova funkcija \varphi(t)= ({\sqrt{2\pi}})^{-1}e^{{-t^{2}}/{2}} (vidi sliku 2). Integral ove gustoće od a do b jednostavno je vjerojatnost da jedinična normalna slučajna varijabla upadne u taj interval.

Neka su \textbf{A}=A_{1},\ldots ,A_{n} i \textbf{B}=B_{1},\ldots ,B_{n} dva niza nezavisnih, jednako distribuiranih slučajnih varijabli te neka je s:\mathcal{A}\times \mathcal{A}\to \mathbb{R} realna funkcija. Ocjenu poravnanja definiramo kao S_{n}=\sum_{i=1}^{n}s(A_{i},B_{i}). Primijetimo da su s(A_{i},B_{i}) slučajne varijable koje su nezavisne i jednako distribuirane za različite indekse i. Ako s \mu označimo njihovo matematičko očekivanje, a sa \sigma^{2} njihovu varijancu, dobivamo iz gore spomenutog teorema sljedeću relaciju Ona određuje asimptotsko ponašanje vjerojatnosti da ocjene poravnanja S_{n} pomaknute za vlastito očekivanje n\mu i podijeljene s {\sqrt{n}\sigma} leže ispod nekog zadanog nivoa x.

Iz prethodne formule izvodimo i približnu formulu za p-vrijednost koja, u slučaju da je ocjena poravnanja primjećenih nizova jednaka s i da je n dovoljno velik, izgleda ovako: gdje je \Phi(x) funkcija definirana u (1).

Primjer. Pretpostavimo da su primjećena dva DNK niza duljine 100.000 realizacije nizova nezavisnih, jednako distribuiranih slučajnih varijabli s uniformnom distribucijom na skupu slova \lbrace \text{A, C, T, G}\rbrace. Odnosno, pretpostavimo da pojava nukleotida na bilo kojem mjestu u nizu ne ovisi ni o tipu nukleotida, ni o mjestu pojavljivanja, ni o nukleotidima na prethodnim pozicijama. Posebno, svako slovo na svakom mjestu pojavljuje se s vjerojatnošću 1/4. Pretpostavimo nadalje da je ocjena poravnanja zadana s pomoću funkcije s:\mathcal{A}\times \mathcal{A}\to \mathbb{R}, Sada je \mu=\mathbb{P}(A_{i}=B_{i})=1/4, a varijanca od s(A_{i},B_{i}) lako se nađe kao \sigma^{2}=3/16. Ako bi score poravnanja bio jednak 25.000, pripadna p-vrijednost iznosila bi 0.5, a u slučaju da je ocjena jednaka 25.200, p-vrijednost bila bi jednaka 2.5731\cdot 10^{-9}. U prvom slučaju nemamo dovoljno jak argument za odbacivanje nulhipoteze. Uočite: ako bismo zaista nasumice izvlačili slova A, C, G, T i tako kreirali dva nezavisna niza duljine 100.000 slova, razumno bi bilo očekivati da će se oni podudarati na približno jednoj četvrtini mjesta. U drugom slučaju pak imamo jak argument za njeno odbacivanje u korist alternative.

Budući da se DNK nizovi tijekom evolucije bitno mijenjaju, ali obično sadržavaju i regije koje ostaju relativno nepromijenjene, lokalna poravnanja s biološke su strane zanimljivija od globalnih. Lokalna sličnost dvaju nizova izražena je npr. preko najduljeg podudarajućeg segmenta. Ako podudaranje poravnatih slova nazovemo uspjehom, onda, drugim riječima, tražimo najdulji niz uspjeha, što možemo interpretirati kao najdulji uzastopni niz jedinica u nizu sastavljenom samo od 0 i 1, ili, što je više u duhu vjerojatnosti, kao najdulji niz uzastopnog pojavljivanja glave prilikom bacanja novčića. Problem ovog tipa riješili su mađarski matematičari Paul Erdös i Alfred Rényi 1970. godine. Heuristički argument iza njihova rezultata je sljedeći. Ako je vjerojatnost uspjeha jednaka p, niz uspjeha duljine m pojavit će se s vjerojatnošću p^{m}. Budući da postoji točno n mogućih nizova uspjeha (po jedan prije svakog bacanja, od kojih su mnogi duljine 0 istina), očekivani će broj nizova uspjeha duljine m biti približno np^{m}. Ako prepostavimo da se najdulji niz pojavljuje samo jednom, njegova duljina R_{n} trebala bi zadovoljavati 1\approx np^{R_{n}}, iz čega dobivamo R_{n}\approx\log_{1/p}{n}. Uočite da R_{n} kod poravnanja predstavlja maksimum skupa \lbrace k: A_{i+j}= B_{i+j} \text{ za sve } j =1,\ldots,k, \text{ i neki } i =0,1,\ldots, n-k \rbrace.

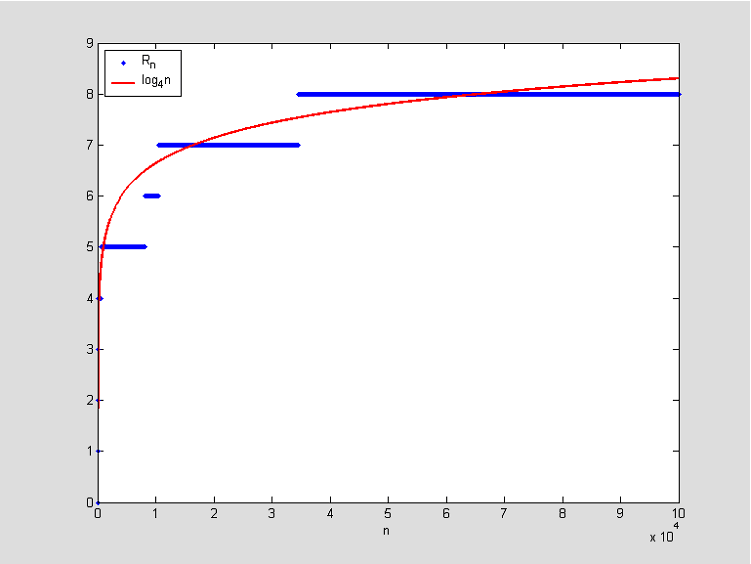
Analogno globalnom poravnanju, htjeli bismo normirati (i eventualno centrirati) vrijednosti R_{n} tako da distribuciju dobivene slučajne varijable možemo aproksimirati nekom poznatom razdiobom. Ovdje se koristimo rezultatom vezanim uz distribuciju maksimuma nizova slučajnih varijabli. Iz tog rezultata zaključujemo da bi aproksimativna distribucija trebala biti standardna Gumbelova. Ako slučajna varijabla Y ima ovu razdiobu, tada vrijedi \mathbb{P}(Y\leq x)=e^{-e^{-x}} za sve realne x. Preciznije, uz oznake q=1-p i \lambda=\ln(1/p), slučajna varijabla imat će, za dovoljno veliki n, aproksimativno standardnu Gumbelovu distribuciju. Iz te činjenice može se izvesti formula za p-vrijednost za isti par hipoteza, no ovaj put korištenjem lokalnog poravnanja. Odnosno, ako smo vidjeli niz podudaranja duljine t, tada vrijedi

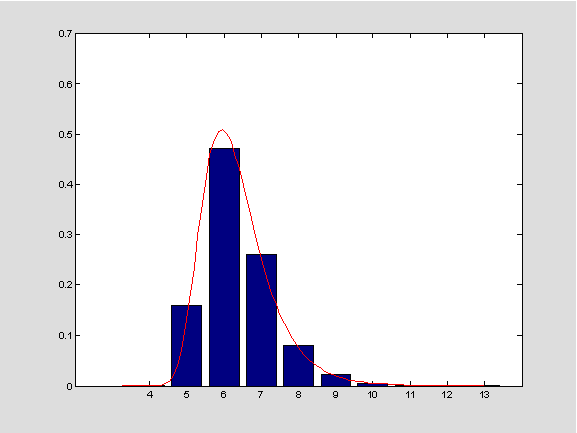
Primjer. Ako ponovno pretpostavimo da su DNK nizovi realizacije nizova nezavisnih, jednako distribuiranih slučajnih varijabli s uniformnom distribucijom i njihova duljina je jednaka 100.000, onda, ako je najdulji primjećeni zajednički niz duljine 10, korištenjem prethodne formule dobivamo da je p-vrijednost približno jednaka 0.069, a ako je najdulji primjećeni zajednički segment duljine 12, pripadna p-vrijednost iznosi 0.0045. Uočimo da je posljednja p-vrijednost manja od 0.05, što je uobičajena granica kod koje odbacujemo nulhipotezu (u ovom slučaju o nezavisnom podrijetlu nizova). Prema tome, uočavanje podudarajućeg niza duljine 12 među nizovima duljine 100.000 bio bi jak pokazatelj sličnosti, dok bismo niz duljine 10 mogli prihvatiti i kao sasvim slučajan.

Napomenimo na kraju da smo i kod lokalnog i kod globalnog poravnanja ignorirali mogućnost indela odnosno pomaka, kao i eventualne zavisnosti između susjednih nukleotida u DNK nizu. Matematički rezultati vrlo bliski gore iznesnima postoje i u ovim i u drugim, zahtjevnijim slučajevima. Statistička analiza DNK nizova i dalje je aktivno područje istraživanja s raširenim primjenama u evolucijskoj genetici, medicini, forenzici i drugdje.