Neke primjene određenog integrala u fizici
1Riječ-dvije o integralnom računu
Problemi računanja površine nekog područja stari su više od 4000 godina. Odgovor na taj problem daje integralni račun. Integral je jedan od ključnih pojmova matematike čiju su ideju računanja prvi oblikovali Isaac Newton i Dottfried Wilhelm Leibniz, dok je prvu strogu definiciju određenog integrala dao Bernhard Riemann. Danas se tehnike integriranja primjenjuju u prirodnim znanostima, inženjerstvu, ekonomiji te brojnim drugim područjima. U fizici, određeni integrali omogućuju precizno računanje kompleksnih pojmova, počevši od klasične mehanike do elektromagnetizma i kvantne mehanike.
Cilj ovog rada je objasniti određeni integral te čitatelju približiti taj apstraktan matematički pojam preko opipljivog svijeta fizike. Poznavanje primjena integralnog računa u fizici uvelike pomaže razumjeti matematičke tehnike, kao i koncepte fizike, što pokazuje povezanost matematike i fizike.
2Riemannov integral ograničene funkcije na segmentu
Računati površinu jednostavnih geometrijskih likova poput pravokutnika, trokuta ili kruga naučili smo još u osnovnoj školi. Postavlja se pitanje kako računati površinu nekog općenitog lika u ravnini? Motivirani ovim pitanjem uvodimo pojam Riemannovog1 integrala funkcije i povezujemo ga s površinom "ispod njezinog grafa". Odmah ćemo promatrati ograničene funkcije na segmentu, jer ćemo se takvima najčešće baviti u problemima iz primjene.
Neka je [a,b] segment realnih brojeva i f:[a,b]\rightarrow \textbf{R} ograničena funkcija. Stoga, postoje realni brojevi
m=\displaystyle \inf_{x \in [a,b]} f(x)\text{ i }M=\displaystyle \sup_{x \in [a,b]} f(x),
tj. infimum i supremum funkcije f. Uočimo, ako je [a_{1},b_{1}] \subseteq [a,b] tada je i restrikcija od f na [a_{1},b_{1}] ograničena funkcija i iz
m \leq f(x) \leq M,\ x \in [a,b]
slijedi
(1)
m \leq m_{1} \leq f(x) \leq M_{1} \leq M, \ x \in[a_{1},b_{1}],
Za prirodni broj n, segment [a,b] podijelimo na n dijelova tako da je
a=x_{0}\lt x_{1}\lt \dots\lt x_{k}\lt \dots\lt x_{n-1}\lt x_{n}=b.
Tada konačan skup točaka P=\lbrace x_{0},x_{1},\dots,x_{n}\rbrace nazivamo subdivizijom ili particijom segmenta [a,b]. Za subdiviziju P^{*} kažemo da je profinjenje subdivizije P ako je P^{*}\subseteq P.
Definicija 1. Neka je [a,b]\subseteq \textbf{R} i n\in \textbf{N}. Za subdiviziju P=\lbrace x_{0}, x_{1},\dots,x_{n}\rbrace definiranu s
x_{i}:=a+ih, h=:\frac{b-a}{n}, \quad i\in \lbrace 0,1,\dots,n\rbrace ,
kažemo da je ekvidistantna.Neka je
M_{k}=\sup\lbrace f(x):x \in [x_{k-1},x_{k}]\rbrace ,\ m_{k}=\inf\lbrace f(x):x \in [x_{k-1},x_{k}]\rbrace ,1\leq k\leq n,
te t_{k} \in [x_{k-1},x_{k}] proizvoljna točka. Definiramo Darbouxove2 i integralnu sumu:
\begin{eqnarray*} s(f,P)=\sum_{k=1}^{n} m_{k}(x_{k}-x_{k-1}) \text{ je donja Darbouxova suma,}\\ \sigma(f,P)=\sum_{k=1}^{n} f(t_{k})(x_{k}-x_{k-1}) \text{ je integralna suma, te}\\ S(f,P)=\sum_{k=1}^{n} M_{k}(x_{k}-x_{k-1}) \text{ gornja Darbouxova suma.} \end{eqnarray*}
Očito vrijedi:
(2)
m(b-a) \leq s(f,P) \leq \sigma(f,P) \leq S(f,P) \leq M(b-a).
\mathcal{I}_{*}(f;a,b)=\sup \mathcal{A}\text{ i }\mathcal{I}^{*}(f;a,b)=\inf \mathcal{B}.
Definicija 2. Broj \mathcal{I}_{*} naziva se donji Riemannov integral funkcije f na [a,b], a broj \mathcal{I}^{*} gornji Riemannov integral funkcije f na [a,b].
Iz pokazanog je jasno da svaka ograničena funkcija f na segmentu [a,b] ima gornji i donji Riemannov integral.
Definicija 3. Za funkciju f:[a,b]\rightarrow \textbf{R} ograničenu na [a,b] kažemo da je R-integrabilna ili integrabilna u Riemannovom smislu ako je
\mathcal{I}_{*}(f;a,b)=\mathcal{I}^{*}(f;a,b).
Tada se broj \mathcal{I}=\mathcal{I}_{*}=\mathcal{I}^{*} naziva integral ili R-integral funkcije f na segmentu [a,b] .Vratimo se sada na problem površine s početka. Neka je T=\lbrace (x,y) \in \textbf{R} \times \textbf{R}:0 \leq y \leq g(x), x\in[a,b]\rbrace pseudotrapez ispod grafa funkcije g:[a,b]\rightarrow \textbf{R}^{+}. Sada površinu pseudotrapeza definiramo s
\int_{a}^{b} g(x)dx
za integrabilnu funkciju g.
3Primjene integralnog računa u fizici
Sada kada smo se malo bolje upoznali s integralnim računom ostaje vidjeti što sve, između ostalog, u području fizike možemo računati preko integrala.
3.1Računanje duljine puta
Promotrimo za početak tijelo koje se giba jednoliko pravocrtno. Ako se tijelo giba brzinom v, put koje je ono prešlo do trenutka t definira se kao: s:=vt. Sada uvedimo tijelo koje se giba, ne nužno jednoliko pravocrtno. Na pravac po kojem se giba tijelo uvedimo koordinatni sustav i početak gibanja označimo s 0 te označimo s v(t) brzinu tijela u trenutku t. Želimo odrediti put koji je tijelo prešlo do trenutka t, tj. s(t).
Neka je dana funkcija brzine v:[0,t]\rightarrow\textbf{R} gdje je t\gt 0. Uzmimo subdiviziju
0=t_{0}\lt t_{1}\lt \dots\lt t_{n}=t,\quad n\in\textbf{N}
segmenta [0,t]. Na proizvoljnom podsegmentu [t_{k-1},t_{k}],k\lt n,k\in\textbf{N}, brzinu tijela aproksimiramo s v(t_{k}*) pri čemu je t_{k}*\in[t_{k-1},t_{k}] proizvoljna točka. Tada se na tom podsegmentu tijelo giba jednoliko pravocrtno pa vrijedi da je s_{k}\approx v(t_{k}*)(t_{k}-t_{k-1}), odnosno
s\approx \sum_{k=1}^{n} v(t_{k}*)(t_{k}-t_{k-1}).
Ova suma je upravo jednaka integralnoj sumi funkcije v pa ima smisla definirati:
s(t)=\int_{0}^{t} v(\tau)d\tau.
Primjer 1. Biciklist Marko vozi utrku i njegova je brzina dana funkcijom v(t)=2t+1, t\gt 0, gdje je vrijeme mjereno u sekundama. Koliko je metara prešao Marko za 10 sekundi?
Prema prethodno izvedenoj formuli imamo da je
Prema prethodno izvedenoj formuli imamo da je
s(10)=\int_{0}^{10} (2\tau+1)d\tau=\tau^{2}\bigg|_{0}^{10}+\tau\bigg|_{0}^{10}=110.
Marko je za 10 sekundi prešao 110\,m.
Napomena 1. Umjesto definiranja prijeđenog puta preko brzine, može se definirati i brzina preko puta. Tada je
za neki trenutak t (vidjeti [1] ). Uočimo da je to u skladu s našom definicijom puta preko brzine uz prirodan zahtjev s(0)=0\,m (tijelo za 0 sekundi prijeđe 0 metara). Integrirajući (3) od 0 do t te primjenom Newton-Leibnitzove formule dobijamo:
(3)
v(t)=s'(t),
\begin{eqnarray*} \int_{0}^{t} s'(\tau)d\tau&=&\int_{0}^{t} v(\tau)d\tau\\ s(t)-s(0)&=&\int_{0}^{t} v(\tau)d\tau\\ s(t)&=&\int_{0}^{t} v(\tau)d\tau. \end{eqnarray*}
Napomena 2. Akceleracija čestice definira se kao promjena brzine u vremenu, tj.
a(t)=v'(t).
Tada primjenom Newton-Leibnitzove formule i integriranjem obje strane dobivamo:
v(t)=\int_{0}^{t} a(\tau)d\tau +v(0),
tj. ako nam je poznata početna brzina možemo izračunati brzinu u proizvoljnom trenutku kao integral akceleracije.
3.2Rad sile
Ako za početak pretpostavimo da na tijelo djeluje konstantna sila F u istome smjeru tada se tijelo pod utjecajem sile F giba jednoliko pravocrtno i prijeđe put s. Tada se rad sile F definira kao W:=F\cdot s.
No, iz iskustva znamo da sila ne mora uvijek biti konstantna. Primjerice, zamislite da idete na autobusni kolodvor i vučete veliki kofer - sigurno ćete na početku vašeg puta imati više energije, odnosno sila koju primjenjujete bit će veća!
Dakle, sila može biti zadana funkcijom f:[a,b]\rightarrow\textbf{R} pri čemu segment [a,b] predstavlja put koje je tijelo prešlo uslijed djelovanja sile f. Da bi smo izračunali rad te sile, napravimo subdiviziju
a=x_{0}\lt x_{1}\lt \dots\lt x_{n}=b, \quad n\in\textbf{N},
segmenta [a,b]. Ako promotrimo proizvoljni podsegment [x_{k-1},x_{k}],k\lt n,k\in\textbf{N}, silu na tom segmentu aproksimirat ćemo s f(x_{k}') pri čemu je x_{k}'\in[x_{k-1},x_{k}] proizvoljna točka. Tada je sila na tom podsegmentu konstantna, tj. gibanje je jednoliko pravocrtno pa je rad sile na tom podsegmentu
W_{k}\approx f(x_{k}')(x_{k}-x_{k-1}),
odnosno na cijelom putu:
W\approx\sum_{k=1}^{n}f(x_{k}')(x_{k}-x_{k-1}).
Primijetimo da je gornji izraz zapravo integralna suma funkcije f na zadanom segmentu [a,b] pa rad sile ima smisla definirati kao integral funkcije f, tj.
W:=\int_{a}^{b}f(x)dx.
Promotrimo kako izračunati rad u nekim konkretnim situacijama.
Primjer 2. Ako je poznato da je potrebna sila od 50\,N da bi se opruga prirodne duljine 10\,cm rastegnula na 20\,cm, izračunajmo koliko je rada potrebno uložiti da bi se opruga rastegnula s 12 na 15\,cm.
Prema Hookeovom zakonu iznos sile koju treba uložiti za produljenje opruge jednak je umnošku koeficijenta elastičnosti k i produljenja opruge x. Možemo iskoristiti Hookeov zakon da izračunamo konstantu elastičnosti k te zadane podatke; x=10cm=0.1\,m i sila f=50\,N. Iz toga slijedi k=500\,N/m, odnosno sila opruge je dana funkcijom f(x)=500x. Stoga je traženi rad jednak:
Prema Hookeovom zakonu iznos sile koju treba uložiti za produljenje opruge jednak je umnošku koeficijenta elastičnosti k i produljenja opruge x. Možemo iskoristiti Hookeov zakon da izračunamo konstantu elastičnosti k te zadane podatke; x=10cm=0.1\,m i sila f=50\,N. Iz toga slijedi k=500\,N/m, odnosno sila opruge je dana funkcijom f(x)=500x. Stoga je traženi rad jednak:
W=\int_{0.02}^{0.05} 500xdx=500 \frac{x^{2}}{2}\bigg|_{0.02}^{0.05}=0.525\,J.
Treba napomenuti da je osim samog iznosa sile važno i njezino usmjerenje. Promotrimo sljedeći primjer.
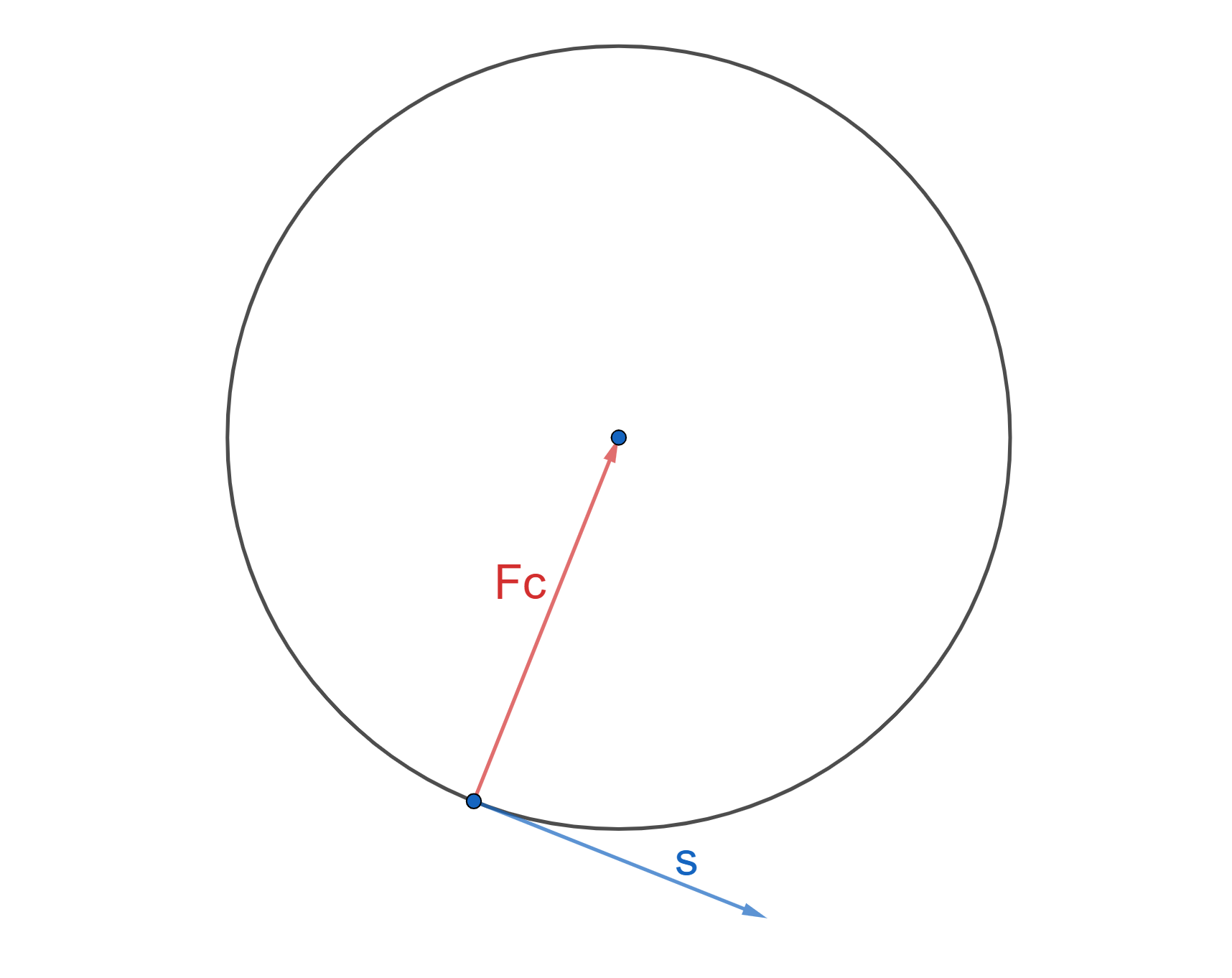
Primjer 3. Dječak uzme igračku koja se sastoji od užeta i loptice na kraju te ju vrti u zraku. Uže na kojem je loptica dugo je 5\,cm, loptica je teška 0.1\,kg, a sestra mu je pomogla izmjeriti brzinu vrtnje loptice koja je stalna i iznosi 15\,m/s. Koliki rad obavi centripetalna sila ako znamo da je loptica napravila 5 krugova?
Centripetalna sila pri stalnoj brzini v iznosi2 ), pa je ona okomita na putanju iz čega slijedi W=F_{c}\cdot s=0\,J, tj. centripetalna sila ne obavlja rad.
Centripetalna sila pri stalnoj brzini v iznosi
F_{c}=m\frac{v^{2}}{r},
gdje je m masa tijela, a r polumjer kružnice po kojoj se to tijelo giba. U ovom slučaju ona iznosi:
F_{c}=0.1\frac{15^{2}}{0.05}=450\,N.
Loptica ukupno prijeđe put od 5 krugova, odnosno 5 puta prijeđe opseg kruga (koji iznosi 2r\pi) pa ne uzimajući u obzir usmjerenje centripetalne sile dobijemo:
W=F_{c}\cdot s=450\cdot 5\cdot 2\cdot0.05\pi\approx706,86\ J.
Međutim, rad sile definiran je kao skalarni produkt, a za njega je bitno i usmjerenje vektora za koje ga računamo. Znamo da je centripetalna sila usmjerena prema središtu kružnice po kojoj se tijelo giba (Slika Sada kada smo vidjeli važnost usmjerenja sile s obzirom na putanju promotrimo sljedeći primjer.
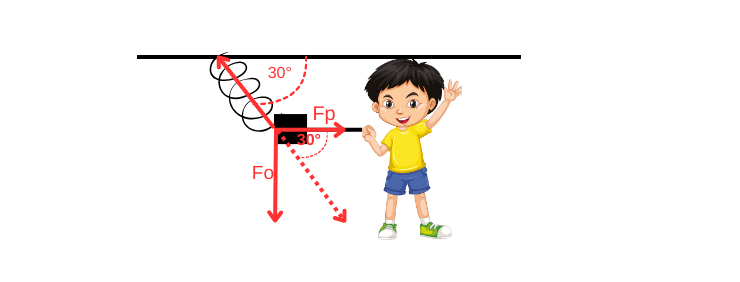
Primjer 4. Dječak vuče lagani blok na opruzi konstante elastičnosti k=800\,N/m kao na Slici 3 . Pri tome je blok postavljen ukoso pod kutom od 30^{\circ} prema horizontali.
Izračunajmo rad koji dječak treba obaviti kako bi povukao blok i oprugu za 10\,cm ako zanemarujemo masu bloka.
Primijetimo da je ovdje elastična sila usmjerena pod kutom s obzirom na smjer putanje pa je potrebno rastaviti silu na komponente.
Neka je F_{o} komponenta okomita na putanju, a F_{p} komponenta paralelna putanji bloka. Iz trigonometrijskih jednakosti slijedi:
Primijetimo da je ovdje elastična sila usmjerena pod kutom s obzirom na smjer putanje pa je potrebno rastaviti silu na komponente.
Neka je F_{o} komponenta okomita na putanju, a F_{p} komponenta paralelna putanji bloka. Iz trigonometrijskih jednakosti slijedi:
F_{o}=F\sin30^{\circ} \quad i \quad F_{p}=F\cos30^{\circ}.
U prethodnom smo primjeru vidjeli da je rad sile okomite na putanju jednak 0 pa nam samo preostaje izračunati rad sile F_{p}. Sada koristeći Hookeov zakon dobivamo ukupan rad:
W=\int_{0}^{0.1} F_{p}(x)dx=\int_{0}^{0.1}800x\cos30^{\circ} dx=800\frac{\sqrt{3}}{2}\frac{x^{2}}{2}\bigg|_{0}^{0.1}\approx 3.46J.
3.3Masa i težište
Neka je dan tanki3 ravni štap duljine l, te funkcija \rho:[0,l]\rightarrow\textbf{R} koja predstavlja linijsku gustoću njegove mase. Ukoliko je ona konstantna kažemo da je štap homogen, a u suprotnom je nehomogen. Tada je masa tog štapa dana s:
m=\int_{0}^{l} \rho(x)dx.
Napomena 3. Umjesto računanja mase cijelog štapa možemo računati masu dijela [0,x]\subseteq[0,l] danog štapa. Tada je:
m(x)=\int_{0}^{x} \rho(\tau)d\tau.
Primjer 5. Na raspolaganju imamo štap duljine 5\,m, linijske gustoće mase \rho:[0,5]\rightarrow\textbf{R} zadane s \rho(x)=x^{3}+2x^{2}+1. Kolika je težina dijela štapa između pravaca x=2 i x=3?
Kako bi izračunali težinu prvo moramo izračunati masu štapa:
Kako bi izračunali težinu prvo moramo izračunati masu štapa:
m=\int_{2}^{3} (x^{3}+2x^{2}+1)dx=\frac{x^{4}}{4}\bigg|_{2}^{3}+2\frac{x^{3}}{3}\bigg|_{2}^{3}+x\bigg|_{2}^{3}=\frac{359}{12}.
Sada je težina jednaka:
F=mg\approx293.5\ N.
m_{1}(\bar{x}-x_{1})=m_{2}(x_{2}-\bar{x}),
dobivamo da je:
\bar{x}=\frac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}.
Veličina mx naziva se moment mase m koja se nalazi u koordinati x, a m_{1}x_{1}+m_{2}x_{2} naziva se moment sustava u odnosu na ishodište.Tešište, moment i masu možemo računati i za općenitije slučajeve, što slijedi u nastavku.
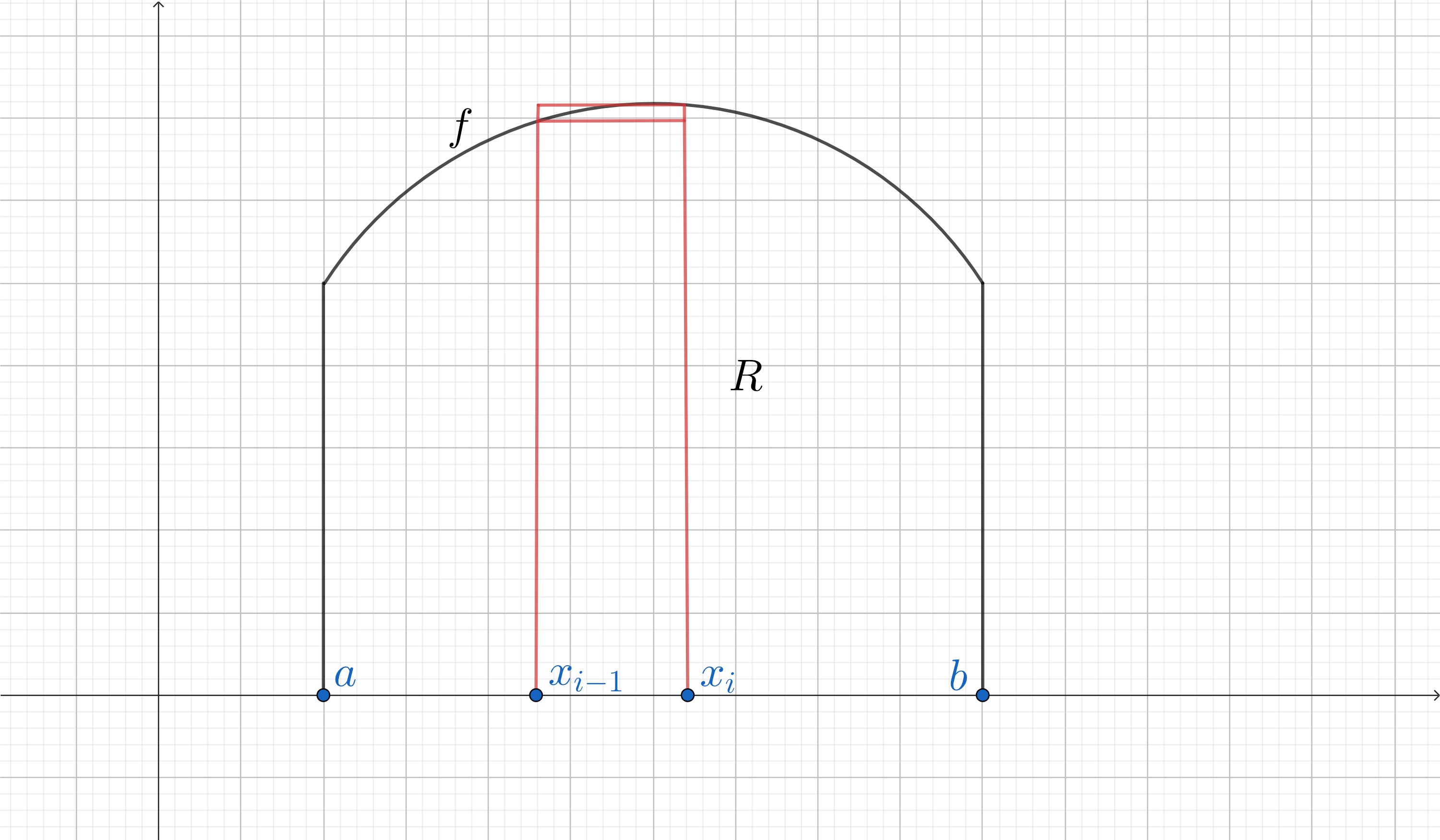
Neka je dana tanka, homogena ploča R, konstantne površinske gustoće mase \rho, koja se nalazi ispod grafa funkcije f:[a,b]\rightarrow\textbf{R^{+}} kao na Slici
Koristimo princip simetrije: ukoliko je homogena ploča R simetrična s obzirom na neki pravac, onda je težište ploče na tom pravcu. Uzmimo ekvidistantnu subdiviziju
a=x_{0}\lt x_{1}\lt \dots\lt x_{n}=b, \quad n\in\textbf{N}
segmenta [a,b] te s \Delta x:=x_{k}-x_{k-1},k\lt n,k\in\textbf{N}, označimo širinu svakog segmenta. Neka je nadalje \bar{x_{k}}=\frac{x_{k-1}+x_{k}}{2} središte tog segmenta. Tada je po principu simetrije težište k-tog pravokutnika u točki (\bar{x_{k}},\frac{1}{2}f(\bar{x_{k}})) i masa mu jednaka: m_{k}=\rho f(\bar{x_{k}})\Delta x. Sada moment ploče s obzirom na os x možemo aproksimirati s:
M_{x}\approx\sum_{k=1}^{n} \rho\frac{1}{2}(f(\bar{x_{k}}))^{2}\Delta x,
odnosno profinjenjem subdivizije dobivamo
M_{x}:=\frac{1}{2}\rho\int_{a}^{b}f^{2}(x)dx.
Analogno definiramo moment s obzirom na os y:
M_{y}:=\rho\int_{a}^{b}xf(x)dx.
Primjer 6. Izračunajte moment sustava koji se sastoji od tanke ploče gustoće 2, koja se nalazi ispod grafa funkcije g:[0,2\pi]\rightarrow\textbf{R} zadane formulom g(x)=\cos x, s obzirom na x i y os.
Prema prethodno izvedenim formulama imamo:
Prema prethodno izvedenim formulama imamo:
\begin{eqnarray*} M_{y}&=&2\int_{0}^{2\pi} x\cos x dx=\bigg|\displaystyle^{u=x\quad \quad \quad u'=dx}_{v'=\cos xdx\quad v=\sin x}\bigg|=x\sin x\bigg|_{0}^{2\pi}+\int_{0}^{2\pi} \sin xdx\\&=&-\cos x\bigg|_{0}^{2\pi}=0, \end{eqnarray*}
M_{x}=\frac{1}{2}2\int_{0}^{2\pi} \cos^{2}xdx=\int_{0}^{2\pi}\bigg(\frac{1}{2}+\frac{1}{2}\cos2x\bigg)dx=\frac{1}{2}x\bigg|_{0}^{2\pi} +\frac{\sin 2x}{4}\bigg|_{0}^{2\pi}=\pi.
Izvedimo sada koordinate težišta homogene ploče R koja se nalazi ispod grafa funkcije f. Momenti sile se ne mijenjaju premještanjem ukupne mase u težište pa slijedi da koordinate težišta (\bar{x},\bar{y}) zadovoljavaju jednakosti
m\bar{x}=M_{y}\text{ i }m\bar{y}=M_{x},
gdje je
m=\rho P=\rho \int_{a}^{b} f(x)dx
ukupna masa ploče R. Sada lako dobijemo izraze za kooordinate težišta:
(4)
\bar{x}=\frac{\displaystyle\int_{a}^{b} xf(x)dx}{\displaystyle\int_{a}^{b} f(x)dx},\quad \bar{y}=\frac{\displaystyle\frac{1}{2}\displaystyle\int_{a}^{b} f^{2}(x)dx}{\displaystyle\int_{a}^{b} f(x)dx}.
Ako se područje R za koje tražimo težište nalazi između krivulja y=f(x) i y=g(x), gdje je f(x)\geq g(x) za svaki x\in[a,b], može se pokazati da su koordinate težišta (\bar{x},\bar{y}) dane s
(5)
\bar{x}=\frac{\displaystyle\int_{a}^{b} x(f(x)-g(x))dx}{\displaystyle\int_{a}^{b}(f(x)-g(x))dx},\quad \bar{y}=\frac{\displaystyle\frac{1}{2}\displaystyle\int_{a}^{b}(f^{2}(x)-g^{2}(x))dx}{\displaystyle\int_{a}^{b}(f(x)-g(x))dx}.
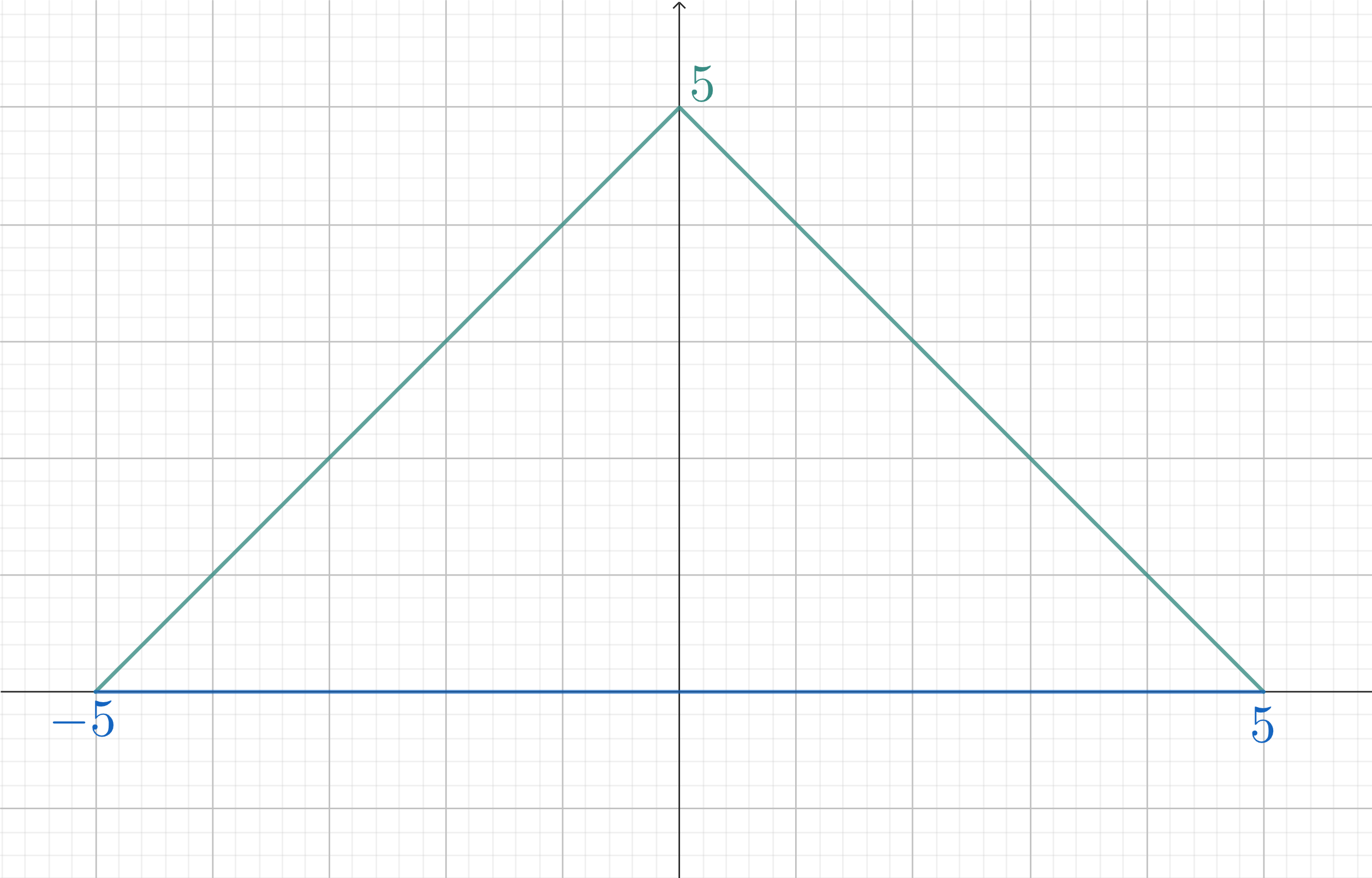
Primjer 7. Markov tata odlučio je napraviti kućicu za vrapce. Krov kućice modelirao je funkcijom f:\textbf{R}\rightarrow\textbf{R},\ f(x)=-|x|+5, pod kućice je paralelan podlozi te su bočne strane ispunjene. Gdje Marko mora zakačiti konac na kućici kako bi ona stajala ravno na drvetu?
Budući da kućica mora biti u ravnoteži zaključujemo da Marko treba zakačiti konac u koordinatama težišta.
Pod kućice je paralelan podlozi i zato ćemo uzeti pravac y=0 kao jednu stranu kućice. Zatim, određujemo njegova sjecišta s funkcijom f, što lako vidimo da su x=-5\text{ i }x=5. Ako promotrimo grafički prikaz ovog područja (Slika6 )
vidimo da je simetrično s obzirom na os y, pa je prema principu simetrije \bar{x}=0.
Sada još trebamo izračunati \bar{y}:
Budući da kućica mora biti u ravnoteži zaključujemo da Marko treba zakačiti konac u koordinatama težišta.
Pod kućice je paralelan podlozi i zato ćemo uzeti pravac y=0 kao jednu stranu kućice. Zatim, određujemo njegova sjecišta s funkcijom f, što lako vidimo da su x=-5\text{ i }x=5. Ako promotrimo grafički prikaz ovog područja (Slika
vidimo da je simetrično s obzirom na os y, pa je prema principu simetrije \bar{x}=0.
Sada još trebamo izračunati \bar{y}:
\begin{eqnarray*} P=\int_{-5}^{5} f(x)dx&=& \int_{-5}^{0} (x+5)dx+\int_{0}^{5} (-x+5)dx\\&=&\frac{x^{2}}{2}\bigg|_{-5}^{0}+5x\bigg|_{-5}^{0}-\frac{x^{2}}{2}\bigg|_{0}^{5}+5x\bigg|_{0}^{5}=10, \end{eqnarray*}
\begin{eqnarray*} \int_{-5}^{5} f^{2}(x)dx&=&\int_{-5}^{0} (x+5)^{2}dx+\int_{0}^{5} (-x+5)^{2}dx\\&=&\int_{-5}^{0} (x^{2}+10x+25)dx+\int_{0}^{5} (x^{2}-10x+25)dx=50, \end{eqnarray*}
te je
\bar{y}=\frac{\frac{1}{2}\cdot 50}{10}=2.5.
Slijedi da Marko treba okačiti konac na koordinatama (0,2.5).
4Zaključak
U ovom radu promatrani su integrali funkcije jedne varijable i njihova primjena u fizici. Nakon uvođenja Riemannovog integrala, proučavane su neke njegove primjene, kao što su računanje duljine puta, rad sile i određivanje koordinata težišta nekog tijela. Nadamo se da će zainteresiranom čitatelju tema biti zanimljiva i korisna, te ga dodatno potaknuti na proučavanje veza između matematike i raznih drugih prirodnih i društvenih znanosti.
Bibliografija
| [1] | Krešimir Burazin, Jelena Jankov, Ivana Kuzmanović, Ivan Soldo, Primjene diferencijalnog i integralnog računa funkcija jedne varijable, Osijek, 2017. |
| [2] | Dr. Miljenko Crnjac, Mr. Dragan Jukić, Dr. Rudolf Scitovski, Matematika, Osijek, 1994. |
| [3] | Dimitrije Hajduković, Matematika 1, Glas, Banja Luka, 1989. |
| [4] | Svetozar Kurepa, Matematička analiza 1, Tehnička knjiga, Zagreb, 1975. |
| [5] |
Šime Ungar, Matematička analiza 1 i 2, skripta, Zagreb, 2018. (javno dostupno na: https://www.pmf.unizg.hr/_download/repository/MATANALuR.pdf) |