Problem prehrane je klasičan problem linearnog programiranja u kojem se minimizira linearna funkcija cilja uz zadana linearna ograničenja. Problem prehrane je i ekonomski zanimljiv problem jer je minimizacija troškova tema koju ekonomisti podučavaju na svim razinama obrazovanja. Dodatno, problem prehrane je važan i ostatku društva jer s jedne strane velik dio svjetske populacije ne ispunjava prehrambene potrebe a s druge strane sve veći dio populacije ima problema s pretilosti. Posebni izazov predstavlja i rast cijena prehrambenih proizvoda, kvaliteta hrane koja se konzumira, ekološka proizvodnja i održivost prehrane, prehrambene navike i utjecaj kulture te zdravstveni problemi vezani uz prehranu.




Problem prehrane jedan je od prvih problema optimizacije koji se proučava već od 1930-ih godina. Inspiriran je željom vojske da zadovolji nutritivne potrebe vojnika ili ratnih zarobljenika uz što manje troškove. Izvorni problem prehrane postavio je George Joseph Stigler 1945. godine te ga je rješavao heurističkom metodom. Njegova procjena je bila da trošak optimalne prehrane iznosi 39.93 USD godišnje (prema cijenama proizvoda iz 1939. godine). Jack Laderman je nešto kasnije rješavao Stiglerov model s tada novom simpleks metodom, što je ujedno bio prvi proračun većih razmjera u optimizaciji. Pokazalo se da su Stiglerova nagađanja o optimalnom rješenju bila pogrešna za svega 24 centa godišnje.




Standardne pretpostavke linearnog programiranja koje vrijede i kod problema prehrane su izvjesnost, proporcionalnost, djeljivost, aditivnost i nenegativnost. Izvjesnost znači da sve konstante, poput npr. jediničnih cijena, količina pojedinih hranjivih tvari u jednoj jedinici pojedinog proizvoda, minimalnih nutrititivnih zahtjeva za pojedinom hranjivom tvari itd., imaju unaprijed poznate vrijednosti. Proporcionalnost kaže da ako je poznato da 1 jedinica proizvoda P sadrži a jedinica određene hranjive tvari, onda x jedinica proizvoda P sadrži ax jedinica navedene hranjive tvari. Djeljivost osigurava da vrijednosti varijabli mogu biti realni a ne samo prirodni brojevi odnosno da je proizvode moguće kupiti „na rinfuzu“ u bilo kojoj količini a ne samo na komade. Npr. moguće je kupiti 0.3 kg jabuka ili 0.42 litre mlijeka. Aditivnost osigurava da možemo zbrajati nutritivne doprinose različitih proizvoda. Npr. ako je poznato da 1 jedinica proizvoda P sadrži a jedinica određene hranjive tvari a 1 jedinica proizvoda Q sadrži b jedinica iste hranjive tvari, onda x jedinica proizvoda P i y jedinica proizvoda Q sadrži ukupno ax+by jedinica tražene hranjive tvari.

Važno je naglasiti da je u praksi često teško zadovoljiti pojedine pretpostavke. Npr. proporcionalnost nije zadovoljena ako se cijena mijenja s porastom količine proizvoda koji se kupuje, što je razumno za očekivati; izvjesnost pada jer su cijene proizvoda podložne promjenama; djeljivost nije uvijek prisutna jer se neke prozvode kupuje upravo na komade i nije moguće kupiti pola proizvoda.




Formulacija optimizacijskog problema, kao što je problem prehrane, osim prikupljanja podataka, traži i definiranje varijabli, funkcije cilja i ograničenja.

Neka je zadano da se izbor hrane provodi između n proizvoda označenih s P_{1},P_{2},\ldots,P_{n} koji su dostupni na određenom tržištu te neka su tržišne cijene po jedinici i-tog proizvoda c_{i},i=1,2,...,n. Neka su hranjive tvari koje se nalaze u navedenim proizvodima označene s T_{1},T_{2},...,T_{m} te neka je a_{ij},i=1,2,...,n, j=1,2,...,m količina j-te hranjive tvari u jednoj jedinici i-tog proizvoda. Matricu A=[a_{ij}] nazivamo nutritivna matrica. Nadalje, neka b_{j},j=1,2,...,m predstavlja minimalni zahtjev za j-tom hranjivom tvari.

Ako sve navedene podatke prikažemo u tablici, dobijemo nutritivnu tablicu kao na slici 1.






Prvi korak u oblikovanju odgovarajućeg matematičkog modela problema prehrane je identificiranje i definiranje nepoznanica pomoću kojih će se kasnije definirati funkcija cilja i ograničenja. Stoga, označimo s x_{i},i=1,2,...,n trenutno još uvijek nepoznatu količinu i-tog proizvoda. Cilj problema prehrane jest upravo u određivanju vrijednosti x_{i}^{*},i=1,2,…,n za nepoznate količine x_{i} proizvoda P_{i} koje je potrebno nabaviti a koje minimiziraju trošak prehrane i istovremeno zadovoljavaju sva ograničenja.

Korištenjem trenutno nepoznatih količina x_{i} proizvoda P_{i} i poznatih jediničnih cijena c_{i} definiramo funkciju cilja kao Funkcija cilja zapravo predstavlja ukupne troškove prehrane pri korištenju x_{i} jedinica proizvoda P_{i} po cijeni c_{i} . Funkciju cilja odnosno ukupne troškove treba minimizirati, Budući jedna jedinica i-tog proizvoda sadrži a_{ij} jedinica j-te hranjive tvari, umnožak a_{ij} x_{i} predstavlja količinu j-te hranjive tvari u x_{i} jedinica proizvoda P_{i}. Stoga zbroj predstavlja ukupnu količinu j-te hranjive tvari konzumirane u svih x_{1},x_{2},...,x_{n} jedinica proizvoda P_{1},P_{2},...,P_{n} redom. Zahtjev da se ukupno konzumira barem b_{j},j=1,2,...,m jedinica j-te hranjive tvari sada se može zapisati kao Dodatno, na sve varijable se postavlja ograničenje nenegativnosti jer nije moguće konzumirati negativnu količinu i-tog proizvoda.

Što je veći broj ograničenja m i broj dostupnih proizvoda n, to je problem prehrane realniji i optimalni obrok potencijalno raznovrsniji [2].

Ako s A označimo nutritivnu matricu [a_{ij}], s b vektor (b_{1},b_{2},...,b_{m}), s c vektor cijena (c_{1},c_{2},...,c_{n}) a s x vektor nepoznanica (x_{1},x_{2},...,x_{n}), problem prehrane možemo u matričnom obliku zapisati kao:



Promotrimo konkretan primjer problema prehrane prema podacima iz diplomskog rada [1].

Iako nutritivne tablice sadrže podatke o velikom broju hranjivih tvari, u ovom primjeru ćemo se zbog jednostavnosti ograničiti na masti, zasićene masti, ugljikohidrate, proteine, kalcij i vitamin C te na ukupan unos energije. Načelno, obroci u danu se dijele na doručak, ručak i večeru, ali kako postoji mogućnost da ljudi ne jedu pojedine obroke u istom dijelu dana svaki dan, odnosno mogućnost da nekad jedu doručak ili neki drugi obrok kasnije ili ranije, model je zamišljen tako da postoje odabrane namirnice ili obroci koja pojedinac treba konzumirati tijekom dana kako bi zadovoljio svoje potrebe za hranjivim tvarima, ali odluka o tome kada će koji obrok konzumirati ostaje na samom pojedincu.




Prvi korak u stvaranju modela prehrane studenta je određivanje preporučenih dnevnih unosa hranjivih tvari kod odrasle osobe. Inače, preporučeni dnevni unos (RDA) je prosječan dnevni unos hranjive tvari koji je dovoljan da zadovolji potrebe gotovo svih (97-98%) zdravih osoba [4].

U drugom koraku je potrebno pronaći izbor namirnica u kojima su zastupljene promatrane hranjive tvari. Iako se na Internetu mogu pronaći podatci o tome koliko koja namirnica sadrži pojedine hranjive tvari, poput npr. USDA FoodData Central [3], točna količina može se očitati i s deklaracija samih proizvoda. Dodatno, preporučene količine vezani za dnevni unos često znaju biti prikazane u tablici na deklaracijama proizvoda.

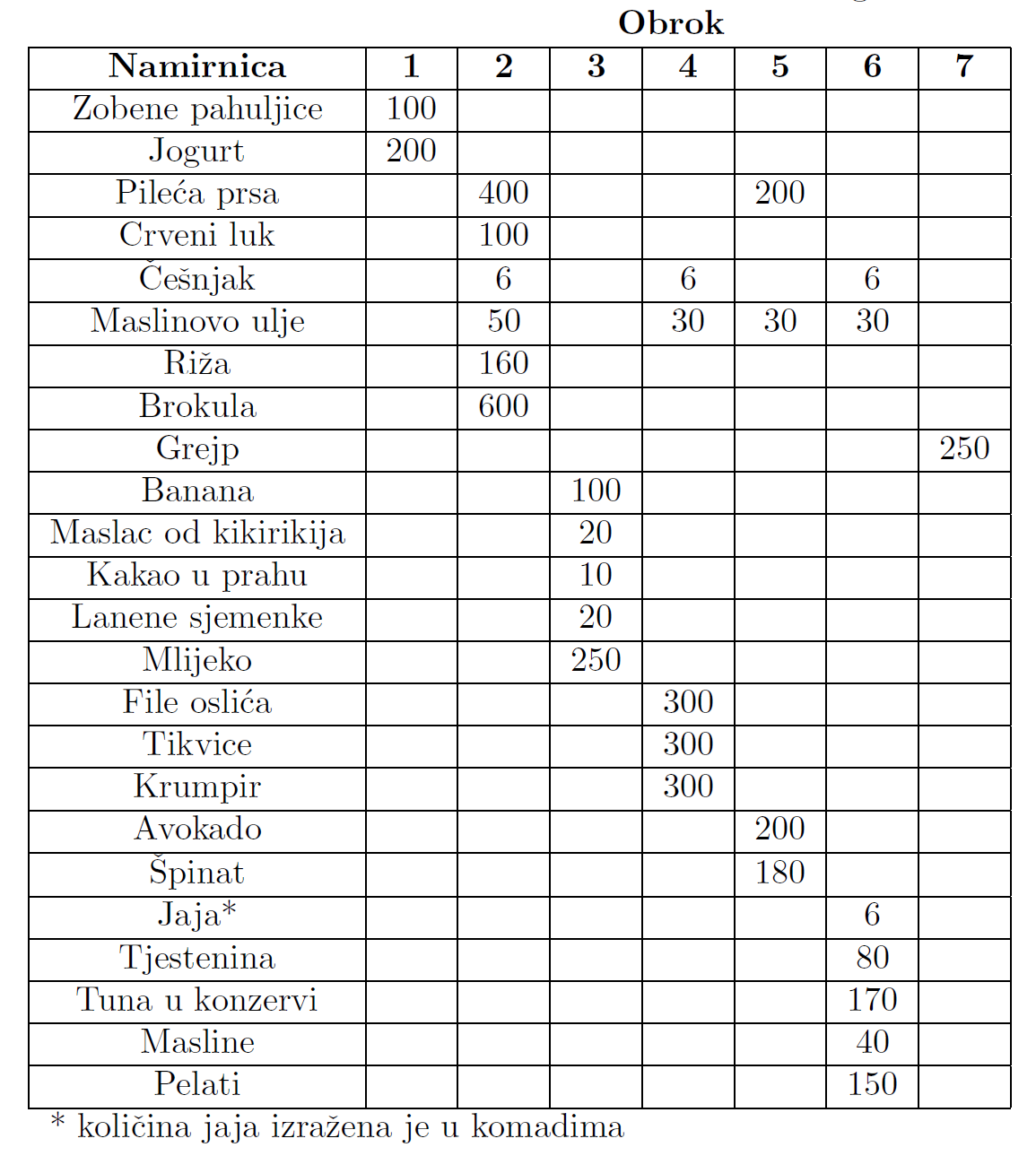
Nakon što su identificirane namirnice koje će se promatrati, potrebno je definirati i dostupne obroke. Obroci su definirani sastojcima navedenim u tablici 1. Detaljne količine namirnica po obroku bit će navedene kasnije u ovom radu.

U slučaju da se pojedini proizvod kupuje u količini koja je veća od količine koja se traži traži u pojedinom jelu, cijena koja će se uzimati u obzir će biti ona koja izražava vrijednost potrebne količine u jelu. Pretpostavlja se da se ostatak proizvoda može iskoristiti u idućim danima i obrocima koji će zahtijevati taj proizvod.

Idealan dnevni unos kalorija varira ovisno o starosti, metabolizmu i tjelesnoj aktivnosti, među ostalim. Generalno, preporučeni dnevni unos kalorija iznosi 2000 kalorija za žene i 2500 kalorija za muškarce [5]. Treba napomenuti da se to odnosi na tjelesno aktivnije osobe, a ovaj model ne uzima nužno u obzir takav profil osobe tako da će se koristiti podatak da je preporučeni unos za prosječnu odraslu osobu 2000 kcal, podatak koji najčešće piše na samim deklaracijama proizvoda.

Minimalna dnevna razina unosa vitamina C je 160 mg, a maksimalna dopuštena količina je 800 mg dok je preporučeni dnevni unos kalcija 800 mg, a maksimalna razina je 1500 mg (NN, 2013).

Što se tiče masti kao hranjive tvari, one se dijele na nezasićene masne kiseline, zasićene masne kiseline i trans-masne kiseline. Za odrasle, raspon preporučenog dnevnog unosa masti je od 20% do 35% ukupnog dnevnog unosa energije, a to se dijeli na maksimalno 10% unosa energije kod zasićenih masnih kiselina i na ostatak koji odlazi na nezasićene i trans masne kiseline [7].

Ostaje pitanje kolika je količina proteina i ugljikohidrata koju čovjek mora unositi dnevno u svoj organizam. Od 10% do 35% kalorija treba dolaziti od proteina, što znači ako je unos kalorija 2000, od 200 do 700 kalorija je iz proteina, a unos proteina je tada između 50 i 175 grama [9]. S druge strane, od 45% do 65% ukupnog dnevnog unosa energije treba biti dobiveno iz ugljikohidrata, što predstavlja od 900 kcal do 1300 kcal, odnosno od 225 g do 325 g ugljikohidrata [8].




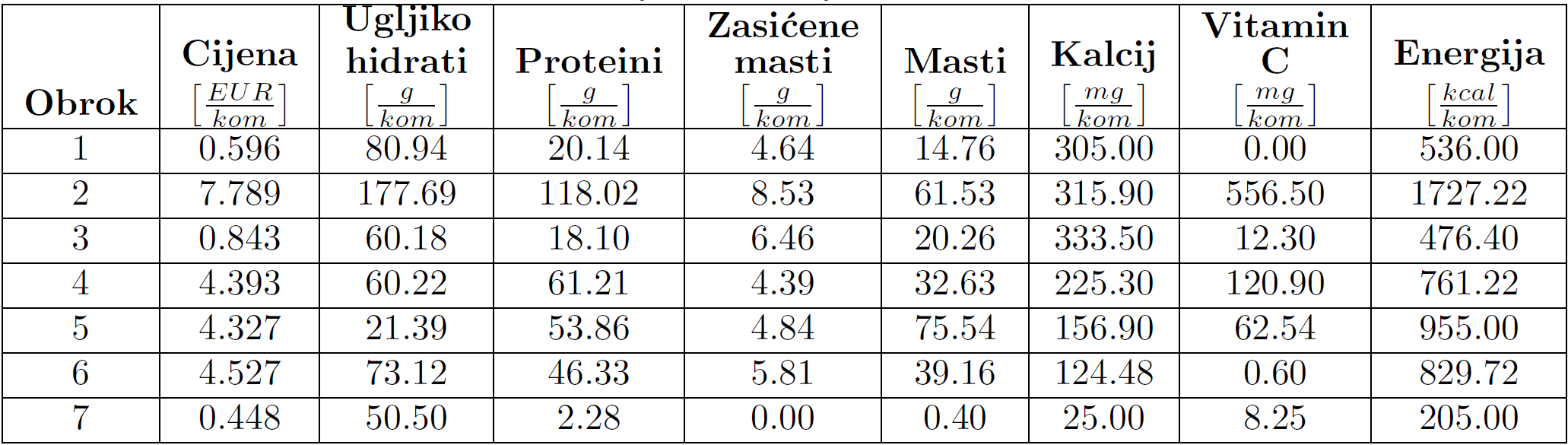
Sljedeći je korak izračunati kolike su količine pojedinih hranjivih tvari i energije u svakom obroku. U receptima obroka se navodi kolika je količina namirnica potrebna za pripremu jela pa će se prema tim količinama dobiti ukupni iznosi hranjivih tvari kod svakog pojedinog obroka. U tablici 2 prikazane su količine namirnica koje se koriste u pojedinim obrocima, izražene u gramima.

Nutritivne vrijednosti svake namirinice mogu se pronaći na web stranicama USDA-a ili na deklaracijama proizvoda. Korištenjem nutritivnih vrijednosti i cijena namirnica, koje su obično izražene na 100 grama namirnice, lako se izračunaju cijene i nutritivne vrijednosti obroka iz tablice 1 te se tako dobije tablica 3.



Da bismo postavili model problema prehrane kako je opisan pomoću tablica 1 do 3 i pomoću prethodno navedenih preporučenih dnevnih unosa pojedinih hranjivih tvari i energije, prvo je potrebno definirati nepoznanice pomoću kojih će se definirati funkcija cilja i ograničenja.

Ono što je nepoznato jest koliku količinu pojedinog obroka treba konzumirati u danu da bi se zadovoljile sve potrebe za hranjivim tvarima ali bez pretjerivanja i uz minimalnu cijenu. Pretpostavmo da svakoga dana možemo birati izmađu svih ponuđenih 7 obroka iz tablice 1. Označimo s x_{i} količinu i-tog obroka koja će bit konzumirana, i=1,2,...,7. Dakle, x_{1} označava količinu obroka 1 – pahuljica s jogurtom, x_{2} količinu obroka 2 – piletine s rižom i brokulom, ..., a x_{7} količinu obroka 7 – voća. Primjerice, x_{3}=2 znači da je potrebno konzumirati 2 obroka 3 odnosno 2 čokoladna banana napitka s kikirikijem, dok x_{4}=1.23 znači da je potrebno konzumirati 1.23 obroka 4 odnosno 1.23 oslića s tikvicama i krumpirom. Dozvoljavamo da se može nabaviti tj. pripremiti i samo dio pojedinog obroka odnosno da nije nužno kupiti i pripremiti isključivo cijeli obrok.

Cilj je minimizirati troškove prehrane pa je stoga funkcija cilja C_{O} zadana kao
Ograničenja su definirana preporučenim dnevnim unosom hranjivih tvari i energije. Svaki dan je potrebno unijeti barem 2000 kcal što znači da mora vrijediti
Preporučeni dnevni unos C vitamina je između 160 i 800 mg odnosno
Primjetimo da se u prethodnim ograničenjima se ne pojavljuje x_{1} jer prvi obrok ne sadrži C vitamin. Nadalje, preporučeni dnevni unos kalcija je između 800 i 1500 mg što daje
Unos masti bi trebao biti između 44 i 78 g, odnosno
Unos zasićenih masti ne smije biti veći od 22g tj.
Preporučen dnevni unos proteina je od 50 do 175 g, odnosno
Slično ograničenje za ugljikohidrate je od 225 do 325 g:
Budući da želimo konumirati što raznovrsnije obroke, postavit ćemo ograničenje da niti jedan obrok ne želimo konzumirati više od dva puta.
I na kraju, nema smisla konzumirati negativne količine obroka pa su
Ako funkciju cilja i sva ograničenja stavimo na jedno mjesto, dobijemo model za optimalan plan prehrane s obrocima:



Problemi linearnog programiranja se općenito rješavaju simpleks metodom. Postoje brojni alati koji automatiziraju izvođenje simpleks metode. Da bismo rješili primjer prehrane s obrocima iz prethodnog poglavlja, u ovom radu ćemo iskoristit Solver alat iz Microsoft Excel-a.


Za početak je potrebno jedan radni list Microsoft Excela popuniti podacima iz tablice 3 i preporučenim dnevnim unosom hranjivih tvari, kao na slici 2.

Funkcija cilja se na slici 2 nalazi u žuto označenoj ćeliji G14 te je u navedenu ćeliju potrebno upisati formulu koja će računati funkciju cilja C_{O}=0.596x_{1}+7.789x_{2}+0.843x_{3}+4.393x_{4}+4.327x_{5}+4.527x_{6}+0.448x_{7}. Formula treba izračunati c^{T}x, odnosno skalarno pomonožiti vektor cijena c, koji se na radnom listu na slici 2 nalazi u rasponu ćelija G4:G10, i vektor nepoznanica x, koji se na radnom listu na slici 2 nalazi u rasponu ćelija D4:D10 i označen je narančastom bojom. Funkcija koja u Excel-u računa skalarni produkt je SUMPRODUCT pa je stoga u žutu ćeliju G14 s funkcijom cilja potrebno napisati =SUMPRODUCT(G4:G10;D4:D10).

Slično, funkcije ograničenja nalaze se u zelenim ćelijama u rasponu H14:N14. Zelena ćelija N14 računa lijevu stranu prvog ograničenja 500x_{1}+1335x_{2}+480x_{3}+840x_{4}+840x_{5}+1280x_{6}+110x_{7} \geq 2000, odnosno računa skalarni produkt A_{1}x, gdje A_{1} označava prvi redak nutritivne matrice A. Zapravo se radi u ukupnoj količini ugljikogidrata koja se unosi pri konzumaciji obroka prema planu opsanom vektorom x. Stoga je Excel formula koju treba upisati u zelenu ćeliju N14 je =SUMPRODUCT(N4:N10;D4:D10).

Slično je potrebno napraviti za proteine, zasićene masti, masti, kalcij, vitamin C i energiju te redom u zelene ćelije H14, I14, J14, K14, L14 i M14 upisati formule =SUMPRODUCT(H4:H10;D4:D10), =SUMPRODUCT(I4:I10;D4:D10), ... , =SUMPRODUCT(M4:M10;D4:D10).

Iako svaka formula u rasponu G14:N14 zapravo računa skalarni produkt "stupca iznad sebe" i "stupca s vektorom x", primijetimo da nije moguće direktno kopirati formulu iz ćelije G14 koja računa ukupnu cijenu. Da bi to bilo moguće i da bismo ubrzali proces upisivanja formula, dovoljno je malo korigirati formulu u ćeliji koja računa ukupnu cijenu tj. funkciju cilja te napisati =SUMPRODUCT(G4:G10;$D4:$D10), kako je prikazano na slici 3 i zatim kopirati formulu na raspon H14:N14. Znak $ fiksira stupac D pa se kod kopiranja formule koristi apsolutno umjesto relativnog adresiranja [10].


Nakon što su postavljene formule za funkciju cilja i lijeve strane svih ograničenja, potrebno je pokrenuti alat Solver (hrv. Rješavatelj) koji se nalazi na Data (hrv. Podaci) kartici na izborniku, kao što je prikazano na slici 4.

Opcije alata Solver prikazane su na slici 5.

Alat Solver nudi brojne opcije koje je potrebno postaviti kako bi se pripremilo sve što je potrebno za rješavanje problema prehrane:

\bullet	Set objective - označiti ćeliju na radnom listu u kojoj se nalazi formula koja računa vrijednost funkcije cilja: u našem primjeru je to ćelija G14
\bullet	To - nudi opcije za maksimizaciju, minimizaciju i postizanje određenog cilja: u našem primjeru je to minimizacija jer žalimo minimizirati troškove prehrane
\bullet	By Changing Variable Cells - označiti ćelije s nepoznanicama tj. varijablama: u našem primjeru je to raspon D4:D10 u kojem se nalaze nepoznanice tj. vektor x
\bullet	Subject to the Constraints - označiti ćelije s ograničenjima: u nađem primjeru je to raspon H14:N14 jer se tamo nalaze formule koje predstavljaju lijeve strane ograničenja

Postoje dvije osnovne mogućnosti za unos ograničenja: pojedinačno i grupno. Pojedinačno ograničenje unosimo tako da biramo opciju Add, nakon čega dobijemo prozor kao na slici 6. Pod Cell reference treba postaviti lijevu stranu ograničenja, zatim biramo znak <=, = ili >= te pod Constraint desnu stranu ograničenja koja se može postaviti upisom konkretne vrijednosti ili oznakom ćelije u kojoj je navedena konkretna vrijednost. Opcija int predstavlja ograničenje cjelobrojnosti, bin ograničenje binarnosti (0 ili 1) a dif ograničenje različitosti (ćelije s lijeve strane moraju biti različite). U našem primjeru, da bismo postavili ograničenje da je potrebno unijeti barem 2000 kcal, Cell reference postavljamo na ćeliju N14 jer se u njoj nalazi formula koja računa ukupan unos energije, zatim biramo znak >= te pod Constraint biramo ćeliju N12 u kojoj je navedena donja ograda 2000 ili upisujemo direktno 2000. Grupno ograničenje postavlja se slično kao pojedinačno samo što je potrebno upisati raspon ćelija koje su redom u određenom odnosu s drugim rasponom. Npr. možemo odjednom označiti da unos ugljikogidrata, proteina, zasićenih masti i masti u rasponu ćelija H14:K14 treba redom biti manji od maksimalnih dnevnih unosa 325, 175, 22 i 78 koji su navedeni u rasponu ćelija H16:K16. Pojedinačno postavljanje ograničenja prikazno je na slici 7 a grupno na slici 8.

Nakon postavljanja minimizacije funkcije cilja, varijabli i ograničenja potrebno je još navesti da su varijable nenegativne x \geq 0 te izabrati metodu za rješavanje modela. Nude se 3 metode prikazane na slici 9:

\bullet	GRG Nonlinear - rješavanje problema nelinearnog programiranja pomoću Generalized Reduced Gradient metode
\bullet	Simplex LP - rješavanje problema linearnog programiranja pomoću simpleks metode koja se u hrvatskoj verziji Excela pomalo nespretno prevodi s Jednostavni LP
\bullet	Evolutionary - rješavanje problema koji se ne mogu riještiti pomoću prethodne dvije metode

Budući da problem prehrane spada u probleme linearnog programiranja izabrat ćemo Simplex LP metodu iako bi i GRG Nonlinear metoda jednako točno riješila linearni problem prehrane. Dodatna motivacija za korištenje simpleks metode je što ona, za razliku od nelinearne metode, nudi mogućnost generiranja izvještaja o analizi osjetljivosti o čemu će biti više riječi nešto kasnije.

Kada popunimo sve što je potrebno, prozor Solvera bi trebao izgledati kao na slici 10 te je Solver spreman za pokretanje pritiskom na gumb Solve, nakon čega u našem primjeru dobijemo poruku da je Solver pronašao rješenje kao na slici 11. Ako nema rješenja jer je funkcija cilja neograničena ili jer nema niti jednog mogućeg rješenja koje zadovoljava sva ograničenja, dobit ćemo odgovarajuću poruku.

Nakon što smo dobili poruku da je Solver riješio naš problem prehrana te iako na prvi pogled izgleda da se ništa nije promijenilo, na slici 12 možemo primijetiti da su se promijenile vrijednosti varijabli u narančastim ćelijama u rasponu D4:D10 u kojima je umjesto 0.00 sada navedeno optimalno rješenje.

Optimalno rješenje našeg problema prehrane sa slike 12 glasi: Ako izdvojimo samo obroke koji se koriste u optimalnom planu prehrane, dobijemo sljedeće:
Navedeno znači da prehrana s obrocima i minimalnom cijenom uključuje 2 obroka 1 tj. piletine s rižom i brokulom, 1.66 obroka 3 tj. čokoladnog banana napitka s kikirikijem i 1.86 obroka 7 tj. grejpa. Navedene obroke bi trebalo rasporediti i konzumirati unutar jednog dana za doručak, ručak, večeru i/ili užinu i to bi nas koštalo 3.42 EUR. Ostali predloženi obroci, obroci 2, 4, 5 i 6 se ne koriste jer jednostavno nisu isplativi tj. ne nude dovoljno hranjivih tvari za cijenu koju je potrebno za njih platiti.

Može se postaviti pitanje imamo li u našem primjeru zadovoljenu pretpostavku djeljivosti odnosno možemo li kupiti samo dio obroka. Odgovor je da u promatranom modelu zbog jednostavnosti pretpostavljamo da možemo konzumirati i samo dio obroka jer npr. ostatak možemo ostaviti za idući dan.

Na slici 12 se vidi da su pri optimalnoj prehrani sva ograničenja zadovoljena: ne konzumira se više od 2 istovrsna obroka, unosi se dovoljno hranjivih tvari i energije ali ne previše. Cijena takve prehrane od 3.42 EUR je minimalna cijena koju treba platiti da bismo zadovoljili sva zadana ograničenja.




Analiza osjetljivosti proučava kako promjene određenih koeficijenata u modelu utječu na promjenu optimalnog rješenja i optimalne vrijednosti funkcije cilja. Ako se promijene cijene obroka odnosno koeficijenti u funkciji cilja, vektor c, analiza osjetljivost nam daje odgovor moramo li sve ponovno računati ili u nekom rasponu optimalno rješenje i/ili optimalna vrijednost funkcije cilja i/ili optimalna baza ostaju nepromijenjeni. Ili, ako se promijene preporuke o zdravoj prehrani u smislu preporučenih dnevnih unosa hranjivih tvari i energije, analiza osjetljivosti nam ponovno daje odgovor u kojem rasponu se preporuke mogu promijeniti a da se ne promijeni optimalno rješenje i/ili optimalna vrijednost funkcije cilja i/ili optimalna baza.

Generiranje izvještaja o analizi osjetljvosti je jedna od opcija Excel Solvera koju on nudi nakon uspješnog rješavanja problema. Potrebno je označiti da želimo izvještaj Sensitivity kao na slici 13 nakon čega Excel Solver na novom radnom listu generira traženi izvještaj. Primjer izvještaja o analizi osjetljivosti za naš primjer dan je na slici 14.

Izvještaj o analizi osjetljivosti na slici 14 podijeljen je na dva dijela: u gornjem dijelu koji je označen s Variable Cells je izvještaj vezan uz promjene koeficijenata u funkciji cilja tj. u vektoru c a u donjem dijelu koji je označen s Constraints izvještaj vezan uz promjene u desnim stranama ograničenja tj. u vektoru b slobodnih koeficijenata u ograničenjima.




Izvještaj o promjenama koeficijenata u funkciji cilja na slici 14 nudi 5 stupaca: Final Value, Reduced Cost, Objective Cofficient, Allowable Increase i Allowable Decrease.

U stupcu Final Value nalazi se optimalno rješenje problema odnosno optimalni plan prehrane dok stupac Objective Ceofficient navodi upravo koeficijente funkcije cilja odnosno cijene obroka. Skalarnim umoškom navedena dva stupca dobit ćemo optimalnu vrijednost funkcije cilja tj. minimalnu cijenu prehrane od 3.42 EUR.

Stupac Reduced Cost, označimo ga s rc_{i}, govori za koliko bi se odgovarajući koeficijent funkcije cilja odnosno cijenu obroka c_{i} trebalo smanjiti da bi obrok postao isplativ odnosno da bi se počeo konzumirati. Vidljivo je za obroke 2, 4, 5 i 6 koji se ne konzumiraju odnosno čiji su x-evi x_{2}^{*}=0, x_{4}^{*}=0, x_{5}^{*}=0 i x_{6}^{*}=0, da su njihove Reduced Cost vrijednosti rc_{2}=3.683, rc_{4}=2.652, rc_{5}=2.623 i rc_{6}=2.141. Za obrok 2 vrijednost rc_{2}=3.683 znači da bi se njegova cijena c_{2}=7.789 treba smanjiti za rc_{2}=3.683, dakle na 4.106, da bi obrok 2 postao isplativ i počeo se konzumirati. Slično je i za obroke 4, 5 i 6. Ugrubo, možemo zaključiti da bi se cijena obroka 2, 4, 5 i 6 trebala otprilike prepoloviti pa da oni postanu isplativi, što je realno teško za očekivati. S druge strane da smo za neki obrok dobili da je njegov Reduced Cost vrlo malen, npr. 0.01 EUR, trebali bismo biti oprezni jer vrlo mala promjena cijene tog obroka, od samo 1 cent, može dovesti do velike promjene u optimalnom rješenju odnosno optimalnom planu prehrane.

Druga ekonomska interpretacija stupaca Reduced Cost jest da je to iznos za koji će se povećati troškovi odnosno funkcija cilja ako prisilimo da se mora konzumirati 1 jedinica nekog obroka koji se trenutno ne konzumira. Npr. ako baš jako volimo obrok 4 - oslić s tikvicama i krumpirom koji trenutno košta c_{4}=4.393 EUR i koji je trenutno neisplativ pa se ne konzumira jer je x_{4}^{*}=0.00, onda će nas svaka jedinica obroka 4 kojeg forsirano guramo u prehranu koštati upravo koliko navodi rc_{4}=2.652 EUR. Dakle ako u modelu postavimo ograničenje x_{4} \geq 1 to će nas dodatno koštati rc_{4}=2.652 EUR pa će trošak takve prehrane umjesto 3.42 EUR biti 3.42+2.65=6.07 EUR.

Kod obroka 3 i 7 su rc_{3}=0.00 i rc_{7}=0.00. Budući da se oba obroka konzumiraju u optimalnom planu prehrane, nema potrebe smanjivati njihovu cijenu jer su oba obroka očito već isplativi. Primjetimo da se oba obroka 3 i 7 konzumiraju u količinama koje su strogo između donje ograde 0.00 i gornje ograde 2.00 odnosno 0.00 \lt x_{3}=1.66 \lt 2.00 i 0.00 \lt x_{7}=1.86 \lt 2.00. Kod obroka 1 je rc_{1}=-0.25 iako se obrok 1 također već konzumira budući da je x_{1}^{*}=2.00. Primjetimo da je vrijednost x_{1}^{*}=2.00 na granici ograničenja x_{1} \leq 2.00 pa je stoga ekonomska interpretacija Reduced Cost vrijednosti rc_{1}=-0.25 za obrok 1 nešto drugačija i predstavlja smanjenje ukupne cijene optimalne prehrane koja trenutno košta 3.42 EUR upravo za vrijednost rc_{1}=-0.25 EUR, ako bismo dozvolili konzumaciju 1 jedinice obroka 1 više nego je trenutno dopušteno tj. kada bismo imali ograničenje x_{1} \leq 3 umjesto x_{1} \leq 2. Dakle, takva prehrana bi koštala 3.42-0.25=3.17 EUR ali samo u slučaju da x_{1}^{*} doista u novom planu prehrane dosegne vrijednost 3.00.

Stupac Allowable Increase, označimo ga s \Delta c_{i}^{+}, govori koliko se može povećati cijena i-tog obroka c_{i} a da se pritom ne promijeni optimalno rješenje x^{*}=(2.00,0.00,1.66,0.00,0.00,0.00,1.86) tj. optimalan plan prehrane. Naravno da će se uz nepromijenjen plan prehrane x^{*} i povećanu cijenu i-tog obroka s c_{i} EUR na c_{i}+\Delta c_{i}^{+} EUR, povećati optimalna vrijednost funkcije cilja za \Delta c_{i}^{+} x_{i}^{*} EUR ali svejedno optimalan plan prehrane ostaje nepromijenjen samo što je sada malo skuplji ali još uvijek najjeftiniji mogući. Slično se interpretira stupac Allowable Decrease, uz oznaku \Delta c_{i}^{-}, samo što on govori koliko se cijena pojedinog obroka može smanjiti a da se pritom ne promijeni optimalno rješenje. Naravno, u ovom slučaju će optimalni obrok pojeftiniti za iznos \Delta c_{i}^{-} x_{i}^{*} EUR.

Napomenimo i da je vrijednost 1E+30 u Excelu oznaka za \infty.

Npr. budući da je \Delta c_{1}^{+}=0.251 a \Delta c_{1}^{-}=\verb|1E+30|, možemo zaključiti da se cijena c_{1}=0.596 može smanjiti za 0.251 ili povećati za \infty, odnosno da se c_{1} može kretati u rasponu [0.345,\infty) a da se pritom optimalno rješenje neće promijeniti. I tako dalje redom za ostale cijene obroka.

Ako usporedimo vrijednosti dopustivog povećanja i smanjenja cijena obroka sa cijenama samih obroka, možemo zaključiti da se sve cijene mogu relativno značajno promijeniti a da se pritom optimalno rješenje neće promijeniti. Većina dozvoljenih promjena kreće se u rasponu od 50% pa do \infty što je dosta široko. Najmanja dozvoljena promjena je \Delta c_{3}^{-}=0.23 što je o odnosnu na c_{3}=0.84 oko 27%.




Izvještaj o promjenama desnih strana ograničenja na slici 14 nudi 5 stupaca: Final Value, Shadow Price, Constraint R.H.Side, Allowable Increase i Allowable Decrease.

U stupcu Final Value nalaze se vrijednosti lijevih strana ograničenja pri optimalnom planu prehrane dok stupac Constraint R.H.Side navodi desne strane ograničenja. Lijeva strana prestavlja unos hranjivih tvari i energije pri optimalnom planu prehrane a desna strana predstavlja preporučene vrijednosti unosa.

Stupac Shadow price, označimo ga s \lambda_{j}, govori za koliko će se promijeniti optimalna vrijednost funkcije cilja odnosno cijena prehrane, ako desnu stranu j-tog ograničenja povećamo za 1 jedinicu. Možemo primjetiti da je \lambda_{j}=0.000 za j=1,2,3,4,5,6,7,8,11 dok je tek \lambda_{9}=0.002 i \lambda_{10}=0.003. Npr. \lambda_{1}=0.000 znači da neće doći do promjene optimalne vrijednosti funkcije cilja ako desnu stranu prvog ograničenja povećamo za 1 jedinicu. Dakle, ako se promijeni preporuka da je potrebno unijeti barem 225 g ugljikohidrata dnevno jer su npr. nova istraživanja pokazala da je potrebno unijeti 1 jedinicu više, 226 g umjesto 225 g, optimalni plan prehrane ostat će nepromijenjen i neće biti ništa skuplji. Navedeno ima smisla jer je prvo ograničenje neaktivno tj. pri optimalnom rješenju je zadovoljeno kao stroga nejednakost. Na slici 14 se prema Final Value vrijednosti 299.55 lijeve strane prvog ograničenja vidi da se pri optimalnoj prehrani već unosi 299.55 g ugljikohidrata pa stoga novi zahtjev u kojem se traži da se unosi 226 umjesto 225 g neće ništa promijeniti. I ne samo to, nego je vidljivo da se zahtjev za povećanim unosom ugljikohidrata može i puno značajnije povećati a da to neće utjecati na optimalnu prehrani niti na njenu cijenu. S druge strane, \lambda_{10}=0.003 govori da će se optimalna vrijednost funkcije cilja odnosno trošak prehrane povećati upravo za 0.003 EUR za svaku jedinicu povećanja desne strane desetog ograničenja. Deseto ograničenje govori da je svaki dan potrebno unijeti barem 2000 kcal energije. Ako nove preporuke kažu da je potrebno unijeti više energije, to ćemo platiti 0.003 EUR za svaku dodatnu jedinicu energije koju unesemo. Napomenimo i da se u ovom slučaju radi o aktivnom ograničenju tj. o ograničenju koje je pri optimalnoj prehrani zadovoljeno kao jednakost: traži se unos 2000 kcal i točno toliko se i unosi. Cijena u sjeni govori koliko košta svaka dodatna jedinica energije koju želimo unijeti ali nam ne govori ništa o novom optimalnom rješenju. Ono će se morati ponovno izračunati i bit če različito od prethodnog optimalnog rješenja ali će ostati očuvana optimalna baze što znači da će i dalje aktivna ograničenja ostati aktivna a nekativna će ostati neaktivna.

Stupaci Allowable Increase i Allowable Decrease imaju sličnu interpretaciju kao prethodno navedeni istoimeni stupci, samo što se ove vrijednosti odnose na dozvoljene promjene desne strane ograničenja. Ako je ograničenje neaktivno, pri promjeni desne strane ograničenja u dozvoljenom rasponu ne mijenja se niti optimalno rješenje niti optimalna vrijednost funkcije cilja. Dakle, i optimalan plan prehrane i njegova cijena se ne mijenjaju. Ako je ograničenje aktivno, mijenja se i optimalno rješenje i optimalna vrijednost funkcije cilja ali optimalna baza ostaje nepromijenjena.

Promotrimo za početak prvo ograničenje kao jedan primjer neaktivnog ograničenja. Vidimo da se u prvom ograničenju traži unos barem 225 g ugljikohidrata a analiza osjetljivosti navodi da se navedena donja ograda od 225 g može povećati za 74.50 g i smanjiti neograničeno, odnosno da se traženi minimalan unos ugljikohidrata može kretatu u rasponu (-\infty,299.50] i pritom neće doći niti do promjene optimalnog plana prehrane niti do promjene njegove cijene. Slično je s gornjom ogradom na unos ugljikohidrata koja je u trećem ograničenju postavljena na 325. Analiza osjetljivosti kaže da se traženi maksimalan unos ugljikohidrata može smanjiti za 25.50 g a povećati neograničeno, odnosno da se može kretati u rasponu [299.50,\infty). Primjetimo da pri optimalnom planu prehrane unosimo 299.50 g ugljikohidrata što je strogo veće od minimalnog potrebnog unosa od 225 g i strogo manje od maksimalnog dozvoljenog unosa od 325 g dnevno.

Kao primjer aktivnog ograničenja može poslužiti deseto ograničenje koje definira minimalan unos vitamina C koji iznosi 160 mg dnevno. Vidimo da u optimalnom rješenju unosimo točno minimalnu potrebnu količinu vitamina C. Prema izvještaju o analizi osjetljivosti, dozvoljeno smanjenje navedene minimalne količine je 113.64 a povećanje 10.625 što znači da se minimalna količina može kretati u rasponu [46.36,149.375]. Budući da se radi o aktivnom ograničenju, promijenit će se i optimalno rješenje i optimalna vrijednost funkcije cilja odnosno i optimalni plan prehrane i njegova cijena. Ipak, navedeni raspon definira raspon u kojem vrijedi cijena u sjeni \lambda_{10}=0.003 i raspon u kojem neće doći do promjene optimalne baze [11].




U ovom radu smo detaljno prikazali kako se korištenjem Microsoft Excela i njegovog alata Solver može riješiti problem prehrane. Postupak je gotovo identičan i za bilo koji drugi problem linearnog programiranja a prilično sličan i za probleme nelinearnog programiranja. Navedeni primjer problema prehrane relativno je jednostavno proširiti s brojnim drugim namirnicama, obrocima, hranjivim tvarima, preporučenim unosima, zdravstvenim ograničenjima i osobnim preferencijama te tako dobiti model koji još bolje prikazuje stvarni problem prehrane. Na kraju rada dane su upute kako generirati i ekonomski interpretirati analizu osjetljvosti vezanu uz promjene cijena ili preporučenih dnevnih unosa hranjivih tvari i energije. Napomenimo i da je postupak rješavanja problema prehrane vrlo sličan i ako se koriste neki drugi alati, poput npr. lpSolve paketa iz R-studio-a, dok je ekonomska interpretacija rezultata i analize osjetljivosti identična.