Kvantni logički sklopovi
Ideja o kvantom računalu pojavila se prije četrdesetak godina kada je u osamdesetim godinama prošlog stoljeća fizičar Richard Feynman održao seriju predavanja te objavio dva ključna članka o mogućnostima izgradnje računala temeljenog na kvantnoj mehanici. Sljedeći velik korak je objava članka Davida Deutscha 1985. godine o „univerzalnom kvantom računalu“, nakon čega je u devedesetim godinama objavljen niz članaka o algoritmima kreiranima za rad na kvantnim računalima (Shorov algoritam, Groverov algoritam pretraživanja, Loydov algoritam ...).
Godine 2001. IBM i Stanford University provode prvu primjenu Shorovog algoritma na 7-qbitnom kvantom računalu. Godine 2010. bilježimo pojavu prvog komercijalnog kvantnog računala, D-Wave One. Devet godina kasnije Google proglašava postizanje „kvantne nadmoći“. Riječ je o terminu kojeg je skovao John Preskill 2012. godine i koji opisuje trenutak u kojemu kvantni sustavi mogu obavljati zadatke koji nadmašuju mogućnost klasičnih računala. Posljednjih deset godina bilježimo ubrzan razvoj kvantnih računala, kako softvera, tako i hardvera. Primjerice, posljednje konstruirano kvantno računalo radi s više od 1000 qbita.
Razvoj kvantnih računala, prirodno, otvara nova područja istraživanja, kako u razvoju hardvera (dakle, samih kvantnih računala), softvera (algoritama konstruiranih za rad na kvantnim računalima), tako i u matematičkoj (logičkoj) formalizaciji rada kvantnih računala. Početkom te formalizacije smatra se von Neumannova aksiomatizacija kojom su kvantni sustavi opisani pomoću kompleksnog separabilnog Hilbertovog prostora.
Unatoč ubrzanom razvoju i bogatom prostoru istraživanja, kvantno računarstvo je još uvijek relativno slabo poznato u široj javnosti, pa čak i široj akademskoj zajednici. Dok se, recimo, Booleova algebra i binarni brojevi kao temelj rada klasičnih računala smatraju općom kulturom, malo tko bi znao iznijeti osnovnu ideju rada kvantnih računala ili pak matematičkih koncepata kojima se ono služi. Smatramo da je stoga korisno na jednom mjestu dati pregled osnova rada i računanja s kvantnim računalima, što je osnovni cilj ovog članka.
Opis kvantne logike iz perspektive primjene kreće od definicije osnovne informacijske jedinice, kvantnog bita, odnosno qbita. Za usporedbu, osnovna informacijska jedinica u primjeni klasične logike, bit, može pohraniti dvije brojčane vrijednosti, 1 i 0. U kvantnom slučaju, osnovna informacijska jedinica qbit može se izmjeriti u dva stanja, koja se u standardnoj Diracovoj notaciji obilježavaju s \left| 0\right\rangle i \left| 1\right\rangle. Fizičku realizaciju kvantnog bita moguće je ostvariti spinom elektrona (spin gore i spin dolje), stanjem polarizacije fotona ili spinom jezgre atoma.
Osnovna razlika između bita i qbita je u tome što qbit može biti u superpoziciji stanja prije mjerenja, dok bit može biti u samo jednom od dva stanja, 0 ili 1. Pored toga, qbite možemo mjeriti na više načina, no nakon prvog mjerenja i kolapsa valne funkcije, svako sljedeće mjerenje dati će isti (bazni) rezultat. To znači da qbit ne ostaje u stanju superpozicije nakon provedenog mjerenja te se informacija iz stanja superpozicije može dobiti samo jednom.
Kvantni bit, qbit, u svakom kvantno-mehaničkom sustavu možemo reprezentirati dvodimenzionalnim kompleksnim vektorom, uz uvjet da pripadni vektorski prostor ima \left| 0\right\rangle i \left| 1\right\rangle za kanonske vektore baze, pri čemu zapisujemo \left| 0 \right\rangle = \left[\begin{matrix}1\\0\\\end{matrix}\right], \left| 1\right\rangle =\left[\begin{matrix}0\\1\\\end{matrix}\right]. Kažemo da je kvantno stanje \left| \psi\right\rangle superpozicija baznih stanja \left| 1\right\rangle i \left| 0\right\rangle ako je netrivijalna linearna kompozicija vektora baze, odnosno ako vrijedi:
Pokazuje se da navedeni skup opisan u Definiciji
Notacija koju koristimo za zapisivanje qbita naziva se Diracovom notacijom, a često je u primjeni i naziv bra-ket notacija. U njoj kao oznaku za qbite (vektore) koristimo grčko slovo \psi, pa se zapis qbita \left| \psi\right\rangle, čita „ket-psi“. U paru s ket-notacijom u koristimo bra-notaciju: za vektor ket-psi \left| \psi\right\rangle=\alpha\cdot \left| 0\right\rangle +\beta\cdot \left| 1\right\rangle=\left[\begin{matrix}\alpha\\\beta\\ \end{matrix}\right] definiramo bra-psi \left\langle\psi\right| = \left[\begin{matrix}\overline{\alpha}&\overline{\beta}\\\end{matrix}\right]. Vidimo kako je bra-psi vektor redak čiji su elementi konjugirane amplitude vektora ket-psi. Posebno, za ket vektore baze vrijedi \left\langle 0\right|=\left[\begin{matrix}1&0\\\end{matrix}\right], \left\langle 1\right|=\left[\begin{matrix}0&1\\\end{matrix}\right].
Takva notacija omogućava nam interpretaciju bra-ket zapisa \left\langle\psi_{1} | \psi_{2} \right\rangle kao skalarnog produkta vektora \left\langle\psi_{1} \right| \cdot \left| \psi_{2} \right\rangle gdje je \cdot oznaka za matrično množenje vektora retka i vektora stupca. Dakle, za \left| \psi_{1} \right\rangle=\left[\begin{matrix}\alpha_{1} \\ \beta_{1} \\ \end{matrix}\right] i \left| \psi_{2} \right\rangle=\left[\begin{matrix}\alpha_{2} \\ \beta_{2} \\ \end{matrix}\right] vrijedi:
Specijalno imamo \left\langle 0 | 0 \right\rangle = 1\cdot 1 + 0\cdot 0 =1 i \left\langle 1 | 1 \right\rangle = 0\cdot 0 + 1\cdot 1 =1 što nam potvrđuje normiranost vektora \left| 0\right\rangle i \left| 1\right\rangle. Također, lako je provjeriti da vrijedi \left\langle 0 | 1 \right\rangle = \left\langle 1 | 0 \right\rangle =0, što potvrđuje ortogonalnost baze. Čitatelju predlažemo da na sličan način provjeri ortonormiranost baza \left\lbrace \left| +\right\rangle,\left| -\right\rangle\right\rbrace i \left\lbrace \left| i\right\rangle,\left| -i\right\rangle\right\rbrace.
Diracova kotacija omogućava nam i interpretaciju zapisa ket-bra, \left|\psi_{1}\right\rangle\left\langle\psi_{2}\right|. Kao što zapis bra-ket opisuje skalarni (unutarnji) produkt, tako ket-bra zapis opisuje tenzorski (vanjski) produkt vektora. Tako za vektore \left| \psi_{1} \right\rangle=\left[\begin{matrix}\alpha_{1} \\ \beta_{1} \\ \end{matrix}\right] i \left| \psi_{2} \right\rangle=\left[\begin{matrix}\alpha_{2} \\ \beta_{2} \\ \end{matrix}\right] vrijedi:
Dakle, ket-bra zapis opisuje linearni operator prikazan gornjom matricom. Bra-ket i ket-bra zapisi međusobno se nadopunjuju u računu s qbitima.
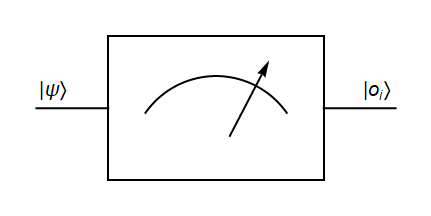
Mjerenje u kvantnoj mehanici je fizički proces u kojem kvantni sustav dolazi u interakciju s klasičnim mjernim aparatom, što dovodi do kolapsa valne funkcije. U slučaju kubita, koji je osnovna jedinica kvantne informacije i može biti u stanju:
Mjerenje može biti provedeno u različitim bazama, ali najčešće se provodi u bazi \left\lbrace \left| 0\right\rangle,\left| 1\right\rangle\right\rbrace. Opisuje se pomoću skupa hermitskih operatora \lbrace \widehat{O}_{i}\rbrace, koji djeluju na vektore stanja i imaju svojstva:2
| \bullet | Svojstvene vrijednosti operatora \widehat{O}_{i} predstavljaju moguće ishode mjerenja. |
| \bullet | Svojstveni vektori operatora \widehat{O}_{i}, |o_{i}\rangle formiraju ortonormiranu bazu Hilbertovog prostora. |
Ako je kvantno stanje |\psi\rangle izraženo u bazi svojstvenih vektora operatora \lbrace \widehat{O}_{i}\rbrace, tada je vjerojatnost da će mjerenje dati rezultat o_{i} (koji odgovara svojstvenom vektoru |o_{i}\rangle) određena pomoću kvadrata apsolutne vrijednosti projekcije:3
Nakon mjerenja, prema postulatima kvantne mehanike, sustav kolabira u odgovarajuće svojstveno stanje |o_{i}\rangle.
Mjerenje uzrokuje kolaps kvantnog stanja. To znači da ako je qbit bio u superpoziciji prije mjerenja, nakon mjerenja ostaje samo u jednom od stanja baze u kojoj se provodi mjerenje. Na primjer, ako je qbit prije mjerenja bio u stanju |\psi\rangle = \frac{1}{2}|0\rangle +\frac{\sqrt{3}}{2}|1\rangle mjerenje će proizvesti |0\rangle s vjerojatnošću P(0)=0.25 ili |1\rangle s vjerojatnošću P(1)=0.75, a nakon mjerenja qbit više neće biti u superpoziciji. Ako odmah nakon mjerenja ponovno mjerimo (isti qbit) u istoj bazi, dobit ćemo isti rezultat kao i u prvom mjerenju sa 100 % vjerojatnosti. Dakle, mjerenje je nepovratno i eliminira superpoziciju, ostavljajući sustav u određenom svojstvenom stanju operatora kojim je provedeno mjerenje.
Kao što smo spomenuli, mjerenja se najčešće izvode u bazi \left\lbrace \left| 0\right\rangle,\left| 1\right\rangle\right\rbrace. Postupak mjerenja zapisujemo na sljedeći način. Mjerenje qbita \left|\psi\right\rangle=\alpha\cdot\left|0\right\rangle+\beta\cdot\left|1\right\rangle je sljedeća operacija:
Dakle, mjerenje stanja \left|\psi\right\rangle daje vrijednost 0 ili 1 s vjerojatnošću ovisnom o amplitudama qbita. Potom stanje qbita kolabira na bazno stanje koje ovisi o rezultatu mjerenja. Na Slici
Iako je qbit definiran kao vektor s kompleksnim amplitudama, tj. kao što smo vidjeli ranije, struktura koja pohranjuje dva stupnja slobode, konačan ishod je prilično mršava informacija u formi jednog bita. No prava snaga kvantnog računala dolazi iz rada s više qbita.
Za razumijevanje rada s qbitima važan nam je još jedan interesantan fenomen, tzv. globalna faza qbita. Ako je |\psi\rangle neki vektor stanja qbita, a za vektor stanja |\psi'\rangle vrijedi
gdje je \varphi \in \mathbb{R}, tada realni broj \varphi nazivamo globalnom fazom.4 Qbiti |\psi\rangle i |\psi'\rangle predstavljaju isto fizičko stanje jer globalna faza ne utječe na rezultat mjerenja. Uistinu, ako stanje |\psi\rangle transformiramo u stanje |\psi'\rangle, vjerojatnost mjerenja ostaje ista:
Ukratko, globalna faza u matematičkoj reprezentaciji kvantnog stanja predstavlja stupanj slobode koji nema fizički značaj jer ne utječe na ishode mjerenja.
Operacije na qbitima provodimo pomoću unitarnih operatora koje zapisujemo pomoću unitarnih matrica.5 Prisjetimo se, za matricu U=\left[\begin{matrix}a&b\\c&d\\\end{matrix}\right], gdje su a,b,c,d\in\mathbb{C}, kažemo da je unitarna ako za njoj konjugirano transponiranu matricu U^{\ast}=\left[\begin{matrix}\bar{a}&\bar{b}\\\bar{c}&\bar{d}\\\end{matrix}\right] vrijedi
Može se pokazati kako je matrica U unitarna ako za njezine vektore stupce \left[\begin{matrix}a\\b\\\end{matrix}\right] i \left[\begin{matrix}c\\d\\\end{matrix}\right] vrijedi da su vektori norme 1 (|a|^{2}+|c|^{2}=|b|^{2}+|d|^{2}=1), te da su međusobno okomiti (ab+cd=0).
Vidjet ćemo da su unitarni operatori ključni za konstrukciju logičkih sklopova na qbitima. Kako bi objasnili njihov rad, uvodimo sljedeće pravilo.
Qbit predstavlja kvantni sustav koji može biti u superpoziciji dva fizička stanja koja označavamo s |0\rangle i |1\rangle. Dva qbita predstavljaju dva takva sustava koja su ekvivalentna sustavu s četiri fizička stanja, koja ćemo označiti s |00\rangle, |01\rangle, |10\rangle. i |11\rangle. (za detalje ekvivalencije vidi
Unitarni operator na sustavu s dva qbita prikazujemo unitarnom kompleksnom matricom U s četiri retka i četiri stupca za koju vrijedi U\cdot U^{\ast}=U^{\ast}\cdot U=I_{4}. Na analogan način definiramo sustave s više od dva qbita. Tako sustav s n qbita prikazujemo kao linearnu kombinaciju 2^{n} baznih vektora u prostoru \mathbb{C}^{2^{n}} s normom 1. Sada možemo definirati tenzorski produkt dva qbita.
Tenzorski produkt dva qbita u stvarnosti predstavlja konkatenaciju dva fizička sustava. Stoga ne čudi da se i u zapisu često izostavlja oznaka \otimes te se tenzorski produkt |x\rangle\otimes|y\rangle piše u skraćenom obliku |x\rangle|y\rangle, |x,y\rangle ili |xy\rangle. Na isti se način bazna stanja |00\rangle, |01\rangle, |10\rangle i |11\rangle mogu promatrati kao tenzorski produkti |0\rangle\otimes|0\rangle, |0\rangle\otimes|1\rangle, |1\rangle\otimes|0\rangle i |1\rangle\otimes|1\rangle.
Promotrimo što se događa ukoliko tenzorski pomnožimo qbite Hadamardove baze (vidi Definiciju
Tako smo dobili prikaz (jednog) tenzorskog produkta vektora Hadamardove baze pomoću vektora kanonske baze, što će nam koristiti kasnije u analizi djelovanja kvantnih algoritama.
Za tenzorski produkt operatora (koje prikazujemo matrično) koristimo standardnu definiciju Kroneckerovog produkta. Za matrice A=[a_{ij}] i B=[b_{ij}], gdje su A,B\in M_{n} na sljedeći način definiramo produkt A\otimes B (naravno, nad poljem \mathbb{C}):
Ilustracije radi, recimo da trebamo odrediti tenzorski produkt matrica A=\left[\begin{matrix}1&-1\\0&2\\\end{matrix}\right] i B=\left[\begin{matrix}1&2\\3&4\\\end{matrix}\right].
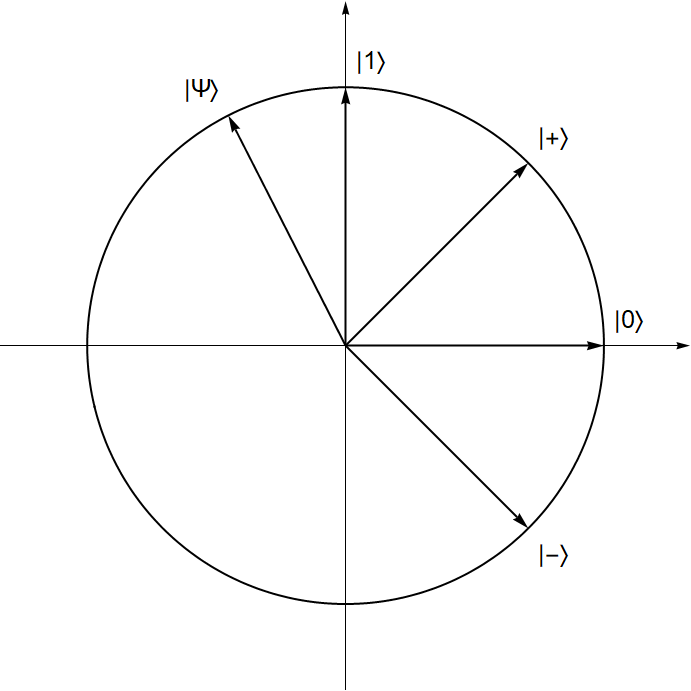
Prostor qbita često se prikazuje vizualno. Za početak, na Slici
Kao što se vidi u Definicijama
Kako je na taj način prikaz prostora qbita nepotpun, standardni način vizualnog prikaza prostora qbita je Blochova sfera, nazvana prema švicarskom fizičaru i nobelovcu Felixu Blochu. Već samo ime govori kako se radi o dvodimenzionalnoj reprezentaciji u prostoru. No kako su qbiti definirani kao dvodimenzionalni vektori nad poljem kompleksnih brojeva, na prvi pogled radi se o strukturi s četiri stupnja slobode.
Jedan stupanj slobode gubi se kroz invarijantnost qbita na globalnu fazu. Naime, jedine mjerljive vrijednosti qbita |\psi\rangle=\alpha\cdot|0\rangle+\beta\cdot|1\rangle gdje su \alpha i \beta kompleksni brojevi različiti od nule su |\alpha|^{2} i |\beta|^{2}. Stoga množenje kvantnog stanja proizvoljnim faktorom oblika e^{i \varphi} (globalnom fazom) ne proizvodi mjerljive posljedice, budući da vrijedi:
Ukoliko kompleksne brojeve \alpha i \beta zapišemo u polarnom obliku, \alpha=r_{\alpha}\cdot e^{\phi_{\alpha} i}, \beta=r_{\beta}\cdot e^{\phi_{\beta} i}, qbit |\psi\rangle = \alpha\cdot|0\rangle+\beta\cdot|1\rangle možemo pomnožiti globalnom fazom e^{-\phi_{\alpha} i} (pri čemu qbit zbog invarijantnosti na množenje globalnom fazom, ostaje isti u odnosu na fizičko mjerenje), nakon čega on prelazi u oblik:
Sada je jasno kako u zapisu qbita danog u jednadžbi
Drugi stupanj slobode gubi se ispunjavanjem uvjeta normalizacije iz Definicije
Zapišemo li kompleksni broj r_{\beta}\cdot e^{{(\phi}_{\beta}-\phi_{\alpha}) i} u Kartezijevim koordinatama, jednadžba
što je jednadžba sfere u realnom trodimenzionalnom prostoru s Kartezijevim koordinatama \left(x,y,r_{\alpha}\right). Ta sfera naziva se Blochovom sferom.6 Uvođenjem sfernih koordinata u zapis qbita, jednadžba
Istaknute točke na Blochovoj sferi su sjeverni i južni pol, odnosno presjecišta sfere s osi z, koja reprezentiraju vektore |0\rangle. i |1\rangle. Presjecišta sfere s osi x reprezentiraju vektore Hadamardove baze |+\rangle i |-\rangle te presjecišta sfere s osi y koja reprezentiraju vektore baze |i\rangle i |-i\rangle. Te istaknute točke nam sugeriraju jedno korisno svojstvo Blochove sfere.
Dokaz: Neka je s |\psi\rangle=\cos{\frac{\theta}{2}}\cdot|0\rangle + e^{\phi i}\sin{\frac{\theta}{2}\ }\cdot|1\rangle dan qbit. Qbit |\xi\rangle reprezentiran njemu suprotnom točkom na Blochovoj sferi tada ima sljedeći zapis.
Sada je (zbog \langle 0 | 0 \rangle=\langle 1 | 1 \rangle=1 i \langle 0 | 1 \rangle = \langle 1 | 0 \rangle = 0):
Po trigonometrijskom identitetu za kosinus zbroja, slijedi \langle \xi | \psi \rangle = \cos{\frac{\pi}{2}} = 0. Kako je skalarni produkt jednak nuli, slijedi da su qbiti |\psi\rangle i |\xi\rangle okomiti. Na sličan se način pokazuje kako je \langle \xi | \xi \rangle =1 te \langle \psi | \psi \rangle =1, što pokazuje da svaki par suprotnih točaka na Blochovoj sferi čini ortonormiranu bazu za prostor qbita. U nastavku teksta vidjeti ćemo kako se djelovanje logičkih sklopova na qbite interpretira na Blochovoj sferi.
Prva grupa logičkih sklopova koju ćemo obraditi su logički sklopovi koji se odnose na transformacije jednog qbita.
Paulijeva logička vrata predstavljaju skup od četiri unitarna operatora:
Jednostavno se vidi da skup Paulijevih vrata \left\lbrace X,\ Y,\ Z,\ I\right\rbrace čini bazu vektorskog prostora linearnih operatora s \mathbb{C}^{2} u \mathbb{C}^{2}. Paulijeva logička vrata su izuzetno praktična za računanje promjene spina pojedinog elektrona, a upravo su spinovi elektrona najčešće korišteni za formiranje qbita u današnjim kvantnim računalima.
Logička vrata X u literaturi se naziva i bit flip (eng. promjena bita) vratima. Ona na qbit (zapisan u standardnoj bazi) djeluju tako da mu zamijene amplitude, odnosno vrijedi X (\alpha |0\rangle + \beta |1\rangle ) = \beta|0\rangle+\alpha|1\rangle. Na Blochovoj sferi, dana transformacija označava rotaciju za \pi oko osi x. Logička vrata X mogu se interpretirati i kao generalizaciju logičkih vrata NE (NOT) u klasičnoj logici, ukoliko se preslikavanje vektora baze |0\rangle \rightarrow |1\rangle i |1\rangle \rightarrow |0\rangle interpretira negacijom. Bit flip vrata zamijene vjerojatnosti da qbit poprimi vrijednost |0\rangle ili |1\rangle.
Logička vrata X u Diracovoj notaciji zapisujemo: X=|1\rangle\langle 0 |+|0\rangle \langle 1|. Lako je provjeriti da taj zapis odgovara matričnom zapisu logičkih vrata X.
Logička vrata Z u literaturi se nazivaju i phase-flip (eng. promjena faze) vratima. Ona na qbit (zapisan u standardnoj bazi) djeluju tako da amplitudi uz vektor |1\rangle (u zapisu u bazi \lbrace |0\rangle,|1\rangle\rbrace) promijene predznak. Logička vrata Z predstavljaju promjenu faze qbita, odnosno rotaciju za \pi oko osi z na Blochovoj sferi.
Logička vrata Y djelovanjem na standardne vektore baze dobivamo Y |0\rangle = i |1\rangle te Y |1\rangle = -i |0\rangle. Na Blochovoj sferi, dana transformacija označava rotaciju za \pi oko osi y, pri čemu se provodi i promjena bita i promjena faze na qbitu.
Logička vrata I predstavljaju operator identiteta, i na ovom mjestu ih navodimo radi potpunosti Paulijeve baze za vektorski prostor logičkih vrata koja djeluju na jednom qbitu. Paulijeva logička vrata X, Y i Z simbolički su prikazana na Slici
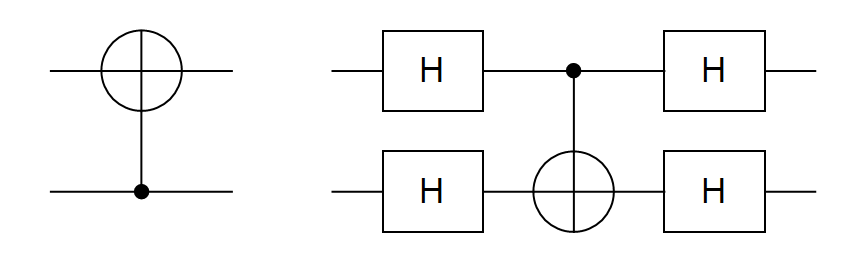
Hadamardova logička vrata zapisujemo pomoću unitarnog operatora
Kada se spin-up ili spin-down elektron pošalje kroz Hadamardova logička vrata, njegov novi „položaj“ možemo opisati kao novčić koji smo postavili na njegov rub te ima 50 % šanse da padne na glavu (spin-up) ili pismo (spin-down). Zbog toga se Hadamardova vrata često koriste na početku izvođenja kvantnog algoritma, jer se na taj način prethodno postavljeni, ili inicijalizirani, qbiti iz definitivnog stanja prebacuju u stanje superpozicije, što omogućava korištenje njihove pune snage. [4] Dakle, osnovna primjena Hadamardovih logički vrata je promjena baze iz baze \lbrace |0\rangle,|1\rangle\rbrace u bazu \lbrace |+\rangle,|-\rangle\rbrace.
Simbolički prikaz Hadamardovih logičkih vrata prikazan je na Slici
Sva prethodno opisana logička vrata pripadaju klasi logičkih vrata koja se nazivaju Cliffordovim vratima. Za tu klasu je karakteristično da koordinatne osi prostora preslikavaju opet u koordinatne osi. No, kako bi bili u mogućnosti opisati univerzalne transformacije, potrebno je koristiti i logička vrata koja ne pripadaju klasi Cliffordovih vrata.
Prikazana logička vrata na Blochovoj sferi opisuju rotaciju za kut \phi oko osi z. Među logičkim vratima faznog pomaka ističe se upotreba tzv. vrata T i vrata S. Vrata T su logička vrata faznog pomaka za \phi=\frac{\pi}{4}, dok su vrata S logička vrata faznog pomaka za \phi=\frac{\pi}{2}. Pokazuje se da za ta vrata vrijedi T^{4}=S^{2}=Z, gdje su Z Paulijeva logička vrata Z.
Brojnost logičkih vrata koja djeluju na jedan qbit je velika, i ovaj tekst je prekratak da bismo istaknuli sva. Širinu prostora konstrukcije novih logičkih vrata zorno opisuju logička vrata \sqrt{NOT}. Radi se o logičkim vratima koja opisuju djelovanje (invertibilnog) operatora čijom uzastopnom kompozicijom dobivamo logički NOT operator, odnosno Paulijeva vrata X. Radi jednostavnosti zapisa za logička vrata \sqrt{NOT} koristiti ćemo oznaku vrata V, kao što je uobičajeno u literaturi (vidi
Istaknimo na početku kako je u klasičnoj Booleovoj algebri navedena konstrukcija nemoguća. Ni za koju funkciju f:\left\lbrace 0,1\right\rbrace \rightarrow\left\lbrace 0,1\right\rbrace ne vrijedi f(f(x))=1-x za svaki x\in\lbrace 0,1\rbrace.
S druge strane u kvantnoj logici možemo konstruirati operator V za koji vrijedi V\circ V=X:
Uistinu vrijedi:
Logička vrata \sqrt{NOT} na Blochovoj sferi qbit rotiraju za \frac{\pi}{2} oko osi x, što je upravo pola rotacije koju na Blochovoj sferi provode Paulijeva vrata X. Može se pokazati kako se vrata \sqrt{NOT} mogu zapisati pomoću vrata H i S , tj. da vrijedi \sqrt{NOT}=H\circ S\circ H.7
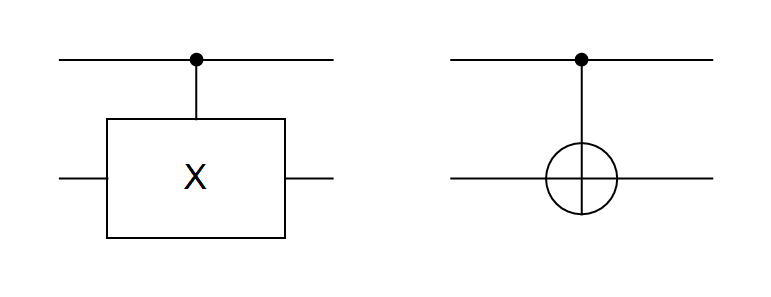
Logički sklopovi koji djeluju na dva qbita reprezentiraju se kompleksnom unitarnom matricom reda 4. Najznačajniji među takvim sklopovima su tzv. controlled Q sklopovi. Radi se o sklopovima kod kojih (arbitrarni) unitarni operator Q djeluje na drugi qbit ako i samo ako je prvi qbit |1\rangle, inače na drugi qbit djeluje jedinični operator I. U Diracovoj notaciji takve je operatore (u oznaci C_{Q}, kao control-Q) moguće zapisati na sljedeći način:
Prelaskom u matrični zapis dobivamo dijagonalnu blok matricu koja za prvi blok ima jediničnu matricu I=\left[\begin{matrix}1&0\\0&1\\\end{matrix}\right], a za drugi blok matricu operatora Q=\left[\begin{matrix}q_{1}&q_{2}\\q_{3}&q_{4}\\\end{matrix}\right]:
Prema prethodno opisanom, operator CNOT matrično zapisujemo na sljedeći način:
Drugi, eksplicitni način za zapis vrata CNOT u Diracovoj notaciji u kojem ne koristimo druge unitarne operatore poput Paulijevih vrata X ili identiteta I, glasi:
Lako se vidi kako CNOT djeluje na vektorima kanonske baze:
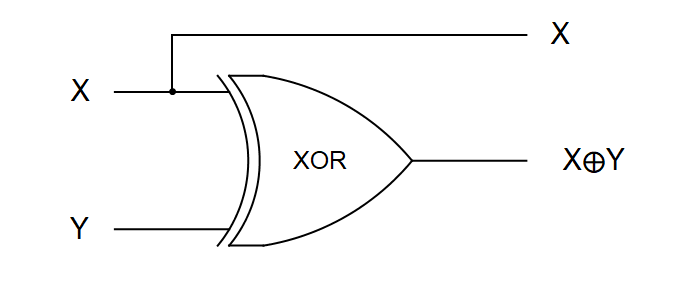
Nije teško provjeriti da se logička vrata CNOT na vektorima standardne baze ponašaju kao klasična reverzibilna logička vrata XOR (logička vrata isključivo ili). Reverzibilnost u klasičnoj digitalnoj paradigmi ostvarujemo čuvanjem informacije o vrijednosti prvog bita, kao što je prikazano na Slici
Djelovanje CNOT logičkih vrata nije simetrično, tj. nije svejedno koristimo li prvi ili drugi qbit kao kontrolni qbit. Štoviše, pogrešno je generalizirati i da je prvi qbit kontrolni qbit u svim upotrebama kontrolnih logičkih vrata. Primjerice, može se pokazati da se kod primjene logičkih vrata CNOT na vektore Hadamardove baze |+\rangle i |-\rangle, drugi qbit ponaša kao kontrolni qbit.
U upotrebi je velik broj kontroliranih Q vrata čija brojnost nadilazi okvire ovog članka. Čitatelje zaineresirane za taj segment kvantnih logičkih sklopova upućujemo na
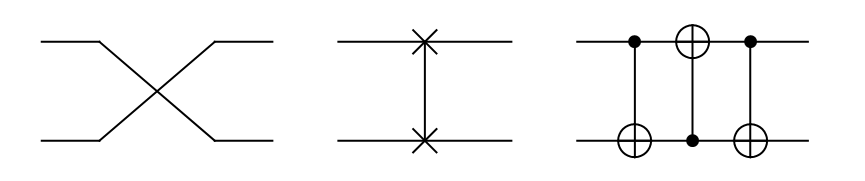
Još jedna logička vrata koja djeluju na dva qbita, a čija je upotreba česta su logička vrata SWAP, čiji se simbolički prikaz nalazi na Slici
U matričnoj, odnosno Diracovoj, notaciji vrata SWAP zapisujemo na sljedeći način:
Vrata SWAP su posebno korisna u fizičkoj izvedbi kvantnog računala, jer omo\-gu\-ća\-va\-ju dovođenje željenih qbita u fizičku blizinu i potreban položaj kao ulaze u pojedina logička vrata, bez presijecanja nositelja qbita.
Jedan od prvih logičkih sklopova formiranih da djeluje na tri qbita je tzv. CCNOT, odnosno Controlled controlled NOT sklop.
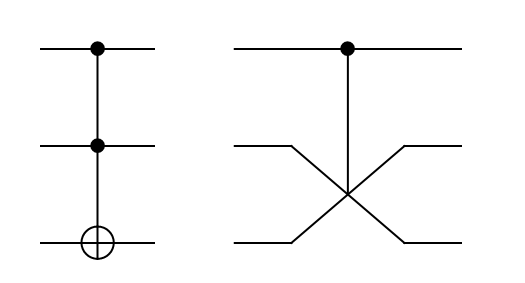
Logička vrata CCNOT nazivaju se još i Toffolijevim logičkim vratima. Radi se o logičkim vratima koja djeluju na tri qbita, od čega su prva dva qbita kontrolni qbiti. Logička vrata CCNOT negiraju posljednji qbit ako su oba kontrolna qbita u stanju |1\rangle. Matricu koja opisuje djelovanje logičkih vrata CCNOT zapisat ćemo pomoću dijagonalne blok matrice, u kojoj su I_{2} i X matrični zapisi odgovarajućih Paulijevih logičkih vrata:
Simbolički prikaz logičkih vrata CCNOT dan je na Slici
dok se logička vrata NOT (\neg) klasične logike realiziraju pomoću
Još jedna interesantna logička vrata koja se primjenjuju na sustavu od tri qbita su logička vrata CSWAP (kontrolirani SWAP). Ta se logička vrata često nazivaju i Fredkinovim logičkim vratima, prema njihovu tvorcu Edwardu Fredkinu. Simbolički prikaz CSWAP logičkih vrata dan je na Slici
Kao i logička vrata CCNOT, logička vrata CSWAP su univerzalna, budući pomoću njih možemo generirati klasične logičke veznike AND i NOT:
Matrično logička vrata CSWAP možemo zapisati u obliku dijagonalne blok matrice oblika:
gdje je I_{2} matrični zapis Paulijevog operatora identiteta, a SWAP matrični zapis logičkih vrata SWAP.
Ovime se ne iscrpljuje pregled kvantnih logičkih vrata, štoviše navedeno treba promatrati kao kratki uvod u tu bogatu temu. Pored brojnih nespomenutih kvantnih logičkih vrata, treba istaknuti kako je dobro izučavana tema i različiti načini faktorizacije, odnosno zapisa kvantnih logičkih vrata pomoću kompozicije nekog skupa logičkih vrata. Čitatelje zainteresirane za tu temu upućujemo primjerice na
Kvantna logička vrata, kao i logička vrata u klasičnoj logici, koristimo za izgradnju kvantnih logičkih algoritama.9 Kako smo pokazali da postoje univerzalna kvantna logička vrata (Toffolijeva i Fredkinova kvantna logička vrata) pomoću kojih je moguće formati klasične logičke veznike AND i NOT, teoretski, svaki se klasični logički algoritam koji je moguće implementirati pomoću klasičnih logičkih vrata, može implementirati i pomoću kvantnih logičkih vrata. Usprkos tome, takva implementacija nije cilj niti osnovna prednost kvantne logike, u prvom redu zbog hardverskih pretpostavki koje zahtjeva izgradnja i upotreba kvantnih računala.
Umjesto toga, cilj kvantne logike je konstrukcija algoritama koji su značajno efikasniji od algoritama koje provodimo pomoću klasične logike. Istaknimo odmah kako su takvi algoritmi (još uvijek) vrlo specifični i vezani uz točno određen tip problema. No i takvi pokazuju velik potencijal za daljnji razvoj, te ne čude velika ulaganja vodećih računalnih kompanija u razvoj kvantnih računala.
U ovom ćemo članku objasniti jedan od prvih formuliranih kvantnih algoritama, Deutschov algoritam. Iako je problem koji algoritam rješava jednostavan, već se i kod njega vidi komparativna prednost koju kvantni algoritam može ostvariti u usporedbi s algoritmima klasične logike.
Deutschov problem pripada skupu tzv. problema upita. Radi se o problemima u kojima nam je cilj postaviti što manje upita (eng. query) kako bismo odredili odgovor na postavljeno pitanje. U tu skupinu problema spadaju i neki drugi složeniji kvantni algoritmi poput Deutsch–Jozsina ili Simonova algoritama (vidi
U Deutschovu problemu dana nam je funkcija f:\left\lbrace 0,1\right\rbrace \rightarrow{0,1}, dakle funkcija koja vrijednosti jednog bita preslikava u drugi bit. Upitima ovdje smatramo računanja pojedinih vrijednosti funkcije f. Stoga nam je cilj odgovoriti na postavljeno pitanje sa što manjim brojem izvršenih upita, odnosno što manjim brojem računanja vrijednosti funkcije f.
Pitanje na koje tražimo odgovor glasi: je li funkcija f balansirana ili konstantna? Funkcija je konstantna ako su obje njezine vrijednosti jednake, odnosno ako sve elemente domene preslikava u broj 0 ili ih sve preslikava u broj 1. S druge strane, funkcija je balansirana ako jednu vrijednost preslika u broj 0, a drugu u broj 1, ili drugim riječima, ako je bijekcija. Dakle, traženi algoritam treba vratiti vrijednost 1 ako je funkcija balansirana, odnosno 0 ako nije.
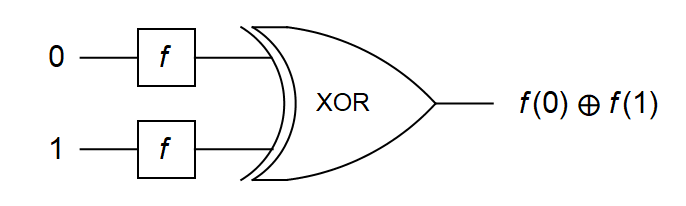
Algoritam klasične logike za rješavanje Deutschovog problema mora postaviti dva upita o vrijednosti funkcije f: mora postaviti upit koliko iznosi f(0) te koliko iznosi f(1). Odgovor na postavljeno pitanje daje primjena logičkog XOR (isključivo ili) veznika na vrijednosti funkcija f(0) i f(1), kao što je prikazano na Slici
S druge strane, kvantni Deutschov algoritam za rješavanje istog problema postavlja samo jedan upit, odnosno samo jednom računa vrijednost funkcije f. No prije nego li promotrimo sam Deutschov algoritam moramo objasniti kako kvantno računalo postavlja upite funkciji f.
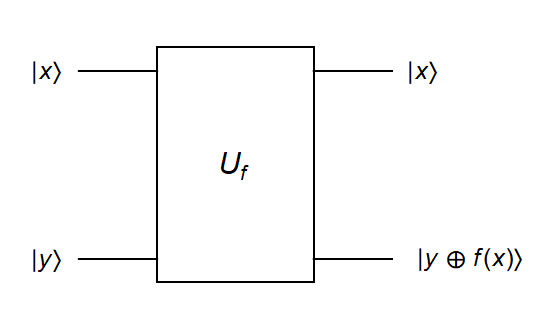
Naime, kvantni logički algoritmi rade isključivo pomoću unitarnih (reverzibilnih) transformacija. Djelovanje funkcije f ne mora biti reverzibilno, budući da funkcija ne mora biti bijekcija. Stoga ćemo (u Diracovoj notaciji) prvo definirati unitarni operator U_{f} kojim ćemo implementirati djelovanje funkcije f, na sljedeći način:
gdje je \oplus zbrajanje modulo 2. Primijetimo kako y\oplus f(x) ostavlja bit y na miru ako je f(x)=0, te ga okreće ako je f(x)=1. Zainteresiranog čitatelja upućujemo na literaturu [8,10] kako bi se uvjerili da je tako definiran operator uistinu unitaran. Simbolički prikaz djelovanja operatora U_{f} prikazan je na Slici 12. Gornji qbit zovemo ulaznim, a donji izlaznim qbitom.11
Snaga kvantnog računa proizlazi iz djelovanja funkcije na superpoziciju ortogonalnih stanja (baze), čime se jednim pozivom funkcije (na opće kvantno stanje) dobiva informacija o djelovanju funkcije na sva ortogonalna bazna stanja. Pametnom konstrukcijom unitarnog operatora U_{f} tako možemo dobiti informacije koje simuliraju paralelno djelovanje kvantnog algoritma na svim stanjima baze, usprkos ograničenju o jednom mjerenju dobivenog rezultata.
Upravo zbog toga kvantni algoritmi značajno (eksponencijalno) dobivaju na efikasnosti pri upotrebi većeg broja qbita (odnosno baznih stanja). Deutschov algoritam prikazuje tu prednost pri upotrebi (samo) dva qbita, no upravo ga to čini dovoljno jednostavnim za razumijevanje procesa koji se odvijaju iza kvantnih algoritama.
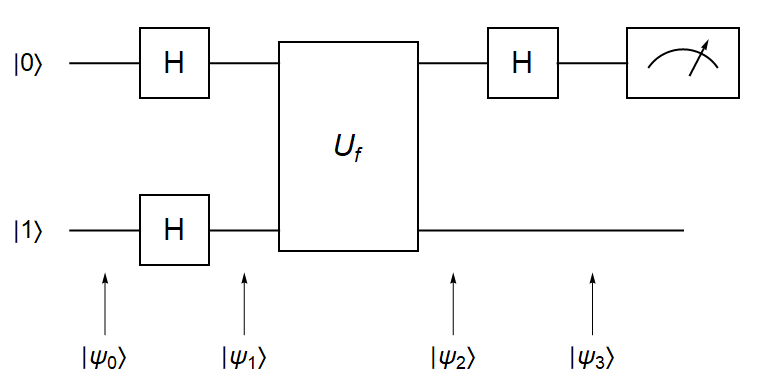
Na Slici
Prođimo računski kroz prikazani algoritam. Ulaz u algoritam je stanje |\psi_{0}\rangle = |01\rangle, na koje potom primjenjujemo unitarni operator H\otimes H. Za taj operator vrijedi:
Sada računamo kvantno stanje |\psi_{1}\rangle (prisjetimo se vektorskog zapisa za |01\rangle iz Definicije
tj. u Diracovoj notaciji
Prisjetimo li se kako izgleda tenzorski produkt vektora Hadamardove baze
Na to kvantno stanje potom primjenjujemo operator U_{f}. Kako je U_{f} |xy\rangle = |x\rangle \otimes |y\oplus f(x) \rangle, raspisivanjem djelovanja operatora U_{f} na
gdje je \oplus zbrajanje modulo 2. Taj izraz možemo pojednostavniti, budući je
gdje je a bilo f(0) ili f(1), tj. poprima vrijednost 0 ili 1. Sada je:
jer je |-\rangle = \frac{|0\rangle-|1\rangle}{\sqrt{2}}.
Vidimo kako u stanju |\psi_{2}\rangle drugi qbit ima vrijednost |-\rangle bez obzira na to kakva je funkcija f. No zato su u vrijednosti prvog qbita sadržane informacije o vrijednostima funkcije f i u 0 i u 1. Još je potrebno te informacije očitati na domišljat način. U tu svrhu izlučimo vrijednost {(-1)}^{f(0)}, pri čemu ćemo iskoristiti činjenicu da je (-1)^{f(1)-f(0)}=(-1)^{f(0) \oplus f(1)}.
Navedeni identitet vrijedi jer f(0) i f(1) mogu poprimiti samo dvije vrijednosti, 0 i 1. Stoga i njihova razlika može poprimiti samo vrijednosti -1, 0 i 1. Ako su vrijednosti f(0) i f(1) jednake (tj. ako je funkcija konstantna), razlika je jednaka nuli, a ako nisu (tj. ako je funkcija balansirana), razlika je jednaka 1 ili -1. U oba slučaja, uvrštavanjem lako provjeravamo istinitost navedenog identiteta. Dakle, vrijedi:
Promotrimo li izraz u zagradi vidimo da vrijedi:
odnosno
Dakle, informacija o tome je li funkcija konstantna ili balansirana pohranjena je u prvom qbitu (pri čemu drugi qbit uvijek ima istu vrijednost). Posljednji korak je primjena Hadamardovih logičkih vrata na prvi qbit, što nam daje kvantno stanje |\psi_{3}\rangle.
Konačno mjerenjem prvog qbita dobivamo vrijednost 0 ako je funkcija konstantna, odnosno 1 ako je balansirana. Istaknimo i kako se primjenom algoritma ispred stanja sustava pojavio faktor (-1)^{f(0)}. No tu se radi o globalnoj fazi koju i tako ne možemo mjeriti pa ne utječe na provođenje algoritma i njegov rezultat.12
Cilj ovog teksta bio je opisati temeljne pojmove i procese u radu kvantnog računala i u izgradnji algoritama kojima se isto služi. Naravno, tema je opsežna i ovim smo člankom tek otvorili vrata zainteresiranim čitateljima. Mnoge su teme ostale neobrađene: od teorijske formalizacije kvantne logike, do načina rada složenijih kvantnih algoritama. No vjerujemo kako će, nakon ovog uvoda te teme biti lakše pronaći, pratiti i razumjeti.
| [1] | Chailloux, A. „Quantum Circuits and Logic Gates“, nastavni materijali Sorbonne Université (2023) |
| [2] | Crooks, G.E. „Quantum Gates“, unpublished (2024) \url{https://threeplusone.com/gates} (pristupljeno: 6. kolovoza 2024) |
| [3] | Glendinning, I. „The Bloch sphere,”, QIA Meeting. Vienna, (2005) |
| [4] |
Ilijić, S. „Kvantna računala“, nastavni materijali, Fakultet elektotehnike i računarstva, Sveučilište u Zagrebu (2022), http://sail.zpf.fer.hr/labs/kvarac/slides/ (pristupljeno: 10. kolovoza 2024) |
| [5] | Krupansky, J., „Feynman’s Three Papers Related to Quantum Computing“, Medium, (2023) https://jackkrupansky.medium.com/feynmans-three-papers-related-to-quantu... (pristupljeno: 25. kolovoz 2024) |
| [6] | McDonald, K.T., „Physics of Quantum Computation“, nastavni materijal, Princeton University (2022) |
| [7] | Roel, J. „Demystifying Quantum Gates – One Qubit At A Time“, Towards Data Science (2018) |
| [8] | de Ronde, C., Domenech, G., Freytes, H. „Quantum Logic in Historical and Philosophical Perspective“, The Internet Encyclopedia of Philosophy, (2016) https://iep.utm.edu/qu-logic/ (pristupljeno: 26. studeni 2024) |
| [9] | Watrous, J., „Fundamentals of Quantum Algorithms“, IBM Quantum Learning, https://learning.quantum.ibm.com/course/fundamentals-of-quantum-algorithms (pristupljeno: 19. kolovoza 2024) |
| [10] |
Wilkins, A., „Record-breaking quantum computer has more than 1000 qubits“, New Scientist, (2023) https://www.newscientist.com/article/2399246-record-breaking-quantum-com... (pristupljeno: 26. studeni 2024) |
| [11] |
„The History of Quantum Computing You Need to Know“, Quantum Insider, (2024) https://thequantuminsider.com/2020/05/26/history-of-quantum-computing/ (pristupljeno 26. studeni 2024) |